Tensor Regression with Applications in Neuroimaging Data Analysis

Abstract

Classical regression methods treat covariates as a vector and estimate a corresponding vector of regression coefficients. Modern applications in medical imaging generate covariates of more complex form such as multidimensional arrays (tensors). Traditional statistical and computational methods are proving insufficient for analysis of these high-throughput data due to their ultrahigh dimensionality as well as complex structure. In this article, we propose a new family of tensor regression models that efficiently exploit the special structure of tensor covariates. Under this framework, ultrahigh dimensionality is reduced to a manageable level, resulting in efficient estimation and prediction. A fast and highly scalable estimation algorithm is proposed for maximum likelihood estimation and its associated asymptotic properties are studied. Effectiveness of the new methods is demonstrated on both synthetic and real MRI imaging data.

1 Introduction

Understanding the inner workings of the human brains and their connection with neuropsychiatric and neurodegenerative disorders is one of the most intriguing scientific questions. Studies in neuroscience are greatly facilitated by a variety of neuroimaging technologies, including anatomical magnetic resonance imaging (MRI), functional magnetic resonance imaging (fMRI), electroencephalography (EEG), diffusion tensor imaging (DTI), and positron emission tomography (PET), among others. The sheer size and complexity of medical imaging data, however, pose unprecedented challenge to many classical statistical methods and have received increasing interest in recent years (Lindquist, 2008; Lazar, 2008; Martino et al., 2008; Friston, 2009; Ryali et al., 2010; Hinrichs et al., 2009; Kang et al., 2012).

In the literature, there have been roughly three categories of statistical methods for establishing association between brain images and clinical traits. The first is the voxel-based methods, which take each voxel as responses and clinical variables such as age and gender as predictors. They generate a statistical parametric map of test statistics or p-values across all voxels (Lazar, 2008; Worsley et al., 2004). A major drawback is that all voxels are treated as independent units and important spatially correlation is ignored (Li et al., 2011; Yue et al., 2010; Polzehl et al., 2010). The second type of solutions adopts the functional data analysis approach. Reiss and Ogden (2010) notably extended functional regression model to incorporate two-dimensional images as predictors. Generalizations to 3D and higher dimensional images, however, is far from trivial and requires substantial research. The third category employs a two-stage strategy. These methods first carry out a dimension reduction step, often by principal component analysis (PCA), and then fit a regression model based on the top principal components (Caffo et al., 2010). This strategy is intuitive and easy to implement. However, it is well known that PCA is an unsupervised dimension reduction technique and the extracted principal components can be irrelevant to the response.

In this article, we formulate a regression framework that treats clinical outcome as response, and images, in the form of multi-dimensional array, as covariates. Most classical regression methods take vectors as covariates. Naively turning an image array into a vector yields an unsatisfactory solution. For instance, typical anatomical MRI images of size 256-by-256-by-256 implicitly require 256³ = 16, 777, 216 regression parameters. Both computability and theoretical guarantee of the classical regression analysis are compromised by this ultra-high dimensionality. More seriously, vectorizing an array destroys the inherent spatial structure of the image that possesses wealth of information.

Exploiting the array structure in imaging data, our new regression method substantially reduces the dimensionality of imaging data, leading to efficient estimation and prediction. The method works for general array-valued covariates and/or any combination of them, and thus it is applicable to a variety of imaging modalities, e.g., EEG, MRI and fMRI. It is embedded in the generalized linear model (GLM) framework, so it works for both continuous and discrete responses. We develop a highly scalable algorithm for maximum likelihood estimation, as well as statistical inferential tools. Regularized tensor regression is also investigated to identify regions of interest in brains that are relevant to a particular response. This region selection problem corresponds to variable selection in the usual vector-valued regression.

The contributions of this article are two-fold. First, from a brain imaging analysis point of view, our proposal timely responds to a number of growing needs of neuroimaging analysis. In the review article, Lindquist (2008) noted the increasing trend and demands of using brain images for disease diagnosis and prediction, for characterization of subjective human experience, and for understanding association between brain regions and cognitive outcomes. Our tensor regression framework offers a systematic solution to this family of problems. Moreover, the framework warrants potential solutions to address questions such as multi-modality imaging analysis, multi-phenotype analysis and imaging genetics (Friston, 2009; Casey et al., 2010), which largely remain as open challenges. Second, from a statistical methodology point of view, our proposal develops a general statistical framework for regression with array covariates. A large number of models and extensions, e.g., quasi-likelihood models (McCullagh and Nelder, 1983), are potential outcomes within this framework. It can also be viewed as a logic extension from the classical vector-valued covariate regression to functional covariate regression and then to array-valued covariate regression.

The rest of the article is organized as follows. Section 2 begins with a review of matrix/array properties, and then develops the tensor regression models. Section 3 presents an effcient algorithm for maximum likelihood estimation. Section 4 provides theoretical results such as identifiability, consistency, and asymptotic normality. Section 5 discusses regularization including region selection. Section 6 presents numerical results. Section 7 concludes with a discussion of future extensions. Technical proofs are delegated to the Appendix.

2 Model

2.1 Preliminaries

Multidimensional array, also called tensor, plays a central role in our approach and we start with a brief summary of notation and a few results for matrix/array operations. Extensive references can be found in the survey paper (Kolda and Bader, 2009). In this article we use the terms multidimensional array and tensor interchangeably.

Given two matrices $\mathit{A}=\left[{\mathit{a}}_1\dots {\mathit{a}}_n\right]\in {\mathbb{R}}^{m\times n}$ and $\mathit{B}=\left[{\mathit{b}}_1\dots {\mathit{b}}_q\right]\in {\mathbb{R}}^{p\times q}$, the Kronecker product is the mp-by-nq matrix A ⊗ B = [a₁ ⊗ Ba₁ ⊗ B … a_n ⊗ B]. If A and B have the same number of columns n = q, then the Khatri-Rao product (Rao and Mitra, 1971) is defined as the mp-by-n columnwise Kronecker product A ⊙ B = a₁ ⊗ b₁ a₂ ⊗ b₂ … a_n ⊗ b_n]. If n = q = 1, then A ⊙ B = A ⊗ B. Some useful operations transform a tensor into a matrix/vector. The vec(B) operator stacks the entries of a D-dimensional tensor $\mathit{B}\in {\mathbb{R}}^{p_1\times \dots \times p_D}$ into a column vector. Specifically, an entry b_i1…iD maps to the j-th entry of vec B, in which $j=1+{\sum }_{d=1}^D(i_d-1){\prod }_{d^{\prime }=1}^{d-1}{p}_{d^{\prime }}$. For instance, when D = 2, the matrix entry x_i1i2 maps to position j = 1 + i₁ − 1 + (i₂ − 1)p₁ = i₁ + (i₂ − 1)p₁, which is consistent with the more familiar vec operation on a matrix. The mode-d matricization, B_(d), maps a tensor B into a p_d × Π_d′≠dp_d′ matrix such that the (i₁, …, i_D) element of the array B maps to the (i_d, j) element of the matrix B_(d), where j = 1 + Σ_d′≠;d(i_d′ − 1) Π_{d″<d′,d″≠d}p_d″. With d = 1, we observe that vec B is the same as vectorizing the mode-1 matricization B₍₁₎. The mode-(d, d′) matricization ${\mathit{B}}_{\left({\mathit{dd}}^{\prime }\right)}\in {\mathbb{R}}^{p_d{p}_{d^{\prime }}\times {\prod }_{d^{″}\ne d,d^{\prime }}{p}_{d^{″}}}$ is defined in a similar fashion (Kolda, 2006). We also introduce an operator that turns vectors into an array. Specifically, an outer product, b₁ ο b₂ ο ⋯ ο b_D, of D vectors ${\mathbf{b}}_d\in {\mathbb{R}}^{p_d}$ is a p₁ × ⋯ × p_D array with entries ${({\mathit{b}}_{1}o{\mathit{b}}_{2}o\cdots o{\mathit{b}}_D)}_{i_1\cdots i_d}={\prod }_{d=1}^D{b}_{{\mathit{di}}_d}$.

Tensor decomposition plays a central role in our proposed tensor regression in Section 2.3. An array $\mathit{B}\in {\mathbb{R}}^{p_1\times \cdots \times p_D}$ admits a rank-R decomposition if

$$\mathit{B}=\sum _{r=1}^R{\beta }_1^{\left(r\right)}o\cdots o{\beta }_D^{\left(r\right)},$$ (1)

where ${\beta }_d^{\left(r\right)}\in {\mathbb{R}}^{p_d}$, d = 1, …, D, r = 1, …, R, are all column vectors, and B cannot be written as a sum of less than R outer products. For convenience, the decomposition is often represented by a shorthand, B = ⟦B₁, …, B_D⟧, where ${\mathit{B}}_d=[{\beta }_d^{\left(1\right)},\dots ,{\beta }_d^{\left(R\right)}]\in {\mathbb{R}}^{p_d\times R}$ (Kolda, 2006; Kolda and Bader, 2009). The following well-known result relates the mode-d matricization and the vec operator of an array to its rank-R decomposition.

Lemma 1. If a tensor $\mathit{B}\in {\mathbb{R}}^{p_1\times \cdots \times p_D}$ admits a rank-R decomposition (1), then

$${\mathit{B}}_{\left(d\right)}={\mathit{B}}_d{({\mathit{B}}_D\odot \cdots \odot {\mathit{B}}_{d+1}\odot {\mathit{B}}_{d-1}\odot \cdots \odot {\mathit{B}}_1)}^{⊺}and\text{vec}\mathit{B}=({\mathit{B}}_D\odot \cdots \odot {\mathit{B}}_1)1_R.$$

Throughout the article, we adopt the following notations. Y is a univariate response variable, $\mathit{Z}\in {\mathbb{R}}^{p_0}$ denotes a p₀-dimensional vector of covariates, such as age and sex, and $\mathit{X}\in {\mathbb{R}}^{p_1\times \dots \times p_D}$ is a D-dimensional array-valued predictor. For instance, for MRI, D = 3, representing the 3D structure of an image, whereas for fMRI, D = 4, with an additional time dimension. The lower-case triplets (y_i, x_i, z_i), i = 1, …, n, denote the independent, observed sample instances of (Y, X, Z).

2.2 Motivation and Basic Model

To motivate our model, we first start with a vector-valued X and absorb Z into X. In the classical GLM (McCullagh and Nelder, 1983) setting, Y belongs to an exponential family with probability mass function or density

$$p(y\mid \theta ,\varphi )=\text{exp}\left\{\frac{y\theta -b\left(\theta \right)}{a\left(\varphi \right)}+c(y,\varphi )\right\},$$ (2)

where θ and ϕ > 0 denote the natural and dispersion parameters. The classical GLM relates a vector-valued $\mathit{X}\in {\mathbb{R}}^p$ to the mean μ = E(Y|X) via g(μ) = η = α + β^⊺X, where g(·) is a strictly increasing link function, and η denotes the linear systematic part with intercept α and the coefficient vector $\beta \in {\mathbb{R}}^p$.

Next, for a matrix-valued covariate $\mathit{X}\in {\mathbb{R}}^{p_1\times p_2}$ (D = 2), it is intuitive to consider a GLM model with the systematic part given by

$$g\left(\mu \right)=\alpha +{\beta }_1^{⊺}\mathit{X}{\beta }_2,$$

where ${\beta }_1\in {\mathbb{R}}^{p_1}$ and ${\beta }_2\in {\mathbb{R}}^{p_2}$, respectively. The bilinear form ${\beta }_1^{⊺}\mathit{X}{\beta }_2$ is a natural extension of the linear term β^⊺X in the classical GLM with a vector covariate X. It is interesting to note that, this bilinear form was first proposed by Li et al. (2010) in the context of dimension reduction, and then employed by Hung and Wang (2011) in the logistic regression with matrix-valued covariates (D = 2). Moreover, note that ${\beta }_1^{⊺}\mathit{X}{\beta }_2={({\beta }_2\otimes {\beta }_1)}^{⊺}\text{vec}\left(\mathit{X}\right)$.

Now for a conventional vector-valued covariate Z and a general array-valued $\mathit{X}\in {\mathbb{R}}^{p_1\times \dots \times p_D}$, we propose a GLM with the systematic part given by

$$g\left(\mu \right)=\alpha +{\gamma }^{⊺}\mathit{Z}+{({\beta }_D\otimes \cdots \otimes {\beta }_1)}^{⊺}\text{vec}\left(\mathit{X}\right),$$ (3)

where $\gamma \in {\mathbb{R}}^{p_0}$ and ${\beta }_d\in {\mathbb{R}}^{p_d}$ for d = 1, …, D. This is our basic model for regression with array covariates. The key advantage of model (3) is that it dramatically reduces the dimensionality of the tensor component, from the order of Π_d p_d to the order of Σ_d p_d. Take MRI imaging as an example, the size of a typical image is 256³ = 16, 777, 216. PIf we simply turn X into a vector and fit a GLM, this brutal force solution is over 16 million-dimensional, and the computation is practically infeasible. In contrast, the multilinear model (3) is only 256 + 256 + 256 = 768-dimensional. The reduction in dimension, and consequently in computational cost, is substantial.

A critical question then is whether such a massive reduction in the number of parameters would limit the capacity of model (3) to capture regions of interest with specific shapes. The illustrative example in Figure 1 provides some clues. In Figure 1, we present several two-dimensional images $\mathit{B}\in {\mathbb{R}}^{64\times 64}$ (shown in the first column), along with the estimated images by model (3) (in the second column labeled by TR(1)). Specifically, we simulated 1,000 univariate responses y_i according to a normal model with mean μ_i = γ^⊺z_i + 〈B, x_i〉, where γ = 1₅. The inner product between two arrays is defined as 〈B, X〉 = 〈vecB, vecX〉 = Σ_i1,…,iD β_i1…iDx_i1…iD. The coefficient array B is binary, with the true signal region equal to one and the rest zero. The regular covariate z_i and image covariate x_i are randomly generated with all elements being independent standard normals. Our goal is to see if model (3) can identify the true signal region in B using data (y_i, z_i, x_i). Before examining the outcome, we make two remarks about this illustration. First, our problem differs from the usual edge detection or object recognition in imaging processing (Qiu, 2005, 2007). In our setup, all elements of the image X follow the same distribution. The signal region is defined through the coefficient image B and needs to be inferred from the association between Y and X after adjusting for Z. Second, the classical GLM is difficult to apply in this example if we simply treat vec(X) as a covariate vector, since the sample size n = 1, 000 is much less than the number of parameters p = 5 + 64 × 64 = 4, 101. Back to Figure 1, the second column clearly demonstrates the ability of model (3) in identifying the rectangular (square) type region (parallel to the image edges). On the other hand, since the parameter vector β_d in a rank-1 model is only able to capture the accumulative signal along the d-th dimension of the array variate X, it is unsurprising that it does not perform well for signals that are far away from rectangle, such as triangle, disk, T-shape and butterfly. This motivates us to develop a more flexible tensor regression model in the next section.

Figure 1.

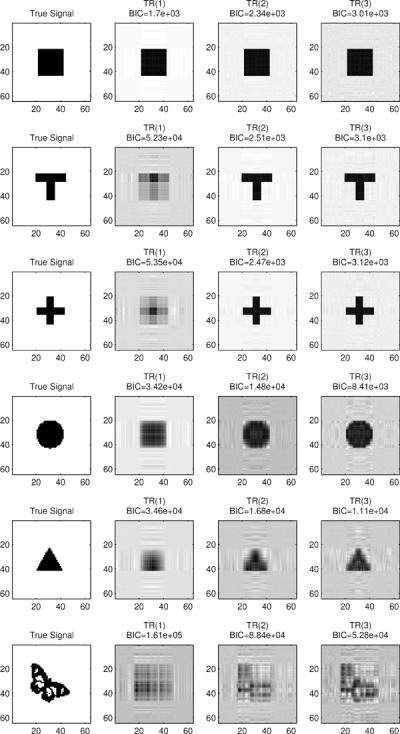
True and recovered image signals by tensor regression. The matrix variate has size 64 by 64 with entries generated as independent standard normals. The regression coefficient for each entry is either 0 (white) or 1 (black). The sample size is 1000. TR(R) means estimate from the rank-R tensor regression.

2.3 Tensor Regression Model

We start with an alternative view of the basic model (3), which will lead to its generalization. Consider a D-dimensional array variate $\mathit{X}\in {\mathbb{R}}^{p_1\times \cdots \times p_D}$, and a full coefficient array B of same size that captures the effects of each array element. Then the most flexible GLM suggests a linear systematic part

$$g\left(\mu \right)=\alpha +{\gamma }^{⊺}\mathit{Z}+\langle \mathit{B},\mathit{X}\rangle .$$

The issue with this model is that B has the same number of parameters, ${\prod }_{d=1}^D{p}_d$, as X, which is ultrahigh dimensional and far exceeds the usual sample size. Then a natural idea is to approximate B with less parameters. If B admits a rank-1 decomposition (1), i.e., B = β₁ ο β₂ ο ⋯ ο β_D, where ${\beta }_d\in {\mathbb{R}}^{p_d}$, then by Lemma 1, we have

$$\text{vec}\mathit{B}=\text{vec}({\beta }_{1}o{\beta }_{2}o\cdots o{\beta }_D)={\beta }_D\odot \cdots \odot {\beta }_1={\beta }_D\otimes \cdots \otimes {\beta }_1.$$

In other words, model (3) is indeed a data-driven model with a rank-1 approximation to the general signal array B. This observation motivates us to consider a more flexible tensor regression model.

Specifically, we propose a family of rank-Rgeneralized linear tensor regression models, in which the systematic part of GLM is of the form

$$\begin{array}{cc}\hfill g\left(\mu \right)& =\alpha +{\gamma }^{⊺}\mathit{Z}+\langle \sum _{r=1}^R{\beta }_1^{\left(r\right)}o{\beta }_2^{\left(r\right)}o\cdots o{\beta }_D^{\left(r\right)},\mathit{X}\rangle \hfill \\ \hfill & =\alpha +{\gamma }^{⊺}\mathit{Z}\langle ({\mathit{B}}_D\odot \cdots \odot {\mathit{B}}_1)1_R,\text{vec}\mathit{X}\rangle ,\hfill \end{array}$$ (4)

where ${\mathit{B}}_d=[{\beta }_d^{\left(1\right)},\dots ,{\beta }_d^{\left(R\right)}]\in {\mathbb{R}}^{p_d\times R}$ ,${\mathit{B}}_D\odot \cdots \odot {\mathit{B}}_1\in {\mathbb{R}}^{{\prod }_d{p}_d\times R}$ is the Khatri-Rao product and 1_R is the vector of R ones.. Equivalently we assume that the tensor regression parameter admits a rank-R decomposition B = ⟦B₁, …, B_D⟧. When R = 1, it reduces to model (3). A few remarks on (4) are in order. First, since our formulation only deals with the linear predictor part of the model, it easily extends to the quasi-likelihood models (McCullagh and Nelder, 1983) where more general mean-variance relation is assumed. Second, for simplicity, we only discuss exponential family with a univariate response. Extension to multivariate exponential family, such as multinomial logit model, is straightforward. Third, due to the GLM setup (2), we call (4) a generalized linear tensor regression model. However, we should bear in mind that the systematic component η is a polynomial rather than linear in the parameters B_d. Finally, the rank-R tensor decomposition (1) is called canonical decomposition or parallel factors (CANDECOMP/PARAFAC, or CP) in psychometrics (Kolda and Bader, 2009). In that sense, model (4) can be viewed as a supervised version of the classical CP decomposition for multi-dimensional arrays.

The number of parameters in model (4) is p₀ + R Σ_d p_d, which is still substantially smaller than p₀ + Π_d p_d. With such a massive reduction in dimensionality, however, it provides a reasonable approximation to many low rank signals. Returning to the previous illustration, in Figure 1, images TR(R) are the recovered signals by the rank-R tensor regression (in third and fourth columns). The square signal can be perfectly recovered by a rank-1 model, whereas rank-2 and 3 regressions show signs of overfitting. The T-shape and cross signals can be perfectly recovered by a rank-2 regression. Triangle, disk, and butterfly shapes cannot be exactly recovered by any low rank approximations; however, a rank 3 tensor regression already yields a fairly informative recovery. Clearly, the general tensor regression model (4) is able to capture significantly more tensor signals than the basic model (3).

3 Estimation

We pursue the maximum likelihood (ML) route for parameter estimation in model (4). Given n i.i.d. data {(y_i, x_i, z_i), i = 1, …, n}, the log-likelihood function for (2) is

$$\ell (\alpha ,\gamma ,{\mathit{B}}_1,\cdots ,{\mathit{B}}_D)=\sum _{i=1}^n\frac{y_i{\theta }_i-b\left({\theta }_i\right)}{a\left(\varphi \right)}+\sum _{i=1}^{n}c(y_i,\varphi ),$$ (5)

where θ_i is related to regression parameters (α, γ, B₁, …, B_D) through (4). We propose an efficient algorithm for maximizing ℓ(α, γ, B₁, …, B_D). A key observation is that although g(μ) in (4) is not linear in (B₁, …, B_D) jointly, it is linear in B_d individually. This suggests alternately updating (α,γ) and B_d, d = 1, …, D, while keeping other components fixed. It yields a so-called block relaxation algorithm (de Leeuw, 1994; Lange, 2010). An appealing feature of this algorithm is that at each iteration, updating a block B_d is simply a classical GLM problem. To see this, when updating ${\mathit{B}}_d\in {\mathbb{R}}^{p_d\times R}$, we rewrite the array inner product in (4) as

$$\langle \sum _{r=1}^R{\beta }_1^{\left(r\right)}o{\beta }_2^{\left(r\right)}o\cdots o{\beta }_D^{\left(r\right)},\mathit{X}\rangle =\langle {\mathit{B}}_d,{\mathit{X}}_{\left(d\right)}({\mathit{B}}_D\odot \cdots \odot {\mathit{B}}_{d+1}\odot {\mathit{B}}_{d-1}\odot \cdots \odot {\mathit{B}}_1)\rangle .$$

Consequently the problem turns into a traditional GLM regression with Rp_d parameters, and the estimation procedure breaks into a sequence of low dimensional GLM optimizations and is extremely easy to implement using ready statistical softwares such as R, S+, SAS, and Matlab. The full estimation procedure is summarized in Algorithm 1. For the Gaussian models, it reduces to the alternating least squares (ALS) procedure (de Leeuw et al., 1976).

Algorithm 1 Block relaxation algorithm for maximizing (5).

Initialize: (α(0), γ(0)) = argmaxα,γ ℓ(α, γ, 0, …, 0), 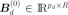a random matrix for d = 1, …, D.

repeat

for d = 1, …, D do

${\mathit{B}}_d^{(t+1)}={\text{argmax}}_{{\mathit{B}}_d}\ell ({\alpha }^{\left(t\right)},{\gamma }^{\left(t\right)},{\mathit{B}}_1^{(t+1)},\dots ,{\mathit{B}}_{d-1}^{(t+1)},{\mathit{B}}_d,{\mathit{B}}_{d+1}^{\left(t\right)},\dots ,{\mathit{B}}_D^{\left(t\right)})$

end for

$({\alpha }^{(t+1)},{\gamma }^{(t+1)})={\text{argmax}}_{\alpha ,\gamma }\ell (\alpha ,\gamma ,{\mathit{B}}_1^{(t+1)},\dots ,{\mathit{B}}_D^{(t+1)})$

until ℓ(θ(t+1)) − ℓ(θ(t)) < ∊

As the block relaxation algorithm monotonically increases the objective function, it is numerically stable and the convergence of objective values ℓ(θ^(t)) is guaranteed whenever ℓ(θ) is bounded from above. Therefore the stopping rule of Algorithm 1 is well-defined. We denote the algorithmic map by M, i.e., M(θ^(t)) = θ^(t+1), with θ = (α, γ, B₁, …, B_D) collecting all parameters. Convergence properties of Algorithm 1 are summarized in Proposition 1.

Proposition 1. Assume (i) the log-likelihood function ℓ(θ) is continuous, coercive, i.e., the set {θ : ℓ(θ) ≥ ℓ(θ⁽⁰⁾)} is compact, and bounded above, (ii) the objective function in each block update of Algorithm 1 is strictly concave, and (iii) the set of stationary points (modulo scaling and permutation indeterminancy) of ℓ(θ) are isolated. We have the following results.

1. (Global Convergence) The sequence ${\theta }^{\left(t\right)}=({\alpha }^{\left(t\right)},{\gamma }^{\left(t\right)},{\mathit{B}}_1^{\left(t\right)},\dots ,{\mathit{B}}_D^{\left(t\right)})$ generated by Algorithm 1 converges to a stationary point of ℓ(θ).

2. (Local Convergence) Let ${\theta }^{\left(\infty \right)}=({\alpha }^{\left(\infty \right)},{\gamma }^{\left(\infty \right)},{\mathit{B}}_1^{\left(\infty \right)},\dots ,{\mathit{B}}_D^{\left(\infty \right)})$ be a strict local maximum of ℓ(θ). The iterates generated by Algorithm 1 are locally attracted to θ^∞ for θ⁽⁰⁾ sufficiently close to θ^∞.

We make a few quick remarks. First, although a stationary point is not guaranteed to be even a local maximum (it can be a saddle point), in practice the block relaxation algorithm almost always converges to at least a local maximum. In general, the algorithm should be run from multiple initializations to locate an excellent local maximum, especially for higher rank models with limited sample size. Second, ℓ(θ) is not required to be jointly concave in θ. Only the concavity in the blocks of variables is needed. This condition holds for all GLM with canonical link such as linear model, logistic model and Poisson log-linear model.

The above algorithm assumes a known rank when estimating B. Estimating an appropriate rank for our tensor model (4) is of practical importance. It can be formulated as a model selection problem, and we adopt the usual model section criterion, e.g., Bayesian information criterion (BIC), −2ℓ(θ)+log(n)p_e, where p_e is the effective number of parameters for model (4): p_e = R(p₁ + p₂) − R² for D = 2, and p_e = R(Σ_dp_d−D+1) for D > 2. Returning to the illustrative example in Section 2.2, we fitted a rank-1, 2 and 3 tensor models, respectively, to various signal shapes. The corresponding BIC values are shown in Figure 1. The criterion is seen correctly estimating the rank for square as 1, and the rank for T and cross as 2. The true ranks for disk, triangle and butterfly are above 3, and their BIC values at rank 3 are smallest compared to those at 1 and 2.

4 Theory

We study the statistical properties of maximum likelihood estimate (MLE) for the tensor regression model defined by (2) and (4). For simplicity, we omit the intercept α and the classical covariate part γ^⊺Z, though the conclusions generalize to an arbitrary combination of covariates. We adopt the usual asymptotic setup with a fixed number of parameters p and a diverging sample size n, because this is an important first step toward a comprehensive understanding of the theoretical properties of the proposed model. The asymptotics with a diverging p is our future work and is pursued elsewhere.

4.1 Score and Information

We first derive the score and information for the tensor regression model, which are essential for statistical estimation and inference. The following standard calculus notations are used. For a scalar function f, ∇f is the (column) gradient vector, df = [∇f]^⊺ is the di erential, and d²f is the Hessian matrix. For a multivariate function $g:{\mathbb{R}}^p\mapsto {\mathbb{R}}^q$, $D_g\in {\mathbb{R}}^{q\times p}$ denotes the Jacobian matrix holding partial derivatives ∂g_i/∂x_j.

We start from the Jacobian and Hessian of the systematic part η ≡ g(μ) in (4). The proof is given in the Appendix.

Lemma 2.

1. The gradient ${\nabla }_{\eta }({\mathit{B}}_1,\dots ,{\mathit{B}}_D)\in {\mathbb{R}}^{R{\sum }_{d=1}^D{p}_d}$ is

   $${\nabla }_{\eta }({\mathit{B}}_1,\cdots ,{\mathit{B}}_D)={[{\mathit{J}}_1{\mathit{J}}_2\cdots {\mathit{J}}_D]}^{⊺}\left(\text{vec}\mathit{X}\right),$$

   where ${\mathit{J}}_d\in {\mathbb{R}}^{{\prod }_{d=1}^D{p}_d\times {p_d}^R}$ is the Jacobian

   $${\mathit{J}}_d=D\mathit{B}\left({\mathit{B}}_d\right)={\Pi }_d\left[\right({\mathit{B}}_D\odot \cdots \odot {\mathit{B}}_{d+1}\odot {\mathit{B}}_{d-1}\odot \cdots \odot {\mathit{B}}_1)\otimes {\mathit{I}}_{pd}]$$ (6)

   and Π_d is the $\left({\prod }_{d=1}^D{p}_d\right)-\mathit{by}-\left({\prod }_{d=1}^D{p}_d\right)$ permutation matrix that reorders vecB_(d) to obtain vecB, i.e., vecB = Π_d vecB_(d).
2. The Hessian $d^2\eta ({\mathit{B}}_1,\dots ,{\mathit{B}}_D)\in {\mathbb{R}}^{R{\sum }_{d=1}^D{p}_d\times R{\sum }_{d=1}^D{p}_d}$ has entries

   $$h_{(i_d,r),(i_{d^{\prime }},r^{\prime })}=1_{\{r=r^{\prime },d\ne d^{\prime }\}}\sum _{j_d=i_d,j_{d^{\prime }}=i_{d^{\prime }}}{x}_{j1,\cdots ,jD}\underset{d^{\prime \prime }\ne d,d^{\prime }}{\Pi }{\beta }_{j_{d^{\prime \prime }}}^{\left(r\right)},$$

   and can be partitioned in D² blocks as

   $$\left(\begin{array}{cccc}\hfill 0\hfill & \hfill \ast \hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill H_{21}\hfill & \hfill 0\hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ast \hfill \\ \hfill H_{D1}\hfill & \hfill H_{D2}\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right).$$

   The block ${\mathit{H}}_{d{d}^{\prime }}\in {\mathbb{R}}^{p_{d}R\times p_{d^{\prime }}R}$ has p_dp_d′R nonzero elements which can be retrieved from the matrix X_(dd′)(B_D ⊙⋯⊙B_d+1 ⊙ B_d−1 ⊙⋯⊙B_d′+1 ⊙ B_d′−1 ⊙⋯⊙ B₁) where X_(dd′) is the mode-(d, d′) matricization of X.

Remark 1: The Hessian d²η is highly sparse and structured. An entry in d²η(B₁,…,B_D) is nonzero only if it belongs to different directions d but the same outer product r.

Let ℓ(B₁,…,B_D|y, x) = ln p(y|x, B₁,…,B_D) be the log-density. Next result derives the score function, Hessian, and Fisher information of the tensor regression model.

Proposition 2. Consider the tensor regression model defined by (2) and (4).

1. The score function (or score vector) is

   $$\nabla \ell ({\mathit{B}}_1,\cdots ,{\mathit{B}}_D=\frac{(y-\mu ){\mu }^{\prime }\left(\eta \right)}{{\sigma }^2}{[{\mathit{J}}_1\cdots {\mathit{J}}_D]}^{⊺}(\text{vec}\left(\mathit{X}\right)$$ (7)

   with J_d, d = 1,…,D, defined by (6).
2. The Hessian of the log-density ℓ is

   $$\begin{array}{cc}\hfill H({\mathit{B}}_1,\cdots ,{\mathit{B}}_D)=& -\frac{{\left[{\mu }^{\prime }\right(\eta \left)\right]}^2}{{\sigma }^2}\left([{\mathit{J}}_1\cdots {\mathit{J}}_D{}^{⊺}]\text{vec}\mathit{X}\right){\left({[{\mathit{J}}_1\cdots {\mathit{J}}_D]}^{⊺}\text{vec}\right)\mathit{X}}^{⊺}\hfill \\ \hfill & +\frac{(y-\mu ){\theta }^{″}\left(\eta \right)}{{\sigma }^2}\left({[{\mathit{J}}_1\cdots {\mathit{J}}_D]}^{⊺}\text{vec}\mathit{X}\right){\left({[{\mathit{J}}_1\cdots {\mathit{J}}_D]}^{⊺}\text{vec}\mathit{X}\right)}^{⊺}\hfill \\ \hfill & +\frac{(y-\mu ){\theta }^{\prime }\left(\eta \right)}{{\sigma }^2}{d}^2\eta ({\mathit{B}}_1,\cdots ,{\mathit{B}}_D),\hfill \end{array}$$ (8)

   with d²η defined in Lemma 2.
3. The Fisher information matrix is

   $$\begin{array}{cc}\hfill I({\mathit{B}}_1,\cdots ,{\mathit{B}}_D)& =E[-H({\mathit{B}}_1,\cdots ,{\mathit{B}}_D\left)\right]=\text{Var}[\nabla \ell ({\mathit{B}}_1,\cdots ,{\mathit{B}}_D\left)d\ell \right({\mathit{B}}_1,\cdots ,{\mathit{B}}_D\left)\right]\hfill \\ \hfill & =\frac{[{{\mu }^{\prime }\left(\eta \right)]}^2}{{\sigma }^2}{[{\mathit{J}}_1\cdots {\mathit{J}}_D]}^{⊺}\left(\text{vec}\mathit{X}\right){\left(\text{vec}\mathit{X}\right)}^{⊺}[{\mathit{J}}_1\cdots {\mathit{J}}_D].\hfill \end{array}$$ (9)

Remark 2: For canonical link, θ = η, θ′(η) = 1, θ″(η) = 0, and the second term of Hessian vanishes. For the classical GLM with linear systematic part (D = 1), d²η(B₁,…,B_D) is zero and thus the third term of Hessian vanishes. For the classical GLM (D = 1) with canonical link, both the second and third terms of the Hessian vanish and thus the Hessian is non-stochastic, coinciding with the information matrix.

4.2 Identifiability

Before studying asymptotic property, we need to deal with the identifiability issue. The parameterization in the tensor model is nonidentifiable due to two complications. Consider a rank-R decomposition of an array, $\mathit{B}=⟦{\mathit{B}}_1,\dots ,\mathit{D}⟧$. The first complication is the indeterminacy of B due to scaling and permutation:

• –scaling: $\mathit{B}=⟦{\mathit{B}}_1{\Lambda }_1,\dots ,{\mathit{B}}_D{\lambda }_D⟧$ for any diagonal matrices Λ_d = diag(λ_d1,…,λ_dR), d = 1,…,D, such that ∐_dλ_dr = 1 for r = 1,…,R.
• –permutation: $\mathit{B}=⟦{\mathit{B}}_1\prod ,\dots ,{\mathit{B}}_D\prod ⟧$ for any R-by-R permutation matrix ∐. For the matrix case (D = 2), a further complication is the nonsingular transformation indeterminancy: ${\mathit{B}}_1{\mathit{B}}_2^{⊺}={\mathit{B}}_{1}O{O}^{-1}{\mathit{B}}_2^{⊺}$ for any R-by-R nonsingular matrix O. Note the scaling and permutation indeterminancy is subsumed in the nonsingular transformation indeterminancy. The singular value decomposition (SVD) of a matrix is unique because it imposes orthonormality constraint on the columns of the factor matrices.

To deal with this complication, it is necessary to adopt a specific constrained parameterization to fix the scaling and permutation indeterminacy. For D > 2, we need to put (D − 1)R restrictions on the parameters B and apparently there is an infinite number of ways to do this. In this paper we adopt the following convention. B₁,…, B_D−1 are scaled such that ${\beta }_{d1}^{\left(r\right)}=1$, i.e., the first rows are ones. This in turn determines entries in the first row of B_D and fixes scaling indeterminacy. To fix the permutation indeterminancy, we assume that the first row entries of B_D are distinct and arranged in descending order ${\beta }_{D1}^{\left(1\right)}>\cdots >{\beta }_{D1}^{\left(R\right)}$. The resulting parameter space is

$$\mathcal{B}=\left\{\right({\mathit{B}}_1,\cdots ,{\mathit{B}}_D:{\beta }_{d1}^{\left(r\right)}=1,\text{for}d=1,\cdots ,D,r=1,\cdots ,R\text{and}{\beta }_{D1}^{\left(1\right)}>\dots >{\beta }_{D1}^{\left(R\right)}\},$$

which is open and convex. The formulae for score, Hessian and information in Proposition 2 require changes accordingly, i.e., the entries in the first rows of B_d, d = 1, …, D−1, are fixed at ones and their corresponding entries, rows and columns in score, Hessian and information need to be deleted. Treatment for the D = 2 case is similar and omitted for brevity. We emphasize that our choice of the restricted space $\mathcal{B}$ is arbitrary and exclude many arrays that might be of interest, e.g., arrays with any entries in the first rows of B_d, d = 1, …, D − 1, equal to zeros or with ties in the first row of B_D. However the set of such exceptional arrays has Lebesgue measure zero. In specific applications, subject knowledge may suggest alternative constraints on the parameters.

The second complication comes from possible non-uniqueness of decomposition when D > 2 even after adjusting scaling and permutation indeterminacy. The next proposition collects some recent results that give easy-to-check conditions for the uniqueness (up to scaling and permutation) of decomposition. The first two are useful for checking uniqueness of a given tensor, while the latter two give general conditions for uniqueness almost everywhere in the D = 3 or 4 case.

Proposition 3. Suppose that a D-dimensional array $\mathit{B}\in {\mathbb{R}}^{p_1\times \cdots \times p_D}$ has rank R.

1. (Sufficiency)(Sidiropoulos and Bro, 2000) The decomposition (1) is unique up to scaling and permutation if ${\sum }_{d=1}^D{k}_{{\mathit{B}}_d}\ge 2R+(D-1)$, where k_A is the k-rank of a matrix A, i.e., the maximum value k such that any k columns are linearly independent.

2. (Necessity)(Liu and Sidiropoulos, 2001) If the decomposition (1) is unique up to scaling and permutation, then min_d=1,…,D rank(B₁⊙⋯⊙B_d−1⊙B_d+1⊙⋯⊙B_D) = R, which in turn implies that min_d=1,…,D (Π_d′≠d rank(B_d′)) ≥ R.

3. (de Lathauwer, 2006) When D = 3, R ≤ p₃ and R(R−1) ≤ p₁(p₁−1)p₂(p₂−1)/2, the decomposition (1) is unique for almost all such tensors except on a set of Lebesgue measure zero.

4. (de Lathauwer, 2006) When D = 4, R ≤ p₄ and R(R − 1) ≤ p₁p₂p₃(3p₁p₂p₃ − p₁p₂ − p₁p₃ − p₂p₃ − p₁ − p₂ − p₃ + 3)/4, the decomposition (1) is unique for almost all such tensors except on a set of Lebesgue measure zero.

Next we give a sufficient and necessary condition for local identifiability. The proof follows from a classical result (Rothenberg, 1971) that relates local identifiability to the Fisher information matrix.

Proposition 4 (Identifiability). Given iid data points {(y_i, x_i), i = 1, …, n} from the tensor regression model. Let ${\mathit{B}}_0\in \mathcal{B}$ be a parameter point and assume there exists an open neighborhood of B₀ in which the information matrix has a constant rank. Then B₀ is locally identifiable up to permutation if and only if

$$I\left({\mathit{B}}_0\right)={\left[{\mathit{J}}_1\dots {\mathit{J}}_D\right]}^{⊺}\left[\sum _{i=1}^n\frac{{\mu }^{\prime }{\left(n_i\right)}^2}{{\sigma }_i^2}\left(\text{vec}{x}_i\right){\left(\text{vec}{x}_i\right)}^{⊺}\right]\left[{\mathit{J}}_1\dots J_D\right]$$

is nonsingular.

Remark 3.1: Proposition 4 explains the merit of tensor regression from another angle. For identifiability, the classical linear regression requires vec $x_i\in {\mathbb{R}}^{{\prod }_{d{p}_d}}$, i = 1, …, n, to be linearly independent in order to estimate all parameters, which requires a sample size n ≥ Π_d p_d. The more parsimonious tensor regression only requires linearly independence of the “collapsed” vectors ${\left[{\mathit{J}}_1\dots {\mathit{J}}_D\right]}^{⊺}\text{vec}{\mathit{x}}_i\in {\mathbb{R}}^{R(d{p}_d-D+1}$, i = 1, …, n. The requirement on sample size is greatly lessened by imposing structure on the arrays.

Remark 3.2: Although global identifiability is hard to check for a finite sample, a parameter point $\mathit{B}\in \mathcal{B}$ is asymptotically and globally identifiable as far as it admits a unique decomposition up to scaling and permutation and ${\sum }_{i=1}^n\left(\text{vec}{\mathit{x}}_i\right){\left(\text{vec}{\mathit{x}}_i\right)}^{⊺}$ has full rank for n ≥ n₀, or, when considered stochastically, E[(vec X)(vec X)^T] has full rank. To see this, whenever ${\sum }_{i=1}^n\left(\text{vec}{\mathit{x}}_i\right){\left(\text{vec}{\mathit{x}}_i\right)}^{⊺}$ has full rank, the full coefficient array is globally identifiable and thus the decomposition is identifiable whenever it is unique.

Generalizing the concept of estimable functions for linear models, we call any linear combination of $\langle {\mathit{x}}_i,{\sum }_{r=1}^R{\beta }_1^{\left(r\right)}o\cdots o{\beta }_D^{\left(r\right)}\rangle$, i = 1, …, n, an estimable function. We can estimate estimable or collection of estimable functions even when the parameters are not identifiable.

4.3 Asymptotics

The asymptotics for tensor regression follow from those for MLE or M-estimation. The key observation is that the nonlinear part of tensor model (4) is a degree-D polynomial of parameters and the collection of polynomials $\{\langle \mathit{B},\mathit{X}\rangle ,\mathit{B}\in \mathcal{B}\}$ form a Vapnik-C̆ervonenkis (VC) class. Then standard uniform convergence theory for M-estimation (van der Vaart, 1998) applies.

Theorem 1 (Consistency). Assume ${\mathit{B}}_0=⟦{\mathit{B}}_{01},\dots ,{\mathit{B}}_{0D}⟧\in \mathcal{B}$ is (globally) identifiable up to permutation and the array covariates X_i are iid from a bounded distribution. The MLE is consistent, i.e., ${\widehat{\mathit{B}}}_n$ converges to B₀ (modulo permutation) in probability, in the following models: (1) normal tensor regression with a compact parameter space ${\mathcal{B}}_0\subset \mathcal{B}$; (2) binary tensor regression; and (3) poisson tensor regression with a compact parameter space ${\mathcal{B}}_0\subset \mathcal{B}$.

Remark 4: (Misspecified Rank) In practice it is rare that the true regression coefficient ${\mathit{B}}_{\text{true}}\in {\mathbb{R}}^{p_1\times \cdots \times p_D}$ is exactly a low rank tensor. However the MLE of the rank-R tensor model converges to the maximizer of function $M\left(\mathit{B}\right)={\mathbb{P}}_{{\mathit{B}}_{\text{true}}}$ ln p_B or equivalently ${\mathbb{P}}_{{\mathit{B}}_{\text{true}}}$ ln(p_B/p_Btrue). In other words, the MLE is consistently estimating the best rank-R approximation of B_true in the sense of Kullback-Leibler distance.

To establish the asymptotic normality of ${\widehat{\mathit{B}}}_n$, we note that the log-likelihood function of tensor regression model is quadratic mean differentiable (q.m.d).

Lemma 3. Tensor regression model is quadratic mean differentiable (q.m.d.).

Theorem 2 (Asymptotic Normality). For an interior point ${\mathit{B}}_0=⟦{\mathit{B}}_{01},\dots ,{\mathit{B}}_{0D}⟧\in \mathcal{B}$ with nonsingular information matrix I(B₀₁, …, B_0D) (9) and ${\widehat{\mathit{B}}}_n$ is consistent,

$$\sqrt{n}\left[\text{vec}\right({\widehat{\mathit{B}}}_{n1},\dots ,{\widehat{\mathit{B}}}_{nD})-\text{vec}({\mathit{B}}_{01},\dots ,{\mathit{B}}_{0D}\left)\right]$$

converges in distribution to a normal with mean zero and covariance I⁻¹(B₀₁, …, B_0D).

5 Regularized Estimation

The sample size in typical neuroimaging studies is quite small, and thus even for a rank-1 tensor regression (3), it is likely that the number of parameters exceeds the sample size. Therefore the p ≫ n challenge is a rule rather than an exception in neuroimaging analysis, and regularization becomes essential. Even when the sample size exceeds the number of parameters, regularization is still useful for stabilizing the estimates and improving their risk property. We emphasize that there are a large number of regularization techniques for different purposes. Here we illustrate with using sparsity regularization for identifying sub-regions that are associated with the response traits. This problem can be viewed as an analogue of variable selection in the traditional vector-valued covariates. Toward that end, we maximize a regularized log-likelihood function

$$\ell (\alpha ,\gamma ,{\mathit{B}}_1,\dots ,{\mathit{B}}_D)-\sum _{d=1}^D\sum _{r=1}^R\sum _{i=1}^{p_d}{P}_{\lambda }(\mid {\beta }_{di}^{\left(r\right)}\mid ,\rho ),$$

where P_λ(|β|, ρ) is a scalar penalty function, ρ is the penalty tuning parameter, and λ is an index for the penalty family. Some widely used penalties include: power family (Frank and Friedman, 1993), in which P_λ(|β|, ρ) = ρ|β|^λ, λ ∈ (0, 2], and in particular lasso (Tibshirani, 1996) (λ = 1) and ridge (λ = 2); elastic net (Zou and Hastie, 2005), in which P_λ(|β|, ρ) = ρ[(λ−1)β²/2 + (2−λ)|β|], λ ∈ [1, 2]; and SCAD (Fan and Li, 2001), in which ∂/∂|β|P_λ(|β|, ρ) = ρ{1_{|β|≤ρ} + (λρ − |β|)₊/(λ − 1)ρ1_{|β|>ρ}}, λ > 2, among many others. Choice of penalty function and tuning parameters ρ and λ depends on particular purposes: prediction, unbiased estimation, or region selection.

Regularized estimation for tensor models incurs slight changes in Algorithm 1. When updating B_d, we simply fit a penalized GLM regression problem,

$${\mathit{B}}_d^{(t+1)}={\mathrm{argmax}}_{Bd}\ell ({\alpha }^{\left(t\right)},{\gamma }^{\left(t\right)},{\mathit{B}}_1^{(t+1)},\dots ,{\mathit{B}}_{d-1}^{(t+1)},{\mathit{B}}_d,{\mathit{B}}_{d+1}^{\left(t\right)},\dots ,{\mathit{B}}_D^{\left(t\right)})-\sum _{r=1}^R\sum _{i=1}^{p_d}{P}_{\lambda }(\mid {\beta }_{di}^{\left(r\right)}\mid ,\rho ),$$

for which many software packages exist. Same paradigm certainly applies to regularizations other than sparsity. The fitting procedure boils down to alternating regularized GLM regression. The monotone ascent property of Algorithm 1 is retained under the modified algorithm. Convex penalties, such as elastic net and power family with λ ≥ 1, tend to convexify the objective function and alleviate the local maximum problem. On the other hand, concave penalty such as power family with λ < 1 and SCAD produces more unbiased estimates but the regularized objective function is more ruggy and in practice the algorithm should be initialized from multiple start points to increase the chance of finding a global maximum. Many methods are available to guide the choice of the tuning parameter ρ and/or λ for regularized GLM, notably AIC, BIC and cross validation. For instance the recent work (Zhou et al., 2011) derives BIC type criterion for GLM with possibly non-concave penalties such as power family, which can be applied to regularized tensor regression models in a straightforward way.

Two remarks are in order. First, it is conceptually possible to apply these regularization techniques directly to the full coefficient array $\mathit{B}\in {\mathbb{R}}^{{\prod }_{d{p}_d}}$ without considering any structured decomposition as in our models. That is, one simply treats vecX as the predictor vector as employed in the classical total variation regularization in image denoising and recovery. However, for the brain imaging data, we should bear in mind the dimensionality of the imaging arrays. For instance, to the best of our knowledge, no software is able to deal with fused lasso or even simple lasso on 64³ = 262, 144 or 256³ = 16, 777, 216 variables. This ultrahigh dimensionality certainly corrupts the statistical properties of the regularized estimates too. Second, penalization is only one form of regularization. In specific applications, prior knowledge often suggests various constraints among parameters, which may be exploited to regularize parameter estimate. For instance, for MRI imaging data, sometimes it may be reasonable to impose symmetry on the parameters along the coronal plane, which effectively reduces the dimensionality by p_dR/2. In many applications, nonnegativity of parameter values is also enforced.

6 Numerical Analysis

We have carried out an extensive numerical study to investigate the finite sample performance of the proposed methods. In this section, we report selected results from synthetic examples and an analysis of a real brain imaging data.

6.1 2D Shape Examples

We first elaborate on the illustrative example given in Section 2.2 with a collection of 2D shapes. We examine the performance of the tensor model under a variety of sample sizes and signal strengths, and compare the estimates with and without regularization. More specifically, the tensor model in Section 2.2 is employed, where the response is normally distributed with mean, η = γ^TZ + 〈B, X〉, and standard deviation σ. X is a 64 × 64 2D matrix, Z is a 5-dimensional covariate vector, both of which have standard normal entries, γ = (1, 1, 1, 1, 1)^T, and B is binary with the true signal region equal to one and the rest zero. We fit both a rank-3 tensor model without regularization, and one with a lasso regularization. For sample size, we examine n = 200, 300, 400, 500 and 750. Note that, for this example, the number of parameters of a rank-3 model is 380 = 5 + 3 × (64 + 64) − 3². As such, there are multiple solutions when n = 200 or 300, and we arbitrarily choose one estimate. For signal strength, we vary the noise level σ = 50%, 20%, 10%, 5% and 1% of the standard deviation of the mean η, respectively.

We summarize the results in three plots: the snapshots of estimates with varying sample size, the snapshots with varying signal strength, and the line plot of the average root mean squared error (RMSE) for estimation of B. For space consideration, only the first plot is presented in Figure 2 (with 10% noise level), and the rest in the supplementary appendix. We make the following observations. First, estimation accuracy steadily increases with the sample size, demonstrating consistency of the proposed method. This can be seen from both the snapshots with improved quality and the decreasing RMSE. Similar patterns are observed with increasing signal strength. Second, regularization clearly improves estimation, especially when the sample size is limited. In practice, when the number of imaging subjects is moderate, regularized tensor regression is recommended.

Figure 2.

Snapshots of tensor estimation with varying sample size. The matrix variate has size 64 by 64 with entries generated as independent standard normals. The regression coefficient for each entry is either 0 (white) or 1 (black).

For this example, we also examined the recovered signals by regularized tensor regression with a fixed sample size n = 500 and varying penalty parameter. The results are reported in the appendix A.2.

6.2 Attention Deficit Hyperactivity Disorder Data Analysis

We applied our methods to the attention deficit hyperactivity disorder (ADHD) data from the ADHD-200 Sample Initiative (http://fcon_1000.projects.nitrc.org/indi/adhd200/). ADHD is a common childhood disorder and can continue through adolescence and adulthood. Symptoms include difficulty in staying focused and paying attention, difficulty in controlling behavior, and over-activity. The data set that we used is part of the ADHD-200 Global Competition data sets. It consists of 776 subjects, with 491 normal controls and 285 combined ADHD subjects. Among them, there are 442 males with mean age 12.0 years and standard deviation 3.1 years, and 287 females with mean age 11.9 years and standard deviation 3.5 years. We removed 47 subjects due to the missing observations or poor image quality. Resting state fMRIs and T1-weighted images were acquired for each subject. The T1-weighted images were preprocessed by standard steps including AC (anterior commissure) and PC (posterior commissure) correction, N2 bias field correction, skull-stripping, intensity inhomogeneity correction, cerebellum removal, segmentation, and registration. After segmentation, the brains were segmented into four different tissues: grey matter (GM), white matter (WM), ventricle (VN), and cerebrospinal fluid (CSF). We quantified the local volumetric group differences by generating RAVENS maps (Davatzikos et al., 2001) for the whole brain and each of the segmented tissue type (GM, WM, VN, and CSF) respectively, using the deformation field we obtained during registration. RAVENS methodology is based on a volume-preserving spatial transformation, which ensures that no volumetric information is lost during the process of spatial normalization, since this process changes an individual's brain morphology to conform it to the morphology of a template. In addition to image covariates, we include the subjects' age, gender, and whole brain volume as regular covariates. One scientific question of interest is to understand association between the disease outcome and the brain image patterns after adjustment for the clinical and demographical variables. We first examined the case with real image covariates and simulated responses. The goal is to study the empirical performance of our methods under various response models. We then showed the performance of the regularized estimation in terms of region selection. Finally, we applied the method to the data with the true observed binary response.

6.2.1 Real Image Covariates and Simulated Response

We first consider a number of GLMs with the real brain image covariates, where η = γ^TZ + 〈B, X〉, the signal tensor B admits a certain structure, η = (1, 1, 1)^T, X denotes the 3D MRI image with dimension 256 × 256 × 198, and Z denotes the vector of age, gender and whole brain volume. We consider two structures for B. The first admits a rank one decomposition, with ${\mathit{B}}_1\in {\mathbb{R}}^{256\times 1}$, ${\mathit{B}}_2\in {\mathbb{R}}^{256\times 1}$, and ${\mathit{B}}_3\in {\mathbb{R}}^{198\times 1}$, and all of whose (90 + j)th element equal to sin(jπ/14) for j = 0, 1, …, 14. This corresponds to a single-ball signal in a 3D space. The second admits a rank two decomposition, with ${\mathit{B}}_1\in {\mathbb{R}}^{256\times 2}$, ${\mathit{B}}_2\in {\mathbb{R}}^{256\times 2}$, and ${\mathit{B}}_3\in {\mathbb{R}}^{198\times 2}$. All the first columns of B_d have their (90 + j)th element equal to sin(jπ/14), and the second columns of B_d have their (140 + j)th element equal to sin(jπ/14) for j = 0, 1, …, 14. This mimics a two-ball signal in the 3D space. We then generate the response through the GLM models: for the normal model, Y ~ Normal(μ, 1), where μ = η; for the binomial model, Y ~ Bernoulli(p), with p = 1/[1 + exp(−0.1η)]; and for the poisson model, Y ~ Poission(μ), with μ = exp(0.01η). Table 1 summarizes the average RMSE and its standard deviation out of 100 data replications. We see that the normal and poisson responses both have competitive performance, whereas the binomial case is relatively more challenging. The two-ball signal is more challenging than a one-ball signal, and overall the tensor models work well across different response types and different signals.

Table 1.

Tensor regression estimation for the ADHD data. Reported are mean RMSE and its standard deviation (in parenthesis) of evaluation criteria based on 100 data replications.

Signal	Param.	Normal	Binomial	Poisson
one-ball	γ	0.0639 (0.0290)	0.2116 (0.0959)	0.0577 (0.0305)
	B	0.0039 (0.0002)	0.0065 (0.0002)	0.0064 (0.0002)
two-ball	γ	0.0711 (0.0310)	0.3119 (0.1586)	0.0711 (0.0307)
	B	0.0058 (0.0002)	0.0082 (0.0003)	0.0083 (0.0003)

6.2.2 Regularized Estimation

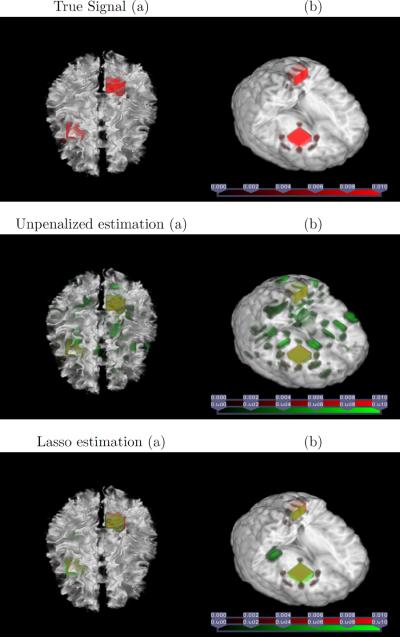
Next we focus on the ability of the regularized tensor regression model to identify relevant regions in brain associated with the response. This is analogous to the variable selection problem in the traditional regression with vector-valued covariates. We employ the two-ball signal and the normal model in Section 6.2.1. Figure 3 shows images with the true signal, the un-regularized tensor regression estimate, and the regularized tensor regression estimates with a lasso penalty, respectively, overlaid on an image of an arbitrarily chosen subject, or on a 3D rendering of a template. The plots clearly show that the true sparse signal regions can be well recovered through regularization.

Figure 3.

Region selection. The true signal regions are colored in red, the estimated signal regions are in green, and the overlapped regions are in yellow. The left panel is the true or estimated signal overlaid on a randomly selected subject, and the right panel is a 3D rendering of the true or estimated signal overlaid on the template

6.2.3 Real Data Analysis

Finally, we analyze the ADHD data with the observed binary diagnosis status as the response. We fitted a rank-3 tensor logistic regression model, since in practice it is rare that the true signal would follow an exact reduced rank formulation. We also applied the regularized estimation using a lasso penalty. Figure 4 shows the results. Inspecting Figure 4 reveals two regions of interest: left temporal lobe white matter and the splenium that connects parietal and occipital cortices across the midline in the corpus callosum. The anatomical disturbance in the temporal lobe has been consistently revealed and its interpretation would be consistent with a finer-grained analysis of the morphological features of the cortical surface, which reported prominent volume reductions in the temporal and frontal cortices in children with ADHD compared with matched controls (Sowell et al., 2003). Moreover, a reduced size of the splenium is the most reliable finding in the corpus callosum (Valera et al., 2007).

Figure 4.

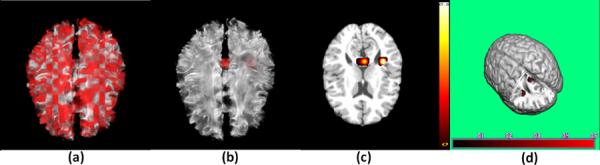
Application to the ADHD data. Panel (a) is the unpenalized estimate overlaid on a randomly selected subject; (b) is the regularized estimate overlaid on a randomly selected subject; (c) is a selected slice of the regularized estimate overlaid on the template; and (d) is a 3D rendering of the regularized estimate overlaid on the template.

7 Discussion

We have proposed a tensor decomposition based approach for regression modeling with array covariates. The curse of dimensionality is lessened by imposing a low rank approximation to the extremely high-dimensional full coefficient array. This allows development of a fast estimation algorithm and regularization. Numerical analysis demonstrates that, despite its massive reduction, the method works well in recovering various geometric as well as natural shape images. Although there has been imaging studies utilizing tensor structure (Li et al., 2005; Park and Savvides, 2007), our proposal, to the best of our knowledge, is the first that integrates tensor decomposition within a statistical regression (supervised learning) paradigm.

A motivation of our work is the recent emergence of large-scale neuroimaging data. Early imaging studies usually have only a handful of subjects. More recently, however, a number of large-scale brain imaging studies are accumulating imaging data from a much larger number of subjects. For instance, the Attention Deficit Hyperactivity Disorder Sample Initiative (ADHD, 2012) consists of 776 participants from eight imaging centers with both MRI and fMRI images, as well as their clinical information. Another example is the Alzheimer's Disease Neuroimaging Initiative (ADNI, 2012) database, which includes 818 participants with MRI, fMRI and genomics data. The proposed tensor regression model aims to address the computational and modeling challenges of such large-scale imaging data. Meanwhile, our approach is equally applicable to smaller scale imaging data, e.g., images acquired from a single lab with a moderate number of subjects. In this scenario, the regularization strategy outlined in Section 5 is expected to play a central role for scientific discovery.

The classical large n asymptotics in Section 4 may seem irrelevant for imaging data with a limited sample size. However, it outlines some basic properties of the proposed tensor regression model and has practical relevance in several aspects. For instance, by choosing a small rank such that the model size p_e is effectively smaller than n, we know that, under the specified conditions, the tensor regression model is consistently estimating the best rank-R approximation to the full model in the sense of Kullback-Liebler distance. A low rank estimate often provides a reasonable approximation to the true tensor regression parameter, even when the truth is of a high rank. This can be seen from our various numerical experiments, where a rank-3 model yields a good recovery of a butterfly shape in Figure 1 and a two-ball structure in Figure 3. Moreover, the regular asymptotics is useful for testing significance of a low rank sparse model in a replication study. Classical hypothesis testes such as likelihood ratio test can be formulated based on the asymptotic normality of the tensor estimates established in Section 4. The explicit formula for score and information in Section 4.1 and the identifiability issue discussed in Section 4.2 are not only useful for asymptotic theory but also for computation.

As the challenge of p ≫ n being a rule rather than exception in brain imaging analysis, regularization is to play a crucial role in practical applications. We consider the tensor regression, with or without regularization, presented in this paper an analog of the hard thresholding in classical regression, where the rank of the model is fixed. Respecting the array structure, the regularized tensor regression yields significantly better estimates than the classical regularization applied to the vectorized tensor covariates. Appendix A.3 presents a numerical comparison with the classical lasso. Currently, we are also investigating another line of regularization through “soft thresholding”. That is, we estimate the tensor regression model without fixing the rank but instead subject to a convex regularization of the rank of the tensor parameter. Results along this line will be reported elsewhere.

The scale and complexity of neuroimaging data require the estimation algorithm to be highly scalable, efficient and stable. The methods in this paper are implemented in an efficient Matlab toolbox. For instance, the median run time of fitting a rank-3 model to the 2D triangle shape in Figure 1 was about 5 seconds. Fitting a rank-3 logistic model to the 3D ADHD data in Section 6.2.3 took about 285 seconds for 10 runs from 10 random starting points, averaging < 30 seconds per run. Appendix A.4 contains more numerical results to study the algorithm stability with respect to starting values as well as computing time. All results were obtained on a standard laptop computer with a 2.6 GHz Intel i7 CPU.

We view the method of this article as a first step toward a more general area of array regression analysis, and the idea can be extended to a wide range of problems. We describe a few potential future directions here. First, although we only present results for models with a conventional covariate vector and an array covariate, the framework applies to arbitrary combination of array covariates. This provides a promising approach to the analysis of multi-modality data which becomes increasingly available in modern neuroimaging and medical studies. Second, we remark that our modeling approach and algorithm equally apply to many general loss functions occurring in classification and prediction. For example, for a binary response Y ∈ {0, 1}, the hinge loss takes the form

$$\sum _{i=1}^n[1-y_i\{\alpha +{\gamma }^{⊺}{z}_i+\langle {\sum _{r=1}^R{\beta }_1^{\left(r\right)}o{\beta }_2^{\left(r\right)}o\cdots o{\beta }_D^{\left(r\right)},x_i\rangle \left\}\right]}_{+}$$

and should play an important role in support vector machines with array variates. Third, in this article rotation has not been explicitly considered in the modeling. When prior knowledge indicates, sometimes it is prudent to work in polar coordinates. For example, the `disk' signal in Figure 1 can be effectively captured by a rank-1 outer product if the image is coded in polar coordinates. A diagonal signal array has full rank and cannot be approximated by any lower rank array, but if changed to polar coordinates, the rank reduces to one. Some of these extensions are currently under investigation. In summary, we believe that the proposed methodology timely answers calls in modern neuroimaging data analysis, whereas the general methodology of tensor regression is to play a useful role and also deserves more attention in statistical analysis of high-dimensional complex imaging data.