Abstract
We use all-atom molecular dynamics simulations on a massive scale to compute the standard binding free energy of the 13-residue antimicrobial peptide indolicidin to a lipid bilayer. The analysis of statistical convergence reveals systematic sampling errors that correlate with reorganization of the bilayer on the microsecond timescale and persist throughout a total of 1.4 ms of sampling. Consistent with experimental observations, indolicidin induces membrane thinning, although the simulations significantly overestimate the lipophilicity of the peptide.
Antimicrobial peptides are a component of the innate immune system of eukaryotes (1). As such, they must interact with pathogenic membranes, either during translocation or by disrupting their structural integrity (2). Here we examine the binding of the 13-residue cationic antimicrobial peptide indolicidin (3) (ILPWKWPWWPWRR-NH2) to a lipid membrane as a first step towards elucidating its mechanism of action.
Molecular solutes interact with lipid membranes in many cellular processes (4). Computational approaches such as molecular dynamics simulations have been widely used to characterize these interactions (5). However, molecular dynamics simulations can require unfeasibly long times to reach equilibrium (6). Therefore, it is common to compute equilibrium properties of solute insertion into lipid bilayers using umbrella sampling (7) simulations in which the solute is restrained along the bilayer normal using harmonic restraining potentials, or umbrellas, centered at values distributed between bulk water and the bilayer center.
It is often assumed that equilibrium properties rapidly attain convergence in umbrella sampling simulations; accordingly, convergence measures are rarely published (8). However, we have recently shown that umbrella sampling simulations require up to 100 ns per umbrella (3 μs in total) to eliminate systematic sampling errors in the standard free energy of binding, Δ, of an arginine side-chain analog from bulk water to a lipid bilayer (8). The fact that umbrella sampling has been used to investigate the bilayer insertion of substantially larger solutes (9) motivates a systematic evaluation of statistical sampling convergence of Δ for indolicidin in a lipid bilayer.
To estimate Δ of indolicidin to a lipid bilayer, we conducted 60 sets of umbrella-sampling simulations while systematically varying the initial conformation. In each umbrella sampling simulation, each umbrella was simulated for 1.5 μs, yielding a total simulation time of 1.4 ms and 60 independent free energy or potential of mean force (PMF) profiles from bulk water to the center of a POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine) lipid bilayer.
The PMF profiles indicate that indolicidin strongly binds to the bilayer, partitioning inside the lipid headgroups (Fig. 1, A and E). Importantly, the mean estimate of Δ decays exponentially with equilibration time teq, indicating that systematic sampling errors in individual simulations continued to decrease throughout the 1.5-μs interval as rare events led to more favorable states (Fig. 1 B). The low frequency of transitions to more favorable states exacerbates the requirement for massive sampling using multiple independent simulations.
Figure 1.
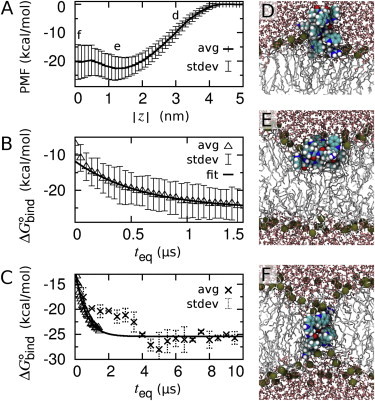
PMF for indolicidin partitioning into a POPC bilayer. (A) Average PMF from 60 independent umbrella-sampling simulations based on 1 < t ≤ 1.5 μs/umbrella. (B) Average Δ from 50-ns time intervals per umbrella (teq < t ≤ teq+50 ns) as a function of equilibration time, teq. (Solid line) Single exponential fit to the mean over 0.5 < teq ≤ 1.5 μs. (C) Mean values of Δ from the 10-μs/umbrella simulations (crosses) together with the mean values of Δ (triangles) and exponential fit from panel B. PMF and Δ profiles obtained from each of the 60 independent simulations are shown in Fig. S1 in the Supporting Material. (D–F) Representative conformations after 1.5 μs of simulation at = (D) 3 nm, (E) 1.2 nm, and (F) 0.0 nm. To see this figure in color, go online.
Computational limitations precluded extending all 60 sets of umbrella-sampling simulations to even longer times. Instead, we identified the two simulations at each umbrella that appeared to be most representative of equilibrium and extended each to 10 μs per umbrella (see Methods in the Supporting Material). The resulting estimates of Δ continued to decrease until teq = 4 μs (68 μs in total), after which they stabilized at the asymptotic limit of the exponential fit of the shorter simulation data (Δ = −26 ± 5 kcal/mol; Fig. 1 C).
As indolicidin approaches the bilayer, it is drawn closer (Fig. 2 A) as salt bridges form between the peptide and the phospholipid headgroups (Fig. 2 B), inducing their protrusion (Figs. 1 D and 2 C). At large separation distances, this state is attained only when the peptide becomes highly extended (Fig. 2, D and E). As indolicidin is inserted more deeply, the surface of the lipid bilayer invaginates (Figs. 1 E and 2 C), maintaining peptide-lipid salt bridges (Fig. 2 B) and leading to the formation of a pore when the solute is near the bilayer center (Figs. 1 F and 2 C, and see Fig. S2, Fig. S3, Fig. S4, and Fig. S5 in the Supporting Material). These Boltzmann-weighted ensemble averages may not be mechanistically representative of nonequilibrium binding events (8,10).
Figure 2.
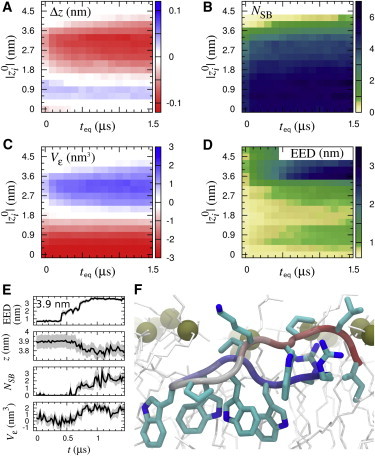
Slow equilibration of bilayer and peptide. (A–D) Color quantifies conformational reorganization for teq < t ≤ teq + 100 ns as a function of teq and ||. (A) Deviation of insertion depth, z, from , Δz ≡ z − ; (B) number of peptide-lipid salt bridges, NSB; (C) volume change of the bilayer’s proximal leaflet in the radial vicinity of the solute, Vε; and (D) peptide end-to-end distance (EED). There is no sampling for t > 0.5 μs at || ≥ 4.5 nm. (E) Representative time-series of a trajectory at = 3.9 nm. (F) Representative conformation at 10 μs for || = 1.2 nm. To see this figure in color, go online.
The reorganization of the peptide, the bilayer, and the ionic interactions between them became more pronounced with increasing simulation time at peptide insertion depths shallower than the global free energy minimum (|| >1.4 nm; Fig. 1 A and Fig. 2, B–D). These conformational transitions are likely the source of the systematic drift of Δ. Reorganization of the bilayer also controls the rate of equilibration during membrane insertion of an arginine side chain (8,9) and a cyclic arginine nonamer (11), suggesting that slow reorganization of lipids around cationic solutes presents a general impediment to simulation convergence.
Consistent with the perturbation of membrane thickness observed by in situ atomic force microscopy (12), our results suggest that indolicidin insertion induces local thinning of the bilayer (Fig. 1, E and F, and Fig. 2, C and F). The different conformational ensembles sampled by the peptide in water and in the lipid bilayer (Fig. 2 D) are consistent with the observations that indolicidin is disordered in solution (13) and adopts stable conformations in the presence of detergent (14). Although the peptide’s conformation continued to change when it was deeply inserted (Fig. 2 D), the amount of water in the bilayer’s hydrophobic core converged relatively rapidly (see Fig. S2). Indolicidin can induce the formation of hydrated, porelike defects (see Fig. S2, Fig. S3, Fig. S4, and Fig. S5) but does not act as a chloride carrier (see Fig. S6 and Fig. S7). Future studies of the mechanism of indolicidin action will examine the effect of multiple peptide binding.
The PMF profile presented in this Letter is strikingly different from that computed by Yeh et al. (15) using different force field parameters for indolicidin partitioning into a DMPC (1,2-dimyristoyl-sn-glycero-3-phosphatidylcholine) bilayer, from which the binding free energy was estimated to be 0 kcal/mol (15). However, that study comprised only 25 ns per umbrella and likely suffers from systematic sampling errors induced by initial conditions (see Fig. S8).
Our estimate of the binding affinity is much larger than the values obtained for indolicidin and large unilamellar POPC vesicles using isothermal titration calorimetry, −7.4 kcal/mol (16), and equilibrium dialysis, −8.8 kcal/mol (13). Such a discrepancy suggests that the relative accuracy of binding free energies for amino-acid side-chain analogs (8,9,17) does not necessarily extend to polypeptides. Although more work is needed to elucidate the source of this discrepancy, this study underlines the importance of attaining convergence before evaluating force-field accuracy.
Importantly, this work also highlights the extensive sampling required to remove systematic errors induced by initial conditions in atomistic simulations of peptides in membranes. Slow equilibration of the system is due to rare transitions across hidden free energy barriers involving reorganization of the membrane. Two simple recommendations are 1), evaluating the time-dependence of ensemble averages, and 2), conducting multiple simulations with different initial conditions. We have recently shown that by using enhanced sampling techniques it is possible to identify the locations of hidden free energy barriers without a priori knowledge (9). Future research will examine strategies for speeding up the crossing of these barriers, such as optimized order parameters including bilayer reorganization and enhanced sampling techniques including a random walk along the order parameter (9).
Acknowledgments
Computations were performed at SciNet (25) and data was stored at SHARCNET, both of which are resources of Compute Canada.
This work was funded in part by National Sciences and Engineering Research Council discovery grant No. RGPIN-418679 and by Canadian Institutes of Health Research operating grants No. MOP-43998 and No. MOP-43949.
Supporting Material
References and Footnotes
- 1.Hancock R.E.W. Cationic peptides: effectors in innate immunity and novel antimicrobials. Lancet Infect. Dis. 2001;1:156–164. doi: 10.1016/S1473-3099(01)00092-5. [DOI] [PubMed] [Google Scholar]
- 2.Epand R.M., Vogel H.J. Diversity of antimicrobial peptides and their mechanisms of action. Biophys. Biochim. Acta. 1999;1462:11–28. doi: 10.1016/s0005-2736(99)00198-4. [DOI] [PubMed] [Google Scholar]
- 3.Selsted M.E., Novotny M.J., Cullor J.S. Indolicidin, a novel bactericidal tridecapeptide amide from neutrophils. J. Biol. Chem. 1992;267:4292–4295. [PubMed] [Google Scholar]
- 4.Stein W. Academic Press; Orlando, FL: 1986. Transport and Diffusion across Cell Membranes. [Google Scholar]
- 5.Saiz L., Klein M.L. Computer simulation studies of model biological membranes. Acc. Chem. Res. 2002;35:482–489. doi: 10.1021/ar010167c. [DOI] [PubMed] [Google Scholar]
- 6.Grossfield A., Feller S.E., Pitman M.C. Convergence of molecular dynamics simulations of membrane proteins. Proteins. 2007;67:31–40. doi: 10.1002/prot.21308. [DOI] [PubMed] [Google Scholar]
- 7.Torrie G.M., Valleau J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. J. Comput. Phys. 1977;23:187–199. [Google Scholar]
- 8.Neale C., Bennett W.F.D., Pomès R. Statistical convergence of equilibrium properties in simulations of molecular solutes embedded in lipid bilayers. J. Chem. Theory Comput. 2011;7:4175–4188. doi: 10.1021/ct200316w. [DOI] [PubMed] [Google Scholar]
- 9.Neale C., Madill C., Pomès R. Accelerating convergence in molecular dynamics simulations of solutes in lipid membranes by conducting a random walk along the bilayer normal. J. Chem. Theory Comput. 2013;9:3686–3703. doi: 10.1021/ct301005b. [DOI] [PubMed] [Google Scholar]
- 10.Kopelevich D.I. One-dimensional potential of mean force underestimates activation barrier for transport across flexible lipid membranes. J. Chem. Phys. 2013;139:134906. doi: 10.1063/1.4823500. [DOI] [PubMed] [Google Scholar]
- 11.Huang K., García A.E. Free energy of translocating an arginine-rich cell-penetrating peptide across a lipid bilayer suggests pore formation. Biophys. J. 2013;104:412–420. doi: 10.1016/j.bpj.2012.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shaw J.E., Alattia J.-R., Yip C.M. Mechanisms of antimicrobial peptide action: studies of indolicidin assembly at model membrane interfaces by in situ atomic force microscopy. J. Struct. Biol. 2006;154:42–58. doi: 10.1016/j.jsb.2005.11.016. [DOI] [PubMed] [Google Scholar]
- 13.Ladokhin A.S., Selsted M.E., White S.H. Bilayer interactions of indolicidin, a small antimicrobial peptide rich in tryptophan, proline, and basic amino acids. Biophys. J. 1997;72:794–805. doi: 10.1016/s0006-3495(97)78713-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rozek A., Friedrich C.L., Hancock R.E.W. Structure of the bovine antimicrobial peptide indolicidin bound to dodecylphosphocholine and sodium dodecyl sulfate micelles. Biochemistry. 2000;39:15765–15774. [PubMed] [Google Scholar]
- 15.Yeh I.-C., Ripoll D.R., Wallqvist A. Free energy difference in indolicidin attraction to eukaryotic and prokaryotic model cell membranes. J. Phys. Chem. B. 2012;116:3387–3396. doi: 10.1021/jp211883u. [DOI] [PubMed] [Google Scholar]
- 16.Andrushchenko V.V., Aarabi M.H., Vogel H.J. Thermodynamics of the interactions of tryptophan-rich cathelicidin antimicrobial peptides with model and natural membranes. Biochim. Biophys. Acta. 2008;1778:1004–1014. doi: 10.1016/j.bbamem.2007.12.022. [DOI] [PubMed] [Google Scholar]
- 17.MacCallum J.L., Bennett W.F.D., Tieleman D.P. Distribution of amino acids in a lipid bilayer from computer simulations. Biophys. J. 2008;94:3393–3404. doi: 10.1529/biophysj.107.112805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 19.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 20.Berger O., Edholm O., Jähnig F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 1997;72:2002–2013. doi: 10.1016/S0006-3495(97)78845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kaminski G.A., Friesner R.A., Jorgensen W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B. 2001;105:6474–6487. [Google Scholar]
- 22.Kandt C., Ash W.L., Tieleman D.P. Setting up and running molecular dynamics simulations of membrane proteins. Methods. 2007;41:475–488. doi: 10.1016/j.ymeth.2006.08.006. [DOI] [PubMed] [Google Scholar]
- 23.Ferrenberg A.M., Swendsen R.H. New Monte Carlo technique for studying phase transitions. Phys. Rev. Lett. 1988;61:2635–2638. doi: 10.1103/PhysRevLett.61.2635. [DOI] [PubMed] [Google Scholar]
- 24.Rokitskaya T.I., Kolodkin N.I., Antonenko Y.N. Indolicidin action on membrane permeability: carrier mechanism versus pore formation. Biochim. Biophys. Acta. 2011;1808:91–97. doi: 10.1016/j.bbamem.2010.09.005. [DOI] [PubMed] [Google Scholar]
- 25.Loken C., Gruner D., Van Zon R. SciNet: lessons learned from building a power-efficient top-20 system and data centre. J. Phys. Conf. Ser. 2010;256:012026. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


