Novel Likelihood Ratio Tests for Screening Gene-Gene and Gene-Environment Interactions with Unbalanced Repeated-Measures Data

Abstract

There has been extensive literature on modeling gene-gene interaction (GGI) and gene-environment interaction (GEI) in case-control studies with limited literature on statistical methods for GGI and GEI in longitudinal cohort studies. We borrow ideas from the classical two-way analysis of variance (ANOVA) literature to address the issue of robust modeling of interactions in repeated-measures studies. While classical interaction models proposed by Tukey and Mandel have interaction structures as a function of main effects, a newer class of models, additive main effects and multiplicative interaction (AMMI) models, do not have similar restrictive assumptions on the interaction structure. AMMI entails a singular value decomposition of the cell residual matrix after fitting the additive main effects and has been shown to perform well across various interaction structures. We consider these models for testing GGI and GEI from two perspectives: likelihood ratio test based on cell means and a regression based approach using individual observations. Simulation results indicate that both approaches for AMMI models lead to valid tests in terms of maintaining the type I error rate, with the regression approach having better power properties. The performance of these models was evaluated across different interaction structures and 12 common epistasis patterns. In summary, AMMI model is robust with respect to misspecified interaction structure and is a useful screening tool for interaction even in the absence of main effects. We use the proposed methods to examine the interplay between the hemochromatosis gene and cumulative lead exposure on pulse pressure in the Normative Aging Study.

INTRODUCTION

Prospective cohort studies examining gene-gene or gene-environment interaction (GGI or GEI) effects on disease-related quantitative traits have received considerable attention in recent years [Bookman et al. 2011, Fan et al. 2012]. The detection of GEI plays a critical role in identifying a sub-population of the genetically susceptible individuals that are strongly affected by an adverse exposure. A better understanding of GEI may lead to the development of more effective disease prevention and intervention strategies. Studies of GEI in relation to disease development are facilitated by life-time characterization of exposure data, which are often available in prospective cohort studies. Repeated measures design in a prospective cohort study may increase power to detect interaction effects [Wong et al. 2003] and provide better ways to handle exposure measurement error. In addition, repeated measures data provide valuable information for delineating potentially time-dependent form of GGI or GEI, thereby permitting a much more detailed assessment of the dynamically evolving interplay between genes and environment.

Cohort studies for GGI or GEI are typically characterized by unequal sample size in each genotype-genotype or genotype-exposure configuration as a result of unbalanced allele frequencies and heterogeneous environmental exposure distributions in a population. A common analysis strategy for such unbalanced data involves modeling GGI or GEI by a product term in a regression setting, implying that the effect of two factors may not be purely additive in their contribution to the quantitative trait. Alternatively, one can try to model the interaction term in the generalized additive mixed model framework with nonlinear exposure and time effects [Lin and Zhang 1999], but tests for such non-parametric, smoothed interaction terms may yield reduced power for moderate sample size. Therefore, flexible yet parsimonious modeling of GGI or GEI is of interest in the longitudinal setting. In this paper, we propose likelihood ratio tests (LRT) for GGI and GEI using a sparse representation of interaction borrowing ideas from the classical ANOVA literature.

Genetic factors (G) and environmental exposures (E) are frequently treated as binary or ordered categorical variables. Consequently, GGI and GEI are often analyzed in the form of a two-way table. Considering G as a row variable with I categories and E as a column variable with J categories, the mean structure of a general two-way classification model for analyzing row × column interactions is given by

$${\mu }_{ij}=\mu +R_i+C_j+{\gamma }_{ij},i=1,\dots ,I,j=1,\dots ,J,$$ (1)

where μ_ij is the the expected (mean) value of a quantitative trait corresponding to the i^th row and the j^th column, μ is the grand mean, R_i is the additive main effect of the i^th row, C_j is the additive main effect of the j^th column, and γ_ij is the non-additive effect of the i^th row and the j^th column. The sum-to-zero conditions,

$$\sum _i{R}_i=\sum _j{C}_j=\sum _i{\gamma }_{ij}=\sum _j{\gamma }_{ij}=0,$$ (2)

ensure identifiability of the parameters in (1), so the degrees of freedom (df) for testing γ_ij in a fully saturated model is (I − 1)(J − 1). While a saturated model (1) is flexible for estimation of γ_ij, the df for interaction tests can increase considerably for finely cross-classified tables, which is inefficient and may result in low power for detecting GGI or GEI.

To improve the power of the test for GGI and GEI in longitudinal cohort studies, we explore alternative parsimonious interaction structures that were proposed in the classical ANOVA literature for testing interaction with only one observation per cell. Several models are summarized in the following:

$$\text{Model}(\text{a}):{\mu }_{ij}=\mu +R_i+C_j+\theta R_i{C}_j$$[Tukey 1949]

$$\text{Model}(\text{b}):{\mu }_{ij}=\mu +R_i+C_j+{\lambda }_i{C}_j$$[Mandel 1961]

$$\text{Model}(\text{c}):{\mu }_{ij}=\mu +R_i+C_j+R_i{\eta }_j$$[Mandel 1961]

$$\text{Model}(\text{d}):{\mu }_{ij}=\mu +R_i+C_j+\theta R_i{C}_j+{\lambda }_i{C}_j+R_i{\eta }_j$$[Tukey 1962]

with constraints ${\sum }_{i=1}^I{\lambda }_i={\sum }_{j=1}^J{\eta }_j$ for models (b) and (c), respectively, and additional constraints ${\sum }_{i=1}^I{\lambda }_i{R}_i={\sum }_{j=1}^J{\eta }_j{C}_j=0$ for model (d). The multiplicative interaction term is proportional to the main effects of one or both factors. The null hypotheses of no interaction for models (a)–(d) are θ = 0, λ_i = 0 (i = 1, …, I − 1), η_j = 0 (j = 1, …, J − 1), and θ = λ_i = η_j = 0 (i = 1, …, I − 2; j = 1, …, J − 2), corresponding to 1, I −1, J − 1, and I + J − 3 df for the tests of interaction effects, respectively. A more flexible potential alternative is the additive main effects and multiplicative interactions (AMMI) model [Gollob 1968, Mandel 1971]

$$\text{Model}(\text{e}):{\mu }_{ij}=\mu +R_i+C_j+\sum _{m=1}^M{d}_m{\alpha }_{im}{\beta }_{jm}+{\gamma }_{ij}^{\ast },$$

where M represents the number of interaction factors being extracted, M ≤ min(I − 1, J − 1), and a residual ${\gamma }_{ij}^{\ast }$ remains if not all interaction factors are used. The terms {α_imβ_jm} can the considered as the weights corresponding to a multiplicative contrast among {γ_ij} with Σ_i α_im = Σ_j β_jm = 0 and Σ_i α_imα_im′ = Σ_j β_jmβ_jm′ = 0 for m ≠ m′. For normalized contrasts ( ${\sum }_i{\alpha }_{im}^2={\sum }_j{\beta }_{jm}^2=1$, {d_m, α_im, β_jm} can be obtained by applying singular value decomposition (SVD) to {γ_ij}. Since the motivation for using an AMMI model is to extract a low rank approximation to the interaction matrix to save df and thus to enhance efficiency for the test, we focus on AMMI models with M = 1 (AMMI1). For all subsequent discussions, model (e) refers to AMMI1 model. The null hypothesis of no interaction for AMMI1 model is H₀ : d₁ = 0.

Models (a)–(e) were conceived from a statistical objective of reducing df and enhancing power of tests for interaction. They have been used in designed genotype-by-environment yield trials in agricultural studies [Freeman 1973, Zobel et al. 1988, Crossa et al. 1990]. These models were not conceived from a mechanistic or human biological perspective. Model (a) has recently been used to test for genetic effects in case-control studies [Chatterjee et al. 2006] and repeated measures data of complex traits [Maity et al. 2009]. Models (a), (b), (c), and (e) have also been applied for GGI effects on quantitative traits in cross-sectional studies [Barhdadi and Dubé 2010]. In unbalanced designs, the sums of squares associated with the two factors and their interaction are not orthogonal to one another. Consequently, the difficulties that arise in applying these nonlinear interaction models to unbalanced data involve obtaining unbiased parameter estimates, partitioning the sums of squares, deriving the appropriate test statistics and their null distributions. Mukherjee et al. [2012] proposed a screening tool for GGI and GEI using cell means from an unbalanced repeated measures array. This approach is appealing due to a closed-form analytical expression of the test statistic. However, violations in the homoscedasticity assumption of cell mean error distributions result in inflated type I error. While their proposed resampling-based method recognizes unbalanced, repeated measures data structure, the test implemented for AMMI models lacks power because it was not based on a theoretically derived pivot but an ad hoc extension of the balanced, cross-sectional case.

To overcome some of the limitations of the previous methods, we propose alternate approaches to explore GGI and GEI using models (a)–(e). We first describe our improved cell-mean approach that properly handles unbalanced data. Specifically, we adapt and modify the test proposed by Boik [1989] under a reduced-rank model for application to GGI/GEI using AMMI models. Next, we extend models (a)–(e) to the repeated measures setting using a mixed-effects modeling framework. We then develop a parametric bootstrap resampling approach by replacing the ad hoc pivot in Mukherjee et al. [2012] with a LRT-based pivot derived from the maximum likelihood under a nonlinear mixed-effects model. The power and type I error of our proposed tests are examined through a series of simulation studies. Lastly, we apply the proposed methods to a GEI study concerning the modifying effects of polymorphisms in the hemochromatosis gene (HFE) on the association between cumulative lead exposure and pulse pressure [Zhang et al. 2010]. Subject- and time-specific contributions to GEI are investigated using outputs from the AMMI model.

METHODS

Likelihood Ratio Test based on Cell Means

Following the notations in (1), let y_ijkh be the h^th measurement corresponding to the k^th individual in the (i, j)^th cell (or equivalently, row i and column j) in a longitudinal cohort study, i = 1, …, I, j = 1, …, J, k = 1, …, N_ij, h = 1, …, n_ijk. Let N denote the total number of individuals, N = Σ_iΣ_j N_ij. Let Ȳ = {Ȳ_ij} be the I × J matrix of sample means with ${\overline{Y}}_{ij}={\sum }_{k=1}^{N_{ij}}{\sum }_{h=1}^{n_{\mathit{ijk}}}{y}_{\mathit{ijkh}}/{\sum }_{k=1}^{N_{ij}}{n}_{\mathit{ijk}}$. Let L be the matrix of main effects, parameterized as $\mathit{L}={\mathbf{1}}_I\mu {\mathbf{1}}_J^{\prime }+\mathit{R}{\mathbf{1}}_J^{\prime }+{\mathbf{1}}_I{\mathit{C}}^{\text{'}}$, where 1_ν is a length-ν vector of ones, and R = (R₁, …, R_I)′, and C = (C₁, …, C_J)′ are the parameter vectors representing row and column effects, respectively. Let Γ be the I × J matrix of interaction effects, so the mean structures of models (a)–(e) can be expressed as E(Ȳ) = L+Γ. Throughout our treatment of the problem, we consider the drop-outs in longitudinal studies to be missing at random, leading to the unbalanced data structure.

We propose to use an empirical variance estimate for the variance of Ȳ_ij (denoted as ${\delta }_{ij}^2$) that accounts for within-subject correlation. Let σ²P(ρ) be a symmetric n_ijk × n_ijk within-subject covariance matrix, where ρ is a s × 1 parameter vector that fully characterizes the correlation matrix P(ρ), and σ² is a scale parameter. Both ρ and σ² can be estimated by Pearson residuals, namely, r̂_ijkh = y_ijkh − ȳ_ijk [Liang and Zeger 1986]. The pooled estimate of σ² is

$${\widehat{\sigma }}^2=\sum _i\sum _j(N_{ij}-1){\widehat{\sigma }}_{ij}^2/(\sum _i\sum _j{N}_{ij}-IJ),\text{where}{\widehat{\sigma }}_{ij}^2=\sum _{k=1}^{N_{ij}}\sum _{h=1}^{n_{\mathit{ijk}}}{\widehat{r}}_{\mathit{ijkh}}^2/(\sum _{k=1}^{N_{ij}}{n}_{\mathit{ijk}}-1).$$

The estimation of ρ is conditional on the correlation structure. For a compound symmetric correlation structure, s = 1, corr(y_ijkh, y_ijkh′) = ρ for h ≠ h′. The pooled estimate for ρ is

$$\begin{array}{c}\widehat{\rho }=\sum _i\sum _j(N_{ij}-1){\widehat{\rho }}_{ij}/(\sum _i\sum _j{N}_{ij}-IJ),\\ \text{where}{\widehat{\rho }}_{ij}=\sum _{k=1}^{N_{ij}}\sum _{h>h^{\prime }}{\widehat{r}}_{\mathit{ijkh}}{\widehat{r}}_{\mathit{ijk}{h}^{\prime }}/\left\{{\widehat{\sigma }}^2\left[\sum _{k=1}^{N_{ij}}\frac{1}{2}{n}_{\mathit{ijk}}(n_{\mathit{ijk}}-1)-1\right]\right\}.\end{array}$$

Finally, the empirical variance estimate for Ȳ_ij is given by

$${\widehat{\delta }}_{ij}^2=\frac{{\widehat{\sigma }}^2}{n_{ij}}+\frac{2{\widehat{\sigma }}^2}{n_{ij}^2}\sum _{k=1}^{N_{ij}}\sum _{h>h^{\prime }}\widehat{\text{corr}}(y_{\mathit{ijkh}},y_{\mathit{ijk}{h}^{\prime }}),\text{where}{n}_{ij}=\sum _{k=1}^{N_{ij}}{n}_{\mathit{ijk}}.$$ (3)

Given δ̂_ij, we maximize the likelihood of Ȳ under the normality assumption on the cell means, namely, $\text{vec}(\overline{\mathit{Y}})~\mathcal{N}\left(\text{vec}(\mathit{L})+\text{vec}(\mathbf{\Gamma }),\text{Diag}({\widehat{\delta }}_{ij}^2)\right)$. Maximizing the log-likelihood is equivalent to least squares fitting of μ_ij subject to weights $1/{\widehat{\delta }}_{ij}^2$. For classical interaction models (a)–(d) involving nonlinearity in the parameters, the maximum likelihood (ML) estimates for L and Γ are obtained using a quasi-Newton method in R [R Core Team 2012] with function ‘optim’ and L-BFGS-B algorithm [Nocedal and Wright 1999]. Quasi-Newton methods are sequential line search algorithms, and generally require only the gradient of the objective to be computed at each iterate. When convergence is reached, we calculate the log-likelihood under the null (ℓ̂₀) and under the alternative (ℓ̂₁) to construct the LRT statistic: −2(ℓ̂₀ − ℓ̂₁). Under H₀, the LRT statistic approximately follows a central chi-square distribution with df = 1, I − 1, J − 1, and I + J − 3 for models (a), (b), (c), and (d), respectively. The comparison of empirical quantiles of the LRT statistics with chi-square quantiles is presented in Supporting Information (Figure S.1).

Boik [1989] proposed the likelihood ratio criterion to test the rank of Γ for unbalanced data without repeated measures. For AMMI1 models, the test for non-additivity is H₀ : d₁ = 0 vs. H_a : d₁ = 1, which is equivalent to H₀: rank(Γ) = 0 vs. H_a: rank(Γ) = 1. Let H_ν be the row-space or column-space projection operator, ${\mathit{H}}_{\nu }={\mathit{I}}_{\nu }-(1/\nu ){\mathbf{1}}_{\nu }{\mathbf{1}}_{\nu }^{\prime }(\nu =I,J)$, and let ${\mathit{K}}_{\nu }{\mathit{K}}_{\nu }^{\prime }$ be a full-rank factorization of Hν with dimension ν × (ν − 1) satisfying ${\mathit{K}}_{\nu }^{\prime }{\mathit{K}}_{\nu }=\mathit{I}$. We have

$$\mathbf{\Gamma }={\mathit{H}}_I\mathbf{\Gamma }{\mathit{H}}_j={\mathit{K}}_I{\mathit{K}}_I^{\prime }\mathbf{\Gamma }{\mathit{K}}_J{\mathit{K}}_J^{\prime }={\mathit{K}}_I\mathbf{\Phi }{\mathit{K}}_J^{\prime },\mathbf{\Phi }={\mathit{K}}_I^{\prime }\mathbf{\Gamma }{\mathit{K}}_J,$$

with rank(Γ) = rank(Φ) = r ≤ p = min(I − 1, J − 1). The elements of Φ form a basis for the set of interaction contrasts. Define K = (K_J ⊗ K_I) so that K′vec(Ȳ) is a linear function of vec(Ȳ) without containing the main effects (because K′vec(L) = 0). Hence, E[K′vec(Ȳ)] = K′vec(Γ) = vec(Φ) and $\text{Var}({\mathit{K}}^{\prime }\text{vec}(\overline{\mathit{Y}}))={\mathit{K}}^{\prime }\text{Diag}({\delta }_{ij}^2)\mathit{K}$.

The goal is to maximize the likelihood function of Ȳ subject to the constraint rank(Γ) = r, which is the same as computing

$$S(r)=\underset{\text{rank}(\mathbf{\Phi })=r}{min}{\left[{\mathit{K}}^{\prime }\text{vec}(\overline{\mathit{Y}})-\text{vec}(\mathbf{\Phi })\right]}^{\prime }{\mathit{W}}^{-1}\left[{\mathit{K}}^{\prime }\text{vec}(\overline{\mathit{Y}})-\text{vec}(\mathbf{\Phi })\right],$$ (4)

where $\mathit{W}={\mathit{K}}^{\prime }\text{Diag}({\delta }_{ij}^2)\mathit{K}$, and ${\delta }_{ij}^2$ is replaced by ${\widehat{\delta }}_{ij}^2$ in (3). The constrained ML estimate Φ̂ is the solution to S(r). Due to the weight matrix W, a direct SVD solution does not exist. Instead, Φ̂ can be obtained by criss-cross regression [Gabriel and Zamir 1979]. Write Φ = AB′, where A and B are (I − 1) × r and (J − 1) × r, respectively. Now (4) becomes a standard weighted least squares problem. Given A⁽ⁿ⁾, B is updated as

$${\mathit{B}}^{(n+1)}={\left[{({\mathit{I}}_{J-1}\otimes {\mathit{A}}^{(n)})}^{\prime }{\mathit{W}}^{-1}({\mathit{I}}_{J-1}\otimes {\mathit{A}}^{(n)})\right]}^{-1}{({\mathit{I}}_{J-1}\otimes {\mathit{A}}^{(n)})}^{\prime }{\mathit{W}}^{-1}{\mathit{K}}^{\prime }\text{vec}(\overline{\mathit{Y}})$$ (5)

In turn, given B⁽ⁿ⁺¹⁾, A is updated as

$${\mathit{A}}^{(n+1)}={\left[{({\mathit{B}}^{(n+1)}\otimes {\mathit{I}}_{I-1})}^{\prime }{\mathit{W}}^{-1}({\mathit{B}}^{(n+1)}\otimes {\mathit{I}}_{I-1})\right]}^{-1}{({\mathit{B}}^{(n+1)}\otimes {\mathit{I}}_{I-1})}^{\prime }{\mathit{W}}^{-1}{\mathit{K}}^{\prime }\text{vec}(\overline{\mathit{Y}})$$ (6)

We alternate (5) and (6) until convergence of (4) is reached, and Φ̂ = ÂB̂′. The LRT statistic is S(0) − S(1), where S(0) = K′vec(Ȳ)W⁻¹K′vec(Ȳ). The asymptotic null distribution of this LRT statistic converges in distribution to the maximum root of a p–variate Wishart matrix with df = max(I −1, J −1) in balanced designs [Boik 1989]. The corresponding 95^th and 99^th percentiles of this distribution can be found in Hanumara and Thompson Jr [1968]. With unbalanced data, under the assumption that N_ij = Σ_j N_ij Σ_i N_ij/Σ_ij N_ij, the null distribution of the LRT is known to be identical to that in balanced designs. Due to correlated nature of the outcome data, these approximations are not directly applicable to our context. However, our numerical work illustrates that using this reference distribution provides a conservative approximation to the test.

Parameter Estimation based on Individual Observations

The cell-means approach provides a quick way of summarizing interaction effects for repeated measures data. In presence of confounders and other covariates, a mixed-effects regression model uses all individual observations and provides a general framework for handling repeated measurements. Let y_ijk denote the length-n_ijk observation vector for subject (i, j, k),

$${\mathit{y}}_{\mathit{ijk}}={\mu }_{ij}{\mathbf{1}}_{n_{\mathit{ijk}}}+{\mathit{Z}}_{\mathit{ijk}}{\mathit{b}}_{\mathit{ijk}}+{\mathit{e}}_{\mathit{ijk}},i=1,\dots ,I,j=1,\dots ,J,k=1,\dots ,N_{ij},$$ (7)

where μ_ij is the mean response value for the (i, j)^th cell, Z_ijk is a n_ijk × q design matrix for the random effects, e_ijk ~ (0, Σ_ijk), not depending on i, j, or k except that its size is n_ijk × n_ijk, and b_ijk is a length-q vector of subject-specific random effects, independent of e_ijk. The random effects are distributed as (0, Ψ), where Ψ is the q × q covariance matrix for the random effects. It follows that the variance-covariance matrix for y_ijk is ${\mathit{V}}_{\mathit{ijk}}={\mathit{Z}}_{\mathit{ijk}}\mathbf{\Psi }{\mathit{Z}}_{\mathit{ijk}}^{\prime }+{\mathbf{\sum }}_{\mathit{ijk}}$.

Classical Interaction Models

To avoid computationally intensive iterations associated with ML estimation for models (a)–(d), we propose a two-step regression procedure to approximate the interaction parameters. The idea is similar to Milliken and Johnson [1989], who applied a two-step regression procedure in two-way tables to estimate nonlinear interaction effects. Let X_ijk be the design matrix with dimension n_ijk × IJ that allows estimation of all plausible effects from the row and column factors. In the first step, we fit a saturated interaction model to the data using a linear mixed-effects model:

$${\mathit{y}}_{\mathit{ijk}}={\mathit{X}}_{\mathit{ijk}}\mathit{\xi }+{\mathit{Z}}_{\mathit{ijk}}{\mathit{b}}_{\mathit{ijk}}+{\mathit{e}}_{\mathit{ijk}},$$ (8)

where ξ = (μ, R₁, …, R_I−1, C₁, …, C_J−1, γ₁₁, …, _{(I−1)(J−1)})′. The log-likelihood function is

$$\ell (\mathit{\xi },\mathbf{\Psi },\mathbf{\sum })=-\frac{1}{2}\sum _{i=1}^I\sum _{j=1}^J\sum _{k=1}^{N_{ij}}\left[n_{\mathit{ijk}}log(2\pi )+log(\mid {\mathit{V}}_{\mathit{ijk}}\mid )+{({\mathit{y}}_{\mathit{ijk}}-{\mathit{X}}_{\mathit{ijk}}\mathit{\xi })}^{\prime }{\mathit{V}}_{\mathit{ijk}}^{-1}({\mathit{y}}_{\mathit{ijk}}-{\mathit{X}}_{\mathit{ijk}}\mathit{\xi })\right].$$ (9)

The variance components are estimated by restricted maximum likelihood (REML) [Patterson and Thompson 1971], and the I × J fixed effect estimates are

$$\widehat{\mathit{\xi }}=\sum _{i=1}^I\sum _{j=1}^J\sum _{k=1}^{N_{ij}}{({\mathit{X}}_{\mathit{ijk}}^{\prime }{\widehat{\mathit{V}}}_{\mathit{ijk}}^{-1}{\mathit{X}}_{\mathit{ijk}})}^{-1}{\mathit{X}}_{\mathit{ijk}}^{\prime }{\widehat{\mathit{V}}}_{\mathit{ijk}}^{-1}{\mathit{y}}_{\mathit{ijk}}.$$ (10)

In the second step, we extract the main effect estimates from ξ̂ and compute the residuals

$${\mathit{r}}_{\mathit{ijk}}={\mathit{y}}_{\mathit{ijk}}-\widehat{\mu }{\mathbf{1}}_{n_{\mathit{ijk}}}-{\widehat{R}}_i{\mathbf{1}}_{n_{\mathit{ijk}}}-{\widehat{C}}_j{\mathbf{1}}_{n_{\mathit{ijk}}}.$$ (11)

Since the interaction term of Tukey’s and Mandel’s models involves main effects, we perform a second regression (without intercept) where the residuals r_ijk are treated as the response variable and the respective specific forms of main effect estimates are treated as the regressors to obtain the corresponding slope estimates. The second-step regression equations for models (a)–(c) are:

$${\mathit{r}}_{\mathit{ijk}}=\theta {\widehat{R}}_i{\widehat{C}}_j{\mathbf{1}}_{n_{\mathit{ijk}}}+{\mathit{\epsilon }}_{\mathit{ijk}}$$ (12)

$${\mathit{r}}_{\mathit{ijk}}={\lambda }_i{\widehat{C}}_j{\mathbf{1}}_{n_{\mathit{ijk}}}+{\mathit{\epsilon }}_{\mathit{ijk}}$$ (13)

$${\mathit{r}}_{\mathit{ijk}}={\widehat{R}}_i{\eta }_j{\mathbf{1}}_{n_{\mathit{ijk}}}+{\mathit{\epsilon }}_{\mathit{ijk}}$$ (14)

with ε_ijk ~ (0, Ω_{ε(nijk×nijk)}). One can select a covariance structure Ω_ε depending on the criterion of model fitting. Note that parameter constraints in (2) are handled in the regressors, and there are I −1 and J −1 regression equations in (13) and (14), respectively. For model (d), we first obtain the estimates of λ_i and η_j then compute the second-step residuals using {R̂_i, Ĉ_j, λ̂_i, η̂_j}, and finally estimate θ (see Supporting Information for details).

AMMI1 Model

Given that the interaction structure of model (e) is derived from a SVD of the matrix of residuals after removing additive effects, we propose to perform SVD to the saturated Γ̂ matrix as obtained from (10). The resulting largest singular value of Γ̂ is an approximation of d̂₁. The corresponding left and right singular vectors are approximations of α̂_i and β̂_j, for i = 1, …, I, j = 1, …, J.

Remark 1

We evaluated the bias and mean squared error (MSE) properties of the two-step regression estimators through simulation. The empirical results indicate that the two-step regression estimators appear to be unbiased, even under misspecified correlation structures (Table S.2 in Supporting Information). The estimator of d₁ for AMMI1 models (obtained by SVD of the estimated saturated interaction matrix), however, slightly over-estimates d₁.

Parametric Bootstrap using a LRT Pivot

We construct a LRT statistic based on the non-iterative two-step regression estimates. First, the log-likelihood under the null hypothesis is obtained by fitting an additive mixed model (denoted as ℓ̂₀), and the log-likelihood under the alternative hypothesis is obtained by the previous two-step regression procedure (denoted as ℓ̂₁). Specifically for calculating ℓ̂₁, we extract μ̂, R̂_i, and Ĉ_j from (10) and obtain the interaction effect estimates from the second-step regression of residuals on a pre-specified structure of main effect estimates for models (a)–(d). Subsequently, an approximate LRT pivot is created, Λ̂ = −2(ℓ̂₀ − ℓ̂₁). Because the parameter estimates used in Λ̂ are not proper ML estimates, the resulting test statistic does not have a standard asymptotic distribution. We use parametric bootstrap to elicit the null distribution of this LRT-based pivot. Since permuting Y or subjects across the configurations of G and E factors can remove both interaction and main effects, we generate pseudo data ${\mathit{y}}_{\mathit{ijk}}^{\ast }$ under the null hypothesis of no interaction while preserving the main effects using the model: ${\mathit{y}}_{\mathit{ijk}}^{\ast }=\widehat{\mu }{\mathbf{1}}_{n_{\mathit{ijk}}}+{\widehat{R}}_i{\mathbf{1}}_{n_{\mathit{ijk}}}+{\widehat{C}}_j{\mathbf{1}}_{n_{\mathit{ijk}}}+{\mathit{Z}}_{\mathit{ijk}}{\mathit{b}}_{\mathit{ijk}}^{\ast }+{\mathit{e}}_{\mathit{ijk}}^{\ast }$, where ${\mathit{b}}_{\mathit{ijk}}^{\ast }~N(0,\widehat{\mathbf{\Psi }}),{\mathit{e}}_{\mathit{ijk}}^{\ast }~N(0,\widehat{\mathbf{\sum }})$. Ψ̂ and Σ̂ are REML estimates from the saturated mixed-effects model in (8). For each simulated null sample, a Λ̂ is computed. Repeating the procedure for a large number of times (e.g., we use 1000) provides an approximate distribution of Λ̂ under H₀. Finally, an empirical p-value is obtained by calculating the proportion of all Λ̂ that exceeds the observed Λ̂.

Simulation Settings

We carried out a series of simulation studies to examine the following properties of the proposed tests: [1] type I error for the LRT using cell means (LRT-CM) and for the parametric bootstrap approach with the LRT-based statistic Λ̂ (LRT-PB); [2] power comparison of AMMI1 to saturated interaction model if AMMI1 model holds; [3] power comparison of LRT-PB to LRT-CM; and [4] performance of models (a)–(e) across classical interaction structures. In addition, we compared relative performances of our proposed tests to existing strategies for testing GGI or GEI, including the standard saturated interaction model and the naive cell mean approach of Barhdadi and Dubé [2010] (not accounting for correlated data). Furthermore, we evaluated the performance of each model in detecting GGI with repeated measures on a quantitative trait under 12 epistasis patterns.

Individual-level outcome Y with n_ijk repeated measures on subject (i, j, k) were generated for a total of N subjects. The general description of the model is given by

$${\mathit{y}}_{\mathit{ijk}}={\mu }_{ij}{\mathbf{1}}_{n_{\mathit{ijk}}}+b_{\mathit{ijk}}{\mathbf{1}}_{n_{\mathit{ijk}}}+{\mathit{e}}_{\mathit{ijk}},k=1,\dots ,N_{ij},$$ (15)

where ${\mathit{e}}_{\mathit{ijk}}~\mathcal{N}(\mathbf{0},{\sigma }_e^2\mathit{I}),b_{\mathit{ijk}}~\mathcal{N}(0,{\sigma }_b^2)$, and {e, b} are mutually independent. Cell means were first generated according to models (a)–(e), and the data vector for each individual with a given mean and a covariance structure was generated from a multivariate normal distribution. The interaction terms in all models were scaled in such a way that they contributed to 15% of the total variation explained by the model, and the remainder was attributed to row and column main effects. While simulating data under an AMMI1 model, we assigned the entire contribution due to interaction effect to the first interaction factor.

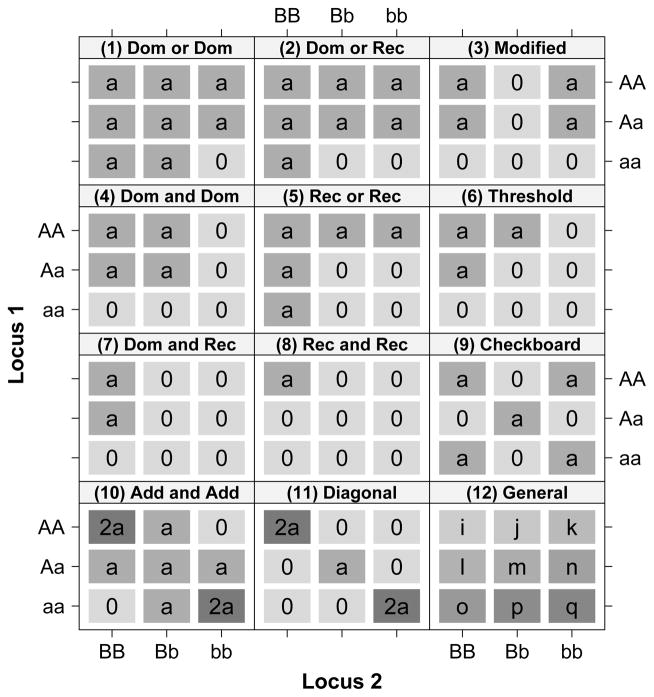
To evaluate model performance in terms of detecting common patterns of GGI, data were simulated according to 12 epistasis models [Barhdadi and Dubé 2010]: (1) dominant or dominant; (2) dominant or recessive; (3) modified model; (4) dominant and dominant; (5) recessive or recessive; (6) dominant and recessive; (7) recessive and recessive [(1)–(7) from [Jung et al. 2009]]; (8) checkerboard; (9) diagonal [(8) and (9) from [Culverhouse et al. 2004]]; (10) threshold; (11) additive and additive; and (12) a general model. The additive and additive model and the general model are purely epistatic models, that is, the quantitative trait depends on genotype from two loci in the absence of any marginal effects. Figure 1 gives a visual representation of the true cell means for the 12 epistasis patterns in our simulation.

Fig. 1.

Cell means (α = 0.5) for12 common epistasis models in the simulation setting

We considered 3 × 3 table settings for all simulations to mimic studies of GGI. In addition, we evaluated the power of AMMI1 models in 9 × 5 table settings as described in [2]. For 3 × 3 tables, minor allele frequencies for the two loci were set at 0.3 and 0.4, respectively. For 9 × 5 tables, combinations of the two loci with allele frequencies 0.3 and 0.4 (resulting in nine categories) along with an environmental exposure with five levels (each with probability 0.2) were considered. Hardy-Weinberg equilibrium was assumed to hold for both loci. We set (i) σ² = 8, ρ = 0.5 (or ${\sigma }_b^2={\sigma }_e^2=4$) and (ii) σ² = 16, ρ = 0.5 (or ${\sigma }_b^2={\sigma }_e^2=8$). We also considered ρ = {0.2, 0.5, 0.8} for the power evaluation of AMMI1 models. Under each simulation setting, 1000 datasets were generated with 1800 and 3600 subjects for 3 × 3 and 9 × 5 tables, respectively. The number of repeated measurements per subject was generated from a multinomial distribution similar to the analysis dataset: n_ijk ∈ {2, 3, 4, 5, 6}, n = {n_ijk : 1 ≤ k ≤ N_ij, 1 ≤ i ≤ I, 1 ≤ j ≤ J} ~ mult(N, p), p = (0.15, 0.2, 0.3, 0.2, 0.15). This is equivalent to generating outcome data missing completely at random.

RESULTS

Simulation Findings

Type I error

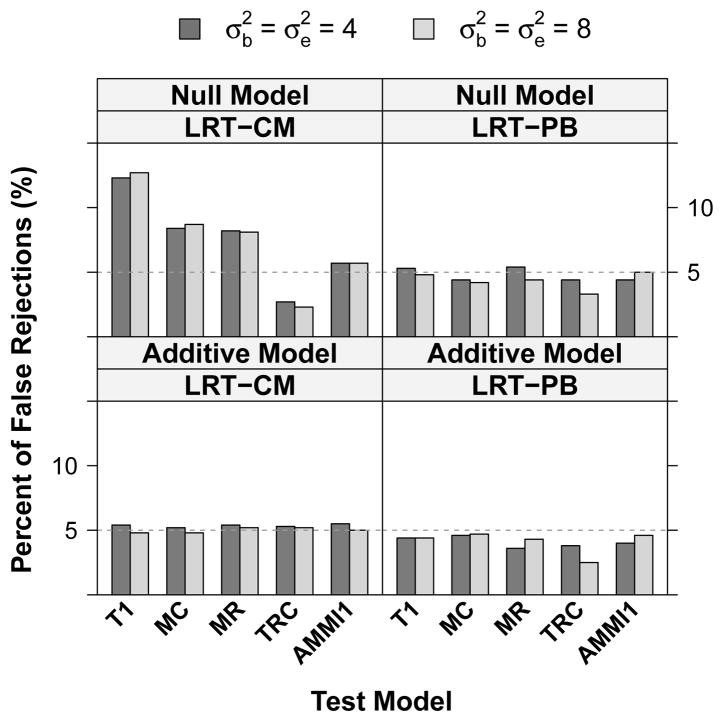
We generated data under an additive model, H₀ :γ_ij = 0 (while R_i, C_j ≠ 0) as well as under a completely null model, H₀ : γ_ij = R_i = C_j = 0 for all i, j. Figure 2 shows the percentage of false rejections for the five interaction models from 1000 simulations at 5% significance level. Under the additive model, the type I error rates for all models using LRT-CM and LRT-PB are maintained at the nominal 5%. Under the null model, type I error rates for models (a)–(e) using LRT-PB as well as for model (e) using LRT-CM are still maintained at 5%. LRT-CM for classical models (a)–(d), however, are either too liberal or too conservative (>12% for model (a), >8% for models (b) and (c), and <3% for model (d)).

Fig. 2.

Type I error for the five interaction tests in a 3 × 3 array setting using the likelihood ratio test with the cell-mean approach (LRT-CM) and the parametric bootstrap test (LRT-PB). 1000 simulation datasets are generated under an additive model (only main effects) and under a completely null model (no main or interaction effects). T1 = Tukey’s one degree-of-freedom non-additivity test (a), MC = Mandel’s column model (b), MR = Mandel’s row model (c), TRC = Tukey’s row-column model (d), AMMI1 = model (e).

Power

The gain in power using an AMMI1 model compared to a saturated interaction model increases as the table dimension increases. In the 3 × 3 array setting, saturated models (4 df for the interaction effects) appear to have similar power to AMMI1 models (data not shown). In the 9 × 5 array setting, AMMI1 models using LRT-CM and LRT-PB clearly have greater power than saturated models when the true interaction only has one interaction factor (Figure 3). The highest observed gain in power for AMMI1 using LRT-PB compared to the saturated model (32 df for the interaction effects) is 11% under three correlation settings. As ρ increases from 0.2 to 0.8, AMMI1 begins to show power gain across a wider range of d₁.

Fig. 3.

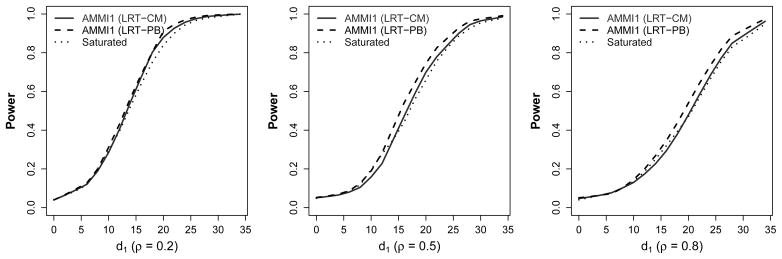
Empirical power (or true positive rate) of AMMI1 model (at α=0.05) using the likelihood ratio test with the cell-mean approach (LRT-CM) and the parametric bootstrap test (LRT-PB), and a saturated interaction model in a 9 × 5 array setting with σ² = 8 and ρ = 0.2, 0.5, and 0.8.

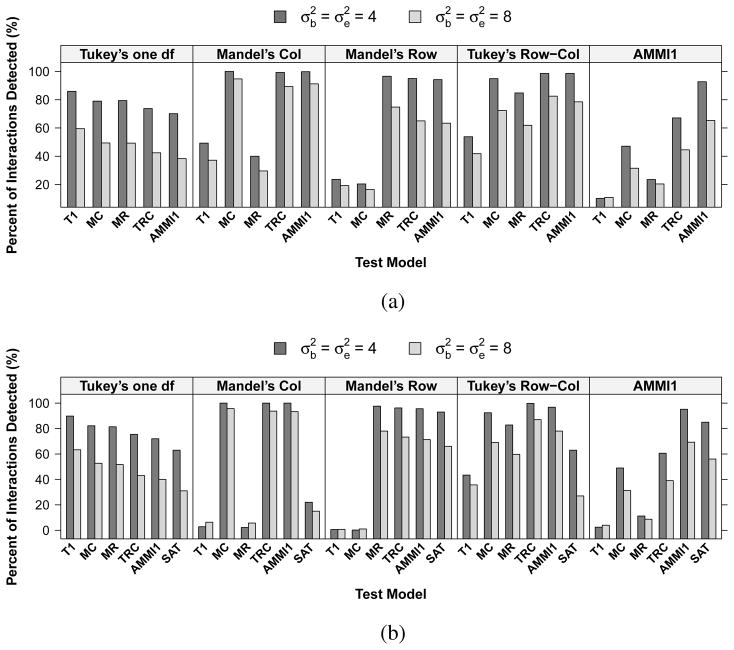
Figure 4 shows the percentage of interactions detected by each test across a set of true simulation models. Overall, the power of LRT-PB is increased by 2–5% compared to LRT-CM. When Tukey’s model (a) is the true model, all other models are able to capture some interactions (70–82% when ${\sigma }_b^2={\sigma }_e^2=4$, 38–53% when ${\sigma }_b^2={\sigma }_e^2=8$). Under Mandel’s column model (b), Tukey’s row-column (d) and AMMI1 (e) are able to detect the interaction (both power >99% when ${\sigma }_b^2={\sigma }_e^2=4$ and >90% when ${\sigma }_b^2={\sigma }_e^2=8$); whereas Tukey’s 1-df model (a) and Mandel’s row model (c) have very low power (both <50% with LRT-CM and <6% with LRT-PB). Similar properties are observed for simulations under Mandel’s row model (c). With Tukey’s row-column model (d) being the simulation model, all alternatives, except model (a), are able to detect the interaction with power greater than 60%. When the true model is an AMMI1 model (e), models (a)–(c) have relatively low power to detect interaction (<50% when ${\sigma }_b^2={\sigma }_e^2=4$ and <32% when ${\sigma }_b^2={\sigma }_e^2=8$). Saturated model has lower power than AMMI1 in most cases.

Fig. 4.

Percentage of interactions detected by different interaction models in the simulation settings corresponding to a 3 ×3 array. Results are based on (a) the likelihood ratio test with the cell-mean approach (LRT-CM) and (b) the parametric bootstrap test (LRT-PB) with test results of using a saturated model for interaction as a comparison. The top label within each box represents the true simulation model. The horizontal-axis labels indicate the models used for testing interaction. T1 = Tukey’s one degree-of-freedom non-additivity test (a), MC = Mandel’s column model (b), MR = Mandel’s row model (c), TRC = Tukey’s row-column model (d), AMMI1 = model (e), SAT = saturated interaction model.

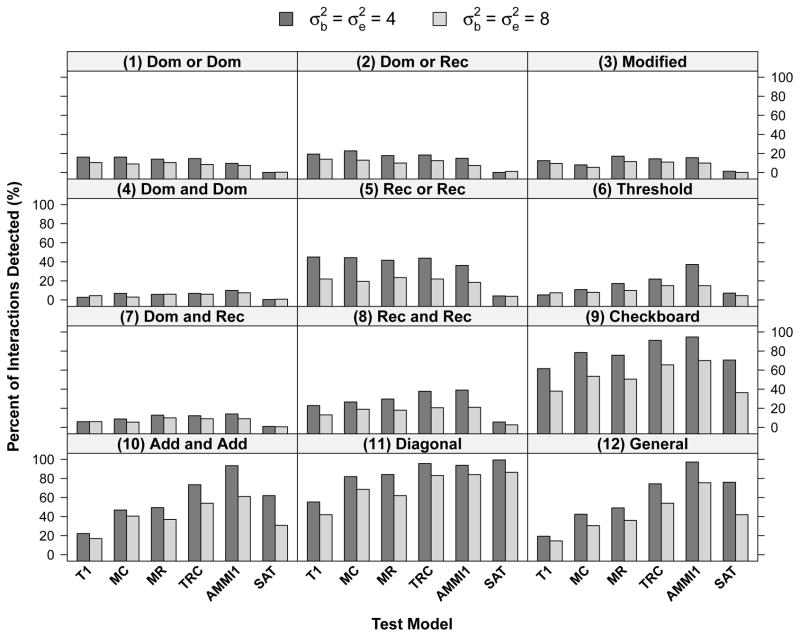
Figure 5 shows the percentages of interaction detected by six interaction models using LRT-PB under 12 common epistasis models. Given the robust performance of model (e), AMMI1 model appears to be a desirable approach for evaluating common epistasis structures, especially when main effects do not exist (e.g., epistasis models (10) and (12)).

Fig. 5.

Percentage of interactions detected (or null hypotheses of no interaction rejected) by each of the interaction models using parametric bootstrap test (LRT-PB) and a saturated model for interaction under 12 common epistasis models. T1 = Tukey’s one degree-of-freedom non-additivity test (a), MC = Mandel’s column model (b), MR = Mandel’s row model (c), TRC = Tukey’s row-column model (d), AMMI1 = model (e), SAT = saturated interaction model.

We also compared our proposed methods with those in Barhdadi and Dubé [2010] in terms of type I error and power. As expected, the tests in Barhdadi and Dubé [2010] assuming balanced data structure and not accounting for within-subject correlation yield inflated type I error (especially for Tukey’s and Mandel’s models) and lower power (see Figure S.2 in the Supporting Information).

Application to the Normative Aging Study (NAS)

The NAS is a multidisciplinary longitudinal study initiated by the U.S. Veterans Administration in 1963 [Bell et al. 1966]. We analyzed 671 participants from a subset of the NAS data who were successfully genotyped for the HFE gene and had baseline measurements of tibia bone lead (a measure of cumulative lead exposure) [Zhang et al. 2010]. The analysis goal was to investigate effect modification by the different HFE alleles on the association between lead exposure and pulse pressure (PP), which is a strong predictor of heart problems for older adults. Since 1991, data had been collected every 3–5 years until 2011 with a median follow-up time of 12 years, including physical examination, blood pressure and laboratory measurements, and questionnaire data. The majority (97%) of the participants were Caucasian. The average age was 66.29 ± 7.14 (range 48–93) at the time of tibia bone lead measurement. More than 96% of subjects had repeated measurements on blood pressure, and over 65% of them had at least four measurements during the study period contributing to a total of 2914 observations.

Two major mutations in the HFE gene (C282Y and H63D mutations) were considered for analysis following Zhang et al. [2010]. Let (AA, Aa, aa) and (BB, Bb, bb) denote wild type, having one variant allele, and having two variant alleles for C282Y and H63D, respectively. As a result of small sample sizes in certain homozygote genotypes (N=5 for aaBB, N=17 for AAbb) and compound heterozygotes (N=14 for AaBb and N=0 for Aabb, aaBb, aabb), we were unable to test for interaction between the two loci. Since the research interest was to compare three mutually exclusive groups (wild type, H63D, C282Y), 14 subjects with compound heterozygotes (AaBb) were excluded from analysis. Consequently, the HFE genotypes were classified into three categories for analysis: AABB, AaBB or aaBB, and AABb or AAbb. The environmental exposure (cumulative lead) was a continuous variable, but to illustrate the proposed methods, we categorized bone lead levels into three groups (Low: ≤15, Medium: (15, 25], and High: >25 μg/g). Table 1 lists the observed cell means of PP and the number of participants for each G × E configuration.

Table 1.

Cell means corresponding to pulse pressure and number of participants (in parentheses) for each configuration of the HFE genotypes and bone lead levels in the Normative Aging Study

HFE gene	Tibia lead levels (μg/g)
	Low: ≤ 15	Medium: > 15 and ≤ 25	High: > 25
Wild-type (AABB)	52.94 (161)	56.16 (149)	56.61 (131)
C282Y (AaBB or aaBB)	51.89 (23)	56.65 (39)	59.10 (23)
H63D (AABb or AAbb)	52.58 (54)	57.72 (53)	64.49 (38)

We applied LRT-CM and LRT-PB to test this GEI effect. According to the Akaike information criterion (AIC) for model fit, we chose a random-intercept mixed-effects model for analysis:

$${\mathit{y}}_{\mathit{ijk}}={\mu }_{ij}{\mathbf{1}}_{n_{\mathit{ijk}}}+b_{\mathit{ijk}}{\mathbf{1}}_{n_{\mathit{ijk}}}+{\mathit{e}}_{\mathit{ijk}},\text{with}{\mu }_{ij}=\mu +R_i+C_j+{\gamma }_{ij},$$ (16)

where $b_{\mathit{ijk}}~\mathcal{N}(0,{\sigma }_b^2)$ is the random-effect coefficient for subject (i, j, k), ${\mathit{e}}_{\mathit{ijk}}~\mathcal{N}(\mathbf{0},{\sigma }_e^2\mathit{I})$ is the random error term, and { ${\sigma }_b^2,{\sigma }_e^2$} are assumed to be constant across individuals. We also considered the model adjusting for baseline age, time since baseline in years, and squared time.

$${\mathit{y}}_{\mathit{ijk}}={\mu }_{ij}{\mathbf{1}}_{n_{\mathit{ijk}}}+{\beta }_1{\text{Age}}_{\mathit{ijk}}+{\beta }_2{\mathbf{Time}}_{\mathit{ijk}}+{\beta }_3{\mathbf{Time}}_{\mathit{ijk}}^2+b_{\mathit{ijk}}{\mathbf{1}}_{n_{\mathit{ijk}}}+{\mathit{e}}_{\mathit{ijk}}.$$ (17)

For LRT-CM adjusting for covariates, cell means were formed by the residuals from a regression of the outcome on covariates other than G and E. This is an ad hoc approach for covariate adjustment since correlations of covariates with G and E are ignored. In general, LRT-PB based on a full regression model with G, E, and covariates will yield more power.

Results for GEI

Table 2 shows the p-values for testing HFE × Lead Exposure interaction using LRT-CM and LRT-PB and the saturated interaction model. Using LRT-CM without adjustment for any covariate, the interaction was significant in all four classical models (p < 0.05), whereas (e) gave a p-value between 0.05 and 0.10. After adjusting for the covariates, model (e) detected the interaction using LRT-CM (p < 0.01). Regardless of covariate adjustment, the interaction was significant for models (a)–(e) using LRT-PB (p < 0.01), and also for the saturated interaction model (p < 0.02). P-values for the GEI effect decreased further for all tests with adjustment for baseline age, time since baseline, and squared time. Given the significant GEI on all models, this interaction may be real and not model dependent.

Table 2.

Analysis results of GEI between HFE genotypes and tibia lead levels in the Normative Aging Study (N=671) using the proposed likelihood ratio test with cell means (LRT-CM) and the parametric bootstrap (LRT-PB) approach (1000 replicates simulated under the null hypothesis)

Model	Hypothesis	p-value
		LRT-CMa	LRT-CMb	LRT-PBa	LRT-PBb
Model (a)	H0 : θ = 0	0.008	0.002	0.002	0.003
Model (b)	H0 : λi = 0 (Lead)	0.029	0.007	0.009	0.008
Model (c)	H0 : ηj = 0 (HFE)	0.015	0.002	0.002	0.001
Model (d)	H0 : θ = λi = ηj = 0	0.035	0.005	0.007	0.002
Model (e)	H0 : d1 = 0	<0.10	<0.01	0.009	0.002
Saturated Model	HFE × Lead			0.015	0.006

^aNo covariate adjustment.

^bAdjusting for baseline age, time since baseline, and squared time. For LRT-CM, residuals from a regression of pulse pressure on all other covariates except lead levels and genotype were used to form the cell means.

According to the SVD of Γ̂_G×E under a saturated interaction model with covariate adjustment, the first and second characteristic roots of Γ̂_G×E were d̂₁ = 5.65 and d̂₂ = 1.24, respectively (Table S.3). The first interaction factor contributed to over 80% of the total contribution to the interaction term. The association between PP and bone lead levels was strongest among H63D variant (AABb or AAbb) carriers, compared to C282Y variant (AaBB or aaBB) carriers and wild-type (AABB) participants. Based on the saturated interaction model estimates, the estimated difference in mean PP for H63D variant carriers with High versus Low lead levels was 9.6 mmHg [95% confidence interval (CI), 0.43–14.83 mmHg]. The same estimated differences were 3.52 mmHg [95% CI, −3.39–10.43 mmHg] and −0.33 mmHg [95% CI, −2.95–2.29 mmHg] for C282 variant carriers and wild-type participants, respectively. Although the underlying mechanisms are poorly understood, the common prooxidant and proinflammatory effects shared by lead exposure and H63D HFE, especially through increased production of monocyte chemo-attractant protein-1 [Zhang et al. 2010], may explain the observed H63D HFE-lead interaction.

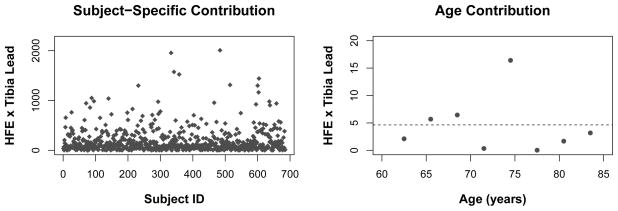
Subject-specific and Age-specific Contributions to GEI

Using the estimates of singular vectors (α̂_im, β̂_jm), we investigated subject-specific and age-specific contributions to GEI in the first and the second interaction factors (m = 1, 2) via the sum of squared deviations [Mukherjee et al. 2012]. Briefly, the variation due to subject (i, j, k) can be calculated by d̂_ijkm = α̂_imβ̂_jmr̂_ijk., where r̂_ijk. is the mean of n_ijk subject-level residuals from (11) after removing main effects. The variation in the contribution of subject (i, j, k) is then (d̂_ijkm − d̂._m)², where d̂._m = Σ_iΣ_jΣ_k d̂_ijkm/N. For the age-specific contribution, we constructed eight three-year age intervals. The first and last intervals contained observations from those who were younger than 65 and who were 83 or older, respectively. The cell means of PP and numbers of participants for genotypes and lead levels based on different age categories are presented in Figure S.3 in the Supporting Information. The contribution due to the t^th age interval is calculated as d̂_tm = Σ_iΣ_j α̂_imβ̂_jmr̂_tij., where r̂_tij. is the average of residuals (11) in the t^th age interval among individuals in the (i, j)^th cell, t = 1, …, 8. The variation in the contribution of the t^th interval is (d̂_tm − d̂._m)², where ${\widehat{d}}_{.m}={\sum }_{t=1}^8{\widehat{d}}_{tm}/8$.

Figure 6 displays subject-specific contributions from the 671 individuals (left panel) and contributions of eight age intervals to the first interaction factor of GEI (right panel). The plot indicates that the modifying effect of the HFE gene on the effect of cumulative lead exposure on PP spiked around age 75. This was due to the fact that the mean difference in PP between the Low and the High bone lead groups became largest in that age interval with H63D (AABb or AAbb), whereas the difference in PP among those with wild-type of HFE (AABB) was the smallest. A stratified analysis by baseline age also indicates time-dependent evidence of interaction effects (see Supporting Information). Figure S.4 shows patterns corresponding to the second interaction factor with substantially less subject-specific and age-specific variability for the GEI. Although these graphical diagnostics do not establish a statistical significance of a G × E × Time term, they provide important insight into longitudinal features of the interaction factors.

Fig. 6.

Subject-specific contributions (left) and age-specific contributions (right) to the first interaction factor in the HFE × Lead interaction based on the Normative Aging Study data.

DISCUSSION

We have proposed new likelihood ratio tests for GGI and GEI effects in longitudinal cohort studies using a sparse representation of interaction structure via Tukey’s and Mandel’s models as well as AMMI1 models. AMMI1 appears to be a robust and flexible model in detecting interaction effects across a spectrum of interaction structures. Moreover, it is relatively powerful in detecting certain epistasis structures with no appreciable main effects but potential interaction. In contrast, Tukey’s and Mandel’s models fail to detect interactions if the interaction structure is misspecified.

Both of our approaches require prior assumptions of the mean structure under the null hypothesis of no interaction and an underlying correlation structure for within-subject measurements. When either part of the model is misspecified, the power and the false rejection rate might be affected. Although this is a generic limitation of parametric modeling, we performed additional simulations to evaluate the influence of misspecification of covariance structure on the proposed tests. We generated data under several common correlation structures (e.g., compound symmetry, autoregressive, unstructured) and analyzed interactions assuming a different correlation structure. The results show that under a misspecification of covariance structure, type I error rates are maintained for LRT-PB but can be slightly inflated for LRT-CM.

In our simulation studies, we did not see a vast difference in the power between LRT-CM and LRT-PB. The correlation across repeated measurements in the LRT-CM approach is accounted for by the weight matrix W. Therefore, the test is not based on naive subject-level averages as in Mukherjee et al. [2012]. The main advantage of LRT-PB is the flexible regression structure that allows all readily available mixed model estimation tools to be used.

We have focused on developing valid tests for the five interaction models, yet there are some limitations. First, a caveat of the ML estimation for classical interaction models (a)–(d) based on cell means is that when the underlying main effects are relatively small, the estimation for interaction parameters would become numerically unstable. Depending on initial values, the final converged estimates might be local ML estimates instead of global ML estimates. Second, SVD of the estimated saturated interaction matrix yields approximate estimates rather than proper ML estimates for AMMI model parameters. Our simulation results indicate that this estimator leads to slight over-estimation of d1. Nevertheless, LRT-PB for AMMI1 still maintains the nominal type I error rate and in general possesses greater power than a saturated interaction model. In addition, how to connect the parameters of the AMMI model to directly interpretable quantities for biological interactions are not clear. At this stage, AMMI model remains a screening strategy for testing non-additivity. Third, covariate adjustment was not considered in our simulation studies. In practice, one can incorporate time effect and other (time-varying) covariates with LRT-CM and LRT-PB, as we did in our data example. Lastly, to our knowledge, no replication study has examined the interaction effect between the HFE gene and cumulative lead exposure on pulse pressure. We randomly split the data in half and analyzed the two halves for GEI as an assessment of internal consistency, and the results were consistent with our findings. As discussed in Zhang et al. [2010], the conclusion from the NAS data analysis may not be generalizable to other populations given that the study population was exclusively white men. Besides, unmeasured confounding factors and interactions with other genetic polymorphisms or environmental factors were not considered.

The proposed analysis strategies are useful for detecting GGI and GEI effects in longitudinal data. A full likelihood-based approach using a general nonlinear mixed-effects model set-up would be more appealing if the appropriate test statistics and their closed form null distributions can be obtained. Further work is required to investigate specialized nonlinear optimization algorithms in the ML framework to replace the two-step estimation and to construct a valid and more efficient test. It is also important to develop a formal test for individual- and time-specific contributions to interactions, which will ultimately lead to better understanding of GGI and GEI.