Tumour Angiogenesis: The Gap between Theory and Experiments

Abstract

A common experimental technique for viewing in vivo angiogenesis utilises tumours implanted into a test animal cornea. The cornea is avascular but the tumour promotes vascularisation from the limbus and the new blood vessels can be readily observed through the transparent cornea. Many of the early mathematical models for tumour angiogenesis used this scenario as their experimental template and as such assumed that there is a large gap, of the order of 2 mm, between the tumour and neighbouring vasculature at the onset of angiogenesis. In this work we consider whether the assumption that there is a significant gap between the tumour and neighbouring vasculature is unique to intra-cornea tumour implants, or whether this characterises avascular tumour growth more generally. To do this we utilise a simple scaling argument, derive a multi-compartment model for tumour growth, and consider in vivo images. This analysis demonstrates that the corneal implant experiments and the corresponding mathematical models cannot be applied to a clinical setting.

1. Introduction

Folkman (Folkman, 1976) proposed that tumours undergo three distinct phases of growth: an initial avascular phase of slow limited growth, then an angiogenesis phase where the tumour cultivates its own blood supply, and finally a phase of rapid vascularised growth. Folkman also proposed that inhibiting angiogenesis could provide an effective anti-tumour therapy.

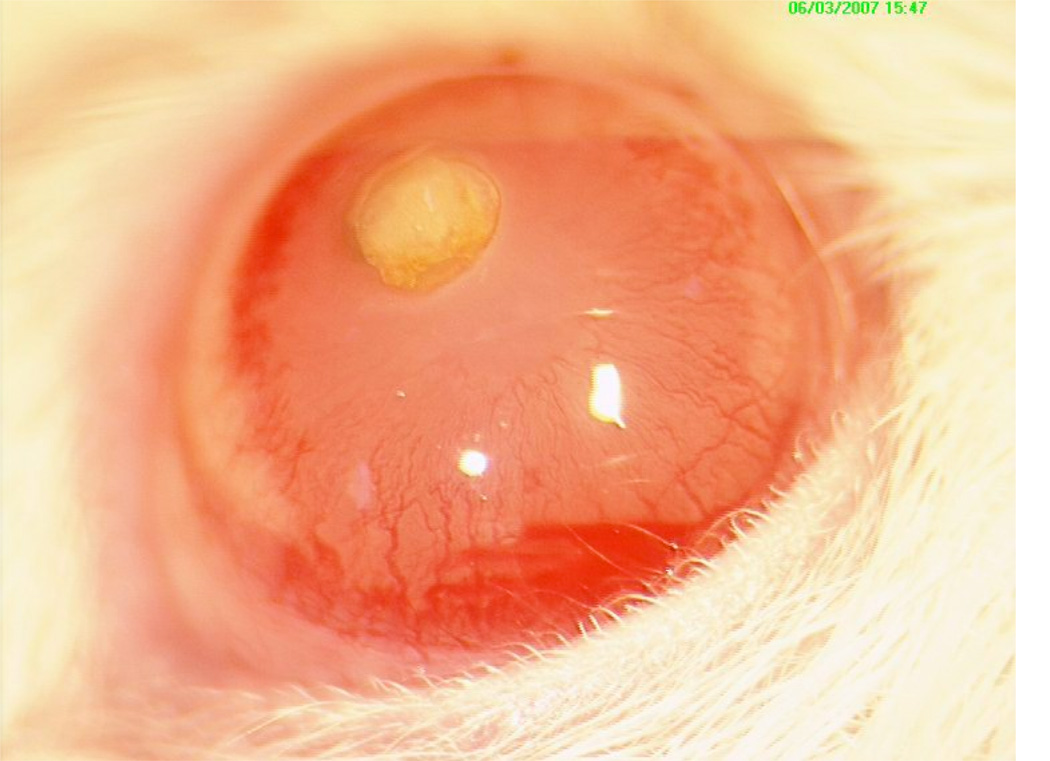
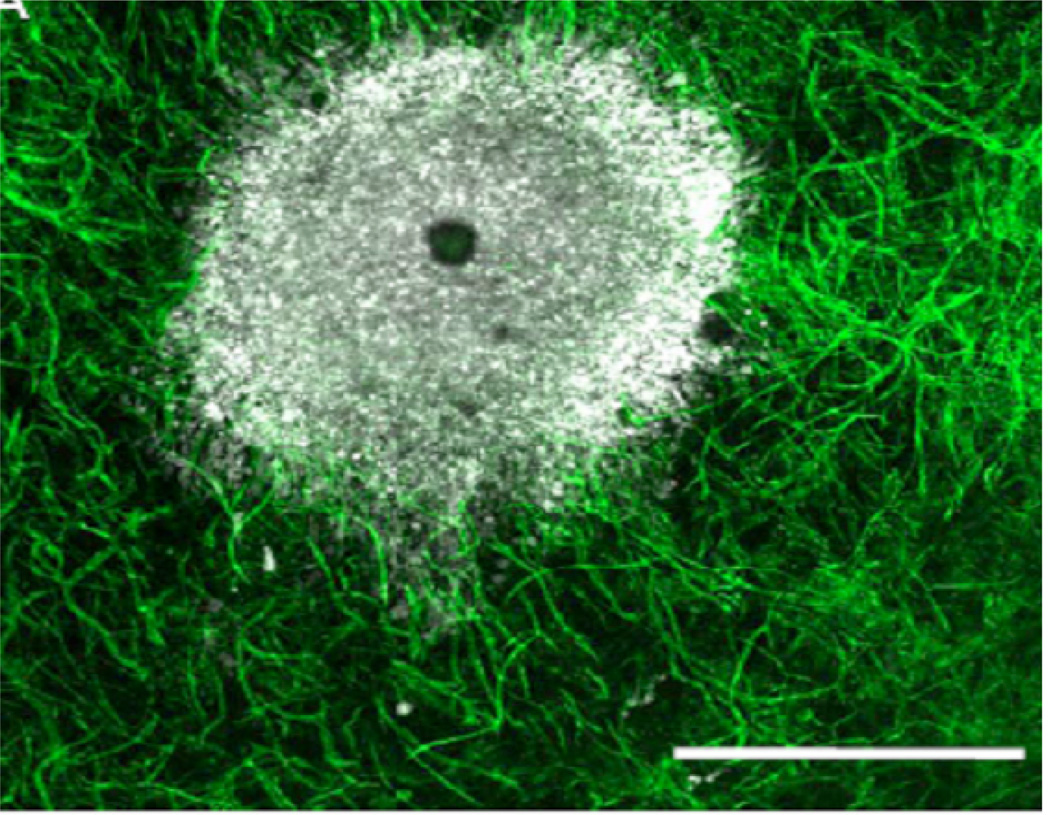
A common technique for observing in vivo angiogenesis with minimal intervention is to implant an avascular tumour into the stroma of the cornea or the aqueous humor of the eye in a test animal (Gimbrone et al., 1974; Ausprunk and Folkman, 1977; Muthukkaruppan et al., 1982). This technique allows the sprouting of capillaries towards and into the tumour to be readily observed through the transparent cornea, as exemplified by Figure 6(a). However, the cornea is a large and uniquely avascular region of tissue. Angiogenesis in this setting takes place with a distance between the tumour and neighbouring vasculature of more than a millimetre, which is much larger than the intercapillary distance typically observed in “normal” vascular tissue (Fait et al., 1998).

Figure 6.

An in vivo avascular tumour and a tumour implanted into a cornea.

(a) Angiogenesis following tumour implantation into a test animal’s cornea (Velpandian).

Many of the initial mathematical and computational models of angiogenesis have been developed to recreate the results of intra-corneal tumour implant experiments by assuming there is a significant gap, of the magnitude of the width of the cornea, between the tumour and the neighbouring vasculature (Balding and McElwain, 1985; Chaplain and Stuart, 1993; Byrne and Chaplain, 1995; Chaplain, 2000; Plank and Sleeman, 2004). These investigations have been very successful at modelling the cornea implant experiments and have been well verified in context; however it is not obvious that a significant gap should exist between a tumour and the neighbouring capillaries when an in vivo tumour grows in “normal” vascular tissue. Furthermore, while many modelling explorations have previously invoked analogous assumptions when considering normally vascularised tissue, recent imaging suggests that there is no significant gap between an in vivo avascular tumour and its neighbouring capillaries (Shubik, 1982), as illustrated by Figure 6(a).

Thus there is a need to explore this potential discrepancy between a modelling framework for vascular tumour angiogenesis and recent observations, and we firstly explore this be utilising a simple scaling argument. For the intra-cornea implant experiments to directly apply to a typical in vivo tumour the in vivo tumour must develop and/or maintain a significant gap between itself and the neighbouring capillaries. Consider a spherical tumour of radius r_tum(t), a function of time t, growing in vascular tissue. Then the volume of the tumour, V_tum, is

$$V_{\text{tum}}=\frac{4{\pi }_{\text{tum}}^3}{3}.$$

Now suppose that following the initiation of cancer in a single cell there is a region of non-cancerous cells between the tumour and the surrounding vasculature which remains of constant width as the tumour grows. To be consistent with the intercapillary distance in vascular tissue the distance between the tumour and neighbouring vasculature should be approximately 50 µm (Fait et al., 1998) and the volume of tissue in such a gap between the tumour and surrounding vasculature (in µm³), V_gap, is then

$$V_{\text{gap}}=\frac{4\pi \{{(r_{\text{tum}}+50)}^3-r_{\text{tum}}^3\}}{3}.$$

It can then be shown that the maintenance of this gap of constant width requires the non-cancerous tissue to increase in volume at the relative rate compared to cancer tissue of

$$\frac{\frac{1}{V_{\text{gap}}}\frac{\mathrm{d}{V}_{\text{gap}}}{\mathrm{d}t}}{\frac{1}{V_{\text{tum}}}\frac{\mathrm{d}{V}_{\text{tum}}}{\mathrm{d}t}}=\frac{r_{\text{tum}}{(r_{\text{tum}}+50)}^2-r_{\text{tum}}^3}{{(r_{\text{tum}}+50)}^3-r_{\text{tum}}^3}.$$

To use this result to compare the cellular proliferation rates of cancerous and non-cancerous cells we recall that tumours of radius three cell widths, which corresponds to a r_tum of approximately 80 µm (Casciari et al., 1992; Buckley et al., 1999) will typically consist of only proliferating cells (LaRue et al., 2004). For this value of r_tum, the tumour radius, we find that the non-cancerous cells must initially proliferate approximately 50% as quickly as the cancerous cells. Having non-cancerous cells proliferate half as quickly as cancerous cells may be faster proliferation than would be anticipated, but is not completely unfeasible for particularly slow growing tumours or tumours growing in tissue with a particularly high cell turnover rate. However in general no obvious mechanism exists which would upregulate non-cancerous cell proliferation to this extent. This suggests that any initial gap between the tumour and the neighbouring vasculature will begin to close as the tumour starts to grow, and will do so rapidly compared to the growth rate of the tumour.

For the mathematical models based upon the intra-cornea experiments to be more widely applicable the assumption that there is a significant gap between the tumour and neighbouring capillaries requires further validation, especially since it appears to demand extreme parameter choices in the context of a simple scaling argument. Alternatively, if no such gap exists at the onset of angiogenesis then this poses the question of what causes the gap to close.

We now consider how the distance between a typical in vivo avascular tumour and the neighbouring capillaries evolves as the tumour grows. In particular we consider whether a significant gap can be maintained between the tumour and capillaries, and if not then why does the gap close and how quickly does it do so. The results of this study will then imply whether or not the mathematical models based upon the intra-cornea implant experiments can be applied in a general context.

2. The Model

To consider how the distance between an in vivo tumour and the neighbouring capillaries evolves as the tumour grows we model the growth of an avascular tumour beginning with a small collection of cells and finishing with an avascular tumour which has reached diffusion limited saturation. We consider populations of healthy non-cancerous cells, proliferating cancerous cells, quiescent cancerous cells and necrotic cells. We assume that the system can be modelled as a continuum of cells and exhibits radial symmetry. These assumptions form an idealised model for avascular tumour growth, but one which constitutes a best case scenario for maintaining a significant gap between the tumour and neighbouring vasculature. If a significant gap between the tumour and neighbouring vasculature cannot be maintained by our idealised model, then we would not expect it to be maintained with the introduction of asymmetries which effectively reduce the gap in at least one direction.

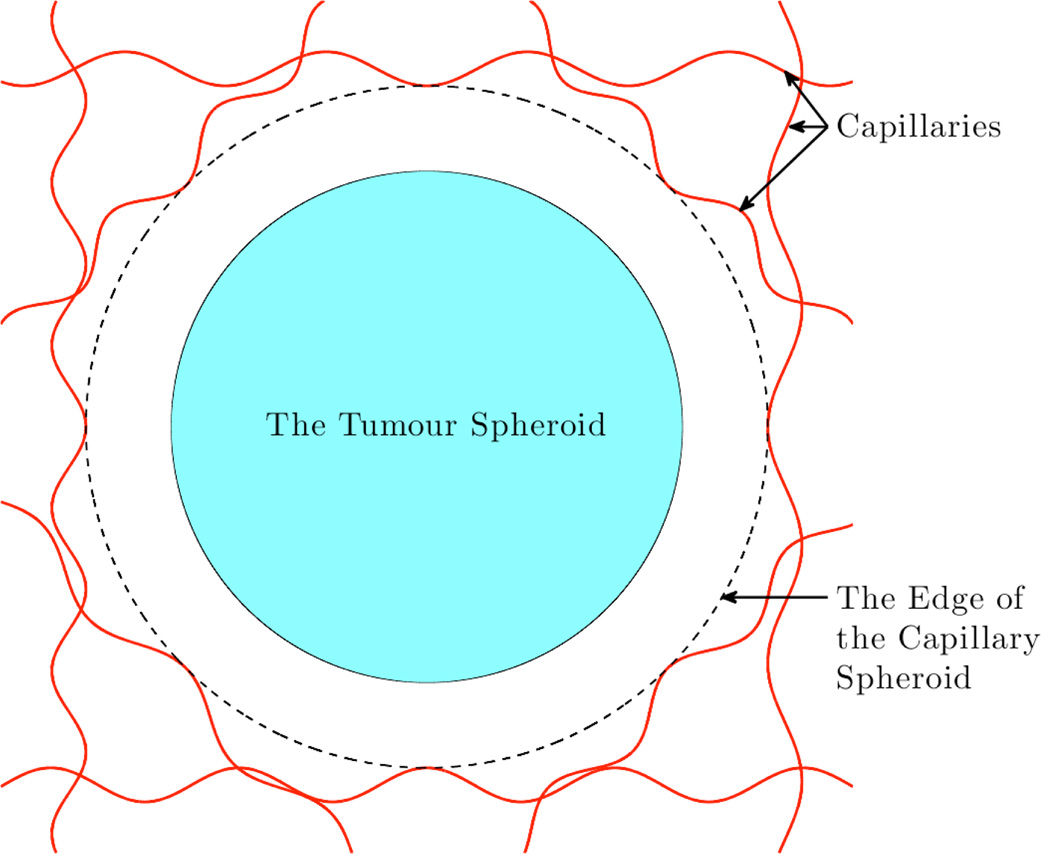
The domain of our model consists of the tumour spheroid and a region of the non-cancerous cells out-side the tumour up to the nearest capillaries, as shown in Figure 1.

Figure 1.

A schematic cross-section of the domain being considered.

We take the rates of mitosis and necrosis per proliferating cell to be k_m(c) and k_d(c) respectively, where c is the local oxygen concentration; k_m(c) is represented by a monotonically increasing function which saturates to a finite rate and k_d(c) is taken to be a monotonically decreasing non-negative function. The Michaelis-Menten based kinetics

$$k_m(c)=\frac{A}{c_m+c},\text{and}{k}_d(c)=B(1-\frac{\sigma c}{c_{\mathrm{d}}+c}),$$

where A, B, c_m, and c_d are constants exhibit these properties and have been shown to provide a good fit to the rate of oxygen consumption by cells (Lin, 1976).

We assume that proliferating cells can become quiescent and vice versa. Whilst the local oxygen concentration can be a factor in determining this change of state, other factors such as cell-cell interaction and the availability of growth factors are also likely to be influential (Mueller-Klieser, 2000). The effect of all these potential factors is too complex to be considered in detail. Instead we note that proliferating cells are generally found on the outer rim of an avascular tumour and quiescent cells are generally observed further towards the tumour’s centre (LaRue et al., 2004; Mueller-Klieser, 2000). To model this we postulate that proliferating cells tend to become quiescent if too far from the edge of the tumour and quiescent cells tend to become proliferative if too close to the edge of the tumour. We also assume that becoming quiescent does not affect a cell’s death rate. The resulting equations for the proliferating and quiescent cell populations are

$$\frac{\partial p}{\partial t}+\nabla \cdot (\underset{¯}{v}p)=[k_m(c)-k_d(c)]p-\alpha pH([S_{\text{tum}}-R]-r)+\beta qH(r-[S_{\text{tum}}-R]),\frac{\partial q}{\partial t}+\nabla \cdot (\underset{¯}{v}q)=-k_d(c)q+\alpha pH([S_{\text{tum}}-R]-r)-\beta qH(r-[S_{\text{tum}}-R]),$$

where p(r, t) and q(r, t) are the densities of proliferating and quiescent cells respectively, v(r, t) is the local cell velocity, S _tum(t) is the radius of the tumour, R is the width of the proliferating rim, α is the rate at which proliferating cells become quiescent outside the proliferating rim, β is the rate at which quiescent cells become proliferative inside the proliferating rim, and H(x) is the Heaviside function (which takes the value 0 if x is negative, and 1 if x is positive).

To investigate whether it is feasible for a significant gap to be maintained between the tumour and the vasculature as the tumour grows we also consider the dynamics of the non-cancerous cells immediately outside the tumour. We assume that non-cancerous cells proliferate more slowly than cancerous cells but otherwise exhibit similar dynamics; in particular we assume that their proliferation depends upon the local oxygen concentration and have the same shaped dependence upon the local oxygen concentration. We also assume that necrotic cells undergo linear degradation. Then the evolution of non-cancerous cells and necrotic cells is given by

$$\frac{\partial h}{\partial t}+\nabla \cdot (\underset{¯}{v}h)=(\lambda k_m(c)-k_d(c))h,\frac{\partial n}{\partial t}+\nabla \cdot (\underset{¯}{v}n)=k_d(c)(h+p+q)-vn,$$

where h(r, t), and n(r, t) are the densities of non-cancerous cells and necrotic cells respectively, λ < 1 is the relative proliferation rate of non-cancerous cells, and ν is the linear degradation rate of necrotic cells. Note that the kinetics of healthy and cancerous cells can be chosen to allow the canceous cells to proliferate at lower oxygen concentrations than the non-cancerous cells. If this is done it is found not to significantly alter our results and the model presented here constitutes the base case scenario for gap maintenance. We estimate the relative proliferation rate of non-cancerous cells, λ, using the fact that in the absence of any tumour the non-cancerous cell population should be in equilibrium. Hence λ is chosen so that in the absence of any tumour, oxygen feedback regulates cell proliferation and necrosis in exactly the way required to maintain the observed intercapillary distance.

We close our model by assuming that the cell volume fraction of tissue is constant, which implies the following equation for the local cell velocity

$$\nabla \cdot \underset{¯}{v}=\frac{V_L(\lambda h+p)k_m(c)}{𝒱}+\frac{(V_N-V_L)(h+p+q)k_{\mathrm{d}}(c)}{𝒱}-\frac{V_{N}vn}{𝒱}.$$

where V_L is the mean volume of a live cell, V_N is the mean volume of a necrotic cell, and 𝒱 is the cell volume fraction, and that oxygen diffuses out of the capillaries and is taken up by living cells. If we assume that the rate of oxygen uptake for the normal processes which keep cells alive also follows Michaelis-Menten kinetics and the rate of additional oxygen uptake required for cell proliferation is proportional to the rate of proliferation, then the evolution of the local oxygen concentration is given by

$$\frac{\partial c}{\partial t}+\nabla \cdot (\underset{¯}{v}c)=\nabla \cdot (D\nabla c)-\gamma k_m(c)(\lambda h+p)-k_n(c)(h+p+q),$$

where c(r, t) is the local oxygen concentration, k_n(c) is the Michaelis-Menten kinetics for the oxygen uptake for normal processes, γ is the constant of proportionality for additional oxygen uptake for mitosis, and D is the diffusion coefficient of oxygen.

We take the initial state of our tumour to be the largest collection of cells which can be assumed to be entirely proliferating, which is a tumour of radius equal to three cell widths (LaRue et al., 2004). We also assume that the tumour front moves with the local cell velocity, so that

$$\frac{\mathrm{d}{S}_{\text{tum}}}{\mathrm{d}t}=\underset{¯}{v}(S_{\text{tum}},t),$$

as do the neighbouring capillaries and that initially the distance between the tumour and vasculature is 50µm, which is consistent with the intercapillary distance (Fait et al., 1998). Again this assumption is the most favourable possible in terms of maintaining a gap. For our final boundary condition we assume the capillary network is a constant source of oxygen.

Where possible we estimate parameters directly from the literature, but it is necessary to estimate some parameters by performing an a posteriori analysis of parameters. To do this we numerically simulate the evolution of the tumour for different values of the unknown parameters and refine the estimates until the modelled tumour growth is consistent with observed tumour growth. In particular we ensure that our modelled tumour’s growth curve, size at saturation, relationship between necrotic core radius and tumour radius, and oxygen diffusion distance are all consistent with observed behaviour. A summary of all the parameters used in our model and their values is presented in Table 1. (Note that the oxygen concentration on the edge of our domain can be non-dimensionalised out of our model and hence need not be estimated explicitly).

Table 1.

The parameters in our model.

Parameter	Description	Value Taken	Reference
A	The maximum rate of proliferation of cancerous cells	1.4 × 10−6 s−1	Grote et al. (1977)
B	The maximum rate of necrosis of cells	2.1 × 10−6 s−1	A posteriori estimation
Ĉm	The non-dimensional critical oxygen concentration in Michaelis-Menten proliferation kinetics	0.1	A posteriori estimation
Ĉd	The non-dimensional critical oxygen concentration in Michaelis-Menten based necrosis kinetics	0.1	A posteriori estimation
σ	A parameter in the cell necrosis kinetic	0.9	A posteriori estimation
α	The rate at which proliferating cells become quiescent outside the proliferating rim	1.4 × 10−6 s−1	A posteriori estimation
β	The rate at which quiescent cells become proliferative inside the proliferating rim	1.4 × 10−6 s−1	A posteriori estimation
R	The width of the proliferating rim	80 µm	LaRue et al. (2004); Casciari et al. (1992); Buckley et al. (1999)
ν	The rate of linear decay of necrotic cells	2.8 × 10−7 s−1	A posteriori estimation
λ	The ratio of the rate of proliferation of non-cancerous cells to cancerous cells	0.3	See text
VL	The mean volume of a live cell	3 × 10−9 cm3	Landry et al. (1981, 1982)
VN	The mean volume of a necrotic cell	1.5 × 10−9 cm3	Landry et al. (1981, 1982)
𝒱	The cell volume fraction	0.66	Buckley et al. (1999)
D	The diffusion coefficient of oxygen	2 × 10−5 cm2 s−1	Grote et al. (1977); Hlatky and Alpen (1985)

Given this model we now simulate the evolution of our tumour whilst paying particular attention to the distance between the tumour and the neighbouring capillaries.

3. Results

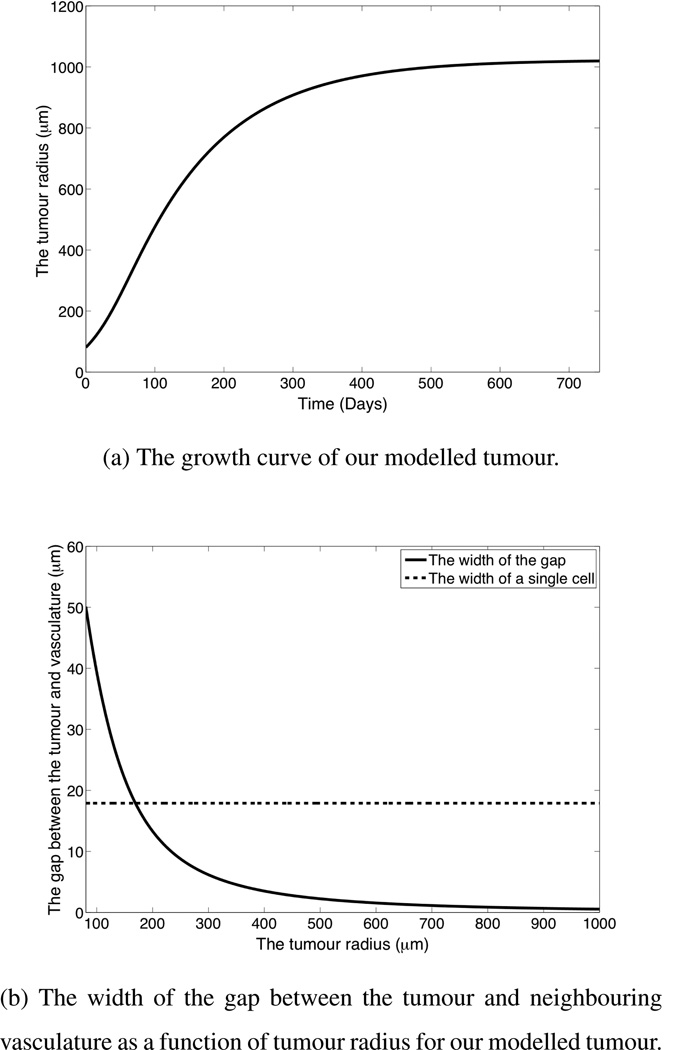
Figure 2 shows the growth dynamics for the modeled tumour. Figure 2(a) shows that our modelled tumour undergoes an initial period of exponential growth, then the growth rate slows and the tumour saturates at a radius of approximately 1 mm, which is consistent with observed tumour growth.

Figure 2.

The growth dynamics of our modelled tumour, given the parameters in Table 1.

Figure 2(b) shows the width of the gap between the tumour and the neighbouring vasculature as the tumour grows. It can be seen that the width of the gap decreases significantly as the tumour grows and the capillaries effectively reach the surface of the tumour well before the tumour growth saturates. Note that the ability of the edge of the tumour to reach the surrounding vasculature relies on the implicit assumption that there to be no obstruction lying between the tumour and vasculature. This assumption is likely to be valid when the tumour is a secondary metastasis, but may not be valid if the tumour is a primary tumour with a basement membrane separating the surrounding vasculature from the tumour.

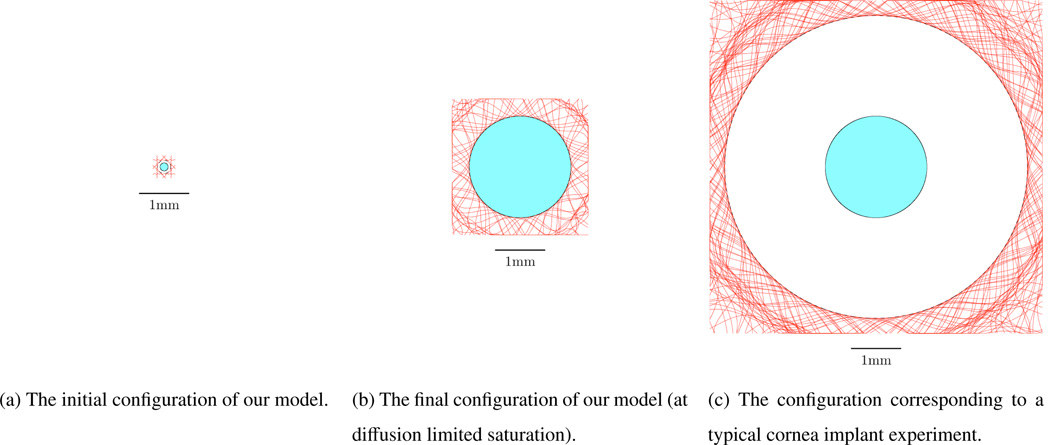
To further highlight this we compare the configurations of the initial state of our modelled tumour, the final state of our modelled tumour, and a typical tumour following an intra-cornea implant in Figure 3. Each of the schematics in Figure 3 is on the same scale with a 1mm scale bar shown. In Figure 3(a) there is initially a small gap of width 50 µm between our modelled tumour and neighbouring capillaries. In Figure 3(b) it can1 be seen that when our modelled tumour has grown to its saturated size, as given by diffusion limited control, there is effectively no gap between the tumour and the vasculature. However, in Figure 3(c) it can be seen that following tumour implantation into the cornea there is a large gap between the tumour and the vasculature. The difference between Figures 3(b) and 3(c) is marked and highlights that the results of our model conflict with observed angiogenesis in the corneal implant experiments where capillaries are seen to sprout towards and into an avascular tumour.

Figure 3.

A schematic comparison of the configurations of the tumour corresponding to (a) the initial conditions taken in our model, (b) the final state of our modelled tumour, and (c) a typical tumour following implantation into the cornea, each to scale with a 1mm scale bar shown. The central shaded regions correspond to the tumour, the red lines outside the tumour represent the capillaries and any unshaded regions correspond to non-cancerous cells.

To investigate whether the lack of a gap between our modelled tumour and the neighbouring vasculature is due to a failing of our model, or whether this properly captures in vivo behaviour, we now suppose that non-cancerous cell proliferation is somehow upregulated so as to maintain a constant gap between the tumour and the neighbouring vasculature as the tumour grows to its saturated size, even though there is no clear biological motivation for such behaviour. It can be shown that the corresponding kinetics of the non-cancerous cells must be

$$\frac{\partial h}{\partial t}+\nabla \cdot (\underset{¯}{v}h)=\frac{2h{v}_{\text{tum}}}{r},$$

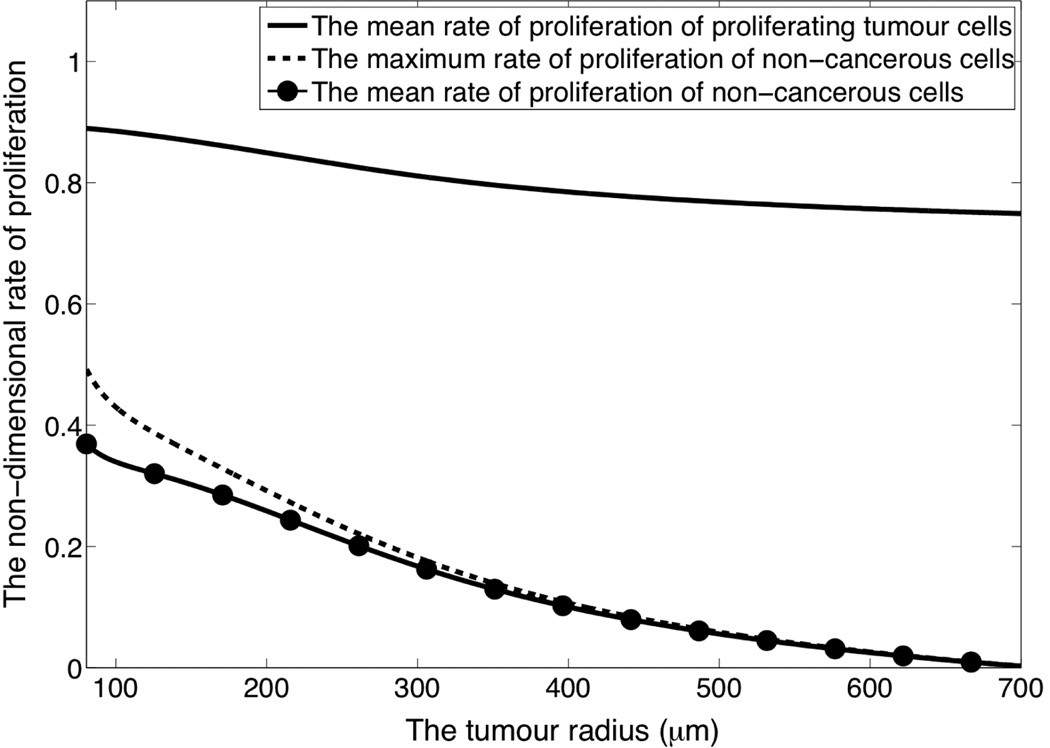
where v_tum is the speed of the tumour front. We now test whether kinetics of this form are feasible by considering the corresponding rates of proliferation of the cancerous cells and non-cancerous cells, which are shown in Figure 4 where a rate of unity corresponds to the proliferation rate of cancerous cells in a limitless oxygen supply. Our modelling shows that to maintain a uniform gap between the tumour and the vasculature some non-cancerous cells are initially required to proliferate at a rate which is 55% that of the tumour cells.

Figure 4.

The rate of proliferation of the different cells types when non-cancerous cell kinetics are chosen to ensure a gap of constant width is maintained between the tumour and neighbouring vasculature as the tumour grows to its maximum size as given by diffusion limited control.

Note that Figure 4 only shows the rate of proliferation required to maintain a gap of constant width. For the initial gap of 50 µm, which is consistent with the intercapillary distance, to evolve into a gap of 2000 µm, which is observed following an intra-cornea tumour implant, requires non-cancerous cells to proliferate on average approximately 160 times faster than this.

4. Discussion and Conclusions

Our modelled tumour showed that simple biologically motivated dynamics for the proliferation of non-cancerous cells caused the distance between the tumour and neighbouring vasculature to decrease quickly compared to the growth rate of the tumour, so that at saturation the neighbouring capillaries effectively lie on the surface of the tumour, unless there is some obstruction which prevents the tumour from reaching the surrounding vasculature. This was despite taking care to ensure that any idealisations in our model contributed to the model being a best case scenario for maintaining the distance between the tumour and vasculature.

Non-cancerous cell proliferation can be forced to maintain a constant gap between the tumour and vasculature, but this requires non-cancerous cells to initially proliferate approximately 55% as quickly as tumour cells, which are typically taken to have lost growth control. This result is consistent with our initial scaling argument, which motivated the problem, which showed that maintaining a uniform gap between a tumour and the vasculature requires the non-cancerous cells to initially proliferate approximately 50% as quickly as the cancerous cells. Whilst the rate of proliferation required to maintain such a gap is high, it is not unfeasible. However the absence of any biologically motivated mechanism which would up-regulate non-cancerous cell proliferation in this way, and having shown that oxygen feedback is not sufficient, suggests that non-cancerous cell proliferation is not generally up-regulated to this extent.

We have found that the rate of proliferation required to maintain a gap of constant width between the tumour and vasculature is high and demands extreme parameter values. However, for an in vivo tumour growing in vascular tissue to evolve into a state which is consistent with that seen following an intra-cornea tumour implant would require non-cancerous cells to proliferate on average approximately 160 times faster that was required to maintain a gap of constant width. This would imply that some non-cancerous cells would be proliferating at least two orders of magnitude faster than cancerous cells which is in conflict with our general understanding of tumour systems. This is clearly impossible. Furthermore, a 2 mm gap between the tumour and neighbouring vasculature would greatly exceed the diffusion distance of oxygen and it is not clear how an in vivo tumour in such a configuration would be supported. From this we conclude that the 2mm gap following intra-cornea tumour implants is unique to that setting and cannot be included in a general model of tumour blood flow dynamics.

Our model assumes that capillaries are carried with the movement of local cells and neglects any angiogenic stimuli or mechanical properties of the capillaries which might resist their movement. We have also neglected any contact inhibition of normal, non-cancerous, cell growth. If any of these effects are included then the non-cancerous cell growth rates required for gap maintenance will be even higher. Hence our model is a best case scenario for gap maintenance and in an in vivo tumour we would expect the gap to close even quicker than it does in our model. Given this and that the gap closes quickly in our modelled tumour we conclude that in a well developed in vivo tumour growing in vascular tissue there will not be a significant gap between the tumour and neighbouring capillaries, unless the presence of a basement membrane prevents the tumour from reaching the surrounding vasculature. In which case our simple scaling argument still applies and the gap between the tumour and surrounding vasculature should only be the width of the basement membrane, which will be relatively thin.

This conclusion implies that mathematical models of angiogenesis should not consider an initial gap between the tumour and the vasculature. Furthermore, the studies based on corneal implants serve as building blocks for developing models for angiogenesis in that setting, but do not immediately translate to a clinical setting. Hence the results and conclusions of models based upon the corneal implants should be disregarded unless they can be replicated in a more general setting. In particular, models based upon the cornea implant experiments are likely to overestimate the importance of angiogenesis and the effectiveness of anti-angiogens. However, if the models based upon the cornea implant experiments can be generalised then these works can then become more biologically accurate and clinically relevant. Furthermore, the new vasculature which is cultivated by tumour angiogenesis tends to be distorted and leaky compared to normal vasculature. The fact that at the initiation of angiogenesis the surrounding capillaries actually lie on the surface of the tumour implies that this leaky distorted vasculature will only exist within the interior of the tumour. This could mean that during treatment healthy tissue will be exposed to less toxicity than predicted by the corneal implant motivated models because less toxic therapy will leak into regions of healthy tissue surrounding the tumour.

These conclusions are supported by experimental observations. The image of the avascular tumour in Figure 6(a) shows small blood vessels growing directly into the periphery of a tumour that was initially avascular. It demonstrates that blood vessels penetrate directly into the tumour-host interface rather than via an elaborate network of vessels adjacent to the tumour edge as seen in the cornea experiments, such as that shown in Figure 6(a). In Figure 6(a) it can be seen that the corneal implant is surrounded by an extremely large region of avascular tissue and the resulting angiogenesis across a large gap between the tumour and vasculature does not represent angiogenesis for an in vivo tumour growing in vascular tissue.

5. Summary

We have considered the evolution of the gap between an avascular tumour and the neighbouring vasculature as the tumour grows. A simple mathematical model illustrates that a well established yet avascular tumour will not exhibit a gap between the tumour and the vasculature and that the neighbouring capillaries effectively lie on the surface of the tumour. These conclusions are reinforced by a simple scaling argument and images of in vivo tumours. This illustrates that mathematical and computational models based on the cornea implant experiments, which assume a significant gap between the tumour and neighbouring vasculature, cannot be immediately applied to a clinical setting.

Figure 5.

An in vivo avascular tumour and a tumour implanted into a cornea.

(a) An in vivo avascular tumour (the white region) growing in a mouse mound chamber. The tumour has been added to the wound chamber in a matrigel disc, and on the outer ring of the disc endothelial buds which were obtained from scrotal fat were place. A 200 µm length bar is shown.