Finding Alternative Expression Quantitative Trait Loci by Exploring Sparse Model Space

Abstract

Sparse modeling, a feature selection method widely used in the machine-learning community, has been recently applied to identify associations in genetic studies including expression quantitative trait locus (eQTL) mapping. These genetic studies usually involve high dimensional data where the number of features is much larger than the number of samples. The high dimensionality of genetic data introduces a problem that there exist multiple solutions for optimizing a sparse model. In such situations, a single optimization result provides only an incomplete view of the data and lacks power to find alternative features associated with the same trait. In this article, we propose a novel method aimed to detecting alternative eQTLs where two genetic variants have alternative relationships regarding their associations with the expression of a particular gene. Our method accomplishes this goal by exploring multiple solutions sampled from the solution space. We proved our method theoretically and demonstrated its usage on simulated data. We then applied our method to a real eQTL data and identified a set of alternative eQTLs with potential biological insights. Additionally, these alternative eQTLs implicate a network view of understanding gene regulation.

1. Introduction

Discovering the relationship between genetic variation and molecular traits, such as gene expression levels, is an essential step for understanding cellular functions at a systems level. Identifying expression quantitative trait loci (eQTLs) through eQTL mapping is one of such endeavors in search of genetic variation that is associated with changes in gene expression levels. An association in eQTL mapping is primarily reflected by a statistical correlation between the genotypes of a genetic variant and the expression levels of the corresponding gene in the samples. These eQTL associations provide a hypothesis that there is some underlying regulatory mechanism for further investigation. (Montgomery et al., 2010; Pickrell et al., 2010; Schlattl et al., 2011; Shabalin, 2012; Stegle et al., 2010; Fusi et al., 2012; Stranger et al., 2007; Stranger et al., 2012).

Many methods have been proposed for eQTL mapping, including a recent propagation of machine-learning approaches (Chen et al., 2012; Kim and Xing, 2012; Lee and Xing, 2012; Fusi et al., 2012; Lee et al., 2010; Wang et al., 2011). These methods either separately examine if the correlation of each pair of traits and genetic variants is significant or characterize their associations as parameters in a machine-learning model. Least absolute shrinkage and selection operator (Lasso) (Tibshirani, 1996) methods, as a type of commonly used machine-learning method, add an l₁ norm regularization term to the loss function, leading to a sparse model that favors a sparse solution with a small number of nonzero terms. The sparsity of these algorithms is justified with an assumption that there are only a small number of associations between genetic variant and traits, given an overwhelmingly large number of variant and trait pairs for genome-wide eQTL mapping. In a solution of Lasso model fitted on observed data, the parameters represent the effect of each genetic variant on a particular trait, and those nonzero terms correspond to the identified eQTL associations. However, neither the pair-wise correlation method nor the Lasso model captures the relationship among the expression levels of multiple genes. Hence, multitask Lasso models (Chen et al., 2012; Lee and Xing, 2012; Lee et al., 2010) were proposed to impose sparsity over all of the variant and trait pairs to take consideration of related genes.

In both Lasso and multitask Lasso models, the weights of genetic variants are computed from an optimization model with its original loss function and l₁ norm of the parameters. Solving the optimization problem results in a solution with the sparse property containing only a limited number of nonzero parameters. The sparseness can be controlled by changing the coefficient of the regularization term. These optimization-based methods have the same assumption that the optimization problem has a single global optimal solution. However, the solution from Lasso methods may be inconsistent in either theory (Zou, 2006) or real situation. In eQTL mapping, the data is usually high dimensional, where the number of genetic variants is much larger than the number of samples, and hence there exists multiple solutions with the same optimal value. In such situations, the solutions resulting from different initializations are inconsistent in terms of the nonzero support of the weights. Thus, the result from a single run of these methods is unreliable, although such a simplistic approach has been widely applied in eQTL mapping. The sparse assumption in these models is also problematic in modeling biological data, since biological systems typically contain redundant and backup mechanisms. (Fishman-Lobell et al., 1992; Korn et al., 2007). Nonetheless, biological redundancy is seldom taken into account in eQTL mapping.

In this article, we propose a novel method to finding the alternative relationship between genetic variants and traits, which shows the redundancy of two genetic variants to a particular trait. Instead of studying a single optimization result, our method explores the space of the optimization solutions by repeatedly running the Lasso method with random initialization parameters. From this randomly sampled solution set, our method has the capability to extract not only the strength of each pair of genetic variant and trait, but also the relationship of two eQTLs regarding their effects on a given trait. We demonstrate the capability of our method both theoretically by a mathematical proof and practically using simulation data. We further apply our method to a real human eQTL data set and find a set of alternative eQTLs with potential biological insights. The remaining article is organized as follows: We describe our method in Section 2, present the results in Section 3, and conclude the article with discussions in Section 4.

2. Method

2.1. Problem definition

We denote X as the observed genotypes of the genetic variants, with D columns for D variants and N rows for N samples. We denote Y as the phenotype data, with P columns for P traits and N rows for N samples. For eQTL mapping, Y includes the expression profiles of all the genes in the samples under investigation. The method of sparse modeling is to find the optimal matrix B with D rows and P columns by minimizing the following square loss function plus a regularization term.

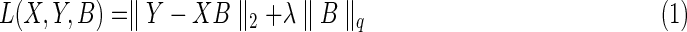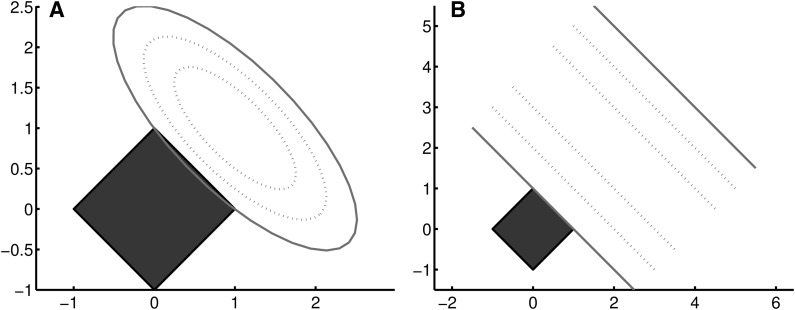
The Lasso method is a special case with q = 1. With l₁-norm, a Lasso model favors a sparse result with a small number of nonzero terms (Candes et al., 2008). In practical situations, there are two cases when multiple solutions exist for a Lasso model, as illustrated in Figure 1.

FIG. 1.

Optimal solutions defined by the contour lines of the loss function and the regularization term. The axes of X and Y correspond to two weights of a solution. Dotted and solid ellipses and lines are the contour of the loss function, and gray boxes show the contour of l₁ regularization term. (A) A strict convex loss function and l₁ regularization term, with optimization error. (B) A nonstrict convex loss function and l₁ regularization term.

As illustrated in Figure 1A, the loss function needs to be symmetric along the line of x = y. In eQTL mapping, the symmetry can be interpreted as two alternative genetic variants with redundant effect on gene expression. Therefore, we utilize this property to find alternative eQTLs, corresponding genes, or even pathways that perform a backup function for system robustness. In this article, we aim to find such variant pairs that are redundant to each other, by investigating multiple solutions sampled from the solution space.

2.2. Our method

The existence of multiple optimization solutions in eQTL mapping prevents us from using a single optimized sparse model to explain the importance of features. In order to investigate the model solution space, we therefore propose a sampling method to generate a set of solutions that is expected to be a representative set covering all the multiple solutions. Consequently, we compute the covariance of the solution vectors as an approximation for the alternative relationship between two genetic variants in eQTL mapping. These identified alternative eQTLs represent a redundant relationship regarding their effect on gene expression.

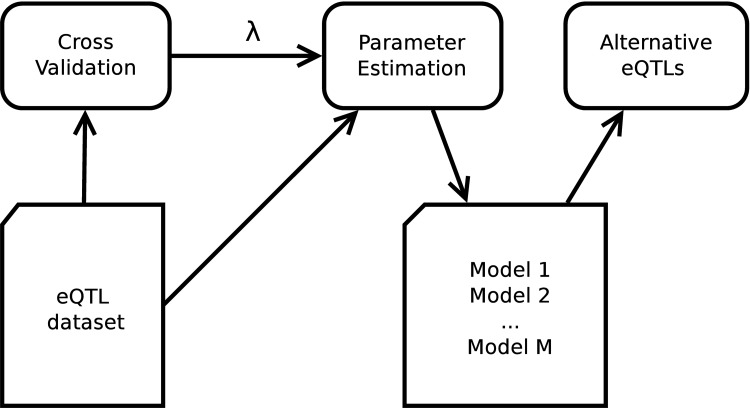
Our method shown in Figure 2 can be summarized as follows. First, we search for an optimal l₁ regularization coefficient, λ, by carrying out a five-fold cross validation. Second, we sample M initialization, 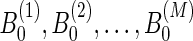independently from a uniform distribution. With these initialization values and λ, we then run Lasso M times and produce M models: 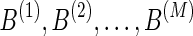. For each pair of genetic variants, we compute the correlation coefficient of their weights in M solutions. Finally, we extract the pairs whose correlation coefficients are equal to or greater than a cutoff c₁ and each of whom has more than c₂ nonzero values out of M models. These extracted pairs are considered as alternative eQTLs that influence the expression levels of a particular gene.

FIG. 2.

The flowchart of our method. From a given eQTL data set with genotypes of genetic variants and expression profiles of genes, our method first finds the coefficient of the regularization term, λ, by a 5-fold cross validation. Then, our method samples M models through parameter estimation with different initializations. From the M models, our method finally screens for alternative eQTLs. eQTL, expression quantitative trait locus.

Our method can be justified in theory by the following claim. Here we describe the claim in a plain way, and the rigorous description and its proof can be found in Supplementary Material (Supplementary Material is available online at www.liebertpub.com/cmb).

Claim: Denote 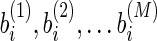and 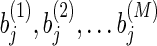as the weights of two features i and j. The correlation coefficient of 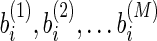and 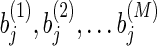among all the M sampled models is negative when the two features have the same effect on the responding variable.

A sketch proof: The claim that two alternative features have the same effect on the responding variable can be viewed the same as the claim that we can exchange the value of the two features, but the responding value is kept the same. From this symmetry, we can derive the conclusion that if 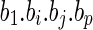is an optimal solution, 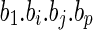is also an optimal solution. Therefore, all the solutions of the optimization problem are paired, which implies that the correlation coefficient of b_i and b_j is negative.

We now justify our method by performing an analysis of suboptimal solution. Optimization methods may produce a solution with error caused by either the numerical precision or the convergence tolerance. We denote B^* as the optimal solution, and B^e as the solution with some small error e, such that 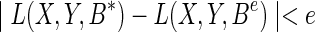. We assume that the loss function L(X,Y,B) has a lower bounded Lipschitz on the difference between a suboptimal solution and an optimal solution. The lower bound is denoted as u₁.

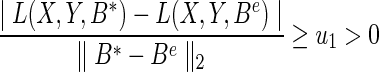Then we have a bound for B^e dependent on the error of loss function.

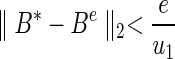Thus, suboptimal solutions are also bounded by u₁ and e, which implies that suboptimal solutions are close to the optimal solution. The error e will approach zero when we implement an optimization method with small tolerance and high precision. Therefore, with a small error e, the correlation coefficient of redundant features in suboptimal solutions should be close to that of the optimal solution.    ■

3. Results

3.1. Simulated data

We design a simulated data set to illustrate how our model can use the correlation of sampled solutions to capture the alternative relationships between two genetic variants. This data set is generated in the following way. X⁽²⁾ and X⁽¹¹⁾ are randomly selected as a pair of alternative genetic variants. Y is the responding variable, which represents the gene expression level in eQTL mapping.

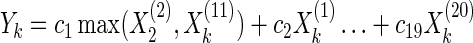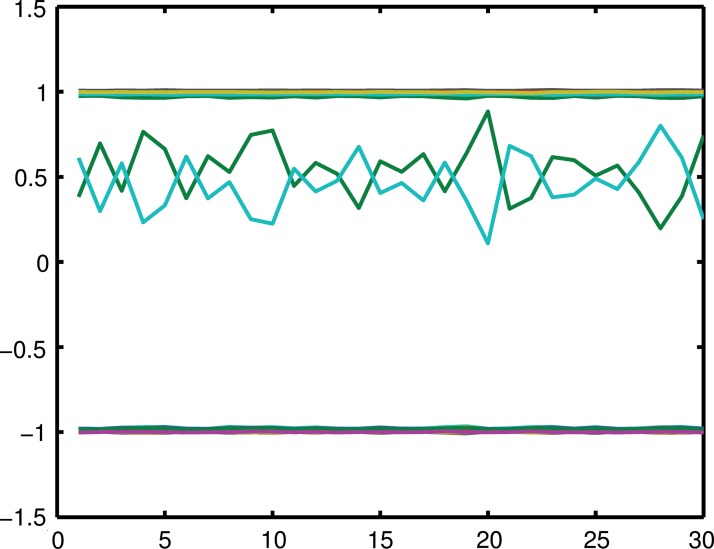
The max function of X⁽²⁾ and X⁽¹¹⁾ indicates that the two variables play the same function in this model. We choose c_i, i = 1.19 randomly from a uniform distribution of {−1,+1}. We perform random sampling for 100 times, where every value of X is sampled from a uniform distribution of {0,1}. We then remove all the samples where the values of (X⁽²⁾,X⁽¹¹⁾) are (0,1) or (1,0). Finally, we solve the Lasso problem on this data set with λ = 0.1 in the regularization term of Equation (1), which is computed through a five-fold cross-validation. We compute 30 solutions using the Lasso model on this simulated data set and compute the correlation between w₂ and w₁₁, the weights of X⁽²⁾ and X⁽¹¹⁾, respectively. The correlation is −0.999 in this simulated data set, as shown in Figure 3. This strong negative correlation between the two weights indicates that these two variants are alternative for their effect on responding variables.

FIG. 3.

Results on the simulated data. This figure shows the parameters of each model computed. X-axis represents the index of the model from 1 to 30. Y-axis shows the parameter value for each model. The weights w₂ and w₁₁ correspond to the green line and the cyan line around y = 0.5. These two weights show a strong negative correlation with each other. The other weights are converged to −1 or +1 in our simulation.

3.2. Real data

We apply our method to a real data set on human eQTL mapping. Specifically, we extract the genotypes of copy number variants (CNVs) for 51 Yoruba individuals in Ibadan, Nigeria (YRI), from The 1000 Genomes Project Consortium (The 1000 Genomes Project Consortium, 2010; Mills et al., 2011). We collect gene expression levels of these same YRI individuals measured by mRNA sequencing (Pickrell et al., 2010). We apply our method to chromosome 20 of the data set, with genotypes of 139 CNVs and expression of 379 genes in 51 individuals. In total, we identify 79 CNV eQTL pairs that alternatively influence the expression of 69 target genes (Supplementary Table S1). These alternative eQTLs have high negative correlation coefficient values among models, and therefore they may alternatively affect the expression of target genes. In contrast, the correlation coefficients of their feature values are low, which prevents such pairs from being discovered by single models or by directly investigating the correlation between the genotypes of each genetic variant and the expression levels of each gene.

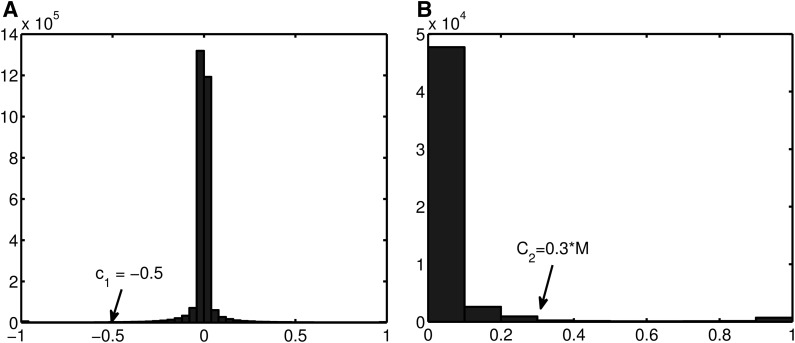
We use M = 100 models with two parameters c₁ = −0.5 and c₂ = 0.3M on this real data set. We choose c₁ = −0.5 to find the negatively correlated alternative eQTLs. We choose c₂ = 0.3M, which implies that the selected alternative eQTLs have nonzero weight in at least 30 models. This parameter enables us to select alternative eQTLs that play significant contribution to the expression level of certain genes not by chance. The histograms of the background distribution of c₁ and c₂ are shown in Figure 4, with arrows indicating the values used to select the most significant alternative eQTLs in our method.

FIG. 4.

The background distribution of c₁ and c₂. Both histograms are computed from 100 Lasso results with random initialization. X-axis represents the values of c₁ and c₂, and Y-axis represents the number of CNV pairs for each value interval of c₁ and c₂. (A) The distribution of the model weight correlation coefficient of all the alternative eQTLs. (B) The distribution of the fraction of the number of models in which a CNV eQTL has nonzero weight, among the total M models. CNV, copy number variant.

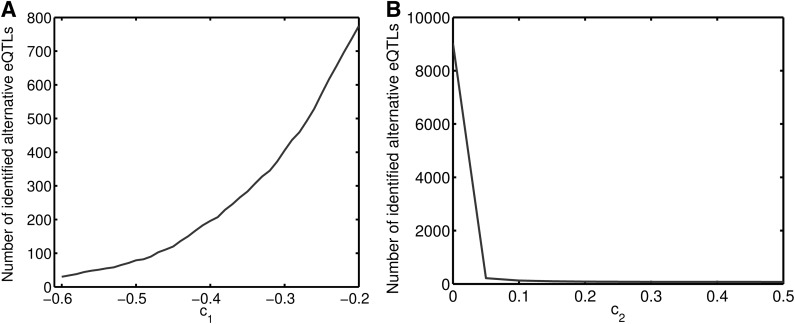
We perform experiments to demonstrate that the resultant set of alternative eQTLs will not change much with a small perturbation of c₁ and c₂. In Figure 5A, we illustrate the number of identified alternative eQTLs with different c₁ values ranging from −0.6 to −0.2 while fixed c₂ = 0.3. Since we are only interested in redundant CNV pairs with negative correlation coefficients, we choose −0.5 as a cutoff, and 79 alternative eQTLs are identified. With c₁ = −0.4, the number of identified alternative eQTLs is 196, which is also a small fraction (2.0%) of the total CNV pairs. With a larger cutoff c₁ = −0.2, which results in many eQTL pairs with low negative correlations, the number of identified alternative eQTLs is close to 800. Therefore, we suggest to carefully tune a cutoff on c₁ according to specific studies. To reflect this observation and keep our model flexible, we allow these parameters to be customized according to different data sets and studies. Figure 5A shows the number of identified alternative eQTLs with different c₂ ranging from 0 to 0.5 while fixed c₁ = −0.5. With c₂ larger than 0.05, the number of identified alternative eQTLs drops from 218 to 75. Considering the total of more than 10⁵ CNV pairs, it is obvious that varying c₁ within the range of 0.05–0.5 would consistently select a small number of alternative eQTLs.

FIG. 5.

The number of identified alternative eQTLs and different values of c₁ and c₂. The left panel shows that the number of identified alternative eQTLs changes with different c₁ ranging from 0 to 0.5 by fixing c₂ = −0.5. The right panel shows that the number of identified alternative eQTLs changes with different c₂ ranging from −0.6 to −0.2 by fixing c₁ = 0.3.

Our results on the real human eQTL data set, as illustrated in Figure 6, reveal a network view of the relationships between genes overlapping with alternative CNV eQTLs, and the target genes for these loci. Particularly, one CNV (chr20:60004020–60004338), overlapping with TAF4, is an alternative CNV eQTL of many other eQTLs targeted for different genes. TAF4 is a subunit of transcription initiation factor TFIID that has been shown to empower transcriptional activation by factors including retinoic acid receptors. TAF4 is an important gene, with the role of mediating promoter responses to various activators and repressors (www.genecards.org) (Safran et al., 2010). One of the alternative CNV eQTLs (chr20:9097570–9097622) overlaps with PLCB4, which has a key role in the intracellular transduction of many extracellular signals in the retina (Safran et al., 2010). MAVS, the mitochondrial antiviral signaling protein, is one example of the target genes whose expression is associated with either of these two CNVs that might take effect by two different pathways. Both TAF4 and MAVS are involved in the pathway of “hsa05168,” which is related to Herpes simplex infection, according to the Kyoto Encyclopedia of Genes and Genomes (www.genome.jp/kegg/). Hence, our results showing that PLCB4 and TAF4 are alternative eQTLs of MAVS may indicate that PLCB4 might either involve the Herpes simplex infection pathway through an alternative route or has an alternative pathway that is different from Herpes simplex infection.

FIG. 6.

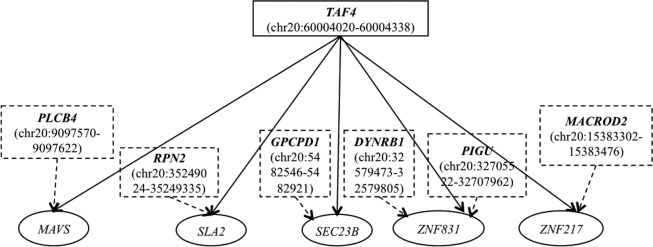
A network view of the relationships between genes overlapping with alternative CNV eQTLs, and the target genes for these loci. The rectangles represent CNV eQTLs and the overlapping genes, with dotted rectangles, represent alternative CNV eQTLs. The ellipses represent target genes whose expression levels are associated with eQTLs. The arrowed lines represent the eQTL mapping identified by our method, where the CNVs are associated with target gene expression.

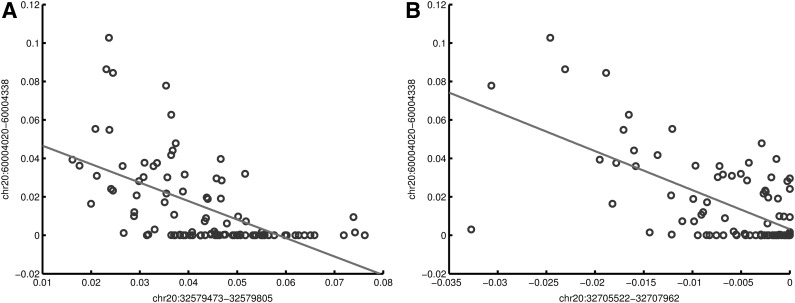
In addition, we observe that one CNV eQTL can have different alternative partners that are associated with the same target gene. For example, as shown in Figure 6, CNV chr20:60004020–60004338, overlapping with TAF4, is associated with the expression of ZNF831. This CNV has two alternative eQTL partners: CNV chr20:32579473–32579805 (overlapping with DYNRB1) and CNV chr20:32705522–32707962 (overlapping with PIGU). Specifically, the pair of (chr20:60004020–60004338, chr20:32579473–32579805) has high negative correlation values in the models running our method, as demonstrated in the scatterplot in Figure 7A. The model weights of these two CNVs regarding the expression level of ZNF831 have a correlation coefficient of −0.574, while their genotypes are not correlated with a small correlation coefficient of 0.075. Comparatively, as shown in Figure 7B, the model weights of the alternative CNV eQTLs (chr20:60004020–60004338, chr20:32705522–32707962) are highly correlated (the correlation coefficient is −0.645), whereas their genotypes have low correlation (the correlation coefficient is −0.174) over the expression of ZNF831. Such an example indicates that there exist multiple alternative CNV partners and corresponding pathways that affect the expression of certain genes.

FIG. 7.

Scatterplots showing model weight correlations of alternative CNV eQTLs. (1) chr20:60004020–60004338 and chr20:32579473–32579805. (2) chr20:60004020–60004338 and chr20:32705522–32707962. The axes represent the model weights of corresponding CNVs. The regression lines show the negative correlations between model weights of CNV pairs.

4. Conclusion

Sparse modeling is a widely studied feature selection method in machine learning. Recent years have witnessed a trend of applying sparse modeling to genetic and genomic studies. However, the problems in such studies usually have different shapes compared with the problems in other machine-learning fields. Usually, biological systems not only desire sparsity for efficiency but also allow redundancy for robustness. The trade-off between efficiency and robustness reminds us to reconsider the sparsity in biological systems and requires careful handling in genomic studies.

In this article we make the first move to address this problem by proposing a novel method to capture the alternative relationships between two genetic variants in eQTL mapping. Our method investigates the space of all the sparse models and prioritizes potential alternative eQTLs. We present both theoretical proof and numerical experiments to support our method. The results on a real eQTL data set further provide evidence that our method serves its goal. In the real eQTL data, we use CNVs from The 1000 Genomes Project as an example. Nonetheless, our method can be applied to study other types of genetic variants, including SNPs and small insertions and deletions.

The alternative genetic variants in eQTL mapping identified by our method point to a systematic or network view of the relationship between genetic entities. These alternative eQTLs may locate at different alternative pathways or regulatory networks that lead to gene expression changes of particular genes. Therefore, a network view of gene regulation could be provided by extensive analysis of such alternative eQTLs using our method.

Our proposed method is focused on identifying redundant relationships among genetic variants for their contribution to gene expression. Such redundant relationship is straightforward yet ubiquitous in biology. In the future, we plan to extend our method to investigate more complex phenomena, including high-order relationships among genetic features.

Although we demonstrate our method in eQTL mapping in this article, this method is not limited to eQTL analysis. Our method can be extended to many other genetic studies as long as optimization is involved. For instance, we can use the same rationale to perform genome-wide association studies where the goal is to find genetic variants associated with various diseases.

Acknowledgments

This work was supported by the National Science Foundation Grant AF-1149811 (CAREER award), the Alfred P. Sloan Research Fellowship, and NIH R01GM089753 grants to J.X., as well as the Wells Fargo Foundation Fund for Faculty Excellence from Charlotte Research Institute and University of North Carolina at Charlotte to X.S.

Author Disclosure Statement

No competing financial interests exist.