Abstract
Drosophila melanogaster, an ancestrally African species, has recently spread throughout the world, associated with human activity. The species has served as the focus of many studies investigating local adaptation relating to latitudinal variation in non-African populations, especially those from the United States and Australia. These studies have documented the existence of shared, genetically determined phenotypic clines for several life history and morphological traits. However, there are no studies designed to formally address the degree of shared latitudinal differentiation at the genomic level. Here we present our comparative analysis of such differentiation. Not surprisingly, we find evidence of substantial, shared selection responses on the two continents, probably resulting from selection on standing ancestral variation. The polymorphic inversion In(3R)P has an important effect on this pattern, but considerable parallelism is also observed across the genome in regions not associated with inversion polymorphism. Interestingly, parallel latitudinal differentiation is observed even for variants that are not particularly strongly differentiated, which suggests that very large numbers of polymorphisms are targets of spatially varying selection in this species.
Keywords: adaptation, clinal variation, population genomics
HOW organisms adapt to the ecological challenges of a new environment remains poorly understood. Indeed, while observations from comparative biology show that organisms often evolve convergent phenotypes when faced with similar selection pressures, we have little insight into how underlying historical and population genetic processes determine the degree of shared or divergent selection responses across populations or species. The latitudinal clines of Drosophila melanogaster provide a rich system for exploring these questions.
While there is general agreement that D. melanogaster evolved in Africa, spread through Eurasia several thousand years ago, and only recently colonized the Americas and Australia (David and Capy 1988; Lachaise et al. 1988; Begun and Aquadro 1993; Keller 2007; Stephan and Li 2007; Duchen et al. 2013), our understanding of the species’ historical biogeography is incomplete. There are at least two potential clines that have received much attention—one in Australia and one in North America—that likely represent independent samplings of shared ancestral variation (Knibb 1982; Hoffmann and Weeks 2007).
Decades of research on D. melanogaster clines have revealed broad shared patterns of adaptive phenotypic divergence along latitudinal transects in the Americas and Australia. For example, several phenotypes including body size, multiple physiological traits, and multiple allozyme variants show parallel clines on these continents (Singh and Long 1992). Paracentric chromosome inversion polymorphism is also well documented as showing similar patterns of clinal variation on the two continents (Voelker et al. 1978; Knibb 1982). Genomic description of the two clines is minimal. The most comprehensive data bearing on the issue of shared clinality on these continents are from tiling array data from Queensland, Tasmania, Maine, and Florida (Turner et al. 2008). These data revealed, perhaps not surprisingly given previous data from phenotypes, inversions, and allozymes, that a considerable portion of clinal variation appears to be shared at the genomic level. Interestingly, however, there were also major differences between the continents. For example, some of the most strongly differentiated regions between northern and southern Australian populations showed no evidence of differentiation between northern and southern populations from North America. However, the technology at that time prohibited a base-level examination. A recent population genomic analysis of the North American cline (Fabian et al. 2012) supported the conclusion from the tiling array analysis (Turner et al. 2008) that there is substantial parallel differentiation on the two continents, but there was no formal comparison of comparable data from the two continents analyzed in the same way. Here we use whole-genome sequencing to elucidate patterns of genomic differentiation in North America and Australia based on genomic sequencing to tease out the degree to which phenotypic convergence in these parallel clines has resulted from convergent evolution at the genetic level. In so doing, we aim to understand the underlying historical and population genetic processes that explain both the degree of shared selection response to latitudinal gradients in these populations and the differences between them.
Materials and Methods
Population samples
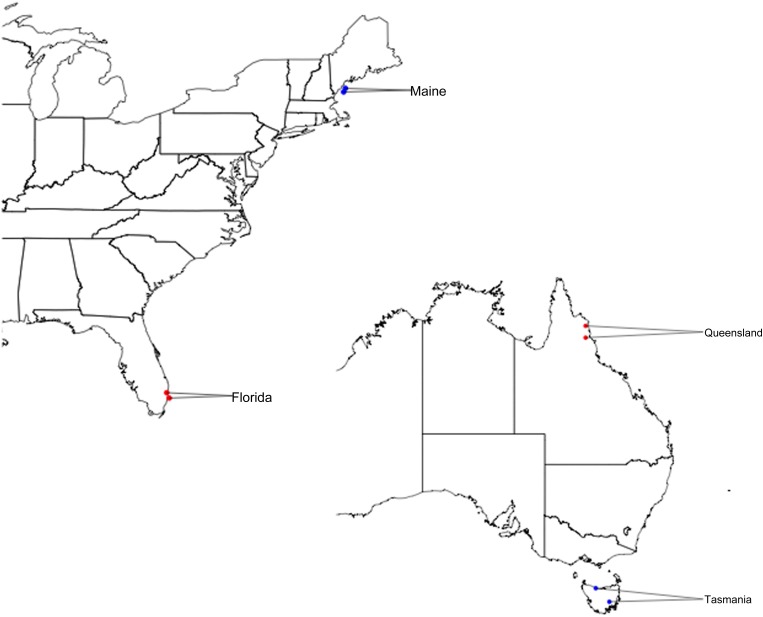
The populations investigated here are from Queensland (QUE), Tasmania (TAS), Maine (MAI), and Florida (FLA) and were described previously (Turner et al. 2008). Figure 1 shows the location of each of the populations sampled from the four different locations. Two samples were taken at each location (see Turner et al. 2008 for details). Sample locations in Figure 1 are labeled red and blue to indicate their low-latitude (red) vs. high-latitude (blue) environment. Two samples from each of the four geographic locations were taken, and these two samples were then pooled for sequencing. For DNA isolation and pooling we used females collected from 16 isofemale lines from MAI, 16 lines from FLA, 17 lines from QUE, and 15 lines from TAS.
Figure 1.
Sampling locations in North America and Australia. In North America more tropical samples come from Florida and temperate samples are from Maine. In Australia tropical flies are from Queensland and temperate collections are from Tasmania.
Genomic sequencing and mapping
Genomic DNA from pooled samples from each location was run on a single lane of an Illumina GA2 sequencer for 2 × 75 cycles, using the standard flow cell, yielding ∼28× coverage apiece. Raw Illumina GA2 image data were phased and filtered for quality, using default GERALD parameters for unaligned reads. Sequencing reads were mapped back to the D. melanogaster reference sequence with BWA v. 0.5.8 (Li and Durbin 2009). As these data are derived from pools of multiple individuals, polymorphism may affect the ability of BWA to align reads harboring SNPs. To control for this effect, we altered the alignment parameters (k, the number of errors allowed in the seed; and n, the number of errors allowed in the whole read) from BWA and compared the number of reads aligned and the accuracy of those alignments (Supporting Information, Table S23). Based on these data, we chose k = 2 and n = 5 for the alignment of all four population samples. Data have been submitted to the Short Read Archive and can be found under bioproject accession no. PRJNA237820.
Postmapping filtering steps
After alignment we further filtered each two-population data set in a number of ways. First, we filtered any bases that were triallelic or had coverage <6 or >40. We also filtered any bases that had only a single read carrying the minor allele on a continent. Next, we used repeat masker (v. 3.3) to filter positions associated with known repeats or low sequence complexity in the reference sequence. We also removed regions of the genome thought to experience reduced rates of crossing over because their associated reduced heterozygosity could reduce the power to detect differentiation and because the larger physical scale of differentiation expected in such regions might compromise one’s ability to identify potential targets of selection. The coordinates corresponding to regions of normal recombination used in our analyses were defined by the Drosophila Population Genomics Project (dpgp.org) and include 2L:844,225–19,946,732; 2R:6,063,980–20,322,335; 3L:447,386–18,392,988; 3R:7,940,899–27,237,549; and X:1,036,552–20,902,578.
Population genetic analysis
Summary statistics of polymorphism and differentiation were calculated following Kolaczkowski et al. (2011). We considered individual populations for single-population summary statistics and pairs of populations for calculations of F st. All downstream analysis uses this pairwise F st information. As the main focus of this article is a comparison of differentiation on two continents, variable coverage across population samples was a potential problem, as it would increase variation in power across sites and continents. To minimize this problem we created a “trimmed” data set. For each position that met the criteria noted in the previous sections the minimum depth among the four population samples was noted and the other three populations were randomly down-sampled to provide equal depth in all four populations. This trimmed data set was the object for the majority of analyses.
Empirical outlier approach
There are benefits and pitfalls of using a genome-wide empirical distribution rather than a model-based approach for the detection of candidates (Beaumont and Nichols 1996; Akey et al. 2002; Teshima et al. 2006; Voight et al. 2006; Pickrell et al. 2009). As in Kolaczkowski et al. (2011), we have, for a few reasons, opted for an empirical rather than a model-based approach for most analyses. First, model-based demographic inference using pooled population genomic data is an unsolved problem. Second, given the pervasive genomic effect of selection on polymorphism in D. melanogaster (Langley et al. 2012), demographic model fitting based on the assumption of strict neutrality is likely to be misleading. Third, because we focus on outliers present on two continents, even if our empirical approach were not optimal, we have a strong expectation that it will reveal a substantial component of parallel adaptive allele frequency change.
As the physical distribution of differentiation in the genome is unknown, we used two complementary approaches. First, we calculated F st in nonoverlapping 1-kb windows throughout the normally recombining portion of the genome on each continent, from which the top 5%, 2.5%, and 1% tails of window F st’s could be identified. Generally we considered differentiated windows to be in either the top 2.5% or the top 1% tail. Shared outlier regions were defined simply as the intersection of the windows occupying the tails of both continents. A second approach was to use individual SNP frequencies throughout the genome to identify candidate differentiated SNPs. This second analysis is useful for generating hypotheses on classes of SNPs that may be under selection or for investigating genome-wide properties of SNPs belonging to different classes (e.g., CDS vs. intergenic).
Whole-genome analysis of parallel differentiation
If parallel differentiation were common even in genomic regions that were not in the shared outlier set, then F st would be positively correlated between continents. We used simulations to determine whether the observed correlation (see Results) was significant. The null model of Coop et al. (2010) was used to simulate divergence from all four populations simultaneously. Shared population history in the model is represented through the covariance matrix associated with the multivariate normal random variable representing population allele frequencies. These simulations assume that the populations were independent (off-diagonal elements set to zero) with continental F st equal to our observed median estimates (∼0.06) and ancestral allele frequencies drawn from the standard neutral site frequency spectrum. Using this model, 10,000 SNPs were simulated and F st at each SNP was computed. From these values a correlation coefficient of F st between continents was calculated, representing one replicate of the simulation. The results reported here are from 100,000 simulation replicates.
We further investigated the question of parallel differentiation at the whole-genome scale by using a clustering analysis. The rationale for this analysis is that SNPs that are targets of spatially varying selection on both continents would lead to clustering of populations by latitude rather than by continent. To examine this question, we created distance trees of the four populations, using SNP frequencies in each population as the input. Three distance metrics were used: cord distance (Cavalli-Sforza and Edwards 1967), Nei’s D (Nei 1972), and Euclidean distance. Trees were constructed using subsets of SNPs with varying levels of F st as defined by the Australian comparison. Distance trees were constructed using neighbor joining (Saitou and Nei 1987). We were particularly interested in asking whether more differentiated SNPs (in Australia) reflect clustering of populations by environment (high latitude vs. low latitude) or by geography (Australia vs. North America) in the four-population tree. Support for the recovered distance tree at each F st cutoff was assessed using nonparametric bootstrapping (1000 replicates), sampling SNPs with replacement from our entire data set.
SNP-level analysis of parallel outliers
We generated lists of candidate selected SNPs by focusing on those that were segregating on both continents and that were strongly differentiated in the same direction (e.g., at a site segregating A/T the T allele was at higher frequency in Tasmania and Maine). Mean F st was calculated for each such SNP for both continents.
Functional annotation
We used the DAVID online functional annotation tools to compare enrichment for functional terms among groups of genes (Huang et al. 2009). DAVID’s tools use a modified Fisher’s exact test (the EASE score) to determine the extent of enrichment for a subset of genes compared to a specified background. We compared subsets to their backgrounds as described in Results and found the most enriched FAT Gene Ontology (GO) terms in each comparison (FAT GO annotation enriches for more specific GO terms, giving less weight to extremely broad terms). In addition, we also used hypergeometric tests in some cases to test for enrichment of specific GO terms over the expected background. These are the marginal inputs to the EASE score used by DAVID. Recently Pavlidis et al. (2012) pointed out that the structure of the genome, particularly the gene length distribution, may lead to spurious enrichments of GO categories among significant windows, even in the absence of true enrichment. While this is so, we present enriched GO categories for the sake of hypothesis generation rather than confirmation.
Results
After mapping and application of the postmapping filters described above, mean coverage from each of the populations was as follows: QUE mean = 26.2×, TAS mean = 26.0×, FLA mean = 36.3×, and MAI mean = 48.9×. The mean for the down-sampled data was 21.6× for each population.
Genomic patterns of polymorphism
Summary statistics of polymorphism in 1-kb windows from the four populations are shown in Table 1. Two patterns are immediately clear. First, high-latitude populations are less polymorphic than low-latitude populations on both continents, genome-wide and for each chromosome arm (all comparisons have P-values <2.2e-16). For example, mean Θπ = 0.0038 vs. Θπ = 0.0045 in Tasmania vs. Queensland, a reduction of ∼16% in Tasmania. The reduction in high-latitude polymorphism is less extreme in North America, representing an ∼10% decrease. The ratios of X-linked vs. autosomal polymorphism (Θπ) range from 0.63 to 0.68 (Queensland = 0.639, Tasmania = 0.676, Florida = 0.632, and Maine = 0.684), similar to previous genome-wide estimates (Sackton et al. 2009; Langley et al. 2012; Mackay et al. 2012). The low-latitude populations have lower ratios of X- to autosomal-linked variation compared to high-latitude populations. This could be explained by differences in operational sex ratio between populations or by systematic differences in selection on X chromosomes and autosomes, which could result from the presence of clinally varying inversions on the autosomes and the absence of such inversions on the X chromosome.
Table 1. Summary statistics of DNA polymorphism from 1-kb windows throughout the recombining portion of the genome.
| Population | Chr | ΘW | Θπ | ΘH | H |
|---|---|---|---|---|---|
| Low latitude | |||||
| Florida | X | 3.54 | 3.12 | 4.22 | −1.089 |
| 2L | 5.92 | 5.47 | 5.90 | −0.421 | |
| 2R | 5.14 | 4.67 | 5.27 | −0.586 | |
| 3L | 5.28 | 4.80 | 5.34 | −0.533 | |
| 3R | 5.27 | 4.82 | 5.16 | −0.333 | |
| GW | 5.05 | 4.60 | 5.18 | −0.579 | |
| Queensland | X | 3.57 | 3.12 | 4.09 | −0.957 |
| 2L | 5.8 | 5.36 | 5.75 | −0.377 | |
| 2R | 4.88 | 4.38 | 4.90 | −0.507 | |
| 3L | 5.39 | 4.87 | 5.23 | −0.353 | |
| 3R | 5.23 | 4.80 | 5.04 | −0.233 | |
| GW | 5.00 | 4.54 | 5.01 | −0.469 | |
| High latitude | |||||
| Maine | X | 3.41 | 3.08 | 3.99 | −0.908 |
| 2L | 5.33 | 4.91 | 5.69 | −0.779 | |
| 2R | 4.86 | 4.49 | 5.05 | −0.558 | |
| 3L | 4.78 | 4.41 | 5.08 | −0.676 | |
| 3R | 4.65 | 4.24 | 4.88 | −0.635 | |
| GW | 4.61 | 4.23 | 4.94 | −0.709 | |
| Tasmania | X | 3.04 | 2.74 | 3.78 | −1.038 |
| 2L | 4.68 | 4.34 | 5.48 | −1.140 | |
| 2R | 4.38 | 4.09 | 4.94 | −0.848 | |
| 3L | 4.27 | 3.96 | 4.92 | −0.968 | |
| 3R | 4.234 | 3.87 | 4.80 | −0.938 | |
| GW | 4.13 | 3.80 | 4.79 | −0.986 |
Mean estimates of 4Nu (1e-03/bp) among 1-kb windows are given and are the pooled-sampling, singleton corrected estimators provided in Kolaczkowski et al. (2011). Chr, chromosome; GW, genome-wide.
A second trend is that high-latitude populations exhibit a greater skew toward high-frequency alleles than do low-latitude populations, as summarized by Fay and Wu’s H statistic (P < 2.2e-16 for both continents). This pattern is consistent across chromosome arms in the Australian samples (all P-values <1e-05). The pattern is observed on three of five chromosomes arms in North America, the two exceptions being the X, which shows greater skew toward high-frequency alleles in Florida than in Maine, and 2R, which shows no significant difference between populations. Taken together, the reductions in polymorphism and greater skew in the frequency spectrum of high-latitude populations are highly suggestive of recurrent local adaptation in these populations. This supports previous investigation of latitudinal differentiation in this species (e.g., Kolaczkowski et al. 2011).
To test whether segregating inversions affect the site frequency spectrum we calculated Fay and Wu’s H in 1-kb windows that overlapped cosmopolitan inversions In(3R)P, In(3R)Mo, In(3L)P, In(2L)t, and In(2R)NS and in windows that did not overlap these inversions. We observed a skew toward high-frequency alleles within regions spanned by inversions relative to outside of such regions (P < 2.2e-16 for both continents). This is suggestive of inversions being a potent target of local adaptation (Hoffmann et al. 2004; Kirkpatrick and Barton 2006; Kolaczkowski et al. 2011; Fabian et al. 2012; Kirkpatrick and Kern 2012). We fitted a linear model to explain variation in 1-kb window H, which included an effect of geography (low latitude vs. high latitude), inversion status, and an interaction effect. Interestingly the interaction was significant along with the main effects, such that windows from high-latitude, inverted regions were significantly more skewed than those from low-latitude, inverted regions. Thus, the inversions within high-latitude populations are the main drivers of this result, suggesting that inversions within low-latitude populations do not harbor a comparatively skewed site frequency spectrum.
Genomic patterns of differentiation
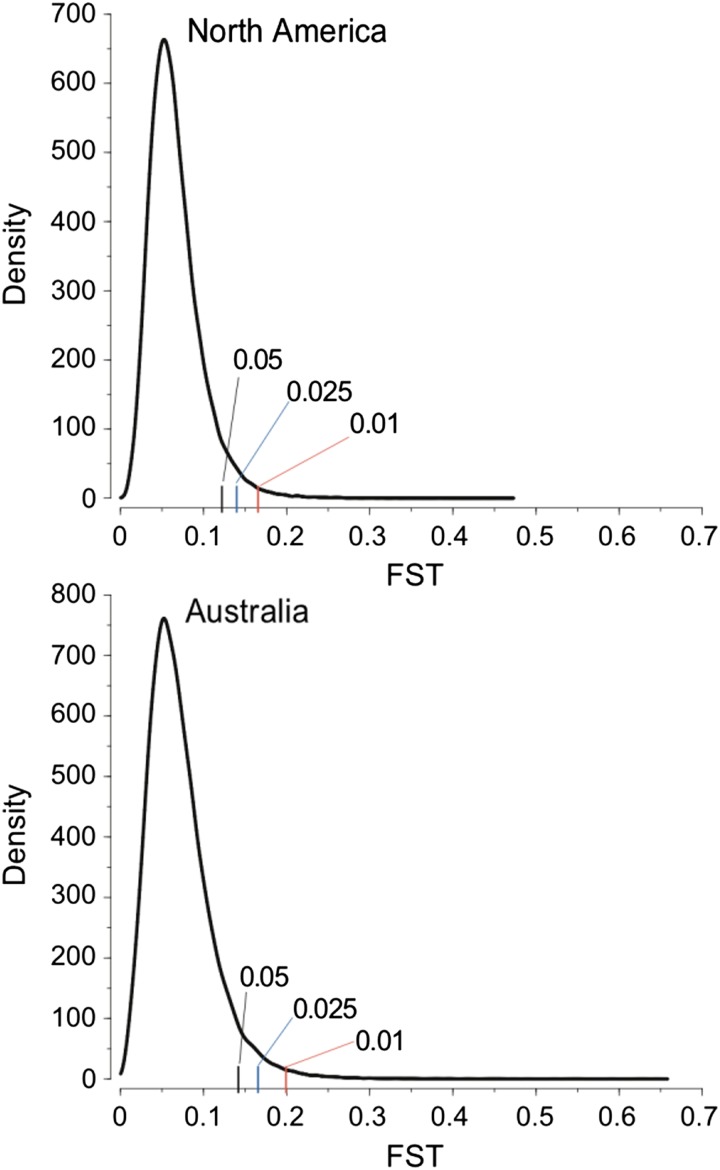
Estimates of F st on the two continents can be found in Table 2 and Figure 2. F st is slightly (but significantly) higher between the Australian populations (mean 1-kb F st = 0.0716) than between the North American populations (mean 1-kb F st = 0.0657). Mean F st from the Australian sample is considerably lower than observed in our previous analysis of the same Australian samples (Kolaczkowski et al. 2011, mean F st = 0.112). We believe this effect is attributable to differences in the alignment procedure (ungapped vs. gapped) used between the two studies or to differences in the quality of the data generated given the technology available at the time of the Kolaczkowski et al. (2011) study.
Table 2. Summary statistics of F st in 1-kb windows from two clines.
| Cline | Mean | SD | 5% | 2.5% | 1% |
|---|---|---|---|---|---|
| Australia | 0.0716 | 0.0392 | 0.1425 | 0.1165 | 0.2002 |
| North America | 0.0657 | 0.0311 | 0.1232 | 0.141 | 0.1658 |
Shown are the mean; the standard deviation; and the 5%, 2.5%, and 1% cutoffs of the empirical distribution of F st.
Figure 2.
Density of F st estimates from 1-kb windows in regions of normal recombination from the North American cline (top) and the Australian cline (bottom), respectively. The 5%, 2.5%, and 1% tail cutoffs are indicated in each population with colored hash marks.
Levels of differentiation are significantly heterogenous among chromosome arms for both continents. (Kruskal–Wallis rank sum test, P < 2.2e-16 for both continents). We calculated the median F st for 1-kb windows that overlap or do not overlap cosmopolitan inversions as above. For both continents, we found that genomic regions overlapping cosmopolitan inversions are more differentiated (Australia inverted region F st = 0.0631 vs. F st = 0.0582 outside of inversions; North America inverted region F st = 0.070 vs. F st = 0.060 outside of inverted regions: Wilcoxon rank sum test P-value <2.2e-16 for both continents). In addition, we looked at a coarse level if 1-kb windows that overlap genes show greater differentiation among populations than nongenic windows. The results from this parsing of the data were not compelling: the difference is extremely small in F st between genic and nongenic windows and leans slightly toward nongenic windows being slightly more differentiated (Australia genic window F st = 0.0638 vs. F st = 0.0649 in nongenic windows; North America genic window F st = 0.0593 vs. F st = 0.0610 in nongenic windows).
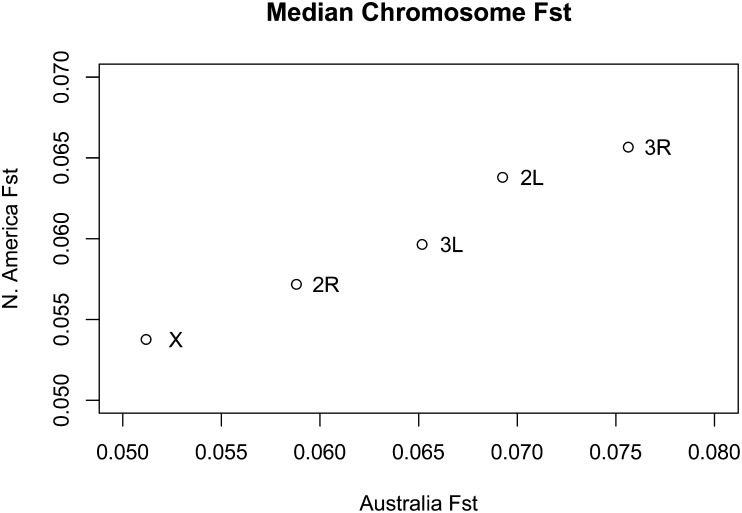
Given the evidence of parallel inversion clines on the two continents, perhaps it is not surprising that the rank order of chromosomal differentiation is the same on both continents (Figure 3). To further investigate this pattern we calculated a nonparametric correlation coefficient of F st for 1-kb windows on the two continents, using the intersection of windows sampled in both clines from the normally recombining portion of the genome. We find the correlation to be surprisingly high, with a Spearman rank correlation ρ = 0.2 (P < 2.2e-16). Correlation coefficients were unchanged in windows that overlapped or did not overlap genes. To test whether this would be expected under a null model of divergence of two pairs of populations from a common ancestor we performed simulations according to the null model of Coop et al. (2010), tuned to represent the level of observed differentiation among populations. None of our simulation draws exceeded a correlation coefficient >ρ = 0.05, indicating that our result is unexpected under a model of independent divergence (P < 1e-4). These results support the idea that parallel differentiation is common and that the cosmopolitan inversions play a role in this parallelism. To further address this question and investigate whether the inverted regions drive the genomic observation, we estimated the correlation between 1-kb F st estimates on the two continents for each chromosome arm and for regions spanned by the common inversions and those not spanned by the inversions. Although the correlation in windowed F st is higher for inverted regions (ρ = 0.195, P < 2.2e-16) than for regions outside of inversions (ρ = 0.143, P < 2.2e-16), both are individually highly significant and unexpected given a model of independent divergence.
Figure 3.
Median F st of 1-kb windows in the recombining portion of each chromosome arm plotted in each clinal comparison. Note that while the scales of the axes are different, reflecting greater absolute differentiation among our Australia samples, rank order of chromosomal differentiation is identical among samples.
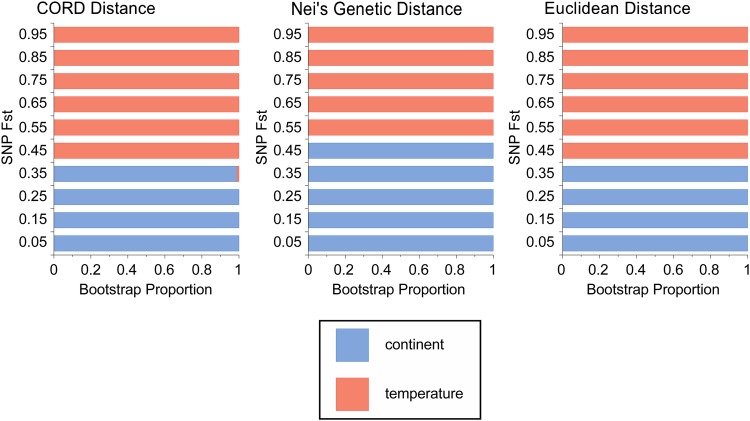
Classically, convergent evolution has been identified when similar phenotypes have been evolved in independent lineages. At the level of the genotype underlying convergent traits, we would expect to observe similar allele frequencies at sites responsible for adaptive differentiation on both continents. To extend our genomic analysis of parallel adaption to the SNP level we created distance trees for the four populations, using SNP frequencies in each population as our input. If F st in the Australian cline were uncorrelated with F st in the North American cline, there should be no bias in which pairs of populations cluster (e.g., Queensland should be paired with Florida or Maine in equal proportion). Figure 4 shows the results of the bootstrap replicates for the distance trees for each of our three metrics, where horizontal lines represent the proportion of replicates that cluster populations by continent (blue) or by temperature (red). The overwhelming result for this analysis is that for those sites that are most differentiated (roughly the top 60% of F st), populations cluster by the environment in which they live rather than by their geographic location, although there is a clear signal separating North American from Australian populations in the least clinally differentiated SNPs. This result is also echoed in average pairwise patterns of F st both at the chromosome arm level and genome-wide (see Table S24, Table S25, Table S26, Table S27, Table S28, and Table S29). These results provide strong evidence for convergent allele frequency differentiation on both continents and moreover suggest that there are substantial numbers of only moderately differentiated SNPs that are targets of spatially varying selection.
Figure 4.
Results for cluster analysis of SNP frequencies. Shown are the proportions of bootstrap replicates that cluster our four sampled populations by either continent (blue) or temperature (red) broken down by the level (percentile) of F st in the Australian cline. These results support convergent evolution of allele frequencies such that more highly differentiated sites cluster populations together on the basis of the environment in which they live rather than geography.
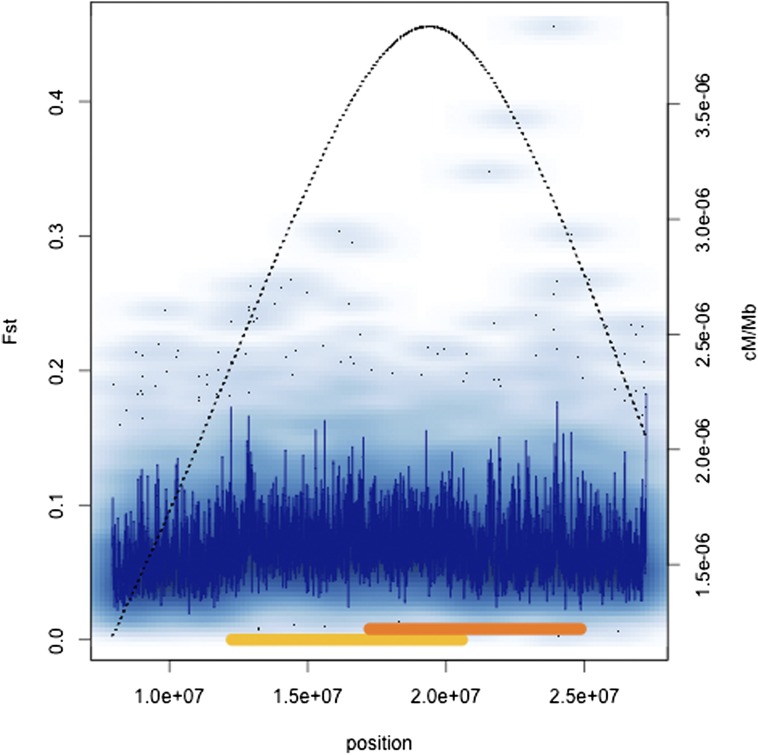
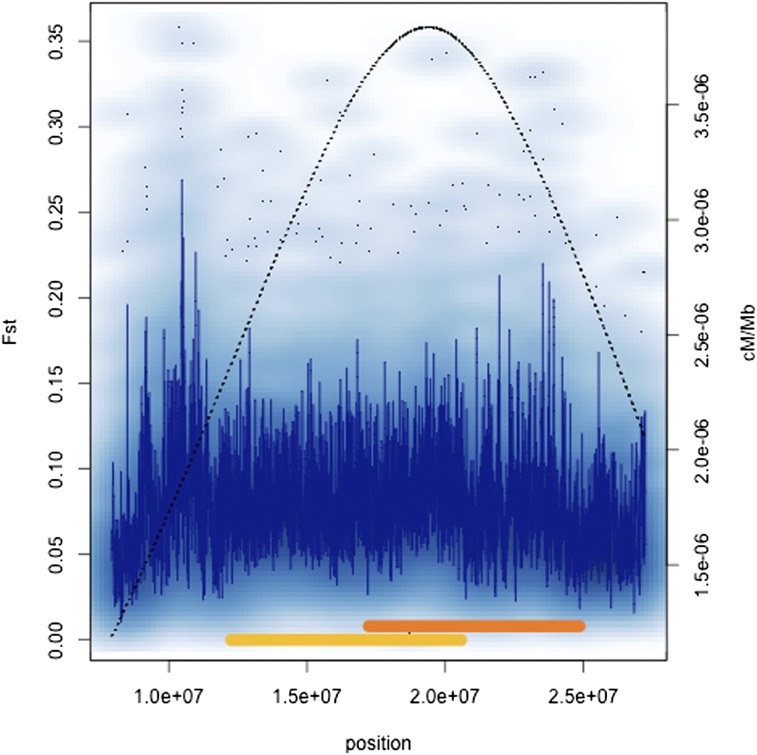
We were also interested in examining the effect of rates of crossing over on F st. Table 3 shows the Spearman rank correlation coefficients between F st and recombination rate both for genome-wide 1-kb window comparisons and on a chromosome-by-chromosome basis. Rate of crossing over explains very little of the variation on a genome-wide basis; Spearman’s ρ ∼ −0.04 in both clinal samples. However, chromosome 3R showed strong positive correlations between recombination and differentiation for both continents. This is notable given that two cosmopolitan inversions, In(3R)P and In(3R)Mo, are known to exhibit geographic differentiation (e.g., Stalker 1976; Voelker et al. 1978). Figure 5 and Figure 6 show F st variation across 3R along with the positions of the rearrangements and our estimates of crossing over for Australian and North American samples, respectively. Figure S1 and Figure S2 show complementary numbers for each chromosome arm for both continents. The chromosome 3R inversions are located in regions of higher crossing in standard homokaryotypic chromosomes, despite the suppression that must occur in inversion heterozygotes. Thus, the correlation between recombination and F st on 3R may be a spurious one driven by the presence of inversions in regions of high recombination in the St karyotype.
Table 3. Correlation coefficients for F st vs. recombination rate (cM/Mb) for each continental comparison by chromosome arm as well as throughout the genome (GW).
| Continent | Chromosome | Spearman’s ρ (F st vs. cM/Mb) | P-value |
|---|---|---|---|
| Australia | X | −0.0286 | 1.02E-04 |
| 2L | 0.0996 | 2.20E-16 | |
| 2R | −0.0966 | 2.20E-16 | |
| 3L | 0.0314 | 3.49E-05 | |
| 3R | 0.1320 | 2.20E-16 | |
| GW | −0.0461 | 2.20E-16 | |
| North America | X | −0.0370 | 4.90E-07 |
| 2L | −0.0039 | 0.5863 | |
| 2R | −0.0237 | 5.29E-03 | |
| 3L | −0.0351 | 3.52E-06 | |
| 3R | 0.1700 | 2.20E-16 | |
| GW | −0.0425 | 2.20E-16 |
Figure 5.
Density scatter plots of F st across chromosome 3R in Australia. The dark blue line represents the running median estimate of F st. The secondary y-axis (dashed black line) shows our estimates of recombination rate across the same region. The positions of In(3R)P and In(3R)Mo are shown with gold and orange bars, respectively. In these plots, density at a position is given by the intensity of the blue cloud, and finer black dots represent outliers.
Figure 6.
Density scatter plots of F st across chromosome 3R in North America. See Figure 5 legend for details.
Outlier windows
The analyses presented in the previous section support the idea that parallel differentiation is common across the genome, but they provide little insight into the associated biology. To investigate biological patterns associated with spatially varying selection we focused on regions of the genome that fall in an empirical tail distribution of F st on both continents.
Table 4 summarizes the numbers of outlier windows recovered at each empirical cutoff along with the intersection counts. Among outlier samples of the 4351 (4352 for North America) windows (top 5%) in each cline, we find overlap at 423 windows. This observation is highly unlikely by chance, using a hypergeometric test (P < 2.2e-16). Indeed, overlap between continents is statistically significant genome-wide at each empirical cutoff tested (Table 4). Focusing on the 5% tail, which given the larger number of windows compared to other cutoffs should provide the most power to detect parallel differentiation, we observe especially high levels of overlap for 3R and 2L, suggesting that cosmopolitan inversions play a significant role in the parallelism. However, the fact that this result is significant on the X chromosome, which harbors no common inversion in these populations, shows that inversions alone cannot explain the whole pattern. Table 5 shows contingency tables comparing the number of genes containing overlapping outlier windows on each continent and their intersection. For example, at the 1% cutoff there are 94 genes that overlap outlier windows on both continents. This is substantially more than expected under independence (Fisher’s exact test, P = 6.93e-27) and further supports the idea that parallelism is common.
Table 4. Counts of outlier 1-kb windows in two clinal samples at three empirical cutoffs.
| Chromosome | Australian count | North American count | Both count | P-value |
|---|---|---|---|---|
| 5% tail | ||||
| X | 727 | 976 | 59 | 0.00067 |
| 2L | 892 | 992 | 93 | 4.12E-10 |
| 2R | 477 | 458 | 38 | 5.15E-07 |
| 3L | 747 | 711 | 47 | 0.00227 |
| 3R | 1508 | 1215 | 186 | <2.2e-16 |
| GW | 4351 | 4352 | 423 | <2.2e-16 |
| 2.5% tail | ||||
| X | 395 | 544 | 16 | 0.1237 |
| 2L | 423 | 464 | 20 | 0.00518 |
| 2R | 274 | 227 | 15 | 4.78E-05 |
| 3L | 339 | 354 | 18 | 0.00021 |
| 3R | 745 | 587 | 41 | 0.00032 |
| GW | 2176 | 544 | 110 | 5.43E-12 |
| 1% tail | ||||
| X | 180 | 233 | 2 | 0.665095 |
| 2L | 148 | 178 | 3 | 0.17059 |
| 2R | 144 | 80 | 5 | 0.00147 |
| 3L | 117 | 145 | 3 | 0.07455 |
| 3R | 282 | 235 | 9 | 0.009 |
| GW | 871 | 871 | 22 | 9.24E-05 |
The total number of windows included in the intersection analysis was 86,216. This included 17,875 windows on chromosome X, 18,470 windows on chromosome 2L, 13,767 windows on chromosome 2R, 17,339 windows on chromosome 3L, and 18,765 windows on chromosome 3R. The number of outlier windows shared by both samples in given in the “Both count” column. P-values are from hypergeometric tests.
Table 5. Comparisons of the numbers of genes overlapped by outlier windows at various empirical cutoffs.
| Australian NS genes | Australian significant genes | |
|---|---|---|
| 5% tail | ||
| North American NS genes | 7,736 | 1,272 |
| North American significant genes | 1,357 | 807 |
| P = 8.309E-120 | OR = 3.62 | |
| 2.5% tail | ||
| North American NS genes | 9,046 | 844 |
| North American significant genes | 934 | 348 |
| P = 1.62E-71 | OR = 3.99 | |
| 1.0% tail | ||
| North American NS genes | 10,152 | 435 |
| North American significant genes | 491 | 94 |
| P = 6.93E-27 | OR = 4.47 |
P-values and associated odds ratios are from Fisher’s exact test on the presented contingency tables. In each case, there is significantly more overlap in genes that contain outlier windows than one would expect under the null model of independence. NS, nonsignificant; OR, odds ratio.
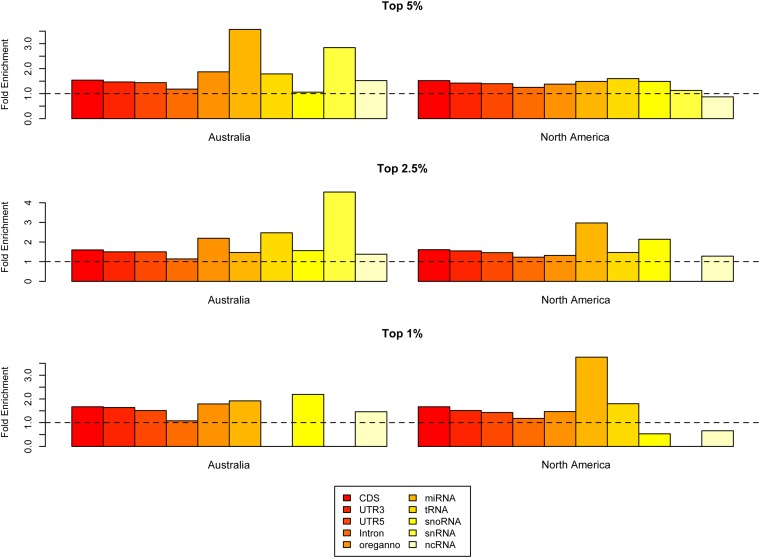
Annotation enrichments at all three empirical cutoffs for both Australia and North America are shown in Figure 7. Generally, we find strong enrichments in multiple functions on both continents but not a great degree of similarity among continents in rank order among annotations. For example, we observed strong enrichments in many classes of RNA genes [including microRNAs (miRNAs) and small nuclear RNAs (snRNAs)] in Australia. Australian outlier windows were also enriched for regulatory elements (Oreganno), CDS, and UTR sequences. In North America, annotation enrichments were generally weaker than those observed in Australia (see Figure 6), yet some functional similarities were present. Outlier windows in the North American sample parallel Australia in enrichments for miRNAs, snRNAs, transfer RNAs (tRNAs), UTRs, and CDS sequences. None of the tests for correlations in annotation enrichments rejected the null hypothesis: 5% tail Spearman’s rank correlation ρ = 0.049 (P = 0.89), 2.5% tail ρ = −0.055 (P = 0.88), and 1.0% tail ρ = 0.212 (P = 0.551). Thus, while there is some evidence of parallel functional enrichment in outlier windows, the pattern is not sufficiently strong to yield a statistical signal.
Figure 7.
Annotation enrichments within outlier F st windows for Australian and North American samples. The dashed line represents no enrichment over what is expected based on the number of bases sampled.
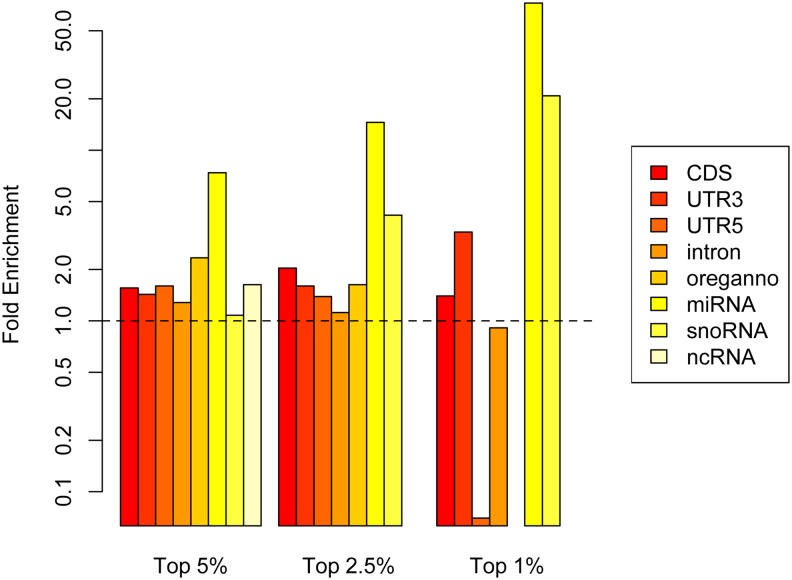
To further investigate the biological properties of shared regions we examined the annotation enrichments for windows in the empirical tail of both continents (shared outliers, Figure 8; note that the y-axis has to be shown on a log scale as some of the enrichments observed are extremely strong). A few functional categories are clear outliers in this analysis: miRNAs, small nucleolar RNAs (snoRNAs), CDS, and 3′-UTRs are strongly enriched in the 1% tail windows. At the 5% and 2.5% cutoffs, miRNAs and CDS are still strongly enriched, with the addition of regulatory elements as annotated in the Oreganno set.
Figure 8.
Annotation enrichments within intersection windows (shared outlier widows among clines). Note the y-axis is shown on a log scale.
Outlier windows overlapping protein-coding genes
We carried out two types of analysis to investigate the biology of parallel differentiation from a gene-centric perspective. First, we carried out a GO enrichment analysis for the protein coding genes hit by outlier windows for each continent separately. Second, we identified the set of genes that are located in the shared outlier windows and then tested them for GO enrichments. The results for each continent are in Table S1, Table S2, Table S3, Table S4, Table S5, Table S6, Table S7, Table S8, Table S9, Table S10, Table S11, Table S12, Table S13, Table S14, Table S15, Table S16, Table S17, and Table S18. There is substantial overlap among the significant GO terms found on each continent, which is not surprising given the excess of shared outlier windows. For example, in the 5% tail for North America and Australia, there are 237 and 199 significant biological process GO terms, respectively, after correction for multiple tests. Of these significant terms, 149 are shared among clines. Similar results were obtained using the 2.5% and 1% cutoffs. Shared significant GO terms point to enrichments in genes involved in such processes as transcription regulation, eye development, wing morphogenesis, and circadian rhythm. Indeed it is worth noting that both wing morphology (e.g., McKechnie et al. 2010) and circadian rhythm phenotypes (reviewed in Kyriacou et al. 2008) are well-studied clinally varying phenotypes. Some interesting behavioral processes are also shared among continents, including learning and memory and olfactory learning. Similarly, high levels of overlapping significant terms are found for the molecular function and cellular component branches of the GO hierarchy. Pavlidis et al. (2012) recently pointed to potential problems with GO-type analyses in the Drosophila genome that may lead to false positives. While this is so, our results for shared significant GO terms are clearly consistent with known features of spatially varying selection in this species and thus are likely not artifactual.
To further examine biological patterns underling genes shared among outlier windows we performed a DAVID analysis. As input, we used the genes that were found in outlier windows (5% tail) on both continents. This list was compared to a background gene list corresponding to those genes found in all the windows in the genome that survived our filtering and were used in our analyses. We limited our analysis to those clusters with enrichment scores >1.301, corresponding to a geometric mean P-value <0.05 of the associated terms in the cluster. This truncation yields 89 significant annotation clusters as predicted by DAVID (see Supporting Information). The single most significant cluster (enrichment score = 11.74) includes terms such as wing disc morphogenesis, wing disc development, appendage development, and metamorphosis. Many of the same genes responsible for wing development appear to be influenced by selection on both continents. Other notable clusters from this analysis include axon guidance and neuronal projection/development (enrichment score = 10.83), eye/photoreceptor development (enrichment score = 8.62), oogenesis and follicle cell development (enrichment score = 8.15), transcriptional regulation (enrichment score = 6.16), EGF signaling (enrichment score = 5.19), adult locomotory behavior (enrichment score = 4.99), olfaction (enrichment score = 3.5), and growth (enrichment score = 3.42). Many of these clusters agree with previous observations (Kolaczkowski et al. 2011; Fabian et al. 2012).
Convergent SNPs
We observed a total of 361,171 SNPs that were segregating on both continents, of which 64% (229,705) were convergent (defined as those SNPs that show the same direction of allele frequency change on both continents). Under the null hypothesis of drift we expect ∼50% of SNPs to be convergent. The large excess of convergent SNPs is indicative of parallel adaptation and is consistent with the neighbor-joining analysis. Convergent SNPs (as defined above) were more differentiated than nonconvergent SNPs, which also strongly supports the inference of natural selection—in North America, mean F st = 0.091 for convergent SNPs and mean F st = 0.075 for nonconvergent SNPs (t-test: P < 0.0001), and in Australia, mean F st = 0.10 for convergent SNPs and mean F st = 0.085 for nonconvergent SNPs (t-test: P < 0.0001).
To further enrich this set of SNPs for targets of selection we identified convergent SNPs that were among the top 10% most differentiated individual SNPs on both continents, which corresponds to F st of at least 0.248 in Australia and at least 0.213 in North America. We refer to these SNPs as strongly convergent SNPs. Strongly convergent SNPs represent ∼1.8% of convergent SNPs (4038 SNPs, Table S19). These SNPs were not enriched for any type of annotation (synonymous, nonsynonymous, UTR, or intronic/intergenic, Table S19) compared either to all other convergent SNPs (chi-square test, P = 0.71) or to all other SNPs that vary on both continents (chi-square test, P = 0.55).
To determine how much SNP convergence was associated with larger spatial scale effects, we determined the proportion of the strongly convergent SNPs that fell within previously defined convergent windows (the 5% “overlap tail” presented above); 5.8% of strongly convergent SNPs fell into these windows. While this represents a small proportion of strongly convergent SNPs, it is a >10-fold excess compared to expectation (only 0.42% of the genome is represented in these windows; chi-square test, P < 0.001). Eleven percent of strongly convergent SNPs fell within the 5-kb region surrounding the 1-kb 5% overlap tail windows, which also represents a significant excess (compared to 2.08% of the genome; chi-square test, P < 0.0001).
A priori, it seems likely that strongly convergent, synonymous SNPs in particular should usually be found within strongly differentiated windows, as it is generally assumed that synonymous SNPs are relatively unlikely to be direct targets of strong spatially varying selection. Indeed, we found that strongly convergent synonymous SNPs were more likely than other (e.g., nonsynonymous) strongly convergent SNPs to be found in an overlap tail window (7.8% compared to 5.5%; Pearson’s chi-square test, P = 0.039). However, this still leaves many synonymous SNPs that do not appear to associate directly with a strongly differentiated window. While some of these SNPs may be strongly convergent due to chance, it seems more probable that these SNPs are associated with differentiated windows that are not sufficiently differentiated to be in the 5% overlap tail. Overall, 137/377 of the 5% overlap tail windows contained at least one strongly convergent SNP, and 181/377 windows had a SNP within 5 kb surrounding the window (2 kb to either side of the window). Thus, the SNP-based analysis shows overlap with the window-based analysis, as expected. However, it also appears that there is substantial information contained in the SNPs that is not contained in the windows, likely because outlier windows are associated with a somewhat larger physical scale of differentiation compared to the set of all parallel outlier SNPs.
One goal of the analysis at the single-nucleotide level is to identify SNPs playing a role in adaptation to high-latitude environments. Thus, we investigated whether genes that carry strongly convergent SNPs share any common biological features. For this analysis, we considered genes that carried either a nonsynonymous or a UTR polymorphism, as these categories of SNP may be more likely to be the direct targets of selection than other categories of SNPs. We performed a DAVID analysis to compare genes carrying at least one strongly convergent UTR or nonsynonymous SNP (303 genes) to a background list of 4893 genes containing at least one UTR or nonsynonymous SNP shared by both continents. We also compared to all Drosophila genes in DAVID’s database. GO categories that were significantly enriched at a false discovery rate <0.10 are shown in Table S20. The comparison to all Drosophila genes recaptured these GO terms as well as showing enrichment for other terms associated with cell membrane function and metal binding. Six nonsynonymous and two 5′-UTR SNPs were among the top 100 most differentiated SNPs in the analysis (these were in the top 1% of F st on both continents). We performed a detailed annotation of these SNPs (Table S21) and found that many of them are associated with genes of known function.
Different nonsynonymous SNPs in the same genes
Convergent evolution can be defined at multiple levels. For example, one might observe adaptive divergence on both continents but at different sites in the same gene. In principle, such convergent changes would support the idea that strong selection on the same gene could have different population genetic outcomes on the two continents, either because of differences in the details of selection (at a focal gene or in the genetic background) or because of differences relating to stochastic events associated with founding events associated with colonization. We generated a list of genes showing high F st nonsynonymous SNPs on both continents but for which the nonsynonymous SNPs are different. We then prioritized them as candidates for convergent evolution (at the gene level) based on the degree of conservation of the corresponding residues in sequenced outgroup species. Our top five candidate genes, hkl, otk, ana1, chm, and trp (summary statistics for and locations of the candidate SNPs in each gene are provided in Table S22), are promising targets of future experimental work.
Continent-specific differentiation
Although the main issue addressed in this article is the degree of shared differentiation on two continents, there are many interesting differences between continents as well. An unknown fraction of such differences could represent false positives or false negatives. However, in a number of cases continent-specific differentiation is characterized by good coverage in all four population samples and substantial physical distances; these are therefore likely to be real. Three excellent examples of strong differentiation in Australia but not in North America are the upd2 region [X chromosome (Kolaczkowski et al. 2011)], the tip of the X chromosome, and the Cyp6g1 region [chromosome 2R (Daborn et al. 2002; Schmidt et al. 2010)] (Figure S3, Figure S4, and Figure S5).
Discussion
Phenotypic convergence of independent lineages across similar environments has been a fundamental, ubiquitous observation of evolutionary biology ever since Darwin. However, the degree to which convergent evolution at the phenotypic level is determined by convergent genetic changes is largely unknown (see Losos 2011 for a recent review). Our data suggest that the parallel phenotypic latitudinal clines in D. melanogaster are reflected in substantial convergent evolution at the genomic level (Table 4, Table 5, and Figure 4). This strongly supports the idea that selection on ancestral variation underlies much of the latitudinal differentiation on multiple continents in this species (Turner et al. 2008; Fabian et al. 2012). The alternative explanation, recurrent selected mutations occurring on multiple continents, not only is unlikely given the short timescales for population divergence in the United States and Australia, but also predicts substantial amounts of large physical scale differentiation, which is not evident. Similar patterns of parallel selection on ancestral variation have also been observed in replicated populations of freshwater sticklebacks (Hohenlohe et al. 2010; Jones et al. 2012). We observed substantial enrichment of convergent allele frequency changes in the United States and Australia, even for SNPs that are not extremely differentiated. This suggests that our empirical tail cutoffs are conservative and that dense sampling of several populations along latitudinal transects on both continents will reveal that a significant fraction of the genome exhibits parallel clines. While inversions are clearly important for latitudinal adaptation in this species, the strong patterns of parallelism observed at the SNP level are not strictly associated with regions spanned by inversions. Better sampling of genomes, populations, and continents will be necessary to quantitatively evaluate alternate models of selection on standing variation. Additional modeling of selection occurring on standing variation in the context of specific demographic models and underlying genomic patterns of linkage disequilibrium will also be important.
Nevertheless, inspection of Table 4 and Table 5 reveals a subset of protein-coding genes that show differentiation on each continent, but in different portions of the genes. For instance, at the 5% tail 807 genes are hit by at least one outlier window on each continent, but only 423 outlier windows are shared. If we ask how many genes in common are hit by only different outlier windows in both clines (i.e., exclude any gene that contains intersecting windows), we find that 374 genes are differentiated over different portions of the gene on each continent. This general pattern was observed at other tail cutoffs (not shown). Thus, while there is an abundance of exact convergence at the molecular level, there may also be adaptive divergence at the same gene that is proceeding through different changes. This situation mirrors what has been seen in other systems, including other Drosophila species, where a large portion of convergent evolution seems to be the result of nonidentical genetic changes (Gompel and Prud’homme 2009; Kopp 2009; Christin et al. 2010).
Supplementary Material
Acknowledgments
A.D.K. was supported in part by Rutgers University and National Science Foundation award MCB-1161367. D.J.B. was supported by National Institutes of Health grant GM084056. C.D.J. acknowledges the support of the University Cancer Research Fund.
Footnotes
Communicating editor: W. Stephan
Literature Cited
- Akey J. M., Zhang G., Zhang K., Jin L., Shriver M. D., 2002. Interrogating a high-density SNP map for signatures of natural selection. Genome Res. 12(12): 1805–1814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaumont M. A., Nichols R. A., 1996. Evaluating loci for use in the genetic analysis of population structure. Proc. R. Soc. Lond. B Biol. Sci. 263(1377): 1619–1626. [Google Scholar]
- Begun D. J., Aquadro C. F., 1993. African and North American populations of Drosophila melanogaster are very different at the DNA level. Nature 365: 548–550. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza L. L., Edwards A. W., 1967. Phylogenetic analysis. Models and estimation procedures. Am. J. Hum. Genet. 19(3 Pt 1): 233. [PMC free article] [PubMed] [Google Scholar]
- Christin P. A., Weinreich D. M., Besnard G., 2010. Causes and evolutionary significance of genetic convergence. Trends Genet. 26(9): 400–405. [DOI] [PubMed] [Google Scholar]
- Coop G., Witonsky D., Di Rienzo A., Pritchard J. K., 2010. Using environmental correlations to identify loci underlying local adaptation. Genetics 185: 1411–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daborn P. J., Yen J. L., Bogwitz M. R., Le Goff G., Feil E., et al. , 2002. A single P450 allele associated with insecticide resistance in Drosophila. Science 297(5590): 2253–2256. [DOI] [PubMed] [Google Scholar]
- David J. R., Capy P., 1988. Genetic variation of Drosophila melanogaster natural populations. Trends Genet. 4(4): 106–111. [DOI] [PubMed] [Google Scholar]
- Duchen P., Živković D., Hutter S., Stephan W., Laurent S., 2013. Demographic inference reveals African and European admixture in the North American Drosophila melanogaster population. Genetics 193: 291–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabian D. K., Kapun M., Nolte V., Kofler R., Schmidt P. S., et al. , 2012. Genome-wide patterns of latitudinal differentiation among populations of Drosophila melanogaster from North America. Mol. Ecol. 21(19): 4748–4769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gompel N., Prud’homme B., 2009. The causes of repeated genetic evolution. Dev. Biol. 332(1): 36–47. [DOI] [PubMed] [Google Scholar]
- Hoffmann A. A., Weeks A. R., 2007. Climatic selection on genes and traits after a 100 year-old invasion: a critical look at the temperate-tropical clines in Drosophila melanogaster from eastern Australia. Genetica 129(2): 133–147. [DOI] [PubMed] [Google Scholar]
- Hoffmann A. A., Sgrò C. M., Weeks A. R., 2004. Chromosomal inversion polymorphisms and adaptation. Trends Ecol. Evol. 19(9): 482–488. [DOI] [PubMed] [Google Scholar]
- Hohenlohe P. A., Bassham S., Etter P. D., Stiffler N., Johnson E. A., et al. , 2010. Population genomics of parallel adaptation in threespine stickleback using sequenced RAD tags. PLoS Genet. 6(2): e1000862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang D. W., Sherman B. T., Zheng X., Yang J., Imamichi T., et al. , 2009. Extracting biological meaning from large gene lists with DAVID. Curr. Protoc. Bioinformatics Chap. 13: Unit 13.11. [DOI] [PubMed] [Google Scholar]
- Jones F. C., Grabherr M. G., Chan Y. F., Russell P., Mauceli E., et al. , 2012. The genomic basis of adaptive evolution in threespine sticklebacks. Nature 484(7392): 55–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller A., 2007. Drosophila melanogaster’s history as a human commensal. Curr. Biol. 17(3): R77–R81. [DOI] [PubMed] [Google Scholar]
- Knibb W. R., 1982. Chromosome inversion polymorphisms in Drosophila melanogaster II. Geographic clines and climatic associations in Australasia, North America and Asia. Genetica 58(3): 213–221. [Google Scholar]
- Kirkpatrick M., Barton N., 2006. Chromosome inversions, local adaptation and speciation. Genetics 173(1): 419–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick M., Kern A., 2012. Where’s the money? Inversions, genes, and the hunt for genomic targets of selection. Genetics 190(4): 1153–1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolaczkowski B., Kern A. D., Holloway A. K., Begun D. J., 2011. Genomic differentiation between temperate and tropical Australian populations of Drosophila melanogaster. Genetics 187: 245–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopp A., 2009. Metamodels and phylogenetic replication: a systematic approach to the evolution of developmental pathways. Evolution 63(11): 2771–2789. [DOI] [PubMed] [Google Scholar]
- Kyriacou C. P., Peixoto A. A., Sandrelli F., Costa R., Tauber E., 2008. Clines in clock genes: fine-tuning circadian rhythms to the environment. Trends Genet 24: 124–132. [DOI] [PubMed] [Google Scholar]
- Lachaise D., Cariou M. L., David J. R., Lemeunier F., Tsacas L., et al. , 1988. Historical biogeography of the Drosophila melanogaster species subgroup. Evol. Biol. 22: 159–225. [Google Scholar]
- Langley C. H., Stevens K., Cardeno C., Lee Y. C. G., Schrider D. R., et al. , 2012. Genomic variation in natural populations of Drosophila melanogaster. Genetics 192: 533–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R., 2009. Fast and accurate short read alignment with Burrows–Wheeler transform. Bioinformatics 25(14): 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Losos J. B., 2011. Convergence, adaptation, and constraint. Evolution 65(7): 1827–1840. [DOI] [PubMed] [Google Scholar]
- Mackay T. F., Richards S., Stone E. A., Barbadilla A., Ayroles J. F., et al. , 2012. The Drosophila melanogaster genetic reference panel. Nature 482(7384): 173–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKechnie S. W., Blacket M. J., Song S. V., Rako L., Carroll X., et al. , 2010. A clinally varying promoter polymorphism associated with adaptive variation in wing size in Drosophila. Mol. Ecol. 19: 775–784. [DOI] [PubMed] [Google Scholar]
- Nei M., 1972. Genetic distance between populations. Am. Nat. 106: 283–292. [Google Scholar]
- Pavlidis P., Jensen J. D., Stephan W., Stamatakis A., 2012. A critical assessment of storytelling: gene ontology categories and the importance of validating genomic scans. Mol. Biol. Evol. 29(10): 3237–3248. [DOI] [PubMed] [Google Scholar]
- Pickrell J. K., Coop G., Novembre J., Kudaravalli S., Li J. Z., et al. , 2009. Signals of recent positive selection in a worldwide sample of human populations. Genome Res. 19(5): 826–837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sackton T. B., Kulathinal R. J., Bergman C. M., Quinlan A. R., Dopman E. B., et al. , 2009. Population genomic inferences from sparse high-throughput sequencing of two populations of Drosophila melanogaster. Genome Biol. Evol. 1: 449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saitou N., Nei M., 1987. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol. Biol. Evol. 4(4): 406–425. [DOI] [PubMed] [Google Scholar]
- Schmidt J. M., Good R. T., Appleton B., Sherrard J., Raymant G. C., et al. , 2010. Copy number variation and transposable elements feature in recent, ongoing adaptation at the Cyp6g1 locus. PLoS Genet. 6(6): e1000998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh R. S., Long A. D., 1992. Geographic variation in Drosophila: from molecules to morphology and back. Trends Ecol. Evol. 7(10): 340–345. [DOI] [PubMed] [Google Scholar]
- Stalker H. D., 1976. Chromosome studies in wild populations of D. melanogaster. Genetics 82: 323–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan W., Li H., 2007. The recent demographic and adaptive history of Drosophila melanogaster. Heredity 98(2): 65–68. [DOI] [PubMed] [Google Scholar]
- Teshima K. M., Coop G., Przeworski M., 2006. How reliable are empirical genomic scans for selective sweeps? Genome Res. 16(6): 702–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner T. L., Levine M. T., Eckert M. L., Begun D. J., 2008. Genomic analysis of adaptive differentiation in Drosophila melanogaster. Genetics 179: 455–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voelker R. A., Cockerham C. C., Johnson F. M., Schaffer H. E., Mukai T., et al. , 1978. Inversions fail to account for allozyme clines. Genetics 88: 515–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voight B. F., Kudaravalli S., Wen X., Pritchard J. K., 2006. A map of recent positive selection in the human genome. PLoS Biol. 4(3): e72. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.