Rapid slice excitation without B₀ gradients using large array coils

Abstract

In a large transmit planar pair phased array with the same power level in each channel, it is shown that controlling the phase shift between neighboring channels can yield different transmit slice thickness. Similarly, variation of the power level can move the slice less or further into the subject for imaging. The technique may be of particular interest as it allows curved slice excitation. These excitation patterns are achieved without complicated RF pulse sequences, i.e., without the use of multi-dimensional RF pulses. Simple simulations based on Biot-Savart law are used to predict the effect of the phase offset and power level variation. Planar and cylindrical formed planar pair coil arrays are both simulated and later built and tested using an MR scanner. The array is flexible and formed around the surface of objects under study, and the excitation is near the surface. Simulation results are compared with actual MRI images with good agreement. This technique is potentially useful for slice excitation in very rapid or ultra-short echo sequences.

Introduction

Both Transmit SENSE (1,2) and B₁ shimming (3,4) have successfully improved B₁ field homogeneity using transmit arrays with as few as two transmit elements. Transmit SENSE, while requiring a more complex pulse sequence and transmit chain, can also be used to generate localized patterns which can be useful in certain applications. In order to accelerate these specialized pulses, and in order to provide increased control in B₁ shimming, the number of transmit channels used in MRI is increasing. As the number of channels increases, it becomes increasingly possible to created tailored RF excitation using just B₁ shimming (5), or classical ‘phased array’ methods (6). Our group has constructed a 64 channel transmit system for purposes of single echo acquisition (SEA) imaging (7), SEA imaging allows a single image per echo acquisition, by fully replacing conventional phase encoding with the image localization provided by the array coils (8,9). For reasons discussed elsewhere, this has to date limited the technique to imaging along surfaces parallel to the array surface. Because speed is the driving interest in SEA imaging, this paper examines the possibility of performing slice excitation directly using the RF field provided by the array coil in transmit mode. It is shown that by optimizing the relative phases and power applied to the elements, it is possible to generate a ‘slice’ of excitation which can be varied in depth away from the array plane, useful for multi-slice or just single slice excitation at different locations. Importantly, by using large arrays, this is done without the use of static field gradients.

A planar pair (10,11) array element was used in SEA imaging. At a location which is very close to the array, the transmit field is mainly from the coil just below it. However, at a distance which is comparable to the coil to coil distance, contributions to the transmit field from nearby channels are on the same order as that from the one below it. In this case, the sensitivity must be considered. The total transmit field will be the sum of all the coils. Figure 1 shows the transmit field of three planar pair coils with fields from two different distances from coils. To achieve the maximum transmit efficiency at a certain point, we want transmit field from all contributing coils to be in phase at that point. This can be achieved by phase shifting the transmit signals applied to neighboring coils. However, this is limited to certain points only. To have the maximum transmit efficiency in a volume is more complicated and thus a numerical method is required.

Figure 1.

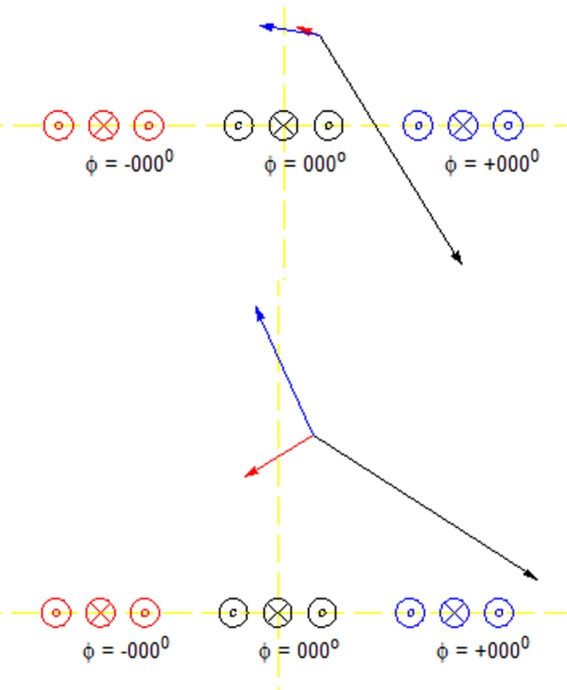
Excitation field of three planar pair coils at different distance from coil. Cross section of the coils is shown. Each coil has its own color, and corresponds to the arrow with the same color. At 0.5 D, where D is the inter-coil center to center distance between neighboring channels, the excitation is mainly contributed by the coil just below it. However, at 1.0 D, excitations from neighboring channels are no longer ignorable.

The transmit field for an array can be simulated. While full wave simulation software packages are widely available today, they are often expensive and/or difficult to use. But more importantly, full wave simulations are often too time consuming and thus not suitable for very large arrays. This is especially a problem when numerous iterations of the simulations become necessary, like in an optimization which is required here. Quasi-static or static simulations can be used when full wave effects can be safely ignored. MATLAB (MathWorks, MA, USA) is used to simulate the behavior of the transmit array. In such an array, the magnetic field pattern is limited to the very near field (millimeters), decaying quickly at increased distances, making it great for quasi-static or static simulations.

Methods

Figure 2 and Table 1 show the geometry and dimensions of the SEA array used in the simulations. The geometries are the same as the arrays which are actually built later for imaging. Two designs are simulated, planar and cylindrical. The cylindrical design is the same as the planar one other than dimensions, but is wrapped around a cylinder. Each design has equal size and spacing across coil elements. The array is placed in such a way that the array elements are aligned with the main magnetic field (Z direction) for both cases. In the planar case, the array is placed in the XZ plain with a phantom placed directly above it, like commonly done in SEA imaging. In the cylindrical case, the array is wrapped around a cylindrical phantom. For both cases, the currents on the three vertical elements are exp(jφ), –2·exp(jφ) and exp(jφ), where φ is the phase of RF excitation at the feeding point of the coil. There is a factor of –2 in the middle element because it carries double the current as compared with the two returning paths, and the direction of the current is opposite to the other two elements.

Figure 2.

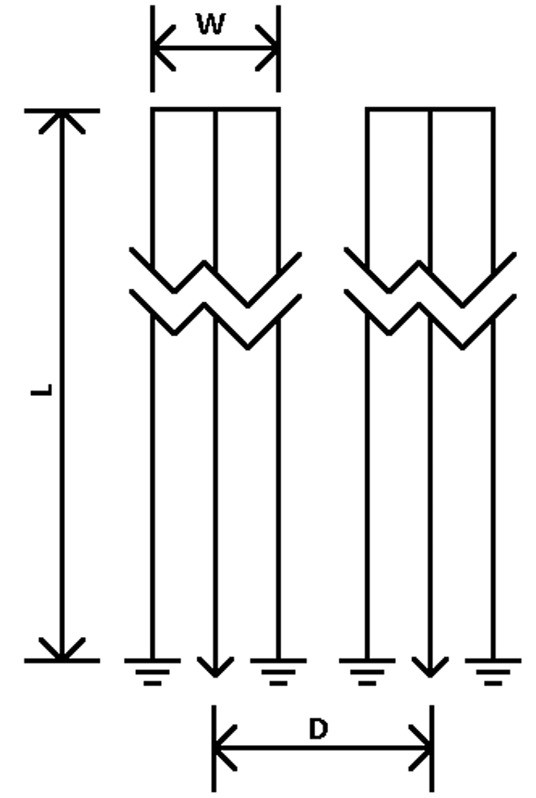
SEA coil geometry used in simulations. For simplicity, only two channels are shown here. The actual arrays used have 64 channels. Each element of the array is long and narrow, so it is truncated in the long direction in the drawing. W is for coil width, L is for coil length and D is for inter-coil center to center distance for nearest neighbors. The exact numbers are shown in Table 1. All these are listed in the unit of mils (1/1,000 inch). SEA, single echo acquisition.

Table 1. SEA coil dimensions used in simulations.

Case	W (mL)	L (mL)	D (mL)
Planar	60	2,980	80
Flexible	130	2,870	160

SEA, single echo acquisition.

The magnetic field generated by a finite length of wire can be calculated from static Biot-Savart law. It is well known that only magnetic field in the transverse plane (XY plane) contributes to the B₁ field. The transmit B₁ field (B₁⁺) can be calculated using:

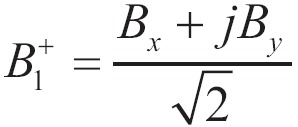[1]

Because the RF currents are expressed in complex scalars to carry both phase and amplitude, B_x and B_y calculated using Eq. [1] are also complex scalars. B₁⁺ is a complex scalar field, containing amplitude and phase of the transmit patterns. When using a uniform volume coil for receiving, the signal strength is proportional to sin(B₁⁺).

The simulations calculate the B₁⁺ field in a slice in the middle of the array, perpendicular to the main magnetic field (Z direction). For planar case, the field of interest (FOI) is above the array. For cylindrical case, the FOI is inside the array. Figure 3 shows the array elements and the FOI, with results, in the planar case.

Figure 3.

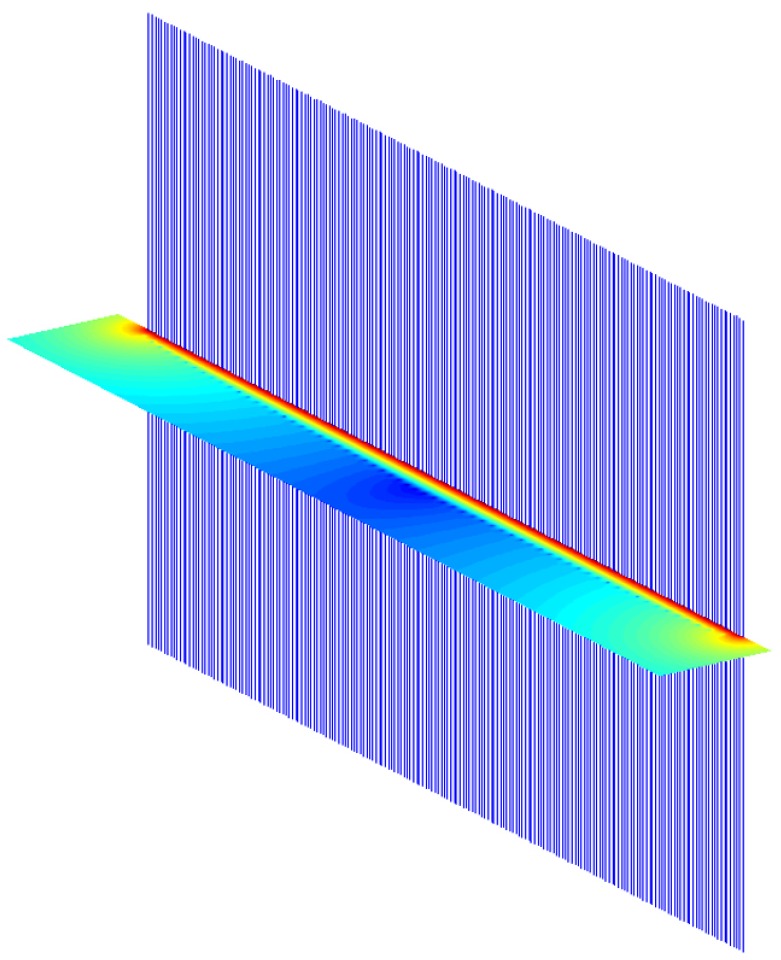
Simulation setup for planar case. The blue vertical lines are the coils. The colored area is the calculated B₁⁺ field, shown in log scale. In this simulation, the phase and amplitude of each coil element is set to be the same. By varying phase offset between neighboring channels, the excitation slice thickness (height of the red area) can be varied greatly.

Results

Varying slice thickness using phase offset

Planar case, transmit only

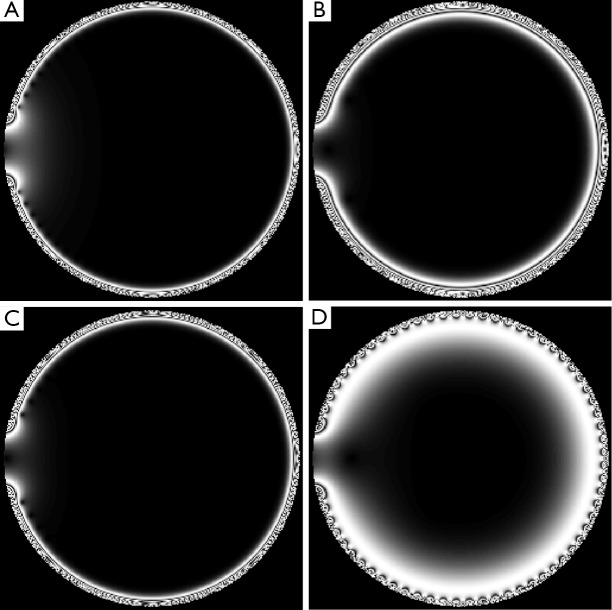
In the simulations, FOI was defined to be 142 mm (the total coil width is 130 mm for 64 channels) by 18.3 mm, 2 mm above the array, with a resolution of 0.2 mm in each direction in the simulation. Pseudo colored area in Figure 3 is the B₁⁺ filed intensity shown in log scale when the phases and power levels are the same across all 64 channels. The intensity of the field drops quickly as we move further away from the array, just as expected. The simulation area has a total width that is actually a little bit wider than the array, so that the “edge effects” can be visualized. Across nearest-neighbor coil element phase shift of 0° to 355°, with a step size of 5° are simulated. Simulated imaging results for 0°, 180°, 20° and 340° are shown in Figure 4 for the same power level.

Figure 4.

Simulated images for planar SEA array, with different phase offset between neighboring channels. By manipulating the phase shift across nearest neighbors, the transmit field slice thickness can be varied. The phase offset was set to be (A) 0°, (B) 180°, (C) 20° and (D) 340°. SEA, single echo acquisition.

The result might seem counter-intuitive that the optimal is neither 0° nor 180° that one might envision initially but around 340° for the coil with the geometry specified in Table 1. This value is related with the coil geometry and area of interest.

It is interesting that the excitation thickness can be manipulated by this phase offset. Here, a 340° phase offset across neighboring channels offer much thicker excitation slice than a 180° phase offset.

For verification of the simulation result, a transmit planar pair array is built for actual MR imaging. The physical coil has the same dimensions as used in the simulation. A photo of the planar transmit planar pair coil array with a uniform phantom is shown in Figure 5. A flat round container is filled with 1 g/L CuSO₄ doped agarose gel to use as a phantom. The whole setup is placed inside a parallel plate volume coil (not shown in the picture) for receiving. This setup is very similar to SEA imaging the only difference being that transmit and receive coils are reversed. A standard spin-echo sequence is used. The “90 degrees” pulses are transmitted using this surface array, while the 180 degrees pulses are transmitted using the volume coil. Please note that the actual transmitted “90 degrees” pulses have different flip angles across the phantom and thus the quotation make here. The 180 degrees pulses produce actual 180 degrees spin flips across the phantom assuming the volume coil is uniform enough. Imaging results using this setup are shown in Figure 6, confirming the simulation results.

Figure 5.

Planar SEA coil array. The traces of the coils are on the bottom side of the FR4 board. The rounded disk shaped container is the phantom which is filled with 1 g/L CuSO₄ doped agarose gel. A spin-echo sequence is used for imaging. The whole setup is placed inside a parallel plate volume coil (not shown in the picture) for transmit of 180° pulses and receiving while the planar SEA coil array is used for transmit of the 90° pulses. SEA, single echo acquisition.

Figure 6.

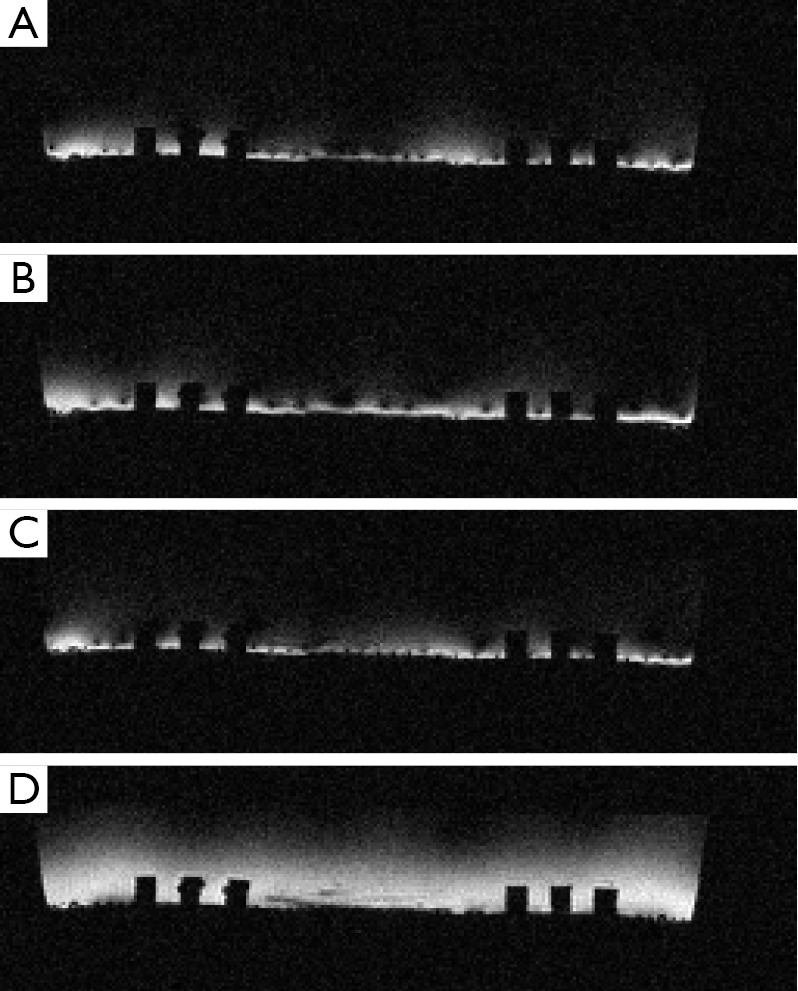
Acquired images of excitation field for planar SEA array. The phase offset is set to be (A) 0°, (B) 180°, (C) 20° and (D) 340°. Images are acquired using standard spin echo pulse sequence with TR 500 ms, TE 30 ms and FOV 140 mm × 140 mm in the axial slice. Please note that although the images are acquired fully encoded, the transmit pattern is achieved in a single shot. SEA, single echo acquisition.

Cylindrical case

Simulations for the cylindrical case are very similar to planar case. A flexible SEA coil array is wrapped around a cylinder. The simulations are only interested in the filed inside the coil. Result from outside has been simply masked out. The flexible SEA array used in this simulation is just about double comparing to the planar SEA array. As a result, similar results are developed. Simulated imaging results for 0°, 180°, 20° and 340° nearest neighbor phase shift are shown in Figure 7. Still 340° gives the thickest excitation slice.

Figure 7.

Simulated images for cylindrical SEA array, with the same power level but different phase offset between neighboring channels. The phase offset is set to be (A) 0°, (B) 180°, (C) 20° and (D) 340°. SEA, single echo acquisition.

Similarly, the cylindrical case is verified using MR images. The experiment setup is shown in Figure 8. A birdcage coil is used to replace the parallel plated used in the planar case experiment. The SEA coil is changed to a flexible one to wrap around the cylindrical shaped phantom. All other parts remain the same as the planar case experiments. Imaging results are shown in Figure 9, indicate optimal phase offset for penetration depth to be around 340°, just as simulation suggested.

Figure 8.

A flexible SEA array wrapped around a cylindrical phantom. The phantom inside is a cylindrical shaped container filled with 1 g/L CuSO₄ doped agarose gel. Using a spin echo sequence, the whole setup is placed inside a birdcage volume coil for transmit of 180° pulses and receiving while the SEA array is used for transmit of 90° pulses. SEA, single echo acquisition.

Figure 9.

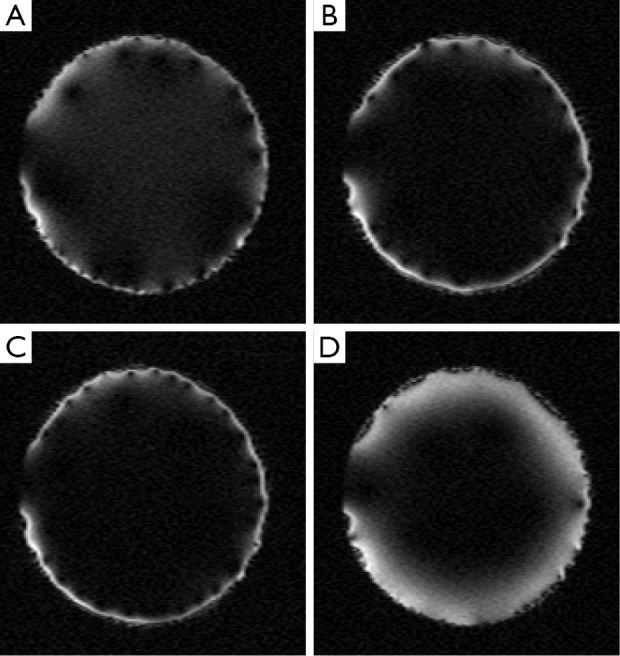
Acquired images for cylindrical SEA array, with different phase offset. The phase offset is set to be (A) 0°, (B) 180°, (C) 20° and (D) 340°. Images are acquired using standard spin echo pulse sequence with TR 500 ms, TE 30 ms and FOV 140 mm × 140 mm. SEA, single echo acquisition.

Varying slice position using RF power level

Besides slice thickness control using the phase offset, excitation slice offset from array can be moved by varying transmit power. In the simulation, by increasing the excitation current, the bright area advances more into the phantom. Here, 180° nearest neighbor phase offset is used. If thinner or thicker slice is needed, this phase offset can be adjusted accordingly. Using the same set as the planar case discussed in the previous section, with varying power, simulations as well as actual images were acquired, shown in Figure 10. Results indicate that the slice profile can be advanced deeper into the phantom with increased power.

Figure 10.

Moving slice of excitation using different transmit power, using simulations and images. Top four images are simulated and bottom four images are actually acquired images. For each group, from top to bottom, the transmit power is increased by 6 dB for each. The bottom one being 2 ms hard pulse for 10 W per channel. Dotted line in actual images is for reference and not artifact in the image. Because of spin couplings and interactions, the “grainy” area that is very close to the array becomes dark in actual images because the excitation phase variations within the voxel causes cancellation. This effectively makes the excitation slice moving into the subject for imaging.

Discussion and conclusions

Using simple phase shifts and flexible array, surface excitation is achieved using a large array of planar pair elements. For the relatively small (in wavelength) arrays considered here, these excitation patterns can be predicted and optimized using simple Biot-Savart law calculations. By varying phase offset between neighboring channels, it is possible to excite different slice thickness. By varying power level, the excitation slice can be moved less or further into the subject for imaging.

While the synthesis of the transmit pattern is simple and quite limited here, they enable surface excitation using a flexible array, allowing a curved slice excitation. Ordinarily this requires a very time consuming multi-dimensional pulse (12). It is also possible to do more interesting excitation patterns. The extension of this work to more complex RF pulses, such as some 2D shaped pulses should be straightforward. For example, it can easily be seen that one can selectively limit the excitation regions in the direction along the surface of the array and orthogonal to the coil elements by turning on only those channels under the interested region. Also excitation selection can be easily limited in Z direction by combining with a simple “slice selection” gradient using z gradient coil. A natural application of this method is to extremely rapid or very short echo time pulse sequences, where slice excitation using shaped RF pulses in gradients can be relatively time consuming.