Summary
Diverse cellular processes require microtubules to be organized into distinct structures, such as asters or bundles. Within these dynamic motifs, microtubule-associated proteins (MAPs) are frequently under load, but how force modulates these proteins’ function is poorly understood. Here, we combine optical-trapping with TIRF-based microscopy to measure the force-dependence of microtubule interaction for three non-motor MAPs (NuMA, PRC1, and EB1) required for cell division. We find that frictional forces increase non-linearly with MAP velocity across microtubules and depend on filament polarity, with NuMA’s friction being lower when moving towards minus-ends, EB1’s lower towards plus-ends, and PRC1 exhibiting no directional preference. Mathematical models predict, and experiments confirm, that MAPs with asymmetric friction can move directionally within active microtubule pairs they crosslink. Our findings reveal how non-motor MAPs can generate frictional resistance in dynamic cytoskeletal networks via micromechanical adaptations whose anisotropy may be optimized for MAP localization and function within cellular structures.
INTRODUCTION
Dynamic networks consisting of microtubules, motor proteins, and non-motor microtubule-associated proteins (MAPs) are employed by cells to carry out mechanical tasks. During cell division, for example, the mitotic spindle segregates chromosomes by physically pulling them apart into two daughter cells (Mitchison and Salmon, 2001). In order to effectively perform work, microtubules are organized by motor and non-motor MAPs into distinct architectures. Within these diverse motifs, microtubules are dynamically growing and shrinking, and can move with a wide range of speeds and in different directions. As a result, MAPs experience forces of varying magnitudes, timescales, and orientations which can modulate their function. Models of forces acting within microtubule networks broadly consider viscous drag parameters that oppose the forces produced by motor proteins, but such drag terms have not yet been linked to the force-dependent microtubule binding of specific non-motor MAPs (Vogel et al., 2009; Wollman et al., 2008).
Thus far, the force-velocity relationships of motor proteins, which consume ATP to generate directed motion and produce force, have been well examined. Single molecule force spectroscopy studies of motor proteins have shown that their stepping velocity can be decreased when they must work against an applied force and can increase when an assisting load is applied (Gennerich et al., 2007; Svoboda and Block, 1994; Valentine et al., 2006). These data suggest that the force-velocity relationship for motor proteins can be asymmetric relative to the polar microtubule, and may be linked to the orientation of a protein’s motor domain binding relative to the microtubule surface. Structural studies have suggested that non-motor MAPs may similarly make precise contacts with microtubule surfaces (Maurer et al., 2012; Subramanian et al., 2010). However, without direct measurements of non-motor MAP microtubule binding under load, we cannot formulate a relationship between force and velocity or determine whether there exist similar asymmetries relative to the polar filament.
Non-motor MAPs are essential for the maintenance of recurring microtubule geometries, such as asters and bundles (Peterman and Scholey, 2009; Subramanian and Kapoor, 2012). Within these motifs, non-motor MAPs achieve distinct localizations, despite the motion of the dynamic microtubule filaments, and it has been proposed that non-motor MAPs can act as brakes against motor protein driven filament sliding or tag unique microtubule features (Braun et al., 2011; Janson et al., 2007; Subramanian et al., 2013). During mitosis, several key MAPs are needed for the establishment of these distinct cytoskeletal motifs. NuMA, for example, is required to assemble spindle poles and asters, concentrating where microtubule minus-ends cluster (Gaglio et al., 1996; Gaglio et al., 1995). One of PRC1’s functions is to selectively crosslink anti-parallel microtubule bundles and accumulate within regions of filament overlap in vitro and in cells (Bieling et al., 2010; Mollinari et al., 2002; Subramanian et al., 2010). This activity of PRC1 is needed to assemble spindle midzones at anaphase and for the proper completion of cytokinesis. EB1 preferentially binds near the plus-end tips of growing microtubules, tracking these ends and recruiting a variety of proteins (Honnappa et al., 2009; Jiang and Akhmanova, 2011; Slep and Vale, 2007). Given such distinct distributions and functions within the dividing cell, these three non-motor MAPs serve as important test cases for microtubule interactions under controlled loads.
Here, we employ optical trapping and TIRF microscopy to characterize the microtubule interactions of NuMA, PRC1, and EB1 under mechanical load, measuring their response across different time-scales and with respect to microtubule orientation. We find that as the proteins move across microtubules, frictional forces develop that scale non-linearly with velocity. Surprisingly, the magnitudes of these forces vary uniquely with respect to filament polarity. NuMA requires less force to pull it towards minus-ends, EB1 requires less force to pull it towards plus-ends, while PRC1 does not exhibit a bias towards either microtubule end. Mathematical models predict, and experiments confirm, that mechanically perturbing parallel microtubules crosslinked by a dimeric NuMA construct leads to clustering of the non-motor MAP towards microtubule minus-ends. In contrast, perturbations to antiparallel microtubules crosslinked by either PRC1 or NuMA do not result in their directional movement. Our results suggest that the micromechanical properties of MAPs may be specifically tuned to self-organize active, non-equilibrium microtubule networks.
RESULTS
NuMA-microtubule binding under load is asymmetric with respect to filament polarity
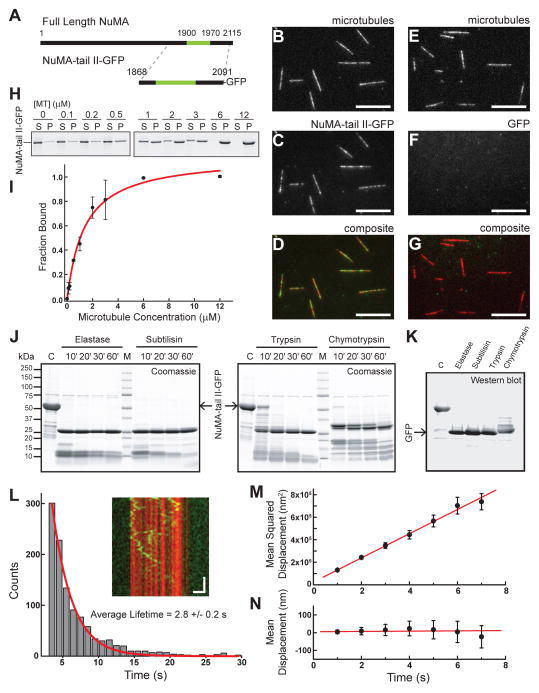
Of the three mitotic non-motor MAPs we examined, human NuMA is less well characterized. Therefore, we first focused on analyzing the biochemical properties of human NuMA. As full-length NuMA is a large (238 kDa) protein, we used a truncation that has been previously shown to recapitulate microtubule binding (Haren and Merdes, 2002), termed the ‘tail II’ domain (Merdes et al., 1996). GFP-tagged human NuMA-tail II (aa: 1868–2091, hereafter NuMA-tail II-GFP) (Figure 1A, S1A) was expressed in bacteria and characterized using four different assays. First, we confirmed that NuMA-tail II-GFP is a soluble monomer by both size exclusion chromatography and fluorescence intensity analysis (Figure S1A, S1C). Second, TIRF-based imaging indicates that NuMA-tail II-GFP binds, without bias, along microtubules (Figure 1B–D), while GFP alone does not (Figure 1E–G). Third, microtubule co-sedimentation assays indicated that NuMA-tail II-GFP binds microtubules with affinity (Kd=1.2 ± 0.2 μM; Hill coefficient: 1.2 ± 0.1) (Figure 1H,I) comparable to that of other MAPs, including PRC1 (Subramanian et al., 2010). Fourth, secondary structure prediction algorithms (results not shown) and limited proteolysis experiments revealed that this domain is not likely to contain stable secondary structure motifs in solution (Figure 1J, S1D); a persistent band at 26 kDa exhibited on the SDS-PAGE gels was confirmed to be the GFP tag (Figure 1K).
Figure 1.
Characterizations of NuMA’s microtubule binding. (A) Schematic depicting full-length NuMA and the truncated NuMA-tail II-GFP used in this study. The microtubule binding domain is highlighted in green (aa: 1900–1970). (B–D) NuMA-tail II-GFP (2 nM, green) binds surface-attached microtubules (red), as visualized via TIRF microscopy (B, microtubules; C, NuMA-tail II-GFP; D, composite). (E–G) GFP alone (2 nM) shows no microtubule localization (Scale bars = 10 μm). (H) Western blot-based analysis (anti-GFP) of NuMA-tail II-GFP’s microtubule binding. NuMA-tail II-GFP concentration was 1 μM. (I) Band intensities from (H) were used to determine fraction of protein bound, and were plotted against microtubule concentration; data were fit to the Hill equation (binding affinity Kd = 1.2 ± 0.2 μM; Hill coefficient = 1.2 ± 0.1 (N = 3 independent experiments). (J) SDS-PAGE analysis of limited proteolysis reactions performed on NuMA-tail II-GFP with four unique proteases reveals multiple low-molecular weight digestion products. (K) The persistent bands at 26 kDa in the gels shown in (J) were confirmed to be GFP by Western blot. (L) Diffusion of NuMA-tail II-GFP on the microtubule lattice plotted as a kymograph (inset: microtubule, red; NuMA-tail II-GFP, green. Vertical scale bar = 5 s, Horizontal scale bar = 2 μm). Histogram of binding lifetimes is fit to a single exponential (characteristic lifetime τ = 2.8 ± 0.2 s, N = 4 independent experiments, n = 1984 single particles). (M) The mean squared displacement of single molecule diffusion events is calculated for NuMA-tail II-GFP (n = 136 traces from N = 4 independent experiments). Fitting MSD = 2Dt + offset yields the diffusion constant, D = 53,700 ± 1,000 nm2/s. (N) Mean displacement analysis of the same diffusion events from (M) are fit to a linear relationship (slope = 0.8 ± 1.6 nm/s).
We next examined the microtubule binding of NuMA-tail II-GFP in the absence of external load. NuMA-tail II-GFP binds and diffuses on the microtubule lattice with a binding lifetime (2.8 ± 0.2 seconds; Figure 1L) similar to what has been measured for other MAPs (Dixit et al., 2009; Subramanian et al., 2010). The diffusion constant was measured using mean squared displacement analysis (D = 53,700 ± 1,000 nm2/s) (Figure 1M). Mean displacement analysis reveals that NuMA-tail II-GFP does not diffuse with a significant bias toward one microtubule end or the other (slope = 0.8 ± 1.6 nm/s) (Figure 1N). Similar analyses in buffer containing higher salt reveal that the binding lifetime decreases and diffusion constant increases for NuMA-tail II-GFP (as well as the other constructs used in this study, Figure S2A–D), consistent with the reported salt-dependence of other MAPs (Subramanian et al., 2010; Weinger et al., 2011). Together, these data indicate that human NuMA-tail II-GFP can bind microtubules with micromolar affinity, can undergo unbiased diffusion on the microtubule lattice, and interacts with microtubules via a region that is likely to be largely unstructured in solution, similar to non-motor MAPs such as tau or MAP2 (Tompa, 2002).
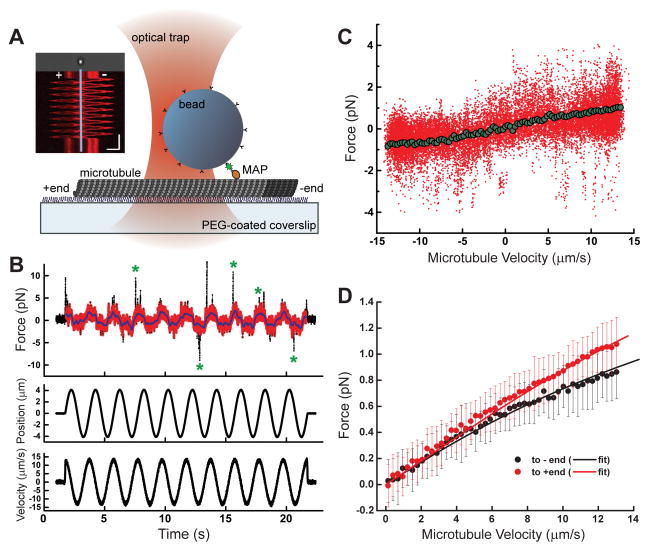
To measure microtubule interactions under applied load, we adapted an optical trap-based methodology used to analyze the drag and unbinding forces generated by motor proteins bound to microtubules (Bormuth et al., 2009; Uemura et al., 2002). Briefly, we employed a calibrated single beam optical trap (Figure S3A–B) to capture microbeads that were sparsely decorated with NuMA-tail II-GFP, such that primarily single NuMA-microtubule interactions were analyzed (Figure S4A–C). To examine the magnitude and directional dependence of bead-bound NuMA’s force response over a wide range of velocities, a polarity-marked microtubule was sinusoidally oscillated (frequency = 0.5 Hz, amplitude = 4 microns) (Figure 2A). Experiments performed using constant velocity ramps (7.5, 10, and 12.5 microns/s) yielded similar findings, consistent with no significant impact of possible force hysteresis in our sinusoidal analysis. (Figure S4F, G). An approximately equal distribution of ‘left’ versus ‘right’ polarity marked microtubules were selected to minimize possible biases in measurements (Figure S3G). Using a calibrated trap we determined the instantaneous force on the bead, and the microtubule position to calculate velocity (Figure 2B).
Figure 2.
Microtubule binding of NuMA under load. (A) Schematic of the optical trapping assay. A bead sparsely coated with NuMA-tail II-GFP is held above a polarity-marked microtubule, which is oscillated via a piezoelectric stage. Inset: kymograph depicts a representative time course of a polarity-marked microtubule’s motion (Scale bars: vertical = 5 s, horizontal = 4 μm). (B) Raw time series data for a single bead/microtubule pair is shown: force (raw data, black; processed data, red), microtubule position, and velocity are simultaneously recorded during 10 periods of oscillation. Green asterisks mark examples of transient force spikes. (C) Force data from (B) is plotted as a function of velocity (raw data, red; binned and averaged data, green). (D) The average force/velocity relationship for ~250 oscillation cycles taken with N = 15 bead/microtubule pairs is shown, with data parsed by dragging direction (black points = towards minus-end, red points = towards plus-end, error bars = SD). Black and red lines are from a fit using the model described in Figure 5 (R2 = 0.9962).
The raw force data (Figure 2B, black points) exhibited two prominent features. First, an oscillatory behavior is observed, with the maximum average force amplitude coinciding with the maximum microtubule velocity. The peak force values are significantly higher than the baseline viscous drag of either an uncoated trapped bead oscillating in the solution or control conditions in which either the MAP or microtubule were not present (Figure S3C–F). Second, infrequent large force spikes were observed (green asterisks, Figure 2B). As these events were also observed with statistically similar regularity in control experiments with MAP-bound beads and no microtubules, we attributed them to transient non-specific interactions (Figure S4D–E). We therefore developed a threshold-based methodology (Supplementary Information) to systematically remove these spikes from the data (Figure 2B, red) for subsequent analysis.
Binning and averaging these data as a function of velocity yields a mean force-velocity profile for each MAP-microtubule pair (Figure 2C). After aligning the data so all microtubule plus-end directed motion corresponded to positive force values, we averaged the force-velocity profiles for 15 unique bead/microtubule pairs, yielding a force-velocity relationship for NuMA’s microtubule binding under load (Figure 2D). The data was fit using a function detailed in Figure 5 (see below). The force was in the sub-pN range, and increased non-linearly up to a value of ~1 pN at the maximum microtubule velocity examined. Remarkably, the frictional force that arose when NuMA-tail II-GFP was dragged towards the plus-end of microtubules was higher than dragging towards the minus-end.
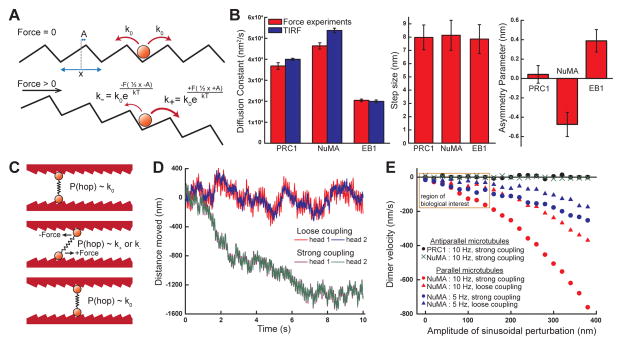
Figure 5.
Quantitative analyses of MAP-microtubule interactions under load. (A) A model depicting the modulation of the rate of diffusion both unloaded and under force. (B) Fits to the force-velocity relationships for all three proteins yield the diffusion constant D (red, force experiments; blue, TIRF imaging), step size between microtubule binding sites x, and asymmetry parameter A. (C) A schematic depicting the behavior of a dimerized microtubule crosslinker with mechanical properties calculated from (B). (D) Time courses of two simulations for dimerized crosslinking MAPs with asymmetric friction under periodic agitation (amplitude = 100nm, frequency = 10 Hz). Stronger coupling between the two microtubule binding domains yields faster directional motion. (E) Calculated dimer velocity as a function of amplitude of perturbation, for different coupling strengths, asymmetry values, and perturbation rates. Using parameters measured for NuMA, a frictionally asymmetric dimer exhibits minus-end directed motion under agitation of two parallel microtubules. A frictionally symmetric dimer (e.g., using PRC1’s measured parameters) or a frictionally asymmetric dimer crosslinking antiparallel microtubules (e.g., NuMA) exhibit no directional motion. (N = 100 independent simulation results per data point; region of primary biological interest at smaller amplitudes is highlighted).
PRC1-microtubule binding under load is symmetric with respect to filament polarity
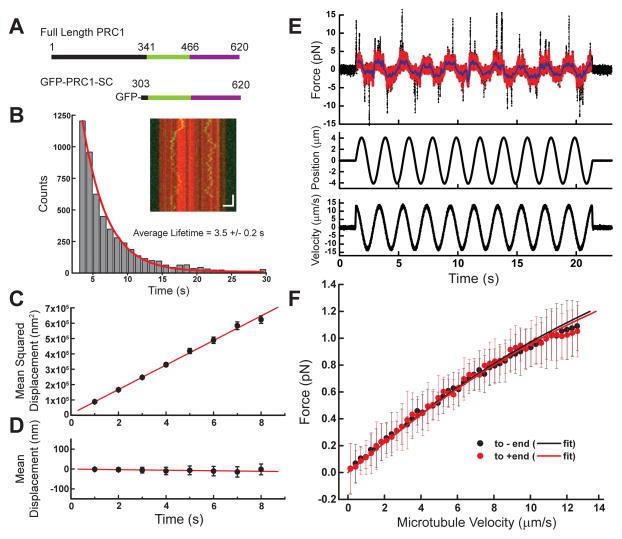
We next focused on human PRC1 microtubule binding, which is mediated by a spectrin domain and an unstructured C-terminus (Figure 3A). As NuMA’s microtubule binding domain was probed in its monomeric form, we sought to do the same with PRC1. To exclude effects of PRC1’s dimerization, we used a monomeric truncated construct consisting of the spectrin and tail domains (PRC1-SC, Kd = 0.6 ± 0.3 μM for microtubules) (Subramanian et al., 2010). We expressed and purified recombinant monomeric GFP-PRC1-SC in bacteria (Figure 3A, S1A). We find that GFP-PRC1-SC diffused on microtubules and resided on the lattice with a lifetime of 3.5 ± 0.2 seconds (Figure 3B). Mean squared displacement analysis revealed the diffusion constant (D = 39,900 ± 500 nm2/s) (Figure 3C), and GFP-PRC1-SC did not diffuse with a significant bias towards either microtubule end (slope = −1.3 ± 0.4 nm/s) (Figure 3D).
Figure 3.
Microtubule binding of PRC1 under load. (A) Schematic depicting full-length PRC1 and the monomeric GFP-PRC1-SC used for single molecule analysis. The microtubule binding regions are highlighted: spectrin domain (green) and unstructured tail (purple). (B) Diffusion of PRC1-SC on microtubules (inset: microtubule, red; GFP-PRC1-SC, green. Scale bars: vertical = 5 s, horizontal = 2 μm). Histogram of binding lifetime is fit to a single exponential (characteristic lifetime τ = 3.5 ± 0.2 s, N = 5 independent experiments, n = 7655 single particles). (C) The mean squared displacement of single molecule diffusion events is calculated for GFP-PRC1-SC (n = 233 traces from N = 5 independent experiments. Diffusion constant, D = 39,900 ± 500 nm2/s). (D) Mean displacement analysis of the same diffusion events from (C) are fit to a linear relationship (slope = −1.3 ± 0.4 nm/s). (E) Raw time series data for a single bead/microtubule pair: force (raw data, black; processed data, red), microtubule position, and microtubule velocity are shown. (F) The average force/velocity relationship for ~150 oscillation cycles taken with N = 9 bead/microtubule pairs (black points = towards minus-end, red points = towards plus-end, error bars = SD). Black and red lines are model fits (R2 = 0.9983).
We next measured the force generated as microtubule-bound PRC1 was subjected to external loads. Data appeared qualitatively similar to that from experiments performed with NuMA, revealing force oscillations that correlated with dragging velocity (Figure 3E). We averaged the force-velocity profiles from 9 independent bead/microtubules pairs (Figure 3F). The mean frictional force response of PRC1 is in the sub-pN range, similar to NuMA, and increases non-linearly as the velocity between the protein and microtubule is increased. However, there is little difference between pulling the protein towards the plus- or minus-end of the microtubule. This is in marked contrast to both our measurements of NuMA’s force response, as well as a previous analysis of a motor protein (Bormuth et al., 2009).
EB1-microtubule binding under load is asymmetric with respect to filament polarity
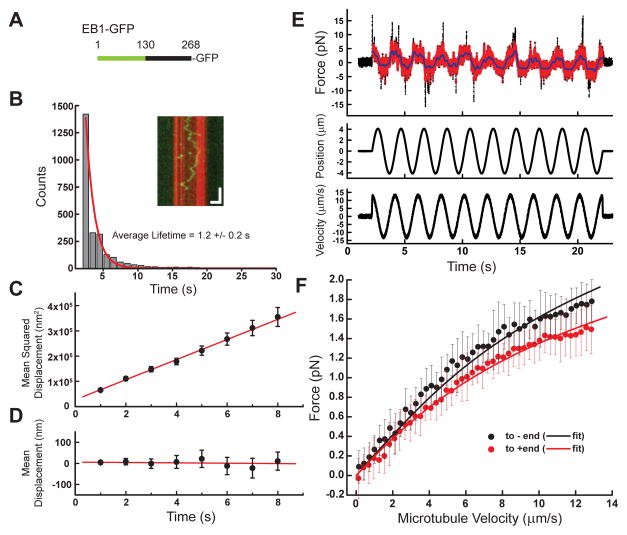
As a final test case, we focused on the human non-motor MAP EB1, whose microtubule binding is mediated by a calponin homology domain and a disordered region in the C-terminus (Buey et al., 2011; Hayashi and Ikura, 2003; Slep and Vale, 2007). To make a direct comparison with NuMA and PRC1, we probed EB1’s microtubule lattice binding. In previous studies, recombinant EB1 has been shown to track the tips of growing microtubules (Bieling et al., 2007), and is known to bind differentially with regard to the tubulin nucleotide binding state, preferring GTPγS (Maurer et al., 2012) or GMPCPP (Zanic et al., 2009) over the GDP-bound state. For all of our experiments, we utilized microtubules polymerized with GMPCPP to facilitate direct comparisons between the different MAPs we examined. We expressed in bacteria the full-length construct with a C-terminus fused GFP, termed EB1-GFP (Figure 4A). EB1-GFP binds and diffuses on the microtubule lattice with a shorter lifetime (1.2 ± 0.2 seconds, Figure 4B), but also a smaller diffusion constant (D = 19,900 ± 500 nm2/s, Figure 4C) than either PRC1-SC or NuMA-tail II, and we did not observe a significant directional bias of diffusion on the microtubule surface (slope = −0.9 ± 1.4 nm/s) (Figure 4D).
Figure 4.
Microtubule binding of EB1 under load. (A) Schematic depicting full length EB1-GFP construct used in this study. The calponin homology domain (aa:1–130) is highlighted (green). (B) Diffusion of EB1 on the microtubule lattice (inset: microtubule, red; EB1-GFP, green. Scale bars: vertical = 5 s, horizontal = 2 μm). Histogram of binding lifetime is fit to a single exponential (characteristic lifetime τ = 1.2 ± 0.2 s, N = 4 independent experiments, n = 2626 single particles). (C) The mean squared displacement of single molecule diffusion events is calculated for EB1-GFP (n = 144 traces from N = 4 independent experiments. Diffusion constant, D = 19,900 ± 500 nm2/s. (D) Mean displacement analysis of the same diffusion events from (C) are fit to a linear relationship (slope = −0.9 ± 1.4 nm/s). (E) Raw time series data for a single bead/microtubule pair: force (raw data, black; processed data, red), microtubule position, and microtubule velocity are shown. (F) The average force/velocity relationship for ~180 oscillation cycles taken with N = 11 bead/microtubule pairs (black points = towards minus-end, red points = towards plus-end, error bars = SD). Black and red lines are model fits (R2 = 0.9946).
Optical trapping experiments reveal that EB1 experiences larger frictional forces when dragged across microtubules than either NuMA or PRC1 (Figure 4E). Binning and averaging force data from 11 separate bead-microtubule pairs reveals that EB1, like NuMA-tail II, experiences an asymmetry in its frictional response, but this asymmetry is inverted relative to the microtubule polarity (Figure 4F). Together, these data reveal the micromechanical properties of three non-motor MAPs under load. Strikingly, these three different MAPs have varied responses with respect to dragging direction across the polar microtubule surface.
A simple model predicts that frictional asymmetry can lead to directional motion in active networks
To quantitatively describe the data, we considered models that account for the force-dependent modulation of a particle’s diffusive behavior. A simple model, which was employed to quantify the frictional response of budding yeast kinesin-8, could be readily applied (Bormuth et al., 2009). Briefly, a protein interacting with a microtubule possesses a diffusion constant that defines the rate at which it hops between binding sites. If a force is applied, this rate is modulated by an Arrhenius-like term that can possess directional asymmetry (Figure 5A; see Supplemental Information for further details). The force-velocity relationships for NuMA, PRC1, and EB1 are all well fit to this model (Figure 2D, 3F, 4F), and three free parameters are extracted: the diffusion constant D, the distance between adjacent binding sites x, and an asymmetric distance parameter A, which represents the change in distance from the binding state to the energy barrier with respect to the direction along which force is applied (Figure 5B).
The diffusion constants for all three proteins, independently measured from both the optical trapping experiments and TIRF imaging, closely agree (Figure 5B). The step size x for all three proteins was found to be ~8nm (Figure 5B), which is consistent with the αβ-tubulin dimer spacing, as well as with the observed binding periodicity from cryo-EM reconstructions of EB1- and PRC1-decorated microtubules (Maurer et al., 2012; Subramanian et al., 2010). It will be important to test whether this is also the case for NuMA. Finally, the asymmetry parameter for PRC1-SC was found to be 0.04 ± 0.09 nm, consistent with a lack of preferred directionality in the force-velocity relationship. NuMA’s asymmetry parameter was determined to be −0.48 ± 0.12 nm, indicating that more force is required to drag the protein away from the minus-ends of microtubules. For EB1, this parameter was determined to be 0.39 +/− 0.10 nm, indicating that more force is required to drag the protein away from the plus-ends of microtubules (Figure 5B). These values quantitatively confirm differences in the frictional symmetry for three different MAPs.
NuMA and PRC1 likely function in the cell as microtubule crosslinkers. In this geometry, two microtubule-binding domains connected via a dimerization region would mechanically crosslink two different microtubules. We devised Monte Carlo simulations for ‘dimerized’ microtubule binding domains possessing the measured mechanical properties to predict how MAPs would behave in the context of crosslinked filaments (Figure 5C, S5A–B, and Supplemental Information). If the microtubules are static, the dimer undergoes 1D diffusion, with no directional preference, regardless of the binding asymmetry. However, if one of two microtubules in a parallel geometry is driven periodically, directional motion of a dimer containing two microtubule-binding domains with frictional asymmetry can emerge. For example, oscillations at 10 Hz with amplitudes on the order of tens to hundreds of nm results in minus-end directed migration at rates on the order of tens of nm/s; the more tightly coupled the domains, the faster the resulting motion (Figure 5D). Therefore, domains which are linked by stiff structural motifs, such as the coiled-coil domains found in many MAPs (Compton et al., 1992; Subramanian et al., 2013), will travel faster than domains which are well separated by floppy or torsionally relaxed coupling domains. Simulations reveal that the asymmetric binding possessed by NuMA-tail II results in the migration of the dimer complex to the parallel microtubules’ minus-ends. In contrast, crosslinkers whose microtubule binding under load is symmetric, such as PRC1 or NuMA crosslinking antiparallel microtubules, do not exhibit directional motion, regardless of how much external perturbation is applied or how tightly the domains are coupled (Figure 5E).
Dimeric NuMA-bonsai-tail II can bundle microtubules and localize to spindle poles
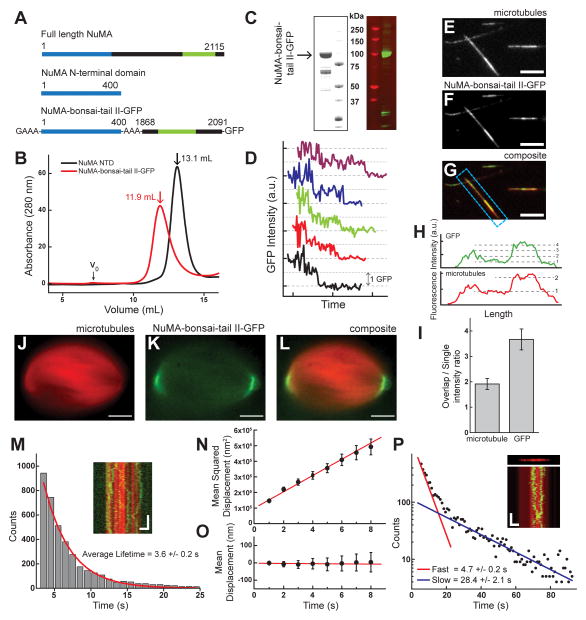
To test these predictions, we designed a dimerized NuMA-tail II construct (Figure 6A). As recombinant full-length NuMA has proven biochemically intractable, we first expressed a portion of the N-terminus, termed NuMA NTD (N-terminal domain, aa 1–400). Light scattering analysis of NuMA NTD revealed that this construct is a dimer (Figure S1B). We next expressed a construct consisting of NuMA-NTD fused to NuMA-tail II-GFP (which we term NuMA-bonsai-tail II-GFP) (Figure 6A). Gel filtration data for both NuMA NTD and NuMA-bonsai-tail II-GFP further reveal that both constructs are dimers (Figure 6B,C). Western blots confirmed the major band to be full length NuMA-bonsai-tail II-GFP (Figure 6C), while mass spectrometry indicated that the minor bands were NuMA derived, but without the GFP tag and would likely not interfere with our fluorescence based analyses (Figure S6A–B). Further efforts to reduce the minor bands (30% of major band) that co-purify with NuMA-bonsai-tail II-GFP over a multistep purification were not successful, likely due to this protein not having well defined secondary structural motifs that would limit adventitious proteolysis (Figure 1J). Finally, we confirmed that NuMA-bonsai-tail II-GFP is dimeric by a photo-bleaching assay (Figures 6D, S1C).
Figure 6.
NuMA-bonsai-tail II-GFP is a dimer that can crosslink two microtubules. (A) Schematic depicting NuMA constructs (dimerization domain, blue; microtubule binding domain, green). (B) Gel filtration profiles for both NuMA-NTD (black) and NuMA-bonsai-tail II (red). Void (V0) and peak volumes indicated. (C) SDS-PAGE gel and a Western blot against GFP in gels run with NuMA-bonsai-tail II-GFP. (D) Sample time courses of fluorescence photo-bleaching shows multiple intensity steps. Traces are offset for clarity. (E–G) Microtubule bundles formed with NuMA-bonsai. Microtubules (E), NuMA-bonsai-tail II-GFP (F), composite (G) are shown (scale bars = 5 μm). (H) Linescans of the bundle highlighted in (G). (I) Comparison of microtubule and GFP intensity between single microtubule and overlap regions for bundles formed with NuMA-bonsai-tail II-GFP (N=17 pairs). (J–L) Localization of NuMA-bonsai-tail II-GFP at the poles of metaphase spindles assembled in Xenopus egg extract. Microtubules (J), GFP signal (K), and composite (L) images are presented (scale bars = 10 μm). (M) Diffusion of NuMA-bonsai-tail II-GFP on the microtubule lattice (inset: microtubule, red; NuMA-bonsai-tail II-GFP, green. Vertical scale bar = 5 s, Horizontal scale bar = 2 μm). Histogram of binding lifetime is fit to a single exponential (characteristic lifetime τ = 3.6 ± 0.2 s, N = 3 independent experiments, n = 3929 single particles). (N) The mean squared displacement of single molecule diffusion events is calculated for NuMA-tail II-GFP (n = 94 traces from N = 3 independent experiments. Diffusion constant, D = 26,000 ± 1,200 nm2/s. (O) Mean displacement analysis of the diffusion events from (N) are fit to a linear relationship (slope = −0.6 ± 0.9 nm/s). (P) Diffusion of NuMA-bonsai-tail II-GFP in microtubule bundle (inset: microtubule, red; NuMA-bonsai-tail II-GFP, green. Vertical scale bar =20 s, Horizontal scale bar = 2 μm). Histogram of binding lifetimes is fit to double exponential (τ 1=4.7 ± 0.2 s, τ2=28.4 ± 2.1 s, N = 3 independent experiments).
We next confirmed that this construct can bundle microtubule pairs by building ‘sandwiches’ and visualizing them by TIRF microscopy. Briefly, NuMA-bonsai-tail II-GFP (50 nM) was added to biotinylated microtubules immobilized on a coverslip surface. Biotin-free microtubules were then added to generate ‘sandwiches’. Microtubules and NuMA-bonsai-tail II-GFP were imaged (Figure 6E–G), and intensity analysis revealed that NuMA-bonsai-tail II-GFP (Figure 6I) has a higher preference (~ 4-fold) for overlap regions than single microtubules. While NuMA-tail II-GFP does not bundle microtubules at similar concentrations (50 nM), it does bundle microtubules at higher concentrations (200 nM), possibly by forming higher order aggregates in the presence of microtubules, and is therefore unsuitable for testing our model’s predictions (Figure S6C–D). We further confirmed that NuMA-bonsai-tail II-GFP localized to the poles of spindles assembled in Xenopus egg extract (Figure 6J–L). NuMA-tail II-GFP also localizes at spindle poles, but forms aggregates and does not present the same characteristic ‘crescent’ localization pattern as NuMA-bonsai-tail II-GFP (Figure S6E–F). We next measured the binding lifetime of NuMA-bonsai-tail II-GFP on single microtubules (3.6 ± 0.2 seconds, Figure 6M), and performed mean squared displacement analysis (D = 26,000 ± 1,200 nm2/s, Figure 6N) and mean displacement analysis (slope = −0.6 ± 0.9 nm/s, Figure 6O). Finally, we measured the binding lifetime of NuMA-bonsai-tail II-GFP in bundles by ‘spiking’ GFP-labelled and unlabeled NuMA-bonsai-tail II to visualize single molecules. By fitting the lifetime data to a double exponential, we were able to measure two populations (fast, 4.7 ± 0.2 seconds and slow, 28.4 ± 2.1 seconds, Figure 6P). We infer that the fast time constant describes ‘passenger’ molecules that bind single microtubules, while the slower time constant describes NuMA molecules that crosslink both microtubules. Together, these data suggest that NuMA-bonsai-tail II-GFP crosslinks microtubules and recapitulates proper spindle pole targeting.
NuMA-bonsai-tail II moves to cluster at the minus ends of mechanically oscillated microtubule pairs
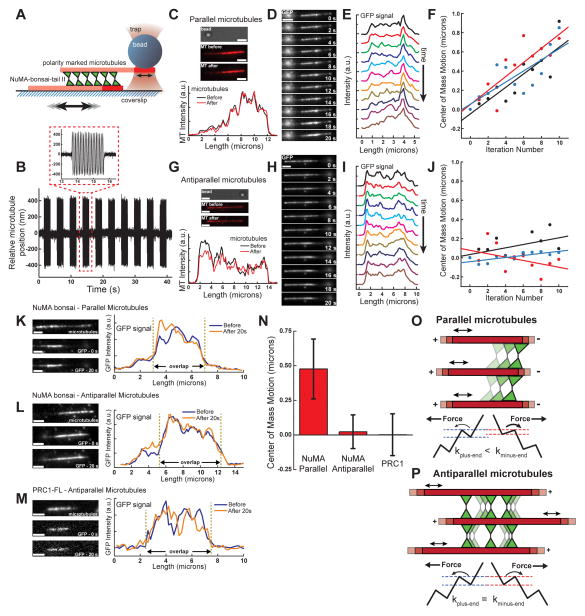
To examine if crosslinking proteins that possess frictional asymmetry move directionally on microtubules, we developed an assay that allowed for the direct manipulation of microtubules crosslinked by dimerized NuMA-bonsai-tail II-GFP. We generated ‘sandwiches’ using polarity-marked microtubules and attached a bead to the end of the free microtubule such that controlled fluctuations between crosslinked microtubules could be generated (Figure 7A). By sinusoidally oscillating the stage and trapping the bead with a greater trap stiffness (0.2 pN/nm), we were able to perturb the relative position of the microtubules within the bundle (Figure 7B).
Figure 7.
Frictional asymmetry can give rise to directional motion of non-motor MAPs in dynamic microtubule arrays. (A) Schematic of the optical trapping assay. (B) Time course of microtubule relative motion. The microtubules are oscillated for 2 seconds, followed by a 2 second pause for imaging. (C) Images of the bead and microtubules, and intensity linescans before and after perturbations are shown for a parallel microtubule ‘sandwich.’ (D) Time course of GFP fluorescence images taken after each microtubule oscillation event. (E) Linescans of GFP intensity from images shown in (D). (F) ‘Center-of-mass’ positions of fluorescence signals taken for 3 parallel microtubule pairs. (G) Images of the bead and microtubules, and intensity linescans before and after perturbations are shown for an antiparallel microtubule ‘sandwich.’ (H) Time course of GFP fluorescence images taken after each microtubule oscillation event. (I) Linescans of GFP intensity from images shown in (H). (J) ‘Center-of-mass’ positions of fluorescence signals taken for 3 antiparallel microtubule pairs. Scale bars = 2 μm. (K–M) Microtubule image, GFP images before and after perturbations, and linescans of GFP intensities for (K) parallel microtubules crosslinked by NuMA-bonsai-tail II-GFP, (L) antiparallel microtubules crosslinked by NuMA-bonsai-tail II-GFP, and (M) antiparallel microtubules crosslinked by PRC1. Scale bars = 2 μm. (N) Change in position of the center of mass of GFP fluorescence after 20 seconds of perturbations at 10 Hz (NuMA, Parallel: N=10; NuMA, Antiparallel: N=9; PRC1, Antiparallel: N=10). (O) MAPs with asymmetric friction would cluster towards microtubule minus-ends in asters. A schematic of the energy landscape under force shows how rates of MAP motion differ with respect to filament polarity. (P) MAPs with asymmetric friction would remain evenly distributed in antiparallel microtubule bundles. A schematic of the energy landscape under force shows how rates of MAP motion remain the same with respect to filament polarity.
We determined the distribution of NuMA-bonsai-tail II-GFP by TIRF microscopy after a series of brief (2 s) bursts of oscillation followed by a pause (2 s) to image the GFP signal. For parallel microtubules pairs (Figure 7C), we observed a time-dependent increase in NuMA density within the overlap region in the direction of the minus ends of the microtubules (Figure 7D). Linescans of the GFP signal were made at each time point (Figure 7E), and the fluorescence ‘center-of-mass’ position was calculated (Figure S7A). This position moved towards the microtubule minus ends at rates of ~50–75 nm/s (Figure 7F). When antiparallel microtubule sandwiches (Figure 7G) were similarly perturbed, we did not observe directional clustering in the GFP intensity (Figure 7H), and the intensity ‘center of mass’ of NuMA-bonsai-tail II-GFP within the bundle remained largely unchanged (Figure 7I,J). Importantly, for each of the antiparallel and parallel bundles examined, the total GFP intensity in the region of microtubule overlap did not significantly vary over the time course of the experiments (Figure S7B–C), indicating that the observed clustering is not due to changes in relative filament geometry. We next analyzed the total displacement of the center-of-mass position of the GFP intensity signal from before perturbation to its value after 20 seconds for NuMA-bonsai-tail II-GFP crosslinking parallel microtubules (Figure 7K), antiparallel microtubules (Figure 7L), and dimeric full length GFP-PRC1 crosslinking antiparallel microtubules (Figure 7M). This analysis indicates that NuMA-bonsai-tail II-GFP moves towards microtubule minus ends when in a parallel configuration, but not in an antiparallel configuration, and PRC1 does not exhibit directional motion within bundles (Figure 7N). We find that faster microtubule oscillations lead to faster NuMA motion in parallel microtubule bundles, in agreement with our predictions (Figure S7D–H).
DISCUSSION
The assembly of microtubule-based structures required for successful cell division depends on non-motor MAPs that must experience significant forces during this dynamic process. We have shown that for three different non-motor MAPs, frictional forces that scale non-linearly with velocity are generated as MAPs move across microtubule surfaces and microtubule binding under load can differ with respect to filament geometry. Further, frictional asymmetry can give rise to directed clustering of crosslinking MAPs within active microtubule networks.
Our measurements of the microtubule binding under load of single non-motor MAPs reveal a relationship between the velocity of MAP motion and frictional force. At low velocities, this relationship is approximately linear, resembling the classic Stokes’ viscous drag relation. Cytoskeletal motifs are frequently organized by clusters of non-motor MAPs, and the collective effect of many frictional elements may lead to significant viscous drag. Our measurements reveal that a single NuMA microtubule binding domain, for example, could produce frictional resistance of ~0.1 pN at microtubule velocities of 1 μm/s, which is the rate at which dynein can step under zero external load (Toba et al., 2006). As NuMA is clustered at spindle poles, we estimate that there could be on the order of 20 NuMA molecules per microtubule (Supplementary Information). If frictional forces scale linearly with MAP number, these interactions would generate a total resistive force of 2 pN per microtubule, which is comparable to forces generated by motor proteins (Mallik et al., 2004; Valentine et al., 2006). The clustered micron-scale distributions of PRC1 at anaphase spindle midzones and EB1 ‘comets’ at the growing ends of microtubules may result in similar scaling of frictional forces in these structures (Bieling et al., 2007; Mollinari et al., 2002). Our data therefore suggests that non-motor MAPs within microtubule networks in cells may function as viscous elements.
Remarkably, despite having similar magnitudes of frictional resistance, the three MAPs in these studies each have a unique asymmetry with respect to the direction of applied load. This asymmetry can be linked to the order in which bonds that mediate the interactions with microtubules are broken. Our studies suggest that under load, ‘peeling’ these interactions away sequentially from one direction requires more work than ‘peeling’ them from the opposite direction. Similar behavior has been shown in experiments performed by ‘unzipping’ a DNA double helix, which revealed that the forces required to mechanically separate the DNA’s paired bases varied when the order in which bases were broken was changed (Hall et al., 2009). As we currently lack detailed structural models for how the MAPs used in this study, particularly their unstructured regions, bind to microtubule surfaces, it is challenging to link our results to specific interactions and the order of their disruption. Our studies also reveal that MAPs that exhibit frictionally asymmetric microtubule binding while crosslinking different filaments can undergo motion if the microtubules are actively driven. Periodic agitation of microtubules may be common within the context of the spindle, as proximal poleward fluxing microtubules can have broad velocity distributions, and entire spindles can undergo oscillations during asymmetric cell division (Pecreaux et al., 2006; Yang et al., 2007). Additionally, the antagonistic activity of plus- and minus-end directed motor proteins is required to organize spindle poles (Gaglio et al., 1996), and can result in instabilities that give rise to fluctuating microtubule sliding behavior (Hentrich and Surrey, 2010). The corresponding region of biological relevance is highlighted accordingly in Figure 5E, suggesting non-motor MAPs possessing frictional asymmetry could move at velocities comparable to those of mitotic motor proteins.
Our analyses of the micromechanics of non-motor MAPs suggest models for how they may contribute to successful cell division. For example, the clustering of NuMA within asters could produce several pN of frictional drag against a single microtubule’s motion, and may be linked to the decrease in microtubule flux velocity observed near spindle poles (Yang et al., 2008). In dividing cells, NuMA has been shown to reside at spindle poles with long lifetimes (~3 minutes) (Kisurina-Evgenieva et al., 2004). These long lifetimes could result in directional motion arising from asymmetric friction of NuMA in response to microtubule fluctuations within the spindle, leading to persistent NuMA localization at spindle poles where microtubule minus-ends cluster (Figure 7O). Longer range transport of NuMA across the spindle could be driven by dynein (Merdes et al., 1996), though biochemical evidence supporting a direct interaction is lacking. Consistent with this model, when dynein/dynactin activity is inhibited in spindles and spindle-like ‘pineapples’, NuMA can still be seen bundling microtubule minus ends at disrupted poles (Heald et al., 1997; Merdes et al., 2000; Mitchison et al., 2013). Similarly, EB1 is known to interact with a variety of proteins that contain a SxIP domain, including microtubule binding proteins kinesin-5, Tastin, and DDA3 (Jiang et al., 2012). If these binding partners interact with both EB1 and other microtubules within dense filament networks, then EB1 may mediate linkages between different microtubules, favoring the maintenance of interactions at microtubule plus-ends. Conversely, a protein that lacks frictional asymmetry or preferentially crosslinks antiparallel microtubules, such as PRC1, would remain uniformly distributed throughout the region of overlap in the face of microtubule fluctuations (Figure 7P). Within the spindle midzone, PRC1’s uniform distribution could persist regardless of external perturbations to the microtubules, contributing to the successful completion of the final stages of cell division.
The directional motion and clustering of non-motor MAPs that lack enzymatic activity appears to be problematic from the perspective of thermodynamics. Models of directional motion for motor proteins consider the hydrolysis of ATP as a symmetry-breaking external source of energy (Bustamante et al., 2001; Magnasco, 1993). Motor proteins can diffuse along the microtubule lattice, but the binding and hydrolysis of ATP serves to rectify the thermal fluctuations and lead to directional motion. The non-motor MAPs examined here, however, do not harness energy from nucleotide hydrolysis. Instead, our results show that external mechanical perturbations coupled with frictional asymmetry can play a similar rectification role and result in the directional motion of non-motor MAPs. It is important to stress that in the absence of such externally applied energy, we predict that crosslinking proteins will diffuse without directional preference, and therefore no useful work is performed via thermal fluctuations alone.
The behavior of non-motor proteins under load can be considered in terms of familiar mechanical analogs. The asymmetric friction described in this work can be likened to a toy finger trap, where pulling in one direction produces more resistance than pulling in the other. Such behavior may inform on the function of non-motor proteins within dynamic polymer networks, including not just microtubules, but also DNA- and actin-based systems. Motor proteins, such as kinesins and myosins in the case of cytoskeletal filaments, and polymerases or helicases in the case of DNA and RNA, can generate external forces that give rise to polymer dynamics. It is likely that these proteins’ frictional resistance to motion will depend on polymer orientation, and additional studies are needed to examine these interactions under load. Our findings suggest that tuned frictional symmetry could result in distinct directional motions and distributions of passively bound non-motor proteins to self-organize complex and diverse biological networks.
EXPERIMENTAL PROCEDURES
Optical Trapping
A 1064nm single mode TEM00 laser (CrystaLaser IRCL-2W-1064, 2 Watt CW laser) was collimated, expanded with a 2X telescope, and steered with a 1:1 telescope onto a NA-1.49 100X Plan Apo TIRF objective (Nikon) which was housed in a Nikon Eclipse Ti microscope. Sample chambers were mounted on a 3-axis piezo-electric stage (Mad City Labs Nano LP-200) which could be moved via computer control (custom built LabView 2010 routines) or driven by an external voltage from a function generator.
After interacting with the trapped bead in the sample volume, the laser light was collected by an NA-1.4 condenser lens (MEL-41410, oil immersion, Nikon), redirected by a dichroic mirror, and focused onto a quadrant photodiode position sensitive detector (QP50-6SD2, Pacific Silicon Sensors, plus homemade electronics). The output signal was digitized using a National Instruments PCI-6251 M-Series DAQ card, and was sampled at 10 kHz for all experiments. Data was acquired and processed using software routines written in LabView.
Sample chamber preparation
Sample chambers were made using 18 mm2 coverslips that had been coated with biotin-PEG/PEG in a 1:75 ratio. Flow chambers (~8–10 μL volume) were built by applying two strips of double-sided tape to a microscope slide and applying the coverslip. Chambers were incubated with casein (0.5mg/mL) in 1XBRB80 (80mM K-PIPES, pH 6.8, 1mM MgCl2, 1mM EGTA) for 2 minutes, then washed with 3 chamber volumes (CV) of 1XBRB80 to remove any unbound protein. Neutravidin at 0.5 mg/mL in 1XBRB80 was incubated for 2 minutes, followed by washing. Next, microtubules, in a buffer containing 1XBRB80, 20μM taxol, and 80mM KCl, were introduced at concentrations such that 10–20 microtubules were visible per field of view were incubated for 5 minutes.
For all experiments, buffer was composed of 1XBRB80 (80mM K-PIPES, pH 6.8, 1mM MgCl2, 1mM EGTA), 20μM taxol, 0.5mg/mL filtered casein, oxygen depletion system (40 μg/mL glucose oxidase, 35 μg/mL catalase, 25mM glucose, 2mM DTT), and the addition of either protein-coated beads (optical trapping) or protein (fluorescence imaging). All experiments were performed at 23°C.
Fluorescence microscopy
Images were acquired with an Andor iXon DU-897 EM-CCD camera (typical exposure time = 200 ms, EM gain = 200). TIRF excitation was achieved with a 488 nm DPSS laser (Spectra-physics) for GFP, and a 561 nm DPSS laser (Cobalt) for X-rhodamine. Image collection was performed with Andor iQ software. Image analysis was performed with both ImageJ and custom-written LabView software.
Supplementary Material
Research Highlights.
Motion along microtubules of non-motor proteins generates friction
Magnitudes of frictional force differ for three proteins needed for cell division
Frictional forces can be anisotropic with respect to filament polarity
Asymmetric friction can lead to motion of proteins in active microtubule networks
Acknowledgments
We would like to thank R. Subramanian for assistance with protein construct design, expression and purification; D. Compton for the gift of NuMA cDNA; and K. Sato and M. Magnasco for helpful discussions about theoretical calculations. The SEC-LS/UV/RI instrumentation was supported by NIH Award Number 1S10RR023748-01 (PI: EFS) S.F. acknowledges postdoctoral support from NIH NRSA Fellowship F32GM099380. K.-C. H. is supported by a Special Fellow Award from The Leukemia & Lymphoma Society. T.M.K. acknowledges support from the NIH (GM65933).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bieling P, Laan L, Schek H, Munteanu EL, Sandblad L, Dogterom M, Brunner D, Surrey T. Reconstitution of a microtubule plus-end tracking system in vitro. Nature. 2007;450:1100–1105. doi: 10.1038/nature06386. [DOI] [PubMed] [Google Scholar]
- Bieling P, Telley IA, Surrey T. A Minimal Midzone Protein Module Controls Formation and Length of Antiparallel Microtubule Overlaps. Cell. 2010;142:420–432. doi: 10.1016/j.cell.2010.06.033. [DOI] [PubMed] [Google Scholar]
- Bormuth V, Varga V, Howard J, Schaffer E. Protein Friction Limits Diffusive and Directed Movements of Kinesin Motors on Microtubules. Science. 2009;325:870–873. doi: 10.1126/science.1174923. [DOI] [PubMed] [Google Scholar]
- Braun M, Lansky Z, Fink G, Ruhnow F, Diez S, Janson ME. Adaptive braking by Ase1 prevents overlapping microtubules from sliding completely apart. Nat Cell Biol. 2011;13:1259–U1201. doi: 10.1038/ncb2323. [DOI] [PubMed] [Google Scholar]
- Buey RM, Mohan R, Leslie K, Walzthoeni T, Missimer JH, Menzel A, Bjelic S, Bargsten K, Grigoriev I, Smal I, et al. Insights into EB1 structure and the role of its C-terminal domain for discriminating microtubule tips from the lattice. Mol Biol Cell. 2011;22:2912–2923. doi: 10.1091/mbc.E11-01-0017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bustamante C, Keller D, Oster G. The physics of molecular motors. Accounts Chem Res. 2001;34:412–420. doi: 10.1021/ar0001719. [DOI] [PubMed] [Google Scholar]
- Compton DA, Szilak I, Cleveland DW. Primary Structure of NuMA, an Intranuclear Protein That Defines a Novel Pathway for Segregation of Proteins at Mitosis. J Cell Biol. 1992;116:1395–1408. doi: 10.1083/jcb.116.6.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixit R, Barnett B, Lazarus JE, Tokito M, Goldman YE, Holzbaur ELF. Microtubule plus-end tracking by CLIP-170 requires EB1. Proc Natl Acad Sci U S A. 2009;106:492–497. doi: 10.1073/pnas.0807614106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaglio T, Saredi A, Bingham JB, Hasbani MJ, Gill SR, Schroer TA, Compton DA. Opposing motor activities are required for the organization of the mammalian mitotic spindle pole. J Cell Biol. 1996;135:399–414. doi: 10.1083/jcb.135.2.399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaglio T, Saredi A, Compton DA. NuMA is Required for the Organization of Microtubules into Aster-Like Mitotic Arrays. J Cell Biol. 1995;131:693–708. doi: 10.1083/jcb.131.3.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gennerich A, Carter AP, Reck-Peterson SL, Vale RD. Force-induced bidirectional stepping of cytoplasmic dynein. Cell. 2007;131:952–965. doi: 10.1016/j.cell.2007.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall MA, Shundrovsky A, Bai L, Fulbright RM, Lis JT, Wang MD. High-resolution dynamic mapping of histone-DNA interactions in a nucleosome. Nat Struct Mol Biol. 2009;16:124–129. doi: 10.1038/nsmb.1526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haren L, Merdes A. Direct binding of NuMA to tubulin is mediated by a novel sequence motif in the tail domain that bundles and stabilizes microtubules. J Cell Sci. 2002;115:1815–1824. doi: 10.1242/jcs.115.9.1815. [DOI] [PubMed] [Google Scholar]
- Hayashi I, Ikura M. Crystal structure of the amino-terminal microtubule-binding domain of end-binding protein 1 (EB1) Journal of Biological Chemistry. 2003;278:36430–36434. doi: 10.1074/jbc.M305773200. [DOI] [PubMed] [Google Scholar]
- Heald R, Tournebize R, Habermann A, Karsenti E, Hyman A. Spindle assembly in Xenopus egg extracts: Respective roles of centrosomes and microtubule self-organization. J Cell Biol. 1997;138:615–628. doi: 10.1083/jcb.138.3.615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hentrich C, Surrey T. Microtubule organization by the antagonistic mitotic motors kinesin-5 and kinesin-14. J Cell Biol. 2010;189:465–480. doi: 10.1083/jcb.200910125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honnappa S, Gouveia SM, Weisbrich A, Damberger FF, Bhavesh NS, Jawhari H, Grigoriev I, van Rijssel FJA, Buey RM, Lawera A, et al. An EB1-Binding Motif Acts as a Microtubule Tip Localization Signal. Cell. 2009;138:366–376. doi: 10.1016/j.cell.2009.04.065. [DOI] [PubMed] [Google Scholar]
- Janson ME, Loughlin R, Loiodice I, Fu CH, Brunner D, Nedelec FJ, Tran PT. Crosslinkers and motors organize dynamic microtubules to form stable bipolar arrays in fission yeast. Cell. 2007;128:357–368. doi: 10.1016/j.cell.2006.12.030. [DOI] [PubMed] [Google Scholar]
- Jiang K, Akhmanova A. Microtubule tip-interacting proteins: a view from both ends. Current Opinion in Cell Biology. 2011;23:94–101. doi: 10.1016/j.ceb.2010.08.008. [DOI] [PubMed] [Google Scholar]
- Jiang K, Toedt G, Gouveia SM, Davey NE, Hua SS, van der Vaart B, Grigoriev I, Larsen J, Pedersen LB, Bezstarosti K, et al. A Proteome-wide Screen for Mammalian SxIP Motif-Containing Microtubule Plus-End Tracking Proteins. Curr Biol. 2012;22:1800–1807. doi: 10.1016/j.cub.2012.07.047. [DOI] [PubMed] [Google Scholar]
- Kisurina-Evgenieva O, Mack G, Du QS, Macara I, Khodjakov A, Compton DA. Multiple mechanisms regulate NuMA dynamics at spindle poles. J Cell Sci. 2004;117:6391–6400. doi: 10.1242/jcs.01568. [DOI] [PubMed] [Google Scholar]
- Magnasco MO. Forced Thermal Ratchets. Phys Rev Lett. 1993;71:1477–1481. doi: 10.1103/PhysRevLett.71.1477. [DOI] [PubMed] [Google Scholar]
- Mallik R, Carter BC, Lex SA, King SJ, Gross SP. Cytoplasmic dynein functions as a gear in response to load. Nature. 2004;427:649–652. doi: 10.1038/nature02293. [DOI] [PubMed] [Google Scholar]
- Maurer SP, Fourniol FJ, Bohner G, Moores CA, Surrey T. EBs Recognize a Nucleotide-Dependent Structural Cap at Growing Microtubule Ends. Cell. 2012;149:371–382. doi: 10.1016/j.cell.2012.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merdes A, Heald R, Samejima K, Earnshaw WC, Cleveland DW. Formation of spindle poles by dynein/dynactin-dependent transport of NuMA. J Cell Biol. 2000;149:851–861. doi: 10.1083/jcb.149.4.851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merdes A, Ramyar K, Vechio JD, Cleveland DW. A complex of NuMA and cytoplasmic dynein is essential for mitotic spindle assembly. Cell. 1996;87:447–458. doi: 10.1016/s0092-8674(00)81365-3. [DOI] [PubMed] [Google Scholar]
- Mitchison TJ, Nguyen P, Coughlin M, Groen AC. Self-organization of stabilized microtubules by both spindle and midzone mechanisms in Xenopus egg cytosol. Mol Biol Cell. 2013;24:1559–1573. doi: 10.1091/mbc.E12-12-0850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchison TJ, Salmon ED. Mitosis: a history of division. Nat Cell Biol. 2001;3:E17–E21. doi: 10.1038/35050656. [DOI] [PubMed] [Google Scholar]
- Mollinari C, Kleman JP, Jiang W, Schoehn G, Hunter T, Margolis RL. PRC1 is a microtubule binding and bundling protein essential to maintain the mitotic spindle midzone. J Cell Biol. 2002;157:1175–1186. doi: 10.1083/jcb.200111052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pecreaux J, Roper JC, Kruse K, Julicher F, Hyman AA, Grill SW, Howard J. Spindle oscillations during asymmetric cell division require a threshold number of active cortical force generators. Curr Biol. 2006;16:2111–2122. doi: 10.1016/j.cub.2006.09.030. [DOI] [PubMed] [Google Scholar]
- Peterman EJG, Scholey JM. Mitotic Microtubule Crosslinkers: Insights from Mechanistic Studies. Curr Biol. 2009;19:R1089–R1094. doi: 10.1016/j.cub.2009.10.047. [DOI] [PubMed] [Google Scholar]
- Slep KC, Vale RD. Structural basis of microtubule plus end tracking by XMAP215, CLIP-170, and EB1. Molecular Cell. 2007;27:976–991. doi: 10.1016/j.molcel.2007.07.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian R, Kapoor TM. Building Complexity: Insights into Self-Organized Assembly of Microtubule-Based Architectures. Dev Cell. 2012;23:874–885. doi: 10.1016/j.devcel.2012.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian R, Ti SC, Tan L, Darst SA, Kapoor TM. Marking and Measuring Single Microtubules by PRC1 and Kinesin-4. Cell. 2013;154:377–390. doi: 10.1016/j.cell.2013.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian R, Wilson-Kubalek EM, Arthur CP, Bick MJ, Campbell EA, Darst SA, Milligan RA, Kapoor TM. Insights into Antiparallel Microtubule Crosslinking by PRC1, a Conserved Nonmotor Microtubule Binding Protein. Cell. 2010;142:433–443. doi: 10.1016/j.cell.2010.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svoboda K, Block SM. Force and Velocity Measured for Single Kinesin Molecules. Cell. 1994;77:773–784. doi: 10.1016/0092-8674(94)90060-4. [DOI] [PubMed] [Google Scholar]
- Toba S, Watanabe TM, Yamaguchi-Okimoto L, Toyoshima YY, Higuchi H. Overlapping hand-over-hand mechanism of single molecular motility of cytoplasmic dynein. Proc Natl Acad Sci U S A. 2006;103:5741–5745. doi: 10.1073/pnas.0508511103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tompa P. Intrinsically unstructured proteins. Trends in Biochemical Sciences. 2002;27:527–533. doi: 10.1016/s0968-0004(02)02169-2. [DOI] [PubMed] [Google Scholar]
- Uemura S, Kawaguchi K, Yajima J, Edamatsu M, Toyoshima YY, Ishiwata S. Kinesin-microtubule binding depends on both nucleotide state and loading direction. Proc Natl Acad Sci U S A. 2002;99:5977–5981. doi: 10.1073/pnas.092546199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentine MT, Fordyce PM, Krzysiak TC, Gilbert SP, Block SM. Individual dimers of the mitotic kinesin motor Eg5 step processively and support substantial loads in vitro. Nat Cell Biol. 2006;8:470–U489. doi: 10.1038/ncb1394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogel SK, Pavin N, Maghelli N, Julicher F, Tolic-Norrelykke IM. Self-Organization of Dynein Motors Generates Meiotic Nuclear Oscillations. Plos Biology. 2009;7:918–928. doi: 10.1371/journal.pbio.1000087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinger JS, Qiu MH, Yang G, Kapoor TM. A Nonmotor Microtubule Binding Site in Kinesin-5 Is Required for Filament Crosslinking and Sliding. Curr Biol. 2011;21:154–160. doi: 10.1016/j.cub.2010.12.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wollman R, Civelekoglu-Scholey G, Scholey JM, Mogilner A. Reverse engineering of force integration during mitosis in the Drosophila embryo. Molecular Systems Biology. 2008;4:13. doi: 10.1038/msb.2008.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang G, Cameron LA, Maddox PS, Salmon ED, Danuser G. Regional variation of microtubule flux reveals microtubule organization in the metaphase meiotic spindle. J Cell Biol. 2008;182:631–639. doi: 10.1083/jcb.200801105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang G, Houghtaling BR, Gaetz J, Liu JZ, Danuser G, Kapoor TM. Architectural dynamics of the meiotic spindle revealed by single-fluorophore imaging. Nat Cell Biol. 2007;9:1233–U1245. doi: 10.1038/ncb1643. [DOI] [PubMed] [Google Scholar]
- Zanic M, Stear JH, Hyman AA, Howard J. EB1 Recognizes the Nucleotide State of Tubulin in the Microtubule Lattice. Plos One. 2009;4:5. doi: 10.1371/journal.pone.0007585. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.