Applications of alignment-free methods in epigenomics

Abstract

Epigenetic mechanisms play an important role in the regulation of cell type-specific gene activities, yet how epigenetic patterns are established and maintained remains poorly understood. Recent studies have supported a role of DNA sequences in recruitment of epigenetic regulators. Alignment-free methods have been applied to identify distinct sequence features that are associated with epigenetic patterns and to predict epigenomic profiles. Here, we review recent advances in such applications, including the methods to map DNA sequence to feature space, sequence comparison and prediction models. Computational studies using these methods have provided important insights into the epigenetic regulatory mechanisms.

INTRODUCTION

A fundamental biological question is to understand the function of the genome. Recent work has shown that the majority of the genome may be functional [1]. However, comprehensive functional annotation of the genome remains a daunting task. Development of computational methods has been essential for functional annotation. In particular, it has been a long tradition to use sequence alignment methods, such as BLAST [2] and FASTA [3], to generate initial biological hypotheses. In the past few years, the computational efficiency of sequence alignment has been improved greatly, enabling the rapid processing of large amounts of sequences [4,5].

Although the power of alignment-based methods has been well-demonstrated in a broad range of applications, their applications are not unlimited. When using a sequence-alignment method, one must make two basic assumptions:

1. The functional elements share common sequence features; and

2. The relative order of these elements is conserved between different sequences.

However, the latter assumption is often violated for cis-regulatory elements, where there is little evidence suggesting the order between different elements would have any significant effect in regulating gene expression. In fact, many important regulatory elements are distal to transcription start sites, and it is the three-dimensional chromatin structure that facilitates their regulatory interactions [6]. As such, the recently developed alignment-free methods [7] have emerged as a promising approach to investigate the regulatory genome.

During the past decade, epigenetics has become increasingly recognized as an important layer of control of gene activities. Epigenetic regulation refers to heritable changes of gene expression that occur without alteration of the DNA base sequence [8]. Using an analogy, we can think that the genomic DNA represents all the potential functions of the ‘software of the cell’, while the epigenetic mechanisms dictate some control on which features are enabled/disabled in each particular cell type, specializing this ‘software’.

While epigenetics and genetics were studied in isolation in early studies, recent studies have shown that they are indeed closely related [9]. It has been increasingly recognized that the genomic sequence plays an important role in guiding epigenetic pattern specificity. However, a major challenge is that, unlike transcription factors (TFs), most epigenetic factors do not or weakly interact with the DNA. While epigenetic factors can be brought to specific DNA sequences through interaction with TFs, they rarely have unique interacting factors [10]. As a result, their association with DNA sequence patterns is, in general, much weaker than TFs.

An emerging field of research is to apply alignment-free methods to study the link between the genome and epigenome. In particular, a number of alignment-free methods have been previously used to predict genome-wide epigenetic patterns and to identify the sequence elements that play a regulatory role in establishing epigenetic patterns. In this article, we review recent progress in this exciting direction.

EPIGENETICS PATTERN AND DNA SEQUENCES

Epigenetic mechanisms include nucleosome positioning, histone modifications and DNA methylation. The primary repeating unit of chromatin is the nucleosome, which consists of 147 bp of DNA wrapped 1.67 times around an octamer of core histone proteins [11]. The N-terminal ends of the histones are unstructured and called the histone tails. Many amino acid residues on the histone tails can be covalently modified, and many of these modifications have distinct biological functions [12]. An important task is to characterize the biological function of the combinatorial states of multiple histone marks [12]. Covalent modification can also occur at the DNA level [13], where the cytosine nucleotide can be methylated at the 5′ position.

The field of epigenomics has been growing rapidly in the past few years, in part because of the development of genome-wide profiling technologies [14–19] and new specialized computational approaches [20–22]. Previous studies have identified strong relationship between epigenetic patterns, TF binding and downstream gene activities. Dynamic changes of epigenetic patterns are strongly associated with developmental control, environmental response and disease susceptibilities. Several computational approaches have been developed to characterize the genome-wide chromatin states [23–28]. Insights obtained from these studies have been essential for developing new therapeutic approaches [29].

The underlying mechanisms for the establishment and maintenance of cell type-specific epigenetic patterns are complex and involve the dynamic interactions among multiple classes of factors, including chromatin modifiers, DNA binding proteins, noncoding RNAs and signaling molecules [10,30]. However, the relative contribution of each factor remains poorly understood. One fundamental question is to what extent the epigenomic patterns are orchestrated by the underlying DNA sequence. Previous studies have shown that, at least for a subset of epigenetic marks, the DNA sequence plays an important role in targeted recruitment to specific genomic regions [31]. Distinct DNA sequence features have been identified to be associated with nucleosome positioning [32], DNA methylation [33] and histone modifications [34], and methods have been developed to predict genome-wide patterns, sometimes with great accuracy. Such a strong association with DNA sequence features may be surprising at first sight, but it is not incompatible with the fundamental property that epigenetic patterns may change without change of DNA sequences. What this means is that the DNA sequence may mark specific regions where epigenetic pattern changes are likely to occur, but the cell type-specific patterns still depend on the activities of chromatin regulators and mediating TFs, which may be further regulated by inputs from various signaling pathways or other mechanisms. Interestingly, the most informative sequence features are those that are traditionally viewed as ‘degenerative’, such as CpG density and poly-A tract [9], posing a severe challenge for alignment-based methods. In the meantime, the development of alignment-free methods has provided a promising alternative to overcoming such challenges.

MAPPING SEQUENCE TO FEATURE SPACE

To identify common sequence features associated with an epigenetic pattern, a major task is to compare multiple DNA sequences. Traditionally, sequence comparison is achieved by multiple sequence alignment and quantified by a quality score [35]. However, it is infeasible to align a large set of sequences because of overwhelming computational cost. Furthermore, for sequence-alignment methods to be effective, one must assume that the underlying sequences are highly conserved, which is often violated in epigenomics.

In contrast, alignment-free methods make no assumption regarding sequence conservation or the order between elements [7]. To compare different sequences, a first step is to project each sequence into a suitably selected feature space, where sequence information is transformed to numerical information, thereby enabling the application of various established mathematical and probabilistic tools for comparison.

In particular, a DNA sequence s is represented as a string of L symbols from a finite alphabet Σ of length r. We indicate as 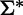the set of all the strings that can be obtained by finite successions of symbols in the alphabet Σ. Any generic string s is mapped to a vector 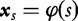(the feature vector) by a particular mapping function , allowing a representation of s into a multidimensional space (the feature space) 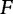, where a particular distance function between the vectors can be adopted to reflect the observed similarities between sequences. Here we summarize a few commonly used representations of feature spaces.

Mapping by word composition and k-mers

One of the most common ways of defining sequence features is by enumerating the frequency of occurrence of a finite set of preselected words. The simplest and most common choice of word list is k-mers, i.e. any string of length k whose symbols are taken in the oligonucleotide alphabet (A,T,C,G). In this case, each sequence s is mapped to a vector in a 4^k dimensional feature space.

In general, each numerical component 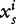of the feature vector is set to the value 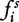that represents the frequency of the i-th k-mer 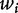in s, each one counted by a sliding window of length k that is run through the sequence s, from position 1 to L − k + 1. Another possible choice is to set 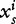to the empirical probability 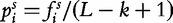, leading to the application of information-based distances.

The mapping of sequences to the space of k-mers is widely used in epigenetic context; it has been used to study the nucleosome positioning [36–38], to characterize the complexity of the sequence associated with particular histone modifications [39], to predict histone modification patterns [40] and to predict DNA methylation patterns [41–43].

Mapping to suffix tree

Because of the large number of possible k-mers, it is often desirable to reduce the complexity by selecting a subset of k-mers for detailed analysis. One of the commonly used techniques to achieve this goal is to use efficient data structures for string operations like suffix tree [44], Burrows–Wheeler transform [45], suffix array [46] and compressed index [47].

A suffix tree T of a string s on a finite alphabet ∑ is defined as a tree containing all the suffixes of s. In particular, each suffix of s corresponds to one path in T. Given a generic string s of length L_s, its suffix tree can be constructed in linear time O(L_s) and the search of any string t with length L_t ≤ L_s in s is O(L_t) (this result holds also for a finite number of mismatches in t). For these reasons suffix trees and related data structures are widely used in sequence-alignment software, such as BWA [48] and BOWTIE [49]. In contrast, in the alignment-free context these structures are used to efficiently evaluate distances or similarity measures based on word composition, where the computational cost scales linearly with respect to the word length. Of particular interest is a distance function proposed by Apostolico et al. [50] based on the enumeration of all the possible k-mers of different and finite length in linear time. A similar idea is used by another study, which defines a general similarity measure [51]. In particular, this measure does not compute all the possible k-mers present in the sequences, but instead calculates only the optimal word length to use. In addition, suffix trees have been used to define distance functions based on compressibility by extensible motifs, i.e. motifs that may contain a finite number of gaps [52].

Suffix trees have been used in the context of epigenomics, for example, to predict hypomethylated regions and CpG islands using hexamer alphabets [53] and to investigate the DNA sequence periodicity associated with nucleosome positioning [54]. In the latter study, Rasheed et al. [55]applied suffix trees to detect repeating dinucleotide subsequences in nucleosomal DNA, using as input a list of known chicken and yeast nucleosomal DNA sequences in the literature. Random sequences extracted from the respective genomes are used as control. Periodicity is detected by searching for subsequences containing recurrent dinucleotides at the following positions:

where p is the period, i a position in the sequence, j an integer and W is the width of the sliding window. They found that around 90% of the nucleosome sequences contain periodic subsequences accordingly to the above criterion, while only 10% of the random sequences have such a property. In this application, the application of suffix tree is essential for achieving sufficient numerical efficiency.

Mapping into spatially extended signal space

A sequence s of length L can also be mapped into a spatially extended signal space. Starting from a finite set of n fixed word length segments w_i, the component 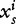is a one-dimensional binary digital signal defined by:

where k is the length of w_i.

An advantage of using this kind of representation is that it takes into account the spatial ‘shape’, which may have favorable binding energy. There are a large number of digital signal processing techniques like convolution, classical Fourier or wavelet analysis that can be used to discover spatially extended patterns.

In the particular problem of nucleosome positioning prediction, the signal representation has shown particular merits. Starting from a training set of nucleosome sequences, the probability density 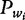of a dinucleotide 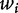at each position of a sequence underlying a nucleosome is estimated. Finally, a convolution operation between 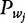and 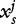is used to score if s underlies a nucleosome [56].

A wavelet transform is a decomposition of a spatially extended signal into the space–frequency domain via a set of basis functions, each related to a common function, called the mother wavelet, by scaling and translation. Wavelet transforms can be viewed as an extension of traditional Fourier analysis in that the signal of interest does not need to be periodic. Yet, similar to Fourier analysis, wavelet methods can be used to systematically investigate the shape of a signal in terms of different frequencies. Wavelet methods have been widely used in many areas of science and engineering [57].

To study the role of DNA sequence periodicity in determining nucleosome positioning, Yuan and Liu [37] applied wavelet analysis to predict nucleosome positioning in yeast by analyzing the DNA sequence information from 199 nucleosomal sequences and 296 linker sequences known in the literature [37,55]. They further truncated each input nucleosome or linker DNA sequence s to 129 bp long. Dinucleotide frequencies, 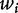are transformed to wavelet coefficients 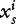for i = 1, … ,16 using the Haar wavelet basis, defined as

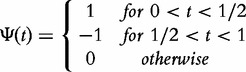This transform involves seven layers of wavelets, each layer corresponding to a specific length scale. The sum of square of the wavelet coefficients at each layer, also called the wavelet energy, is then used to summarize the sequence features with the aim to quantify the contribution of different spatial frequencies. They find modest prediction power (AUC = 0.84) in predicting nucleosome positioning, but the nucleosome-depleted regions are highly predictable.

A major benefit of the wavelet approach is its ability to detect position-specific signals across multiple length scales, allowing combinations of both small-scale and large-scale motifs to contribute to the overall targeting signal. To date, the wavelet approach has only been applied to investigate the spatial distribution of dinucleotides. In general this can be naturally extended to longer k-mers, but there is an additional computational cost compared with simply using word counts.

COMPARISON OF SEQUENCES IN THE FEATURE SPACE

Once DNA sequences are mapped to numerical vectors in a feature space F, they can be easily compared by using traditional mathematical tools, such as a distance or dissimilarity function, d, which is a two-variable function on F satisfying the following conditions:

1. d(x,y) ≥ 0

2. d(x,y) = d(y,x)

3. d(x,x) = 0

Generally speaking, there are three main classes of distance functions that have been applied to epigenetic studies: geometrical, correlation and information-based distances.

Geometrical distance functions capture the concept of physical distance between two objects. They are strongly influenced by the magnitude of changes in the measured components of vectors x and y, making them sensitive to noise and outliers. The most adopted geometrical distance is the ‘Euclidean distance’:

Correlation distance functions capture linear dependencies between the coordinates of two vectors. The most adopted distance belonging to this class is the ‘Pearson's correlation distance’:

where 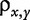is the Pearson correlation between x and y.

Information-based distance functions are defined via well-known quantities in information theory, such as entropy or relative entropy. They have the advantage of capturing nonlinear statistical dependencies between two discrete variables. The entropy measures the degree of uncertainty associated with a random variable and typically is represented in units of bits. The mathematical definition is as follows.

Given a multivariate random variable X with possible values {x₁,…, x_n} and its associated probability mass function P(X), the entropy is defined as

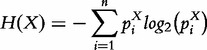where .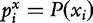

The concept of entropy can be extended to ‘relative entropy’ or ‘Kullback–Leibler divergence’, which quantifies the similarity between two random variables X and Y:

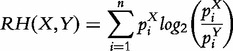While relative entropy is not symmetric, it can be symmetrized by the following transformation:

and the result is called the Kullback–Leibler distance. To evaluate the Kullback–Leibler distance between a pair of DNA sequences, the occurrence of each k-mer is viewed as a random variable following a binomial distribution whose parameter is estimated by its overall frequency.

The idea described above has been used to define an unbiased quantitative measure for DNA sequence specificity called the Motif Independent Measure (MIM) [39]. Starting from a set of random sequences, the method uses their empirical probabilities of k-mers (default k = 4) to estimate their Kullback–Leibler divergence distribution, and uses this distribution as the null model to establish the level of specificity. Of note, this approach does not assume the existence of any distinct sequence motif. The authors apply this approach to analyze a published ChIP-seq dataset of the enhancer mark H3K4me1 [1,58,59]. They find that the sequence specificity associated with the H3K4me1 peaks is highly cell type-specific, which is highest in embryonic stem cells, suggesting different targeting mechanisms. Of note, no distinct motif sequences are identified in the H3K4me1 targets, suggesting a motif-independent utility of this approach in evaluating sequence specificity.

The concept of entropy has also been applied to investigate the relationship between nucleosome positioning and DNA sequences. For example, Levitsky et al. [60] identify differences in entropy levels between different classes of nucleosomal DNA sequences, which may be associated with conformational and physicochemical property differences, based on analysis of an existing nucleosome sequence database [61].

Kernels for sequences comparison

Another class of sequence comparison methods is the string kernels, which have recently gained significant popularity and been successfully applied to a wide range of problems [62,63].

Consider two generic sequences s and t, and a generic feature space F where an inner product is defined, a kernel is any 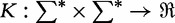such that there exists a mapping satisfying:

where 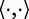denotes the inner product in F.

Classical examples of kernels are:

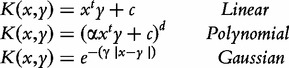It is straightforward to transform a kernel to a distance function, as follows:

In computational biology, a popular choice is subsequence kernel, which is defined in a number of steps. First, given a sequence 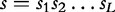, the index set 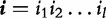of length l is defined as a monotonically increasing set of positive integers whose values are no greater than L. Denote by 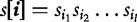the subsequence (allowing gaps) of s that corresponds to the index set. Second, each index set i is associated with a gap-penalizing weight, 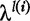, where 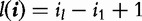and λ < 1 is a predetermined constant. Third, the sequence s is mapped into a 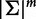dimensional feature space through the following mapping:

for every subsequence u of length m. Finally, the subsequence kernel is defined as the dot product between any pair of sequences:

As such, indels are tolerated yet penalized in a suitable manner.

Because of the poor numerical efficiency, effort has been taken to develop a more efficient algorithm based on recursive strategies. As a result, the numerical complexity is improved to O(mL_sL_t) [64], where L_s and L_t are the lengths of the two considered sequences.

Sequence comparison using complexity/compression measures

Another class of distance functions has been recently introduced based on an extension of the Kolmogorov complexity, which intuitively can be viewed as a measure of the computational resources needed to generate such sequences. The mathematical definition is as follows.

The conditional Kolmogorov complexity 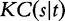between two generic strings s and t is the length of the shortest binary program written in a generic programming language that computes s giving t as input. The Kolmogorov complexity 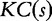of a string s is defined as 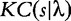where λ stands for the empty string.

Li et al. [65] define the universal similarity metric (USM) for strings based on the Kolmogorov complexity:

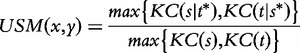where 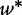denotes the shortest program that produces the generic sequence w on an empty input. USM represents a lower bound for all the distance and similarity functions.

It is difficult to exactly compute the value of USM; therefore, it is commonly approximated by the following formula:

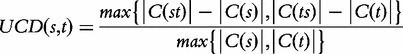where st and ts denote the concatenations of the sequences s and t, C is a compression algorithm and C(s) its output on a string s. Details about this approximation can be found in the work of Ferragina et al. [66]. Complexity-based approaches have been used, for example, to distinguish nucleosome-enriched and -depleted regions [67].

PREDICTION OF EPIGENETIC PATTERNS IN SEQUENCE FEATURE SPACE

While epigenetic patterns are typically not strongly associated with any distinct DNA sequence features, accurate prediction models have been built by combining multiple sequence features. There are three main classes of approaches, as described below.

Regressors and classifiers

Regression analysis is the process of determining how a variable y (the response) is related to a multivariate variable X (whose components are called covariates). Assuming that y and X are associated via a prespecified, possibly nonlinear functional relationship y = h(X, β) with an unknown coefficient β, the regression procedure infers the values of β based on a finite number of observed data. Classification is similar to regression but for discrete values of y. The choice of a particular function form of h is related to the so called empirical risk:

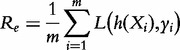where 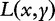is the loss function such that it is non-negative and 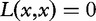. Empirical risk minimization is the process of choosing a function 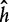that minimizes the empirical risk:

where H is a particular class of function. In binary classifications, the linear hyperplanes 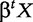can be used to define the set H of binary linear classifier as:

A commonly used regressor is the logistic regression (LR), which is a member of the generalized linear models suitable for binary responses [68]. In LR one obtains the logarithm of the odds of the success outcome, and finally uses a log-linear model:

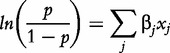where p represents the probability of the success outcome, 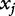represents the covariate values, and the β_js are unknown coefficients that are numerically estimated, often with the maximum likelihood procedure.

In the context of epigenomics, Yuan and Liu [37] use wavelet energies as covariates of an LR model to predict the likelihood of an arbitrary sequence being classified as a nucleosomal or a linker sequence. They find that the genome-wide nucleosome-depleted regions can be predicted with high accuracy from the DNA sequence alone.

In Yang et al. [41] an LR model, based on k-mers, is used to study cell type-specific DNA methylation susceptibility at three different resolutions: promoters, CpG dinucleotides and CpG segments. They predict, with reasonable accuracy, methylation patterns across different human cell types. Furthermore, they also identify k-mers that partially explain the tissue-specific methylation patterns.

Support vector machines

Support vector machines (SVMs) [69] are binary linear classifiers. They search for the optimal hyperplane 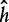that maximizes the geometric margin, which is the distance of the hyperplane to the nearest training data point of any class. The main advantage of SVM is that it provides a solution to the global optimization problem, thereby reducing the generalization error of the classifier.

The formulation of SVM can be easily extended to build a nonlinear classifier by incorporating a generic kernel of the class H:

While no systematic tools have been developed to automatically identify the optimal kernel for a particular application, intuition-based kernel designs often seem to be sufficient in practice.

Peckham et al. [36] have applied SVM to predict nucleosome positions in yeast from DNA sequences using genome-scale nucleosome positioning information identified by a tiling array experiment [20]. In particular, each input sequence is represented by k-mers with lengths up to 6 bp, using a linear kernel. Genome-wide nucleosome positions are predicted using a hidden Markov model to detect peaks of the SVM-predicted scores. Similarly, using a linear kernel, SVM has also been applied to predict histone modifications patterns [40].

In addition, Lee et al. [70] have applied SVM to predict enhancer locations. In this study, they used ChIP-seq data of EP300/CREBBP [71] to define enhancers, and also used a linear kernel for prediction. Interestingly, a subset of the identified sequence elements can be associated to sequence motifs of TFs that are known to play a tissue or developmental stage-specific role in gene regulation.

Classification trees and random forests

Classification trees are complex classifiers based on the idea of representing the function h as a set of discrimination rules in a feature space in term of discrete data structures called rooted trees [72]. A rooted tree is a direct and acyclic graph composed of a set of nodes and a set of paths that connect the nodes. The root is a special node where all paths ultimately originate from, whereas the leaf nodes are where the paths terminate. Each node represents a binary rule that splits the feature space according to the value of a predictive feature, and a path from the root to leaf nodes represents a series of rules that are used to recursively divide the feature space into smaller subspaces, where a common class label is assigned. This approach can also be extended using an ensemble of trees, called forests, to make classification, and the results from individual trees are aggregated, for example, by majority voting. The most used methods in this context are decision trees [73], random forests [74] and probabilistic sum of trees [75]. The tree-based models have been used successfully, for example, to predict target regions of a chromatin remodeling complex based on TF binding and motif sequences [76] or for the identification of DNA binding protein [77].

An ensemble version of classification trees, called the Bayesian additive regression trees (BART), has been developed by Chipman et al. [75]. Previous work has shown that the BART model has competitive performance with other methods, such as SVMs [78]. An advantage of BART is that, by enumerating the frequency of usage of each predicting variable, it can serve as an effective way for variable selection.

Liu et al. [76] apply the BART model to predict the genome-wide polycomb target genes in mouse embryonic stem cells. The Polycomb group complexes (PRC1 and PRC2) are responsible for synthesizing the repressive H3K27me3 mark and play an important role in development. ChIP-chip experiments identify nearly 3000 genes whose promoters are occupied by PRC2 complex in mouse embryonic stem cells; these target genes are highly enriched for developmental regulators, which are activated during cell differentiation in a cell type-specific manner. Using the BART model, Liu et al. [76] compare the promoter sequences of the target and nontarget genes and find that the model has good classification accuracy (AUC = 0.83).

There are a number of variations of tree-based models in the literature using different learning strategies and, as a result, the computational complexities are very different. For example, classic approaches like the ID3 or C4.5 [79] have a complexity of O(n² m) in the case of n discrete features or O(n² m³) for n continuous features [80]. Random forests instead have a complexity of O(tn m log m), where t is the number of trees in the forest. The complexity of the BART approach instead is dominated by the Markov chain Monte Carlo sampling, which has been shown to have, in the case of large samples, a stochastic complexity of O(n²) [81]) and is O(t m n²).

In contrast, the complexities of SVM and LR can be highly variable depending on the specific optimization problem. Fast implementation of the LR optimizer involves a computation that is O(m n²) [82].

In the case of SVM, the optimization problem is a quadratic-programming one, and it is noteworthy that the best solvers have O(m³) complexity [83], in addition to the cost, k(n), associated with the precomputation of the kernel matrix. For the linear kernel, k(n) is equal to n², but this cost can be significantly greater for more complex kernels. Numerically efficient implementations have been developed [83].

To date, effective prediction models have been developed for nucleosome positioning, histone modification and DNA methylation, providing strong evidence that DNA sequence plays an important role in guiding these factors. A summary of the methods discussed in this article is presented in Table 1.

Table 1:

A summary of alignment-free methods that either have been applied to epigenomics or may be suitable for epigenomics

Epigenetic mark	Feature space mapping	Similarity/distance function	Prediction model
Nucleosome positioning/occupancy	Word composition [36,37,38] Suffix tree [54] Signal space [37,56] Entropy [37,60]	Kernel [36] Information based Complexity based [67]	Logistic regression [37] Support vector machine [36] Tree models
DNA methylation	Word composition [41,42,43] Suffix tree [53] Signal space Entropy	Kernel [43] Information based Complexity based	LR [41,43] Support vector machine [43] Tree models
Histone modifications/chromatin regulatory elements (enhancers)	Word composition [39,40,70,76,34] Suffix tree Signal space Entropy	Kernel [40,70] Information based Complexity based	LR [34] Support vector machine [70,40] Tree models [76]

As summarized in Table 2, each method has its strengths and weaknesses. For example, SVM models provide usually highly competitive prediction accuracies, but the results are often difficult to interpret in terms of the underlying features. On the other hand, the tree-based models may perform less efficiently in terms of prediction accuracy, but their results can be easily interpreted. Furthermore, some methods, such as LR, are more numerically effective than others, although not parallelizable. These properties should be taken into consideration for model selection.

Table 2:

A comparison of prediction models that have been applied to epigenomics

Prediction model	Time complexity	Parallelizable	Easy to interpret
SVM/kernel based	O(m3) for the QP solver and O(k(n)) for the computation of the kernel matrix, where k(n) is the computational cost of the kernel used	Yes	No
LR	O(m n2)	No	Yes: it is easy to check the contribution of each feature in the model.
Tree based	ID3 or C4.5: O(n2 m) discrete features, O(n2 m3) continuos features BART: O(t m n2) Random Forest: O(tn m log m)	Yes	Yes: it is easy to check the contribution of each feature and also combinatiorial rules in the features space.

DISCUSSION

In this article, we have reviewed a number of recent applications of the alignment-free methods to epigenomics, whose connection with the DNA sequences has not been well recognized until recently. Because of the limit of space and our knowledge, we have only touched upon a small set of existing studies and apologize for the omission of any important studies. Nonetheless, it is evident that the alignment-free methods have offered new biological insights into DNA methylation patterns [41–43], histone modifications [70] and nucleosome positioning [37,38]. We think that the power of alignment-free methods mainly lies on their flexibility, robustness and numerical efficiency.

Most previous studies either focus on a specific epigenetic mark or consider different marks independently, but in reality there is often strong association between different marks. For example, it is well known that nucleosome positioning influences DNA methylation patterns [84]. Similarly, DNA methylation is known to be positively correlated with H3K9 methylations and negatively correlated with H3K4 and H3K27 methylations [17,85]. Taking these correlations into account may result in more powerful predictive models.

The DNA sequence is only one of many factors that affect epigenetic patterns. The effect of additional factors, such as transcription, replication and histone-mediated self-propagation, varies greatly among different epigenetic marks, providing an intrinsic limit for any sequence-based prediction model. One important question is whether the lack of prediction power is because of the inferiority of computational method or such intrinsic limitations. This is in part addressed by the MIM method [39], but more study is warranted.

It is important to recognize that correlation is not equivalent to causal mechanisms. Causal relationship can only be established if it can be demonstrated that perturbation of the potential effector indeed has the predicted effect. To test whether a predicted DNA element is required for the establishment of epigenetic pattern, the most direct way is to genetically delete the element in question from the genome and then use a suitable experimental assay to evaluate whether the local epigenetic pattern changes as predicted. Recently developed genome-editing tools, such as TALEN [86] and CRISPR [87], are extremely useful for such validations.

CONCLUSIONS

Alignment-free methods have provided important computational tools for functional annotation of biological genome and for linking genome with epigenome. Conversely, the applications themselves have also provided important insights that can be used to develop more accurate and efficient methods. Close interactions between computational and experimental biologists will likely result in significant advances in both frontiers.

Key Points.

• There has been a lot of progress in applications of alignment-free methods to study the link between the genome and epigenome.

• Feature space representation enables the detection of weakly associated sequence features.

• Alignment-free methods are useful for prediction of epigenomic patterns.

• Different alignment-free methods have different strengths and weaknesses.

FUNDING

This research was supported by the NIH grant HG005085 to GY.

Biographies

Luca Pinello is Research Fellow at the Department of Biostatistics and Computational Biology at Dana-Farber Cancer Institute and at the Harvard School of Public Health, Boston, USA. His research is focused on new computational approaches to investigate different epigenetic factors that regulate the chromatin structure and dynamics.

Giosuè Lo Bosco is Assistant Professor of Computer Science at the Department of Mathematics and Computer Science at the University of Palermo, ITALY. His research focuses on the design and development of machine-learning tools.

Guo-Cheng Yuan is Associate Professor at the Department of Biostatistics and Computational Biology at Dana-Farber Cancer Institute and at the Harvard School of Public Health, Boston, USA. His research focuses on epigenomics and gene regulatory networks.