Packing Interface Energetics in Different Crystal Forms of the λ Cro Dimer

Abstract

Variation among crystal structures of the λ Cro dimer highlights conformational flexibility. The structures range from a wild type closed to a mutant fully open conformation, but it is unclear if each represents a stable solution state or if one may be the result of crystal packing. Here we use molecular dynamics (MD) simulation to investigate the energetics of crystal packing interfaces and the influence of site-directed mutagenesis on them, in order to examine the effect of crystal packing on wild type and mutant Cro dimer conformation. Replica exchange MD of mutant Cro in solution shows that the observed conformational differences between the wild type and mutant protein are not the direct consequence of mutation. Instead, simulation of Cro in different crystal environments reveals that mutation affects the stability of crystal forms. Molecular Mechanics Poisson-Boltzmann Surface Area binding energy calculations reveal the detailed energetics of packing interfaces. Packing interfaces can have diverse properties in strength, energetic components, and some are stronger than the biological dimer interface. Further analysis shows that mutation can strengthen packing interfaces by as much as ~5 kcal/mol in either crystal environment. Thus, in the case of Cro, mutation provides an additional energetic contribution during crystal formation that may stabilize a fully open higher energy state. Moreover, the effect of mutation in the lattice can extend to packing interfaces not involving mutation sites. Our results provide insight into possible models for the effect of crystallization on Cro conformational dynamics and emphasize careful consideration of protein crystal structures.

Introduction

X-ray crystallography is the most important tool for structural biology. Yet protein X-ray images capture just a single snapshot of the dynamic solution ensemble and are under the influence of crystal packing. Although there are many cases for which multiple structures of the same protein exist in different conformations,¹ it is often unclear how each structure relates to the solution ensemble. While such structural polymorphisms may arise due to the presence of substrate or from mutation, there are many cases of proteins in multiple conformations for no apparent reason.^2–8 Such cases could be due to differences in crystal packing instead of representing natural solution dynamics, and complicate the functional interpretation of protein X-ray data.

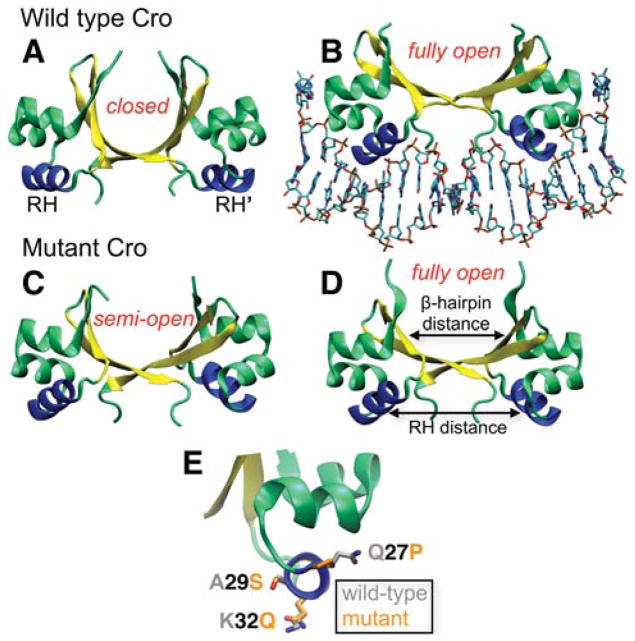
To examine the effect of the crystal environment on protein conformation, we consider the Cro transcription factor from bacteriophage λ as a model system. λ Cro functions as a homodimer and is a paradigm system for studying protein-DNA interactions,^9–12 gene regulation,^13,14 and protein fold evolution.^15,16 In the dimer, the relatively rigid subunits display an α+β fold and are connected by a plastic β-sheet region that permits a hinge-like motion between the two domains (Fig. 1A). Several crystal structures are available for Cro and range from a wild type (WT) closed conformation in the apo state¹⁷ (Fig. 1A) to an open DNA-bound form¹⁸ (Fig. 1B). This observation initially indicated a textbook example of induced conformational transition. However, two new apo crystal structures challenge this mechanism and bring into question the dominant solution form, as neither structure resembles the previously solved DNA-free conformation.⁴ Both of the new structures were crystallized as the same mutant (Q27P, A29S, and K32Q; “PSQ”). One of them (PSQ form 1, Fig. 1D) closely resembles the DNA-bound open conformation, while the other (PSQ form 2, Fig. 1C) displays a structure intermediate of the WT closed and open dimer forms (“semi-open”). The mutations are located on the surface of the DNA recognition helix (RH, Fig. 1E) and there is no clear explanation for why they would have resulted in dimer structures different from the original DNA-free closed conformation.⁴ An NMR ensemble is also available for the Cro dimer,¹⁹ but the models display a significant degree of conformational heterogeneity among one another and differ from the X-ray structures. Thus, the nature of the Cro dimer solution ensemble remained in question.

Figure 1.

Crystal structures of the λ Cro dimer. (A) WT apo, closed; (B) WT DNA-bound, fully open; (C) PSQ mutant form 2, semi-open; and (D) PSQ mutant form 1, fully open (PDB IDs 5CRO¹⁷, 6CRO¹⁸, 2ECS⁴, and 2OVG⁴, respectively). Both mutant crystal forms are in the apo state. For each dimer, the flexible β-hairpin region is colored yellow and the RHs are shown in blue. “Open” and “closed” dimers are defined based on the intersubunit distance between the hairpins as shown in (D). (E) Location of the RH mutations: Gln27Pro, Ala29Ser, and Lys32Gln, with the side-chains of the WT and mutant residues shown in gray and orange, respectively. The side-chain coordinates of the WT apo (5CRO) and PSQ form 1 (2OVG) X-ray structures are shown along with the backbone of 5CRO.

We recently examined the various Cro dimer X-ray and NMR models by reconstructing the solution ensemble using replica exchange molecular dynamics (REMD).^20,21 Closed and semi-open dimers similar to the WT DNA-free and PSQ form 2 crystal structures, respectively, dominate the solution ensemble, while the NMR models are largely inaccessible. The predominance of both closed- and open-like conformations supports a conformational selection model^22,23 for DNA binding. Fully open conformations similar to the WT DNA-bound and PSQ form 1 X-ray structures are accessible but unstable. This prompted the question: Why are unstable, fully open conformations observed in the crystal structures? In the case of bound Cro, DNA-protein interactions would stabilize the fully open state. However, for the DNA-free fully open conformation (PSQ form 1), mutations participate in crystal packing and may affect the resulting crystal form. To investigate this possibility, in this study we simulate WT and mutant Cro in the crystal environment.

Crystal MD simulations entail a greater degree of methodological complexity than standard solution MD simulations and are still relatively rare. Previous crystal MD studies have focused on force field evaluation,^24–26 solute diffusion in crystals,^27,28 modeling the crystallization solvent,²⁹ and the effect of crystal packing on protein conformational dynamics.^30–36 A more recent study employed crystal simulation in combination with the Molecular Mechanics Poisson-Boltzmann Surface Area (MM-PBSA) method^37,38 to expedite the ranking of protein-ligand binding energies.³⁹ In a similar vein, here we employ the MM-PBSA approach with crystal simulations to quantitatively evaluate the energetics of crystal packing interfaces in different crystal environments of WT and mutant Cro. To our knowledge, this is the first application of the MM-PBSA approach to crystal packing interfaces, and our results lead to a fuller understanding of the relationship between the X-ray data and the solution ensemble.

Materials and Methods

REMD

REMD^40,41 combines principles from traditional MD and Monte Carlo (MC) simulation to improve sampling of the conformational energy landscape of biomolecules. Several identical copies of the system, each existing at a unique temperature, are simulated by MD and allowed to exchange temperature states at regular intervals through an MC move. Crossing of energy barriers at higher temperatures permits exploration of a wider range of conformational space than standard MD simulation. Previous REMD simulations begun from three distinct starting configurations (two X-ray structures and an NMR model) of the WT Cro dimer converged to a similar region of conformational space,^20,21 which indicates that the REMD protocol we employ is sufficient to capture the major conformational dynamics of Cro. The initial configuration for REMD in this study is the fully open PSQ form 1 mutant dimer X-ray structure (PDB ID: 2OVG).⁴ A detailed description of the set-up and equilibration and production runs for REMD can be found in a prior publication.²⁰ In brief, we simulate 24 total replicas in the NVT ensemble at temperatures exponentially distributed between 287.9 and 338.7 K.

Crystal set-up and simulation

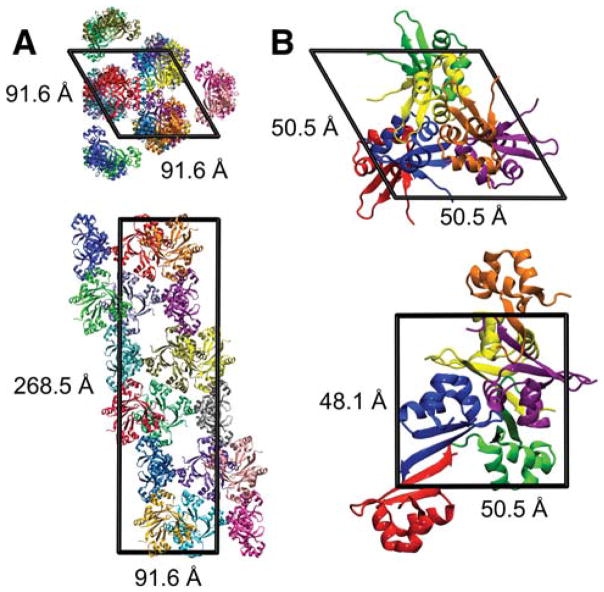
Crystals of the WT closed Cro dimer (PDB ID: 5CRO,¹⁷ 2.3 Å) grew in space group R32 with unit cell parameters a = b = 91.6 Å, c = 268.5 Å, and γ = 120° (Fig. 2A). The asymmetric unit (AU) is a tetramer (chains A, B, C, and O), and 18 AUs (72 total chains) are present in the unit cell. Crystals of the DNA-free fully open mutant Cro dimer (PDB ID: 2OVG,⁴ 1.35 Å) grew in space group P3₂21 with parameters a = b = 50.5 Å, c = 48.1 Å, and γ = 120° (Fig. 2B). The AU corresponds to one protein chain, and six total chains are present in the unit cell. The 5CRO and 2OVG crystals were grown at the same pH (7.5) with similar concentrations of salt −1.5 M lithium sulfate/0.1 M Hepes sodium salt (2OVG) and ~1.2 M phosphate (5CRO). While the 2OVG crystal was cryo-cooled for data collection, no cryoprotectants are reported. Data collection for the 5CRO crystal occurred at room temperature. A previous crystal MD study indicates that detailed modeling of the crystallization mixture may better preserve the protein structure during simulation than a water-solvated lattice.²⁹ However, the actual concentration of solutes in crystal is in general unknown since it is unclear whether the concentration of solutes is the same in the mother liquor and in the resulting crystal. Thus, instead of modeling the crystallization mixture in detail, we approximate the solvent environment of the lattice with explicit water molecules and neutralizing ions (see below). Several previous crystal MD studies have employed such an approach.^26,30,31,35 The resulting concentration of counterions in the simulated unit cells is more dilute than the salt concentrations reported for the original solution mixtures that resulted in crystal formation.

Figure 2.

Simulated unit cells: (A) 5CRO (closed Cro, originally solved as WT)¹⁷ and (B) 2OVG (fully open Cro, originally solved as mutant).⁴ The top and bottom panels show projections along the c and a axes, respectively. The 5CRO AU contains four monomers forming a tetramer, and 72 total monomers are in the unit cell. The 2OVG AU comprises one monomer, and 6 total monomers are in the unit cell. In both lattices, each AU is shown as a different color and the functional dimer is formed between adjacent monomers with the largest packing interface (e.g., between the blue and red monomers in B).

In both the 5CRO and 2OVG crystals, the biological dimer is formed between two neighboring chains that share the largest crystal packing interface. For simulation, we construct the protein coordinates of the unit cells by applying symmetry operations to the AU using the UnitCell²⁹ program that is part of AmberTools.⁴² Unobserved terminal residues of the X-ray structures are added by alignment with an NMR model (PDB ID: 1COP).¹⁹

The fully open dimer form in the 2OVG lattice contains three mutations in the RH helix: Q27P, A29S, and K32Q (Fig. 1E). The 5CRO and 2OVG Cro lattices are constructed with both WT and mutant residue composition, resulting in four total systems for crystal MD simulation (Table S1 of Supporting Information). Computational mutagenesis is performed on the AUs using the SCWRL4 program.⁴³ The WT (Gln27/Ala29/Lys32) and mutant (Pro27/Ser29/Gln32) monomers have overall +5 and +4 charges, respectively, and one neutral histidine (His35, protonated at N_ε). We use the AddToBox program²⁹ to add solvent molecules to the interstices of the unit cell. TIP3P water molecules and neutralizing Cl⁻ counterions are added at distances of 1.5 Å and 4 Å from each other, respectively, and 3 Å away from any protein atom.²⁹ The solvated and neutralized unit cells are the initial coordinates for simulation. The equilibrated unit cells (see below) are used for test runs in the NPT ensemble to determine the density of the system (Fig. S1). The 2OVG WT and mutant unit cells have a density of ~1.17 g/mL and contain ~1,650 waters and ~11,280 total atoms. The 5CRO unit cells have a density of ~1.11 g/mL and comprise ~42,100 waters and ~202,100 total atoms. Implementation of periodic boundary conditions creates neighboring unit cells to form the crystal. A summary of the simulations performed is presented in Table S1.

To perform simulation, we use Amber10⁴⁴ and the FF99SB parameter set.⁴⁵ The FF99SB force field outperformed other models during the testing of several force fields with crystal MD simulation of a high-resolution X-ray structure.²⁵ Energy minimization and equilibration are executed in several stages for the 5CRO and 2OVG lattices. Unfavorable contacts between solvent coordinates are first relaxed during 40,000/20,000 (5CRO) and 4,000/2,000 (2OVG) steepest descent (SD)/conjugate gradient (CG) cycles with harmonic restraints applied to all protein atoms (500 kcal mol⁻¹ Å⁻² force constant). Contacts between solvent atoms and protein side-chains are then minimized during 40,000/20,000 (5CRO) and 7,000/4,000 (2OVG) SD/CG cycles with the same restraints applied to protein backbone atoms. A final minimization stage of 20,000/10,000 (5CRO) and 4,000/2,000 (2OVG) SD/CG steps initially relaxes the unobserved termini added for simulation. To rigorously sample configurations of the added termini for the much larger 5CRO unit cell, positional restraints are applied to all protein atoms and the system is heated to 600 K for 400 ps of dynamics with a 0.5 ps time step. The system is cooled back down to 300 K where restraints are removed from side-chain atoms. For both systems, backbone restraints are gradually relaxed over several equilibration steps.²⁹ One hundred picosecond increments of dynamics are performed sequentially with 500, 250, 125, and 64 kcal mol⁻¹ Å⁻² restraints. From this point, the restraints are reduced in half in 50 ps increments until a value of 0.125 kcal mol⁻¹ Å⁻². Another 150 ps of dynamics is performed with 0.0625 kcal mol⁻¹ Å⁻² restraints still on all protein backbone atoms. The total time for this initial equilibration phase at 300 K is 1 ns. The equilibrated unit cells served as the initial configurations for production dynamics. While a greater degree of conformational variation can be accounted for by including multiple unit cells³⁶ for the lattice originally solved as mutant protein (2OVG), such an approach is impractical for the lattice originally solved as wild type (5CRO), as a single solvated unit cell of the latter comprises more than 200,000 atoms. To maintain a consistent approach for simulation of both crystal environments, we simulate a single unit cell in each case.

Production dynamics for the 5CRO and 2OVG unit cells is performed for 12 ns and 30 ns, respectively. These lengths correspond to effective simulation times of 216 ns (5CRO) and 180 ns (2OVG) per AU (Table S1). The simulations are run in the NVT ensemble with periodic boundary conditions at 300 K (which closely corresponds to the crystallization temperature of both lattices^4,17). Several other studies have performed crystal MD in the NVT ensemble.^{26–28,30,31,35,39} Other than SHAKE restraints⁴⁶ applied to bonds involving hydrogen atoms, no other positional restraints are placed on the system during the production phase. We use the velocity Verlet algorithm with a 2 fs time step. A 10 Å non-bonded cutoff is employed in direct calculations of electrostatic and van der Waals interactions, and the particle mesh Ewald method with a grid spacing of 1 Å is used to calculate long-range electrostatics. Temperature control is performed using a Langevin thermostat with a friction coefficient of 1 ps⁻¹. Coordinates are saved every 1 ps and the trajectories are analyzed with ptraj⁴² and VMD.⁴⁷

Evaluation of packing interface energetics using the MM-PBSA approach

Packing interfaces are defined between any two monomers with a pair of non-hydrogen atoms within 4 Å using the ncont program that is part of CCP4.⁴⁸ All residues within this distance of the neighboring chain are considered part of the interface. For residues with multiple conformations, we consider alternate conformation A. Interfaces defined in this manner are consistent with those listed in the Protein Data Bank in Europe Proteins, Interfaces, Structures and Assemblies (PDBePISA) database.⁴⁹ In total, 14 unique interfaces are identified in the 5CRO lattice, four of which involve a mutation site (Fig. S2), and six unique interfaces are present in the 2OVG lattice, one of which includes a mutation site (Fig. S3). Each crystal packing interface can be identified and evaluated with 3D viewing software in the PDBePISA server (http://www.ebi.ac.uk/msd-srv/prot_int/) using the 5CRO and 2OVG PDB IDs and the source and target chain symmetry operations listed in Tables I and II.

Table I.

5CRO lattice: MM-PBSA energies of crystal packing interfaces^a

Interfaceb	ΔEvdwc	ΔEele	ΔEele + ΔGPB	ΔGtot
1	−73.46 ± 0.74d	191.26 ± 11.45	36.62 ± 2.08	−49.19 ± 1.60
	−76.19 ± 1.46	44.54 ± 11.73	36.11 ± 1.94	−52.57 ± 1.76
2	−73.47 ± 0.86	241.91 ± 8.42	41.18 ± 1.27	−44.37 ± 0.98
	−73.94 ± 1.02	73.65 ± 9.42	35.11 ± 1.18	−50.57 ± 1.13
3	−10.49 ± 0.77	8.98 ± 3.72	−5.07 ± 1.52	−19.78 ± 1.62
	−10.07 ± 0.91	−30.12 ± 5.43	−1.85 ± 1.97	−15.92 ± 1.75
4	−8.99 ± 0.66	7.07 ± 5.07	−4.67 ± 1.35	−17.94 ± 1.18
	−8.89 ± 0.54	−15.55 ± 9.73	1.30 ± 2.24	−11.25 ± 2.14
5	−47.27 ± 0.66	62.35 ± 4.26	3.73 ± 1.22	−52.58 ± 1.35
	−45.61 ± 0.87	31.83 ±11.04	9.67 ± 2.22	−44.29 ± 2.20
6	−48.18 ± 0.58	64.25 ± 4.99	4.46 ± 1.59	−52.73 ± 1.71
	−46.38 ± 0.75	21.16 ± 6.03	9.35 ± 1.94	−45.56 ± 1.94
7	−23.18 ± 1.71	92.14 ±10.72	8.43 ± 1.38	−19.62 ± 1.64
	−23.00 ± 1.13	18.69 ± 7.24	8.84 ± 0.99	−18.98 ± 1.07
8	−20.72 ± 1.91	80.54 ± 6.38	14.13 ± 1.20	−10.65 ± 1.08
	−15.86 ± 1.47	29.45 ± 4.91	10.66 ± 1.04	−8.53 ± 0.89
9e	−21.12 ± 0.80	272.41 ± 3.23	16.95 ± 0.92	−7.85 ± 0.53
	−19.53 ± 1.19	143.22 ± 2.86	12.96 ± 0.58	−9.92 ± 1.08
10	−46.28 ± 0.39	340.35 ± 4.75	26.09 ± 0.79	−25.89 ± 0.70
	−42.00 ± 0.82	217.03 ± 3.83	21.74 ± 0.73	−25.65 ± 0.90
11	−23.43 ± 0.73	232.25 ± 3.01	17.87 ± 0.31	−9.76 ± 0.68
	−21.09 ± 0.84	137.38 ± 3.42	15.18 ± 0.62	−9.56 ± 0.45
12	−44.91 ± 0.55	266.81 ± 3.21	20.76 ± 0.55	−29.97 ± 0.58
	−42.76 ± 0.40	199.12 ± 3.12	22.95 ± 0.41	−25.31 ± 0.67
13	−16.78 ± 0.96	273.33 ± 2.65	14.39 ± 0.60	−5.24 ± 0.67
	−21.09 ± 0.89	159.84 ± 2.80	13.71 ± 0.72	−10.87 ± 0.62
14	−15.45 ± 0.85	346.50 ± 3.59	13.15 ± 0.46	−4.94 ± 0.61
	−16.56 ± 0.66	174.10 ± 2.24	11.19 ± 0.39	−8.14 ± 0.55

^aFor each packing interface, MM-PBSA energies (kcal/mol) are presented for the WT (rows with normal font) and mutant (rows with italicized font) crystal simulations.

^bThe source and target chains for each interface are the following: 1: A(x,y,z), C(x,y,z); 2: B(x,y,z), O(x,y,z); 3: A(x,y,z), O(x,y,z); 4: B(x,y,z), C(x,y,z); 5: A(x,y,z), B(x,y,z); 6: C(x,y,z), O(x,y,z); 7: C(x,y,z), A(-y-1,x-y-1,z); 8: B(x,y,z), A(-y-1,x-y-1,z); 9: B(x,y,z), A(-x-2/3,-x+y-1/3,-z-1/3); 10: B(x,y,z), B(-x-2/3,-x+y-1/3,-z-1/3); 11: B(x,y,z), B(x-y-2/3,-y-4/3,-z-1/3); 12: C(x,y,z), C(y,x,-z); 13: O(x,y,z), C(y,x,-z); 14: O(x,y,z), O(-y-1,x-y,z). For the heterotypic interfaces (1, 2, 3, 4, 5, 6, 7, 8, 9, 13, and 14), each energy term is averaged over 18 unique copies in the unit cell. Energy terms for the homotypic interfaces (10, 11, and 12) are averaged over nine unique copies.

^cΔE_vdw: van der Waals energy; ΔE_ele: MM electrostatic energy; ΔE_ele + ΔG_PB: net electrostatic contribution (where ΔG_PB is the electrostatic solvation free energy, determined using the PB equation); ΔG_tot: total binding energy. The individual solvation free energy terms (ΔG_np and ΔG_PB) are not presented.

^cStandard errors are computed as σ/N^1/2, where σ is the standard deviation of the averages over the total number of copies (N) of an interface in the unit cell.

^dInterfaces with mutation sites (9, 11, 13, and 14) are denoted by bold and underlined font.

Table II.

2OVG lattice: MM-PBSA energies of crystal packing interfaces^a

Interfaceb	ΔEvdwc	ΔEele	ΔEele + ΔGPB	ΔGtot
1	−79.99 ± 5.31d	224.47 ± 19.94	43.08 ± 7.56	−49.56 ± 2.76
	−77.03 ± 0.07	79.47 ± 18.24	37.14 ± 1.91	−52.13 ± 1.79
2	−10.35 ± 1.79	346.29 ± 8.50	11.37 ± 2.05	−0.73 ± 0.57
	−14.26 ± 1.51	244.82 ± 7.04	12.43 ± 1.45	−3.96 ± 0.40
3e	−26.12 ± 2.04	119.31 ±11.94	18.25 ± 1.33	−12.06 ± 1.82
	−31.71 ± 0.66	46.24 ± 8.10	19.66 ± 1.41	−17.12 ± 1.11
4	−28.48 ± 1.18	261.88 ± 7.93	22.37 ± 1.83	−11.30 ± 0.96
	−27.62 ± 1.82	149.00 ± 5.87	20.21 ± 1.82	−12.59 ± 0.94
5	−12.17 ± 1.12	267.78 ±11.33	13.35 ± 1.14	−1.78 ± 0.89
	−5.55 ± 0.61	134.99 ± 1.85	5.79 ± 0.55	−1.45 ± 0.22
6	−9.16 ± 1.41	92.96 ±16.55	4.47 ± 1.18	−6.90 ± 2.14
	−6.92 ± 1.78	63.46 ±17.88	5.55 ± 1.43	−3.43 ± 0.87

^aFor each packing interface, MM-PBSA energies (kcal/mol) are presented for the WT (rows with normal font) and mutant (rows with italicized font) crystal simulations.

^bThe source and target chains for each interface are the following: 1: A(x,y,z), A(-x,-x+y,-z-1/3); 2: A(x,y,z), A(-x,-x+y,-z+2/3); 3: A(x,y,z), A(-y+1,x-y+1,z-1/3); 4: A(x,y,z), A(x-y,-y+1,-z+1/3); 5: A(x,y,z), A(y-1,x,-z); 6: A(x,y,z), A(y,x,-z). For the heterotypic interfaces (3, 4, and 5), each energy term are averaged over six unique copies formed by the simulated unit cell. Energy terms for the homotypic interfaces (1, 2, and 6) are averaged over three unique copies.

^cThe energy term designations follow as in Table I.

^dStandard errors are computed as in Table I.

^eInterface 3 contains the Q27P mutation site and is denoted by bold and underlined font.

We use the MM-PBSA method^37,38 as implemented in Amber10⁴⁴ to compute binding free energies of the crystal packing interfaces. For two chains (A and B) forming an interface in the crystal, the MM-PBSA method calculates the binding free energy (ΔG_bind) as

$$\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}={\mathrm{G}}_{\text{AB}}-({\mathrm{G}}_{\mathrm{A}}+{\mathrm{G}}_{\mathrm{B}}),$$

where G_AB is the free energy of the AB complex and G_A and G_B are free energies of the individual chains. The individual free energies can be decomposed as

$$\mathrm{G}={\mathrm{E}}_{\text{MM}}+{\mathrm{G}}_{\text{np}}+{\mathrm{G}}_{\text{PB}}-{\text{TS}}_{\text{solute}}$$

E_MM is the gas-phase energy of the protein, calculated with the molecular mechanics (MM) potential. G_np represents the nonpolar contribution to the free energy of solvation, computed by the empirical equation ${\mathrm{G}}_{\text{np}}=\mathrm{\gamma }\text{SA}$, where γ=0.0072 kcal mol⁻¹ Å⁻² and SA is the solvent accessible surface area as determined by the LCPO algorithm.^50–52 G_PB is the electrostatic contribution to the solvation free energy, calculated with the Poisson-Boltzmann (PB) equation.^53,54 Dielectric constants of 80.0 and 1.0 are used for solvent and solute, respectively. We also compute the electrostatic contribution using the Generalized Born⁵⁵ counterpart to the PB equation, which yields similar trends in the relative binding energies (results not shown). TS_solute is the solute configurational entropy, which is typically calculated with normal mode analysis.

We extract the individual protein chains and the complex formed by the interface from a single trajectory. This approach is valid since no significant conformational rearrangement is observed in the confined crystal medium (Figs. S4 and S5). In this approach, the bonded terms of E_MM cancel one another in the calculation of ΔG_bind. Significant computational cost and uncertainty are associated with computing the contribution of TS_solute to the free energy. This term is commonly excluded when analyzing the relative stability between similar complexes,³⁸ as is the case for the WT and mutant crystal interfaces. Thus, we do not compute the entropic contribution to the free energy. The MM-PBSA energies are averaged over snapshots extracted every 10 ps from 2–12 ns and from 15–30 ns during the production runs of the 5CRO and 2OVG lattices, respectively. The mean energies are then averaged over each instance of an interface in the unit cell. The number of instances of an interface in the unit cell depends on whether the interface is heterotypic (different surface patches interact across an interface formed between two crystal neighbors) or homotypic (identical surface patches interact across an interface formed by two chains).⁵⁶ Heterotypic interfaces have as many instances as the number of AUs in the unit cell, while homotypic interfaces have half as many occurrences. Tables I and II list the class (heterotypic or homotypic) for each interface and the symmetry relationships between the chains forming the interfaces. We also perform MM-PBSA calculations for equal-length, non-overlapping trajectory segments, which yield essentially the same results (Tables S2 and S3).

Results

Conformational energy landscape of mutant Cro

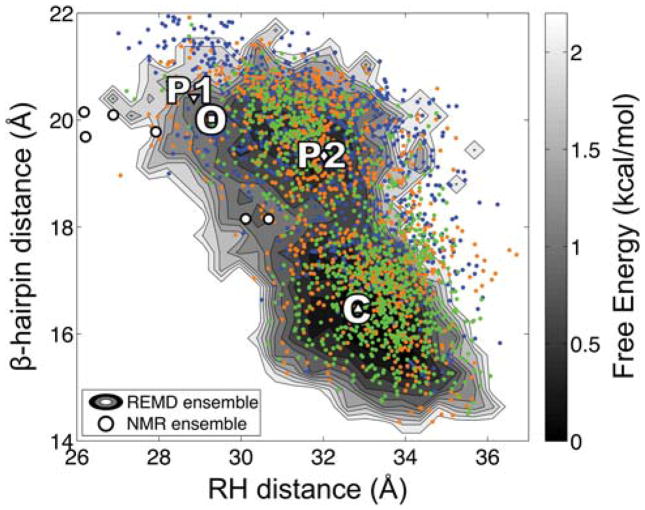
One possible explanation for the conformational difference between WT and mutant Cro would be the direct effect of mutation on the conformational dynamics in solution. To examine whether mutation alters the conformational preference of the dimer in solution, we perform REMD simulation starting from the fully open PSQ form 1 mutant. Conformational sampling is analyzed by measuring two intersubunit distances between the β-hairpins and the RHs (Fig. 1D) to allow for comparison to a free energy surface previously constructed from REMD of the WT protein.²⁰ The reaction coordinates for the mutant simulation are plotted over this free energy surface in Figure 3. The coordinates for the fully open initial configuration are indicated by the filled upside-down triangle, “P1”. Over the course of simulation, the mutant trajectory progressively samples dimer conformations in good agreement with previous simulations of WT Cro. This observation agrees with a previously run REMD simulation started from an NMR model,²¹ which markedly differs from the X-ray structures (3.5 to 4.9 Å RMSD) and rapidly converges to a region of conformational space that overlaps with the WT trajectories. The RH distance of closed-like dimers for mutant Cro is shifted by ~1 Å toward larger values compared to simulation of the WT protein, but closed-like (C) and semi-open (P2) dimers still dominate the ensemble, while fully open dimers (P1 and O) are rarely sampled. These observations support the notion that the conformational differences observed between WT and mutant Cro X-ray structures do not directly arise from the effect of mutation on the solution dynamics. Instead, the observation of the fully open conformation in the PSQ form 1 X-ray structure may be attributed to crystal packing. To investigate this hypothesis, we perform simulation of WT and mutant Cro in different crystal environments (Fig. 2).

Figure 3.

Comparison of conformational sampling during solution simulation of WT and mutant Cro. The coordinates corresponding to the β-hairpin and RH distances for snapshots extracted from REMD simulation of mutant Cro are plotted over the two-dimensional free energy surface computed from REMD simulations of the WT Cro dimer.²⁰ Blue, orange, and green points represent snapshots extracted from 0–10, 10–20, and 20–30 ns, respectively, during the mutant trajectory. The coordinates of the four X-ray structures are indicated on the surface: WT apo (C, closed), WT DNA-bound (O, fully open), PSQ mutant form 1 (P1, fully open) and form 2 (P2, semi-open). The coordinates of P1 denote the initial configuration for simulation of the mutant dimer. The NMR models are indicated by circles. Details pertaining to the construction of the free energy surface can be found in a previous publication.²⁰

Local dynamics in solution and in the crystal

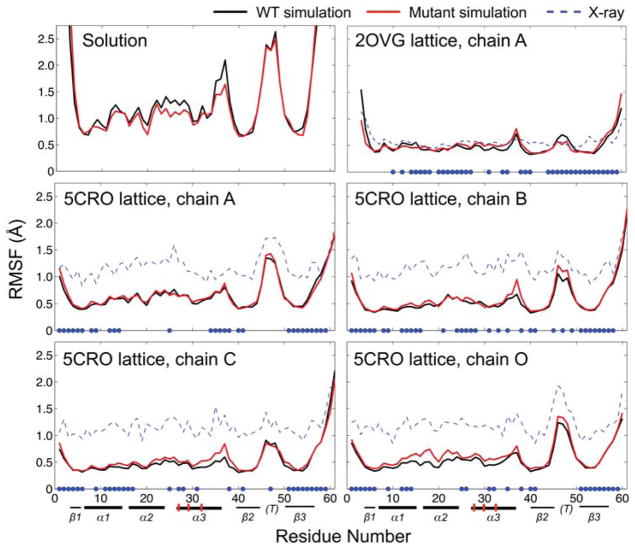
We assess local protein dynamics of Cro during solution and crystal simulation by computing Cα root mean square fluctuations (RMSFs, Fig. 4). A previously reported REMD trajectory²⁰ beginning from the closed dimer is used to calculate RMSFs for the WT protein in solution. In solution simulation, the highest RMSF peak is observed in the flexible turn of the β2β3-hairpin (residues 46–48). Residues 23–28 and 35–38 encompass short random coil stretches and show slightly higher RMSFs in the WT than in the mutant trajectory. The RMSFs from solution simulation are higher in magnitude than those calculated from the NMR models, but show a similar overall trend (Fig. S6).

Figure 4.

Residue RMSFs for Cro monomers during WT (black) and mutant (red) solution REMD and crystal MD simulation for the 5CRO and 2OVG crystal structures. Residues participating in a crystal contact are denoted by blue dots on the horizontal axis. Secondary structure elements are indicated below the residue numbers: bold lines are α-helices, thin lines are β-strands, and “(T)” denotes the flexible turn in the β2β3-hairpin region. The mutation sites in the α3 helix (RH) are marked with vertical red hashes.

As expected, the RMSFs in the crystal trajectories are dampened in comparison to solution simulation. RMSFs are computed for the Cα atoms of each residue observed in the crystal structures with the relationship RMSF = (3B/8π²)^1/2, where B is the B-factor. Results are averaged over both dimer subunits for solution simulation and over all instances of the protein chains in the unit cell for the crystal simulations. The fluctuations calculated from the experimental B-factors in the 5CRO lattice are higher than those of the 2OVG lattice, as the data collection temperatures for 5CRO and 2OVG were 290 K¹⁷ and 100 K,⁴ respectively. In both lattices, the pattern of per residue dynamics during crystal MD correlates well with the location of crystal contacts and shows a similar trend as the RMSFs from experiment. Within both lattices, relatively minor differences in WT and mutant RMSFs are observed. The chains in the 5CRO crystal simulation show a similar RMSF trend as the solution trajectories, with the highest fluctuations occurring in the β2β3-hairpin region. On the other hand, the RMSFs about the β-hairpin in the crystal trajectories of the 2OVG lattice are diminished to values comparable to those observed for residues in the more rigid α-helical region. This indicates that the extensive crystal contacts in the 2OVG lattice (which was originally solved with the mutant sequence) affect not only the overall magnitude of fluctuations, but also the local dynamics relative to other regions of the molecule.

Comparison of crystal packing energetics of WT and mutant Cro in different crystal environments

To quantitatively evaluate the energetics of crystal packing interfaces in the WT and mutant lattices, we perform MM-PBSA binding energy calculations. The energy contributions for all interfaces in the simulated 5CRO and 2OVG lattices are listed in Tables I and II, respectively. (Images of each interface are presented in Figures S2 and S3.) Although we list the total MM-PBSA energy as ΔG_tot, we run the crystal simulations in the NVT ensemble and do not compute the configurational entropy contribution, so this term technically represents the enthalpic component of the Helmholtz free energy. Thus, we refer to the total value as a general binding energy.

As is shown in Figure 5, the MM-PBSA binding energy decreases approximately linearly as the interface surface area increases. The largest interfaces in both lattices form the biological dimer (interfaces 1 and 2 in the 5CRO lattice and interface 1 in the 2OVG lattice) and the calculations exhibit a consistent interaction energy near −50 kcal/mol. Except for interfaces 5 and 6 in the 5CRO lattice, all other non-biological interfaces in both lattices are roughly equal to or less than the average size of a crystal packing interface (the vertical dashed line at 570 Ų)⁵⁷ and exhibit binding energies between −5 and −30 kcal/mol.

Figure 5.

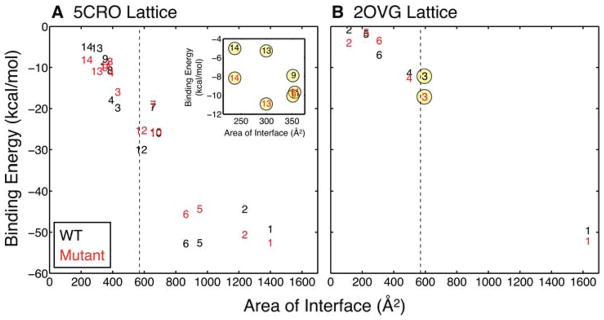
MM-PBSA binding energies versus the size of the interfaces in the (A) 5CRO and (B) 2OVG simulated lattices. Data points are denoted by their corresponding interface number for both WT (black) and mutant (red) simulations. Interfaces involving a mutation site are indicated with yellow circles. The dashed line designates the average area of a crystal packing interface (570 Ų).⁵⁷ The inset in (A) expands the region for the smallest interfaces in the 5CRO lattice. The largest interfaces – interfaces 1 and 2 in the 5CRO lattice and interface 1 in the 2OVG lattice – form the biological dimer. The interface surface area is computed as the difference in solvent accessible surface area between the two isolated monomers and the complex using VMD.⁴⁷

All interfaces in the WT lattices exhibit higher values of MM electrostatic energies (ΔE_ele) than those of the mutant lattices (Tables I and II). This observation may be attributed to the K32Q mutation, which results in an overall charge closer to neutral for the mutant compared to the WT monomer (+4 and +5, respectively). Thus, the polar contribution to the free energy of solvation (ΔG_PB) plays a more significant role in offsetting the positiveΔE_ele values in the WT lattices. The net electrostatic contribution to complex formation is determined by the interplay of ΔE_ele and ΔG_PB. While the individual terms are large in most cases, the net electrostatic energy (ΔE_ele + ΔG_PB) is generally smaller in magnitude (Tables I and II). For most interfaces, ΔE_ele + ΔG_PB is positive, indicating that the net electrostatic energy disfavors the association of protein chains in the crystal. Exceptions are the 5CRO interfaces 3 and 4, which have negative or roughly zero ΔE_ele + ΔG_PB in the WT and mutant simulations, respectively (Table I). Intersubunit salt bridging between Arg4 and Glu2′ at interfaces 3 and 4 (discussed below) is a likely explanation for why these interfaces are the only ones for which the net electrostatic contribution is negative. On the other hand, the MM van der Waals energies (E_vdw) and, to a lesser degree, the non-polar contribution to solvation (ΔG_np) favor complex formation, and together outweigh the net electrostatics.

We present the total MM-PBSA binding energies for different sets of interfaces in the 5CRO and 2OVG lattices in Table III. The differences between the sets in the WT and mutant simulations are shown in bold in the bottom row, and negative and positive values correspond to greater stability for the WT and mutant sequences, respectively. When considering all interfaces (“All”), WT and mutant Cro appear to be more stable in the lattices in which they were originally solved, although the difference in binding energy is smaller in magnitude than the standard error in the calculation. This trend holds for the subset of interfaces that do not involve a mutation site (“No site”), and the difference in energy is greater than the error for this subset in the 5CRO lattice. Interestingly, in both lattices, the subset of interfaces with a mutation site (“With site”) yields a more favorable binding energy in the mutant trajectories. The difference in binding energy for this subset is positive and roughly two (2OVG) and three (5CRO) times as large as the standard error. This observation indicates that packing interfaces with a mutation site are stronger in the mutant simulations regardless of the crystal environment.

Table III.

Total binding energies for crystal packing interfaces in the simulated lattices^a

	5CRO lattice (originally solved as WT)b			2OVG lattice (originally solved as mutant)c
	All	No site	With site	All	No site	With site
WT	−350.51 ± 14.93d	−322.72 ± 12.44	−27.79 ± 2.49	−82.33 ± 9.14	−70.27 ± 7.32	−12.06 ± 1.82
mutant	−337.12 ± 17.15	−298.63 ± 14.45	−38.49 ± 2.70	−90.68 ± 5.33	−73.56 ± 4.22	−17.12 ± 1.11
difference	−13.39 ± 22.74	−24.09 ± 19.07	10.70 ± 3.67	8.35 ± 10.58	3.29 ± 8.45	5.06 ± 2.13

^aThe sum of MM-PBSA binding energies (kcal/mol) for the WT and mutant lattices are presented for three different sets of crystal packing interfaces: all interfaces (“All”), those without a mutation site (“No site”), and those that involve a mutation site (“With site”). Differences between the energies in the WT and mutant simulations are defined as WT – mutant and are shown in bold in the last row.

^bFourteen total interfaces are present in the 5CRO lattice, four of which involve a mutation site.

^cSix total interfaces are present in the 2OVG lattice, one of which involves a mutation site.

^dStandard errors for the WT and mutant binding energies are computed as in Tables I and II. For the difference in energy terms (bold numbers), the standard errors are reported as the square root of the sum of the squares of the WT and mutant errors.

Crystal packing energetics is also analyzed as a function of the interaction energy per monomer for the WT and mutant sequences (Table IV). For each unique chain the unit cell, we compute the interaction energy per monomer as one half of the sum of the binding energies of all interfaces in which the chain participates. While we observe differences in the interaction energies for the WT and mutant simulations, the results are within the standard error of the calculation. Nevertheless, the general trend of the interaction energies presented in Table IV, as well as the total interface energies shown in Table III, are consistent with experiment in that the sequence with the lowest overall energy is realized in the actual crystal. We note that while the MM-PBSA approach provides a detailed description of the interaction energy between protein chains in the crystal, other forces that influence crystal formation (e.g., translational entropy and pH)^58,59 are not captured by the calculation.

Table IV.

Interaction energies per monomer in the simulated crystals^a

	5CROb				2OVGc
	chain A	chain B	chain C	chain D	chain A
WT	−79.83 ± 3.91	−84.52 ± 3.25	−87.34 ± 3.69	−63.53 ± 2.80	−41.17 ± 4.57
mutant	−75.10 ± 4.38	−79.89 ± 4.39	−82.27 ± 4.10	−65.53 ± 3.00	−45.34 ± 2.67
difference	−4.73 ± 5.87	−4.64 ± 5.47	−5.08 ± 5.52	2.00 ± 4.10	4.18 ± 5.29

^aThe interaction energies (kcal/mol) for the independent monomers in the 5CRO and 2OVG lattices are computed as one half of the sum of the energies over each interface in which the chain participates. For the WT and mutant sets, the errors are reported as in Tables I and II. For the differences, the standard errors are computed as in Table III.

^bIn the 5CRO AU, chain A participates in six crystal packing interfaces (1, 3, 5, 7, 8, 9), chain B in seven (2, 4, 5, 8, 9, 10, 11), chain C in six (1, 4, 6, 7, 12, 13), and chain O in five (2, 3, 6, 13, 14).

^cSince the 2OVG AU contains just one monomer, every chain (A) is equivalent and participates in all six crystal packing interfaces.

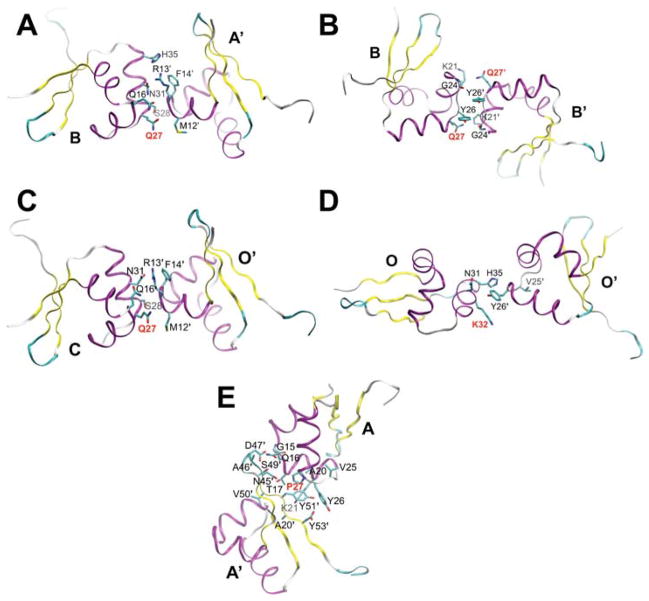
Energetics of interfaces involving RH mutations

In the 5CRO lattice, the RH mutation sites are located within the four smallest interfaces (interfaces 9, 11, 13, and 14; Fig. 6A–D). Interfaces 9 and 13 contain the Q27P mutation site and exhibit a stronger binding energy during the mutant trajectory compared to the WT simulation. More favorable net electrostatics and van der Waals interactions appear to account for the stabilization for the mutant protein at interfaces 9 and 13, respectively (Table I). Interface 11 also incorporates the Q27P mutation, but does not exhibit a difference in interaction energy in the WT and mutant sequences. Interface 14 involves the K32Q mutation and is stabilized in the mutant simulation relative to the WT sequence, in large part due to a decrease in the net electrostatic energy that likely arises from a decrease in charge repulsion between interface chains (Table I).

Figure 6.

Crystal packing interfaces involving mutation sites: 5CRO interfaces (A) 9 (353 Ų), (B) 11 (356 Ų), (C) 13 (300 Ų), and (D) 14 (237 Ų) and (E) 2OVG interface 3 (597 Ų). Residues are labeled with one-letter/number designations and the mutation sites are indicated with bold red labels. In the ribbon representation, purple, yellow, and teal/white represent α-helix, β-strand, and turn/coil secondary structure elements, respectively. At the mutation sites, the original residue composition is shown, i.e. 5CRO is shown as WT (Q27 and K32) and 2OVG is displayed as mutant (P27). The A29S mutation does not participate in crystal packing.

In the 2OVG lattice, the Q27P mutation participates in the largest crystal packing interface other than the biological dimer interface (interface 3; Fig. 6E). Replacing the mutant residues with their WT counterparts weakens interface 3. The net electrostatics for this interface is similar in the WT and mutant simulations, while ΔE_vdw is ~5 kcal/mol more favorable for the mutant versus the WT sequence (Table II). The latter observation is likely because the smaller cyclic side-chain of Pro27 in the mutant protein allows for better packing against Tyr51 of the neighboring chain compared to the longer and polar side-chain of Gln27 in the WT protein (Fig. 6E). Overall, the MM-PBSA calculations show that interfaces with mutation sites are more stable with the mutant sequence relative to the WT protein in both of the simulated lattices.

Energetics of interfaces without mutation sites

Mutation also affects interfaces that do not involve mutation sites. The most notable differences in the MM-PBSA binding energies between the WT and mutant lattices for interfaces without mutation sites occur at interfaces 1–6 in the 5CRO unit cell and represent interactions within the tetrameric AU (Fig. 7A–C). Among this set, interfaces 1 and 2 both form the biological dimer (A/C and B/O, Fig. 7A), and appear to be affected by the neighboring interfaces 3–6. (The stability of the dimer interface is further considered in the Discussion.)

Figure 7.

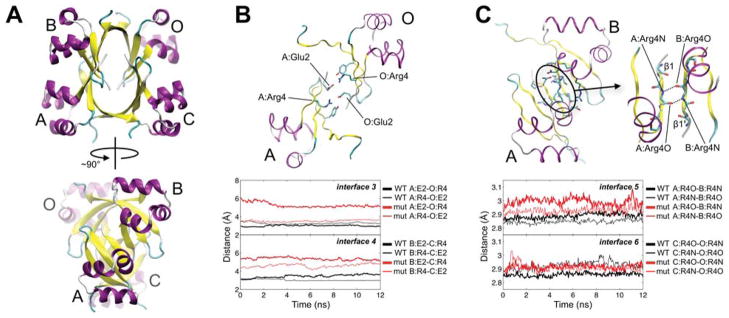
Packing interfaces in the tetrameric 5CRO AU. (A) The tetramer is rotated by ~90° to emphasize the extensive β-strand interaction. Chains A/C and B/O (interfaces 1 and 2, respectively) form the biological dimer. (B) Interfaces 3 (chains A/O) and 4 (chains B/C) involve salt bridging between Arg4 and Glu2 of a neighboring subunit (interface 3 is shown). The overtime inter-residue distance between Glu2 and Arg4 at interfaces 3 and 4 in the WT and mutant 5CRO crystal simulations is plotted below the interface. The distance is measured between the centers of mass of Arg4 Nη1/Nη2 and Glu2 Oε1/Oε2. (C) Interfaces 5 (chains A/B) and 6 (chains C/O) comprise interaction between β1 strands. Interface 5 is shown with a close-up of the β1-β1′ strand region to highlight the backbone hydrogen bonding between Arg4 of each subunit. The over-time distance between the backbone nitrogen and oxygen of Arg4 in the neighboring subunits at interfaces 5 and 6 during the WT and mutant simulations is plotted below the interface. A running average over 50 ps is used for all plots. An image of this interface with all contacting side-chains labeled is presented in Fig. S2. Secondary structure designations follow as in Figure 6.

Interfaces 3 (chains A/O) and 4 (chains B/C) involve an intersubunit salt bridge between Arg4 and Glu2 of a neighboring chain (Fig. 7B). Differences in the energetics for these two interfaces in the WT and mutant trajectories may be governed by the strength of this interaction. Due to the symmetry of the interfaces, the salt bridge can form between two intersubunit pairs (Arg4-Glu2′ and Glu2-Arg4′). Interestingly, the overall binding energies and net electrostatics for interfaces 3 and 4 become more favorable with the formation of this interaction. In the simulation of the WT 5CRO lattice, the salt bridge is maintained for all four possible Arg4-Glu2′ pairs at interfaces 3 and 4 throughout simulation and contributes to favorable net electrostatics. (Fig. 7B and Table I). In contrast, the trajectory of the mutant 5CRO lattice maintains the salt bridge for just one (interface 3) or zero (interface 4) of the four Arg4-Glu2 pairs, and the net electrostatics and ΔG_tot are less favorable than in the case of the WT protein.

Interfaces 5 and 6 form the two largest non-biological dimer interfaces in the 5CRO lattice, and are formed through interaction between β1-strands in the tetrameric AU (Fig. 7C). These interfaces exhibit stronger binding energies than the biological dimer interface in the WT 5CRO simulation. In the mutant simulation, interfaces 5 and 6 are significantly destabilized relative to the WT trajectory, and are weaker than the dimer interface (Fig. 5 and Table I). Throughout simulation, a key main-chain hydrogen bond between Arg4N and Arg4O′ in the β1-strands of the participating chains is longer for the mutant compared to the WT protein (Fig 7C), indicating that the strands move farther apart in the mutant lattice. The formation of new backbone hydrogen bonds between the β1-strands is not observed. Overall, the trends in hydrogen bonding at interfaces 5 and 6 and in salt bridging at interfaces 3 and 4 reveal a loosening of the 5CRO tetrameric AU upon incorporating the mutant sequence.

Other interfaces in the 5CRO lattice highlight the diverse nature of crystal packing interfaces. While interfaces 8 and 10 exhibit similar total binding energies, the van der Waals interactions and the net electrostatics contribute differently for the WT and mutant sequences. At both interfaces, ΔE_vdw is stronger for the WT sequence and ΔE_ele + ΔG_PB is more favorable for the mutant protein by similar magnitudes. For interface 12, both of these contributions are slightly more favorable in the WT simulation.

In the 2OVG lattice, differences in the binding energies between the WT and mutant simulations for interfaces without mutation sites occur for the first and third smallest interfaces (2 and 6). Interface 2 is more stable in the mutant trajectory and interface 6 is stable by approximately an equal amount in the WT simulation. E_vdw accounts for this difference at interface 2 and, to a lesser degree, at interface 6 (Table II). Interface 4 involves the RH of one monomer, but no mutation sites, and exhibits similar E_vdw, ΔE_ele + ΔG_PB, and ΔG_tot in the WT and mutant trajectories. At interface 5, ΔE_vdw is more favorable for the WT protein, and this effect is offset by a more favorable net electrostatic contribution of roughly the same magnitude for the mutant sequence. The stability of the biological dimer interface (interface 1) is similar in the WT and mutant 2OVG lattice simulations and is considered further in the Discussion. Overall, the MM-PBSA calculations show that the effect of mutation in the lattice is not relegated to interfaces directly involving mutation sites. Allosteric effects arising from mutation in the crystal lattice are the target of current investigation.

Discussion

Protein X-ray structures are perhaps the most valuable information for discussions of structure-function relationships. While conformational variation within and between X-ray models may indicate solution dynamics critical for function, such heterogeneity could instead arise from crystal packing. We address this issue by considering different crystal forms of the Cro dimer.

Influence of the crystal environment on Cro conformation

Our simulations allow us to propose models for the effect of crystallization on Cro conformational dynamics.⁶⁰ Two dominant interconverting states (closed and semi-open) exist in solution simulation, and crystallization may nucleate from either conformer. Since closed and semi-open states closely correspond to available X-ray structures, they appear to fit “as is” to the lattice during crystallization without significant structural rearrangement. This scenario represents a “conformational selection” model.^22,23 In the case of WT Cro, the lattice selects the closed dimer, while for mutant Cro, due to a new set of packing interfaces, the lattice can take the semi-open conformer.

However, such a model does not account for why an unstable fully open mutant is observed by X-ray crystallography in the absence of DNA. In this case, a dominant solution form may initially interact with the lattice. The strengthening of crystal packing interfaces involving the mutated residues could then deform the dimer structure away from a conformational energy minimum toward a higher energy state. Given that this “biasing energy” can be quite strong, such a deformation may proceed from either basin (closed or semi-open). Lattice stabilization of a higher energy solution conformer is consistent with an “induced fit” model.⁶¹ The possibility of both a conformational selection and an induced fit model for crystallization underscores the complexity of the influence of the crystal environment on protein conformational dynamics and the need to carefully consider X-ray structures. It should be noted that although we argue that the fully open crystal structure does not reflect the dominant solution form of Cro, it still represents a functionally relevant conformation. This further emphasizes Cro flexibility, which is undoubtedly essential for its DNA-binding mechanism.

Energetics of crystal packing interfaces

Currently there is no general consensus for how strongly crystal packing can affect protein conformation. Our combination of crystal MD and MM-PBSA calculations presents a practical approach toward addressing this issue and yields new understanding into how crystal packing influences the Cro dimer.

As previously noted by Hall et al.,⁴ Cro crystals exhibit extended β-sheet structure. In the WT apo (closed) and PSQ form 2 (semi-open) crystal structures, interaction between β1 strands of neighboring dimers results in a pseudo-symmetric anti-parallel β-sheet (see Fig. 7A for the case of 5CRO). This extended β-sheet structure was proposed to distort Cro conformation away from its dominant solution form.⁴ Such β-sheet interaction is not present in the crystals of fully open Cro. While our MM-PBSA calculations show that the β-sheet interaction in the 5CRO lattice of closed Cro is as strong as the dimer interface, these interactions do not appear to alter dimer conformation, since closed and semi-open dimers similar to the WT apo and PSQ form 2 Cro X-ray structures, respectively, are the dominant species in the simulated solution ensemble.^20,21 The observation that the two X-ray structures exhibiting the extended β-sheet structure (which lacks any realized biological implication⁴) correspond to the two stable dimer solution states shows that extensive contacts between protein molecules in the crystal do not necessarily distort protein conformation. Comparison of crystal packing energetics in the two crystal environments of mutant Cro (PSQ forms 1 and 2) would provide insight as to why extended β-sheet structure formed in one mutant X-ray structure (form 2) but not in another (form 1). However, the crystals for PSQ forms 1 and 2 were grown at different pHs (7.5 and 5.5, respectively) and such a comparison is perhaps well suited for a combination of crystal and constant pH^62,63 simulation methods, which would broaden our capability to quantitatively evaluate protein energetics in different crystal environments.

We also glean further insight into the Cro dimer interface. In contrast to solution simulation,^20,21 closed biological dimers in the tetrameric AU of the 5CRO crystal environment are either similar (interface 1) or destabilized (interface 2) with respect to the fully open dimer of the 2OVG lattice. This apparent discrepancy can be explained in terms of intersubunit salt bridging. During solution simulation, a salt bridge between Arg4 and Glu53 of the adjacent chain stabilizes closed-like dimers. The tetrameric AU of the 5CRO lattice satisfies a similar pattern of intersubunit salt bridging between Arg4 and Glu2 of a neighboring monomer at interfaces 3 and 4 (Fig. 7B). Despite differences in the strength of the salt bridges in the WT and mutant crystal simulations, interfaces 3 and 4 exhibit favorable binding energies and act across the interface of the closed biological dimer. No such salt bridge across the dimer interface is present in the 2OVG crystal of fully open Cro. Taking into account the intersubunit salt bridging as part of the dimer interface, the closed dimer conformation in the 5CRO crystal environment becomes more energetically favorable than the fully open form of the 2OVG lattice, consistent with previous solution simulations. Experimental validation of the intersubunit salt bridge in stabilizing the closed dimer could come from mutating Arg4 to a charge-neutral residue (while preserving the WT composition of all other residues) and then crystallizing Cro to determine if a closed conformation is still achieved.

Furthermore, we gain understanding about the effect of mutation on packing interface energetics in the Cro crystals. Mutational modification is a common approach for facilitating protein crystallization. Such mutations are often located on the protein surface and participate in crystal contacts.⁵⁶ In the case of the PSQ Cro crystal structures, the mutated residues reside on the surface of the RH, relatively far away from the flexible β-hairpin hinge region, and contribute to crystal packing. It has been unclear whether the mutations are the direct cause of the conformational differences between WT and mutant Cro, or if they affect crystal packing so as to favor a different crystal form. Our simulations reveal that the mutations do not significantly alter Cro conformation in solution. Instead, the mutated residues form crystal contacts, and packing interfaces involving a mutation site exhibit a stronger binding energy during crystal simulation with the mutant sequence in comparison to the wild type protein. Notably, this effect can be as strong as ~5 kcal/mol in either crystal environment, providing a significant additional energetic contribution during crystallization that could alter dimer conformation (i.e., to a more open state). For Cro the same set of mutations resulted in two new apo crystal forms that exhibit large-scale conformational differences in comparison to the originally solved WT apo X-ray structure. While one mutant crystal form is consistent with a stable solution state (semi-open PSQ form 2), the other is unstable in solution (fully open PSQ form 1),^20,21 further emphasizing the complex nature of the crystal environment. Nevertheless, the effect of mutation works serendipitously in the case of Cro, as the set of mutant and WT X-ray structures fully describes the range of conformational space available to the dimer in solution.

Conclusion

The presence of an apo Cro X-ray structure in a fully open conformation similar to its DNA-bound structure suggests that the functional dimer form is a well-populated member of the solution ensemble. However, mutations in the DNA-free fully open X-ray structure (PSQ form 1) may alter the conformational preference of the dimer. In this study, enhanced sampling of mutant Cro reveals that the mutations do not alter the dominant solution states of the dimer. Instead, simulation of WT and mutant Cro in the crystal environment supports the notion that mutation influences crystal packing. In particular, comparison of MM-PBSA energies for crystal packing interfaces involving a mutation site shows that incorporating the mutant sequence into the originally solved WT lattice (5CRO) strengthens the interfaces. Conversely, replacing the mutant residues with their WT counterparts in the originally solved mutant lattice (2OVG) destabilizes crystal packing for interfaces with mutation sites. Mutation can stabilize a single packing interface by as much as ~5 kcal/mol in either of the two crystal environments. Thus, even though the mutations do not significantly affect the dominant dimer states in solution, they appear to provide an additional energetic contribution during crystal formation that could shift the conformational ensemble toward a higher energy state (i.e., a more open conformation). Moreover, interfaces without mutation sites can exhibit differences in relative stability. This effect is either apparent in the overall binding energy of the WT and mutant sequences or more subtle through differences in the balance between the van der Waals and the net electrostatic contributions that lead to similar total binding energies for the two sequences. Overall, the current work sets a foundation for studies focusing on other energetic factors at play in crystal packing so as to more fully elucidate the affect of the crystal environment on protein conformational dynamics.