Abstract
We developed a novel scheme based on the Grand-Canonical Monte-Carlo/Brownian Dynamics (GCMC/BD) simulations and have extended it to studies of ion currents across three nanopores with the potential for ssDNA sequencing: solid-state nanopore Si3N4, α-hemolysin, and E111N/M113Y/K147N mutant. To describe nucleotide-specific ion dynamics compatible with ssDNA coarse-grained model, we used the Inverse Monte-Carlo protocol, which maps the relevant ion-nucleotide distribution functions from an all-atom MD simulations. Combined with the previously developed simulation platform for Brownian Dynamic (BD) simulations of ion transport, it allows for microsecond- and millisecond-long simulations of ssDNA dynamics in nanopore with a conductance computation accuracy that equals or exceeds that of all-atom MD simulations. In spite of the simplifications, the protocol produces results that agree with the results of previous studies on ion conductance across open channels and provide direct correlations with experimentally measured blockade currents and ion conductances that have been estimated from all-atom MD simulations.
1. Introduction
The use of beta-barrel proteins for the sequencing of ssDNA was proposed as early as 1996 and rapidly drew attention for its apparent simplicity and potential for rapid and cost-efficient genome sequencing1. The strand of DNA is electrophoretically driven through a protein nanopore, such as alpha-hemolysin (αHL) or Mycobacterium smegmatis porin A (MspA), by an applied electrical potential, resulting in the reduction (blockade) of ionic current in a sequence-dependent manner. The analysis of the blocking events can subsequently be used to infer the DNA sequence. The direct signal readout removes errors associated with the chemical reactions that are needed in the existing sequencing methods, thus reducing cost and increasing the efficiency. The key challenge of this method is to achieve a contrast between nucleotides (or corresponding blockade) that is resolvable by current equipment. The use of the high potential bias that is required to drive DNA in a well-controlled manner is usually prohibitive, as it increases the associated noise and thereby makes sequencing more challenging. A variety of methods has been proposed to address this challenge with the use of polymerases or sequence expansion2-6, but these additions will unavoidably affect the operational costs and will most likely make such techniques financially impractical.
These rapid advances in experimental studies suggest that protein nanopore techniques could be developed into a robust and relatively cheap method for DNA sequencing. The main challenge facing these techniques is to elucidate the physical mechanism underlying polymer translocation through biological pores. Captured single stranded DNA (ss-DNA) is a large and floppy biopolymer with low degrees of freedom and with conformational dynamics that modulate ion flow across the pore7,8. The molecular details of DNA capture and escape are also a source of debate. However, most researchers agree that specific DNA-protein interactions could and should be exploited to amplify the signal and increase the contrast between nucleotides. The targeted modification of a biological pore requires detailed information about the dynamics of a floppy ssDNA molecule in confinement and its effect on ion currents9. A natural approach to this problem is to use all-atom Molecular Dynamics (MD) simulations8,10,11 and subsequently construct a rational picture of DNA dynamics in a nanopore confinement. This approach has been proven to be useful in the elucidation of the microscopic factors that govern DNA dynamics in the nanopore12. However, it is apparent that the slow conformational dynamics of DNA limit the usefulness of this method if it is applied to sequence-dependent ion transport. Simulations up to several micro-seconds in length are required to obtain comprehensive sampling, which is prohibitive for large systems of nanopores embedded in lipid bilayers (up to 300,000 atoms). To increase the ion conductance sampling in all-atom simulations with applied voltage, the applied bias must be large (up to 2 V) compared to experimental voltages of 100 to 150 mV. The use of a strong force may lead to (a) the damage of the pore itself and (b) to the overextension of the captured strand, which would impede direct comparisons to the experimental data.
A convenient alternative can be found in the Brownian Dynamics (BD) simulations that explicitly model the degrees of freedom due to mobile ions13,14 and (or) captured polymers15 but treat protein and solvent degrees of freedom implicitly. The influence of the surrounding media is incorporated implicitly via random stochastic, electrostatic and repulsive forces due to the buffers, protein and membrane charges that are pre-computed by solving the Poisson-Boltzmann equation. This modeling allows for the construction of a multi-ion potential of mean force (PMF) for simulations of ion transport. The main challenge of applying this technique directly for studies of ion current through DNA-blocked nanopores is in elucidating the parameters for ion-ion and ion-polymer potentials. One recently proposed approach is based on the explicit use of a potential grid from the atomistic MD simulation of a nanopore with a captured DNA strand. This approach allows for the construction of static maps that capture the highly inhomogeneous field inside the nanopore. An important step forward was made in 2012, when Comer and Aksimentiev showed that the sampling of DNA dynamics in a model nanopore is sufficient for the construction of PMF maps from all-atom MD16 and their subsequent use for ion permeation studies. The great advantage of this approach is in its computational performance and relatively simple implementation. The most obvious limit is its need for a complete description of ssDNA dynamics and its mutual coupling to ion distributions in the pore; e.g., it is assumed that the PMF reconstructed for an ion inside the channel with a captured nucleotide is fully converged. In other words, it is assumed that such a PMF that does not explicitly take into account that DNA dynamics can be used to represent some “mean” conformation of a polynucleotide, effectively modulating ion transport across the pore. While this lack of consideration can be justified in the case of tightly controlled ssDNA translocation across solid-state nanopores, it is hardly the case for many biological nanopores, where ssDNA exhibits significant conformational dynamics. For example, several experimental studies reported excess noise in measured ion currents for solid-state and biological nanopores with captured ss-DNA. This suggests that measured current levels are modulated by the conformational dynamics of the molecular DNA, with a slow time-component, similar to the flickering gating observed in ion channels1,17,18. The structural origins of conformational transitions for captured polymers are largely unknown, but it was recently suggested that proteins in nanopores exhibit well-defined structural transitions on the time-scale of micro- to milliseconds; e.g., the time-scales are comparable in resolution to low-noise electrophysiological recordings. The extension of static PMF maps to new nanopores (or even mutant versions of known nanopores) would require the re-parameterization of a 3D PMF grid and thus additional MD simulations. For example, if one is to study a floppy polymer, such as ss-DNA, in a new pore with different surface charges, one would need to first perform all-atom MD/PMF computations to obtain the required maps first.
An alternative approach is to combine the explicit treatment of ions and ssDNA degrees of freedom, while representing the nanopore and the solvent using mean-field approaches. We have recently implemented this strategy with the BROMOC program, which uses a well-established coarse-grain model for DNA and ad-hoc DNA-ion interaction potentials from primitive electrolyte models15. The natural problem for an extension of Grand Canonical Monte-Carlo/Brownian Dynamics (GCMC/BD)-based techniques to nanopore sequencing is its lack of potential functions for describing the interactions between ions and nucleotides at an atomic resolution. To circumvent this challenge here, we used an approach based on the reverse reconstruction of interaction potentials from known atomistic distribution functions with statistical mechanics relationships that were mapped onto a coarse-grain model. We used the Inverse Monte-Carlo (IMC) method developed by Lubartcev and colleagues19-25 to obtain a set of ion-ion and ion-nucleotide interaction potentials from all-atom MD simulations, and then mapped these potentials onto the coarse-grained DNA model of our choice. This allowed us to study the ion permeation of the membrane proteins by including solvent-mediated interactions in our potential functions in combination with a previously developed GCMC/BD approach.
The main purposes of this study were twofold. First, we aimed to test and establish the validity of effective potential mapping from all-atom MD onto a coarse-grained model of ss-DNA. Second, we wanted to elucidate the microscopic factors that give rise to base-specific transport through the α-HL and its mutant nanopore and through the synthetic Si3N4 nanopore in presence of a single-stranded (ss-) and double-stranded (ds-) polynucleotides that blocked ion passage. The paper is organized as follows. We first describe in detail the Inverse Monte-Carlo method, ion-DNA interaction potentials and their implementation as part of the BROMOC simulation scheme. In the Results and Discussions section, we describe our study of open pore conductance across three widely used sequencing systems: the αHL (WT and its NYN-modification) nanopore9 and the Si3N4 nanopore. Next, we test our method for its ability to predict ssDNA dynamics in αHL (WT and its NYN-modification), dsDNA dynamics in Si3N4 and DNA-dependent ion currents in both pores.
2. Methods
To provide better descriptors for the ion distributions observed in the all-atom MD simulations mapped onto a coarse-grain DNA model and implemented in BROMOC-D,15 we developed improved pairwise interaction potentials between DNA sites and their counter-ions. The idea of this method was to map the distribution functions obtained from all-atom simulations onto a coarse-grained representation of the system of interest. We used well-established and carefully tested DNA models developed by De Pablo and colleagues26. The parameters of the model and its melting thermodynamics in the presence of explicit and implicit counter-ions were tested as described previously in De Biase et al. 15 The Inverse Monte-Carlo (IMC) scheme for developing sets of effective potentials was adopted from Lubartcev et al23,25. Effective ion-nucleotide potentials allow for an accurate description of solvent-mediated effects based on matching distribution functions. The Radial Distribution Functions (RDF) required for the development of effective potentials from IMC iterations were obtained from the all-atoms MD simulations for all possible ion-ion and ion-DNA bead pairs. Afterwards, using the new pairwise ion-ion interaction potential, the excess chemical potentials were obtained. In this section, we also describe the methods for the simulations preformed on the synthetic and biological nanopores used to validate our methodology. All of the program codes (Fortran-90) developed for this paper are freely available by request from the authors.
MD simulations
Radial distribution functions between nucleotide sites (base, sugar, phosphate), individual ions (K+, Cl-) and ion-ion pairs were obtained from six series of separate simulations in 1 M of aqueous KCl solution with and without deoxy-oligonucleotides: (a) ss-poly(dA)14, (b) poly(dC)14, (c) poly(dG)14, (d) poly(dT)14, (e) 5′-CGCGAATATTCGCG-3′, (f) no DNA. B-DNA geometry was constructed using the 3D-DART27 web portal. Next, single stranded B-DNA was solvated in a truncated octahedron box with 21232±210 TIP3 water, 141 Cl- anions and 154 K+ cations for (a-e), and 153 Cl- anions and 153 K+ cations for (f), all by using the CHARMM-GUI portal28,29. The MD simulations were performed using NAMD30 2.8 with the standard CHARMM27 force field31,32 The initial system was minimized to 5000 steps, followed by 0.6 ns of equilibration in the NPT ensemble at 1 atm and 300K, according to the Langevin Piston method33 and the Lowe-Andersen thermostat34 and as implemented in NAMD30,35. The van der Waals interactions were switched off at 14–16 Å using a force-switching function36. Long-range electrostatic interactions were calculated using the particle-mesh-Ewald method, with a grid spacing of 0.75 Å for the fast Fourier transformation, κ = 0.34 Å−1 and a sixth-order B-spline interpolation37. All bond lengths involving hydrogen atoms were fixed using the SHAKE function to enable a 2-fs time step38. The DNA atoms were restrained to enable exact structural mapping onto the coarse-grain model used for the parameterization of the distribution functions from the inverse Monte-Carlo runs. A production run of 25.6 ns simulations was performed in the NVT ensemble for all systems to obtain the site-ion distribution functions (a-f). The trajectory was saved every 0.5 ps, and the average final box volume was approximately 216 × 103 Ǻ3.
An All-Atom Molecular Dynamic Simulation of Synthetic Nanopores
We used a silicon nitride (Si3N4) partition as a model for the synthetic nanopores. The Si3N4 layer was built, after which the atoms were removed to create a solid-state nanopore with the same dimensions as those used in the experimental studies. The all-atom MD simulations were performed using the program NAMD30 2.9 with periodic boundary conditions. CHARMM-GUI28,29} and Aksimentiev's lab protocols were used to build membrane-inserted pores and the Si3N4 system39,40. A Langevin thermostat was applied to the non-hydrogen atoms (Si3N4) with a damping constant of 1.0 ps−1 to maintain a temperature of 298.15 K. Interactions between all atoms of the systems, including atoms from the water, ions, and nucleic acids, were calculated using the C27 CHARMM force-field31,32. The rigid version of the TIP3 water model, as implemented in NAMD2.9, was used.
After assembly, each system was minimized with the gradual removal of heavy atom constraints, equilibrated for 5 ns in the CPT ensemble and subjected to 60-100 ns runs with applied voltage in the NVT ensemble12. The non-bonded parameters were obtained from Comer et al.40 To maintain the nanopore during the MD simulations, a harmonic potential was applied on the heavy atoms to ensure an appropriate dielectric constant of the surface (ε ∼ 7.5) and bond length. The model pore was generated using the numerical recipe provided by Comer & Aksimentiev for the construction of a phantom pore16. The repulsive potential was used to modulate DNA adhesion to the pore walls. The nanopore is wide enough (with an effective radius ∼8 Å) to allow the transport of a DNA duplex. It has been proposed that due to differences in the blocking volume and mechanics of DNA transport, it may still be possible to sequence double-stranded DNA. We ran the MD simulations for the open pores and for systems containing the 3′-CGG, 3′-GCC, 3-′GTA and 3′-TAC oligomers. The salt concentration (C=1.75 M) and applied voltage (180 mV) were held constant. An example of a simulated system is shown in Figure 1.
Figure 1.
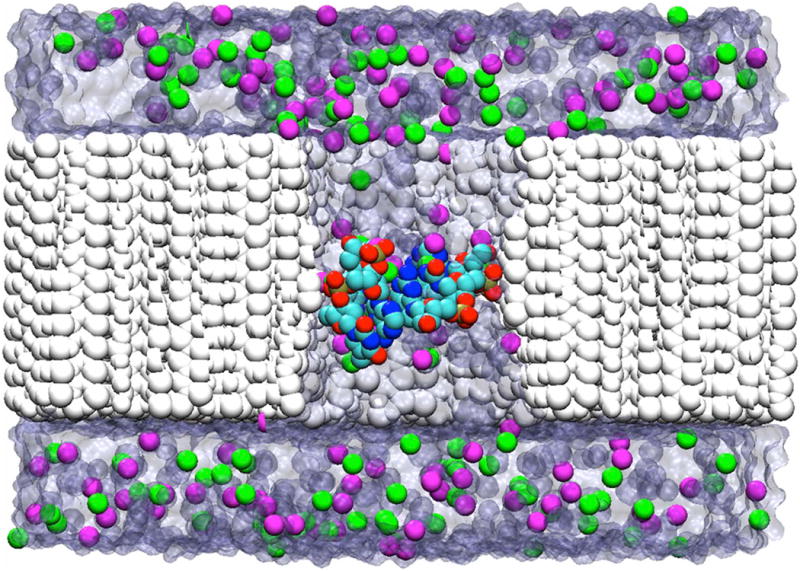
A sagittal view of the all-atom MD simulation setup with different dsDNA trimers blocking a nanopore perforated in the Si3N4 partition, shown in white. The blocking DNA molecule is shown as a ball-and stick, while the K+ and Cl- counterions are shown as magenta and green spheres, respectively. The solvent molecules are shown in transparent navy.
Site Definition in the Coarse Grain Model of DNA
The site definitions and equilibrium geometry correspond to de Pablo's DNA coarse grain model.26 The positions of the DNA bead centers were slightly adjusted (maintaining the rest of the force field) to aid matching for the ssDNA and ion interaction between the all-atom and coarse-grained simulations. This has no impact on the performance of the coarse-grain DNA model and faithfully reproduces the melting thermodynamics as reported by de Pablo and colleagues26. In the revised DNA model, the phosphate site (P) of the CG-model coincides with the phosphorous positions, and the sugar site (S) is located at the geometric center of the sugar atoms: C4′, O4′, C1′, C2′ and C3′. For the bases, the A, C, G, and T sites are positioned at the geometric center of all heavy atoms for each base.
DNA geometrical parameters
Based on de Pablo's paper26, BROMOC builds DNA by the periodical replication (set of rotation and translation) of the primary nucleotide coordinates, which are composed of the sugar, phosphate and base coordinates. The new set of coordinates for the nucleotide sites are generated based on our coarse definition of DNA. We built an all-atoms double-stranded B-DNA structure using the 3D-DART27 web portal with a sequence that contains a total of 100 nucleotides composed of an equal number of each base in a completely random order. The sequence was:
5′AATACACTGAGTAGCCCGTGAGTATACTATTCTCTCCATCCATCGAATGGGTAGAACTCCGGTGTCACCTAGAAGGCGTGGCTCACAAGTGAGTCGTTGCGCAACGACTCACTTGTGAGCCACGCCTTCTAGGTGACACCGGAGTTCTACCCATTCGATGGATGGAGAGAATAGTATACTCACGGGCTACTCAGTGTATT-3′.
The coordinates of the primary nucleotide and replication parameters were adjusted using the PRAXIS algorithm41 to minimize the root mean square deviation between the constructed DNA (using de Pablo's parameters as the initial set of parameters for the primer nucleotides) and the coarse-grained DNA structure. These new parameters (Table 1) were used in BROMOC in combination with the obtained effective potentials.
Table 1.
Our structural coarse grain DNA Model: Cartesian coordinates of primary nucleotide elements (S, P, Ab, Cb, Gb, Tb) and replication parameters: internucleotide distance (id) and internucleotide angle (ia). Distances are in Å and angles in degrees. Parameters correspond to B form of DNA. Complementary nucleotide is located in cylindrical coordinates at (r,-θ,-z). The position of the next contiguous nucleotide is located in cylindrical coordinates at (r, θ+ia, z+id).
| x | y | z | |
|---|---|---|---|
| Phosphate (P) | -0.32844965 | -9.07673263 | -1.03892416 |
| Sugar (S) | 2.59584871 | -6.51694259 | 1.34359750 |
| Adenine base (Ab) | 0.39843739 | -2.57129265 | 0.15848098 |
| Cytosine base (Cb) | -2.34190887 | -3.49182521 | 0.24690508 |
| Guanine base (Gb) | 0.80597851 | -2.05254712 | 0.10838747 |
| Thymine base (Tb) | -0.37157162 | -3.35015493 | 0.24317884 |
Inter-nucleotide distance: 3.41899065
Inter-nucleotide angle: 36.29094497°
Evaluation of the Radial Distribution Functions
For the RDF computation from the MD simulations, atomistic DNA coordinates were converted to coarse-grained DNA site coordinates as described above. The RDF functions for the effective potential parameterization were computed for 15 X-Y pairs, where X=P, S, A, C, G, T, K, Cl and Y=K, Cl. The RDF tables were computed for every 0.1 Å (dx). RDF was calculated for each saved frame (f), with F as the total number of frames. The RDF was computed for each particle, where N or M are the total number of particles for each respective type index number i or j. The RDFs for the identical pairs (gii(x)) were obtained from eq. 1, while the hetero-pairs of RDF (gij(x)) were evaluated using eq. 2. V is the truncated octahedron box volume calculated by the scalar triple product of its three periodic vectors as for a parallelepiped. Periodic boundary conditions were used to center all atoms during the RDF calculations using the lattice vectors from the MD simulations.
| (1) |
| (2) |
The special case of the spherical finite system
Calculations of RDF in BROMOC simulations were performed in finite spherical boundaries. Periodic Boundary Conditions are not yet available for the BROMOC simulations. We normalize our RDFs by considering the volume of intersection of two spheres. The volume of intersection (vi) between two spheres is computed as described in eq. 3.
| (3) |
Here, d is the distance between the two sphere centers, r1 is the radius of sphere 1 and r2 is the radius of sphere 2. If one sphere is contained inside the other, the volume is equivalent to the volume of the contained sphere.
Sphere 1 is the system sphere of radius 65 Å and volume V, centered at the origin. Sphere 2 has a radius equivalent to the distance between particle i and j centered at either i or j location (ri, rj, respectively). The RDF was computed and normalized as shown in eq. 4 and 5.
| (4) |
| (5) |
The Implementation of the Effective Potentials in BROMOC15
The effective potential tables do not cover a strong-repulsion region of the potential function between 0 and ∼3 Å. The repulsive wall for each energy function is introduced using eq. 6. Parameters a and b were adjusted to fit the first two data points of the effective potential tables. The potential functions for distances greater than 25 Å were smoothed to zero with eq. 8 and the parameter c was adjusted to match last data point at the end of each potential table. The second term in eq. 8 accounts for the electrostatic interaction between particles i and j. The discreet data points are splined using the second order polynomial formula shown in eq. 7. For each data point in the effective potential tables, a set of l, m and n parameters were obtained. All parameters were adjusted so that each contiguous eq. 7 and its derivative matched at every point. For the first data point, eq. 7 was adjusted so that the head function and its derivative coincided at this point. The last eq. 7 parameters are adjusted to match the tail function and its first and second derivatives. For the computation of forces, the first derivatives of eq. 6, 7 and 8 are used. To achieve these conditions, the data points need to be slightly modified using a particular developed algorithm implemented in the BROMOC code. Therefore, the obtained numerical forces and energies are smooth and continuous.
| (6) |
| (7) |
| (8) |
Excess Ion Chemical Potentials
The Grand-Canonical Monte Carlo (GCMC) procedure relies on the excess chemical potential (μ) as an input to control the number of particles in the system. Excess chemical potential depends on the effective solvent-mediated ion-ion interaction potentials, and must therefore be parameterized for a developed set of K-K, K-Cl and Cl-Cl effective potentials. We used an empirical fit of parameters with an initial guess obtained from the solution of the hyper-netted-chain (HNC) equation14,42-44. We used a single GCMC buffer that covered a cubic box of 75×75×75 Å3. The GCMC input needs initial values for the concentration (ci) and for the excess chemical potential (μ) and will output a real concentration (co) of ion for each type. We iteratively varied the excess chemical potential values (μ) (at fixed ci) to find the matching point between the input (ci) and the output concentrations (co). The corresponding μ for each ci is found when ci equals co. The output concentration (co) was computed by averaging the concentrations obtained from the particle counts and the system volume. Once co of the ions was acquired for each μ (at a particular value of ci), co and μ the data were adjusted using eq. 9, and the proper μ was extrapolated for the corresponding ci value.
| (9) |
Excess chemical potentials were retrieved for concentrations (c) ranging from 0.1 to 3 M. The c vs. μ plot was fitted using eq. 10. The parameters obtained for K+ and Cl- are shown in Table 2.
Table 2.
Parameters of eq. 5 adjusted for K+ and Cl-. Correlation coefficient of 0.99995 was obtained for both. 24 data points used from 0.1 to 3 M.
| Eq. 5 parameters | Cl- | K+ |
|---|---|---|
| a0 | -1.875192 | -1.981815 |
| a1 | 2.091497 | 2.247552 |
| a2 | -0.8698114 | -1.023529 |
| a3 | 0.1632971 | 0.2325105 |
| a4 | 8.732315 × 10-4 | -1.153873 × 10-2 |
| (10) |
With this equation, any μ within the concentration range can be extrapolated.
Evaluation of ion currents
Here, we describe the method used to compute ion currents. First, a counting point along the z-axis was selected (the channel was aligned along z-axis). For every time step, ions crossing this point in direction of the positive axis were counted as forward crossing (nf) or backward crossing (nb) for the opposite direction. The effective crossing was the difference between the forward and backward crossing and was determined for each type of ion and subsequently combined with the net charge (q) to obtain the total current (I). The current for a given time-interval (Δt) was then determined then by eq. 11. The average current for the time course (t) of a given trajectory can be computed with eq. 12. In all cases, the current is expressed in pico-Amperes (pA) units. Ion counters were located in several positions along the channel, and the variance in current counting was found to be insignificant, as expected for a steady state situation.
| (11) |
| (12) |
However, it should be noted that for all of the simulations, steady states of the ion currents were achieved during the simulation time, and the variance between the different counting zones was less than 0.5 %.
Ion Diffusion in the proximity of DNA
It was shown that the ion diffusion was reduced in the proximity of DNA. For the implementation, we used an empirical formula from Comer et al.16. The diffusion constant was determined according to eq. 13, where Dbulk is the diffusion coefficient in the bulk, d(r) is the minimum distance between the ion and DNA surfaces at position r, D0 is the diffusion coefficient at distance d=0, and b is a characteristic distance over which diffusivity approaches its bulk value. The minimum distance was computed from the distance between the ion and the DNA site centers minus the closest proximity distance obtained from the effective potential tables. The DNA site that minimizes this distance was chosen.
| (13) |
BROMOC Simulation Setup
BROMOC 15 utilizes the GCMC/BD method, which separates the electrostatic forces into static and reaction field contributions for enhanced computational efficiency and allows off-lattice dynamics of the explicit mobile ion while keeping the proper thermodynamic boundary conditions of ion concentrations using GCMC algorithm of Im, Seefeld and Roux43. We used the method developed by Luo, Egwolf et al. to assess the reaction field component for the GCMC/BD simulations45 with Generalized-Born formulation. The details of the Poisson-Boltzman computations required for obtaining static and repulsive field maps can be found in De Biase et al.15. In all BROMOC simulations, the biological pores were treated as rigid structures, with a dielectric constant of 2, surrounded by a high dielectric solvent (εw= 80) and embedded in an implicit membrane (εm= 2) of 38 Å in thickness (Figure 2).
Figure 2.
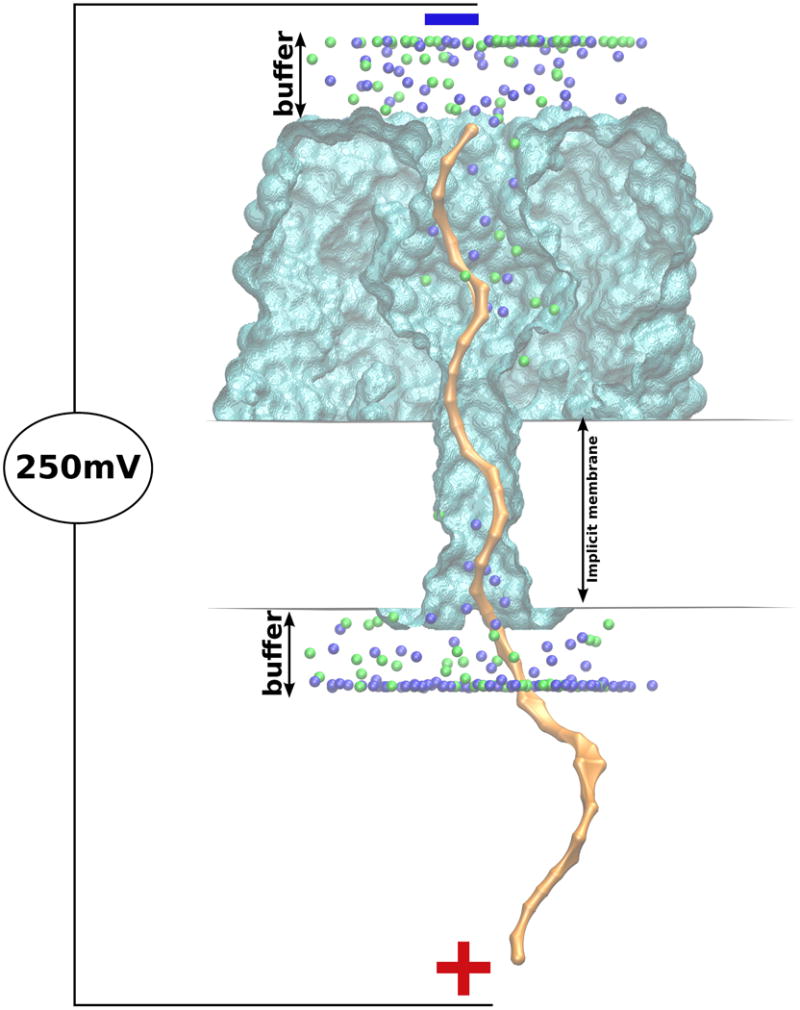
Setup for BROMOC simulation box. αHL (or αHL-NYN) is presented as a rigid structure (cyan surf), with ssDNA (yellow surf) threaded through it. The buffer regions contain a salt solution of KCl (ions are represented as green and blue spheres).
The synthetic nanopore has a dielectric constant of 7.5, with a partial charge distribution set according to the Comer at al.16 The cylindrical region (with εc= 80 and radius of 14.5 Å and 8.0 Å) was introduced to mimic the water-filled pore environment in the αHL simulations and the Si3N4 nanopore, respectively. The simulation box covered the entire length of the pore-DNA systems, with the GCMC buffers located approximately 20 Å away from its boundaries. The structure for wild type αHL was taken from PDB entry:7AHL. SCWRL3.0 protocol46 was used to generate the E111N/M113Y/K147N (αHL-NYN) mutant of αHL. αHL-NYN was proposed to provide a better discrimination between the different nucleotides9 by reducing the primary confinement zone of the nanopore. The BROMOC setup for studies of the beta-barrel proteins considered here was analogous to the setup previously reported.15 In addition to open-pore current-voltage relations, we have considered studies of four different homo-polymeric strands (ss-poly(dA)40, ss-poly(dC)40, ss-poly(dT)40) with readily available experimental data. Two different orientations were studied. The 3′ or 5′ end of the polynucleotide was immobilized by harmonic restrains at the wide entrance of the pore to mimic the effect of the streptavidine tethers used in experiments. All simulations of the pore blockade by DNA molecules were performed at V=250 mV and C=1 M at T=293.38 K. Each model had 25 separate simulations (using 25 different initial ssDNA strand structures obtained from short BROMOC equilibrium runs at a higher temperature and higher diffusivity, 330K and 0.1 Å2/ps, respectively). A uniform diffusion coefficient of 0.001 Å2/ps was assigned to all the nucleotides. This value was obtained by adjusting the diffusivity to match the simulated and experimental DNA translocation rates as well as from reviews of literature on nucleotide bulk diffusion.15 Unless otherwise noted, the proximity correction of ion diffusion around the DNA sites was used as proposed by Comer and Aksimentiev16. While position-dependent diffusion may be important for obtaining a 1:1 correspondence with the experimental data47, the reduction of the DNA diffusion coefficient profile in the nanopore to a single dimension was a considerable theoretical challenge by itself. It should be noted, however, that the passive diffusion of the strand is a secondary factor in translocation under applied forces (see below) and in Ref. 48
3. Results and Discussion
Inverse Monte Carlo Simulations for Effective Potentials
Atomistic RDFs were used to obtain effective potentials with the Inverse Monte Carlo (IMC) technique.23,24 The set of atomistic RDFs from the MD simulations was used to optimize iteratively RDFs generated from the Monte Carlo (MC) cycles by adjusting the trial effective ion-ion and ion-DNA pairwise interaction potentials to include many-body effects and solvent screening, as described previously25. The periodic box vectors, number of ions and DNA nucleotides in the MD and MC simulations were exactly the same. The temperature was set at 300K and a dielectric constant of 80 was used. The DNA structure was obtained from MD and converted to a coarse grain configuration. During the MC scheme, the DNA configuration was kept static such that only the ions were allowed to move. First, sets of effective potentials were determined for ion pairs (K-Cl, K-K, Cl-Cl). Then, these effective potentials were used as first guess for the IMC procedures with the DNA (MD simulations a-e). Ion pair effective potentials were left unchanged in every IMC iteration step and the just DNA-Site–Ion potentials were adjusted. Therefore, five sets of DNA-Site-Ion pair effective potentials were determined. The Effective Potential tables were binned every 0.1 Å between an interval of 3 and 25 Å. Figure 3 shows an example of the RDF from an all-atom MD and the resulting effective potential used in the BROMOC simulations with a coarse-grained model of ss-DNA. A complete set of Pairwise Effective Potential Tables obtained from 5′-CGCGAATATTCGCG-3′ can be found in the Supporting Information.
Figure 3.
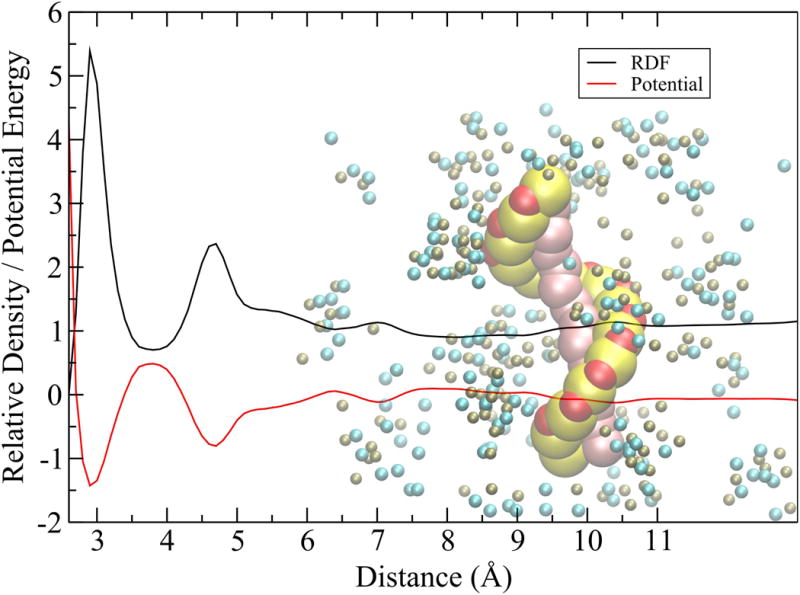
Schematic illustration of the effective potential for the sugar-ion radial distribution function (black) and the corresponding solvent-mediate effective potential (red). Potential energy is shown in kcal/mol.
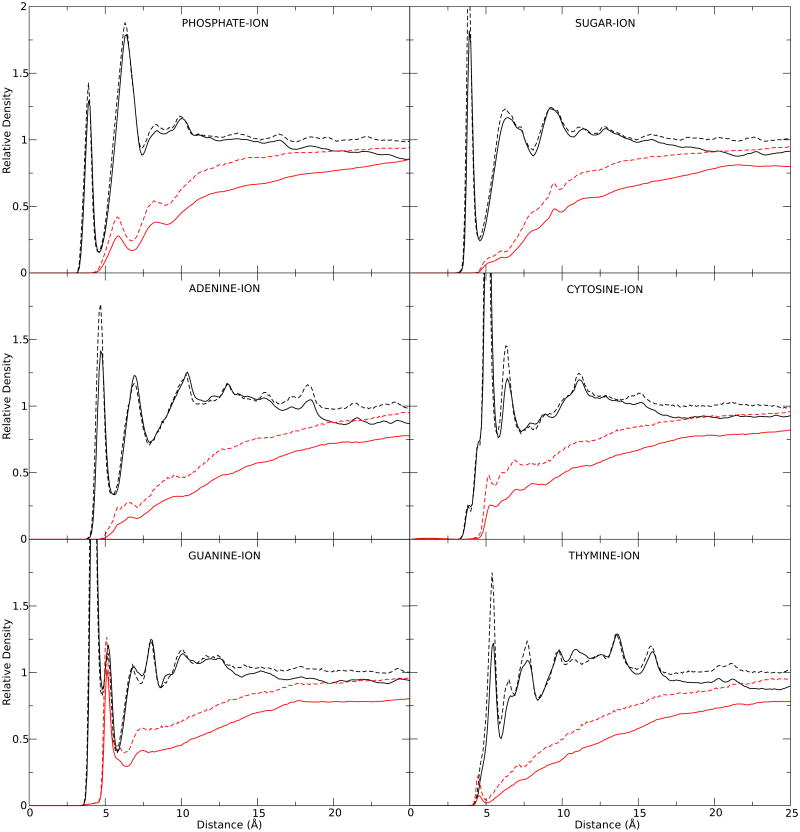
To test the obtained effective potentials (EFPOT) from the IMC scheme, RDFs were calculated using BROMOC and our EFPOT, and compared to the MD RDFs. Brownian Dynamic simulations were then performed using BROMOC. The system contained 784 Cl-, 797 K+ and the DNA oligomer 5′-CGCGAATATTCGCG-3′ in a 65 Å radius sphere. A time step of 20 fs was used, building a trajectory by taking a snapshot every 1 ps. The GCMC iteration was deactivated to keep constant number of ions to match a MD concentration of ∼1 M. The system was electrically neutral. The resulting RDFs for the coarse-grain simulations were determined to be in excellent agreement between BROMOC with the effective potentials and MD shown in Figure 4. While fairly minor, the differences may be attributed to four factors: 1) Different cutoff schemes used in the MD and BD iterations, 2) The effects of coarse-graining; the explicitly treated DNA atoms were averaged and projected on a single site, 3) The usage (in MD) and non-usage (in BD) of the Ewald summation, and 4) To variations in the effective concentration of each electrolyte between both simulations due to the pre-imposed electro-neutrality condition, different box volumes and non-equal relation in the DNA-Box volumes.
Figure 4.
RDF between MD (Dashed line) and BROMOC (Solid Line) for DNA Site-K+ (black) and DNA Site-Cl- (red).
Open-Pore Conductance from atomistic MD and BROMOC simulations with effective potentials
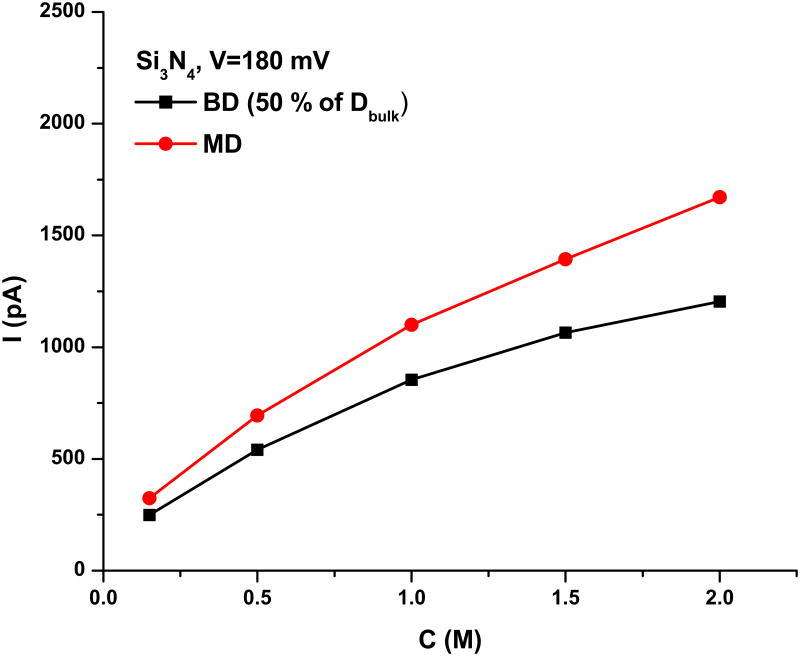
To determine the performance of ion-ion solvent-mediated effective potentials, we chose to study the ion conductance and its dependence on concentration in several systems with potential for nanopore sequencing applications. First, we explored open pore conductance for the selected synthetic nanopore Si3N4. The resulting concentration dependence of the conductance, which can be used to test the accuracy of the developed chemical potentials, is shown in Figure 5.
Figure 5.
Concentration-dependence of ion conductance in a model nanopore. All BD simulations were run with a position-dependent scaling of the diffusion constant for mobile ions. This was set to 50 % of the bulk value inside the pore, with a switching region of 4 Å.
The general agreement between the MD and BD simulations is good, providing a uniform scaling of the diffusion constant of the BD simulations (scaled down by 50 %)13. While exact matching may be reached by varying the diffusion coefficient inside the nanopore, BD simulations with developed effective potentials are sufficiently accurate in capturing the apparently slow conductance saturation at higher concentrations. Both methods produced non-selective pores. Next, we computed open-pore conductance across αHL and its NYN variant, where the main pore constriction was removed. The simulations of the open pore conductance for αHL and its variants have been previously reported 14,15. The open pore conductance at V=120 and 250 mV (experimental voltage) with C= 1 M of KCl is predicted to be between ∼ 1.2 and 1.3 nS, with the diffusion correction, and between ∼1.5 and 1.8 nS without the correction, both of which are consistent with the values obtained in previous studies13. We experimentally measured that the open-pore conductance in this salt is between 1.1 and 1.2 nS, and it can therefore be concluded that the developed potentials faithfully reproduce the electrophysiological measurements reported for the αHL systems. In summary, it can be concluded that the developed effective ion-ion parameter allow for the accurate capturing of concentration-dependent transport and the accurate description of ion permeation in a variety of biological pores.
Sequence-Specific Ion Conductance in Nanopores
dsDNA Triplex Blockade of the Si3N4 Nanopore
The current across a synthetic nanopore depends on the conformational dynamics of blocking dsDNA as well as on its chemical composition. To test whether BD simulations with effective potentials can detect differences in the chemical compositions of the dsDNA triplexes, we performed both MD and BD simulations (for C=1.5 M KCl and V=180 mV) across the system. The DNA duplex displayed a strong propensity to melt and diffuse away from the nanopore in the course of simulation for both the all-atom and coarse-grained simulations. To prevent the dsDNA from denaturing, a harmonic potential was used to control the inter-strand distance. We did not use a single specific conformation of dsDNA (“tilted state” according to Comer at al16), allowing for the blocking molecules to exist in all conformational states while inside the nanopore. The ssDNA and dsDNA molecules captured by nanopores are known to exhibit broad and sometimes very broad distributions of residual currents. Furthermore, it is well known that residual currents may differ in different experiments run on the same nanopore system. The slow conformational dynamics of captured DNA are actually excess noise in the ion current, suggesting that the characteristic time-scale of the ion transport modulation by a polymer is between hundreds of microseconds and milliseconds7,8,29. Therefore, we decided to run a swarm of BD simulations using different starting structures of dsDNA . As expected, this increased the errors associated with the measured residual currents.
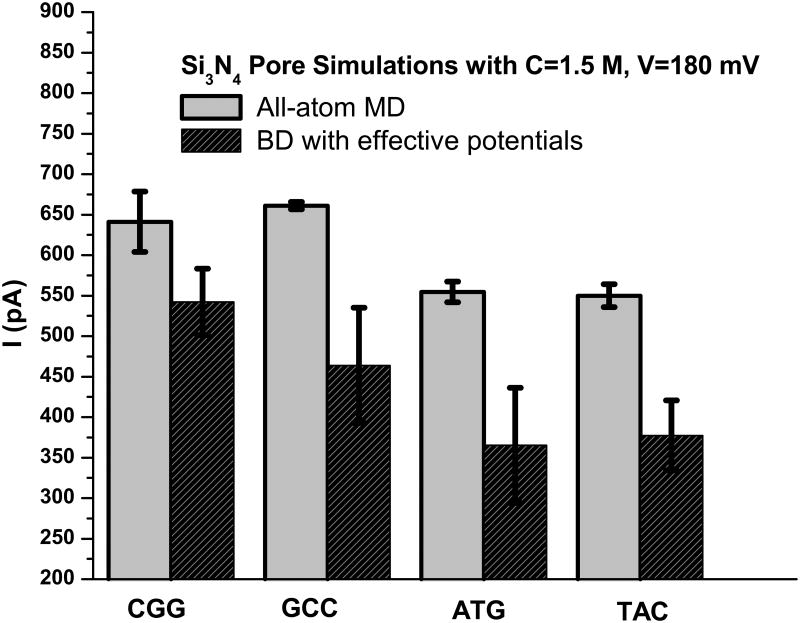
It was found that the dsDNA triplex blocks ∼ 60 (MD) to 70 % (BROMOC) of the current across the nanopore. The residual current across the blocked nanopore is ∼700 to 1000 pA for C=1.5 M and V=180 mV and display considerable fluctuations correlating to dynamics of blocking DNA molecule. Only the last 50 ns of the MD simulations for blocking triples were used to obtain the data shown in Figure 6.
Figure 6.
Summary of nucleotide-specific blocked currents across the Si3N4 nanopore. All BD values were obtained with DNA proximity diffusion scaling (Eq. 7).
We found that under the simulation conditions of the MD studies, the GCC DNA triple blocks the least current. The BD simulations also found that CGG was the nucleotide that was least effective in blocking the pore, while the ATG/TAC triplets produced the most effective blockade. The relative errors are higher for the BD simulations, as they are an average of 25 independent runs of 1 μs each. Importantly, both methods provide a similar ranking of the sequence specific residual currents for nucleotide types; e.g., GCC ∼ CGG > TAC ∼ ATG. Sampling of nucleotide dynamics may be a challenge in relatively short MD simulations used in this work.
Simulations of nucleotide-dependent blockade currents in α-Hemolysin
Next, we examined the performance of these methods using studies of ssDNA (PolyA40; PolyC40 and PolyT40) dynamics in biological nanopores. We computed open pore and blocking currents for the αHL and αHL-NYN pores using BROMOC with effective potentials. Our results were compared to previously reported results and recent unpublished results from Electronic Bioscience LTD. While an exact agreement between experiment and theory is not expected, the results shown in Table 3 (see also Figure 7) demonstrate that there is a direct correlation between the simulated and measured currents. Most of the experimental measurements are performed at a very high salt concentration to ensure greater conductance. While this is experimentally advantageous, this concentration range is known to cause both MD and BD to fail in the accurate description of ion-ion correlations. Therefore, we decided to use a KCl concentration of C=1 M and a voltage comparable to that of the experiment. With this setup, we can directly compare trends such as blocked currents, orientations and nucleotide dependent blockage. It should be noted that BD systematically underestimates the blocked currents compared to the experimental data. However, our approach is capable of capturing the characteristic differences between the WT-αHL and αHL-NYN pores observed experimentally. For instance, open pore current calculations show that the NYN mutation increases the conductance of the pore, which was also observed experimentally (Electronic Bioscience (EBS) unpublished data). While it is obvious that our method partially underestimates the pore blockade for αHL, our results for the αHL-NYN pore exhibit better correlation with the experimental data in terms of the computed residual currents. This can be rationalized by the use of electrostatic maps that assume a rigid protein structure. The presence of the first constriction in the pore, e.g., αHL vs. αHL-NYN, leads to a deep pore block due to the high barriers around it. The removal of the first constriction zone formed in αHL by E111-M113-K147 in the αHL-NYN mutant led to a significance increase (compared to the WT) in the residual current. To test whenever the computed residual currents display any dependence on the local diffusion constant of the ions, we performed simulations without proximity diffusion (PROXDIFF) correction around the DNA sites. We found (Table 3 and Figure 7) that proximity diffusion plays almost no role in the computed residual currents in all studied cases (PolyA40/ C40 /T40 in αHL).
Table 3.
Comparison of blocking current between BROMOC and available experiments. Currents in pA.
| ss-DNA | Entrance Orientation | BROMOC | Exp. 151 | Exp. 2* | ||
|---|---|---|---|---|---|---|
| PROXDIFF on | PROXDIFF off | |||||
| αHL | ||||||
| Open Pore | 416.6 ± 9.1 | 116 ± 3 | 212 ± 5 | |||
| PolyA40 | 3′ | 4.1 ± 2.7 | 4.6 ± 3.4 | 18.6 ± 0.6 | 26.9 | |
| 5′ | 6.1 ± 2.4 | 6.0 ± 2.2 | 22.0 ± 0.6 | 33.1 | ||
| PolyC40 | 3′ | 16.3 ± 11.2 | 14.3 ± 9.6 | 21.7 ± 0.6 | 30.3 | |
| 5′ | 18.4 ± 5.5 | 20.8 ± 6.2 | 20.3 ± 0.6 | 33.5 | ||
| PolyT40 | 3′ | 11.2 ± 5.0 | 13.5 ± 4.3 | 19.2 ± 0.6 | 28.5 | |
| 5′ | 13.9 ± 3.2 | 13.1 ± 3.9 | 18.5 ± 0.6 | |||
| αHL-NYN | ||||||
| Open Pore | 474.7 ± 6.4 | - | 216.3 | |||
| PolyA40 | 3′ | 18.6 ± 6.4 | - | - | 29.2 | |
| 5′ | 20.3 ± 8.9 | - | - | 33.5 | ||
| PolyC40 | 3′ | 31.5 ± 8.6 | - | - | 37.2 | |
| 5′ | 34.9 ± 9.0 | - | - | 37.7 | ||
| PolyT40 | 3′ | 29.9 ± 5.4 | - | - | - | |
| 5′ | 28.6 ± 8.6 | - | - | - | ||
PROXDIFF: Ion Diffusion in proximity of DNA
Communicated by Electronic Bioscience (EBS).
Standard Deviation obtained from 25 independent BROMOC simulations.
Conditions:
αHL/BROMOC: C = 1 M KCl, Vmp = 250mV.
αHL/Exp 1: C = 1M of KCl, Vmp = 120 mV.
αHL-NYN/Exp 2 conditions: C = 3M of NaCl, V = 120 mV.
Figure 7.
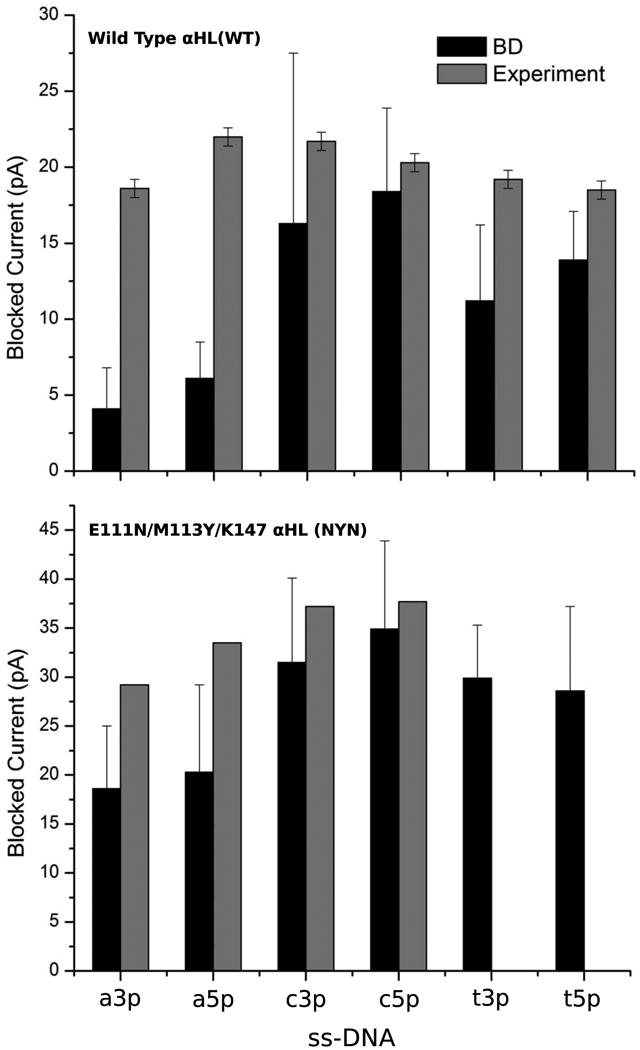
A bar graph summarizing the comparison of blocking currents from the wild type (WT) and mutant (NYN) alpha-hemolysin nanopores. Bromoc vs available experimental data. a3p = PolyA40 (3′) a5p = PolyA40 (5′) c3p = PolyC40 (3′) c5p = PolyC40 (5′) t3p = PolyT40 (3′) t5p = PolyT40 (5′).
It is reassuring that the developed method allows for an accurate discrimination between the different nucleotides in the confinement of αHL and αHL-NYN. While differences in the A and C blocking levels are very small, the simulation results suggest that A blocks more than C in both the 3′ and 5′ entrances. This supports previous reports from the lab of H. Bayley as well as more recent low-noise measurements from EBS San-Diego. The results are somewhat inconsistent with the blockade sequence reported by Purnell at all.49 It was also found that while 5′ entry tends to block less than the 3′ entry, the overall contrast is better for nucleotide threaded from the 3′ end first. Interestingly, the results of the BD simulations, which show considerably lower residual currents than those reported from patch-clamp measurements of the alpha-hemolysin pore in lipid bilayers, are in excellent agreement with the reported residual currents in recent study, in which the aHL pore itself was captured by a solid-state nanopore. This assembly was used for measurements of the residual current after blockade with a variety of ssDNA molecules50. This approach should result in lower conformational dynamics of the biological pore itself and lead to significant DNA blockade compared to previous studies performed in lipid bilayers.
5. Conclusions
We extended the Inverse Monte-Carlo protocol to develop a set of ion-ion and ion-nucleotide effective potentials compatible with a modified reported model of ss-DNA. We implemented a new feature that uses effective potentials in BROMOC, our developed GCMC/BD package. We evaluated the performance of the developed potentials for studies of ion permeation across biological and synthetic model nanopores. We found that effective interaction potentials combined with the GCMC/BD protocol from previous work provided a correct qualitative description of nucleotide-specific ion transport and ion transport across open (non-blocked) pores. Our system reproduces key features of residual ion currents in the presence of blocking ssDNA molecules, which corrects the blockade ordering (A<T<C) and the orientation dependence of the blockade (e.g., 3′ vs 5′ entrance) for the blocking of alpha-hemolysin by ss-DNA. The studies of the blockade of synthetic nanopores by double-stranded DNA oligomers demonstrate an excellent correlation between the residual currents computed from the all-atom MD and the coarse-grained BD using the effective potentials developed in this work. Combining the BD simulations using explicit ions/DNA with effective potentials has proven to be a powerful and fast computational tool for characterizing the transport of ions and DNA across nanopores. Moreover, this method is capable of performing up to millisecond simulations with a high level of molecular detail, taking into account implicit solvent effects and protein electrostatics.
Supplementary Material
Acknowledgments
This work was supported by the Natural Sciences and Engineering Research Council (NSERC) Discovery grant program (RGPIN 340946-07) and the NIH team grant (NHGRI Grant R01 HG005095), and a Resource Allocation Award from WestGrid, Canada. SYN is an Alberta Innovates Technology Futures New Faculty. We would like to acknowledge EBS San-Diego for providing us with their unpublished data on the αHL and αHL-NYN systems. We are also very grateful to Geoffrey A. Barrall, Eric Ervin and Prithwish Pal (EBS) for their helpful discussion.
References
- 1.Kasianowicz JJ, Brandin E, Branton D, Deamer DW. Proc Natl Acad Sci USA. 1996;93:13770–13773. doi: 10.1073/pnas.93.24.13770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Benner S, Chen RJA, Wilson NA, Abu-Shumays R, Hurt N, Lieberman KR, Deamer DW, Dunbar WB, Akeson M. Nat Nano. 2007;2:718–724. doi: 10.1038/nnano.2007.344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hornblower B, Coombs A, Whitaker RD, Kolomeisky A, Picone SJ, Meller A, Akeson M. Nat Methods. 2007;4:315–317. doi: 10.1038/nmeth1021. [DOI] [PubMed] [Google Scholar]
- 4.Wilson NA, Abu-Shumays R, Gyarfas B, Wang H, Lieberman KR, Akeson M, Dunbar WB. ACS Nano. 2009;3:995–1003. doi: 10.1021/nn9000897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Derrington IM, Butler TZ, Collins MD, Manrao E, Pavlenok M, Niederweis M, Gundlach JH. Proc Natl Acad Sci USA. 2010;107:16060–16065. doi: 10.1073/pnas.1001831107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lieberman KR, Cherf GM, Doody MJ, Olasagasti F, Kolodji Y, Akeson M. J Am Chem Soc. 2010;132:17961–17972. doi: 10.1021/ja1087612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Timp W, Comer J, Aksimentiev A. BIophys J. 2012;102:L37–L39. doi: 10.1016/j.bpj.2012.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Timp W, Mirsaidov UM, Wang DQ, Comer J, Aksimentiev A, Timp G. IEEE Trans Nanotech. 2010;9:281–294. doi: 10.1109/TNANO.2010.2044418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Stoddart D, Maglia G, Mikhailova E, Heron Andrew j, Bayley H. Ang Chem Intl Ed. 2010;49:556–559. doi: 10.1002/anie.200905483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lu D, Aksimentiev A, Shih AY, Cruz-Chu E, Freddolino PL, Arkhipov A, Schulten K. Phys Biol. 2006;3:40–53. doi: 10.1088/1478-3975/3/1/S05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bhattacharya S, Derrington IM, Pavlenok M, Niederweis M, Gundlach JH, Aksimentiev A. ACS Nano. 2012;6:6960–6968. doi: 10.1021/nn3019943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wells DB, Bhattacharya S, Carr R, Maffeo C, Ho A, Comer J, Aksimentiev A. Optimization of the molecular dynamics method for simulations of DNA and ion transport through biological nanopores. Humana Press; 2011. [DOI] [PubMed] [Google Scholar]
- 13.Lee KI, Jo S, Rui H, Egwolf B, Roux B, Pastor RW, Im W. J Comput Chem. 2012;33:331–339. doi: 10.1002/jcc.21952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Noskov SY, Im W, Roux B. Biophys J. 2004;87:2299–2309. doi: 10.1529/biophysj.104.044008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.De Biase PM, Solano CJF, Markosyan S, Czapla L, Noskov SY. J Chem Theor Comp. 2012;8:2540–2551. doi: 10.1021/ct3004244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Comer J, Aksimentiev A. J Phys Chem C. 2012;116:3376–3393. doi: 10.1021/jp210641j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Akeson M, Branton D, Kasianowicz JJ, Brandin E, Deamer DW. Biophys J. 1999;77:3227–3233. doi: 10.1016/S0006-3495(99)77153-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lathrop DK, Ervin EN, Barrall GA, Keehan MG, Kawano R, Krupka MA, White HS, Hibbs AH. J Am Chem Soc. 2010;132:1878–1885. doi: 10.1021/ja906951g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mirzoev A, Lyubartsev AP. Phys Chem Chem Phys. 2011;13:5722–5727. doi: 10.1039/c0cp02397c. [DOI] [PubMed] [Google Scholar]
- 20.Lyubartsev AP, Marcelja S. Phys Rev E. 2002;65 doi: 10.1103/PhysRevE.65.041202. Art:041202. [DOI] [PubMed] [Google Scholar]
- 21.Lobaskin V, Lyubartsev A, Linse P. Phys Rev E. 2001;63 doi: 10.1103/PhysRevE.63.020401. Art: 020401. [DOI] [PubMed] [Google Scholar]
- 22.Lyubartsev AP, Laaksonen A. Chem Phys Lett. 2000;325:15–21. [Google Scholar]
- 23.Lyubartsev AP, Laaksonen A. J Chem Phys. 1999;111:11207–11215. [Google Scholar]
- 24.Lyubartsev AP, Laaksonen A. Phys Rev E. 1997;55:5689–5696. [Google Scholar]
- 25.Lyubartsev AP, Laaksonen A. Phys Rev E. 1995;52:3730–3737. doi: 10.1103/physreve.52.3730. [DOI] [PubMed] [Google Scholar]
- 26.Knotts TA, Rathore N, Schwartz DC, De Pablo JJ. J Chem Phys. 2007;126:084901. doi: 10.1063/1.2431804. [DOI] [PubMed] [Google Scholar]
- 27.Van Dijk M, Bonvin AMJJ. Nucl Acid Res. 2009;37:W235–W239. doi: 10.1093/nar/gkp287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jo S, Kim T, Iyer VG, Im W. J Comput Chem. 2008;29:1859–1865. doi: 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- 29.Jo S, Lim JB, Klauda JB, Im W. Biophys J. 2009;97:50–58. doi: 10.1016/j.bpj.2009.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Feller SE, Mackerell AD. J Phys Chem B. 2000;104:7510–7515. [Google Scholar]
- 32.Yin DX, Mackerell AD. J Comput Chem. 1998;19:334–348. [Google Scholar]
- 33.Feller SE, Zhang YH, Pastor RW, Brooks BR. J Chem Phys. 1995;103:4613–4621. [Google Scholar]
- 34.Koopman EA, Lowe CP. J Chem Phys. 2006;124 doi: 10.1063/1.2198824. Art. 204103. [DOI] [PubMed] [Google Scholar]
- 35.Lowe CP. Europhys Lett. 1999;47:145–151. [Google Scholar]
- 36.Steinbach PJ, Brooks BR. J Comput Chem. 1994;15:667–683. [Google Scholar]
- 37.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. J Chem Phys. 1995;103:8577–8593. [Google Scholar]
- 38.Barth E, Kuczera K, Leimkuhler B, Skeel RD. J Comput Chem. 1995;16:1192–1209. [Google Scholar]
- 39.Aksimentiev A, Brunner RK, Cruz-Chu E, Comer J, Schulten K. IEEE Nanotechnol Mag. 2009;3:20–28. doi: 10.1109/MNANO.2008.931112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Comer J, Dimitrov V, Zhao Q, Timp G, Aksimentiev A. Biophys J. 2009;96:593–608. doi: 10.1016/j.bpj.2008.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Brent RP. Algorithms for Minimization without Derivatives. Prentice-Hall, Englewood Cliffs; Toronto, Canada: 2002. [Google Scholar]
- 42.Roux B, Yu HA, Karplus M. J Phys Chem. 1990;94:4683–4688. [Google Scholar]
- 43.Im W, Seefeld S, Roux B. Biophys J. 2000;79:788–801. doi: 10.1016/S0006-3495(00)76336-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Roux B, Berneche S, Im W. Biochem US. 2000;39:13295–13306. doi: 10.1021/bi001567v. [DOI] [PubMed] [Google Scholar]
- 45.Luo Y, Egwolf B, Walters DE, Roux B. J Phys Chem B. 2010;114:952–958. doi: 10.1021/jp906790f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang Q, Canutescu AA, Dunbrack RL. Nat Protocols. 2008;3:1832–1847. doi: 10.1038/nprot.2008.184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Simakov NA, Kurnikova MG. J Phys Chem B. 2010;114:15180–15190. doi: 10.1021/jp1046062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Luan B, Aksimentiev A. Phys Rev Lett. 2008;101 doi: 10.1103/PhysRevLett.101.118101. Art:118101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Purnell RF, Mehta KK, Schmidt JJ. Nano Lett. 2008;8:3029–3034. doi: 10.1021/nl802312f. [DOI] [PubMed] [Google Scholar]
- 50.Aguilar-Cabello S, Balme S, Chaaya AA, Bechelany M, Balanzat E, Janot JM, Pochat-Bohatier C, Miele P, Dejardin P. Nanoscale. 2013;5:9582–9586. doi: 10.1039/c3nr03683a. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.