A Versatile Omnibus Test for Detecting Mean and Variance Heterogeneity

Abstract

Recent research has revealed loci that display variance heterogeneity through various means such as biological disruption, linkage disequilibrium (LD), gene-by-gene (GxG), or gene-by-environment (GxE) interaction. We propose a versatile likelihood ratio test that allows joint testing for mean and variance heterogeneity (LRT_MV) or either effect alone (LRT_M or LRT_V) in the presence of covariates. Using extensive simulations for our method and others we found that all parametric tests were sensitive to non-normality regardless of any trait transformations. Coupling our test with the parametric bootstrap solves this issue. Using simulations and empirical data from a known mean-only functional variant we demonstrate how linkage disequilibrium (LD) can produce variance-heterogeneity loci (vQTL) in a predictable fashion based on differential allele frequencies, high D’ and relatively low r² values. We propose that a joint test for mean and variance heterogeneity is more powerful than a variance only test for detecting vQTL. This takes advantage of loci that also have mean effects without sacrificing much power to detect variance only effects. We discuss using vQTL as an approach to detect gene-by-gene interactions and also how vQTL are related to relationship loci (rQTL) and how both can create prior hypothesis for each other and reveal the relationships between traits and possibly between components of a composite trait.

INTRODUCTION

Most statistical tests for single locus association with quantitative traits look for mean differences between genotypes or alleles (via average excess in additive models [Álvarez-Castro and Yang 2012]). Most of these linear models assume that the factors have equal variances. There are a few of scenarios where deviations from this assumption not only violate the model but also can be biologically meaningful and result in identifying important loci. Typical genome-wide association studies (GWAS) rely on linkage disequilibrium (LD) to identify physical regions of association with a trait assuming that a marker associated with the trait is due to LD with one or more functional variants in close proximity. It generally assumes that this association will be made due to mean differences; however, even if the functional variant has no variance heterogeneity, the locus in LD with it will likely have an inflation of variance within its genotypes due to being a mixture of genotypes from the functional variant [Balding 2009]. Under certain circumstances, this can lead to variance heterogeneity.

A functional locus may also have different variances across genotypes whether or not there are differences in genotypic means. A number of papers have focused on variance heterogeneity as a result of gene-by-gene (GxG) or gene-by-environment (GxE) interactions [Deng and Pare 2011; Paré et al., 2010; Struchalin et al., 2010]. These loci with variance heterogeneity are referred to as variance-heterogeneity quantitative trait loci (vQTL) [Rönnegård and Valdar 2012]. If a genotypic effect at one locus were dependent on the genotype of another locus, the variance of that genotype would derive from a composite of multiple distributions with different means, even if the variances were the same, resulting in an inflated variance for that genotype. These papers suggest that vQTL are an avenue to identifying loci involved in GxG. Loci with heterogeneous variance may also be related to gene-by-environment (GxE) interactions with similar consequences as the GxG cases.

Here we present a method which tests for differences in genotypic means and variances simultaneously, while allowing adjustment for covariates. We present a description of the method and some analytical results and simulations based on some of the scenarios along with comparisons to other basic tests for differences in means alone, variances alone, and tests for both. Using data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI), we present a real world example of the inflated variance due to LD with a known functional variant. This cases study uses a non-synonymous variant in the matrix metallopeptidase 3 (MMP3) gene and surrounding markers in LD that are very strongly associated with MMP3 protein levels in cerebrospinal fluid (CSF).

MATERIALS AND METHODS

A new omnibus likelihood ratio test for both mean and variance heterogeneity

Assume n subjects are genotyped. For subject i = 1, … n, let y_i denote the quantitative phenotype value and let G_i = 0, 1, or 2, denote the genotype for the SNP of interest, corresponding to major allele homozygous, heterozygous, and minor allele homozygous, respectively. We further define dummy variables X_i1 = I_(Gi=1) and X_i2 = I_(Gi=2). Let Z_i = (Z_i1, … , Z_im) denote the m covariates, such as sex, age, and principle components capturing population substructure. To allow both mean and variance differences across genotype groups, we have the following regression model:

$$y_i={\alpha }_0+Z_i\alpha +X_{i1}{\beta }_1+X_{i2}{\beta }_2+{\epsilon }_i,{\epsilon }_i~N(0,{\sigma }_{G_i}^2).$$ (M1)

Simultaneously testing mean and variance difference is equivalent to testing the null hypothesis H₀: β₁ = β₂ = 0 and ${\sigma }_0^2={\sigma }_1^2={\sigma }_2^2$, and the alternative hypothesis is H_α : at least one of “=”does not hold. We propose to use the likelihood ratio test (LRT) to test model M₁ against the null model:

$$y_i={\alpha }_0+Z_i\alpha +{\epsilon }_i,{\epsilon }_i~N(0,{\sigma }^2).$$ (M2)

In matrix notation, model M₁ is y = Cγ + ε, where y = (y₁, … , y_n)′, the ith row of the design matrix C is (1, Z_i, X_i1, X_i2), γ = (α₀, α′, β₁, β₂)’ and ε = (ε₁, … , ε)′ ~ with V being diagonal matrix $({\sigma }_{G_1}^2,\dots ,{\sigma }_{G_n}^2)$. Therefore, y~N(Cγ, V). The log-likelihood of y under M_i is

$$l\left(\gamma ,V\right)=-\frac{1}{2}\left\{n\log \right(2\pi )+\log \mid \mathit{V}\mid +{(\mathit{y}-C\gamma )}^{\prime }{\mathit{V}}^{-1}(\mathit{y}-\mathit{C}\gamma \left)\right\}$$ (1)

Taking partial derivative of l(γ, V) with respect to γ, we have

$$\frac{\partial l}{\partial \gamma }=-C^{\prime }{V}^{-1}C\gamma +C^{\prime }{V}^{-1}y.$$

Equating it to 0, we can see (1) is maximized over γ for any fixed V: $\tilde{\gamma }={\left(C^{\prime }{V}^{-1}C\right)}^{-1}{C}^{\prime }{V}^{-1}y$, which is also the generalized least squares (GLS) estimator of γ. The maximum likelihood estimate (MLE) of V can be found by maximizing the profile log-likelihood for V, obtained from plugging $\tilde{\gamma }$ in (1):

$$\begin{array}{cc}\hfill & l_P\left(\mathit{V}\right)=-\frac{1}{2}\left\{n\log \right(2\pi )+\log \mid \mathit{V}\mid +{(\mathit{y}-C\tilde{\gamma })}^{\prime }{\mathit{V}}^{-1}(\mathit{y}-\mathit{C}\tilde{\gamma }\left)\right\}\hfill \\ \hfill & =-\frac{1}{2}\{\log \mid \mathit{V}\mid +y^{\prime }{V}^{-1}[\mathrm{I}-C{\left(C^{\prime }{V}^{-1}C\right)}^{-1}{C}^{\prime }{V}^{-1}\left]\mathit{y}\right\}-\frac{n}{2}\log \left(2\pi \right)\hfill \end{array}$$

The MLE of γ is then $\widehat{\gamma }={\left(C^{\prime }{\widehat{V}}^{-1}C\right)}^{-1}{C}^{\prime }{\widehat{V}}^{-1}y$, where $\widehat{V}$ is the MLE of V. The LRT for both mean and variance difference is $LR{T}_{MV}=-2\left\{l\right({\widehat{\gamma }}_{M_2},{\widehat{V}}_{M_2})-l({\widehat{\gamma }}_{M_1},{\widehat{V}}_{M_1}\left)\right\}$, where the MLE of γ and V are obtained under the full model M₁ and the null model M₂, respectively. For large sample size n, LRT_MV approximately follows χ²(4) distribution. Similarly, for variance difference only or mean difference only, we test model M₁ against

$$y_i={\alpha }_0+Z_i\alpha +X_{i1}{\beta }_1+X_{i2}{\beta }_2+{\epsilon }_i,{\epsilon }_i~N(0,{\sigma }^2),$$ (M3)

$$\mathrm{or}{y}_i={\alpha }_0+Z_i\alpha +{\epsilon }_i,{\epsilon }_i~N(0,{\sigma }_{G_i}^2),$$ (M4)

respectively. The LRTs are $LR{T}_V=-2\left\{l\right({\widehat{\gamma }}_{M_3},{\widehat{V}}_{M_3})-l({\widehat{\gamma }}_{M_1},{\widehat{V}}_{M_1}\left)\right\}$ and $LR{T}_M=-2\left\{l\right({\widehat{\gamma }}_{M_4},{\widehat{V}}_{M_4})-l({\widehat{\gamma }}_{M_1},{\widehat{V}}_{M_1}\left)\right\}$, both of which approximately follow χ²(2) for large n. If we are willing to assume an additive mean effect model, a one degree-of-freedom LRT_M test can be performed. The above models are described in terms of discrete genotypes; however, they can easily be modified to accommodate additive models for both means and variances as well as dominance for the mean. Specifically, If we assume that in the full model M₁ the variance depends on the genotype as a linear function of the number of minor alleles/imputed dosage, i.e., additive model for the variance, we have y~N(Cγ, V), where $\mathit{V}={\sigma }_0^2\times diag(1,1,\dots ,1)+\delta \times diag(G_1,G_2,\dots ,G_n)$ and G_i is the number of minor alleles the ith subject carries. It follows that the variance of y_i is, respectively, ${\sigma }_0^2$, ${\sigma }_0^2+\delta$ or ${\sigma }_0^2+2\delta$, for major allele homozygous, heterozygous, or minor allele homozygous. δ can be either positive or negative; however, we impose a constraint $\delta >-\frac{{\sigma }_0^2}{2}$ such that the variance of y_is are all positive. The corresponding LRT_V tests against the null model υ~N(Cγ, V), where $\mathit{V}={\sigma }_0^2\times diag(1,1,\dots ,1)$, leading to a χ²(1) test as the full and null models differ by one free parameter δ. It is noted that, should an additive model for the variances be desired, an additive model for the means should also be assumed with the mean model Cγ modified accordingly. We have implemented the above tests in R code found via the link at the end of the article along with a file of examples implementing the functions.

Parametric bootstrap LRT

LRT_V is closely related to Bartlett’s test for equality of variances [Bartlett 1954],which is well known to be not robust to violation of the normality assumption, even subtle deviation from the normal distribution [Conover et al., 1981; Struchalin et al., 2010]. We also observe in our simulation study that for non-normal quantitative traits, LRT_MV and LRT_V can have inflated Type I error, while LRT_M still controls Type I error satisfactorily. In light of the superior performance of the proposed LRTs when the normality assumption does hold, we propose the following parametric bootstrap-based LRT procedure for non-normal traits. The parametric bootstrap is widely used in genetics when the null distribution of the test statistic is unknown and covariates are present [Bůžková et al., 2011; Davison and Hinkley 1997]. We carry out the parametric bootstrap-based LRT as follows:

1. Obtain parameter estimates ${\widehat{\gamma }}_{M_2}={(\widehat{{\alpha }_0},{\widehat{\alpha }}^{\prime })}^{\prime }$ under the null model M₂ from the original data

2. Calculate the residuals: $r_i=y_i-C_i{\widehat{\gamma }}_{M_2}$ for i = 1, … , n.

3. Permute the r_i’s to generate the $r_i^{\ast }$’s and create new trait values $y_i^{\ast }=C_i{\widehat{\gamma }}_{M_2}+r_i^{\ast }$ for i = 1, … , n.

4. Replace the y_i’s by the $y_i^{\ast }$’s and recalculate the test statistic $LR{T}_{MV}^{\ast }$ for i = 1, … n.

5. Repeat steps (3)-(4) for B times

The parametric bootstrap p-value is $\frac{\#\{LR{T}_{MV}^{\ast \left(b\right)}\ge LR{T}_{MV},b=1,\dots ,B\}+1}{B+1}$, where LRT_MV is the test statistic computed from the original data. Parametric bootstrap-based LRT_V can be similarly performed by fitting the null model M₃ in step (1) and calculating resampled test statistic $LR{T}_V^{\ast }$ in step (4).

Comparison with other methods for testing variance heterogeneity

Double GLM (DGLM)

Rönnegård and Valdar [2011] proposed to employ the double generalized linear models (DGLMs;[Smyth 1989]) to detect mean and variance differences simultaneously. Specially, both mean and variance of the quantitative trait depend on the genetic factor via $y_i={\alpha }_0+Z_i\alpha +X_{i1}{\beta }_1+X_{i2}{\beta }_2+{\epsilon }_i,{\epsilon }_i~N(0,{\sigma }_i^2)$, and $\log \left({\sigma }_i^2\right)=\log \left({\sigma }^2\right)+X_{i1}{\theta }_1+X_{i2}{\theta }_2$. To test equality of both means and variances, we test the null hypothesis H₀: β₁ = β₂ = 0 and θ₁ = θ₂ = 0. The DGLM is implemented in the R package “dglm”. We can see that the DGLM is equivalent to model M₁. As a result, inflation of Type I error is expected for traits deviating from the normal distribution as confirmed by our simulation study. Rönnegård and Valdar [2011] proposed to apply Box-Cox transformation on traits that appear to deviate from normal distribution. Here we demonstrate using simulations that, as the variance test is very sensitive to even subtle deviation from the normal distribution, Box-Cox transformation prior to testing does not guarantee that the Type I error be controlled. This is even true when the residuals are simulated from the distribution of total cholesterol, which is generally considered as normally distributed.

Levene’s Test

Levene’s test has been shown to be a powerful and robust test for equality of variances [Conover et al., 1981; Gastwirth et al., 2009; Levene 1960], and has been used for detecting vQTLs [Paré et al., 2010; Shen et al., 2012; Struchalin et al., 2010]. For ease of exposition, we rewrite the n trait values according to the genotype groups: y_kj for k = 0,1,2 and j = 1, . . , n_k with ${\sum }_{k=0}^2{n}_k=n$. The test statistic is the ANOVA F-test applied to the absolute differences between each observation and the mean of its group $d_{k_j}=\mid y_{k_j}-{\stackrel{‒}{y}}_{k.}\mid$. The resulting F statistic is $F=\frac{(n-3){\sum }_{k=0}^2{n}_k{({\stackrel{‒}{d}}_{k.}-{\stackrel{‒}{d}}_{..})}^2}{(3-1){\sum }_{k=0}^2{\sum }_{j=1}^{n_k}{(d_{k_j}-{\stackrel{‒}{d}}_{k.})}^2}$, which, because of non-normality of d_kj, approximately follows an F(2, n – 3). When n is large, F is well approximated by χ²(2). In addition, Brown and Forsythe [1974] proposed to use the group median ${\tilde{y}}_k$ instead of the group mean in defining individual deviation d_kj for more robust results and this version of Levene’s test is more commonly used [Paré et al., 2010; Shen et al., 2012]. Levene’s test is implemented in the R function “levene.test” in the “lawstat” package. Potential limitations of Levene’s test include no covariates are allowed and only equality of variances, but not means, can be tested.

Lepage Test

Lepage test is a rank-based non-parametric test for either location or dispersion difference [Hollander and Wolfe 1999; Lepage 1971]. For two-sample comparison, it combines Wilcoxon rank sum test statistic for location (median) and Ansari-Bradley test statistic for dispersion [Ansari and Bradley 1960]. Hothorn et al. [2006] extended the Lepage test to K-sample problems (K ≥ 2) to combine the Kruskal-Wallis (KW) test statistic for location and the Fligner-Killeen (FK) test statistic for dispersion, and implemented it in the R package “coin”. Note that the Wilcoxon rank sum test is a special case of the KW tests for two-sample location test, while the FK test was found to perform as well as Levene’s test in a previous comparative study [Conover et al., 1981]. These nonparametric tests cannot adjust for covariate effects.

Simulation studies

In order to compare the power of different tests and their robustness to non-normality assumptions, we simulated a common SNP with a minor allele frequency (MAF) of 0.4, mimicking the functional SNP in the real data example and two sets of quantitative traits, one normally distributed and the other non-normally distributed. For each set, we considered four scenarios: 1. Genotypes have no effects on quantitative traits; 2. Genotypes affect means of quantitative traits; 3. Genotypes affect variances of quantitative traits; and 4. Genotypes affect both means and variances of quantitative traits. The quantitative traits (y_i) were generated using the model: y_i = X_i1β₁ + X_i2β₂ + ε_i, where X_i1 is an indicator variable for the heterozygous genoty X_i2 is an indicator variable for the minor allele homozygote genotype. Without mean effects, β₁ = β₂ = 0; when genotypes affect means, β₁ = −.03, β₂ = −.08. For normally distributed quantitative traits, we simulated ε_i from N(0, 0.23²) for scenarios without variance effects. For scenarios with variance effects, ε_i was generated from N(0, 0.23²), N(0, 0. 25²), and N(0, 0. 29²) corresponding to major allele homozygous, heterozygous, and minor allele homozygous, respectively. The mean and variance effect sizes and MAF were specified to mimic the observed ones in the real data analysis described below.

For non-normally distributed quantitative traits, ε_i was simulated from a t-distribution (df=5) and scaled with a scale parameter of 0.19 for scenarios without variance effects so that the variance of ε_i was comparable to that of normally distributed ε_i. For scenarios with variance effects, we simulated ε_i from t-distributions with df = 10, 5, and 3, corresponding to major allele homozygous, heterozygous, and minor allele homozygous, respectively, and scaled all the ε_i with a scale parameter of 0.19. For each scenario, we simulated 1000 replicates with sample size of 1000 in each replicate. Empirical power/Type I error was calculated as the proportion of replicates with statistically significant effects at the threshold level of 0.05. 10,000 resamplings were performed for each replicate when using parametric bootstrap LRT.

To further compare different tests when there are covariates to adjust for, following the simulation setup in Demissie and Cupples [2011], we generated quantitative traits (y_i) using the model: y_i = Z_iα + X_i1β₁ + X_i2β₂ + ε_i, where Z_i is a covariate, X_i1 and X_i2 are the same as defined above. We considered two cases: 1. Z_i is independent of X_i1 and X_i2; 2. Z_i is correlated with X_i1 and X_i2, where Z_i is a confounder. For case 1, (X_i, Z_i)′ were generated from N(μ, Σ), where $\mu =\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0.5\hfill \end{array}\right)$, $\sum =\left(\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right)$. For case 2, (X_i, Z_i)′ were generated from N(μ, Σ), where $\mu =\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0.5\hfill \end{array}\right)$, $\sum =\left(\begin{array}{cc}1\hfill & \hfill 0.6\\ 0.6\hfill & \hfill 1\end{array}\right)$. X_i was then categorized using dummy variables X_i1 and X_i2, corresponding to a SNP with MAF of 0.4. We kept Z_i as a continuous variable. We used α = 0.2 and also considered four different scenarios as described previously. Simulation of QTL effects was the same as the previous simulation study for normally distributed quantitative traits. In each scenario, 1000 replicates were generated with a sample size of 1000 in each replicate. For Levene’s test and all the non-parametric tests, quantitative trait effects were analyzed after adjusting for the covariate using a two-stage approach, i.e., the first stage fitted a covariate only model to obtain ${\widehat{y}}_i=Z_i\widehat{\alpha }$ and the second stage tested the association between the residual $y_i-{\widehat{y}}_i$ and the SNP. When using LRT and linear regression (LR), quantitative trait effects and covariate effect were analyzed simultaneously. 10,000 resamplings were performed for each replicate when using parametric bootstrap LRT_MV.

Real data analysis: application to the Alzheimer’s Disease Neuroimaging Initiative (ADNI)

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu). ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada [Trojanowski et al., 2010; Weiner et al., 2010]. For up-to-date information, see www.adni-info.org. We obtained CSF MMP3 protein levels and genetic data from 293 individuals from the Alzheimer’s Disease Neuroimaging Initiative. Using these data, we tested SNPs within 100 kilobases of the known functional SNP rs679620 for association with CSF MMP3 protein levels using LRT_MV, LRT_M, LRT_V, and LR, respectively. All tests adjusted for age, gender and principal components from population stratification analyses.

RESULTS

Empirical Type I error/power of different tests in the four simulated scenarios were summarized in Table I. For normally distributed quantitative traits (Table I A), the false positive rates were all close to 0.05 when there is no effect. In other words, Type I errors were well controlled for all the tests. Among the joint tests that test for heterogeneity in means and variances simultaneously, the non-parametric Lepage test had larger power than LRT_MV in all the scenarios, but not substantially; while LRT_MV and parametric bootstrap LRT_MV had almost identical performance. Different mean tests were comparable in all the scenarios. LRT_V stood out as the most powerful variance test. In addition, the simulation study results confirmed that LRT_M is equivalent to the mean test of DGLM (DGLM_M), and LRT_V is equivalent to the variance test of DGLM (DGLM_V). When there was only a mean effect, joint tests lost power in comparison with mean tests. Similarly, joint tests were not as powerful as variance tests when only variance heterogeneities existed. However, the power of joint tests was not much less for the mean or variance only scenarios and the joint tests were substantially more powerful when there were both mean and variance heterogeneity.

Table I.

Comparison of empirical Type I error/power of different tests in four simulated scenarios. PB:Parametric Bootstrap; LR:Linear Regression; KW:Kruskal-Wallis; FK:Fligner-Killeen.

A. Simulated normally distributed quantitative traits.
Simulated effects	joint tests			mean tests				variance tests
	LRTMV	LRTMV(PB)	Lepage	LRTM	LR	KW	DGLMM	LRTV	Levene	FK	DGLMV
No effect	0.044	0.040	0.049	0.045	0.045	0.042	0.045	0.052	0.060	0.060	0.052
Mean	0.800	0.801	0.862	0.893	0.891	0.862	0.893	0.065	0.063	0.060	0.065
Variance	0.764	0.760	0.774	0.046	0.063	0.054	0.046	0.831	0.786	0.779	0.831
Mean & var	0.978	0.975	0.983	0.828	0.855	0.820	0.828	0.842	0.796	0.784	0.842

B. Simulated non-normally distributed quantitative traits.
Simulated effects	joint tests		mean tests			variance tests
	LRTMV(PB)	Lepage	LRTM	LR	KW	LRTV(PB)	Levene	FK
No effect	0.038	0.039	0.037	0.038	0.037	0.044	0.040	0.041
Mean	0.513	0.930	0.869	0.876	0.933	0.056	0.045	0.041
Variance	0.795	0.449	0.060	0.100	0.050	0.810	0.676	0.437
Mean & var	0.967	0.985	0.795	0.848	0.927	0.853	0.700	0.459

C. Tests that cannot control Type I error for non-normally distributed quantitative traits.
Simulated effects	LRTMV	LRTV	DGLMV	DGLMV Box-Cox transformation
No effect	0.246	0.325	0.325	0.172

It is well known that variance tests are sensitive to violation of the normality assumption [Conover et al., 1981; Struchalin et al., 2010]. When quantitative traits were simulated from t-distributions, we observed substantial Type I error inflations of LRT_MV, LRT_V and DGLM_V (Table I C). Rönnegård and Valdar [2011] suggested Box-Cox transformation to correct for inflated Type I error. However, the simulation study shows that Box-Cox transformation did decrease the inflated Type I error of DGLM_V, but it was still well above 0.05. We did not include the tests with inflated Type I error in the power comparison since it would not be meaningful to compare the powers of tests if their Type I errors cannot be controlled.

Table I B demonstrated that all the mean tests, non-parametric tests and Levene’s test were robust to violation of the normality assumption. In addition, parametric bootstrap LRT_MV and parametric bootstrap LRT_V can also correct Type I error inflation. When quantitative traits were non-normally distributed, Lepage test was more powerful than parametric bootstrap LRT_MV if only mean effects existed, while parametric bootstrap LRT_MV had higher power if there were only variance effects. For both mean and variance effects, the two tests had comparable performance. Comparing different mean tests, the KW test was the best. We also noticed that linear regression (LR) had inflated Type I error (0.1) when non-normally distributed quantitative traits only had variance heterogeneity. Parametric bootstrap LRT_V had the highest power among variance tests. The relative performance of different tests did not change when the significance level α was set at 0.01 (Supplemental Table 1) or when the SNP to be tested had a lower MAF (Supplemental Table 2 and 3). A simulation study was also performed to show that the versatile omnibus test for mean and variance heterogeneity we propose here can model mean and variance using the additive genetic model (Supplemental Table 4).

In genome-wide association studies, there are often confounders or covariates to adjust for. However, Levene’s test and all the nonparametric tests cannot incorporate covariates without resorting to a two-step approach. Demissie and Cupples [2011] and Che et al. [2012] showed that a two-stage residual-outcome regression analysis can introduce bias and cause loss of power. Table II summarized the simulation studies comparing one-step tests and two-step tests when there was a covariate to adjust for. When the simulated covariate was independent of the QTL, we did not observe inflated Type I error or loss of power of two-step tests (Table II B). However, when the QTL was correlated with the covariate, which was a confounder in this case, both Lepage test and the KW test lost power (Table II A). This simulation study only included one moderate correlated confounder (see details in the Methods section). We would expect more substantial loss of power for both Lepage test and the KW test when there are highly correlated confounders or multiple confounders to adjust for, which is often the case in common genome-wide association studies [Che et al., 2012].

Table II.

Comparison of empirical Type I error/power between one step tests and two-step tests in four simulated scenarios adjusting for a covariate. PB:Parametric Bootstrap; LR:Linear Regression; KW:Kruskal-Wallis; FK:Fligner-Killeen.

A. QTL is correlated with the covariate (confounder).
Simulated effects	one-step tests					two-step tests
	LRTMV	LRTMV(PB)	LRTM	LRTV	LR	Lepage	KW	FK	Levene
No effect	0.047	0.049	0.053	0.061	0.049	0.026	0.029	0.058	0.055
Mean	0.624	0.619	0.730	0.048	0.736	0.551	0.578	0.040	0.040
Variance	0.736	0.726	0.051	0.822	0.055	0.749	0.031	0.756	0.764
Mean & var	0.951	0.948	0.707	0.829	0.747	0.948	0.560	0.775	0.782

B. QTL is independent of the covariate.
Simulated effects	one-step tests					two-step tests
	LRTMV	LRTMV(PB)	LRTM	LRTV	LR	Lepage	KW	FK	Levene
No effect	0.057	0.053	0.048	0.045	0.051	0.044	0.048	0.046	0.043
Mean	0.779	0.780	0.866	0.046	0.869	0.844	0.857	0.044	0.047
Variance	0.722	0.718	0.040	0.823	0.059	0.751	0.047	0.762	0.767
Mean & var	0.978	0.979	0.811	0.845	0.853	0.983	0.833	0.786	0.795

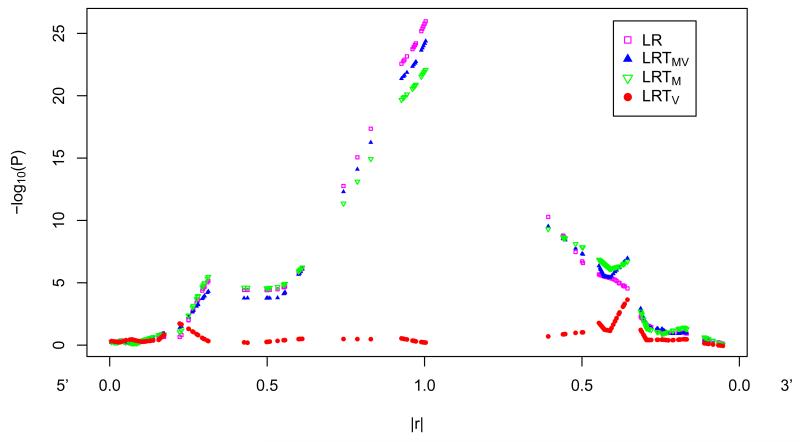
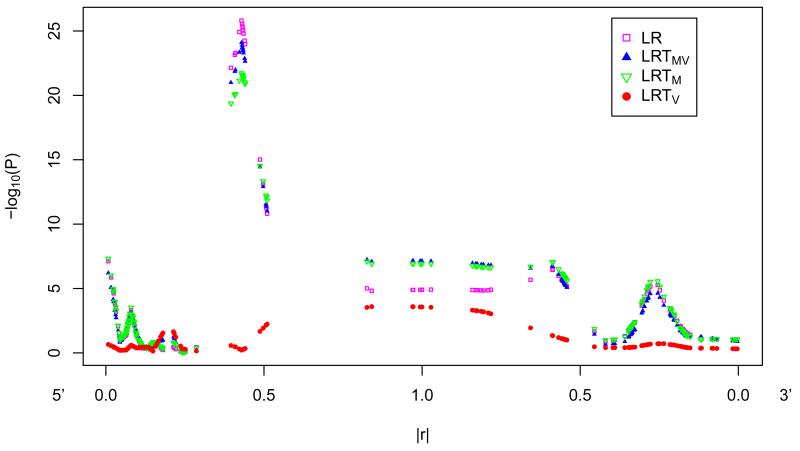
To investigate if variance heterogeneity can be due to in LD with a functional SNP with mean heterogeneity, we performed association analysis of MMP3 SNPs with MMP3 protein levels in CSF. SNP rs679620 of MMP3 gene showed extremely strong association with MMP3 protein levels in CSF (p=6.36E-26) and showed mean heterogeneity but no variance heterogeneity. SNP rs679620 is a nonsynonymous variant in the matrix metallopeptidase 3 (MMP3) gene that results in a change from Lysine to Glutamic acid at amino acid position 45 in the MMP3 protein and has been implicated in several human disease processes [Niu and Qi 2012]. The association analysis of SNPs surrounding rs679620 with MMP3 protein levels in CSF (Figure 1) illustrated that SNPs in LD with the functional SNP showed both mean and variance heterogeneity. Mean heterogeneity fades as LD (|r|) with the functional SNP decreases. However, variance heterogeneity begins to rise and peak in a short interval where LD (|r|) is less than 0.5 (r² < 0.25) with the functional SNP (Figure 1A). To determine if detected variance heterogeneity is due to LD with a true functional variant with mean heterogeneity, instead of true functional variance heterogeneity, we would expect a strong signal of mean heterogeneity among SNPs in LD with the detected SNP with variance heterogeneity (Figure 1B). Using the real MMP3 genetic data, we also performed association analysis with a simulated quantitative trait on a common variant (supplemental Figure 2), and a simulated quantitative trait on an uncommon variant (supplemental Figure 3), separately. Consistent mean and variance heterogeneity patterns due to LD (|r|) were observed from simulation studies.

Figure 1.

Test statistics (−log₁₀(P values)) for association between SNPs within 100kb of functional SNP rs679620 and MMP3 protein levels in Cerebralspinal Fluid. A. Lowess of test statistics (−log₁₀(P values)) against LD (|r|) with the functional SNP rs679620, from 5′ and 3′ separately. B. Lowess of test statistics (−log₁₀(P values)) against LD (|r|) with the SNP having the smallest p-value of LRT_V, from 5′ and 3′ separately. (See supplemental Figure 1 for plots without smoothing.) LR: linear regression; LRT_MV: likelihood ratio test testing both mean and variance heterogeneity; LRT_M: likelihood ratio test testing mean heterogeneity; LRT_V: likelihood ratio test testing variance heterogeneity.

In addition to LD measurement |r|, we also explored the relationship between variance heterogeneity and LD measurement D’ (supplemental Figure 2 and 3). We found a distinct relationship between variance heterogeneity and D’, compared with the relationship between variance heterogeneity and |r|. If a functional variant is common with only a mean effect, it is likely that any relatively uncommon variant in high D’ with it will show a variance heterogeneity peak but it will occur for relatively low |r| values (roughly according to our limited data and simulations 0.5 > |r| > 0.1, which translates to 0.25 > r² > 0.01). For the opposite situation, if we have a relatively uncommon functional variant with only a mean effect, it is likely that any common functional variant in high D’ with it will show variance heterogeneity at about the same distance (|r|<0.5 and r² < 0.25) as the prior case. In addition to the simulation and real data analysis results, we also analytically demonstrated why variance heterogeneity can arise due to LD with a functional locus with only mean effect (see supplemental text).

DISCUSSION

We have demonstrated how our method has utility for finding loci that affect trait means, variances, or both without a great sacrifice in power. This provides a nice way to identify classes of loci that may ordinarily be missed by most traditional single locus tests without sacrificing power to detect traditional loci that only affect means. In addition, as other papers have noted, loci that affect variances (vQTL) automatically become a priori hypotheses for GxG interactions. This greatly increases power and reduces computation over standard GxG analyses by reducing the number of tests to the number of loci (i.e. a standard GWAS) instead of every possible pair of loci (n choose 2).

Approach to detecting vQTL

The ability to detect variance heterogeneity is inherently less powerful (regardless of test type) than detecting mean differences. This is primarily because means are the first moment and variances are the second moment. We propose for studies interested in detecting vQTL, the LRT_MV test should be used. For multiple independent tests and using the Bonferroni, the LRT_MV test controls Type I error with normally distributed traits and non-normally distributed traits with the parametric bootstrap. Under the global null, the Type I error is controlled for the LRT_V test if it is only performed for globally significant LRT_MV. If there is an underlying mean effect and no variance effect we find a slight Type I inflation of the LRT_V test using the Bonferroni correction based on the number of globally significant LRT_MV tests (see Section 7 in the supplemental text). Nevertheless, the Bonferroni correction for the variance test appeared to work well in both scenarios. Further investigation is warranted to more comprehensively study the properties of the multiple testing procedure entailed by the two-stage tests proposed here.

Our proposed LRT_V test is as powerful as the commonly used Levene’s test for variance heterogeneity, while the latter does not allow adjustment for covariates, which may not be desirable in GWAS of complex traits. Another interesting finding in our study is that the nonparametric Lepage test is a powerful and robust alternative to the LRT_MV for simultaneous detection of mean and variance heterogeneity, with the only disadvantage of not being able to accommodate covariates. The LRT_MV is only slightly less powerful than LRT_V when there are variance only effects yet dramatically more powerful when there are both mean and variance effects. While we may not be able to detect variance effects at the border of genome-wide significance for an LRT_V test, with the LRT_MV we would detect any that are nominally above genome-wide significance for LRT_V. We would also be able to detect loci with real variance effects that are not strong enough for genome-wide significance alone unless they are coupled with a mean effect. Shen et al. [2012] suggested that many loci may show both mean and variance effects, some of which neither would be strong enough for detection by themselves. The recently discovered vQTL in the FTO gene for BMI [Yang et al., 2012] is a locus with very strong mean effects and moderately strong variance heterogeneity effects. While it was difficult to reach genome-wide significance for the vQTL alone with this locus, it would be very easy with the LRT_MV test and a subsequent LRT_V subtest. While the LRT_V subtest may have a mildly inflated Type I error, the p-value from any of their separate datasets (see Table 2 of Yang et al. 2012) would still be highly significant after correcting for inflation.

While DGLM produces statistic for mean only and variance only tests identical to our LRT_M and LRT_V tests, they are slower computationally and are not amenable to the parametric bootstrap which we have shown is essential for maintaining appropriate Type I error. And so far it has not led to an omnibus test like our LRT_MV in their paper or implemented in their R package. Typically, vQTL studies do a set of genome-wide vQTL tests and also a separate set of genome-wide traditional mean tests. The LRT_MV test would explicitly avoid the usually unacknowledged issue of doing all of the tests twice while still having power to detect instances of each scenario, mean effects, variance effects, and both. In fact, in the long run it probably has the best chance of identifying vQTL as a byproduct of a locus with both mean and variance effects.

The LRT_MV test also has an advantage over a traditional linear regression in general because traditional linear regression may have Type I error inflation in the presence of variance heterogeneity. Variance heterogeneity is a common part of loci in LD with a functional variant with mean effects as demonstrated here. While the type I error inflation tends to mislead a means test in a scenario where we would actually like an association (i.e. the bias points towards situations we are interested in finding), it is not very satisfying to use a test that is giving you the “right” answer for a partially wrong reason. The parametric bootstrap version of LRT_MV does not have this inflation and can actually lead us through subtests of LRT_M and LRT_V to understand to some extent what is contributing to the association. After identifying vQTL via LRT_MV and subsequent subtests, a descriptive plot of LRT_V and LRT_M may reveal the patterns we identified if it is due to LD with a mean functional variant (Figure 1).

Parametric Bootstrap and Computation

It is disheartening to find that in general we recommend doing the parametric bootstrap to control Type I error because tests for testing variance heterogeneity are much more sensitive to deviations from normality. We tried many different transformations and found that none of them appropriately controlled Type I error. Inverse normal transformation was used in the meta-analysis to identify SNPs in association with height or BMI variability [Yang et al., 2012]. However, Struchalin et al. [2010] showed that inflated Type I error of a variance test due to normality deviation cannot be controlled even after inverse normal transformation if the SNP effects mean heterogeneity [Struchalin et al., 2010, Figure 2B]. In addition to inflated Type I error, Beasley et al. [2009] demonstrated that inverse normal transformation can reduce statistical power in some circumstances.

For computational efficiency we suggest a series of options, with the least computational first. The first is to do the standard parametric test; this is sufficient if there is no inflation in the Quantile-Quantile plots. Type I error inflation can also be detected by permuting the phenotype with respect to a random SNP to create an empirical null distribution and compare it with the theoretical asymptotic null distribution. If there is inflation then we suggest a single set of parametric bootstraps can be performed to create a null distribution for all tests for that particular phenotype. We found that this distribution is valid for all the SNPs in the sample for a particular phenotype despite varying minor allele frequencies (see supplemental text and Supplemental Figure 4). Beyond these suggestions, the most intensive options are to do bootstrap replicates for each preliminarily significant SNP or each SNP separately. The full set of bootstrap replicates for a given SNP can be discontinued if the p-value is more than 0.1 after 100 bootstrap replicates.

vQTL or LD

As we have shown, a locus associated with variance heterogeneity of a trait could be a true vQTL or could be due to LD with a functional variant. Variance heterogeneity due to LD only appears when the r² value is relatively low and D’ is high. This imposes the condition that the two variants have very different allele frequencies. Any two loci in high D’ with similar allele frequencies will by definition have high r², in which case variance heterogeneity (due to LD) across genotypes will not be possible because the alleles AND genotypes would be highly correlated. Whereas if they are of disparate allele frequency the D’ could be high while the overall correlation is low and the minor allele of the rarer variant would only be seen on one of the allelic backgrounds creating variance heterogeneity across genotypes. Wray [2005] quantified the maximum r² as a function of the two loci’s minor allele frequencies and their difference. To determine if the putative vQTL is due to LD, if it is common we should look for relatively low frequency variants with large mean effects in high D’ with it but relatively low r² (see Results). If it has a relatively low frequency, we should look for common variants with mean effects in high D’ with it but relatively low r². Unless we have all available variants, it will be harder to rule out LD as cause for a putative vQTL when it is common because we may not have sampled all of the low frequency variants in the region.

Scale

The scale of measurement of a trait can determine what pattern of association a locus has with the trait (i.e. mean and/or variances) [Rönnegård and Valdar 2012]. This can also be influenced by various transformations. Biologically, if a locus affects the mean of an unmeasured trait that subsequently has an exponential (or other nonlinear) effect on the measured trait, the locus may display variance heterogeneity with respect to the measured trait. While the interpretation of the locus as a vQTL may not fully describe the inherent underlying relationship, it is still a vQTL for the trait of interest at that scale and gives us a link to the system for which we may uncover the true biology. The test itself allows us to identify loci related to the trait and get a foot in the door. Knowledge of the various ways that this pattern can occur allows us to realize that multiple inferences are possible and that we must pursue our suspected or favorite inference but also take it with a grain of salt. That can be said for just about any pattern identified by a statistical test. With this knowledge in hand, we can develop and test hypotheses related to the range of known possibilities with further biological knowledge and/or trait measurements.

vQTL and rQTL

Once a locus is found to be significant, it can be determined if the effect is due primarily to means, variances, or a combination of both. If variance heterogeneity plays a role, this vQTL could then be used in a GxG analysis. vQTL are theoretically connected to work by James Cheverud who developed the concept of a relationship locus (rQTL) [Pavlicev et al., 2008; Pavlicev et al., 2011]. An rQTL is a locus where the relationship between two traits varies by genotype (i.e. within genotype beta coefficients for the bivariate regression of the two traits differ). Theoretically and empirically, they have been shown to be involved in GxG or GxE interactions. An rQTL can be due to covariance and/or variance (i.e. vQTL) differences across genotypes. In order for an rQTL to exist, one of the interacting loci has a pleiotropic effect on the two traits resulting in some form of relationship between them. The other locus disrupts this pleiotropic relationship by an interaction with the pleiotropic locus for only one of the traits or by opposing interaction affects for each of the traits (i.e. differential epistasis). Finding a vQTL automatically makes it a candidate for being an rQTL with the current trait and some other. Many quantitative traits studied in relation to human disease are risk factors. An rQTL for a disease endpoint and a risk factor acts to modulate (enhance or reduce) the risk. Any vQTL found for a quantitative risk factor is potentially an rQTL and could therefore act to modulate the relationship between that risk factor and disease. Both the vQTL and/or any interacting loci for that risk factor establish a priori hypotheses for these rQTL relationships.

Another important relationship between rQTL and vQTL is that they are theoretically interchangeable through linear combinations of traits. A locus that is a rQTL for two traits and only affects the covariances is a vQTL for any linear combination of the traits such as one of the principle components of the traits or even a composite trait such as the addition of traits 1 and 2. Fundamentally, it means that a vQTL for a trait may suggest that the trait itself is a composite of multiple traits for which the locus is an rQTL. Most biological traits that we measure are composites of multiple factors due to the highly modular forms of biological systems. For example total cholesterol is a composite of the many different types of lipoproteins such as low-density lipoprotein, high-density lipoprotein and very low-density lipoprotein, which themselves are composites of multiple types. That same vQTL for the composite trait may also be an rQTL for the composite trait and some other trait.

Variance heterogeneity gives us another window into gene-by-gene interactions and can also be a tool for identifying loci in LD with functional loci in a region. Our method allows us to leverage both mean and variance heterogeneity to identify important loci and also to shed light on how they may be related to our traits of interest. Just before submitting this manuscript, we discovered a paper published ahead of print in Genetic Epidemiology [Aschard et al., 2013] that describes a nonparametric method to test for different overall distributions across genotypes which would be another way to test for mean and variance effects simultaneously.

The LRT_MV, LRT_M and LRT_V tests are implemented in R using the “nlme” package, which is posted on our website at https://sites.google.com/site/utpengwei/