‘Particle genetics’: treating every cell as unique

Abstract

Genotype-phenotype relations are usually inferred from a deterministic point of view. For example, quantitative trait loci (QTL), which describe regions of the genome associated with a particular phenotype, are based on a mean trait difference between genotype categories. However, living systems comprise huge numbers of cells (the ‘particles’ of biology). Each cell can exhibit substantial phenotypic individuality, which can have dramatic consequences at the organismal level. Now, with technology capable of interrogating individual cells, it is time to consider how genotypes shape the probability laws of single cell traits. The possibility of mapping single cell probabilistic trait loci (PTL), which link genomic regions to probabilities of cellular traits, is a promising step in this direction. This approach requires thinking about phenotypes in probabilistic terms, a concept that statistical physicists have been applying to particles for a century. Here, I describe PTL and discuss their potential to enlarge our understanding of genotype-phenotype relations.

Genetics has largely remained ‘Newtonian’

When Isaac Newton described the link between forces and energy (momentum) in what is known as his 2nd principle, classical mechanics was born. Scientists could compute speeds and trajectories, and this knowledge initiated a profound transformation of occidental societies. New techniques appeared and the philosophical apprehension of the world was modified. It is tempting to consider that the Newtonian revolution of genetics took place during the mid-20th century. When heredity (genes) was linked to biochemistry (enzymes), molecular biology was born. As happened three centuries earlier with mechanics, this discovery profoundly transformed society, in technological and philosophical terms. Over a few decades, it became plausible to explain and predict phenotypes from combinations of genetic and environmental determinants. Current research in genetics is probably still largely influenced by this excitement. Genomics has scaled up investigations and findings but did not profoundly change the (sometimes caricatural) view of a deterministic genotype-phenotype control.

Most quantitative genetics studies are based on QTL (see Glossary) mapping or whole-genome association. In both cases, the phenotype is assumed to derive from the genotype in a deterministic manner. Mutations that are searched are those that cause an increase in trait values in individuals carrying them. An arsenal of statistical methods can efficiently detect them when this increase is large enough. However, mutations contributing little to the phenotype escape detection because their effect is small compared with intragenotype variation. Unfortunately for our understanding, these ‘small-effect’ variants seem to be particularly important: they are abundant [1]; they were proposed to contribute to the ‘missing heritability’ of complex traits [1,2]; and evolutionary selection might largely act through them [3]. Detection of these loci can be improved by studying larger cohorts and by applying judicious models that include cofactors (e.g., environmental factors) and nonadditivity. However, staying in a deterministic framework might be limiting when the small contribution of the locus is due to incomplete penetrance of the trait. If the genotype does not comprehensively predict the phenotype, as seen in heritable cardiac arrhythmia [4], polydactyly [5], and various cancer-predisposing syndromes [6], then adopting a probabilistic approach might be more appropriate.

Major macroscopic events can result from microscopic properties

Rare events occurring in a few cells can have dramatic consequences at the macroscopic level. We are all examples of this, because the macroscopic physiology of our body largely results from only two germ cells contributed by our parents. Peculiarities in these cells or their progenitors can potentially change our everyday life. Another striking example is cancer: macroscopic tumors appear from a single cell that escaped proliferation controls. Anticancer treatments do not eradicate all tumor cells, and the (few) cells that persist represent the major threat for clinical outcomes. Therefore, cancer is a statistical issue of controlling the probability that cells become tumorous (risk factors), and the probability that they escape elimination by the organism and treatment (persistence). The latency of infectious pathogens is also a statistical issue. HIV-1 can persist in a small reservoir of resting cells that later ‘reactivate’ infection and disease. This mechanism of persistence represents an enormous challenge for long-term therapy [7,8]. Bacterial resistance to antibiotics represents a similar challenge [9]. Thus, some macroscopic phenotypes cannot be fully apprehended without taking into account cell-to-cell differences.

However, if genetics has remained Newtonian, are we prepared for microscopic considerations? Objects of atomic scale violate Newton’s laws. Colleagues from physics can study and manipulate these objects because their predecessors formulated the quantum theory. The revolutionary concept considered that the parameters of a particle did not determine its position and speed but changed the probability that the particle be at a given position or have a certain speed. Colleagues from statistical physics describe particles by wave functions, which carry this probabilistic information. Without this description, the diffraction of light or the spreading of liquid helium away from its container escape understanding.

As any other matter, cells comprise atoms and the fact that quantum properties appear at higher and higher resolution is obvious. However, the consideration that multicellular organisms are statistical systems of cells has not been clearly formulated. Until only recently, biochemistry and molecular biology tests have typically been conducted on extracts of millions of molecules or cells. Therefore, most experimental readouts report averaged values. Physiological trait measurements often reflect the averaged contribution of billions of cells to the function of an organ. However, biological processes, as mechanics, look profoundly different at lower scales. When gene expression is monitored at the single cell level, bursts can be observed corresponding to activity fired in some cells and not others. This had been noticed long ago [10] and is now extensively studied. Therefore, our scientific language is changing: what we used to call the ‘level’ of transcription is replaced by more discrete terms such as ‘burst size’ and ‘burst frequency’ [11]. Single molecule studies have also revealed unanticipated activity dynamics [12].

Regarding phenotypes, microscopic heterogeneities can become apparent when traits are observed at single cell resolution. For example, the induction of apoptosis by tumor necrosis factor-related apoptosis-inducing ligand (TRAIL) in cancer cell lines was shown to vary among individual cells [13], as did the activation of nuclear factor (NF)-κB by TNF-α in mouse fibroblasts [14] and the triggering of proliferation in response to epidermal growth factor (EGF) stimulation [15]. Phenotypic variability among human cell cultures can be driven by local population contexts, such as local cell density [16], and nonuniform mechanical stress can generate heterogeneities within tissues [17]. Thus, the deterministic view of genetic control seems to be challenged by single cell analysis. Even though macroscopic traits result from the collective contribution of billions of cells, they do not necessarily follow the average of these contributions. Therefore, our classical apprehension of phenotypes might have long been blurred by the law of large numbers.

Cells and molecules: the particles in biological sciences

The boundary between Newtonian and quantum mechanics is a frontier between orders of magnitude. For the law of large numbers to apply, identical particles must be numerous enough in the object considered so that probabilistic considerations are not needed. What are the typical orders of magnitude under consideration in biological systems? For example, in a system such as a human body, how many particles (cells) are there? With the very crude approximation of an average cell size of 10 μm and a density of 1, a 100-kg human body comprises 10¹⁴ cells. Given that various body parts are devoid of cells, a lower estimate (10¹³) was proposed based on DNA mass [18]. However, many cells divide, and the total number of cell divisions in a human body in the course of a lifetime was said to be in the order of 10¹⁶ [19]. Notably, these numbers cover only human cells and not our microbiome, which is approximately ten times more abundant [20] and much more proliferative. To realize how big these numbers are, one can visit the Great Dune of Pyla near Arcachon, France. This tall (>100 m) sand dune is made of tiny quartz grains and its volume is estimated at 60 million m³. A 50-ml sample of sand from the dune weighed 80 g and 97 grains weighed 4 mg; therefore, the dune has approximately 2.5 × 10¹⁸ grains. Thus, the few hundred campers staying near the dune will altogether have produced in their lifetime as many human cells as the dune grains.

Not only are cells incredibly numerous, but they also differ substantially. Cell identity is often categorized as a cell ‘type’, which reflects a particular tissue, function, morphology, and differentiation state. However, even within cell types, cells have a large amount of variability. The stochastic nature of gene expression mentioned above illustrates that intracellular concentrations of molecules can range significantly among so-called ‘identical’ cells [21]. And cells also differ in the identity of these molecules. First, somatic mutations generate intra-cell type heterogeneities. Considering a somatic mutation rate of 10^-6 per cell division for a human protein of middle size [22], the chance that one of the 20 000 human protein-coding sequence [23] gets mutated at every division is very high (approximately 2%). In addition, mutations also arise in nondividing cells, as shown recently for active transposition in brain neurons [24]. Second, fidelity of mRNA molecules is largely imperfect, with abundant nucleotide misincorporations and splicing errors [25], and transcript boundaries are extremely heterogeneous among individual molecules [26]. Third, DNA-coding sequences do not strictly dictate the final identity of intracellular proteins. Errors in translation can generate ‘mistakes’ in approximately 15% of the proteome [25]. Finally, individual protein molecules change with time. They are dynamically modified at many sites, accumulate oxidative damages, occasionally fail to fold into functionally equivalent conformations, and do not necessarily localize to the same subcellular compartments and macromolecular complexes. For all these reasons, multicellular organisms are dynamic mosaics of a huge number of cells that differ far beyond their differentiation type, and all these aspects can impact the relation between genotype and phenotype.

Nondeterministic genetic effects

The nonlinearity of biochemical reactions sometimes makes the analysis of single cell statistics essential. Properties such as cooperation, threshold effects, or feedback loops provide cells with the ability to switch between phenotypic states [27,28]. Genetic variation affecting these properties might change the probability of single cell outcomes without necessarily affecting the average trait value. Understanding trait variation in this context requires a statistical description of the behavior of individual cells.

Nondeterministic outcomes of genetic mutations can be studied on experimental organisms. In the Caenorhabditis elegans nematode, skinhead (skn)-1 mutants were shown to generate elevated variability in expression of ending (end)-1 transcripts. As a result, some but not all skn-1 mutant embryos did not achieve proper intestinal development [29]. Nonlinear dependencies between phenotypic outcomes and molecular regulations can also be studied by directly manipulating the dosage of genes involved in developmental pathways. A recent study described how C. elegans vulval development can tolerate up to a fourfold variation in EGF signaling without any phenotypic perturbation. Combining dosage perturbations in EGF and Notch signaling enabled the authors to draft an experimental phase diagram of developmental outcomes as a function of quantitative variation in the two pathways [30]. These experiments are important because they estimate the boundaries within which developmental processes are robust.

In humans, a particularly interesting example is the case of autosomal dominant (AD) mutations predisposing to cancer [6]. A large number of such mutations cause diseases characterized by a wide spectrum of symptoms (syndromes), with varying clinical expressivity, and several considerations on AD mutations illustrate the need to perform genetics in a nondeterministic framework (Box 1). In addition, a surprising correlation was recently reported between morbidities of Mendelian disorders and complex diseases, suggesting that many Mendelian disease-causing mutations have probabilistic effects on complex traits [31].

Other informative observations are those collected on fluctuating asymmetry. Some organs, such as animal limbs or plant leaves, are represented more than once in the same individual. This offers the possibility to observe nondeterministic trait variation directly. For example, any difference between the left and right wing of a fly cannot be attributed to age, diet, or any environmental effect because the two wings developed simultaneously in the same animal. Fluctuating asymmetry (FA) quantifies such intraindividual morphological differences and provides a valuable readout of nondeterministic phenotypic outcomes. When measured on numerous individuals, FA enables phenotypic variability to be quantified, even if the causes of these differences remain unknown at the molecular and cellular level. A remarkable experiment showed that elevated FA and, therefore, phenotypic variability, can have large heritability. By designing successive crosses between Drosophila melanogaster flies displaying high FA, the authors were able to fix elevated FA from an outbred population [32]. This demonstrates that different levels of phenotypic noise can segregate in the wild. This likely explains the different levels of cell-cell trait variability that were recently observed in natural yeast strains[33,34]. Finding sources of phenotypic noise in the wild complements an earlier observation from an in-lab evolution experiment. Extreme selection on Pseudomonas fluorescens bacteria for phenotypic switching generated genotypes causing intraclonal trait bimodality [35]. These examples show that some genotypes can have nondeterministic consequences on phenotypic traits. To really understand how these genetic effects contribute to the physiology and evolution of living systems, classical genetics must be revised.

Mapping macroscopic and single cell probabilistic trait loci

From Mendelian mapping to current whole-genome association studies (GWAS), genetic linkage is always based on a simple principle: observing phenotype and genotype on a set of individuals, and deriving correlations. A genetic locus of sufficiently large effect on the phenotype is detected because data points (individuals) display covariation between the genotype at the locus and the phenotype. In this framework, all the microscopic diversity discussed above is compressed in a single parameter: the phenotype of the individual. The ability to acquire parameters on single cells from every individual has not yet been fully exploited.

Common traits are classically dissected by mapping QTL. A QTL is detected when one can reliably reject the null hypothesis of no difference in mean trait value between carriers of one allele and carriers of other alleles at the locus. Sometimes, the test is applied on the median value instead. In multilocus scans, more genotype combinations are considered, and the null hypothesis is also an equal mean (or median) trait value across genotypes. Therefore, QTL are mapped within a statistical framework, but they have a deterministic nature because they affect the average or median trait value of all individuals of the same genotype. If a genetic locus changes trait properties other than its mean or median, it is likely not detected. For example, interindividual variance might be changed, thereby generating more individuals with extreme trait values (Figure 1B). To better account for the probabilistic nature of common traits, one can consider the trait probability density function instead of the observed trait values only. This function not only relates to the trait expressivity, but also provides the probability of observing the trait at a given value, as does penetrance for dichotomous traits. Using this function, it is possible to refine the concept of QTL by considering any change of the trait density function in response to genetic variation. Let us define a probabilistic trait locus (PTL) as any DNA polymorphism that modifies a trait probability density function. Under this definition, all QTL are PTL because they affect the mean or median trait value and, therefore, the trait density function. However, the reverse is not true: a PTL may change various properties of the trait probability without necessarily affecting its average.

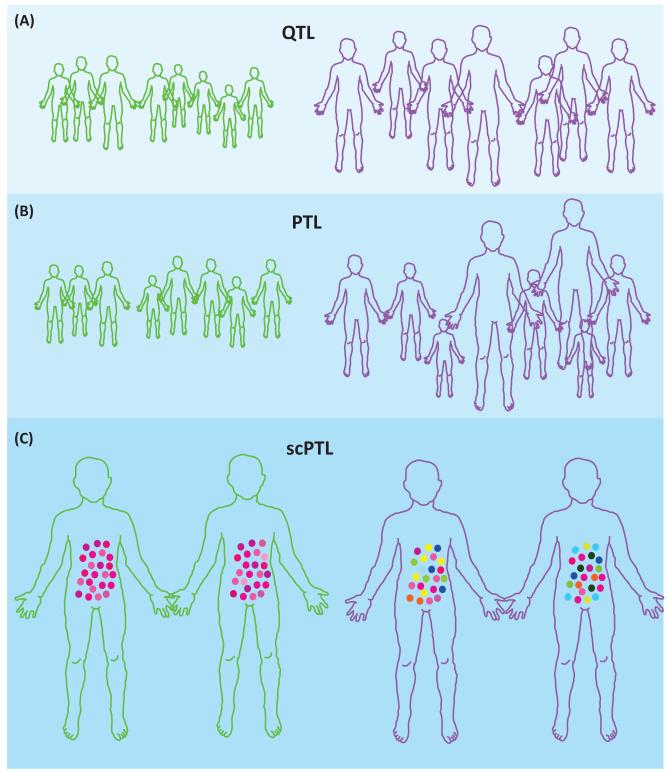
Figure 1. Quantitative trait loci (QTL), probabilistic trait loci (PTL), and single cell (sc)PTL effects.

In each case, two genotypes at a given locus are compared, as indicated by the color outline of individuals (green versus purple). (A) The locus is a QTL and the purple genotype increases the trait value, as indicated by the size of individuals. (B) The genotype is a PTL and the purple genotype increases the trait variance without changing the mean trait value of individuals. (C) Individual cells of a tissue are represented by dots, colored by their value of a single cell quantitative trait. Here, the locus is a scPTL: the purple genotype increases single cell trait variance within the tissue. This may or may not change the macroscopic phenotype of individuals.

Although not specifically named this way, PTL mapping has already been reported in several studies that looked at within-genotype interindividual trait variation. The earliest example was a QTL mapping strategy applied to stochastic variation in yeast gene expression [36]. The approach was recently followed up to derive additional PTL [37]. In these studies, the trait of interest was the expression level of a GFP construct reporting the activity of the yeast methionine-requiring (MET)17 promoter. Probability density functions were tracked by flow cytometry and several loci were associated with a change in variance and not mean of MET17 promoter activity. These loci can be qualified as expression (e)PTL because they affect the density function of a gene expression trait. Notably, three DNA polymorphisms causing increased variability were discovered. One was a uracil-requiring (ura)³ mutation that is widely used as an auxotrophic marker in yeast laboratories. Given that URA3 activity can affect transcriptional elongation efficiency, this ePTL revealed that elongation impairments increased the levels of stochasticity in gene expression [36]. Another ePTL was a frame-shift mutation in ethionine resistance conferring (ERC)-1, a transmembrane transporter gene, which reduced MET17-GFP expression variability. A third one was the promoter region of the methionine uptake (MUP)1 gene, also encoding a transmembrane transporter, which probably increased the sensitivity of cells to microenvironmental fluctuations [37]. Another study also mapped ePTL using a transcriptomic data set of Arabidopsis thaliana [38]. Within-genotype coefficient of variation of mRNA levels were considered as quantitative traits and genetic loci linked to them were identified. Many, but not all of them were also eQTL affecting mean expression. An apparently similar observation was made in humans, where the fat mass and obesity associated (FTO) gene locus was associated with both mean and variability of obesity in a GWAS study [39]. However, in this case, variability was measured across individuals sharing a common allele at the FTO locus, but differing at numerous other loci and each having a specific history of exposure to various environmental factors. Therefore, the observed PTL effect of FTO could result from fully deterministic gene–gene or gene–environment interactions that remain challenging to characterize. In this regard, the effect is comparable to results from a previous study mapping QTL of genetic and environmental robustness in mice [40]. Using approximately 20 animals from each of 19 inbred lines, the authors mapped numerous ‘robustness QTL’ conferring different levels of across genetic-background or interindividual variability without altering median trait values. A detailed dissection of the underlying gene–gene and gene–environment interactions would require more lines and animals, but the results already indicate the presence of abundant genetic loci implicated in trait buffering. Interestingly, the nonparametric method described in this mouse study can be applied to variability among isogenic individuals sharing a common environment and, therefore, provides a direct way to map ePTL systematically [40].

These pilot studies illustrate the feasibility and potential of PTL mapping. However, carrying out genetic mapping at the level of individuals without exploiting single cell data faces a major limitation: sample size. It is well known in statistics that testing differences in variance or other high-order moments of a distribution requires larger samples than testing differences in median or mean. This issue has been explored in a quantitative genetics model: a single nucleotide polymorphism (SNP) causing a change in phenotypic variance with a 1.1 multiplicative effect requires a minimum of 10 000 observations to be detected by GWAS [41]. Given the large samples already needed for classical QTL and GWAS studies, the experimental effort to identify PTL in a systematic approach seems enormous. To bypass this limitation, an attractive possibility is to remember that a single individual can provide of a huge number of cells.

If a genetic locus has an intrinsically nondeterministic effect on molecular or cellular regulation, then it likely affects the density function of one or more single cell traits. This trait can be a gene expression level or any other intracellular concentration, a cellular shape, a cell division rate, a rate of secretion, or any other quantity relevant to the macroscopic phenotype under study. When this single cell trait can be measured experimentally on many cells collected from each individual of a cohort, the single cell trait density function can be estimated. This is the case, for example, if the trait is the cell size of a class of macrophages. Its density function can be obtained by drawing blood from donors, extracting macrophages, labeling the ones of interest with appropriate cell surface markers and analyzing them by flow-cytometry. I now define a single cell (sc)PTL as a genetic locus changing a single cell trait density function. Mapping scPTL can bypass the issue of statistical power because samples of large size (many cells) are available from every individual. Thus, comparing variances or other higher order moments of the single cell trait density function becomes possible. Therefore, using flow cytometry or other high-throughput single cell measurements [42] to map scPTL might prove more powerful than mapping PTL of traits exhibited by the individual.

In what situation would scPTL mapping succeed and QTL detection fail? A scenario is presented in Figure 2, where a cellular quantitative trait is monitored and cells with high trait values are pathogenic. A trait like this can be, for example, the expression level of an oncogene such as v-erb-b2 erythroblastic leukemia viral oncogene homolog 2 (ERBB2), which can trigger tumorigenic processes when it is overexpressed in a single cell [43]. Alleles at a scPTL locus can change the statistical distribution of the trait among cells without necessarily changing the mean expression level (Figure 2A). This can be, for example, a variant in the promoter of the ERBB2 gene that increases cell-to-cell variability in ERBB2 expression [11]. In this case, some ERBB2 genotypes will increase the fraction of pathogenic cells appearing in the body and, therefore, will increase disease risk. The phenotype of the individuals (disease versus healthy) is poorly contrasted by the genotype because many individuals at risk are healthy (e.g., their immune system managed to clear the pathogenic cells). Owing to this low penetrance, standard QTL or GWAS detection has poor power (Figure 2B). By contrast, if single cell data are available, it becomes apparent that all carriers of the predisposition allele display a modified distribution of the single cell trait. Every individual is then highly informative for the genetic linkage test, and the scPTL can be detected (Figure 2C).

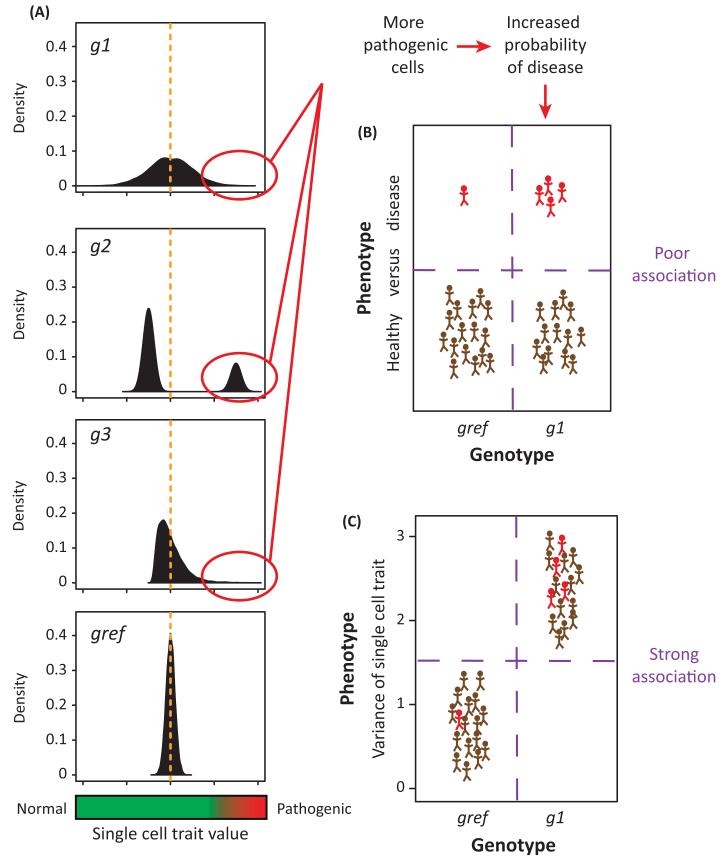
Figure 2. A scenario where single cell probabilistic trait loci (scPTL) mapping has greater potential than a classical approach.

(A) A single cell trait, such as the expression level of an oncogene, is pathogenic at high values. Graphs represent distributions of the trait value (x-axis) among isogenic cells for four individuals having genotype g_ref, g₁, g₂, and g₃, respectively, at a given locus. This locus is a scPTL because the distributions are significantly different, but it is not a QTL because the mean trait value (orange broken line) is the same in all four individuals. Genotypes g₁, g₂, and g₃ generate more pathogenic cells than genotype g_ref, thereby increasing disease risk. (B) Corresponding data set used if a classical approach is applied. Brown and red symbols represent healthy and diseased individuals, respectively. Due to incomplete penetrance, only few individuals carrying the g₁ genotype at the locus display the disease. Therefore, the correlation between the macroscopic phenotype (disease versus healthy) and the genotype (g_ref versus g₁) is weak. (C) Data set used for scPTL mapping. Symbols represent the same individuals as in (B). This time, the phenotype on the y-axis is the variance of the distributions shown in (A). All g₁ individuals display greater phenotypic values compared with g_ref controls. This greater correlation between the ‘microscopic’ phenotype and the genotype enables detection of the locus.

Concluding remarks

The huge mosaic of cells that forms an individual constitutes both a challenge and an opportunity. There is no chance that we will exhaustively describe this complex system by ‘Newtonian’ deterministic laws inherited from molecular biology, and this might seem bad news. But fortunately, experimental measures are accessible to estimate probability functions from single cells and, therefore, the genetic properties of these functions can be dissected. A ‘particle’ approach will probably not revolutionize genetics in general. However, for diseases that depend on the behavior of rare cells, several genetic factors might have been missed by classical QTL studies and GWAS because their reduced penetrance makes their overall effect small. The scPTL approach has the potential to reveal such variants. It is now, more than ever, time to talk to statistical physicists, to invite them to train our students, and to think in probabilistic terms about the roots of phenotypic control.

Box 1. Possible nondeterministic effects of haploinsufficiency.

Neurofibromatosis 1 is a typical case of an autosomal dominant disorder displaying a range of disease severity. It is caused by heterozygous loss-of-function mutations of the NF1 gene, and symptoms vary from café au lait stains on the skin to severe malignancy [46]. Variability in disease appearance and expressivity can be interpreted in two complementary ways. Mutations might appear in ‘two hits’: a first mutation is inherited from the parental germline and a second one occurs later somatically. This secondary mutation can occur via loss of heterozygosity, or via a novel mutation hitting the wild type allele. In this two-hit model, the probabilistic nature of the trait among carriers of the first mutation is strictly associated with the probability of the occurrence of the secondary mutation. The model remains deterministic in terms of genotype–phenotype control: heterozygous cells are healthy and homozygous −/− cells are pathogenic. The alternative interpretation is that haploinsufficiency alone might produce a subpopulation of pathogenic cells as a result of improper regulation of enzymatic activity in some heterozygous cells. In this case, the genotype–phenotype control is probabilistic because most heterozygous cells are healthy but some of them become pathogenic.

Note that this alternative model does not necessarily exclude the ‘two-hit’ interpretation: if the probabilistic cellular trait affects the mutation rate of the wild type allele, then haploinsufficiency facilitates secondary mutations and the two-hit model also applies. Possible nondeterministic consequences of haploinsufficiency have been discussed [47] and explored in simulations [48,49]. Two scenarios are particularly plausible. First, haploinsufficiency might increase sensitivity to differential allelic expression. Two alleles of a gene are not necessarily ‘fired’ simultaneously. If they both encode a fully functional protein, these temporal allelic differences do not generate significant fluctuations in gene activity. By contrast, firing a null allele is a dead-end and fluctuations between allelic transcription rates might generate variable enzymatic activity in −/+ heterozygous cells (Figure IA). Second, haploinsufficiency can render cells particularly sensitive to molecular noise because of the nonlinearity of enzymatic reactions. This is illustrated in Figure isB, where heterozygosity suppresses buffering against fluctuations. Experimental evidence supporting such scenarios is scarce, but an important observation is the elevated variability in single cell traits that has been observed among Nf1^−/+ melanocytes compared with Nf1^+/+ control samples [50].

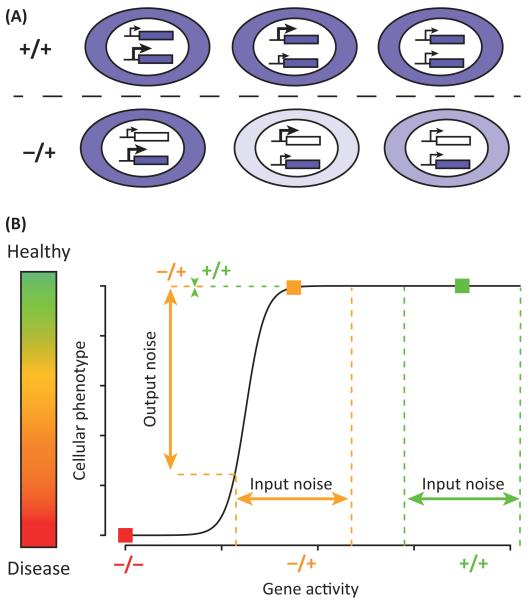
Figure I. Possible nondeterministic consequences of haploinsufficiency.

(A) Diversity from fluctuations in allele-specific expression. Color of the cytoplasm represents the concentration of functional gene product (darker color indicates a higher concentration). (B) A cellular outcome is represented as a quantitative trait, from disease-causing low levels to healthy full levels, as a function of the activity of a gene product. The heterozygous genotype produces normal mean level activity but an increased variability in the outcome. Note that the ‘input noise’ reflects variability in enzymatic activity, which can correspond to various parameters, such as variation in concentration or in the proportion of molecules that have the required post-translational modifications, subcellular localization, or conformation.

Glossary

Expression probabilistic trait locus (ePTL)

a PTL where the trait of interest is the abundance of a gene product.

Expression quantitative trait locus (eQTL)

a QTL where the trait of interest is the abundance of a gene product. In some studies, eQTL refers to traits of mRNA levels and pQTL refers to traits of protein levels.

Penetrance

probability that an individual of genotype g displays a phenotype [44]. Usually associated with qualitative traits, such as disease versus control.

Probabilistic trait locus (PTL)

a DNA polymorphism modifying a quantitative trait density function. A PTL is not necessarily associated with a change in mean trait value. It may affect the variance, skewness, normality, bimodality, or any other property of the trait density function. Genetic buffers of environmental or genetic perturbations are not PTL under this definition. They may affect interindividual variability across different environments or genotypes without necessarily modifying a trait density function defined within a precise environmental and isogenic context.

Quantitative trait density function

probability density function f of a quantitative trait among individuals of the same genotype g, such that $P={\int }_{t_1}^{t_2}f(g,t)$ is the probability that one individual of genotype g displays a trait value falling within the interval [t₁,t₂]. To be informative, this function must be defined for given values of environmental, age, gender, and other factors that may obviously affect the trait in a deterministic manner. Here, ‘same genotype’ refers to fully isogenic individuals, such as isogenic strains or lines of experimental organisms. For many outbred organisms, trait density functions cannot be directly observed.

Quantitative trait locus (QTL)

a DNA polymorphism underlying the genetic variation of a quantitative trait [45]. It is usually mapped within genetic intervals defined by markers. If it is precisely identified, its molecular implication can be studied. In most studies, QTL are associated with a change in mean or median trait value.

Single cell probabilistic trait locus (scPTL)

a DNA polymorphism modifying a single cell quantitative trait density function. A scPTL is not necessarily a PTL if the difference in single cell properties does not modify the probability of a macroscopic trait of an individual.

Single cell quantitative trait density function

probability density function of a single cell quantitative trait, defined for cells of a given genotype, differentiation state, and environmental context. This can refer to individual cells of the same tissue within an individual (Figure 1C, main text), or cells of a clonal microbial colony.

Trait expressivity

degree to which trait expression varies among individuals of genotype g. Often used to describe traits that can be discretized, such as the clinical severity of syndromes. Expressivity E of trait T reflects the extent of trait variation but not the probability that an individual expresses T at a given level. If f is the quantitative trait density function of T for genotype g, then E(T,g) corresponds to all values of T where f >0.