Mechanisms of noise robust representation of speech in primary auditory cortex

Significance

We show that the auditory system maintains a robust representation of speech in noisy and reverberant conditions by preserving the same statistical distribution of responses in all conditions. Reconstructed stimulus from population of cortical neurons resembles more the original clean than the distorted signal. We show that a linear spectrotemporal receptive field model of neurons with a static nonlinearity fails to account for the neural noise reduction. Although replacing static nonlinearity with a dynamic model of synaptic depression can account for the reduction of additive noise, only the combined model with feedback gain normalization is able to predict the effects across both additive and reverberant conditions.

Abstract

Humans and animals can reliably perceive behaviorally relevant sounds in noisy and reverberant environments, yet the neural mechanisms behind this phenomenon are largely unknown. To understand how neural circuits represent degraded auditory stimuli with additive and reverberant distortions, we compared single-neuron responses in ferret primary auditory cortex to speech and vocalizations in four conditions: clean, additive white and pink (1/f) noise, and reverberation. Despite substantial distortion, responses of neurons to the vocalization signal remained stable, maintaining the same statistical distribution in all conditions. Stimulus spectrograms reconstructed from population responses to the distorted stimuli resembled more the original clean than the distorted signals. To explore mechanisms contributing to this robustness, we simulated neural responses using several spectrotemporal receptive field models that incorporated either a static nonlinearity or subtractive synaptic depression and multiplicative gain normalization. The static model failed to suppress the distortions. A dynamic model incorporating feed-forward synaptic depression could account for the reduction of additive noise, but only the combined model with feedback gain normalization was able to predict the effects across both additive and reverberant conditions. Thus, both mechanisms can contribute to the abilities of humans and animals to extract relevant sounds in diverse noisy environments.

Vocal communication in the real world often takes place in complex, noisy acoustic environments. Although substantial effort is required to perceive speech in extremely noisy conditions, accurate perception in moderately noisy and reverberant environments is relatively effortless (1), presumably because of the presence of general filtering mechanisms in the auditory pathway (2). These mechanisms likely influence the representation and perception of both speech and other natural sounds with similarly rich spectrotemporal structure, such as species-specific vocalizations (3–5). Despite the central role this robustness must play in animal and human hearing, little is known about the underlying neural mechanisms and whether the brain maintains invariant representations of these stimuli across variable soundscapes causing acoustic distortions of the original signals.

Several theoretical and experimental studies have postulated that the distribution of linear spectrotemporal tuning of neurons found in the auditory pathway could support enhanced representation of temporal and spectral modulations matched to those prevalent in natural stimuli (6, 7). Others have attributed this effect to nonlinear response properties of neurons (8) and adaptation with various timescales (9). In this study, we tested the noise robustness of auditory cortical neurons by recording responses in ferret primary auditory cortex (A1) to natural vocalizations that were distorted by additive white and pink (1/f) noise or by convolutive reverberation. We sought to determine whether neural population responses to speech and vocalization in these noisy conditions encode important stimulus features while suppressing the noise, therefore resulting in less distorted representation of the signal. In addition, we tested whether the robust neural representations can be explained solely by static spectrotemporal receptive field models of neurons (10) or whether additional dynamic nonlinear mechanisms such as synaptic depression (ability of synapses to weaken rapidly, in response to increase presynaptic activity) (11, 12) or gain normalization (division of neural responses by a common factor that relates to the overall activity) (13–15) are necessary to account for this phenomenon.

Results

Neural Responses to Clean and Distorted Auditory Signals.

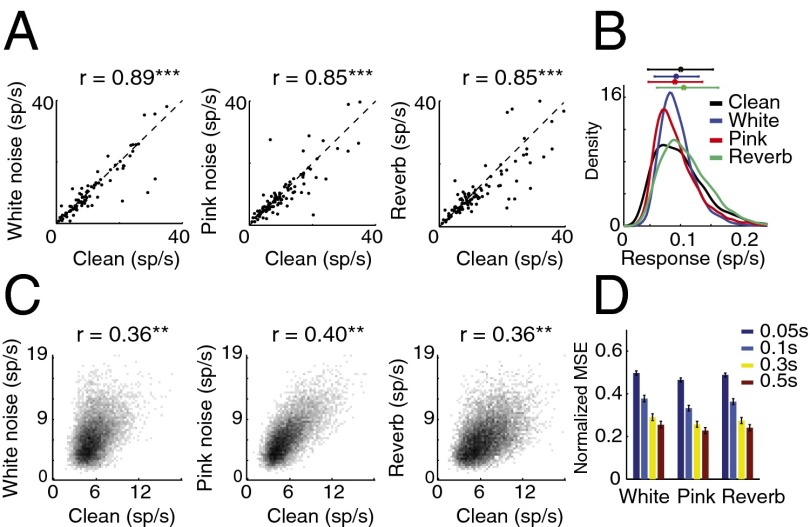
We first examined the effect of stimulus distortions (white and pink additive noise and reverberation) on single-unit responses in A1 by comparing the responses of neurons to clean (undistorted) speech and to the same speech signal in noisy conditions. We chose additive white noise and pink noise due to their simple spectral profile and stationary characteristics, therefore simplifying the comparison of masking effects across different speech samples (16). Reverberation, in contrast, is a convolutive distortion resulting in temporal smearing of the stimuli. Fig. 1A shows the firing rate of single neurons for clean and for each of the three distortions, averaged over the entire stimulus period. The high correlation values between stimulus conditions (r = 0.89, 0.85, and 0.85 for clean versus white noise, pink noise, and reverberation, respectively, P < 0.001, t test) show a relatively constant level of neural spiking activity in the different conditions, despite the highly variable stimulus statistics. This stability is also evident in the overlapping histograms of neural spike rates measured on a much finer time scale (20-ms bins), shown in Fig. 1B, where we did not observe a significant change in firing profile of neurons. The high level of stability suggests a mechanism that normalizes the level of neural activity across different noisy and reverberant conditions.

Fig. 1.

Single-neuron responses to clean and distorted speech. (A) Effect of stimulus distortions on the average firing rate of neurons. Each point indicates the average response of a single neuron to clean (horizontal axis) and distorted speech (vertical axis). Correlations between responses in each pair of conditions appear over each plot. Most neurons did not exhibit a significant change in their firing rate, and the correlations between conditions were significant (***P < 0.001, t test). (B) Histogram of neural spike rates in clean and distorted conditions. Horizontal bars at the top show mean and SD for each condition. (C) Joint histogram of instantaneous neural responses at fine time scales (20-ms bins) to clean speech and to the same speech samples in noise (r = 0.36, 0.40, and 0.39, P < 0.001, t test). (D) Normalized MSE difference between neural responses to clean and distorted speech for different bin sizes.

To examine the relative timing of spikes in clean and distorted conditions, we measured the joint histograms of neural population responses in clean versus each of the three noisy conditions as shown in Fig. 1C. These joint distributions reveal the relationship between instantaneous responses to the same stimulus in clean and in each distorted condition (10-ms bins), where a diagonal structure indicates consistent response between conditions. The divergence from the diagonal in Fig. 1C indicates the impact of stimulus distortions on the neural responses. However, a small but significant correlation value remains (r = 0.36, 0.4, and 0.36, P < 0.01, t test), suggesting the preservation of the responses to stimulus features across all distortions. We measured the mean-squared error (MSE) between neural responses in clean and in distorted conditions to quantify the degradation of neural responses in noise as a function of bin size, as shown in Fig. 1D. This analysis shows greater degradation as finer temporal details of neural responses are taken into account, confirming the loss of precisely phase-locked responses of single neurons to stimulus features in noise. Together, these results show that the neural responses to distorted stimuli are degraded, particularly changing the precise temporal profile of spiking activity. However, they also suggest a normalization mechanism in the auditory pathway that results in maintained statistical properties of firing patterns as shown in Fig. 1 B and C.

Reduced Distortions in Stimuli Reconstructed from the A1 Population Response.

Although the single-neuron analysis provides a quantitative measure of the change in neural responses to acoustically distorted stimuli, it is hard to gain insight about what aspects of the stimulus are preserved by the population response in noisy conditions. To overcome this difficulty, we used stimulus reconstruction techniques (17, 18) to map the population neural responses to a stimulus spectrogram, which could be easily compared with the original clean and noisy spectrograms. The reconstruction filters were fitted to the responses in the clean condition and used to reconstruct the stimulus from responses in distorted conditions.

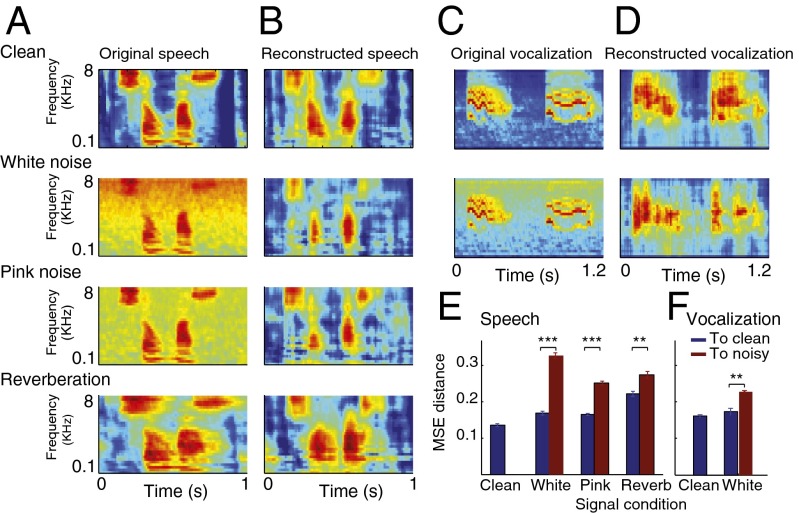
The original spectrograms of the clean and the three types of distorted speech are illustrated in Fig. 2A. Spectrograms reconstructed from the neural responses for the same conditions are shown in Fig. 2B and Fig. S1. In all three conditions, both for additive noise and reverberation, the reconstructed spectrograms showed significantly improved signal-to-noise ratio, seen visually as suppressed background activity (for additive noise) and reduced smearing in Fig. 2B (for reverberation). We quantified this effect by measuring the MSE between the reconstructed and original spectrograms as shown in Fig. 2E. The difference between the reconstructed and clean spectrograms (blue bars) in all three conditions is significantly smaller than the noisy spectrograms (red bars, P < 0.01, t test). To confirm that the same effects occur for species-specific vocalizations as for speech, we performed the same analysis on A1 responses to ferret vocalizations in additive white noise, and observed the same pattern of noise robustness (Fig. 2 C−F, P < 0.01, t test). We should point out that even though the reconstruction filters were estimated from neural responses to clean speech, the imposition of this prior does not guarantee that the reconstruction from noisy responses will have improved signal-to-noise ratio. To explore whether the observed denoising is due to reconstruction filters or to dynamic changes in the neural response properties, we next used the same reconstruction filters obtained from clean neural responses (Fig. 2B) and reconstructed the spectrograms from simulated neural responses.

Fig. 2.

Reduced stimulus distortions in spectrograms reconstructed from the A1 population response. (A) Original and (B) reconstructed spectrograms of clean and distorted speech. The reconstructed spectrograms from the population response of A1 neurons to the clean and distorted speech were more similar to the spectrogram of the clean speech signal (first panel in A) than to those of the distorted signals (second through fourth panels in A). (C) Original and (D) reconstructed spectrogram of clean and noisy ferret vocalization sounds, showing a similar effect as in A and B. (E and F) MSE distance between the spectrograms reconstructed from neural responses and clean (blue) or noisy (red) original spectrograms. In all distortions, reconstructions were closer to the clean than to the noisy stimuli (**P < 0.01, t test), both for speech and ferret vocalization sounds. Error bars were estimated across different speech samples.

Nonlinear Mechanisms Contribute to Noise-Robust Responses.

To explore possible neural mechanisms that could produce noise-robust representation in A1, we simulated neural activity using the spectrotemporal receptive field (STRF), which is commonly used to characterize functional properties of auditory neurons (10, 19, 20):

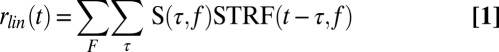where 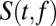is the spectrogram of the stimuli, and the parameter V_th indicates the spiking threshold for each neuron, fitted to the data to maximize the correlation value of the neuron’s predicted response. In addition to a classic STRF, consisting of a linear filter followed by a static nonlinearity (10) ( 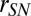in Eq. 2), we explored the dynamic effects of a subtractive nonlinearity modeling input synaptic depression (SD) (21) and a multiplicative nonlinearity modeling feedback gain normalization (GN) (15) (Fig. 3A). A model incorporating both dynamic nonlinear elements is defined at a high level as

where 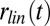is defined in Eq. 1, and A(t) and B(t) are defined as:

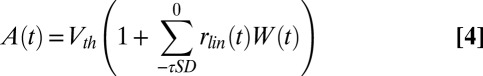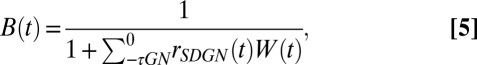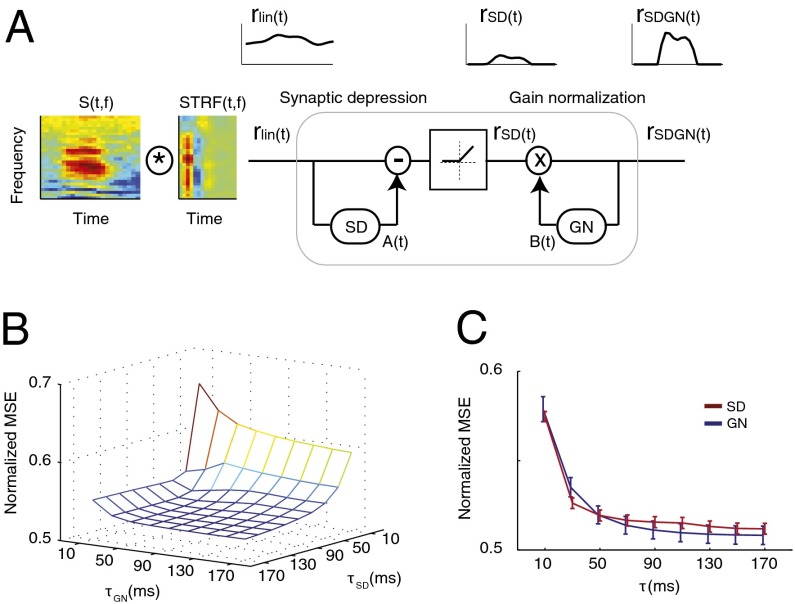
where 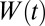is the Hann function, added to emphasize the most recent history of stimulus and response (see Methods). The SD component, A(t), performs a feed-forward subtraction reducing the output of the linear filter, r_lin(t), proportionally to the preceding input stimulus history. The GN component, B(t), is a feedback operation, scaling the final response proportionally to the short-term history of the predicted output response. We compared this dynamic model to a model with only a static nonlinearity (SN) in which both A(t) and B(t) were fixed at constant values. We also studied the effects of the SD and GN stages individually by keeping either A(t) (GN only) or B(t) (SD only) constant.

Fig. 3.

Simulating the neural responses in clean and noise using static and dynamic models. (A) Schematic of the model to simulate neural responses including linear STRF, a feed-forward subtractive model of SD and a feedback multiplicative model of GN. The synaptic depression stage [r_SD(t)] eliminates the baseline stimulus energy, whereas the gain normalization stage normalizes the predicted output. (B) MSE distance of predicted neural responses to actual neural responses in distorted conditions as a function of SD and GN integration windows. (C) MSE distance of predicted to actual noisy responses for SD and GN models separately.

Both the SD and GN modules depend critically on temporal integration parameters tau (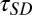 and 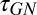) that specify the duration of the stimulus (SD) or response (GN) that influences the neural response (see Methods for details). To study how these parameters influence the predicted responses, we measured the MSE difference between responses predicted by the model and actual responses to the noisy speech stimuli (Fig. 3 B and C). We also measured the effects of varying tau for SD and GN components separately by averaging MSE measurements as shown in Fig. 3C. We observed significant improvement in prediction error as we increased both time constants from 0 ms. Performance ceased to improve beyond a value of 70 ms for the SD module and 90 ms for the GN module. Thus, for subsequent simulations, we fixed the time constants at these values. Although effective here, these values should not be interpreted too strictly as upper bounds. Our experiments did not probe the entire range of possible distortions or nonstationary distortions, particularly for reverberation, which can have longer echo times.

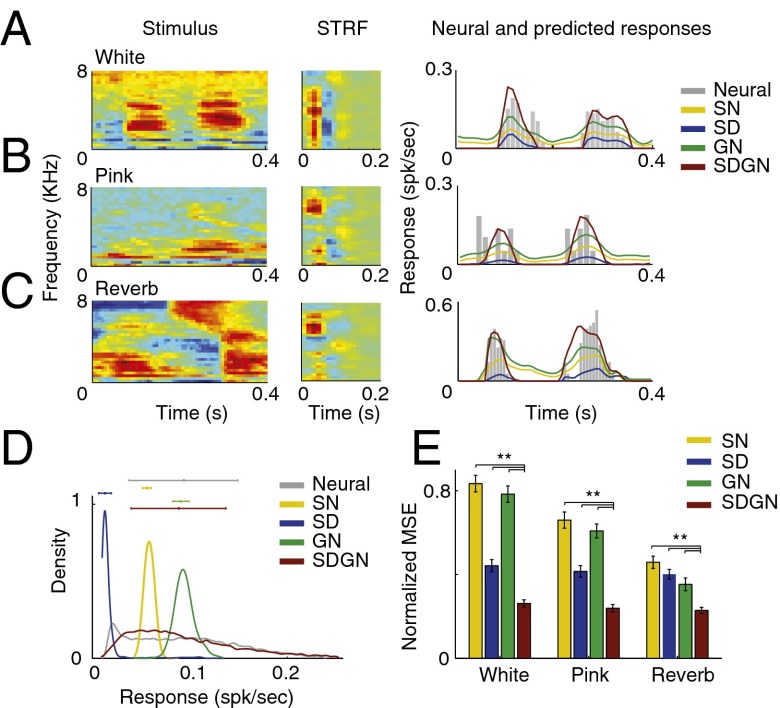
Responses by the different static and dynamic models to distorted speech are compared in Fig. 4. The responses predicted by the SN model do not suppress the additive noise, as shown by the predicted neural activity even in the absence of the stimulus (Fig. 4 A and B, yellow line). The SN model also predicts a prolonged response to reverberant stimuli, reflecting the temporal smearing caused by this distortion (Fig. 4C, yellow line). The GN model alone (Fig. 4 A−C, green line) also fails to decrease the noise and merely scales the average spike rate. By contrast, the SD model alone predicts the suppressed noise floor in additive noise conditions, but also (erroneously) predicts a significantly reduced overall spiking rate (Fig. 4 A−C, blue lines). This reduction, however, is compensated for in the predictions of the SDGN model, resulting in suppression of noisy distortions while preserving the overall neural firing activity (Fig. 4 A−C, red lines). These observations are quantified in the histograms of predicted responses for the different models (Fig. 4D), where the SDGN model produces the most similar histograms for the clean and noisy conditions and replicates the neural data (Fig. 1B). Finally, we quantified the MSE difference between responses predicted by the different models in each distorted condition to actual neural responses in the same conditions, shown in Fig. 4E. Responses predicted by the SDGN model were significantly more similar to the actual responses than SN, SD, or GN alone (P < 0.01, t test, n = 91, 101, and 97 for white, pink, and reverberation conditions, respectively). Although inclusion of either dynamic mechanism individually results in more accurate prediction of the neural response, the actual neural data are best predicted when both mechanisms are combined. More specifically, the subtractive SD model is more effective than the multiplicative GN in additive noise conditions (blue vs. green bars for white and pink noise in Fig. 4E), but not in reverberation.

Fig. 4.

Example predicted neural responses in noisy conditions. (A−C) Examples of distorted spectrograms and their corresponding actual and predicted neural response for SN, SD, GN, and SDGN models for (A) white noise, (B) pink noise, and (C) reverberation. The predicted responses using the SN and GN models encode the noise even in the absence of the stimulus. The predicted responses using SD model alone, however, are able to eliminate the noise floor by removing the average baseline activity, but result in a significant reduction in spike rate. SDGN model produces the most similar predicted response to actual neural data. (D) Histogram of predicted neural responses for SN, SD, GN, and SDGN models show their overall effect on predicted responses. (E) MSE distance of predicted to actual noisy neural responses for SN, SD, GN, and SDGN models shows the efficacy of SDGN (**P < 0.01, t test).

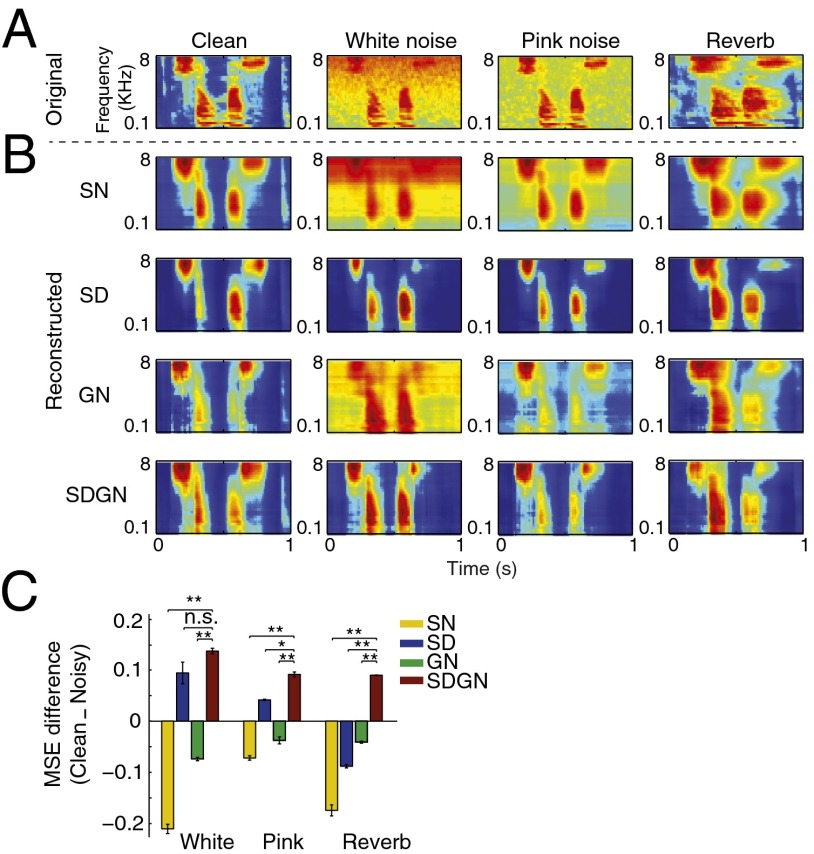
To study how the different models encoded clean and noisy speech at the population level, we applied the reconstruction analysis to the simulated responses. We used the same reconstruction filters obtained from neural responses to clean speech, as in the analysis in Fig. 2. The original and reconstructed spectrograms for the SN, SD, GN, and SDGN models are shown in Fig. 5. As expected, the reconstructed spectrograms for the SN and GN models contain both speech and noise and a relatively smeared response in the reverberant conditions. The SD model reduces the noise level but at the expense of excessive overall response suppression that fades the finer features of the speech signal. Reconstructed spectrograms for the SDGN model produced spectrograms most similar to the original clean signals (Fig. 2A) and to the reconstruction from actual neural data (Fig. 2B).

Fig. 5.

Original and reconstructed spectrograms from predicted neural responses. (A) Original spectrograms of an example speech sample in white and pink noise and in reverberation. (B) Reconstructed spectrograms from predicted neural responses using SN, SD, GN, and SDGN models in different noisy conditions. Suppression of acoustic distortion while preserving the speech signal was achieved only in the predicted responses of SDGN model. (C) Difference between MSE distances of reconstructed spectrograms and original clean and noisy spectrograms showing a significant enhancement of the speech signal and suppression of the distortion for SDGN predicted responses (red bars, **P < 0.01, t test).

We used the MSE distance metric to compare the reconstructions for the different models quantitatively, as shown in Fig. 5C. This analysis confirms the significant enhancement of the speech signal and suppression of distortions for the SDGN model (red bars, Fig. 5C, t test, Bonferroni correction). Note also that the reconstructed spectrograms from the SD model were closer to the clean stimulus for additive white and pink noise (blue bars, Fig. 5C), but the only model that also reduced the reverberant distortions was the combined SDGN model. Based on these observations, we conclude that a simple higher-level read-out stage (simulated by linear reconstruction in our study) that is estimated only in clean condition will generalize to distorted speech, because the responses themselves adapt to the changing condition, eliminating the need for reestimation of a decoding model. This self-normalization of the responses is advantageous for subsequent stages of information processing by reducing the variability of the signal that simplifies adaptation to novel conditions.

Improved Phoneme Discriminability in Reconstructed Speech.

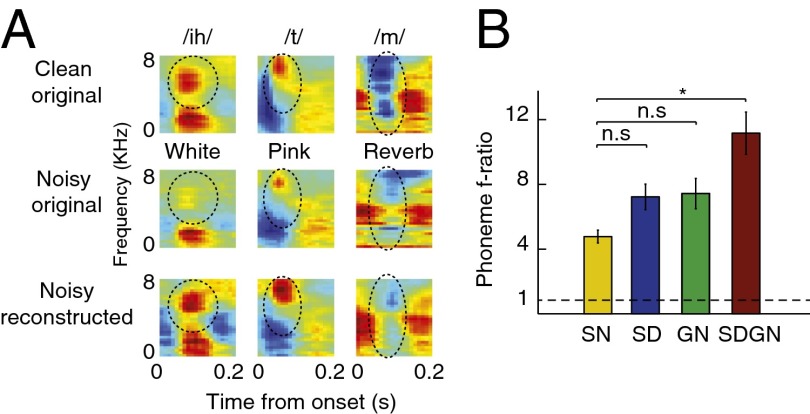
Phonemes are the smallest units of speech that can change meaning within a language (22). Their robust representations in neural data are therefore crucial for speech comprehension. As with other natural sounds, it is likely that basic neural mechanisms contribute to the stability and robustness of their representations in early stages of auditory processing (23). To examine the effect of distortions on phoneme category representation, we measured the mean phoneme spectrograms averaged over all of the instances of individual phonemes (24). Fig. 6A compares three examples of phoneme average spectrograms over clean speech, noisy speech, and reconstructions using neural responses to the noisy stimulus. The first example is a closed vowel /ih/, which is characterized by two separated spectral peaks (i.e., for[ant frequencies (22), with the second higher frequency peak circled]. As can be seen in the average spectrograms in white noise, the second formant is heavily masked by the background noise, but it is restored in the reconstructed spectrograms from the actual neural responses. The second example is a plosive phoneme (/t/), characterized by a silence gap followed by a high-frequency noise burst (22). This profile is diminished in additive pink noise, but is enhanced again in the reconstructed spectrograms from the neural responses (Fig. 6A, second column). Finally, the third example shows the spectrogram of the nasal /m/, which is characterized by reduced acoustic energy in middle to high frequencies (22). This specific profile is masked in reverberation (Fig. 6A, second row), but is restored in the reconstructed spectrogram (Fig. 6A, third row).

Fig. 6.

Difference between MSE distance of reconstructed spectrograms and original clean and noisy spectrograms. (A) Examples of average phoneme spectrograms in original clean, original noisy, and reconstructed noisy samples. Different distortions heavily mask the acoustic features of phonemes, such as second formant of vowel /ih/ in white noise (circled), spectral peak of plosive /t/ (circled), or midfrequency gap of nasal /m/ (circled). These features are highly restored in the reconstructed spectrograms from neural responses to distorted speech. (B) Phoneme separability index estimated from reconstructed spectrograms using SN, SD, GN, and SDGN predicted responses, showing a significant improvement in phoneme discriminability by SDGN model (*P < 0.05, t test).

To determine whether the models also enhance the essential acoustic characteristics of phonemes in distorted conditions, we used a phoneme separability analysis to compare the ratio of between-class to within-class variability of simulated responses to different phonemes (F statistics) (25). In this measure, a ratio of 1 indicates complete overlap between responses to different phonemes, whereas higher values imply better discriminability. We estimated this ratio across all phonemes for the reconstructed spectrograms from responses predicted by the SN, SD, GN, and SDGN models, as shown in Fig. 6B. Although neither the SD nor the GN model showed a significant improvement, the SDGN shows significantly better phoneme discriminability compared with the SN model (Fig. 6B, P < 0.05, t test, Bonferroni correction).

Discussion

We observed robust representation of natural vocalizations in the primary auditory cortex (A1) of ferrets even when stimuli were distorted by additive noise and reverberation. Despite substantial changes in neuronal activity at the single-cell level (4, 6), stimulus information encoded across the neural population remained remarkably stable across distorted stimulus conditions. This robustness was demonstrated by quantitative comparison of original clean spectrograms to reconstructions based on the neural population response to the distorted stimuli. In particular, spectral cues such as formants (e.g., the high-frequency peak of vowel /ih/) are enhanced in the reconstructions despite their weakness in the noisy spectrograms. Dynamic cues that are smoothed out by the reverberation (e.g., the midfrequency gap of the nasal /m/) are also well preserved in the population responses. This enhanced signal representation may explain the persistence of phoneme discriminability even under noisy conditions (16), and contribute to the overall representation of phonetic features in the auditory cortex (26).

A classic STRF model, consisting of linear spectrotemporal filtering followed by a static nonlinearity, cannot account for the observed noise suppression. Instead, we found that a dynamic nonlinear model is necessary, accounting for both feed-forward, subtractive synaptic depression (21, 27) and feedback, multiplicative gain normalization (14, 15, 28). Although the synaptic depression model alone can account partly for the suppression of additive noise, the combined depression/gain control model is necessary to replicate the neural data in more complex distortions such as reverberation. We found that although the interaction between neuronal tuning properties and the spectrotemporal profile of a distortion is an important factor in how the neuron’s response changes for distorted signals (6), the presence of a distortion in spectrograms reconstructed using the static STRF model (SN) (Fig. 5B) demonstrates that the observed enhancement of the stimuli in neural data cannot be explained exclusively by static, linear spectrotemporal filtering.

Our findings have important implications for theoretical models of optimality in neural coding. Encoding models derived in clean signal conditions may not be sufficient to account for the encoding of spectrotemporally rich signals in complex noisy environments. A previous study of A1 that focused only on the representation of clean speech did not identify a functional role for divisive normalization (21), but studies with other noise stimuli have suggested that it might play a role (28). More generally, the relevance of environmental noise is well established in studies of neurophysiology (4), psychoacoustics (16), and automatic speech processing (29). Similarly, our results demonstrate that characterizing the neural encoding of natural stimuli in multiple noisy conditions will be required to understand neural representations over their full dynamic range.

Limitations and Scope.

Although this study focused on the response properties of neurons in A1, mechanisms with functional properties similar to synaptic depression and gain normalization have also been reported in subcortical areas in the auditory pathway, including inferior colliculus (30), cochlear nucleus (31), and auditory nerve (32). These mechanisms are likely to contribute to the overall reduction of signal distortions in areas providing input to A1, and the nonlinear dynamic properties reported here are likely the combined effect of all these processes throughout the auditory pathway (33). Moreover, although the underlying signal enhancement mechanisms need not be the specific models of synaptic depression and gain normalization used in this study, they likely share functional and dynamic properties with the mechanisms we showed are able to effectively replicate the neural data. Therefore, we propose these mechanisms as plausible processes underlying the signal enhancement observed in the cortex.

One of the limitations of the present study is that behavioral data from the ferrets were not obtained to forge a link between neural activity and perception of signals in noise. Although we cannot conclude that the neurophysiological response properties we have described here are necessarily essential for behavior, several existing studies using synthetic stimuli (34) and speech (23) have demonstrated that ferrets and rodents are able to perceive target sounds in noisy conditions similar to those used in this study. The functional properties observed for speech and conspecific vocalizations in distorted conditions may reflect computational strategies used in these behaviors, and future studies that combine our unique computational approach and behavior paradigms promise valuable new insight into the general problem of identifying signals in the background of interfering sources (5). Although our focus in this study was to determine how different mechanisms contribute to the formation of the cortical representation under convolutive and additive distortions, a wider range of conditions is necessary to expand the findings and to determine how these mechanisms contribute to signal enhancement in various stationary, nonstationary, and, ultimately, competing vocalizations (35).

Methods

Single-unit neurophysiological activity was recorded from A1 of four head-restrained, quiescent adult female ferrets during passive listening to speech stimuli. The protocol for all surgical and experimental procedures was approved by the Institutional Animal Care and Use Committee at the University of Maryland and is consistent with National Institutes of Health Guidelines.

Neurophysiological Recording.

After implant surgery, animals were habituated to head restraint and to the recording setup over a period of several weeks before the onset of neurophysiological experiments. Experiments were conducted in a double-walled acoustic chamber (Industrial Acoustics). Small craniotomies (∼1–2 mm in diameter) exposing the dura were made over A1 before recording sessions. Electrophysiological signals were recorded using tungsten microelectrodes (2-8 MΩ; FHC) and were amplified and stored using an integrated data acquisition system (Alpha Omega).

At the beginning and end of each recording session, the craniotomy was thoroughly rinsed with sterile saline. At the end of a recording session, the craniotomy was filled with a silicone ear impression material (Gold Velvet II-Part Silicon Impression System, Precision Laboratories Inc.) that provided a tight seal in the well, thus protecting the craniotomy while the animals were returned to their home cages. Necessary steps were taken to ensure the sterility during all procedures.

Recording sites were verified as being in A1 based on their relatively narrow frequency tuning, short latency, and tonotopic organization. Spike sorting of the raw neural traces was completed off-line using a custom principal component analysis clustering algorithm (21). Our requirements for single-unit isolation of stable waveforms included that each unit be at least 80% isolated from other activity and that the waveform and spike shape remain stable throughout the experiment. We characterized isolation using a Gaussian noise model that quantified the overlap between individual waveforms and background hash. An isolation level of 80% indicates that 80% of the spikes are attributed to a single unit rather than the background noise.

Auditory Stimuli and Preprocessing.

Experiments and simulations described in this report used clean and distorted speech. Speech stimuli were phonetically transcribed continuous speech from the TIMIT database (36). Thirty different sentences (16-KHz sampling) spoken by 15 male and 15 female speakers were used to ensure a wide variety of voices and contexts. Vocalizations were recorded from ferret kits and adults using a digital recorder (44-KHz sampling) in a sound-attenuating chamber (IAC). Recordings spanned the range of vocalizations observed in the laboratory, including kit distress calls, adult play vocalizations, and adult aggression calls. Each sentence or vocalization was 3 s long plus a 1-s interstimulus interval. Stimuli were repeated five times during the neurophysiological recordings; therefore the entire stimulus period for a single condition (clean or distorted) was ∼600 s.

Three types of distortion were applied to the clean signals: additive white noise, additive pink noise, and convolutive reverberation. In the first two conditions, we added frozen noise (i.e., noise segments were the same in each presentation of the same speech token, but randomly generated for each speech sample), white noise at 0 dB, and pink (1/f noise) noise at 6 dB signal-to-noise ratio. In the third condition, we added reverberation to clean speech by convolving the samples with the simulated impulse response of a highly reverberant room (exponentially decaying random Gaussian noise, decay time constant = 300 ms). All sounds were played at 75 dB. These three types of distortion represent examples of noisy situations and contexts where human listeners exhibit robust speech recognition (29).

Because of experimental limitations, the number of neurons tested in each distortion condition for each ferret varied (white noise, total n = 91, 29–41 per animal; pink noise, total n = 101, 9–41 per animal; reverberation, total n = 97, 9–45 per animal). In all cases, responses were also obtained for the same neurons during presentation of the clean stimulus (speech or vocalizations).

For analysis, speech auditory spectrograms were generated from the sound waveforms using a bank of constant-Q band-pass filters, logarithmically spaced along spectral axis (30 channels, 125–8000 Hz) (37). Because of the logarithmic spacing of the frequency axis, white noise has greater relative power in the high-frequency bands, whereas pink noise with a 1/f spectrum looks flat on logarithmic scale (Fig. 2A).

Reconstructing Sound Spectrograms from Neural Responses.

Optimal prior reconstruction is a linear mapping between the response of a population of neurons and the original stimulus (17). In this method, the reconstruction filter, g(τ, f, n), is computed to map the neural population responses, R(t, n), back to the sound spectrogram, Ŝ(t, f):

where n indexes neurons. This function g(.) is estimated by minimizing the mean-squared error between actual and reconstructed stimulus (17).

Quantifying Reconstruction Accuracy.

To make unbiased measurements of the accuracy of the reconstruction, a subset of validation data (10%) was reserved from the data used for estimating the reconstruction filter. The estimated filter was used to reconstruct the stimulus in the validation dataset, and reconstruction accuracy was measured by the normalized MSE distance between the reconstructed and original stimulus spectrogram, averaged over frequency and time.

Phoneme Discriminability Index.

We measured a phoneme discriminability index (F statistics) that reflects both the representation similarity of instances of the same phoneme and the separation between different phoneme classes. This measure is defined as the ratio of between-phoneme to within-phoneme variability spectrogram representations, where ratios (ρ) larger than 1 imply less overlap between the representations of different phonemes.

Measurement of Spectrotemporal Receptive Fields.

We characterized each neuron by its STRF, estimated by normalized reverse correlation of the neuron’s response to the auditory spectrogram of the speech stimulus (10). Although methods such as normalized reverse correlation can produce unbiased STRF estimates in theory, practical implementation requires some form of regularization to prevent overfitting to noise along the low-variance dimensions. This in effect imposes a smoothness constraint on the STRF. Regression parameters were adjusted using a jackknife validation set to maximize the correlation between actual and predicted responses (10). The estimated STRF models were not optimized jointly with the addition of various nonlinearities, due to the limited amount of data available for fitting (38).

Simulation of Neural Responses With and Without Nonlinear Normalization.

We predicted the response of neurons to novel speech samples using their measured STRFs (10) (Eqs. 1 and 2). To study the effect of nonlinear mechanisms on noise robustness of neural responses, we extended the linear model by adding a subtractive model of SD (21), and a multiplicative model of GN (15) to the output of the linear model (Eq. 3 and Fig. 3A). W in Eqs. 4 and 5. is the Hann function, added to emphasize the most recent history of stimulus and response:

and τ is the same as the time constant used in A(t) and B(t) (τ_SD and τ_GN, respectively) and specifies the duration of the temporal integration window. The integration windows τ_SD and τ_GN were fit to the data (after first fitting the linear STRF and V_th), using cross-validation analysis (Fig. 3 B and C) to minimize the MSE between predicted and actual neural responses. Because synaptic depression only influences stimulus channels providing input to a neuron, we limited the stimulus integration region of the SD model, A(t), to the same spectral bands that modulated the neural responses, defined by the STRF of the neuron (8, 21). For the SD only model, we set B(t) = 1, and for the GN only model, we set A(t) = V_th. Computationally, the SD stage is a feed-forward computation that subtracts the short-term baseline of the stimulus. The GN stage, on the other hand, operates as a feedback and normalizes the short-term average of the predicted output.