A general method for diagonal peak suppression in homonuclear correlated NMR spectra by spatially and frequency selective pulses

Graphical abstract

Highlights

• •General method for the suppression of peaks along the diagonal for any homonuclear correlated spectra.
• •More reliable NOESY intensities due to the removal of artifacts from the huge diagonal peaks.
• •The overall appearance of the spectra is not changed.
• •Far less susceptible to magnetic field inhomogeneity in the z-direction by slice selective excitation.

Abstract

Homonuclear two- and multidimensional NMR spectra are standard experiments for the structure determination of small to medium-sized molecules. In the large majority of homonuclear correlated spectra the diagonal contains the most intense peaks. Cross-peaks near the diagonal could overlap with huge tails of diagonal peaks and can therefore be easily overlooked. Here we present a general method for the suppression of peaks along the diagonal in homonuclear correlated spectra. It is based on a spatially selective excitation followed by the suppression of magnetization which has not changed the frequency during the mixing process. In addition to the auto correlation removal, these experiments are also less affected by magnetic field inhomogeneities due to the slice selective excitation, which on the other side leads to a reduced intensity compared to regular homonuclear correlated spectra.

1. Introduction

In a typical 2D homonuclear correlated spectrum the diagonal contains the most intense peaks, although all the relevant information is contained in the cross peaks. These intense signals can obscure nearby cross peaks. Furthermore, the diagonal is often responsible for the so called t₁-noise, artifacts along the indirect dimension. Intense diagonal peaks also limit the dynamic range of the spectrometer, leading to a lower sensitivity of low intensity signals. The stronger the diagonal peaks in relation to the cross peaks are, the bigger are the problems they cause. In particular, NOESY-type spectra, where the intensity ratio of diagonal versus cross peaks is quite extreme, often suffer from strong diagonal peak artifacts which can easily obscure nearby cross peaks.

Several different strategies for diagonal peak suppression have been reported in the literature. The first approach is based on suppressing diagonal peaks by recording two spectra, a regular 2D spectrum and one containing only the diagonal [1,2]. The latter is obtained by setting the mixing time to zero. Subtraction of the diagonal-only spectrum from the regular one provides a diagonal-free spectrum. However, this approach only works if there is no significant relaxation during the mixing time and does not alleviate the t₁-noise or dynamic range problem since one still has to record datasets with a diagonal. In addition, by using this technique, the acquisition of two different comparable spectra requires a high accuracy of the parameter settings. Otherwise subtraction artifacts will lead to insufficient suppression of the diagonal [2–4]. The second method destroys the magnetization of the excited nucleus by a defocus, mixing, refocus sequence [5]. The mixing period is implemented between two 90° pulses. The magnetization of the excited nucleus, which has not been transferred during the mixing period, undergoes a 180° rotation. A last 90° pulse transfers this magnetization into the z-direction leading to no visible signal of the diagonal in the spectrum. This method leads to an unusual appearance of the 2D spectra, showing cross peaks on diagonals with a slope Δω₁/Δω₂ = 2. Another method, which has been used to suppress diagonal peaks in a NOESY spectrum uses a combination of two jump-and-return sequences before and after the mixing and a pulsed field gradient to suppress magnetization that evolved with the same frequencies before and after mixing [6]. By this approach the signal intensities in the 2D spectrum are modulated by a sheared sinusoidal profile with zero intensity on the diagonal as a result of the jump-and-return sequences. For multidimensional (3D and 4D) ¹⁵N-edited NOESY-type spectra the suppression of diagonal peaks has also been described by selecting only magnetization transfer pathways where the spin-state has been changed. This approach, which allows the observation of cross peaks underneath the diagonal, only works on TROSY-type spectra on proteins and for ¹⁵N-bound protons [7–13]. Especially for 3- and 4D NOESY type spectra diagonal peak suppression is very convenient as it makes the use of sparse data sampling techniques much easier due to a significant reduction of the spectral dynamic range [10,11].

2. Theory and methods

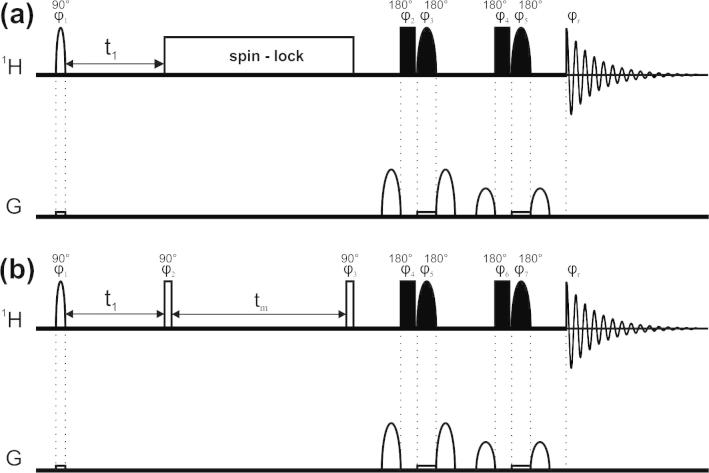
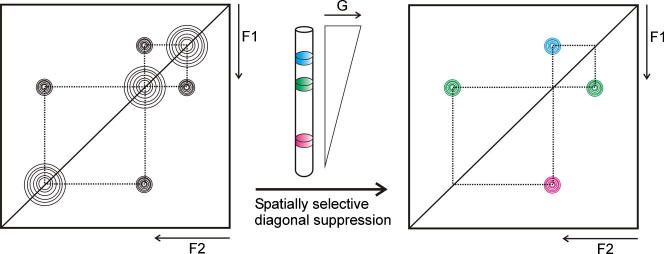
Here we present a completely different, generally applicable, approach for diagonal peak suppression in homonuclear two- and multidimensional spectra, which is based on transforming a homonuclear system into a spatially-separated heteronuclear system by using frequency-selective pulses during a weak field gradient [14–20]. To obtain a diagonal peak suppressed homonuclear 2D spectrum we use the pulse sequences shown in Fig. 1. A selective 90° pulse during a weak gradient excites different signals in different slices of the NMR sample tube. After the mixing period (shown for TOCSY and NOESY type spectra) the excited signals that did not change their frequency significantly during mixing (i.e. the diagonal peak signals but also any underlying or very close-by cross peaks) can be suppressed by using any signal/solvent suppression scheme, when applied during the same weak gradient field. For this purpose we used an excitation sculpting scheme (a combination of a hard and a selective 180° pulse sandwiched by two strong gradients) [21]. To increase the efficiency of the diagonal suppression this element was repeated with different purging gradient strength.

Fig. 1.

The pulse sequence of a diagonal suppressed TOCSY experiment is shown in (a). The slice-selective excitation is achieved by a 40 ms EBURP-2 pulse, applied during a weak magnetic field gradient (∼1 G/cm). After the evolution and TOCSY mixing, for which we used a 12.5 kHz DIPSI-2 sequence at 500 MHz, the originally excited magnetization, which would produce the diagonal peaks is suppressed by two consecutive excitation sculpting blocks. The latter contain 4 ms rectangular shaped selective 180° pulses during a field gradient which has the same strength of the one used during initial excitation. The following phase cycling was used for (a): φ₁ = x, −x; φ₂ = x, x, y, y; φ₃ = −x, −x, −y, −y; φ₄ = x, x, x, x, y, y, y, y; φ₅ = −x, −x, −x, −x, −y, −y, −y, −y; φ_r = x, −x, −x, x, −x, x, x, −x. The pulse sequence of a diagonal suppressed NOESY experiment is shown in (b). The selective 90° and 180° pulses are the same as in a. The phase cycle for (b) is: φ₁ = x, x, −x, −x; φ₂ = x; φ₃ = x, x, x, x, −x, −x, −x, −x, y, y, y, y, −y, −y, −y, −y; φ₄ = φ₆ = x, x, x, x, y, y, y, y; φ₅ = −x, −x, −x, −x, −y, −y, −y, −y; φ₇ = x, y; φ_r = x, −x, −x, x, x, −x,−x, x, y, −y, −y, y, y, −y, −y, y. 90° and 180° pulses are indicated by white and black bars, respectively.

The method of spatially dependent selective spin excitation in solution NMR has been used previously, for example for homonuclear broadband decoupling [14–18,20]. Because of the weak field gradient, the resonance frequencies of the NMR signals are shifted, depending on the position in the sample. The range of frequency shifts of these signals is given by

$$\mathrm{\Delta }\omega =sG\gamma$$ (1)

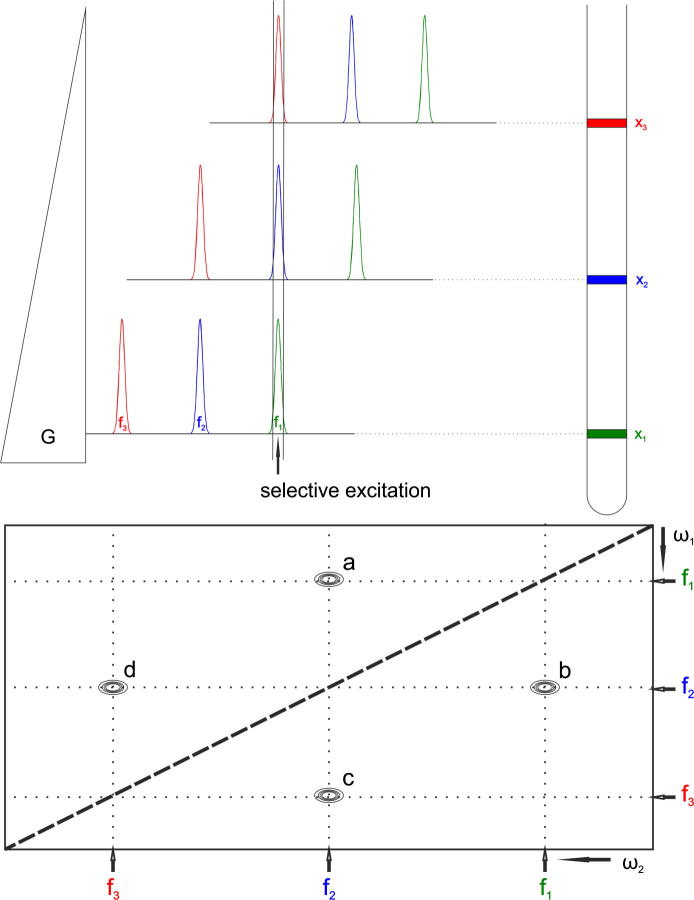
where G is the strength of the gradient, γ is the gyromagnetic ratio and s is the sample length to be measured, in our case about 1 cm. Therefore, if we want to use a selective pulse to excite a range of 10 ppm of a proton spectrum on a 500 MHz spectrometer we need at least a gradient strength of 1.2 G/cm. The spatial dependence of the resonance frequencies is shown in Fig. 2.

Fig. 2.

Top panel: The principle of the selective excitation during a weak field gradient: Small, continuous, variations of the magnetic field lead to a shifting of the spectrum. A selective pulse applied in the middle leads to the excitation of all resonances, but each signal is irradiated in a different slice of the sample tube. Bottom panel: A schematic example of a diagonal suppressed homonuclear 2D spectrum, where proton 2 correlates with proton 1 and 3, but 1 not directly with 3. Auto-correlation (diagonal) peaks are suppressed by using an excitation sculpting block on the signals that were originally, selectively excited in the same slice.

For a better understanding we illustrate the presented method by a hypothetical molecule. The molecule has three protons with different chemical shifts and only the proton with the resonance frequency f₂ shows a correlation to the other two protons 1 and 3 (Fig. 2), whereas 1 is not directly correlated with 3. In the slice x₁ the selective pulse only excites the nuclei with frequency f₁ (green¹), in x₂ only f₂ (blue) and in x₃ only f₃ (red). During t₁ the chemical shift in the indirect dimension evolves. If we stop the experiment here, Fourier transformation would yield a 2D spectrum where only the diagonal peaks are visible. During the mixing period, the magnetizations of the individual nuclei are partly transferred to their correlation partners. The polarization of f₂ is partly moved to the nuclei with f₁ and f₃. The magnetization at x₁ is transferred from protons with f₁ to protons with f₂ and at x₃ some magnetization is now at protons with f₂. If we would end the experiment at this point, the appearance of the resulting spectrum would be like a regular 2D spectrum including diagonal- and cross peaks. Subsequently, the magnetization which is on-resonance during the weak gradient field is destroyed by two excitation sculpting blocks. So, the part of the magnetization that is not transferred during the mixing sequence, and which produces the diagonal peak is removed right before the start of acquisition. The result is that in slice x₁ the only remaining magnetization is from protons with f₃ (peak a in Fig. 2). In slice x₂ protons with f₂ in the indirect dimension have remaining magnetizations of f₁ and f₃ (peaks b and c) and in slice x₃ protons with f₃ in t₁ have peaks at f₂ (peak d). Correlation peaks which are underneath the diagonal (from two correlated nuclei which happen to have the same chemical shift) are of course also suppressed by this method and cannot be observed. This spatially-selective approach for diagonal peak suppression can be applied to any kind of homonuclear two- (and multi-) dimensional NMR spectrum simply by replacing the first 90° excitation pulse by a selective one applied during a weak gradient and using an on-resonance signal suppression scheme right before acquisition, which is also applied during a weak gradient field. Due to the slice-selective excitation the sensitivity of the proposed scheme is reduced when compared to a regular 2D experiment. It is determined by the width of the excitation slice. The width of this slice is determined by the strength of the gradient (∼1–1.5 G/cm to excite all protons in the spectrum). We used typically a gradient of 1.5 G/cm, which covers ∼10 ppm ¹H frequency at 500 MHz. The width of the excited sample slice is also determined by the width of the excitation pulse. On the other hand the selectivity of the pulse determines how close signals can be to the diagonal to still be observable. However, if the pulse gets too selective, the excited sample slices gets smaller, which reduces the sensitivity. The thickness of the slice excited during the weak gradient corresponds to the ratio Δω_ex/Δω, with Δω_ex being the excitation bandwidth of the selective pulse and Δω the frequency shift range induced by the weak gradient in the detected sample volume length. Therefore, the reduction percentage in signal/noise Δ(S/N) of a spatially selectively excited spectrum compared to a regular one is given by

$$\mathrm{\Delta }\frac{S}{N}=\frac{\mathrm{\Delta }{\omega }_{\text{ex}}}{{\gamma }_{\mathit{GS}}}$$ (2)

The residual signal/noise ratio of a spatially selectively excited spectrum, relative to a regular one is shown as a function of gradient strength and excitation bandwidth in Supplementary Fig. S1. For the selective pulse it is also important that it does not produce excitation sidebands and gives little phase distortions across the excitation region. We obtained best results using an E-BURP2 shaped pulse [22] for excitation. As a compromise between selectivity and sensitivity we employed a 40 ms pulse. The selective 180° pulse used in the excitation sculpting blocks is less demanding as far as the excitation profile is concerned and we typically used a 4 ms square pulse. The longer this “purging” pulse is the sharper the region around the diagonal which is suppressed. However, this pulse cannot be made too selective due to diffusion between the excitation and the diagonal suppression. Diagonal peaks which are excited at the beginning in a very narrow slice then start to diffuse during the pulse sequence and it is important that the pulse used during the excitation sculpting block acts on all spins that were excited in a slice, including the ones that changed their location by diffusion. Therefore, the width of the suppressed diagonal can be made narrower for larger, more slowly diffusing molecules. In the case of negligible diffusion during the pulse-sequence (proteins and other large molecules) the bandwidth of the selective pulse used to suppress the diagonal peaks can be as narrow as the original excitation pulse. However, the purging pulse must not be more selective than the excitation pulse since this would lead to cancellation of diagonal peaks in slices narrower than the excitation slices and therefore reintroduce diagonal peaks from nearby sample tube regions. One nice feature, inherent to slice-selective excitation, is its insensitivity to poor shimming (magnetic field inhomogeneities) along the z-direction [23]. Therefore, the signals obtained in our diagonal-suppressed spectra are characterized by very narrow line-widths, even if the magnetic field is not very homogenous.

NOESY spectra of lysozyme were recorded on a Bruker AVANCE III 700 MHz NMR spectrometer using a 5 mm TCI cryo probe at 298 K. All other spectra were acquired on a Bruker AVANCE III 500 MHz spectrometer using a 5 mm TCI probe at 298 K. For all 2D experiments data matrices of 1024 × 128 complex data points were acquired and, after zero filling to twice the number of points, multiplied by a 60° phase-shifted squared sine-bell window function in both dimensions. The highly derivatized sugar methyl-4,6-O-benzylidene-2,3-O-ditosyl-α-glucopyranoside was obtained from Prof. Karl Dax at the Graz University of Technology. All other compounds were from Sigma Aldrich (St. Louis, USA) in the highest purity available.

3. Results and discussion

As test examples for the presented approach we acquired diagonal peak free TOCSY and NOESY spectra of a highly substituted monosaccharide (methyl-4,6-O-benzylidene-2,3-O-ditosyl-α-glucopyranoside [24]) dissolved in CDCl₃ as well as a diagonal-free NOESY spectrum of the protein lysozyme (14 kDa). In solution, methyl-4,6-O-benzylidene-2,3-O-ditosyl-α-glucopyranoside partly losses its benzylidene moiety and consists of an almost equimolar mixture of the fully protected and 4,6-deprotected form (Fig. 3).

Fig. 3.

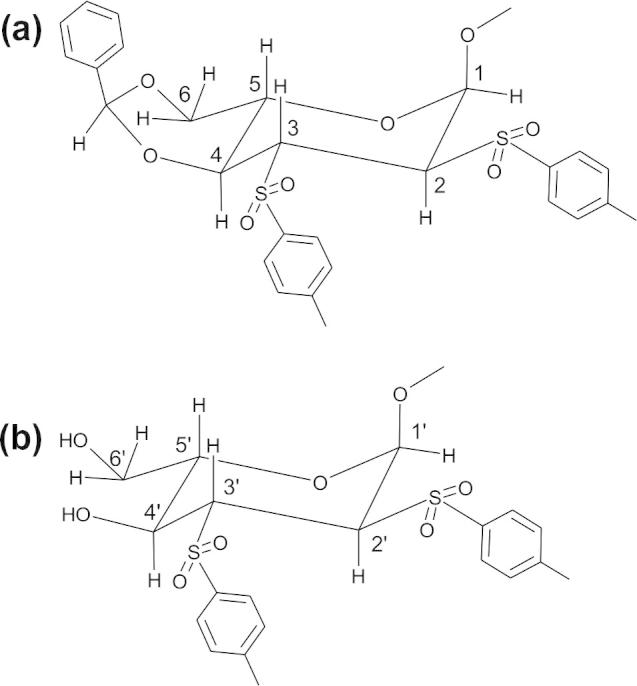
The chemical structures of (a) methyl-4,6-O-benzylidene-2,3-O-ditosyl-α-glucopyranoside and its degradation product (b) methyl-2,3-O-ditosyl-α-glucopyranoside.

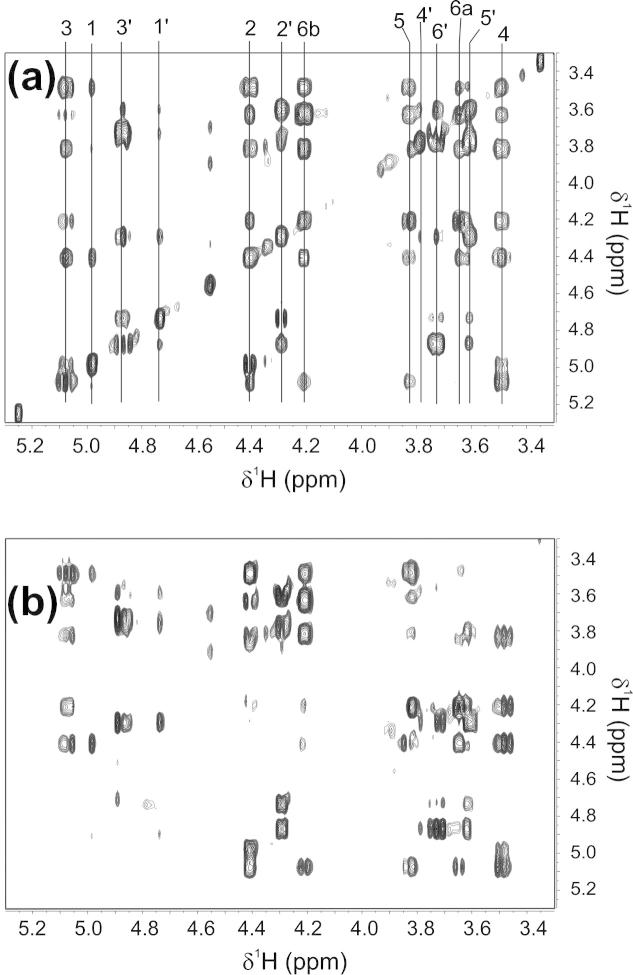
The regular TOCSY of methyl-4,6-O-benzylidene-2,3-O-ditosyl-α-glucopyranoside (60 mg dissolved in 600 μl CDCl₃) (Fig. 4a) was recorded with 8 scans and 16 were accumulated for the diagonal peak suppressed version (Fig. 4b).

Fig. 4.

Close-up views of the most crowded regions of a regular TOCSY (a) and diagonal suppressed version (b) of the derivatized glucopyranosides. The increased resolution of the diagonal-free spectrum, which results from it being less affected by magnetic field inhomogeneities can be seen for example by better resolved scalar couplings of the signal at 3.5 ppm. The assignment (see Fig. 3 for the labeling scheme) is indicated in the regular TOCSY spectrum.

Both spectra were recorded with a mixing time of 80 ms and 6000 Hz spectral width in both dimensions. All diagonal peaks are completely removed in the diagonal suppressed version while peaks close to it can still be observed. The width of the diagonal suppressed region depends on the selectivity of the pulse used for the excitation sculpting. In our case a 4 ms square pulse was employed but it should be changed to a longer, more selective pulse if signals even closer to the diagonal need to be observed. The lower sensitivity of the diagonal-free spectrum, which results from the slice selective excitation during the gradient can be somewhat compensated by increasing the receiver gain because of the absence of strong diagonal peaks. For molecules which require smaller spectral widths the strength of the weak gradient can be reduced which increases the signal/noise ratio. The higher resolution of the diagonal-free spectrum results from the better magnetic field homogeneity in the slices where the signals are detected [6] compared to the complete detected sample volume of a regular TOCSY.

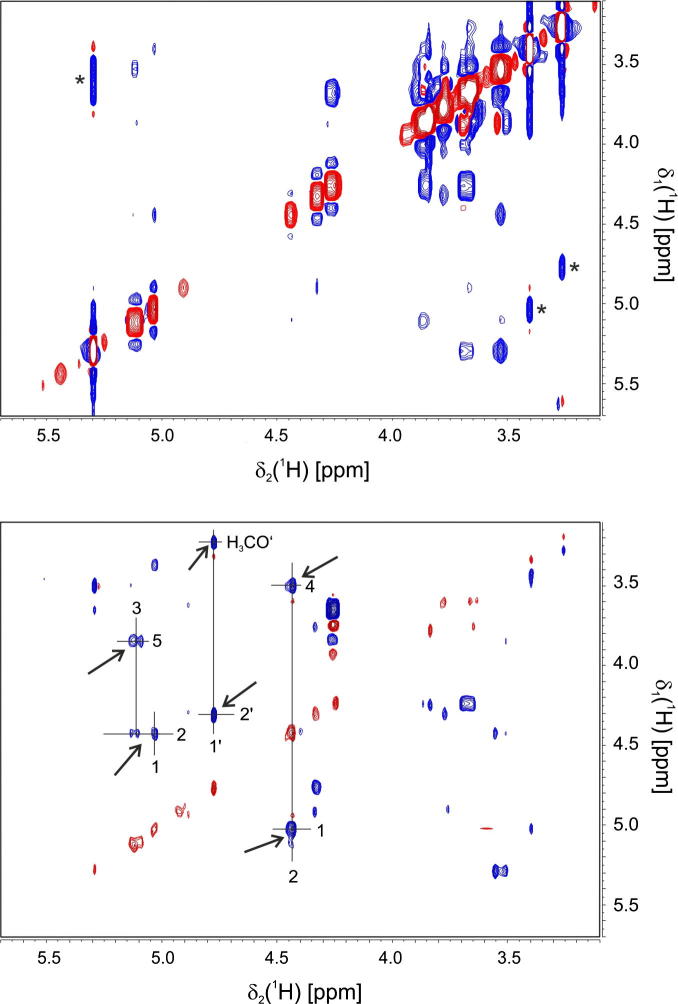
Artifacts from the diagonal are typically much more severe in NOESY type spectra. Especially the weak NOEs of small molecules (ωτ_c < 1) often lead to cross peaks which are hidden in the tails of huge nearby diagonal peaks. This can be seen in Fig. 5, which shows a close up of a regular (top) and diagonal peak suppressed 2D NOESY (bottom) of methyl-4,6-O-benzylidene-2,3-O-ditosyl-α-glucopyranoside with mixing times of 700 ms.

Fig. 5.

A close-up view of the most crowded region of a regular NOESY (top) and a diagonal-suppressed NOESY (bottom) spectrum of methyl-4,6-O-benzyliden-2,3-O-ditosyl-α-glucopyranoside. Positive and negative peaks are colored red and blue, respectively. Peaks that are made stronger by intense diagonal peaks are marked by asterisks. Signals which are more intense in the diagonal-free spectrum are assigned and indicated by arrows.

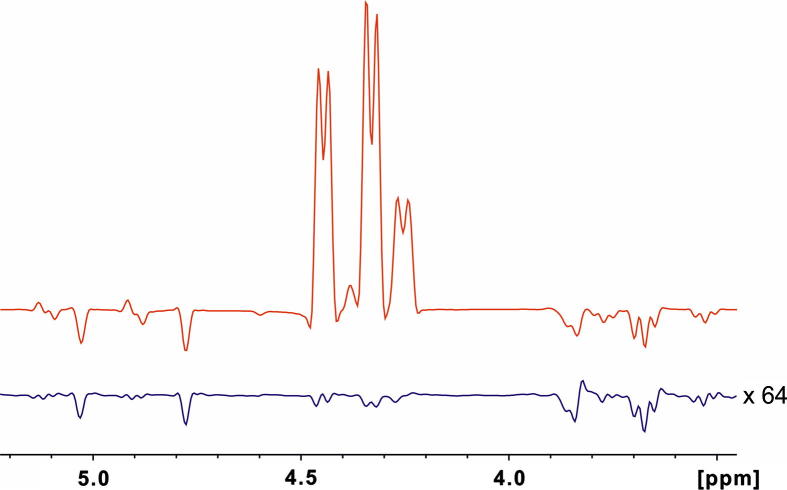
Positive and negative peaks are colored red and blue, respectively. Close to the diagonal it is difficult to differentiate artifacts from real peaks in the regular NOESY spectrum. This is most pronounced in the region between 3.1 and 3.8 ppm. Some peaks are visible only in the diagonal-free spectrum (indicated by arrows), while others are stronger in the regular NOESY (marked by asterisks). All peaks which are stronger in the regular NOESY correspond to signals that show strong diagonal peaks. On the other hand the peaks which are seen only in the diagonal free spectrum have relatively weak diagonal peaks in the regular NOESY spectrum. This is probably a result of the elevated baseline along the ω₁-direction. Cross peaks at the same ω₂-frequency of a strong diagonal peak appear stronger than they are. In the regular NOESY some of the very strong cross peaks have much weaker counterparts on their symmetrized position. In contrast, the diagonal suppressed NOESY shows cross peak intensities which are much more similar on both sides of the diagonal. To confirm that all peaks observed in the diagonal-free NOESY are actual NOE peaks and not artifacts, their assignment is indicated. They all correspond to proton pairs which are close in space, like axial protons on the same side of the glucose ring (2–4 and 3–5) or neighboring protons (1–2, 1′–2′). The regular NOESY experiment (Fig. 5a) was recorded with 32 scans per increment and the diagonal suppressed NOESY spectrum (Fig. 5b) by using 256 scans per increment and otherwise identical parameters. To experimentally determine the signal/noise changes of the regular versus the spatially-selective, diagonal-suppressed NOESY spectrum, representative traces at the frequency 4.3 ppm for two short NOESY spectra recorded with the same acquisition parameters (number of scans, increments, receiver gain, etc.) and processing scheme is shown in Fig. 6. As expected, for a selective pulse with an excitation bandwidth of ∼80 Hz and a 1.2 G/cm gradient the signal/noise ratio drops to about 2% of a regular NOESY spectrum.

Fig. 6.

Traces taken along the signals at ∼4.3 ppm in the indirect dimension of a short regular NOESY (red) and a diagonal suppressed version (blue) of the glucopyranosides with absolutely equal acquisition and processing parameters. The trace from the diagonal suppressed NOESY is multiplied by 64, showing the expected lower sensitivity of the slice-selective pulse sequence. For these comparative NOESY spectra 64 scans and 64 complex data points in the indirect dimension were recorded.

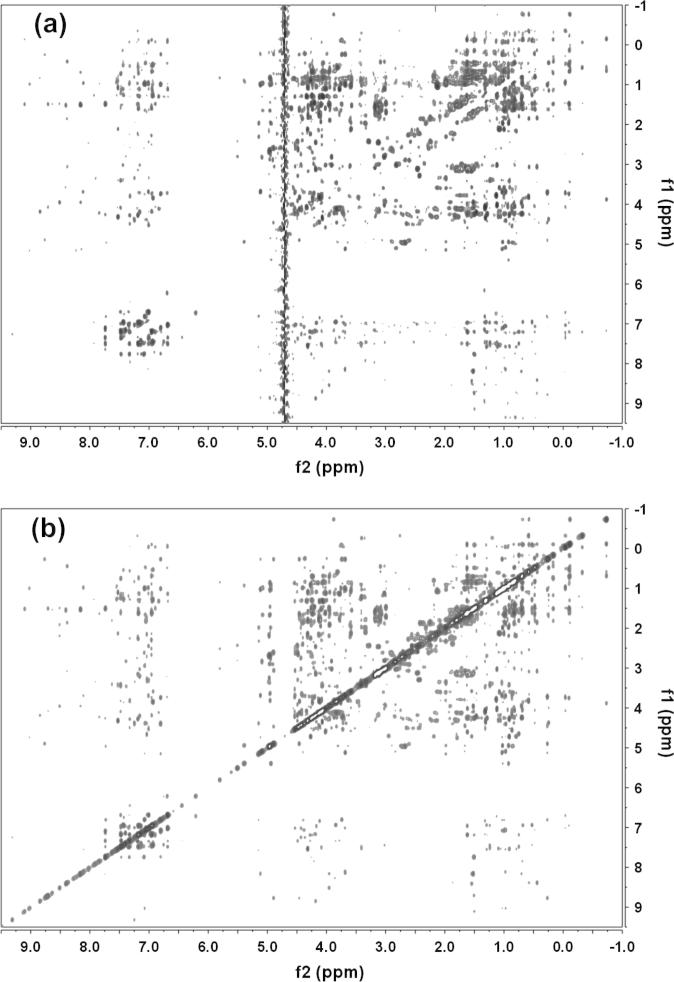
To evaluate the performance of the diagonal suppression scheme also on bigger, faster relaxing molecules, we acquired a diagonal suppressed NOESY spectrum of the 14 kDa protein lysozyme (3 mM) in D₂O solution. As can be seen in Fig. 7, the presented approach leads to a complete removal of all diagonal peaks, while the cross peaks are unaffected.

Fig. 7.

Diagonal-free (a) and regular NOESY (b) spectra of a 3 mM solution of lysozyme in D₂O. For both spectra 256 increments, with a spectral width of 8000 Hz were recorded. For the regular NOESY 64 scans were accumulated for each increment and 256 scans were used for the diagonal suppressed version. The mixing time was 150 ms.

Both spectra were recorded with a mixing time of 150 ms and 8000 Hz spectral width in both dimensions. Sixty-four scans were acquired for the regular NOESY and 512 for the diagonal free version. The total duration of the pulse-sequence of the presented approach is not much longer than a regular NOESY. Only the first pulse is now 40 ms instead of the hard pulse and the diagonal suppression is technically the same as the typical solvent suppression. Therefore, any additional relaxation losses of the diagonal-free spectrum, relative to the regular experiment, are minimal. When solvent suppression is needed in diagonal-free spectra, we use presaturation of the water signal before the first selective 90° pulse, rather than adding another excitation sculpting/watergate sequence prior to acquisition to keep relaxation losses to a minimum (see Supplementary Fig. S2).

4. Conclusions

We have presented a generally applicable approach to obtain diagonal peak free homonuclear correlated spectra. It relies on the slice selective excitation during a weak gradient field. Signals that do not change the frequency during the mixing are removed by excitation sculpting right before the acquisition. Due to this spatially selective excitation the magnetic field is very uniform for each signal and therefore cancels most of the magnetic field inhomogeneities along the z-direction. However, as a result, the sensitivity is reduced compared to a regular spectrum. To the best of our knowledge this is the first generally applicable diagonal peak suppression method which does not change the relative cross peak intensities or the appearance of the spectrum and does not rely on the subtraction of individual spectra.

Appendix A. Supplementary material

Supplementary data 1

Fig. S1. Signal/noise ratio of a spatially selective versus a regular NMR spectrum (in %) as a function of the excitation bandwidth Δω_ex and the strength of the applied weak gradient, shown as a 3D plot in (a) and a contour plot in (b) and Fig. S2. Two-dimensional diagonal suppressed (a) and regular (b) TOCSY spectra of a 6 mM solution of lysozyme in 90% H₂O/10% D₂O, 50 mM KPi pH 5.0. Water suppression was achieved by 1 s of presaturation at a power level of 250 Hz. Only 16 scans for each of the 64 increments were accumulated for both spectra, resulting in a diagonal suppressed spectrum showing only the strongest cross peaks. The intensity of the regular TOCSY was reduced by a factor of 64.