Prefailure and Failure Mechanics of the Porcine Ascending Thoracic Aorta: Experiments and a Multiscale Model

Short abstract

Ascending thoracic aortic aneurysms (ATAA) have a high propensity for dissection, which occurs when the hemodynamic load exceeds the mechanical strength of the aortic media. Despite our recognition of this essential fact, the complex architecture of the media has made a predictive model of medial failure—even in the relatively simple case of the healthy vessel—difficult to achieve. As a first step towards a general model of ATAA failure, we characterized the mechanical behavior of healthy ascending thoracic aorta (ATA) media using uniaxial stretch-to-failure in both circumferential (n = 11) and axial (n = 11) orientations and equibiaxial extensions (n = 9). Both experiments demonstrated anisotropy, with higher tensile strength in the circumferential direction (2510 ± 439.3 kPa) compared to the axial direction (750 ± 102.6 kPa) for the uniaxial tests, and a ratio of 1.44 between the peak circumferential and axial loads in equibiaxial extension. Uniaxial tests for both orientations showed macroscopic tissue failure at a stretch of 1.9. A multiscale computational model, consisting of a realistically aligned interconnected fiber network in parallel with a neo-Hookean solid, was used to describe the data; failure was modeled at the fiber level, with an individual fiber failing when stretched beyond a critical threshold. The best-fit model results were within the 95% confidence intervals for uniaxial and biaxial experiments, including both prefailure and failure, and were consistent with properties of the components of the ATA media.

Introduction

ATAA are dilatations of the arterial wall that result primarily from a weakening in the middle smooth muscle layer, or media, of the artery [1–3]. Aneurysm dissection and rupture pose serious risk of mortality and are the primary concerns for patients with an ATAA [1–4]. Cystic medial degeneration (which can be caused by disease, injury, or hereditary condition [2,3]), weakens the aortic wall, allowing for the formation of aneurysms and subsequent dissections. Aneurysm growth and dissection is further driven by increased hemodynamic loading within the media [5]. Ascending aortic dissection, the most prominent failure mode, occurs when the hemodynamic stresses within the media exceed the capacity of its collagen and elastin constituents allowing blood to pass into the medial lamella and peel it apart (delaminate) [6]. Ultimately, this tear can propagate axially along the length of the aorta, either proximally or distally, and in the absence of clinical intervention, may lead to further complications such as ischemia, aortic regurgitation, cardiac tamponade, aortic rupture, and death [1].

Ascending aortic aneurysms have an incidence rate of 10.4 per 100,000 person-years [7], with significant risk of dissection or rupture [7]. Clinically, ATAA management balances the risk of aneurysm rupture with the risk of surgery-related complications and death [2,3]. Risk of rupture is correlated with aneurysm diameter [2,7]; aneurysms greater than 6 cm in diameter exhibit a significantly higher risk of rupture [2]. Thus, for patients without valvular disorders, current guidelines indicate surgical intervention for ATAA diameters greater than 5.5 cm and monitoring for those less than 5.5 cm [2].

In spite of clinical guidelines and what is known about the pathogenesis of aneurysms, dissection and rupture occur in a significant number of patients whose aneurysms are less than 5.5 cm in diameter [8], suggesting that a better understanding of the dissection process is needed. Experimental studies have investigated the mechanical failure of aortic media [6,9,10], but only a few theoretical models have attempted to emulate this response [11–13]. The most notable work to date, by Gasser and Holzapfel [12], employs constitutive FE modeling with two independent continuous and cohesive zones to model the fiber network and ground matrix, respectively. While the Gasser–Holzapfel model is capable of describing the mechanical behavior of the aorta, it fails to capture complex fiber-fiber and fiber-matrix interactions or address failure at the microscopic scale. A model employing microscale mechanics and structure to determine the macroscale response would have potential to incorporate greater anatomical detail and could be applied to a broader range of conditions. This work represents an initial attempt to apply such multiscale concepts to the mechanics of the ATA.

The objectives of this study were (1) to characterize the prefailure and failure response of healthy porcine ascending aorta tissue under uniaxial and biaxial loading and (2) to describe that response with a multiscale, FE damage model. The model has been shown to be effective for prefailure and failure behavior of collagen gels [14] and has been applied to prefailure behavior of decellularized arterial wall [15].

Methods: Experiment

ATA from adolescent male swine (∼6 months old, 88 ± 11.5 kg) were collected following in vivo atrial ablation studies. Immediately upon harvesting, specimens were stored in 1% phosphate-buffered saline solution (PBS) at 4 °C overnight. All experiments were performed within 24 h of tissue dissection.

A ring from the ascending aorta was cut distal to the aortic valve and proximal to the brachiocephalic trunk (Fig. 1(a)). The ring was cut open at its superior edge to obtain a flat, rectangular tissue sample, and the intima, adipose tissue, and adventitia were removed (Fig. 1(b)). Then, the rectangular tissue specimen was cut into dog-bones (uniaxial) and/or cruciforms (biaxial), both axially and circumferentially aligned, for mechanical testing. Samples were immersed in 1% PBS at room temperature during mechanical testing. Verhoeff's stain was used to texture the luminal surface of the media for optical displacement mapping (Figs. 1(c) and 1(d)). Once prepared, the sample was subjected to uniaxial or biaxial testing.

Fig. 1.

(a) Porcine aortic arch. Black dotted lines demarcate ascending aortic ring. White star symbolizes a marker used to keep track of tissue sample orientation. (b) Ascending aortic ring with intima, adventitia, adipose, and loose connective tissue removed. Axial and circumferential directions shown with white arrows. (c) Undeformed, typical uniaxial sample in CIRC orientation with speckling prior to loading. Arrow indicates orientation and direction of pull. (d) Undeformed, typical biaxial sample with speckling prior to loading. Arrows indicate orientation and direction of pull.

Uniaxial Extension to Failure.

Rectangular tissue strips (∼20 mm × 5 mm) with the long axis in either the circumferential (CIRC) or axial (AXI) orientation were cut. A 5 mm circular biopsy punch was used to create a dog-bone shape (Fig. 1(c)). Several samples in both orientations were obtained from a single aorta. Images of each sample were taken to determine its initial unloaded dimensions.

Mechanical testing was conducted on a computer-controlled, uniaxial testing machine (MTS, Eden Prairie, MN). Samples were placed in a custom rig. Samples were extended at a rate of 3 mm/min until failure, and force was measured using a 5 N load cell. The deformation of the tissue’s luminal surface was recorded (∼157 pixels/mm) at a rate of one image per 5 s.

The force measured was divided by the undeformed cross-sectional area at the failure point in the neck in order to calculate the first Piola–Kirchhoff Stress. Image analysis and strain tracking was performed per our previous studies (e.g., Ref. [16]) to determine the local Green strain. Samples that did not fail in the neck region of the dog-bone (∼28% of samples) were not included in the analysis. Peak tensile stress was evaluated at the point of failure.

Equibiaxial Extension.

Biaxial samples were created by cutting a cruciform shape from an approximately square (∼20 × 20 mm) section of tissue such that the CIRC and AXI directions remained parallel to the arms. An unloaded biaxial sample is shown in Fig. 1(d).

The biaxial testing method was similar to that of previous studies (e.g., Ref. [16]) with a slight preload (∼0.1 N) applied to each cruciform arm. Samples were loaded onto a biaxial tester (Instron, Norwood, MA) with four 5 N load cells using a custom rig. Each sample was preconditioned with nine equibiaxial extensions to 40% grip strain. Following preconditioning, an experimental equibiaxial extension was performed at a strain rate of 3 mm/min to 40% grip strain, a subfailure load in contrast to the failure loading for uniaxial samples. During this extension, images of the tissue’s speckled luminal surface and the forces at each grip were recorded.

Again, local Green strain was determined using image analysis and strain tracking per our previous studies [16]. Forces in the axial and circumferential arms were divided by the respective undeformed cross-sectional areas in order to calculate the first Piola–Kirchhoff stress.

Methods: Model

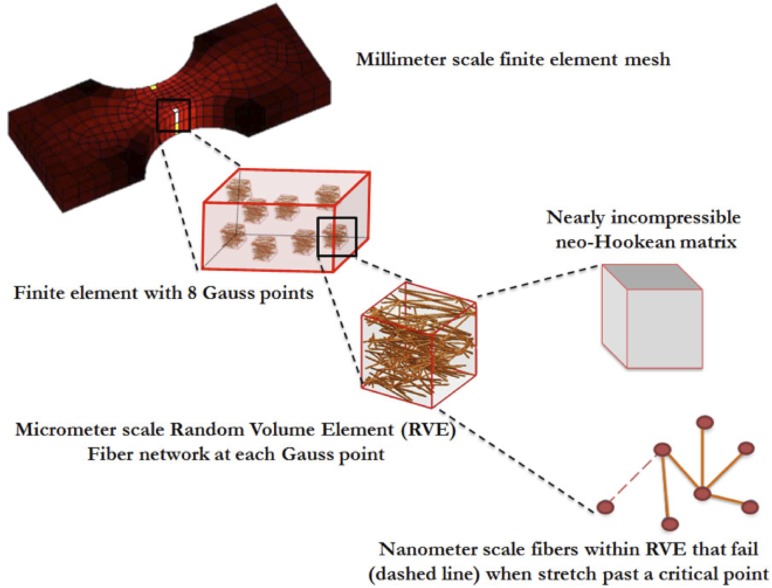
The multiscale model (Fig. 2, Refs. [14,15,17]) was made up of elements at three scales: the finite element (FE) domain at the millimeter (mm) scale, representative volume elements (RVE) at the micrometer (μm) scale, and the fibers with radii at the nanometer (nm) scale. Each FE element contained eight Gauss points, and each Gauss point was associated with an RVE. Each RVE was comprised of a discrete fiber network in parallel with a nearly incompressible neo-Hookean component to represent the nonfibrous material (matrix) [15]. The matrix and fiber network were functionally independent, with the sole exception that fiber network failure dictated simultaneous matrix failure. Stresses developed by the network and the matrix were additive (Table 1). Matrix material was considered homogenous throughout the model; however, each element was assigned a unique set of fiber networks, and new networks were generated for each iteration.

Fig. 2.

Synopsis of multiscale model. Uniaxial or biaxial geometries are developed into millimeter sized finite element meshes. Each element consists of eight Gauss points that dictate its stress-strain response. Each Gauss point consists of representative volume elements (RVE) that consist of a nanoscale fiber network in parallel with a nearly incompressible neo-Hookean matrix. Deformation of the macroscale structure causes the fiber network to stretch and reorient to reach force equilibrium. Fibers that stretch beyond a critical value are considered failed and their modulus of elasticity is reset to a near-zero value.

Table 1.

Governing equations applied within the model, as well as the scale at which each equation and its parameters are applied

Equation	Description	Scale	Parameters
${\sigma }_{ij,j}=\frac{1}{V}{\displaystyle {\oint }_{\partial V}({\sigma }_{\mathit{i}\mathit{j}}{}^L- {\sigma }_{\mathit{i}\mathit{j}})u_{k,i}{n}_{k}dS}$	Macroscale Volume-Averaged Stress Balance [16]	Tissue	σ: macroscale averaged Cauchy stress
			V: RVE volume
			σL: microscale stress
			u: RVE boundary displacement
n: normal vector to RVE boundary
${\sigma }_{\mathit{ij}}=\frac{1}{V}\int {\sigma }_{\mathit{ij}}^L\hspace{1em}\mathit{dV}=\frac{1}{V}\sum _{\mathit{bc}}{x}_i{f}_j$	Volume-Averaged Stress of RVE [16]	Network	bc: boundary for all RVE cross links
			x: boundary coordinate
f: force acting on boundary
$F_f=\frac{E_f{A}_f}{\mathrm{ß}}\left({\text{e}}^{\mathrm{ß}{\text{ε}}_{\text{G}}}-1\right)$	Fiber Constitutive Equation [15,17–19]	Fiber	Ff: fiber force
$\mathrm{and}\mathrm{\hspace{1em}}{E}_f\approx 0\mathrm{\hspace{1em}}\mathrm{when}\hspace{1em}{\lambda }_f>{\lambda }_{\mathrm{crit}}$			Ef: Young’s modulus of fiber at infinitesimal strain
			Af: fiber cross-sectional area
			εG: fiber Green strain
			ß: fitting parameter for fiber nonlinearity
			λf: fiber stretch
λ crit: fiber stretch at failure
${\sigma }_{\mathit{ij}}^m=\frac{G}{J}(B_{\mathit{ij}}-{\delta }_{\mathit{ij}})+\frac{2\mathit{Gv}}{J(1-2v)}{\delta }_{\mathit{ij}}\ln \left(J\right)$	Matrix Governing Equation [4]	Matrix	σM: matrix Cauchy stress
			G: shear modulus
			J: deformation tensor determinant
			B: left Cauchy–Green deformation tensor
$v$: Poisson’s ratio

The macroscale and microscale stress and strain were coupled as described previously [18], and the corresponding governing equations are outlined in Table 1. In brief, displacements applied to the macroscale model were passed down to individual RVEs. Pre-oriented Delaunay networks within the RVE stretched and rearranged in response to the displacements, generating net forces on the boundary network nodes. From these net forces, a volume-averaged stress was determined for each Gauss point within the element. The macroscopic displacement field was updated until the overall Cauchy stress balance was satisfied. Rigid boundary conditions were placed at the edges of the grip while the rest of the surface was free to move. Model simulations were run at the Minnesota Supercomputing Institute on 32-core parallel processors, with clock times averaging 4–6 h per simulation.

Model Specification and Parameter Estimation.

Table 2 summarizes the key parameters of the model. The orientation of the fiber network, which plays a critical role in the mechanical response, was described by an orientation tensor Ω. The components of Ω correspond to the degree of alignment in the coordinate directions, with the trace of Ω equal to 1 by construction (further details in Ref. [15]). Previous studies have shown that collagen fibers within the arterial media have strong preferential orientation in the circumferential direction (Ω_θθ) while some percentage of fibers are mainly oriented in the axial direction (Ω_zz) and even smaller percentage in the radial direction (Ω_rr) [19–23]. Based on those studies, the average orientation for collagen fiber networks in the media [Ω_θθ Ω_zz] was extrapolated to be [0.62 0.37] [20]. The initial network orientation tensor components [Ω_θθ Ω_zz Ω_rr] were, therefore, specified to be [0.6, 0.3, 0.1] ± [0.039, 0.040, 0.006]—an orientation state close to that measured in Ref. [20] and with a small amount of alignment in the r direction to maintain the integrity of the network. A single network was used to represent the combined contribution of the collagen and elastin components, with a volume fraction of 5% [15]. Fiber radius was set to 100 nm to replicate fiber geometry reported for elastic lamellae in arterial walls [24,25]. The matrix was modeled as nearly incompressible with a Poisson’s ratio, v, of 0.49.

Table 2.

Values for parameters used within the model, as well as justification for parameter values. The last four parameters in the table (shown in bold) were regressed to the combined uniaxial/biaxial data set.

Symbol	Description	Value	Justification
Ω	Network Orientation	Ωθθ = 0.6, Ωzz = 0.3	Extrapolated from structural histology [20]
Ωrr = 0.1
Af	Cross-sectional area	31,416 nm2	Elastin fiber radius 100 nm [24,25]
Φ	Fiber volume fraction	0.05	Based on Ref. [17]
ν	Poisson’s ratio	0.49	Nearly incompressible [15]
wu, lu, tu	Uniaxial undeformed dimensions	Width = 5.00 mm	Measured in experiment
		Length = 13.0 mm
Thickness: 1.5 mm
wb, lb, tu	Biaxial undeformed dimensions	Width = 6.00 mm	Measured in experiment
		Grip-to-Grip Length = 15.0 mm
Thickness: 1.5 mm
Ef	Fiber modulus of elasticity	2.51 MPa	Fit to data
λcrit	Lambda critical fiber failure	2.17	Fit to data
G	Matrix shear modulus	1.7 kPa	Fit to data
ß	Non-linearity fitting parameter	2.35	Fit to data

Four model parameters—fiber small-strain Young’s modulus E_f, critical fiber failure stretch λ_crit, matrix shear modulus G, and a nonlinear fitting parameter, ß—were regressed to the experimental data. The model was fit up to the maximum experimental stress, rupture and 40% strain, for uniaxial and biaxial experiments, respectively, while not including post rupture or unloading conditions. A value of 31.4 kPa was used as an initial guess and an upper bound for the matrix shear modulus based on the work of Holzapfel [26]. Fitted parameters were chosen to minimize the total sum of squared error between the model and experimental force curves for both the uniaxial and biaxial configurations. Both simulations were repeated for ten iterations. Each iteration used unique randomly selected networks that were generated using the same network criteria, Table 1.

Statistical Analysis

Unless otherwise specified, all p-values were calculated using unpaired two-tailed t-tests with Bonferroni correction and assuming equal variances (GraphPad Prism v. 5.03). A p-value less than 0.05 was deemed significant. All values are reported as mean ±95% confidence intervals.

Results

Uniaxial Extension to Failure.

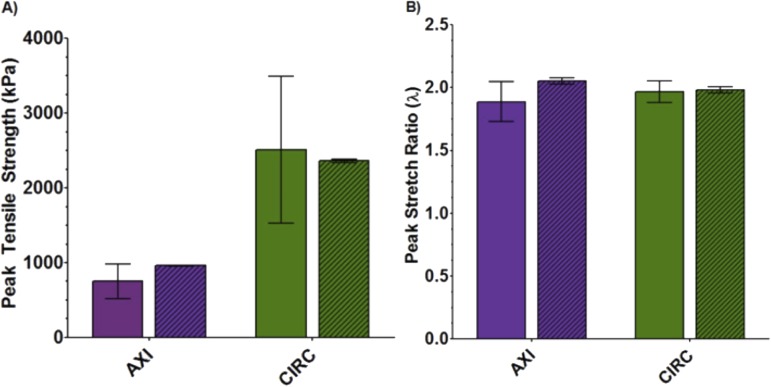
Uniaxial samples from both CIRC (n = 11) and AXI (n = 11) orientations were loaded to failure. The stress-strain response was nonlinear, characteristic of many tissues (Fig. 3) [27]. As expected, anisotropic behavior was observed in the tensile strength of the tissue. Peak stress was significantly (p < 0.001) higher in the CIRC versus AXI orientation (Fig. 4(a); 2510 ± 979 kPa versus 750 ± 228 kPa). Model simulation results showed similar anisotropy (p < 0.001) (Fig. 4(a); 2362 ± 10.3 kPa versus 958 ± 3.6 kPa) when using the parameters (Table 2) that were regressed to the combined uniaxial and biaxial data sets. In comparing experimental and model results, no statistically significant difference in the CIRC direction (p = 0.74) was observed. For the AXI direction, the tensile strength predicted by the model was within the 95% confidence interval for the experiments, but there was statistical significance (p = 0.046) due to the tighter confidence intervals for the model.

Fig. 3.

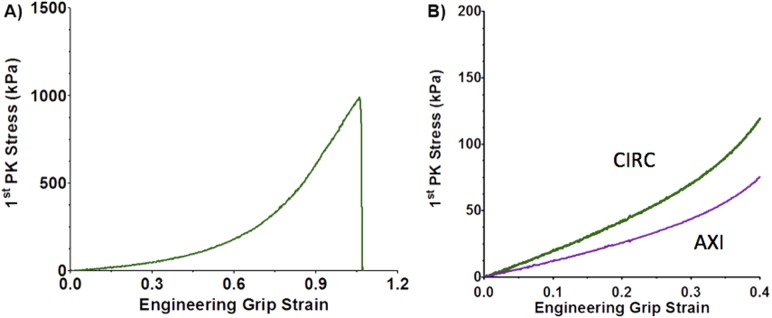
(a) Typical measured uniaxial grip stress versus grip strain response in the CIRC orientation. (b) Typical measured equibiaxial grip stresses versus grip strain.

Fig. 4.

(a) Peak tensile strength of ascending aortic samples for both uniaxial experiment (solid, n = 11) and model (diagonal lines, n = 10). (b) Peak stretch of ascending aortic samples for both uniaxial experiment (solid, n = 11) and model (diagonal lines, n = 10).

The media on the inner curvature of the arch is typically thicker than the outer [28], likely because the vessel remodels to balance the higher circumferential wall stresses caused by the curvature [29]. To verify that this remodeling does not affect the failure mechanics of the tissue, we compared the peak stress and strain of samples taken from the inner and outer curvature. Regional analysis found no significant difference in peak stress between uniaxial samples taken from the interior versus exterior of the aortic arch for either the CIRC or AXI orientations (p-values ranged form 0.10 to 0.28). No significant difference in peak stretch was observed between interior and exterior AXI uniaxial samples; however, a significant difference (p = 0.04) was observed for CIRC uniaxial samples. Samples near the exterior of the arch exhibited only 9.6% larger peak stretch than those from the interior.

No significant difference was noted in experimental peak stretch between the CIRC and AXI directions (Fig. 4(b); 1.99 ± 0.07 versus 1.92 ± 0.16, p = 0.36); however, model results between the two directions was significant (Fig. 4(b); 1.98 ± 0.003 versus 2.05 ± 0.003, p < 0.001). In comparing the experimental and model results, there was no statistically significant difference in peak stretch for either the CIRC (p = 0.74) or AXI (p = 0.07) orientation.

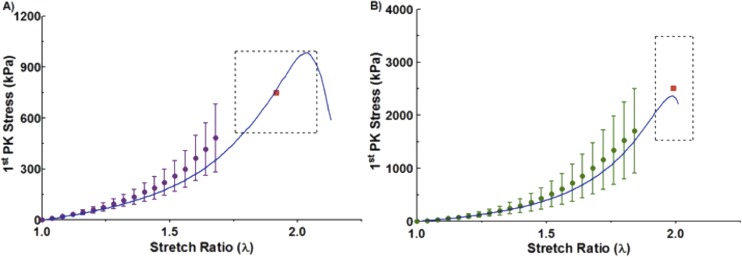
The averaged experimental stress-stretch curves for both the CIRC and AXI orientations are shown in Fig. 5 along with the best-fit model curves. The specified and regressed model parameters of Table 1 allowed the model to match the experimental prefailure and failure results to within the 95% confidence intervals for both orientations.

Fig. 5.

First Piola–Kirchhoff stress as a function of stretch ratio for the experiment (dots with 95% confidence interval) and model (solid blue line). Colored dots represent the mean experimental stress and error bars depict the 95% confidence interval. The red square indicates the mean peak tensile strength and stretch, and the surrounding dotted black box indicates the 95% confidence interval for the peak experimental stress and stretch with (a) being experimental and model results in the AXI orientation and (b) being experimental and model results in the CIRC orientation.

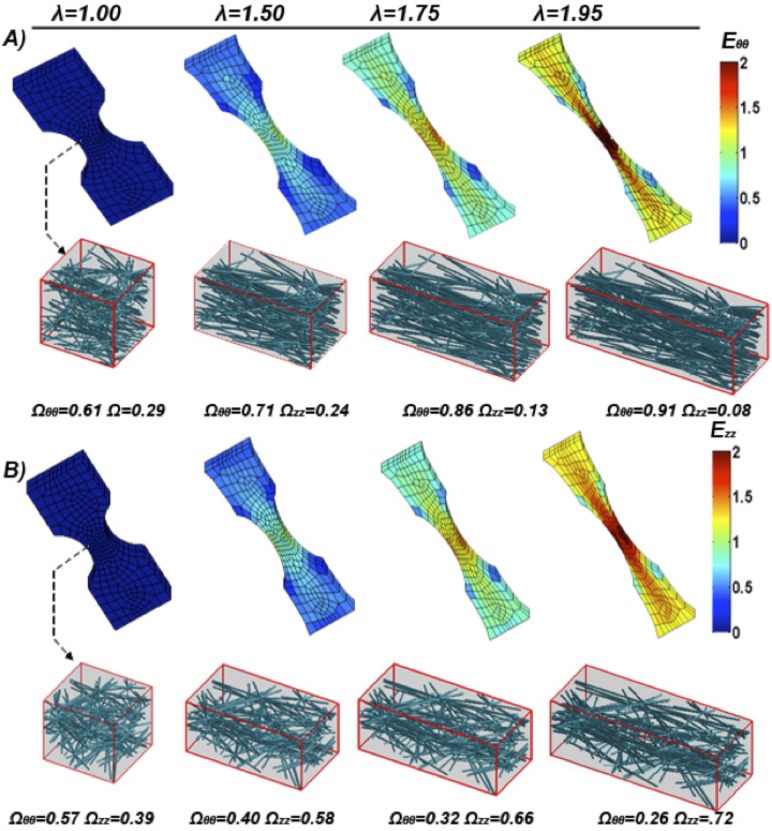
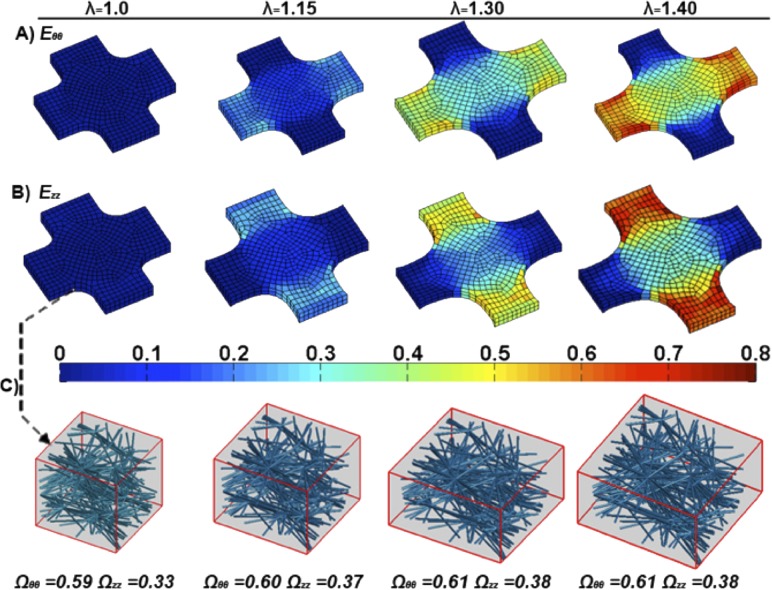
The neck region of the simulated uniaxial samples (both CIRC and AXI) experienced the largest strains and stresses (not shown), as expected, and also the largest degree of fiber reorientation (Figs. 6(a) and 6(b)). Fibers within the neck region were analyzed for their mean fiber orientation tensor Ω. As the simulated uniaxial sample is stretched, fiber alignment changes from its initial orientation tensor [Ω_θθ Ω_zz Ω_rr] ∼ [0.6 0.3 0.1] and steadily increases along the direction of stretch.

Fig. 6.

(a) Model circumferential Green strain E_θθ along the axis of pull plotted over the deformed model mesh at given sample stretches (λ). A representative neck region RVE network is shown and its corresponding fiber orientation tensor. (b) Model axial Green strain E_zz along the axis of pull plotted over the deformed model mesh at a given sample stretch (λ). A representative neck region RVE network is shown and its corresponding fiber orientation tensor.

Equibiaxial Extension.

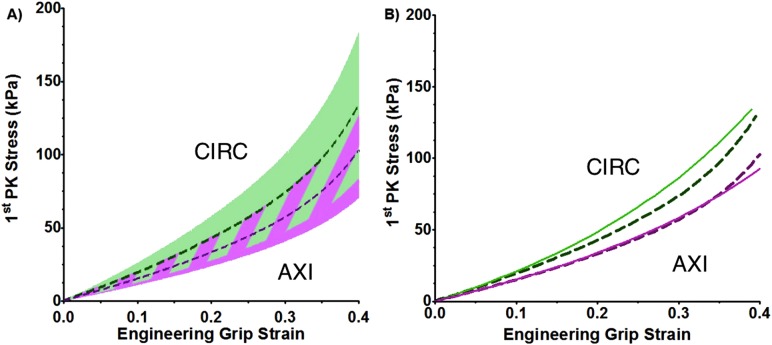
Biaxial samples (n = 9), as with uniaxial samples, exhibited a nonlinear stress-strain response, characteristic of biological tissues (Fig. 3(b)) [27]. As all samples exhibited similar nonlinear behavior, it is reasonable to consider the mean response (Fig. 7(a) dotted lines). The tissue showed similar directional dependence under equibiaxial loading as under uniaxial loading. At peak extension, the stress ratio (CIRC to AXI) was 1.44. The 95% confidence intervals for the two orientations overlapped each other (Fig. 7(a) shaded area).

Fig. 7.

(a) Mean first Piola–Kirchhoff stress as a function of grip strain for the biaxial experiment (dashed purple line for AXI and dashed green line for CIRC, n = 9) with 95% confidence interval (purple and green shaded areas, respectively). The striped shaded area represents overlap of the 95% confidence interval of the two orientations (p < 0.05). (b) Mean biaxial model first Piola–Kirchhoff stress as a function of grip strain (solid purple line for AXI and solid green line for CIRC, n = 10) compared to mean experimental results (dashed purple and green lines, respectively, n = 9).

The biaxial model (Fig. 7(b) solid line) was in good agreement with the experiments. Stresses in the CIRC direction were slightly overpredicted but remained well within the 95% confidence interval (Fig. 7(b)).

Similar to the uniaxial simulations, regions with higher strains had greater changes in fiber rotation and fiber stretch (Fig. 8). However, regions with the largest strain, the arms, are not the region of interest (Figs. 8(a) and 8(b)). Figure 8(c) depicts an element from the central region of the biaxial sample, showing the change in its fiber orientation. Even at 40% strain, in-plane fiber orientation of the elements in this region showed little change.

Fig. 8.

(a) Model equibiaxial Green strain E_θθ plotted over the deformed model mesh at various sample stretches (λ). (b) Model equibiaxial Green strain E_zz plotted over the deformed model mesh at various sample stretches (λ). (c) A sample center region RVE network is shown and its corresponding fiber orientation tensors for the stretches depicted in (a) and (b).

Fitted Model Parameters.

The model parameters (fiber small-strain Young’s modulus E_f = 2.51 MPa, critical fiber failure stretch λ_crit = 2.17, matrix shear modulus G = 1.7 kPa, and the nonlinear fitting parameter ß = 2.35) were regressed to the experimental data from both the uniaxial and biaxial experiments.

Discussion

This study investigated tensile properties of the porcine ascending thoracic aorta using uniaxial and biaxial extensions. Subsequently, we applied a multiscale model to emulate the ex vivo testing results. García-Herrera et al. [30] performed uniaxial tests using young (25 ± 3 years), healthy, human ascending aortic tissue and observed similar anisotropic behavior, peak stretch, and tensile values. Their reported values of 2180 ± 240 kPa for CIRC and 1140 ± 100 kPa for AXI [30] are similar to our reported tensile values (2510 ± 979 kPa and 750 ± 228 kPa for CIRC and AXI, respectively). Vorp et al., however, observed no significant difference in tensile strength between AXI and CIRC oriented human specimens [31], possibly due to older subjects (51 ± 6 years). Peak stretch at failure showed no significant difference between the CIRC and AXI cases and was similar to values reported by García-Herrera et al. [30] (2.35 ± 10 versus 2.00 ± 0.1 in CIRC and AXI, respectively) and to our values (1.92 ± 0.16 and 1.99 ± 0.07 for AXI and CIRC, respectively).

An equibiaxial study by Nicosia et al. [32] on healthy, porcine aortic root wall showed similar directional dependence with stresses at 30% strain, approximately equaling 50 kPa and 90 kPa in the AXI and CIRC directions, respectively, comparable to our results of 58.4 kPa and 76.2 kPa. Unlike the results presented by Nicosia et al., which remained linear up to 40% strain [32], our results were pronouncedly nonlinear. The experimental results are consistent with other studies [30–32]. Having confirmed that our experimental data are consistent with previous studies, we will focus on the model for the remainder of the discussion.

The advantage of a multiscale model is to link observed macroscale properties to changes in microscale structure (Table 1 and Fig. 2). The model was able to capture the anisotropic response in both the uniaxial and biaxial simulations, in agreement with our experimental results. It is important to note that our study, similar to other studies, is however limited in that physiological strain rates are higher than those used; thus, the model should be seen as approaching the quasi-static limit. The model demonstrated smaller confidence intervals (for both peak tensile strength and peak stretch) relative to experimental results, suggesting the method to model fiber failure could be modified to increase variance. Variance could be increased by using a stochastic element for fiber failure or introducing more variability in the model networks. A stochastic failure model would be consistent with the wide range of failure lengths seen for fibers such as collagen, where λ_crit can range from 1.2 to 1.7 [33].

In-plane fiber rotation (in the area of interest) was more prevalent in uniaxial than biaxial simulations (Figs. 6 and 8). Fibers in the uniaxial CIRC simulations were predominately aligned in the direction of pull and, therefore, could only stretch and not rotate at the onset of macroscale strain. Fibers in uniaxial AXI simulations were predominately aligned perpendicular to the direction of pull; therefore, when macroscale strain was applied, fibers first rotated and then extended. The rotation of fibers resulted in lower forces for the same amount of macroscale strain in uniaxial AXI results. The model permits for free rotation of fibers, which overestimates a fiber’s capacity to rotate, as in vivo obstacles such as neighboring fibers and matrix are not taken into account in fiber rotation.

An important simplification of the tissue microstructure in the model was that a single, idealized network of uniform-diameter fibers was employed in parallel with a neo-Hookean component to account for all structural contributions including collagen, elastin, extracellular matrix, cells, and interstitial fluid. Even with this simplification, the complex mechanical response was still captured by the model. We had expected the neo-Hookean component to dominate at low strain, representing elastin, while the fiber network would dominate at high strains, representing collagen. Therefore, initial model fiber parameters were chosen to simulate collagen, but those values led to vastly overpredicted forces (data not shown). When fiber model parameters were fit to the experimental data, the resulting values (Table 2) described the behavior of elastin more closely than collagen, suggesting that elastin plays a dominant role dictating behavior in the tissue. A previous study also indicated that intrinsic elastic properties dictate distensibility of the aorta [34]. In addition, a collagen-based fiber network would not be able to achieve a stretch of 2.0 since collagen fibers have a λ_crit closer to 1.4 [17], while elastin can reach stretches up to 3 [35]. Histological evidence supports a large elastin contribution as studies have shown more elastin than collagen exists in the ascending aorta (by dry weight 35% elastin, 22% collagen [19]). Hence, our fitted λ_crit value of 2.17 represents the combined effect of the two proteins. Our fitted value (2.51 MPa) of small strain Young’s modulus is within the range of values reported for elastin (estimated 0.3–10 MPa) in vessel walls [26,36,37].

We have investigated the biomechanical tensile properties of the aortic media in the circumferential and axial orientations, which are relevant to rupture of the vessel, but dissection of ATAA also depends on the strength of the tissue in the shear and radial tension [38]. Fitting the model to data from different experiments is an important test, and it will be valuable in the future to examine how the model behaves under different loading configurations (e.g., inflation, shear, peeling) that better represent failure as seen in ATAA and to determine whether the model can have predictive in addition to analytical value. To properly investigate the radial and shear loading conditions the simplified microstructural organization of this model will need to be revised/expanded. Currently, the model does not consider the concentric, circumferential layers of elastin, collagen, and smooth muscle, which form the medial lamellae [39]. Unlike the current study, which considers the failure of the fibers within the lamellae, a study with radial and shear loading would involve the failure of the connections between the lamellae. Therefore, the lamellae’s structure is an essential component in modeling dissection of ATAA, and a two fiber network model, similar to Lai et al. [14], that models collagen and the elastic lamellae separately could provide better insight.

In spite of the simplifications, the good agreement between the model and the experiment, for both prefailure and failure behavior in uniaxial and biaxial tests, indicates a high potential for use in the more complex geometry, architecture, and loading configuration that arise in ATAA.