Phenotypic switching in gene regulatory networks

Significance

Phenotypes of an isogenic cell population are determined by states of low and high gene expression. These are often associated with multiple steady states predicted by deterministic models of gene regulatory networks. Gene expression is, however, regulated via stochastic molecular interactions at transcriptional and translational levels. Here, we show that intrinsic noise can induce multimodality in a wide class of regulatory networks whose corresponding deterministic description lacks multistability, thus offering a plausible alternative mechanism for phenotypic switching without the need for ultrasensitivity or highly cooperative interactions. We derive a general analytical framework for quantifying this phenomenon, thereby elucidating how cells encode decisions, and how they retain memory of transient environmental signals, using common gene regulatory motifs.

Abstract

Noise in gene expression can lead to reversible phenotypic switching. Several experimental studies have shown that the abundance distributions of proteins in a population of isogenic cells may display multiple distinct maxima. Each of these maxima may be associated with a subpopulation of a particular phenotype, the quantification of which is important for understanding cellular decision-making. Here, we devise a methodology which allows us to quantify multimodal gene expression distributions and single-cell power spectra in gene regulatory networks. Extending the commonly used linear noise approximation, we rigorously show that, in the limit of slow promoter dynamics, these distributions can be systematically approximated as a mixture of Gaussian components in a wide class of networks. The resulting closed-form approximation provides a practical tool for studying complex nonlinear gene regulatory networks that have thus far been amenable only to stochastic simulation. We demonstrate the applicability of our approach in a number of genetic networks, uncovering previously unidentified dynamical characteristics associated with phenotypic switching. Specifically, we elucidate how the interplay of transcriptional and translational regulation can be exploited to control the multimodality of gene expression distributions in two-promoter networks. We demonstrate how phenotypic switching leads to birhythmical expression in a genetic oscillator, and to hysteresis in phenotypic induction, thus highlighting the ability of regulatory networks to retain memory.

An increasing number of single-cell experiments have been reporting bimodal gene expression distributions (1–3), providing evidence that gene regulatory interactions encode distinct phenotypes in isogenic cells. Cellular decision-making is undermined by epigenetic stochasticity, in that fluctuations allow cells to switch reversibly between distinct phenotypic states, as has been observed in bacteria (4), yeast (5), and cancer cells (6). It has been argued that such stochastic transitions in gene activity can affect stem cell lineage decisions (7, 8). Similarly, they may present advantageous strategies when cells make decisions in changing environments (9). Here, we develop a quantitative methodology which allows us to explore the implications of phenotypic switching, and the phenomena associated with it.

It is known that gene regulatory networks involving slow promoter switching may lead to distinct expression levels having significant lifetimes; hence, overall expression levels are characterized by bimodal distributions (10–12) or, more generally, by mixture distributions. However, it remains to be resolved how modeling can generally describe and parameterize these distributions. A positive resolution is crucial for the development of testable quantitative and predictive models, e.g., when investigating the sensitivity of bimodality against variation of model parameters, for estimating rate constants from experimentally measured distributions, in the design of synthetic circuitry with tunable gene expression profiles, but, most importantly, when determining the implications of phenotypic decision-making.

A class of theoretical models based on the Chemical Master Equation (CME) predicts bimodal protein distributions in the absence of bistability in the corresponding deterministic model (12, 13), some of which have been verified experimentally (1, 4, 14). Recent efforts to quantify this type of cell-to-cell variability have been limited to particular simple examples (8, 12, 13), which is mainly due to the difficulty of obtaining analytical solutions from the CME. It therefore remains unclear when bimodality is observed in more complex gene regulatory networks, and how the resulting phenotypic variability can be quantified.

The conventional linear noise approximation (LNA) of the CME represents a systematic and commonly used technique for the quantification of gene expression noise (15). Whereas the LNA is valid for many common biochemical systems, it fails to predict distributions with more than a single mode, as its solution is given by a multivariate Gaussian distribution which is strictly unimodal. The reason is that the implicit assumption underlying the LNA, namely, that all species are present in large molecule numbers, cannot be justified for general gene regulatory networks, because most genes occur in only one or two copies in living cells. Hence, the conventional LNA is too restrictive to describe distributions that are observed in gene regulation.

Here, we present a methodology which extends the range of validity of the LNA to gene regulatory networks that, in the absence of deterministic multistability, display more than a single mode in distribution. The underlying key idea is to treat promoter dynamics exactly using the CME, while approximating mRNA and protein distributions in the limit of large molecule numbers via a conditional LNA. The overall cell-to-cell variability can then be decomposed into individual Gaussian components, each of which is characterized by three quantities: the fractional lifetime of each state, as well as the mode and the width of each distribution component. Explicit (closed-form) expressions are presented here for all of these quantities.

Our approach thus allows us to explore phenomena accompanying multimodality that, to the authors' knowledge, could not be investigated previously. In the process, we identify a tradeoff between transcriptional and posttranscriptional control as being key for the regulation of phenotypic diversity. We analyze how slow noise in protein production rates can be integrated into digital responses by genetic oscillators including birhythmicity and all-or-none responses. In contrast with current thought (16), we demonstrate that bistability is not required for generating hysteretic responses in gene regulatory networks, and we identify an optimal time window for this effect to be observed.

Results

General Model Formulation.

We consider general gene regulatory networks which are composed of a number of promoters that can be in 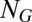states and a set of 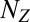corresponding gene expression product species. The overall state of the network is then described by the vector 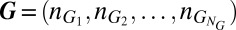, where 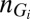denotes the number of promoters in state i, as well as by the vector of concentrations of gene expression products 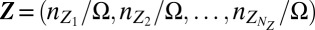, which comprises all RNA and protein species of interest; here, Ω is the cell volume. Assuming well-mixed conditions, the joint probability distribution 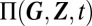is described by the CME (SI Appendix 2) for the regulatory network illustrated in Fig. 1. We assume promoter state transitions to occur either via unspecific effects such as chromatin remodeling or DNA looping, or via transcriptional regulation. Apart from transcription and translation, we allow for gene products to be involved in general posttranscriptional, posttranslational, as well as translational regulation.

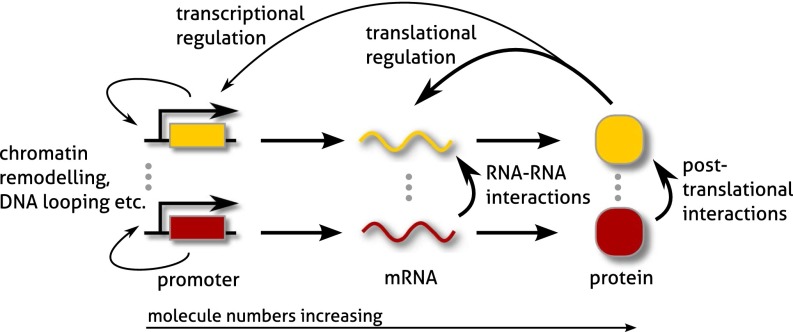
Fig. 1.

Modeling gene regulatory interactions. Representation of a regulatory network consisting of promoters from which mRNA is transcribed, followed by translation of protein in accordance with the central dogma. Each gene expression pathway involves reactions that modify gene expression products posttranscriptionally and posttranslationally, as well as regulatory interactions that change the promoter state such as chromatin remodeling or DNA looping. In addition, we consider upstream regulation via transcription factors (transcriptional feedback) or via RNA-binding proteins (translational feedback). We define a slow promoter network as one in which reactions that alter its state are less frequent (light arrows, slow) compared with ones that leave it unchanged (heavy arrows, fast). The separation of physiological abundances, with only one or two copies of each promoter per cell, but few to tens of mRNA and tens to thousands of protein molecules, is taken into account explicitly by the conditional LNA.

The above formulation involves two biochemical timescales of interest: those of reactions that change the promoter state, and those of reactions which involve only gene products. Specifically, it follows that, if the former reactions occur less frequently than the latter or vice versa, the timescales of promoter and gene product species must be well separated. In effect, the corresponding CME can be decomposed into an equation for the conditional fast species and one for the slow ones (17). Further, one can show (SI Appendix 4) that fast promoter dynamics implies unimodality in the absence of bistability. We derive a conditional LNA that predicts multimodal mixture distributions in the case of slow promoter dynamics. Later, we also demonstrate how this extended LNA can be applied to obtain estimates for gene expression distributions that are uniformly valid over all timescales.

Gene Expression Distributions from Slow Promoters.

Gene regulatory networks expressing more than a single phenotype can be characterized by mixture distributions (18). Intuitively, it might be expected that we can describe the probability distribution 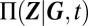, given a certain promoter state G, under the assumption that any reactions affecting promoters vary on a much slower timescale than those that affect only gene products. Averaging these conditional distributions over all possible promoter states then yields

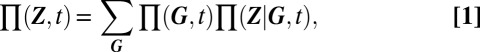as can be deduced using Bayes’ theorem. Qualitatively, we may associate (i) the set of the different modes of the mixture components with the set of distinguishable phenotypes, (ii) their relative weights with the probability for a given phenotype to be observed, and (iii) the spread of these components with the phenotypic variability.

Quantitatively, the question of when the mixture distribution 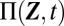is multimodal can only be answered once the components 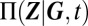and the associated weights 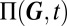in Eq. 1 have been derived from the CME; in practice, however, these cannot be evaluated in closed form. We address this issue by defining a systematic approximation procedure that makes use of the system size expansion for the gene expression products while retaining the discreteness of promoter states. In the limit of sufficiently large molecule numbers of gene products, these distributions can then be approximated via an LNA for the conditional variables of the CME (SI Appendix 3.2). We therefore introduce the ansatz

for the conditional LNA which, for each promoter state, separates the gene product concentration into its conditional average 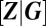and the fluctuations 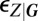about it. Similarly to the conventional LNA, the conditional averages in the above equation are determined from a set of conditional rate equations at quasisteady state,

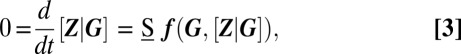where we only account for those reactions in Fig. 1 that affect gene products; moreover, because we assume that the latter are fast, we evaluate Eq. 3 at steady state. Here, 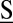denotes the corresponding stoichiometry, whereas 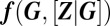are the associated rate functions, with the promoters being in state G.

A particular advantage of the above procedure is that it allows us to predict the relative weight of the mixture components in Eq. 1. These are given by the probability of the promoter state 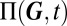, and determine the variability on the slow timescale. Specifically, under stationary conditions, they may be interpreted as the fractional lifetimes of a certain phenotype. The CME governing the slow promoter transitions can then be derived using the ansatz in 2 (see also SI Appendix 3.2), and is given by averaging over the fast conditional protein fluctuations:

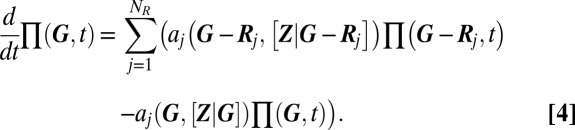Here, the vector 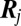represents the stoichiometry of the jth of 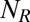slow promoter transitions for , whereas 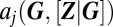is the associated propensity, where protein concentrations have been replaced by their conditional averages, as given by Eq. 3. The above CME can typically be solved in a straightforward manner, as (i) its state space is necessarily finite due to promoter conservation, (ii) it involves only linear reactions, and (iii) physiological copy numbers concern only one or two individual promoters. Specifically, for a single promoter with 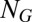internal states, the right-hand side of Eq. 4 reduces to 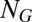linear rate equations, where the rates only depend on the conditional means of gene product concentrations from which a solution for multiple identical gene copies can be derived (SI Appendix 3.7).

The remaining quantity to be determined is the conditional distribution by means of the LNA of the CME. Recalling that reactions affecting the promoter state are slow, it can be shown (SI Appendix 3) that the conditional gene product distribution assumes a quasistationary state: 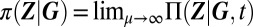, where μ is the ratio of slow and fast reaction timescales. We note that, in contrast with the case of fast promoter fluctuations, the above equation implies 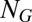conditional product distributions. It follows from the system size expansion that the conditional distribution 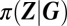is approximately Gaussian in the limit of sufficiently large molecule numbers of gene products (SI Appendix 3.2.1) and, hence, that the modes of the mixture components are given by the gene product concentrations about which the conditional distributions are centered:

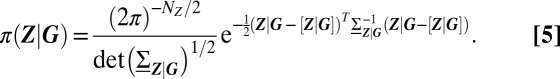In particular, the set of significantly different modes determines the set of distinguishable phenotypes that are expressed. By the Gaussian property, these are equal to the expectations of gene product concentrations 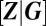, conditioned on the promoter state. The size of fluctuations and, ultimately, the form of the resulting conditional distributions, is determined by the conditional covariances 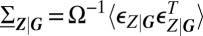, which satisfy the linear matrix equation 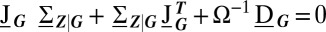. Here, 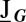is the Jacobian of the conditional rate equations, Eq. 3, expressed as function of G; similarly, 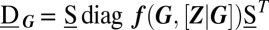. Specifically, the stationary covariance 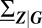is then a measure for the variability of each phenotype over short timescales.

In sum, the procedure outlined above thus yields closed-form expressions for (i) the component modes 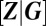that determine the set of observable phenotypes, (ii) the relative weights 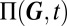in the mixture, which measure phenotype stability, and (iii) the covariance matrices 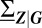of the conditional distributions that quantify the variability of each phenotype. The decomposition given by the solutions of Eqs. 3–5 fully determines the gene expression distribution in Eq. 1 and, hence, characterizes general gene regulatory networks that involve slow promoters.

Next, we demonstrate the utility of this conditional LNA for the quantification of multimodality by applying it to a number of exemplary gene regulatory networks. In the process, we elucidate several phenomena that are known to be induced by slow promoter fluctuations, but that are beyond the scope of standard solution techniques for the CME, or of the conventional LNA.

Binary Promoter Switching: Interpolation of Unimodal and Bimodal Distributions.

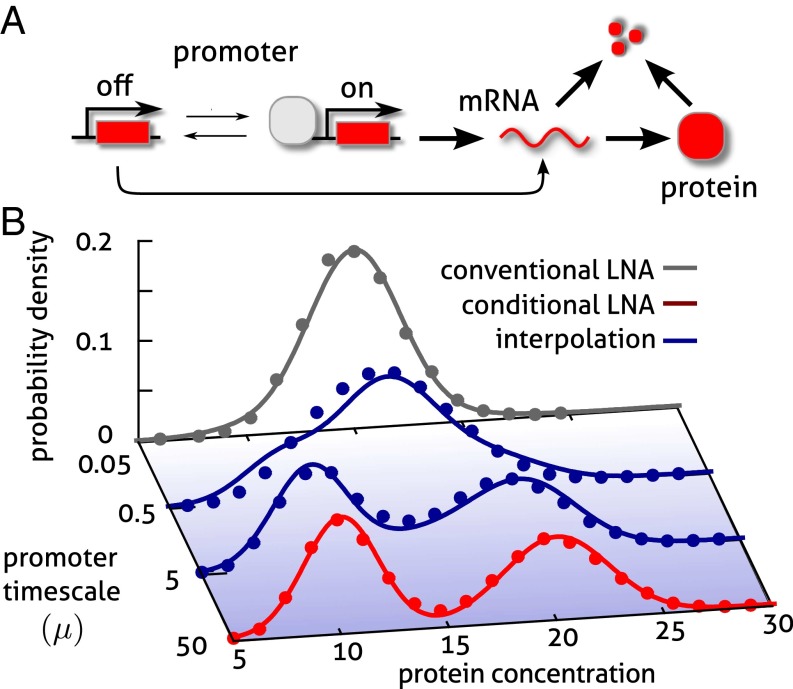
In eukaryotic gene regulation, the action of RNA polymerases and transcription factors (TFs) can be hindered by the fact that the chromatin structure is dynamic, rendering binding sites temporarily inaccessible (19). A recent study suggests that bimodal gene expression of the lactose operon of Escherichia coli relies on similar long-lived states, which, however, stem from TF-mediated looping of DNA (4). These additional promoter states can be described by a simple two-stage model of gene expression involving transcription from a promoter that fluctuates randomly between two different states of gene activity (Fig. 2A); see also refs. 10, 11, 19.

Fig. 2.

Binary promoter switching. (A) Gene expression from a single promoter switching between states of low or high activity. (B) The resulting gene product distributions show a strong dependence on the timescale of promoter switching (μ). For fast promoter fluctuations, the protein distribution is clearly Gaussian, and well predicted by the conventional LNA (solid gray). For slow fluctuations, however, the distribution displays two modes, corresponding to either state of promoter activity, and is well described by the conditional LNA (solid red). The intermediate regime for which protein lifetimes become comparable to switching frequency is approximated by the above interpolation formula (Eq. 6, solid blue); that formula is in good agreement with stochastic simulation of the full network via SSA (dotted) over the whole range of promoter timescales. Parameter values are given in SI Appendix, Table S1.

The limiting distributions for this simple model are shown in Fig. 2B for different values of promoter switching and protein lifetimes. For slow promoter fluctuations, one observes the characteristic bimodal distribution that results from the mixture of two Gaussian distributions, as predicted by our theory (solid red) derived in SI Appendix 3.4 and verified by stochastic simulation (dotted). For fast fluctuations, the distribution is clearly unimodal and follows closely the conventional LNA (solid gray). Subsequently, we assume that the intermediate regime in which there is no timescale separation can be fit by an interpolation formula between the solution of the conventional LNA 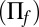and that of the conditional LNA ,

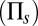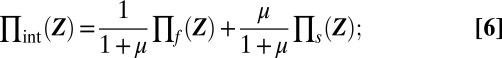here, we have defined μ as the ratio of protein degradation and the sum of promoter off rates and on rates. The overall good accuracy of this interpolation (solid blue), including the case where promoter switching and protein lifetimes are of the same order, is encouraging (Fig. 2B). The conditional LNA thus represents a simple tool for predicting the modality of gene product distributions in gene regulatory networks over broad ranges of timescale separation.

Global Control of Gene Expression Promotes Multimodality.

During the development of hematopoietic stem cells, the two antagonistic TFs Gata and Pu are responsible for the erythroid-myeloid lineage decision. The underlying two-gene regulatory motif consisting of two mutually repressing genes represents a toggle switch (20) and has been shown to exhibit multimodal protein distributions, including committed and primed states in cell differentiation, even in the absence of cooperative binding (8). Here, we study how fine-tuning of this transcriptional response can be achieved through translational feedback control. We model the latter by inhibition of target mRNA (shown in yellow in Fig. 3A) by the repressor protein (shown in red), which is actively degraded upon binding.

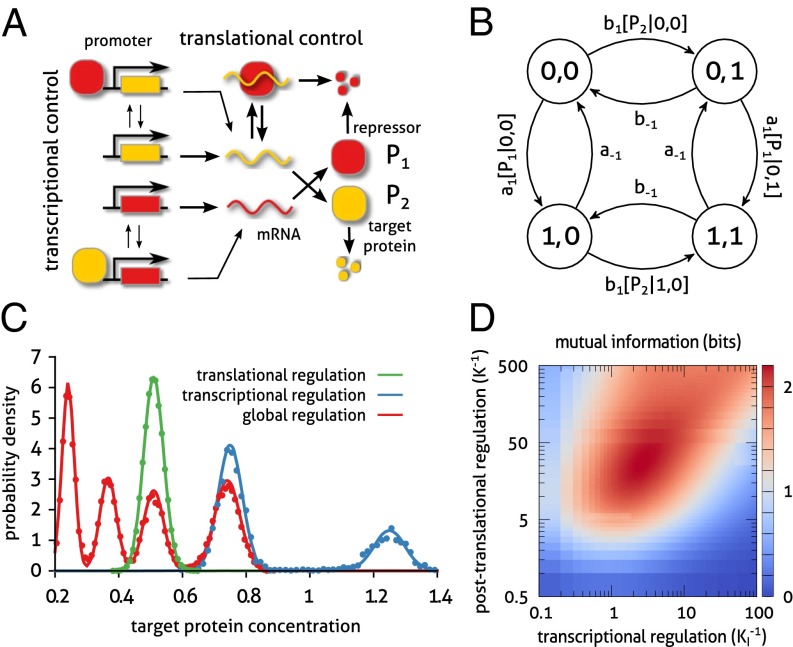
Fig. 3.

Global control of gene expression promotes multimodality. (A) Noncooperative transcriptional regulation of two mutually repressing promoters including translational regulation which is mediated by binding of the repressor protein (red) to the mRNA species of the target protein (yellow). (B) The transition graph of the CME for the two-promoter network derived from Eq. 4 contains four slow states: (0,0) – no TF bound; (1,0) – repressor 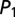bound; (0,1) – target 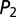bound; and (1,1) – both TFs bound. The parameters 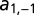and 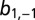correspond to the rate constants of DNA binding and unbinding of repressor and target proteins, respectively. (C) We compare the effect of exclusive translational (green), exclusive transcriptional (blue), and global control (red) on the modality of the target protein distributions: the conditional LNA (solid) predicts that these are uni-, bi-, and tetramodal, respectively, which is in excellent agreement with stochastic simulation of the full network via SSA (dotted). (D) We analyze the mutual information shared between repressor and target proteins (as a measure of regulation), calculated from the conditional LNA as a function of the inverse promoter binding constant (K) and the inverse mRNA inhibition constant 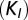. We find that optimization of the mutual information is a tradeoff between both types of regulation (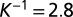, , 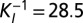2 bits of information). The optimal target protein distribution corresponds to (B, red). Parameter values are given in SI Appendix, Table S2.

We compare the corresponding probability distributions in three regimes: (i) exclusive translational regulation, (ii) exclusive transcriptional regulation, and (iii) both transcriptional and translational regulation, which we term global control. The CME derived from Eq. 4 describing the slow switching of both promoters is given by a Markov chain with four states (Fig. 3B) and is analytically tractable (SI Appendix 5.1). We now discuss the qualitatively different solutions that are obtained in the three regimes. In regime (i), i.e., with translational control 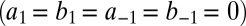, we expect unimodality, as posttranscriptional regulation does not affect promoter activity (Fig. 3C, green). In regime (ii), with transcriptional control, we have 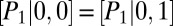and 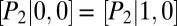; hence, the transition graph (Fig. 3B) shows that promoter binding occurs independently for the two proteins. We observe a bimodal protein distribution that is characteristic of a toggle switch (Fig. 3C, blue). Finally, in regime (iii), we have 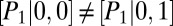and 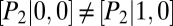due to global control, which implies that repressor binding changes the rate of target protein binding (and vice versa) and, hence, that regulation is allosteric. We note that such regulation can also be achieved for promoters positioned at distant loci on the chromosome. In the latter case, we observe up to four modes in the target protein distribution (Fig. 3C, red), each corresponding to a combinatorial state of the two promoters. We emphasize that our conditional LNA correctly predicts all three regimes, as well as that it contains the conventional LNA (Fig. 3C, green) as a special case.

Thus, we have shown that allosteric regulation of two-gene networks can be achieved through a combination of both slow transcriptional and fast translational regulation. Next, we investigate if there exists an optimum for which the gene expression products are highly regulated. To that end, we calculate the mutual information of the two protein species as a measure of regulation strength. The mutual information can be readily found from the explicit form of the probability distribution, as predicted by the conditional LNA (SI Appendix 5.1); its use is motivated by the belief that, in highly regulated systems, there is a high degree of statistical dependence between the two protein species. However, for the case of the globally regulated circuit, both types of regulation contribute to the overall promoter state for the mutual information at its optimum (Fig. 3D), as can be seen from the transition graph (Fig. 3B). The target protein distribution resulting from optimal regulation is displayed in Fig. 3C. Specifically, as the protein species share roughly two bits of information at that optimum, we are able to distinguish all four different phenotypes among a cell population. As we have demonstrated, this diversity cannot be realized by transcriptional or translational regulation alone, but rather through an allosteric effect induced by global control.

Birhythmicity in the Expression of a Genetic Oscillator.

Many physiological properties are encapsulated in the dynamics of gene regulatory networks. In human cancer cells, the response of the p53-Mdm2 feedback loop to irradiation is binary, with some cells displaying noisy oscillations, whereas others show no rhythmic expression (21). Here, we explore the possibility that similar responses can be induced by a stochastic phenotypic switch based on a negative feedback network whose deterministic counterpart exhibits neither oscillatory nor bistable behavior. In particular, using analytical expressions for the power spectra characterizing stochastic oscillations (SI Appendix 3.6), we demonstrate how slow promoter fluctuations can induce birhythmicity or phenotypic switching between oscillatory and steady-state expression levels.

We consider the binary expression of a regulatory protein due to DNA damage and repair under weak irradiation conditions. The protein activates a kinase of an ultrasensitive signaling cascade that is composed of two reversible phosphorylation modules (Fig. 4A). The phosphorylated kinase in the second module, which is considered the output of the system, also down-regulates gene expression through negative feedback and, hence, induces oscillatory dynamics.

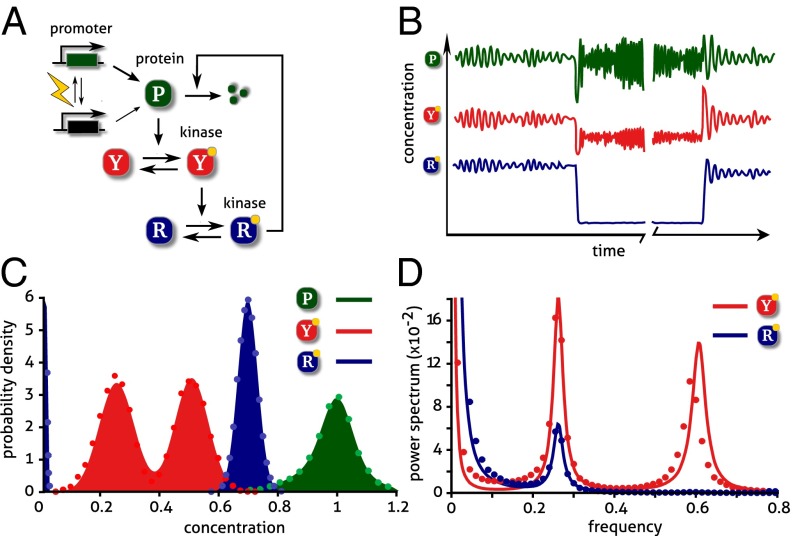
Fig. 4.

Birhythmicity in the expression of a genetic oscillator. (A) Binary expression of a protein P that activates a kinase of an ultrasensitive signaling cascade involving kinases Y and R. The latter also down-regulates gene expression through negative feedback, causing the expression levels of all involved proteins to oscillate. Promoter switching is caused by DNA damage and repair triggered by weak irradiation. (B) Sample paths for all protein concentrations from stochastic simulation are shown for DNA damage and repair events. We observe that the oscillation baseline of P (blue) displays only little variation over large variations in the oscillator period. By contrast, the binary behavior of the oscillation baseline is amplified downstream in the ultrasensitive cascade, leading to switching between oscillatory and silent oscillator modes (blue). (C) Baseline variations are quantified by probability distributions which discriminate well the binary switch in the oscillator output (R, blue) that is not present in the input distribution (P, green; concentration scaled by a factor of 2). (D) We analyze the power spectra of both kinases, observing birhythmic behavior in Y (red), but only a single frequency in R (blue), the oscillator output, which demonstrates the amplification of the all-or-none response. We note the increase at low frequencies, which is a reminiscence of phenotypic switching over long timescales. Our theoretical predictions for the distributions and power spectra (solid) agree well with stochastic simulation of the full network via SSA (dotted). Parameter values are given in SI Appendix, Table S3.

Comparing the oscillatory time courses for all three components, as obtained using the stochastic simulation algorithm (SSA), we find that the regulatory protein and the two signaling proteins display binary variation in their oscillation baseline and period (Fig. 4B). Specifically, the baselines of the protein expression levels are indistinguishable in both the on state and the off state, whereas those of the signaling proteins show significant variation. This amplification is due to the high sensitivity of the signaling module to protein variation, which is well represented by the distributions of signaling proteins displaying two modes (Fig. 4C).

However, these stationary distributions cannot capture the period variability that is observed in the oscillatory time series (Fig. 4B); the latter are quantitatively better described by the corresponding power spectra, which can be derived in closed form using the conditional LNA (SI Appendix 5.2). The birhythmicity of the first signaling protein is well captured by the predicted power spectrum (Fig. 4D), which shows two distinct frequencies. Instead, in the output of the signaling cascade, we observe only a single frequency, which is due to ultrasensitivity almost fully depleting the off state, as can be seen by the large component near zero in distribution (Fig. 4C). These findings are confirmed by stochastic simulation, via SSA, of the full network (Fig. 4 C and D, dotted). Remarkably, for a variant of this circuit with two gene copies, our theory predicts an additional rhythm that does not correspond to those of any of the individual promoter states, but that arises as an emergent property of the mixture (SI Appendix, Fig. S3). We hence conclude that slow gene expression noise, amplified by ultrasensitive pathways, can drastically change the dynamics of intracellular networks.

Phenotype Induction: Transient Bimodality and Hysteresis.

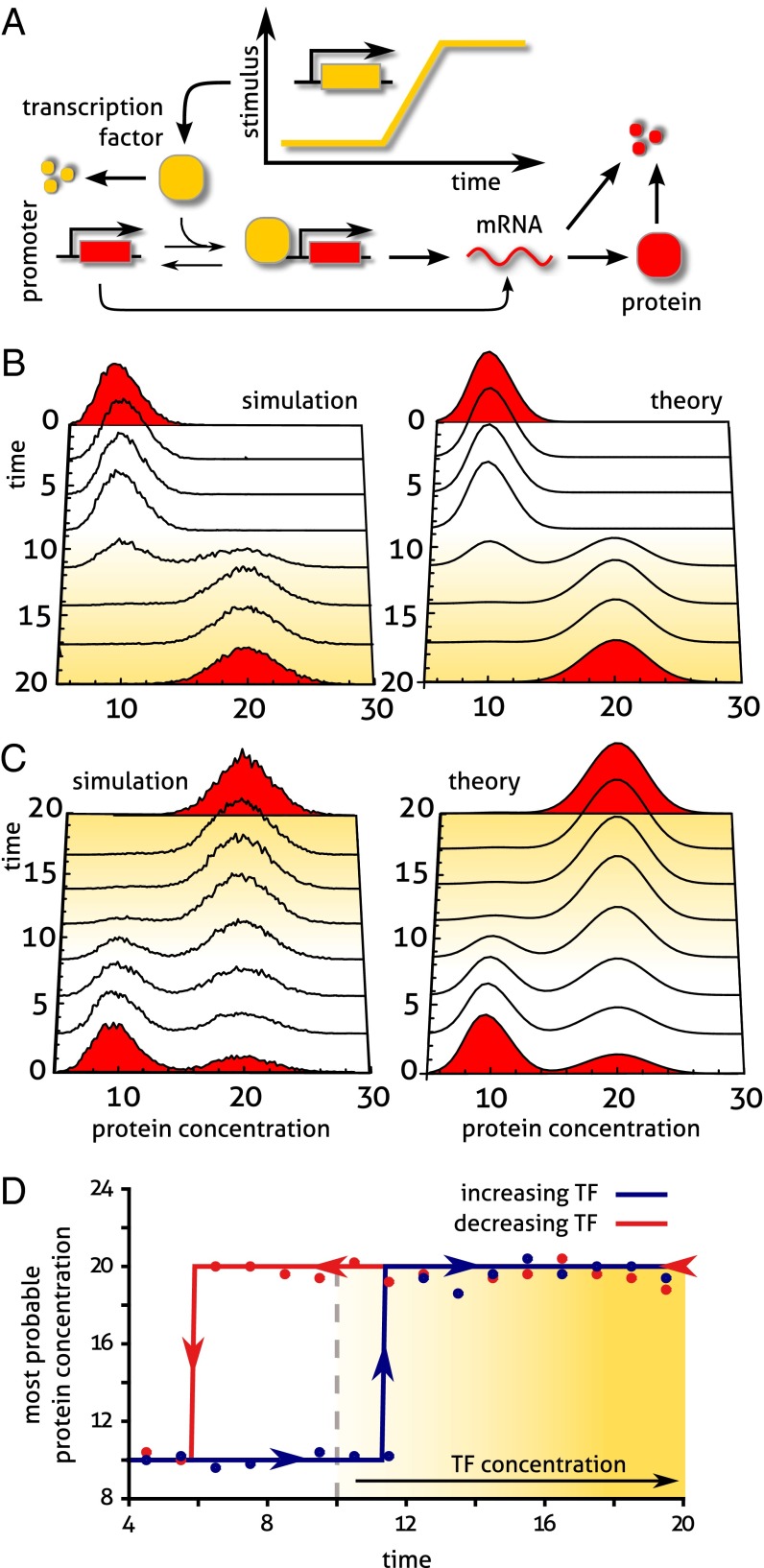
Bimodality is often observed transiently during stress responses such as osmotic, oxidative, or heat shock. Transient activation of the HOG pathway in budding yeast cells, for example, results in bimodal protein distributions of the induced genes after rapid nuclear translocation of TFs (2). An open question is whether isogenic cells exposed to the same, but changing, stress conditions express the same phenotypes (22). Here, we argue that slow promoter kinetics can account for these differences in phenotype induction due to hysteresis.

Intuitively, it is clear that slow promoter kinetics can lead to different transient phenotypes during induction, e.g., when the promoter is neither fully activated nor repressed. It is, however, less obvious what memory effects are associated with that switching. We consider a hypothetical induction experiment in which an externally controlled inducer activates the expression of TF (Fig. 5A). Note that the corresponding deterministic system exhibits no bistability irrespective of TF concentration because of noncooperative binding. We then compare two experimental protocols: (i) an increasing induction ramp which carries the promoter from the inactive to the active state, and (ii) the corresponding reverse experiment. In the case where both experiments yield similar results, the system is memoryless, whereas it displays hysteresis otherwise.

Fig. 5.

Phenotype induction. (A) We consider a hypothetical induction experiment in which a TF induces the expression of a slow promoter, such as, for instance, in response to osmotic or heat shock. Here, the external stimulus is assumed to be controlled via a ramp of TF input (or production) rate. Because TF degradation is assumed to be fast, its concentration follows the instantaneous induction rate. (B) The probability distribution of protein obtained from an induction experiment which carries the promoter from the inactive to the induced state displays transient bimodality. Here, the stimulus is assumed to be a ramp between times 10 and 20, as shown in A. (C) The same experiment is carried out in the reverse direction: A decreasing ramp leading from the fully induced to the depleted promoter state also shows transient bimodality which is, however, persistent for much longer times. The resulting probability distribution is reminiscent of the induction history, indicating hysteresis. We also note that, at each time point, the protein distributions obtained from stochastic simulation of the full network (Left) agree well with the predictions of our conditional LNA (Right). (D) We quantify the apparent hysteresis phenomenon associated with an increasing and then decreasing stimulus by comparing the global modes of either distribution, i.e., the most probable protein concentrations, which result in a hysteresis loop. The difference between forward and reverse induction, as predicted by the conditional LNA (solid), is in good agreement with simulation (dotted). Parameter values are given in SI Appendix, Table S4.

We characterize the hysteresis effect based on analytical solutions to the protein distributions for both experiments (SI Appendix 5.3). When the induction rate is increased from zero to some high value, the conditional LNA predicts transient bimodality immediately after the onset of the ramp (Fig. 5B). The reverse experiment (Fig. 5C) is realized by decreasing the induction rate from that high value to zero, starting from the induced state. Although transient bimodality is again observed, it persists for a much longer time, and even after the induction rate has dropped to zero, which indicates memory of the induced state. Given that TF dynamics is much faster than the induction kinetics, this asymmetry is caused by the interplay of slow promoter binding and induction timescales.

A quantitative measure is provided by the global maxima of the distributions which correspond to the most likely concentrations observed in either experiment. The maximum switches rapidly after TF concentration is increased, whereas switching occurs only after TF has been removed in the reverse experiment (Fig. 5D). Hence, reversible induction results in a hysteresis loop, which is also well predicted by the conditional LNA.

Finally, the maximum hysteretic response is achieved when the induction rate is much faster than the promoter dynamics, but slower than TF degradation, i.e., when the induction ramp can be approximated by a step function. In that limit, we compare the timescale of induction to that of the reverse experiment 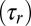; their ratio measures the degree of hysteresis (SI Appendix 5.3):

where 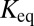is the DNA-dissociation constant and 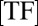denotes the concentration of TF after induction. It follows that a memory effect is observed either for strong binding sites, or when the perturbation 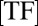is sufficiently large. The hysteresis phenomenon persists when induction rate and promoter dynamics evolve on similar timescales (Fig. 5 C and D); it is, however, absent for very slow induction, as expected. The existence of such optimal time windows for observing hysteresis hence provides an experimentally testable protocol with which to probe slow promoter dynamics.

Discussion

We have presented an analytical methodology for the quantitative study of multimodal distributions that arise from gene regulation involving slow promoters. In the literature, different methodologies have been used to describe simple gene regulation models on the basis of a separation of timescales. Qian et al. (12) obtain a factorization of the stationary probability density for an autoregulated gene; similarly, Innocentini et al. (23) have considered a multistate promoter without feedback. These methodologies require the corresponding protein distributions to be obtained analytically, which becomes generally intractable when posttranscriptional mechanisms based on bimolecular protein interactions are considered or when the full time dependence of the distribution function is desired. A promising approach that is based on conditional moments (24) overcomes many of the limitations imposed by timescale separation; however, it does not yield systematic estimates for the distributions of the more abundant species. Our conditional LNA thus fills a gap in the modeling literature, as it is, to our knowledge, the first methodology to provide closed-form expressions for gene product distributions in general regulatory networks. Whereas our LNA-based approach correctly takes into account physiological gene copy numbers, it can become inaccurate when some gene products of interest are present only in very low molecule numbers (SI Appendix 3.4, Fig. S1). Finally, we note that our gene-centric methodology does not incorporate effects of cell growth and division and, hence, cannot account for growth phenotypes that have been described (25).

As we have shown, our approach provides a simple tool (i) to identify cellular phenotypes in such networks that cannot be quantified via deterministic models, (ii) to study a wide class of network architectures, and to identify parameter ranges over which multimodality can be observed, and (iii) to identify dynamical characteristics of multimodal systems that have not been described previously. Specifically, we have demonstrated how the interplay of transcriptional and translational feedback may be exploited to encode complex phenotypes in many-gene networks. We have quantified how phenotypic switching shapes birhythmic expression patterns in genetic oscillators. Further, we have proposed a previously unidentified mechanism for generating hysteresis in gene induction experiments that display transient bimodality. Remarkably, our procedure remains highly accurate when the underlying gene regulatory network is also deterministically multistable (SI Appendix 5.4, Fig. S4). The conditional LNA presented here hence serves to advance our understanding of cellular memory and decision-making.