Bacterial promoter repression by DNA looping without protein–protein binding competition

Abstract

The Escherichia coli lactose operon provides a paradigm for understanding gene control by DNA looping where the lac repressor (LacI) protein competes with RNA polymerase for DNA binding. Not all promoter loops involve direct competition between repressor and RNA polymerase. This raises the possibility that positioning a promoter within a tightly constrained DNA loop is repressive per se, an idea that has previously only been considered in vitro. Here, we engineer living E. coli bacteria to measure repression due to promoter positioning within such a tightly constrained DNA loop in the absence of protein–protein binding competition. We show that promoters held within such DNA loops are repressed ∼100-fold, with up to an additional ∼10-fold repression (∼1000-fold total) dependent on topological positioning of the promoter on the inner or outer face of the DNA loop. Chromatin immunoprecipitation data suggest that repression involves inhibition of both RNA polymerase initiation and elongation. These in vivo results show that gene repression can result from tightly looping promoter DNA even in the absence of direct competition between repressor and RNA polymerase binding.

INTRODUCTION

The Escherichia coli lactose (lac) operon provides the classic paradigm for understanding negative and positive control of bacterial gene expression (1). This genetic switch measures glucose and lactose concentrations so that genes necessary for lactose catabolism are expressed at high levels only in the absence of glucose and the presence of lactose (2). Gene control at lac depends upon the homotetrameric lac repressor (LacI) protein (3) whose DNA binding is weakened when allolactose or isopropyl β-D-1-thiogalactopyranoside (IPTG) are bound to allosteric sites. In the absence of glucose, the binding of catabolite activator protein (CAP) near the lac promoter stabilizes RNA polymerase binding and gene expression, while LacI binding directly occludes the lac promoter (4). Classic experiments have shown that the local concentration of LacI is enhanced by DNA looping between auxiliary operators (5–12). We and others have used elements of this control system to analyze the apparent physical properties of DNA both in vitro and in vivo (11,13–19).

It has long been apparent that DNA looping in bacterial transcriptional control occurs in a variety of promoter/operator configurations (20). While there is evidence that direct repressor-RNA polymerase competition occurs for upstream loops in lac (18) [but not putative O₃–O₂ loops and see (21,22)], ara and deo (23), there are important examples such as the galactose (gal) operon where RNA polymerase does not directly compete with repressor proteins for DNA occupancy within a DNA loop (24,25). Repression in such cases suggests that either additional co-repressor proteins are recruited as direct obstacles to RNA polymerase binding, and/or that bending the promoter DNA into a tight loop is inherently repressive. This latter concept has been supported by several prior in vitro experiments (26–29). Here, we test this concept for the first time using quantitative experiments in living E. coli cells.

Repression by promoter constraint in a small DNA loop could reflect at least four mechanisms. First, the topological position of the promoter (i.e. outer or inner helical face of the tight DNA loop) could create a steric obstacle inhibiting RNA polymerase diffusion to the promoter. Second, promoter DNA distorted by tight bending might be poorly recognized by RNA polymerase holoenzyme, thus inhibiting closed complex formation. Third, conversion of an RNA polymerase closed complex to the open complex might be inhibited if helix opening is unfavorable in a tightly constrained DNA loop. Fourth, promoter escape and transcription elongation by RNA polymerase might be inhibited in the context of a tightly constrained DNA loop. Here we report the results of systematic in vivo gene expression experiments using components of the lac operon to quantitate some of these effects. We show that capturing an E. coli promoter within a tightly constrained DNA loop of ∼100 base pairs (bp) causes at least ∼100-fold promoter repression in the absence of any direct binding competition between RNA polymerase and repressor protein. An additional ∼10-fold repression is observed as a periodic function of promoter topology (inner versus outer helical face) within the DNA loop. The efficiency of RNA polymerase cross-linking to DNA only partly mirrors these effects, suggesting that transcription initiation and elongation may both be inhibited by tight DNA looping.

MATERIALS AND METHODS

Bacterial strains

FW102 (the kind gift of F. Whipple) is a Strep^R derivative of CSH142 [araD(gpt-lac)₅] that has been described (30). Expression constructs were confirmed by diagnostic polymerase chain reaction amplification following conjugation and selection (31).

DNA constructs

DNA looping constructs were based on plasmid pJ992, created by modifications of pFW11-null (30) as previously described (31). Construct sequences are shown in Supplementary Figures S1 and S2 with descriptions in Supplementary Table S1. The O₂ operator normally present within the lacZ coding region was destroyed by site-directed mutagenesis (14). The experimental strong UV5 promoter does not contain a CAP binding site. lacZ looping constructs were placed on the single copy F128 episome by homologous recombination between the constructed plasmids and bacterial episome, followed by bacterial conjugation. F128 carries the lacI gene producing wild-type levels of repressor. Bacterial conjugation and selections were as previously described (31).

In vivo DNA looping assay and data fitting

Analysis of lac reporter gene expression was performed as described (31). Raw β-galactosidase reporter activity (E) is presented in Miller units. The repression ratio (RR) is given by E_induced/E_repressed, where induction is obtained by addition of 2 mM IPTG. Curve fitting with a thermodynamic model of lac promoter accessibility was performed using a simplex and inductive search hybrid algorithm (SIH) (32). A non-linear least-squares refinement to each set of pooled E values (repressed and induced) is performed with five adjustable parameters for each as described below (and see Table 1).

Table 1. Parameters (95% confidence interval) fit to a thermodynamic model of lac promoter accessibility.

Parameter	−IPTG	+IPTG
hr (bp/turn)	12.45 ± 0.14	12.13 ± 0.02
Capp (× 10−19 erg cm)	2.26 ± 0.02	8.32 ± 0.19
KSmax	1403 ± 29	440 ± 1
KNSSL	269 ± 9	18 ± 0.2
spoptimal (bp)	44.89 ± 0.01	45.03 ± 0.02

Thermodynamic model

The thermodynamic model described here is reminiscent of previous approach analyses (14,33), but the model parameters have different definitions and interpretations. The current model is based on the premise that promoter repression is sensitive to the occupancy of the downstream lac O₁ operator at equilibrium. The extent of promoter repression is then modeled by evaluating the distribution of possible states of this operator. If a singly bound repressor exists at O₁ (‘single bound’), repression is modest because transcription elongation can, with high probability, disrupt the bound repressor. In contrast, repressor bound to the downstream operator by virtue of DNA looping from the strong upstream O_sym operator has the potential to cause more complete promoter repression by RNA polymerase exclusion through the mechanisms in question here. In the current model, the distance between the downstream and upstream operators is held constant within each of two loop families. The face of the helix occupied by the promoter is then systematically changed in a manner that influences O_sym–O₁ loop stability: if the promoter is accessible and productively engaged by RNA polymerase, the loop is destabilized by the action of elongating RNA polymerase. If the promoter is inaccessible, the loop is specifically stabilized from disruption by RNA polymerase elongation (‘specific stabilized loop’), and the repressed state is favored. Other unstable slightly repressed states might include repressor delivered to O₁ by transfer mechanisms (e.g. sliding or hopping) from the distal operator. Other stable repressed states could involve repressor delivered by looping to pseudo-operator sites near O₁ creating nonspecific stabilized loops (‘NS stabilized loop’).

A partition function for the system expresses the sum of possible unlooped and looped states of the O₁ operator:

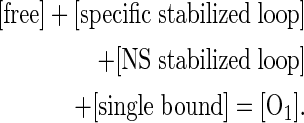(1)

This expression can be cast in terms of the equilibrium constants for the different states:

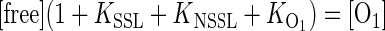(2)

where

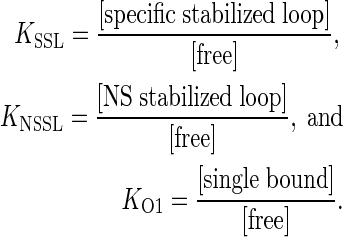The constant cellular concentration of LacI has been absorbed into each of the equilibrium constants; we assume one or low copy number DNA template so there is no interaction between separate DNA molecules and no depletion of LacI.

The fraction of bound (repressed) O₁ operators is given by the sum of the statistical weights of the bound forms divided by the total partition function:

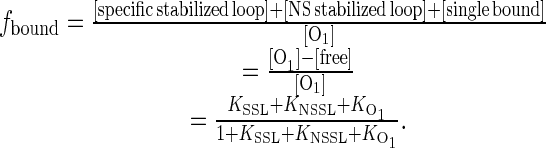(3)

Experimentally, the fraction bound is given by

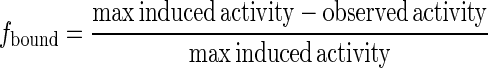(4)

where the maximum induced activity is potentially different for each E. coli strain background. Control experiments with isolated O₁ operators are used to determine 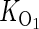(under both repressing and inducing conditions).

Torsional flexibility of the stabilized repression loop is modeled by formulating a helical-phasing-dependent equilibrium constant for specific stabilized loop formation, K_SSL. A sum of Gaussians expresses the total probability of twist deformations needed to bring the promoter into phase with the repressors (i.e. bury the promoter on the inner face of the DNA loop):

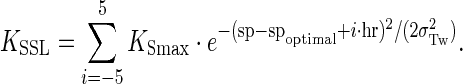(5)

The parameter sp gives the actual spacing (bp) between the promoter and operator O₁ centers for a given construct, sp_optimal is the spacing (bp) for optimal repression, hr is the DNA helical repeat, K_Smax is the equilibrium constant for maximal stabilized (when the promoter and O₁ operator are optimally phased) DNA loop formation, and σ_Tw is the apparent standard deviation of the torsion angle between the promoter and O₁ operator (given thermal fluctuations, the intrinsic resistance to twist of the DNA loop, the additional torsion angles accessible by the conformational space of the repressor, and the allowed torsion angles of the DNA loop that are inaccessible to polymerase due to steric occlusion). Summation over the integer i captures all possible overtwisting or undertwisting needed to give the helical phasing required for optimal promoter burial and polymerase exclusion. For a given loop size (operator center to operator center), σ_Tw is calculated as:

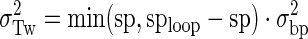(6)

where sp_loop is a constant for each loop family (either 89.5 bp or 100.5 bp) and σ_bp is the standard deviation of twist per base pair given by

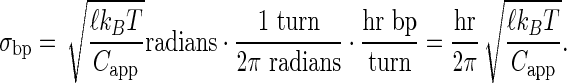(7)

in units of bp twist increments. Here, ℓ is the average base pair separation (3.4 Å), k_B the Boltzmann constant, T the absolute temperature, and C_app the apparent torsional modulus for the DNA in the loop. Variability in the possible torsion angles permitted in a protein–DNA loop increases the apparent σ_Tw (reducing C_app), whereas steric occlusion of polymerase eclipses a certain fraction of otherwise allowed torsion angles decreasing the apparent σ_Tw (increasing C_app). Thus, this fitting procedure models the ability of the promoter to sample inside (inaccessible) and outside (accessible) surfaces of the DNA loop given a fixed spacing from the flanking operators.

To summarize, the theoretical f_bound is modeled as a function of DNA promoter–operator length (sp), with five adjustable parameters: hr, C_app, K_Smax, K_NSSL, and sp_optimal. Predicted absolute activities are calculated using this theoretical f_bound and the measured maximal induced activity. Possible effects of architectural proteins such as HU are absorbed into the fit thermodynamic model parameters here.

Chromatin immunoprecipitation

E. coli cultures were grown to log phase in 50 ml cultures of Luria-Bertani medium at 37°C in the presence or absence of 2 mM IPTG. Cross-linking of DNA and protein complexes was accomplished with the addition of 37% formaldehyde (Sigma) to a final concentration of 1% in the presence of 10 mM sodium phosphate [pH 7.6]. Cultures were maintained at room temperature with constant gentle swirling for 20 min. Reactions were quenched with cold 2 M glycine (200 mM final concentration). Cells were harvested by centrifugation, washed three times with 4 ml cold phosphate buffered saline and resuspended in 1 ml FA lysis buffer [100 mM Tris-HCl 8.0, 300 mM NaCl, 2% Triton X-100, 0.2% sodium dodecyl sulphate, 1 mM phenylmethylsulfonyl fluoride (PMFS) and protease inhibitor mix (Roche)]. Cells were lysed and cellular DNA was sheared by sonication and further analyzed as described (18). All chromatin immunoprecipitation (ChIP) data are included in Supplementary Table S2.

Structural modeling

DNA supercoiling was modeled as a plectonemic superhelix with circular arcs as end caps forming the apical loops, as described previously (33). While the actual size of apical loops in vivo is unknown, this simple geometric model can be compared with more sophisticated theoretical treatments (34–38) and experimental electron microscopy (EM) and atomic force microscopy (AFM) images of plasmid DNA (39–41). A uniform plectonemic superhelix was generated from a 500 bp domain with helical repeat of 11 bp/turn, superhelical density of −0.18, superhelix pitch angle of 60°, center-to-center superhelix diameter equivalent to 8 bp and DNA radius equivalent to 4 bp. By absorbing all of the superhelicity into a minimum-radius plectonemic superhelix, the negative writhe per helical turn of DNA in the plectoneme is much greater than physiological (30). Scaling of this initial plectonemic superhelix by a factor of ∼3.5 resulted in a final plectoneme with apical radius of ∼46 Å and center-to-center superhelix diameter of ∼28 Å. These dimensions are consistent with EM and AFM results as well as Monte Carlo simulations suggesting that at physiological salt concentrations the diameter of apical loops is 1–3 times larger than the plectonemic superhelix diameter (38–43). This scaling procedure effectively increases the superhelix diameter.

RESULTS AND DISCUSSION

Experimental design

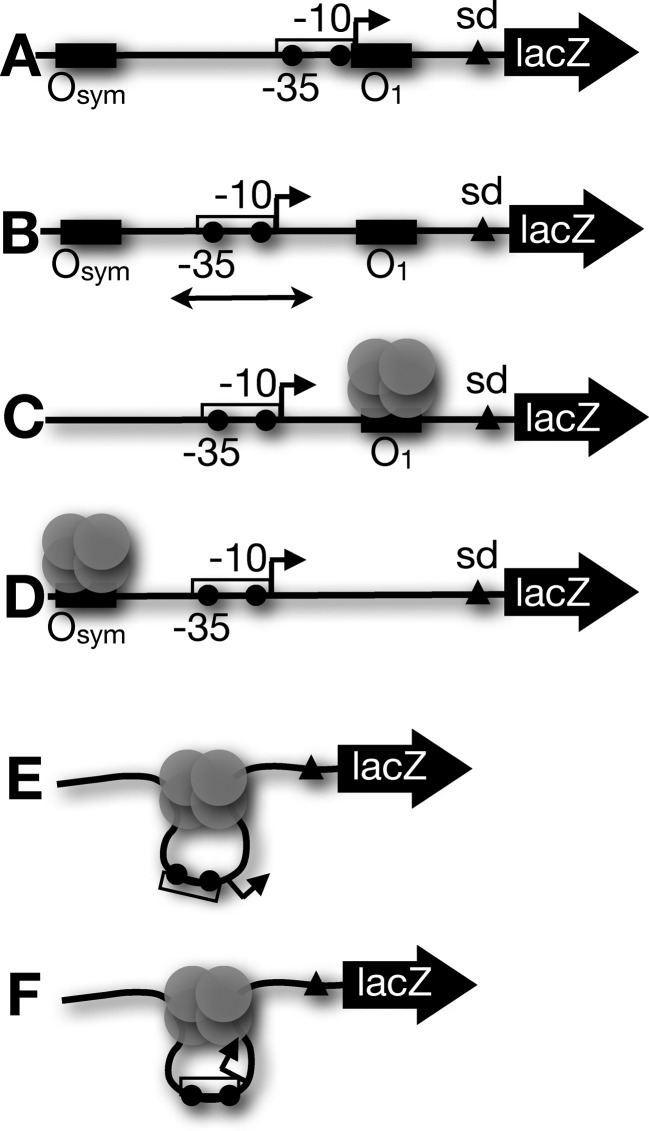
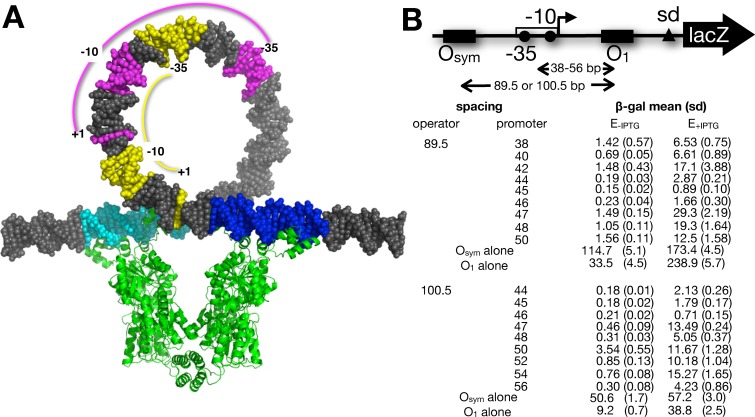
The experimental design for this study is illustrated in Figure 1 (approximately to scale) and Figure 2A. We have previously analyzed in vivo repression and protein binding for promoter constructs that simulate the wild-type lac configuration (Figure 1A) where RNA polymerase and LacI compete for DNA binding (14,18,33), with operator identities chosen to tune the dynamic range of repression (44). The third far-downstream O₂ lac operator is deleted to simplify these analyses. In this wild-type configuration (45), DNA looping may repress the lac promoter by a combination of three effects: (i) direct competition between repressor and RNA polymerase for DNA binding, (ii) tightly looping the promoter DNA and (iii) steric hindrance if the promoter is on the inner face of the DNA loop. We sought to deconvolute these three effects by placing the regulated promoter centrally between operators (Figure 1B) so that the first effect is eliminated: LacI and RNA polymerase do not directly compete for DNA binding. Control constructs (Figure 1C and D) allow study of repression by isolated downstream or upstream repressors in the absence of specific looping. DNA loop formation (Figure 1E and F) then imposes promoter bending strain (Figure 1E) or promoter bending strain combined with promoter steric hindrance on the inner face of the DNA loop (Figure 1F). The different configurations of promoters and repressors are depicted to scale in the context of a conventional DNA loop illustration in Figure 2A. To study repression of promoters in these configurations, we created two families of favorable (twist relaxed) repression loops (Supplementary Figures S1 and S2). In each family, the E. coli UV5 promoter is placed centrally between two operators such that there is no binding competition between RNA polymerase and LacI, and the operators are separated (center-to-center) by an integral number of helical turns of DNA (14,33). Each family of constructs then systematically positions the promoter on different helical faces of the looped DNA to deconvolute the repressive effect of DNA deformation, per se, from topological repression due to steric effects of promoter occupancy on the inner versus outer face of the DNA loop. The two loop families differ only in loop size (Supplementary Figure S1, 89.5 bp: ∼8 DNA turns or Supplementary Figure S2, 100.5 bp: ∼9 DNA turns, measured center-to-center between O_sym–O₁ operators). We have previously shown in detail (14,16) that these operator spacings in our system define optimal untwisted loops, although these optimal lengths are slightly different from those reported by the Müller-Hill group (6).

Figure 1.

Schematic illustration of research design. (A) Conventional arrangement of lac operon elements. A strong lac operator (here O_sym, filled rectangle) lies upstream of a promoter (open rectangle) with −35, −10 elements and transcription start point (filled circles and broken arrow, respectively) that overlap downstream operator (here O₁) such that repressor and RNA polymerase directly compete for DNA. (B) Arrangement of lac elements in present study. The test promoter is positioned centrally so binding by RNA polymerase is not occluded by LacI. The promoter position can be systematically varied (double-headed arrow) to explore face-of-the-helix effects. (C) Control construct with only downstream O₁ operator. (D) Control construct with only upstream O_sym operator. (E) Schematic illustration of DNA looping by tetrameric LacI for a construct of the type shown in (B). Here, the promoter is exposed on the outer face of the tightly bent DNA. (F) As in (E) except the promoter has been shifted by 5 bp (one half helical turn) to face the inward surface of the looped DNA.

Figure 2.

DNA looping constructs and data. (A) Scale space-filling models showing lac loop geometry studied here. 100.5 bp DNA loop is shown stabilized by the lac repressor tetramer (green; pdb code 1Z04) engaged with upstream O_sym (cyan) and downstream O₁ (blue) operators in the conventional model. This conventional model depicts the simplifying assumption that lac repressor does not deform its bound operators, and depiction of this conventional model is not meant to imply that there are not superior loop models. The positions of the wild-type lac promoter −35, −10 and +1 elements (yellow) are contrasted with an example of promoter elements in this study (magenta) where promoter and operator do not overlap. The diagram was rendered using the 3D-DART tool (57). (B) β-galactosidase expression data from constructs with the indicated operator and promoter spacings (mean, standard deviation in parentheses). Promoter spacing indicates distance (bp) between the center of O₁ and the center of the UV5 promoter. Operator spacing indicates distance (bp) between the centers of O₁ and O_sym operators. Results for constructs with single operators are shown.

Previous in vivo experiments have shown that transcription initiation and elongation from a UV5 promoter on an unlooped template (e.g. Figure 1C) displace the downstream repressor tetramer such that gene expression is reduced only by a factor of ∼7, whether the downstream obstacle is repressor bound to a single O₁ operator (14) or a repressor anchoring a downstream loop that does not include the test promoter (18). This prior result agrees with previous reports (18,46) and sets a baseline for quantitative comparison of repression of promoters centered within strained DNA loops (Figure 1E and F) compared to an unstrained control (Figure 1C).

Loop-dependent repression

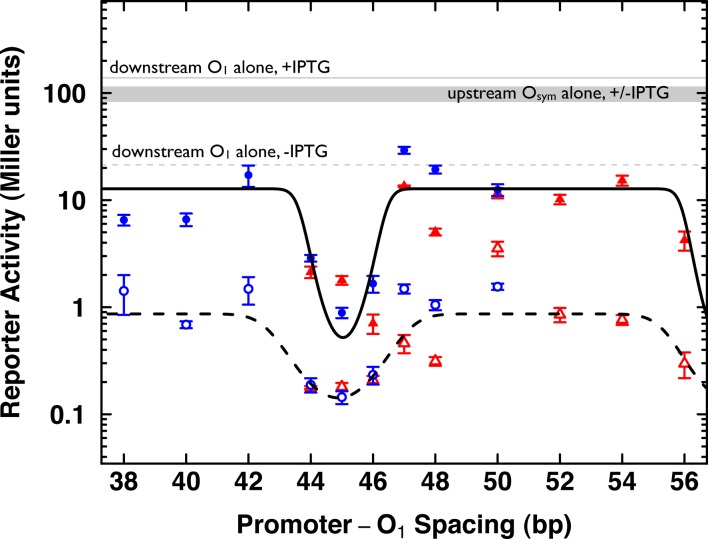
The experimental constructs were transferred to the large E. coli F′ episome by standard methods (14), and live cells were assayed for lacZ reporter gene expression in the absence and presence of saturating IPTG inducer concentrations. The pooled experimental results are shown in Figures 2 and 3. Reporter activity is shown on a logarithmic scale in Figure 3 as a function of the center-to-center spacing of the UV5 promoter and downstream O₁ operator. Open and closed symbols show data collected in the absence and presence, respectively, of IPTG inducer. Bold solid and dashed lines show fits to a thermodynamic model (parameters given in Table 1), while gray solid and dashed lines show average data for reference constructs bearing single operators.

Figure 3.

Reporter activity in vivo. β-galactosidase activity (Miller units) is shown on a logarithmic scale (y-axis) as a function of the center-to-center spacing (x-axis) between promoter and downstream O₁ operator. Data from 89.5 bp (blue circles) and 100.5 bp (red triangles) constructs are shown in the absence (open symbols, dashed black fit line) and presence (filled symbols, solid black fit line) of IPTG induction. Average reporter activities of promoter constructs with an isolated downstream O₁ operator in the absence (dashed gray) and presence (solid gray) of IPTG are shown. Similarly, average reporter activities for promoter constructs with an isolated upstream O_sym operator in the absence or presence of IPTG fall in the gray shaded region of the graph. Black lines show best fits to a thermodynamic model of promoter accessibility.

Several important conclusions are immediately evident from the data in Figure 3. The gray reference data for single operator controls show induced expression near a value of 100, with only ∼5-fold repression (score ∼20) when the isolated downstream O₁ operator is occupied, as expected. There is little effect of isolated upstream O_sym operator occupancy. In dramatic contrast, when the centrally positioned UV5 promoter is constrained on a tight DNA loop (Figure 3, open symbols; 8 DNA turns: blue; 9 DNA turns: red), the promoter is repressed between ∼100-fold (score ∼1) and ∼1000-fold (score ∼0.1), depending on the helical face occupied by the promoter. As shown by the fit to the thermodynamic model (Figure 3, dashed bold line and Table 1, sp_optimal) the most repressive spacings are near 45 bp where the promoter binding site for RNA polymerase faces the inside of the constrained DNA loop.

Table 1 reveals that the maximal stabilized looping equilibrium constant, K_Smax, is weakened by IPTG induction, as expected. Interestingly, and consistent with previous experiments (14,18,33), significant residual DNA looping persists even in the presence of saturating IPTG inducer (Figure 3, filled symbols; solid bold curve fit to thermodynamic model). This residual looping results in ∼10-fold residual repression with face-of-the-helix effects again responsible for a further ∼10-fold repression for promoter spacings near 45 bp (Table 1). This result presumably reflects the combination of residual DNA binding by the LacI-IPTG complex and the strong cooperativity of simultaneous LacI tetramer binding to favorably spaced operators. In fact, we cannot rule out that favorable cooperative interactions exist between surfaces of lac repressor and trapped unproductive RNA polymerase (21,22), perhaps contributing to this strong residual repression.

Examination of the parameters in Table 1 also illustrates several key differences from DNA studied in vitro. First, the apparent helical repeat (hr) value of ≥12 bp/turn is larger than the common value of ∼10.5 measured in vitro. This difference is attributed to DNA supercoiling. The apparent torsional modulus (C_app) equals or exceeds by 3-fold the commonly reported value for C in vitro (∼2.4 × 10⁻¹⁹ erg cm). This difference is an anticipated feature of the model, since C_app captures not only the intrinsic twist resistance of the looped DNA but also additional flexibility imparted by LacI participation in the loop (previously shown to decrease C_app ∼3-fold) as well as the steric occlusion of polymerase from the inside of the tightly strained DNA loop (which acts to increase C_app). Considering the loop shown in Figure 2A, if only the outer 50% of the DNA surface is sterically accessible to engage polymerase, this would appear as a 50% reduction in the allowed variation in DNA twist, or a 2-fold increase in C_app.

Together, these results clearly demonstrate strong repression simply by tight bending of promoter DNA, with the potential for even greater repression when the promoter is unfavorably positioned on the inner face of the DNA loop.

Correlating gene expression and protein binding

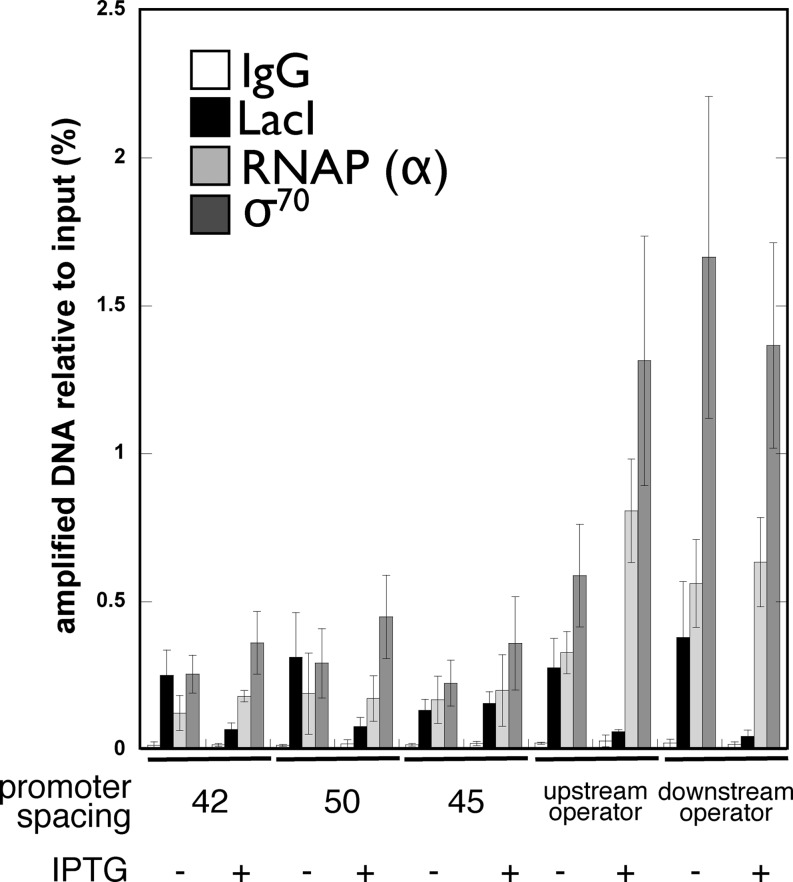
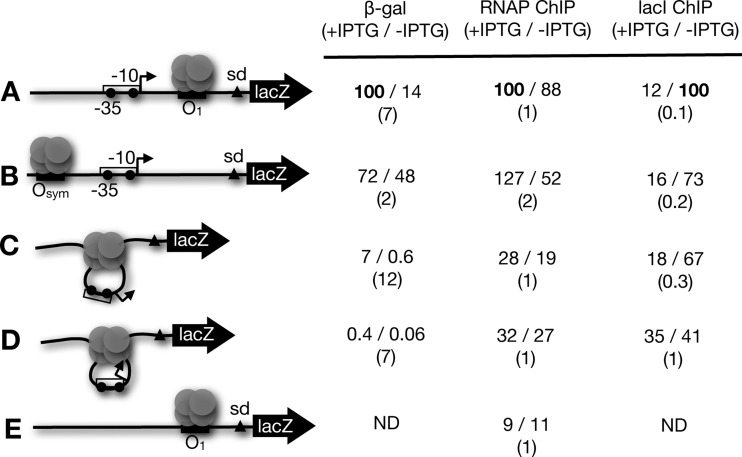
We wished to determine whether regulatory protein occupancy of experimental constructs was quantitatively correlated with gene expression as might be expected. Results of quantitative ChIP studies are shown in Figure 4 (and Supplementary Table S2). Figure 4 shows amplification of recovered target DNA, as a percent of input, after formaldehyde cross-linking in vivo and immunoprecipitation with nonspecific IgG or antibodies to LacI, the α subunit of RNA polymerase, or the σ⁷⁰ transcription initiation factor. Indicated promoter–O₁ spacings of 42 and 50 bp place the promoter on the outside face of the DNA loop, while the 45 bp spacing places the promoter on the inside face of the loop. Single operator control constructs were also included and all experiments were repeated in the absence or presence of IPTG inducer. The experimental results are in qualitative agreement with expectations. LacI occupancy tends to decrease in the presence of inducer and RNA polymerase holoenzyme subunits are enriched on the single operator control constructs with modest effect of inducer. It is noteworthy, however, that promoter cross-linking to RNA polymerase holoenzyme subunits is not strictly anti-correlated with the level of cross-linked LacI. This is emphasized in the representative results shown quantitatively in Figure 5. Here, both gene expression and ChIP data are normalized so that the maximal value is set at 100 to facilitate comparison. Maximal gene expression, RNA polymerase binding and minimal LacI binding are observed for single operator controls (Figure 5A and B) under induced conditions, as expected. An isolated downstream repressor (Figure 5A) creates ∼7-fold repression, with little effect on RNA polymerase binding and a LacI cross-linking change of ∼8-fold upon induction. Repression due to an isolated upstream repressor (Figure 5B) is only ∼2-fold with a corresponding ∼2-fold change in RNA polymerase binding and ∼5-fold reduction of LacI cross-linking upon induction. These results can be compared to gene expression and protein binding data for tightly looped DNA (Figure 5 C and D). For the construct with the promoter exposed on the outside face of the loop (Figure 5C), there is a ∼4-fold reduction of LacI cross-linking upon induction. Interestingly, this construct shows ∼12-fold increase in reporter expression but only ∼1.5-fold increase in RNA polymerase cross-linking upon induction. This result suggests that a significant fraction of cross-linkable RNA polymerases are engaged unproductively (in closed complexes and/or abortive initiation) at this promoter, implying that the tight DNA loop can inhibit transcription initiation by bound RNA polymerase. This pattern is also observed when the promoter faces the inside of the tight DNA loop (Figure 5D). Here, a further ∼7-fold repression (from ∼250-fold to ∼1700-fold) is observed while the change in RNA polymerase cross-linking is small. These interpretations are further supported by the observation that RNA polymerase cross-linking is several-fold lower for a control template lacking any promoter (Figure 5E). Interestingly, when promoter and operator overlap (as in the wild-type lac operon), it has previously been shown RNA polymerase occupancy of the promoter detectable by ChIP is more sensitive to the change from repression to induction (18).

Figure 4.

Chromatin immunoprecipitation data. Quantitation of amplified immunoprecipitated DNA is indicated as a percentage of input for the indicated conditions within the indicated 89.5 bp DNA looped constructs and controls and for antibodies with the indicated specificities (or IgG control).

Figure 5.

Summary of gene expression and protein cross-linking data. Representative schematic illustrations (left) are shown with data normalized to the maximum signal (set to 100) for both β-galactosidase reporter (first data column) and ChIP data for RNA polymerase (RNAP; second data column) or LacI (third data column). The first value in each data pair represents inducing conditions. The ratio of normalized values is shown in parentheses below. ND: not done.

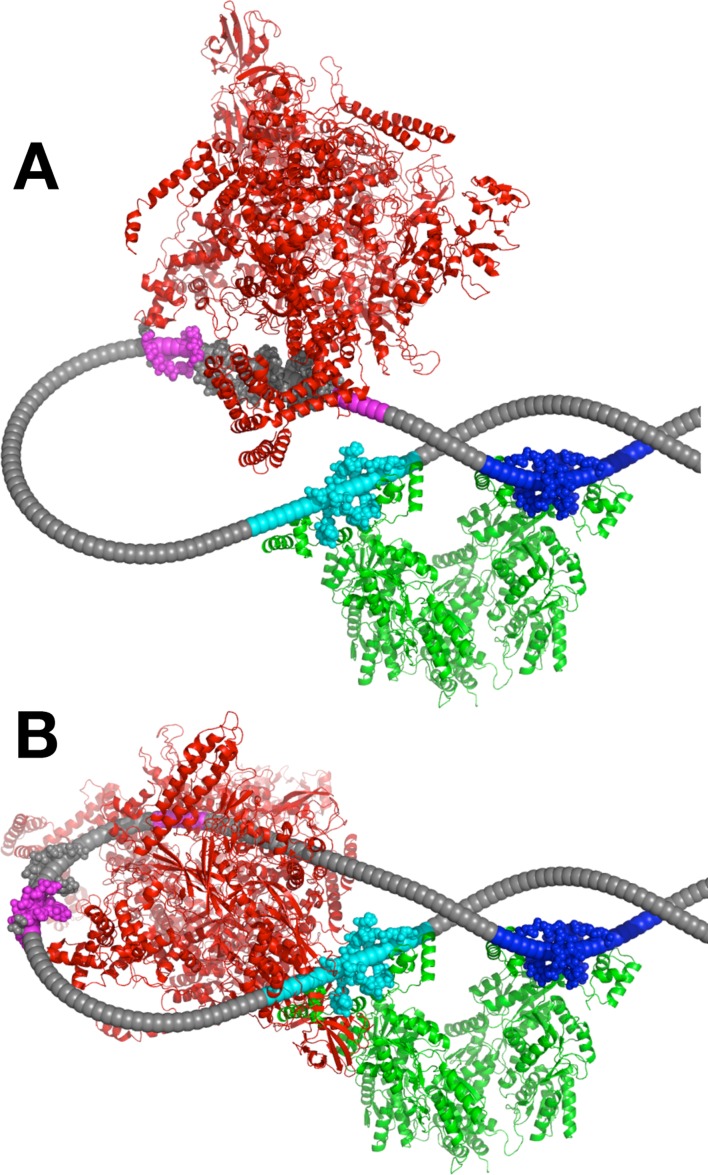
Our interpretation of these experimental results is shown in Figure 6. LacI tetramer is shown capturing the apex of a negatively supercoiled DNA plectoneme. DNA pre-bending in this hypothetical structure helps to rationalize the paradox that there is no apparent difference in DNA bending free energy change for formation of DNA loops of different sizes in vivo, even in the absence of various nucleoid proteins such as HU (14,15,33). The extent of promoter distortion in such a structure would depend on the exact position of the promoter relative to the apex of the plectoneme. For the position shown in Figure 6A, promoter DNA distortion is minimal, though changes in DNA conformation thought necessary for subsequent wrapping of RNA polymerase during transcription initiation (47) would be dramatically disfavored in this complex. Changing the promoter position by 5 bp rotates it to face the inside of the DNA loop (Figure 6B), creating dramatic steric clashes that likely account for the ∼1000-fold repression observed in our in vivo experiments for such cases. Interestingly, the theoretical work of Czapla et al. (34) suggests that loop length could play a role in determining the relative probabilities of loop conformations shown in Figure 2A versus Figure 6A.

Figure 6.

Interpretive repression model. DNA repression loop (arbitrary example length 111.5 bp) anchored by LacI (green; pdb code 1Z04) binding to upstream (cyan) and downstream (blue) operators is depicted at the apex of a negatively supercoiled plectoneme, in contrast to the conventional model in Figure 2A. A scale representation of RNA polymerase holoenzyme (red; PDB code 4IGC) is shown for promoter positions facing outward (A) or inward (B), emphasizing the impacts of template strain and steric hindrance on repression. Note that the DNA diameter is reduced for clarity (but see crystallographic DNA atoms shown at protein binding sites). Potential operator deformation by repressor has not been modeled here. Superhelical DNA parameters are discussed in Materials and Methods.

Comparison with previous experiments

It is useful to compare the present in vivo results with previous in vitro studies of DNA binding and transcription in the context of tightly looped DNA. It has been hypothesized that Ultrabithorax promoter repression in Drosophila involves DNA loops anchored by the even-skipped gene product (28). In vitro tests of Drosophila RNA polymerase recruitment by basal transcription factors showed that constraining the promoter on a ∼250 bp DNA minicircle caused strong repression (48). This result led the authors to propose that DNA constraint into a tight loop was inconsistent with transcription initiation.

Elegant in vitro experiments testing T7 RNA polymerase elongation on tightly bent ∼100 bp DNA minicircles have also been reported (27). Effects on initial DNA promoter recognition were not measured per se but it was shown that the rate and processivity of transcription elongation by the single-subunit phage T7 RNA polymerase were reduced by ∼100-fold on the tightly strained templates. This result is consistent with the notion that DNA wrapping, unwinding and other conformational changes required for RNA polymerase elongation are disfavored by the looping constraint. Both of these in vitro experiments used circular DNAs to simulate DNA looping. Such models do not constrain DNA thermal rotation along the helix axis, meaning that the promoter DNA is free to sample ‘inside’ and ‘outside’ faces during the experiment (biased by any intrinsically curved or anisotropically flexible DNA sequences). In contrast, loops anchored by repressor proteins introduce defined ‘inside’ and ‘outside’ promoter geometries as described in the current in vivo work.

An important previous qualitative in vitro study of this kind measured transcription from tandem E. coli gal promoters facing opposite DNA faces constrained in 11 helical turns of DNA (26). The authors interpreted these results as indicating that repression could result from resistance of the constrained loop to unwinding.

While the current work focuses on transcriptional repression by tight DNA looping in a bacterial model system, it is interesting to compare these concepts to constraints on protein recognition caused when nucleosomal DNA is constrained to a similar radius of curvature on the surface of a eukaryotic histone octamer. It has long been known that such DNA distortion can block transcription factor binding, even when the binding site is exposed on the outer nucleosome surface (49), and it has been argued that DNA distortion by tight bending may play a major role in blocking sequence-specific recognition by proteins (50). Luger et al. also point out that the unique geometry of the tightly bent DNA double helix could create unique binding sites for proteins that bind selectively to such distorted structures. This concept may apply to the recruitment of architectural proteins such as bacterial HU to tightly looped DNA (51,52). For example, a recent report by Boedicker et al. proposes a model where HU binds within the lac repression loop in E. coli(58). These authors argue that HU binding overcomes the sequence dependence of the DNA bending energy.

Finally, we note that RNA polymerase localization at apical loops has been reported (53), and it has since been proposed that nonspecific DNA binding proteins and transcription factors may act in part by controlling the formation of short plectonemic regions and thereby the availability of apical loops (54). While imaging techniques such as EM and AFM offer direct observation of DNA loops between bound proteins (55), more sophisticated methods will be needed to distinguish protein participants and operon positions relative to apical loops in the bacterial nucleoid.

SUMMARY AND CONCLUSIONS

We have used elements of the lac control system of E. coli to show, for the first time, that tight DNA looping can repress a bacterial promoter in vivo in the absence of direct protein–protein binding site competition between RNA polymerase and repressor. This work confirms and expands the results of previous in vitro experiments, and helps to explain how a wide range of promoter–operator arrangements lead to gene control in bacteria. The fundamental result is that RNA polymerase and repressor binding sites need not overlap for repressor proteins to strongly inhibit transcription. Constraining a promoter in a tight DNA loop is sufficient for dramatic repression, introducing considerable flexibility in the functional positioning of cis-regulatory elements for gene control. The present in vivo work shows quantitatively that repression within looped DNA arises from a combination of DNA distortion effects on transcription initiation and elongation (∼100-fold) and face-of-the-helix effects on promoter access (∼10-fold). Unresolved in these experiments are the detailed repressive roles of bending deformation versus resistance of constrained DNA to twisting and unpairing. It is likely that each effect plays a role given the dramatic DNA conformational changes thought necessary for transcription initiation by RNA polymerase. Restraining a promoter in a small DNA loop will prevent the necessary development of compensating writhe upon base unpairing for open complex formation. Negative supercoiling is known to potentiate RNA polymerase binding to DNA, and restraining a promoter in a DNA minicircle decreases binding unless the minicircle is negatively supercoiled (56). This unpairing resistance of tightly looped DNA could provide a major mechanism for the observed promoter repression in vivo.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online, including Supplementary Figures S1–S2 and Supplementary Tables S1–S2.

FUNDING

Mayo Graduate School, the Mayo Foundation; National Institutes of Health [GM75965 to L.J.M]. Funding for open access charge: Mayo Foundation.