Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Apr 10;4:4644. doi: 10.1038/srep04644

Platonic Scattering Cancellation for Bending Waves in a Thin Plate

M Farhat 1,a, P-Y Chen 2, H Bağcı 1, S Enoch 3, S Guenneau 3, A Alù 2,b
PMCID: PMC4027886  PMID: 24844801

Abstract

We propose an ultra-thin elastic cloak to control the scattering of bending waves in isotropic heterogeneous thin plates. The cloak design makes use of the scattering cancellation technique applied, for the first time, to the biharmonic operator describing the propagation of bending waves in thin plates. We first analyze scattering from hard and soft cylindrical objects in the quasistatic limit, then we prove that the scattering of bending waves from an object in the near and far-field regions can be suppressed significantly by covering it with a suitably designed coating. Beyond camouflaging, these findings may have potential applications in protection of buildings from earthquakes and isolating structures from vibrations in the motor vehicle industry.

In the past few years, metamaterials have become an attractive research focus for physicists and engineers due to their ability to control electromagnetic, acoustic, and elastic waves in ways that cannot be achieved using “regular” materials. Consequently, exciting applications of metamaterials ranging from sub-wavelength imaging to cloaking have been reported1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22. Soon after the advent of negative refraction and sub-wavelength imaging1, it has been shown that dielectric or conducting objects could be made “invisible” to electromagnetic waves by coating them with plasmonic materials2,3. A promising route to electromagnetic invisibility relies on the scattering cancellation phenomenon, where the fields scattered from a coating with negative (local) polarizability are specifically designed to cancel the fields scattered from the object2,4,5,6,7. The scattering cancellation technique has been proven relatively robust to changes in the design parameters, geometry, losses, and frequency of operation8,9. It has also been used to make electrodes or metal films transparent to THz10 or GHz11 radiation. Experimental evidence of such invisibility devices has recently been demonstrated in the microwave regime12,13,14. An alternative route to designing invisibility devices makes use of coordinate transformations15,16 to mold the wave flow in desired manners17,18,19,20,21,22. It should also be mentioned here that with their possible applications in stealth technology, noninvasive probing, and sensing, electromagnetic invisibility cloaks open promising avenues for new technologies in medicine, defense, and telecommunications23,24.

Cloaking ideas and designs for acoustic waves have also been developed. The possibility of two-dimensional acoustic cloaking for pressure waves in transversely anisotropic fluids has recently been shown25. Subsequent investigation of this cloaking idea for concentric layers of solid lattices behaving as artificially anisotropic fluids in the homogenization limit has been provided26. Following a similar approach, a micro-structured metallic structure has been designed as a cloak for surface liquid waves; the design has been validated experimentally around 10 Hz27. Additionally, three-dimensional acoustic cloaking for pressure waves in fluids has been envisaged; this cloak makes use of the fact that the scalar wave equation retains its form under geometric transforms28,29. Like in electromagnetic cloaking, the scattering cancellation technique offers an alternative path towards acoustic cloaking30,31,32. However, cloaking fully coupled pressure and shear elastodynamic waves in solids is a more elusive task, since the Navier-Stoke's equations do not retain their form under geometric transforms33,34. Although the theoretical foundation of these cloaking effects is well established35,36, the inherent requirement of singular bulk metamaterial properties that can hardly be met in practice still hinders the practicality of cloaking devices37,38.

In this Report, a biharmonic wave equation with appropriate boundary conditions, which describes the propagation of bending waves, is derived from the generalized elasticity theory39,40 and is used in designing a cloak that operates in thin plates. The idea behind the cloak design is to choose a coating material with density ρc satisfying ρc < ρ0 or ρc < 0 and to conceal an object with density ρs > ρ0. Here, ρ0 represents the density of the surrounding medium.

The parameters of the cloak are deduced using the scattering cancellation technique applied to a platonic metamaterial coating2. Note that the term “platonic” was coined by McPhedran in reference to thin plates while investigating wave propagation in complex thin plate elastic artificial materials41,42,43. Recent advances in the field of high frequency homogenization in platonics provide a theoretical foundation for understanding frequency dependent effective mass density taking negative or less than unity values44.

We then analyze the response of the platonic cloak concealing a cylindrical obstacle in the presence of a plane wave elastic excitation (harmonic vibration of the plate in the vertical z-direction). It is assumed that the out-of-plane dimension of the obstacle is negligible compared to its in-plane dimensions41,42. We show that in the quasistatic limit, i.e. for 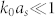Inline graphic, where k0 is the bending wavenumber in the surrounding medium and as is the in-plane dimension of the scatterer, the scattering is dominated by the zeroth-order multipole, unlike in the electrodynamics case where the first significant order is the dipolar one. This is not the only fundamental difference between electrodynamic/acoustic and elastic wave scattering phenomena: the fourth order biharmonic partial differential equation, which typically describes the propagation of bending waves in ultra-thin plates, is not equivalent to the vector/scalar wave equations that describe electromagnetic or acoustic wave propagation. For instance note that propagating and evanescent waves coexist even in homogeneous thin plates. Consequently, one can anticipate that a new cloaking method and new relevant physics are introduced following this route.

Results

It has been recently shown that the elasticity equations are not invariant under coordinate transformations33. Indeed, equations describing the propagation of elastodynamic waves under a time harmonic dependence e−iωt read (in a weak sense)

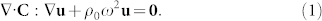graphic file with name srep04644-m1.jpg

Here, ρ0 is the (scalar) density of an isotropic heterogeneous elastic medium, C is the rank-four symmetric elasticity tensor (which has up to 34 entries even for thin plates), ω is the wave angular frequency, and u is the associated three-component vector displacement field. In most practical applications, the lateral dimension is significantly larger than the plate thickness making the Kirchhoff assumption for thin plates applicable39,40. Under this assumption, shear deformation and rotary inertia are negligible. For such a structure, Eq. (1) reduces to the scalar fourth order biharmonic equation

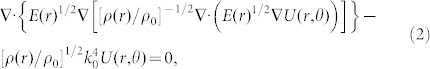graphic file with name srep04644-m2.jpg

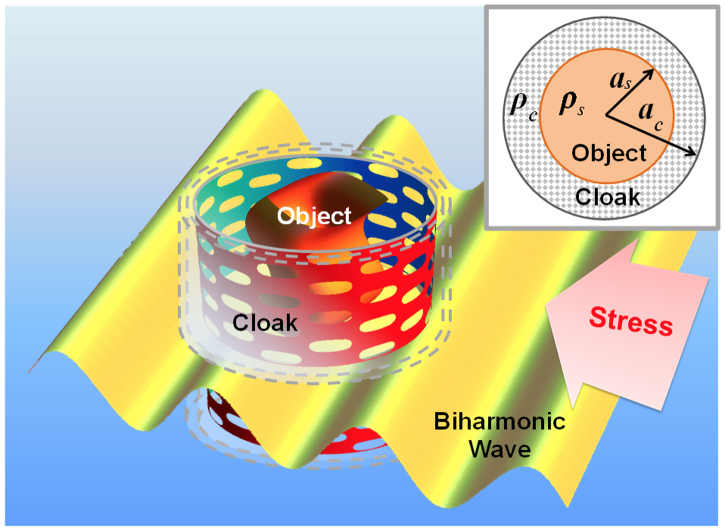
where U(r, θ) is the displacement in the vertical z-direction (assuming a cylindrical coordinate system due to the symmetry of the structure), E(r) is the relative Young modulus, ρ(r) is the density, 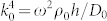Inline graphic, D0, and ρ0 are the bending wavenumber (to the power four), rigidity and density in the thin plate, respectively, and h is the plate thickness. Consider the structure shown in the inset of the Fig. 1. An object of radius as is coated with a shell of outer radius ac. For r < as (inside the object), ρ(r) = ρs and the bending wavenumber is ks. For as < r < ac (inside the shell), ρ(r) = ρc and the bending wave number is kc. Object, shell, and thin plate all have the same rigidity D(r) = D0, same relative Young modulus E(r) = 1, and same Poisson's ratio v(r) = v0. Without loss of generality, we assume that this structure is illuminated by a plane wave propagating in the x-direction. The displacement field of the incident plane wave is expressed as 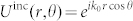Inline graphic, equivalently it can be expanded as 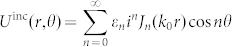Inline graphic, where the coefficients ε0 = 1 and εn = 2, n ≥ 2. The scattered field, Usca(r, θ), must be finite at r = 0 and it satisfies the radiation condition at r → ∞. Thus, it is expressed as

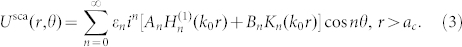graphic file with name srep04644-m3.jpg

Similarly, fields inside the shell and the object are expressed as

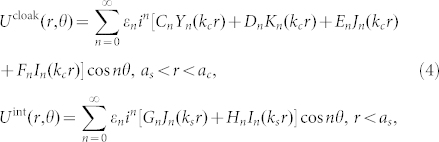graphic file with name srep04644-m4.jpg

respectively. Here, 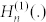Inline graphic, Jn(.)and In(.), and Yn(.)and Kn(.)are cylindrical Hankel functions of the first kind, Bessel and modified Bessel functions, and Bessel and modified Bessel functions of the second kind, respectively. To solve for the coefficients in the above equations, continuity of the field U, its derivative in radial direction ∂U/∂r, the bending momentum Mr, and the radial component of the generalized Kirchhoff stress Vr is enforced at the boundaries at r = as and r = ac, for each azimuthal order n (see supplemental materials45 for explicit expressions of the bending momentum and the generalized Kirchhoff stress in cylindrical coordinates). This yields a matrix system of equations in scattering unknown coefficients An and Bn. The far-field scattering amplitude (or differential scattering cross-section) 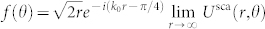Inline graphic is a measure of the cloaked object's visibility in direction θ46. The total scattering cross-section, σsca, is the integral of f(θ) over all angles, i.e. 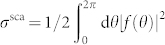Inline graphic. It may thus be expressed as

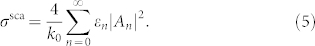graphic file with name srep04644-m5.jpg

Note that coefficients Bnare absent in Eq. (5) since the modified Bessel functions Kn(k0r) have no contribution to the scattered field as r → ∞. Generally speaking, the possibility for an observer to detect the object in the far-field is determined by the value of σsca. As a result, minimizing or completely canceling σsca would lead to the undetectability (invisibility) of the object in the far-field, independent of the observer's position. This can be achieved by canceling the coefficients 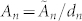Inline graphic that significantly contribute to the scattering. Here, 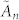Inline graphic is given by the determinant:

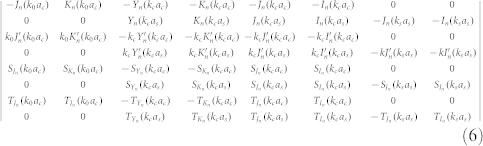graphic file with name srep04644-m6.jpg

where

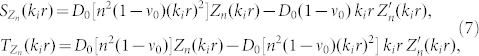graphic file with name srep04644-m7.jpg

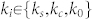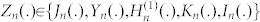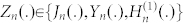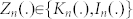where Inline graphic and Inline graphic. Upper and lower signs in Eq. (7) should be selected for Inline graphic and Inline graphic, respectively. The expression of dn could be obtained from Eq. (6) by replacing Jn(.) by Hn(.) in the first column (see supplemental materials45). Given the general complexity of this expression, it is instructive to analyze the low frequency limit corresponding to elastically small obstacles and shells, i.e. 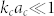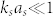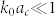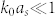Inline graphic, Inline graphic, Inline graphic, and Inline graphic. 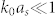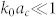Note that with the parameters in our study, it is sufficient to impose only Inline graphic and Inline graphic. Under this assumption, σsca in Eq. (5) is dominated by the monopole term A0:

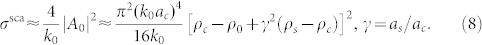graphic file with name srep04644-m8.jpg

Note that here, terms scaling with (k0ac)m, m ≥ 3, in expressions of An, n ≥ 0, are safely assumed to be zero for 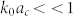Inline graphic. It is clear from Eq. (8) that σsca of elastically small obstacles in a thin plate scales with 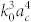Inline graphic. Also, as γ → 1 and ρc → ρ0 (no shell, only bare object), Eq. (8) reduces to

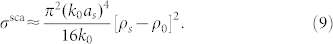graphic file with name srep04644-m9.jpg

By enforcing A0 = 0, i.e. σsca ≈ 0, in Eq. (8), we can derive the quasistatic design rule for cloaking:

graphic file with name srep04644-m10.jpg

which relates ρc, ρs, as, and ac. It is found that, to satisfy Eq. (10), ρc must take negative values for ρs > ρ0 and values larger than ρ0 for ρs < ρ0.

Figure 1. Geometry under investigation: An object at the center of a thin elastic plate lies on the trajectory of a planar bending wave, incident from right to left in presence of a cylindrical shell that may act as a platonic cloak.

Figure 1

Open in a new tab

Inset shows a top view of the cloak and object.

For larger objects, retardation effects become important and numerical calculations using the full 8 × 8 matrix in Eq. (6) are necessary to analyze the problem.

It is interesting to investigate two additional types of obstacles, namely when a “clamped” and a stress-free boundary conditions are set on the inner boundary of the system (r = as), while the same conditions of continuity of U, ∂U/∂r, Mr and Vr as before are hold on the outer boundary (r = ac). For the first case, we have U = ∂U/∂r = 0 whereas Mr and Vr are unconstrained. The 8 × 8 system in Eq. (6) reduces thus to a 6 × 6 system (see supplementary materials45). Applying the analysis described before to this case reveals that the monopole scattering coefficient A0 ≈ −1 in the quasistatic limit regardless of the cloak's parameters. This means that the resulting scattering amplitude 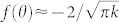Inline graphic (or the scattering cross-section σsca ≈ 4/k) becomes singular in the quasistatic limit (all other scattering coefficients tend to zero). This is unique to elastic waves, because a very small object would scatter infinitely and it has no equivalent in electromagnetics or acoustics46. This discussion shows that it is not possible to use shells of tailored density, in the quasistatic limit, to cancel the monopole scattering of a clamped obstacle since their corresponding coefficients differ by a factor (k0ac)2.

For the stress-free boundary conditions, Mr and Vr are set to zero on r = as whereas the same continuity conditions hold for the other parameters. We obtain here also a 6 × 6 system (see supplementary materials45). By applying the analysis above, we show that the monopole scattering coefficient of a stress-free hole of radius as cloaked with a shell of density ρc and radius ac = as/γ, is given by 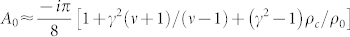Inline graphic. We see then that it is possible to find values of the density of the shell ρc and ratio γ that make A0 vanish thereby canceling the scattering from the cloaked object in the quasistatic regime. 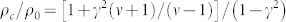This condition is found to be Inline graphic.

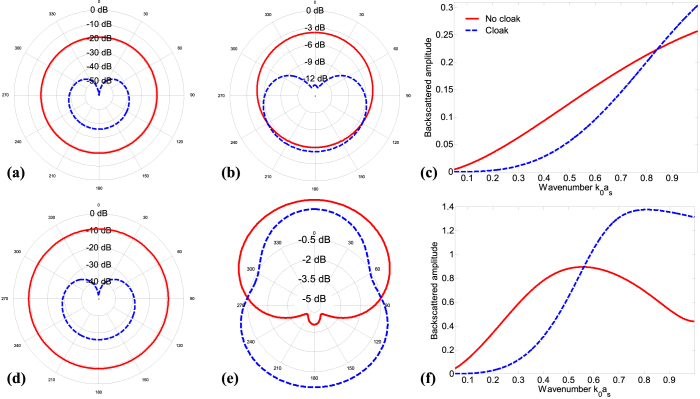
In all the results presented in the rest of the Report, in-plane dimension of the object is set to as = 1 m. Figure 2 shows the dependence of the scattering amplitude |f(θ)| on k0as for ρs/ρ0 = 0.1 [Figs. 2(a), 2(b) and 2(c)] and ρs/ρ0 = 10 [Figs. 2(d), 2(e) and 2(f)]. We show here that curves of scattering amplitude |f(θ)| vs. θ in logarithmic scale contain angular information about the scatterer [Figs. 2(a), 2(b) and 2(d), 2(e)] and curves of normalized backward scattering amplitude 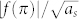Inline graphic vs. k0as [Figs. 2(c) and 2(f)] give insight into the spectral dependence of the object visibility for an observer placed at the angular position of the illumination (mono-static scattering). The simulations are carried out for the first scenario (soft object e.g. soil) for k0as = 0.1 (quasistatic limit) and k0as = 1 (Mie scattering). It is clearly seen that, for the soft object with ρs/ρ0 = 0.1 [Figs. 2(a) and (d)] and the rigid object with ρs/ρ0 = 10, [Figs. 2(b) and 2(e)], the scattering amplitude |f(θ)| is circularly symmetric for k0as = 0.1. This is due to the fact that scattering is dominated by the monopole term A0. The scattering behavior of soft and rigid objects is quite different for different values of k0as. For the soft object [Figs. 2(a), 2(b), solid red lines] A0 is still dominant for k0as = 1, and no significant angular dependence is observed. For the rigid object, [Figs. 2(e), solid red line], higher order multipoles start to contribute quite significantly to the overall scattering when the size is increased to k0as = 1. This has consequences on cloaking behavior. Consider the soft and rigid objects cloaked with shells with ρc = 1.3ρ0 and ρc = −2ρ0, respectively. For both shells, γ = 0.5, i.e. ac = 2as. Note that these values satisfy Eq. (10). Scattering amplitude |f(θ)| and normalized backward scattering amplitude 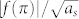Inline graphic of the cloaked objects are shown in Fig. 2 (dashed blue lines). Scattering reduction is clearly observed for both objects in the long wavelength limit while in the Mie scattering regime only the soft object gets cloaked in every direction.

Figure 2. Scattering amplitude |f(θ)| in logarithmic scale for the soft object (ρs/ρ0 = 0.1) with (a) k0as = 0.1 and (b) k0as = 1 and for the rigid object (ρs/ρ0 = 10) with (d) k0as = 0.1 and (e) k0as = 1.

Figure 2

Open in a new tab

The dashed blue line represents the cloaked scenario whereas the solid red line stands for the bare object. Plots in (c) and (f) are the normalized backward scattering amplitude 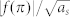Inline graphic vs. k0as for soft and rigid objects, respectively.

Also, curves of 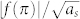Inline graphic vs. k0as in Figs. 2(c) and 2(f) show that the scattering from the rigid object undergoes a more dynamic variation in k0as-range [0, 1], contrary to the scattering from the soft object, where only one broad maximum is observed in the same k0as- range. This is associated with the fact that higher densities correspond to smaller effective wavelengths in the object, thus causing several internal resonances even for moderately sized objects. In addition, scattering reduction is more pronounced and broader for cloaking of the soft object [Fig. 2(c) and 2(f)].

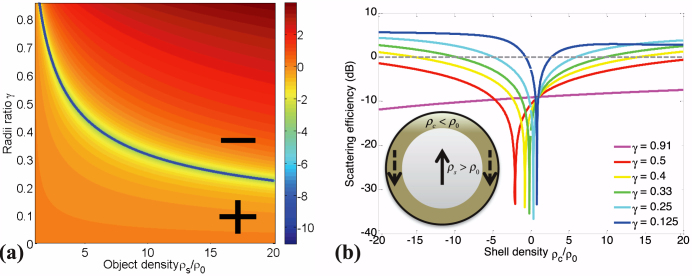
We now analyze how introducing a suitably designed negative density shell can drastically lower the overall scattering. We schematically indicate the scattering, in analogy with the polarization in the electromagnetic case, with vertical arrows of opposite direction: the positive (solid) arrow stands for ‘positive' scattered wave, whereas the negative (dashed) one corresponds to scattering with opposite phase [inset of Fig. 3(b)]. Figure 3(a) shows the contours of |ρc/ρ0| (in logarithmic scale) that fulfill Eq. (10) for varying values of ρs/ρ0 and γ. The solid blue line in the figure represents the case ρc = 0 and + or - sign indicates whether the required shell density is positive or negative. Let esca represent the scattering efficiency computed by the ratio of scattering cross-sections of the cloaked and bare objects. Figure 3(b) plots esca vs. ρc/ρ0 for a cloaked object with ρs/ρ0 = 10 for various values of γ and for k0as = 0.1 (the quasistatic limit). Figure 3 clearly shows that for certain values of ρc, significant scattering reduction is achieved, and this is also obtained for different values of γ. We notice that, for an ultrathin cloak (in the limit of γ ≈ 1), there is no dip in esca; instead the scattering reduction can be quite broadband for thicker shells. For instance, the shell with γ = 0.5 and ρc/ρ0 = −2 significantly suppresses the scattering. This agrees well with the result given by Eq. (8), which considers only the zeroth-order multipole. As schematized in the inset of Fig. 3(a), a platonic cover with relative density less than unity may induce an out-of-phase monopolar mode with respect to the local elastic displacement field, thus permitting dramatic cancellation of the field scattered from the object. For other values of γ, different values of ρc/ρ0 ranging from negative values to low positive (less than unity), are required to achieve significant cancellation of scattering.

Figure 3.

Figure 3

Open in a new tab

(a) Contour plot of the solutions of Eq. (10). (b) Scattering efficiency esca of the cloaked object with ρs/ρ0 = 10 vs. ρc/ρ0 for various values of γ and k0as = 0.1. The inset gives the sketch of cloaked object with arrows marking opposite phase of scattered wave in core and shell.

In reality, while modeling the frequency response of the cloaking phenomenon, one needs to take into account the inherent dispersion characteristics of the shell material since it is not possible to have a negative and frequency independent density due to causality considerations47. A negative density metamaterial may be achieved in acoustics by mimicking the way we achieve negative permittivity in electromagnetics with low frequency homogenization in high contrast periodic media47,48,49,50,51,52, or high frequency53 and high order homogenization54 in moderate contrast media. For elasticity, spring mass or inertial resonator metamaterials could lead to the desired effect near the resonance frequencies55. We suppose in the following that the material comprising the shell follows a classic Drude-like model of the type 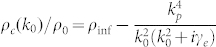Inline graphic [notice the fourth order dependence on k0 stemming from the nature of the biharmonic equation], where ρinf = 1, and kp and γe are the plasma wavenumber and Ohmic loss, respectively. This model can be obtained via a homogenization applied to a composite shell with high contrast inclusions, and is in all ways analogous to that derived in56. This Drude dispersion is plotted in Fig. 4(a) with parameters kpas = 0.15 and 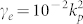Inline graphic. Figure 4 (b) plots scattering efficiency esca of an object cloaked with a shell made of Drude material vs. k0as for various values of γe. For this example, ρs/ρ0 = 10 and γ = 0.5. Here, 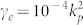Inline graphic, (blue solid line), 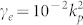Inline graphic, (green dashed line), and 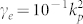Inline graphic, (orange dotted line) correspond to small, moderate, and high Ohmic losses, respectively.

Figure 4.

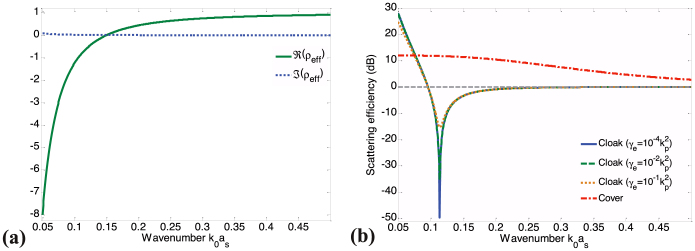
Figure 4

Open in a new tab

(a) The Drude-like density dispersion of the shell material with kpas = 0.15 and 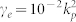Inline graphic. (b) Scattering efficiency esca of the cloaked object with ρs/ρ0 = 10 vs. k0as for various values of γe and γ = 0.5.

These curves are obtained using Eqs. (2) and (3), consistent with rigorous elastic scattering theory46 and validated against results obtained using a finite elements commercial software57. It is clear that the presence of a cloak with negative effective density may allow for a drastic reduction of the overall scattering at a desired wavenumber (k0as = 0.11 in this example), independently of the angle of observation. It is stressed here that the scattering cross-section can be reduced by over five orders of magnitude compared to the uncloaked scenario and by six orders of magnitude compared to the case of an obstacle of the same size and density ρc/ρ0 = 10. A slight broadening of the cloaking dip and a corresponding deterioration of the effect may be noticed when elastic loss γe is increased.

Discussion

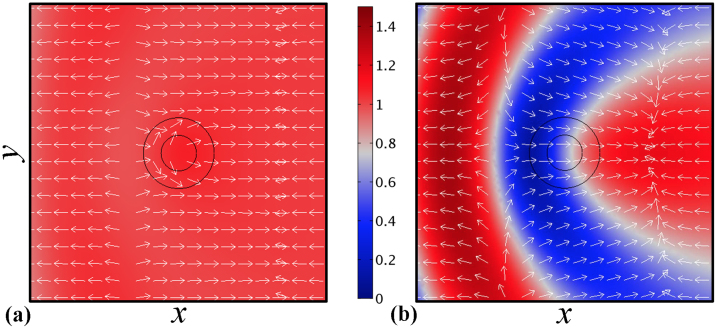
We have put forward a technique to cloak objects from elastic waves governed by the scalar fourth order biharmonic equation. The functionality of the obtained cloak could be seen in Fig. 5, where we plot the amplitude distribution of the scattered elastic displacement field U in the presence of cloaked [Fig. 5(a)] and uncloaked [Fig. 5(b)] objects. When it is surrounded by the negative density platonic shell (following the Drude-like model described above), the field amplitude is constant and equal to unity everywhere in space, in contrast to the considerably perturbed fields in the uncloaked case. The scattering reduction can be attributed to the proper choice of mass density of the platonic shell, in view of the scattering reduction predicted in Figs. 3 and 4.

Figure 5. Time-averaged displacement field distributions (vector direction with white arrows, amplitude indicated by the contours) in linear scale of a rigid elastic object with ρs/ρ0 = 10 cloaked by a Drude-like shell (a) and on its own for comparison (b).

Figure 5

Open in a new tab

The structures are illuminated with a unit-amplitude plane wave (k0as = 0.11) propagating in the x-direction from right to left.

In summary, we proposed a design of an elastic cloak based on the scattering cancellation technique, inspired by earlier applications in electrodynamics and acoustic scenarios. Here, however, the challenge is associated with the fact that a different, more complex analytical form governs bending waves. The cloaking mechanism introduced here presents significant advantages in comparison with transformation acoustic designs: there is no need of anisotropy and inhomogeneity of the material parameters. Using a homogeneous isotropic platonic shell with low or negative density we have been able to greatly reduce the scattering from soft and highly rigid objects as well as from stress-free holes. It should also be noted here that the proposed technique cannot be used to cloak clamped objects in the quasistatic limit. However, cloaks made of layered shells have the potential to overcome this problem at higher frequencies (where scattering from clamped objects is finite) by adding extra degrees of freedom to cancel more than one scattering coefficient, as previously demonstrated in electromagnetic cloak designs58.

Experimental realization of this idea may be within reach in the near future (note for instance that lensing of bending waves via negative refraction was theoretically predicted using the biharmonic plate model in41,42 and experimentally confirmed in a thin Duralumium plate in59 and a theoretical proposal for cloaking via geometric transforms in the biharmonic operator was also experimentally confirmed in37,38), allowing for exciting applications in scenarios in which it is desirable to suppress the scattering from obstacles in thin plates in the motor vehicle and airplane industry, in which the scattering of bending waves in thin plates generated by engines may be totally suppressed, or smart secure buildings, protecting them from bending and other types of seismic vibration damages caused by scattering from neighboring buildings60.

Methods

Analytical methods based on scattering Mie theory of cylindrical objects in thin elastic plates are used to obtain the numerical simulations in this Report (for further details and physical insight, see supplementary material45). The vertical displacement of the plate is the solution of the fourth order partial differential equation of Kirchhoff. We proceed, as is usually done, by expanding the impinging plane waves and the scattered fields in terms of Bessel and Hankel functions in polar coordinate system centered with the object to be cloaked. We then apply four elastodynamic boundary conditions on each cylindrical interface in order to obtain the scattering coefficients for waves, which uniquely determine the displacement fields everywhere. The displacement field distributions and scattering cross sections are computed using Bessel developments and Eq. (6) respectively. In the quasistatic limit, where the size of the elastic core sphere is much smaller than the wavelength and only the lowest-order Mie coefficient is important, an analytical formula is obtained [Eq. (10)] and it gives similar results to the full-wave simulations. Proper convergence for all the results is reached. The simulations given in Fig. 5 are obtained using the commercial finite-elements software COMSOL Multiphysics.

Author Contributions

M.F., P.-Y.C. and A.A. conceived the theoretical idea. M.F. conducted the numerical simulations and wrote the manuscript text. P.-Y.C., H.B., S.E., S.G. and A.A. discussed the implementation of the concept and reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary materials

srep04644-s1.pdf (203.2KB, pdf)

Acknowledgments

P.-Y.C. would like to thank Donald D. Harrington Dissertation Fellowship; S.G. wishes to thank the European Research Council for an ERC starting Grant. A.A. was supported by the DTRA grant No HDTRA1-12-1-0022.

References

  1. Pendry J. B. Negative refraction makes a perfect Lens. Phys. Rev. Lett. 85, 3966–3969 (2000). [DOI] [PubMed] [Google Scholar]
  2. Alù A. & Engheta N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 72, 016623 (2005). [DOI] [PubMed] [Google Scholar]
  3. Milton G. W. & Nicorovici N. A. On the cloaking effects associated with anomalous localized resonance. Proc. Roy. Lond. A 462, 3027–3059 (2006). [Google Scholar]
  4. Mühlig S., Farhat M., Rockstuhl C. & Lederer F. Cloaking dielectric spherical objects by a shell of metallic nanoparticles. Phys. Rev. B 83, 195116 (2011). [Google Scholar]
  5. Farhat M., Mühlig S., Rockstuhl C. & Lederer F. Scattering cancellation of the magnetic dipole field from macroscopic spheres. Opt. Express 20, 13896–13906 (2012). [DOI] [PubMed] [Google Scholar]
  6. Farhat M., Rockstuhl C. & Bagci H. A 3D tunable and multi-frequency graphene plasmonic cloak. Opt. Express 21, 12592–12603 (2013). [DOI] [PubMed] [Google Scholar]
  7. Xi S., Chen H., Zhang B., Wu B. I. & Kong J. A. Route to low-scattering cylindrical cloaks with finite permittivity and permeability. Phys. Rev. B 79, 155122 (2009). [Google Scholar]
  8. Alù A. & Engheta N. Plasmonic materials in transparency and cloaking problems: mechanism, robustness, and physical insights. Opt. Express 15, 3318–3332 (2007). [DOI] [PubMed] [Google Scholar]
  9. Chen P. Y., Soric J. & Alù A. Invisibility and cloaking based on scattering cancellation. Adv. Mater. 24, 281–304 (2012). [DOI] [PubMed] [Google Scholar]
  10. Malureanu R. et al. A new method for obtaining transparent electrodes. Opt. Express 20, 22770–22782 (2012). [DOI] [PubMed] [Google Scholar]
  11. Song Z., He Q., Xiao S. & Zhou L. Making a continuous metal film transparent via scattering cancellations. Appl. Phys. Lett. 101, 181110 (2012). [Google Scholar]
  12. Edwards B., Alù A., Silveirinha M. G. & Engheta N. Experimental verification of plasmonic cloaking at microwave frequencies with metamaterials. Phys. Rev. Lett. 103, 153901 (2009). [DOI] [PubMed] [Google Scholar]
  13. Rainwater D. et al. Experimental verification of three-dimensional plasmonic cloaking in free-space. New J. Phys. 14, 013054 (2012). [Google Scholar]
  14. Xu S. et al. Experimental Demonstration of a Free-Space Cylindrical Cloak without Superluminal Propagation. Phys. Rev. Lett. 109, 223903 (2012). [DOI] [PubMed] [Google Scholar]
  15. Pendry J. B., Schurig D. & Smith D. R. Controlling electromagnetic fields. Science 312, 1780 (2006). [DOI] [PubMed] [Google Scholar]
  16. Leonhardt U. Optical conformal mapping. Science 312, 1777–1780 (2006). [DOI] [PubMed] [Google Scholar]
  17. Schurig D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006). [DOI] [PubMed] [Google Scholar]
  18. Cai W., Chettiar U. K., Kildiev A. V. & Shalaev V. M. Optical cloaking with metamaterials. Nat. Photonics 1, 224–227 (2007). [Google Scholar]
  19. Smolyaninov I. I., Smolyaninova V. N., Kildishev A. V. & Shalaev V. M. Anisotropic metamaterials emulated by tapered waveguides: application to optical cloaking. Phys. Rev. Lett. 102, 213901 (2009). [DOI] [PubMed] [Google Scholar]
  20. Valentine J., Li J., Zentgraf T., Bartal G. & Zhang X. An optical cloak made of dielectrics. Nat. Mater. 8, 568–571 (2009). [DOI] [PubMed] [Google Scholar]
  21. Ergin T., Stenger N., Brenner P., Pendry J. B. & Wegener M. Three-dimensional invisibility cloak at optical wavelengths. Science 328, 337–339 (2010). [DOI] [PubMed] [Google Scholar]
  22. Zhang B. Electrodynamics of transformation-based invisibility cloaking. Light: Science & Applications 1, 32 (2012). [Google Scholar]
  23. Alù A. & Engheta N. Cloaking a sensor. Phys. Rev. Lett. 102, 233901 (2009). [DOI] [PubMed] [Google Scholar]
  24. Alù A. & Engheta N. Cloaked near-field scanning optical microscope tip for noninvasive near-field imaging. Phys. Rev. Lett. 105, 263906 (2010). [DOI] [PubMed] [Google Scholar]
  25. Cummer S. A. & Schurig D. One path to acoustic cloaking. New J. Phys. 9, 45 (2007). [Google Scholar]
  26. Torrent D. & Sanchez-Dehesa J. Acoustic cloaking in two dimensions: a feasible approach. New J. Phys. 10, 063015 (2008). [Google Scholar]
  27. Farhat M., Enoch S., Guenneau S. & Movchan A. B. Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Phys. Rev. Lett. 101, 134501 (2008). [DOI] [PubMed] [Google Scholar]
  28. Chen H. & Chan C. T. Acoustic cloaking in three dimensions using acoustic metamaterials. Appl. Phys. Lett. 91, 183518 (2007). [Google Scholar]
  29. Cummer S. A. et al. Scattering theory derivation of a 3D acoustic cloaking shell. Phys. Rev. Lett. 100, 024301 (2008). [DOI] [PubMed] [Google Scholar]
  30. Guild M. D., Haberman M. R. & Alù A. Plasmonic-type acoustic cloak made of a bilaminate shell. Phys. Rev. B 86, 104302 (2012). [Google Scholar]
  31. Guild M. D., Haberman M. R. & Alù A. Plasmonic cloaking and scattering cancelation for electromagnetic and acoustic waves. Wave Motion 48, 468–482 (2011). [Google Scholar]
  32. Guild M. D., Alù A. & Haberman M. R. Cancellation of acoustic scattering from an elastic sphere. J. Acoust. Soc. Am. 129, 1355–1365 (2011). [DOI] [PubMed] [Google Scholar]
  33. Milton G. W., Briane M. & Willis J. R. On cloaking for elasticity and physical equations with a transformation invariant form. New J. Phys. 8, 248 (2006). [Google Scholar]
  34. Brun M., Guenneau S. & Movchan A. B. Achieving control of in-plane elastic waves. Appl. Phys. Lett. 94, 061903 (2009). [Google Scholar]
  35. Farhat M., Guenneau S., Enoch S. & Movchan A. B. Cloaking bending waves propagating in thin elastic plates. Phys. Rev. B 79, 033102 (2009). [Google Scholar]
  36. Norris A. N. Acoustic metafluids. J. Acoust. Soc. Am. 125, 839–849 (2009). [DOI] [PubMed] [Google Scholar]
  37. Farhat M., Guenneau S. & Enoch S. Ultrabroadband elastic cloaking in thin plates. Phys. Rev. Lett. 103, 024301 (2009). [DOI] [PubMed] [Google Scholar]
  38. Stenger N., Wilhelm M. & Wegener M. Experiments on elastic cloaking in thin plates. Phys. Rev. Lett. 108, 014301 (2012). [DOI] [PubMed] [Google Scholar]
  39. Timoshenko S. Theory of Plates and Shells (McGraw-Hill, New York, 1940). [Google Scholar]
  40. Graff K. F. Wave Motion in Elastic Solids (Dover, New York, 1975). [Google Scholar]
  41. Farhat M., Guenneau S., Enoch S., Movchan A. B. & Petursson G. G. Focussing bending waves via negative refraction in perforated thin plates. Appl. Phys. Lett. 96, 081909 (2010). [Google Scholar]
  42. Farhat M., Guenneau S. & Enoch S. High directivity and confinement of flexural waves through ultra-refraction in thin perforated plates. EPL-Europhys. Lett. 91, 54003 (2010). [Google Scholar]
  43. Movchan N. V., McPhedran R. C., Movchan A. B. & Poulton C. G. Wave scattering by platonic grating stacks. Proc. R. Soc. A-Math. Phys. Eng. Sci. 465, 3383–3400 (2009). [Google Scholar]
  44. Antonakakis T. & Craster R. V. High-frequency asymptotics for microstructured thin elastic plates and platonics. Proc. R. Soc. Lond. A-Math. Phys. Eng. Sci. 468, 1408–1427 (2012). [Google Scholar]
  45. Supplemental materials section.
  46. Norris A. N. & Vemula C. Scattering of flexural waves on thin plates. J. Sound Vibr. 181, 115–125 (1995). [Google Scholar]
  47. Mei J., Ma G., Yang M., Yang J. & Sheng P. [Dynamic Mass Density and Acoustic Metamaterials] Acoustic Metamaterials and Phononic Crystals [Deymier, P. A. (ed.)] [159–200] (Springer-Verlag, Berlin, 2013). [Google Scholar]
  48. Li J. & Chan C. T. Double-negative acoustic metamaterial. Phys. Rev. E 70, 055602(R) (2004). [DOI] [PubMed] [Google Scholar]
  49. Liu Z., Chan C. T. & Sheng P. Analytic model of phononic crystals with local resonances. Phys. Rev. B 71, 014103 (2005). [Google Scholar]
  50. Mei J., Liu Z., Wen W. & Sheng P. Effective dynamic mass density of composites. Phys. Rev. B 76, 134205 (2007). [DOI] [PubMed] [Google Scholar]
  51. Wu Y., Lai Y. & Zhang Z. Q. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys. Rev. Lett. 107, 105506 (2011). [DOI] [PubMed] [Google Scholar]
  52. Zhou X., Liu X. & Hu G. Elastic metamaterials with local resonances: an overview. Theor. Appl. Mech. Lett. 2, 041001 (2012). [Google Scholar]
  53. Craster R. V., Kaplunov K. & Pichugin A. V. High-frequency homogenization for periodic media. Proc. R. Soc. A-Math. Phys. Eng. Sci. 466, 2341–2362 (2010). [Google Scholar]
  54. Liu Y., Guenneau S. & Gralak B. Causality and passivity properties of effective parameters of electromagnetic multilayered structures. Proc. R. Soc. A-Math. Phys. Eng. Sci. 469, 20130240 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Bigoni D., Guenneau S., Movchan A. B. & Brun M. Elastic metamaterials with inertial locally resonant structures: Application to lensing and localization. Phys. Rev. B 87, 174303 (2013). [Google Scholar]
  56. Farhat M., Chen P. Y., Guenneau S., Enoch S. & Alù A. Frequency-selective surface acoustic invisibility for three-dimensional immersed objects. Phys. Rev. B 86, 174303 (2012). [Google Scholar]
  57. COMSOL Multiphysics, http://www.comsol.com (2014).
  58. Alù A. & Engheta N. Plasmonic and metamaterial cloaking: physical mechanisms and potentials. J. Opt. 10, 093002 (2008). [Google Scholar]
  59. Dubois M. et al. Flat lens for pulse focusing of elastic waves in thin plates. Appl. Phys. Lett. 103, 071915 (2013). [Google Scholar]
  60. Brulé S., Javelaud E., Enoch S. & Guenneau S. Seismic metamaterial: how to shake friends and influence waves? arXiv:1301.7642 (2012).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary materials

srep04644-s1.pdf (203.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES