A Bottom-Up Approach to Understanding Protein Layer Formation at Solid-Liquid Interfaces

Abstract

A common goal across different fields (e.g. separations, biosensors, biomaterials, pharmaceuticals) is to understand how protein behavior at solid-liquid interfaces is affected by environmental conditions. Temperature, pH, ionic strength, and the chemical and physical properties of the solid surface, among many factors, can control microscopic protein dynamics (e.g. adsorption, desorption, diffusion, aggregation) that contribute to macroscopic properties like time-dependent total protein surface coverage and protein structure. These relationships are typically studied through a top-down approach in which macroscopic observations are explained using analytical models that are based upon reasonable, but not universally true, simplifying assumptions about microscopic protein dynamics. Conclusions connecting microscopic dynamics to environmental factors can be heavily biased by potentially incorrect assumptions. In contrast, more complicated models avoid several of the common assumptions but require many parameters that have overlapping effects on predictions of macroscopic, average protein properties. Consequently, these models are poorly suited for the top-down approach. Because the sophistication incorporated into these models may ultimately prove essential to understanding interfacial protein behavior, this article proposes a bottom-up approach in which direct observations of microscopic protein dynamics specify parameters in complicated models, which then generate macroscopic predictions to compare with experiment. In this framework, single-molecule tracking has proven capable of making direct measurements of microscopic protein dynamics, but must be complemented by modeling to combine and extrapolate many independent microscopic observations to the macro-scale. The bottom-up approach is expected to better connect environmental factors to macroscopic protein behavior, thereby guiding rational choices that promote desirable protein behaviors.

1. Introduction

Protein adhesion and layer formation at solid-liquid interfaces is a common process, but despite more than two decades of extensive research,^[1–2] many questions remain. Ultimately, research in this field seeks fundamental understanding that relates the surface coverage and biofunctional properties of the layer to environmental conditions such as the concentration of different protein species in solution, surface chemistry, temperature, pH, salt concentration, pressure, solvent, and many others.

Insight into interfacial protein behavior impacts a variety of applications. Chromatographic separations seek to tune the affinity of the interface to reversibly bind different protein species.^[3–7] Membrane filtration processes can suffer from protein adsorption that occludes membrane pores and decreases the filtration rate.^[8–9] In many different types of biosensors, non-specific protein adsorption to the sensor surface can obscure signal from the desired, specific interaction.^[10–12] Surfaces may also induce protein denaturation and/or aggregation, which can damage therapeutic protein drugs in vitro or participate in disease processes in vivo (e.g. amyloid plaque formation in Alzheimer’s disease).^[13–16]

Many applications seek to attract proteins to, rather than repel them from, solid-liquid interfaces. For example, coating surfaces with extracellular matrix proteins like collagen and fibronectin can promote cell adhesion and spreading in tissue engineering applications.^[17–18] It may also be desirable to passivate surfaces with a monolayer of ‘inert’ protein like albumin in order to prevent adsorption of more pathological proteins that can stimulate inflammatory responses.^[19–20] An important question in these applications is whether other plasma proteins will exchange with pre-adsorbed albumin when the passivated surface is exposed to blood.^[21–22] Still other applications like biosensing or targeted drug delivery rely on specific receptor-ligand interactions^[23–24] and therefore the interface cannot be designed to completely repel all proteins. An ideal surface for these applications would allow transient protein adsorption while preventing interactions that lead to irreversible, non-specific adhesion.

Interfacial protein behavior is often measured by exposing a surface to protein solution and measuring the net accumulation over time, until saturation coverage is reached.^[25–31] The contact solution can then be replaced with one that does not contain protein, allowing net migration away from the surface to be measured over time.^{[28–29,32–33]} In addition to protein coverage, the average protein conformation can be measured using spectroscopic techniques based on infrared (IR),^[34] circular dichroic (CD),^[35] or fluorescence signals.^[36] These data can be interpreted using models of protein-surface interactions,^[37–39] leading to parameters that describe microscopic interfacial protein behaviors and how they vary with environmental factors. Such parameters may include: rate constants for adsorption, desorption, and unfolding, average surface area per protein, and irreversibly adsorbed fraction.^[40]

This top-down approach to understanding protein-surface interactions is widely practiced but leads to conclusions that depend heavily on the underlying assumptions in the models. Unfortunately, models that are easily applied to experimental data often neglect important complexities that have been observed in detailed studies of interfacial protein behavior. For example, it is common to use a Langmuir model,^[41] or any one of several related models,^[42] to extract adsorption rate constants from variation in the average macroscopic protein surface coverage with time or concentration of protein in solution. Experiments may be repeated at different temperatures, and the resulting rate constants fit to the Arrhenius equation to determine an activation energy barrier that is assumed to represent the protein-surface interaction. However, this article will highlight that basic models of protein surface coverage neglect important protein-protein interactions that are influenced by interfacial diffusion and subtle orientational and conformational effects; these are kinetic processes with characteristic energy barriers independent of those for adsorption. The resulting apparent adsorption energy barrier will reflect contributions from many different physical processes, making it difficult to draw conclusions about the fundamental protein-surface interactions from these experiments. In contrast, more sophisticated models^[43–51] are available but often involve a large number of parameters and, except for a few limiting regimes, require numerical implementation. Consequently, it is impractical to use these more detailed models to extract microscopic parameters from macroscopic observations with good statistical confidence.

New experimental techniques permit direct observations of interfacial protein behaviors at the single-molecule level.^[52] However, it is not always straightforward to reconcile these microscopic and macroscopic observations. For example, while PEG-coated surfaces often demonstrate better anti-fouling behavior relative to hydrophobic surfaces,^[33,53–57] single-molecule measurements of surface residence times for isolated fibrinogen molecules were found, on average, to be longer on PEG-coated surfaces.^[58] Thus it is important to recognize that any one single-molecule experiment measures only a subset of the parameters in a larger system.

In light of the strengths and weaknesses of the experimental and theoretical approaches described above for understanding interfacial protein behavior, it seems appropriate to adopt a bottom-up approach in which microscopic observations from single-molecule experiments are fed into sophisticated models of protein layer formation, which are then used to predict macroscopic behaviors. In this approach, direct measurements are made of the relationship between environmental conditions and microscopic behaviors; modeling then combines the perspectives of many microscopic observations. While practical considerations force the top down approach to adopt a simplified view of protein behavior in order to describe the system with few parameters, the bottom-up approach permits a more sophisticated description of the system, so long as it is possible to independently specify many of the necessary input parameters.

This article will first provide an overview of models that are commonly used to describe macroscopic observations of protein monolayer formation in Section 2. Section 3 contains an overview of microscopic interfacial dynamics within the context of assessing the underlying assumptions in Section 2. Section 4 introduces more complicated models of protein layer formation and how they may be used to integrate experimental observations of microscopic dynamics, leading to a bottom-up, multi-scale approach to understanding interfacial protein behavior. Section 5 provides a critical assessment of single-molecule tracking (SMT) as an experimental tool to quantify microscopic dynamics while Section 6 summarizes the main conclusions and suggests how future research may advance the bottom-up approach described here.

2. Basic Models of Protein Monolayer Formation

The goal of this section is to outline the top-down approach to understanding protein monolayer formation, using a Langmuir model to demonstrate how parameters describing microscopic dynamic processes are extracted from transient and steady-state measurements of protein surface coverage. The Langmuir model has been widely criticized for deficiencies in describing protein adsorption and more complicated alternative models have been proposed that better describe experimental data.^[1] However, the Langmuir model is easy to understand, with a simple mathematical form that is derived in many of the cited references, and is therefore used as a representative of the broad class of top-down models that make ad hoc assumptions about microscopic protein dynamics in order to predict the macroscopic behavior.

When attempting to model the macroscopic surface coverage as a function of time after exposure to protein solution of constant concentration, at minimum one must consider the possibility that proteins can adsorb to and desorb from the surface as well as the fact that an interface has a finite area available for direct protein-surface contact. If interactions between different proteins are neglected, both adsorption and desorption are generally considered to be homogeneous first-order processes, each characterized by a single rate constant. The assumption of finite surface area is important because accumulation of protein on the surface decreases the area available for subsequent protein adsorption. For modeling purposes, a reasonable ad hoc assumption is that the surface can be decomposed into a lattice of adsorption sites that are completely filled by an adsorbed protein, with no interactions between sites. With the further assumption that adsorption and desorption are not rate-limited by diffusion to and from the interface, protein surface coverage (θ) as a function of time (t) is given by the Langmuir model (equation 1).^[38]

$$\theta (t)=\frac{c}{c+k_d/k_a}(1+e^{-(k_{a}c+k_d)t})$$ (1)

where c is the concentration of protein in solution and k_a and k_d are the first-order adsorption and desorption rate constants, respectively.

Qualitatively, equation 1 captures the fact that increasing protein concentration in bulk solution increases interfacial surface coverage and that the rate of net accumulation decreases as surface coverage increases. When fitting this model to experimental data to determine k_a and k_d, the steady-state surface coverage is the best indicator of the ratio k_d/k_a. While kinetic behavior at short times is most sensitive to k_a (where θ << 1), in practice this value can be highly error-prone due to the fact that techniques for measuring macroscopic surface coverage are often least accurate at low surface coverage. The corresponding desorption experiment, in which a surface at steady-state coverage is exposed to a solution with c = 0, can be used as an independent measure of k_d. In this case, desorption kinetics are expected to follow equation 2, which is valid only if readsorption of protein to the interface can be neglected. However, in practice, even if the bulk solution is presented with a large volume per area of interface such that the average protein concentration is negligible after desorption,^[59] a significant concentration boundary layer will be established that permits readsorption and alters the apparent desorption kinetics. The effect of the concentration boundary layer can be minimized using flow to remove desorbed protein. However, high shear rates at the interface invite questions whether shear is contributing to the observed desorption behavior.

$$\theta (t)=\frac{c}{c+k_d/k_a}{e}^{-k_{d}t}$$ (2)

Although experimental data of proteins desorbing from solid-liquid interfaces often appear to exhibit a distribution of characteristic decay constants^{[28,33,60–61]} (i.e. are not well-described by a single exponential decay constant) the use of equation 2 is required in order to compare k_d between adsorption and desorption experiments. Furthermore, surface coverage in desorption experiments generally reaches a non-zero value at long times rather than decaying to zero as predicted by equation 2. This behavior indicates the presence of an irreversibly bound fraction whose origins will be discussed in more detail in Section 3.3. For modeling within the Langmuir framework, however, an ad hoc correction can be made by adding a constant to equation 2 to represent the irreversible population.

The final step in the top-down approach is to vary environmental factors in order to determine their effects on the adsorption and desorption rates. For example, variation of k_a with temperature would yield an apparent activation energy barrier for adsorption (i.e. an Arrhenius analysis) that could be compared to predictions based on different intermolecular forces between protein and surface. It should be noted that, strictly speaking, an Arrhenius analysis is only correctly applied to parameters derived from the Langmuir model described above. Whereas both the Langmuir and Arrhenius models assume that desorption is an elementary process, characterized by a single energy barrier, many variants on the Langmuir model (discussed below) assume a distribution of energy barriers. A distribution of energy barriers would create a distribution of rate constants, each with different temperature-dependent behavior. Although this situation is not accounted for in the Arrhenius model of rate constants, the Arrhenius model is still used to interpret non-elementary protein adsorption kinetics.^[42]

The steady-state form of equation 1, θ(c) = c/(c+k_d/k_a), is often called the Langmuir isotherm. Although the Langmuir isotherm predicts that θ→1 for c >> k_d/k_a, it is often observed that θ(c) levels off at values significantly less than unity at high c. This phenomenon can be explained by a random sequential adsorption model (RSA), which does not assume regularly-spaced adsorption sites.^[62–65] Rather, adsorption occurs at random (i.e. off-lattice in the context of the Langmuir model) locations on the surface, leaving gaps between neighboring proteins that are too small to permit adsorption of a new protein. The maximum surface coverage in the RSA, often called the ‘jamming’ limit, depends on the assumed geometric footprint of the protein, with 2D circles or squares both expected to reach maximum area coverage between 0.54–0.56.^[37] However, protein mobility, specifically desorption and diffusion, would allow molecular rearrangements that eventually lead to a close-packed state with significantly higher surface coverage (e.g. 2D close packed circles yield θ ≈ 0.91, squares yield θ = 1). In practice, maximum surface coverage often falls somewhere between the close-packed and jamming limits.^[66–67] Perhaps more importantly, the neglect of desorption in the RSA model leads to significantly different kinetic predictions than the Langmuir model. Section 3 will present evidence that both desorption and interfacial diffusion play an important role in protein layer formation. Consequently, the kinetic behavior predicted by RSA is almost certianly wrong despite the fact that it partially explains the observation of a steady-state surface coverage below that of a close-packed monolayer. In practice, it is common to include the idea of imperfect packing into the Langmuir model by multiplying equation 1 by a constant, θ_max, such that

$$\theta (t)={\theta }_{\mathit{\text{max}}}\frac{c}{c+k_d/k_a}(1+e^{-(k_{a}c+k_d)t})$$ (3)

An ad hoc rationale for this additional parameter involves the notion that even in mobile systems, an object may exclude an interfacial area (due to molecular motions or repulsive enthalpic pairwise interactions) greater than its physical size. An important consequence of introducing a third parameter into equation 3 is that the determination of k_d/k_a is made with greater uncertainty and it becomes more important to determine k_d independently, as described above. Alternatively, coarse-grained structural models have led to statistical-thermodynamic theories that can provide semi-quantitative predictions of excluded volume effects and place reasonable bounds on θ_max.^[68]

The Langmuir and RSA models are not the only available descriptions of protein adsorption. For example, the Temkin^[69] and Elovich^[70] models postulate that the surface contains different types of sites for possible adsorption, with a uniform distribution of site-protein binding energies. Proteins first adsorb to sites that are most strongly binding, followed by subsequent adsorption to weaker sites. The macroscopic net adsorption rate appears to decrease over time because proteins are forced to find progressively weaker adsorption sites. This model was a better description of histidine-containing proteins onto copper-chelating surfaces than the Langmuir isotherm.^[71] In contrast, the Langmuir–Freundlich^[72] and Tóth^[73] models assume a Gaussian-shaped distribution of binding energies. Still other models assume the presence of discrete ‘states’, which may arise from different protein orientations or conformations, and allow for interconversion between these states on the surface.^[74–78] There are many such alternative ad hoc models^{[49–51,63–65,79]} that have advantages in describing specific subsets of protein-surface combinations and have been reviewed elsewhere.^[1] Like the Langmuir model, their common characteristic is that they all seek to extract unknown parameters, representing unobservable microscopic protein behavior, from the macroscopically observable surface coverage. Thus, given just the one observable property of surface coverage, a many-parameter model would risk over-fitting the data, and certainly it is very difficult to claim that a given model provides a unique description of the data, compared to the vast number of alternative models.

3. Microscopic Protein Dynamics

Numerous experimental studies highlight the fact that interfacial protein behavior is both more dynamic and more complex than assumed in models described in the previous section. This section will review some of this work and discuss its implications in the context of protein layer formation.

3.1 Adsorption and Desorption

Even at the macroscopic level, both adsorption and desorption are readily apparent using surface plasmon resonance,^[80–81] optical waveguide lightmode spectroscopy,^[82–83] quartz crystal microbalance,^[83–87] ellipsometry,^[83,88] and total internal reflection fluorescence (TIRF) spectroscopy.^[78] However, new perspectives on these processes have been provided by single-molecule tracking (SMT) experiments that are based on TIRF microscopy.^[89–90] In SMT, fluorescently-labeled proteins are observed, one-by-one, to adsorb, diffuse in the interfacial plane, and desorb. The time between adsorption and desorption is a direct measure of a protein’s surface residence time, and large numbers of these observations can be used to construct a probability distribution of surface residence times.

In one set of SMT studies, surface residence time distributions showed that the mean desorption rate constant for two different proteins, fibrinogen (Fg) and bovine serum albumin (BSA), on model hydrophobic, hydrophilic, and PEG-coated surfaces were of the order of 1–10 s⁻¹ when measured by SMT with temporal resolution of 0.2–2 s.^[58,91] In contrast, apparent desorption rate constants extracted from macroscopic measurements varied between 10⁻⁴–10⁻² s⁻¹ on different hydrophilic and hydrophobic surfaces for these same proteins.^[85] While the hydrophilic surfaces in these different studies carried opposite charges, it is at least possible to directly compare the hydrophobic trimethyl and octyl self-assembled monolayer surfaces where it is clear that desorption appears many orders of magnitude faster when observed at the single-molecule level than at the macroscopic level. Because SMT is a direct measurement of the elementary process of desorption, it must be concluded that the apparent, macroscopic desorption rate represents contributions from multiple desorption pathways that are characterized by different rate constants. In other words, it is an oversimplification to model protein desorption as a single, first-order process.

Interestingly, a different set of SMT studies, with a much lower temporal resolution of several tens of seconds, analyzed total BSA coverage as a function of time with a Langmuir model and found apparent desorption rate constants between 10⁻³–10⁻² s⁻¹.^[92–93] Thus, it seems reasonable to conclude that there is a significant population of adsorbed protein that is in rapid dynamic equilibrium with the bulk solution as well as a population with much slower dynamic behavior. In fact, multiple populations are often observed in SMT experiments on proteins, peptides, and DNA, and the shorter-lived populations are generally found to represent a much greater fraction of the full ensemble.^{[90,92,94–96]}

Part of the discrepancy between microscopic and macroscopic desorption rates may be explained to the behavior of protein aggregates. In SMT studies, surface residence time distributions of Fg and BSA could be described as the sum of contributions from multiple, independent, simultaneously occurring first-order processes (Figure 1A).^[58,91] Furthermore, fluorescence intensity data showed that some degree of heterogeneity could be explained by the presence of protein oligomers and that the mean desorption rate decreased systematically with increasing oligomer size. However, even the surface residence time distributions of the individual oligomeric states could not be described with a single, first-order rate constant. This suggests that both protein monomers and aggregates can interact with a surface in different ways that may be the result of different conformational states or orientations relative to the surface (see Section 3.3).

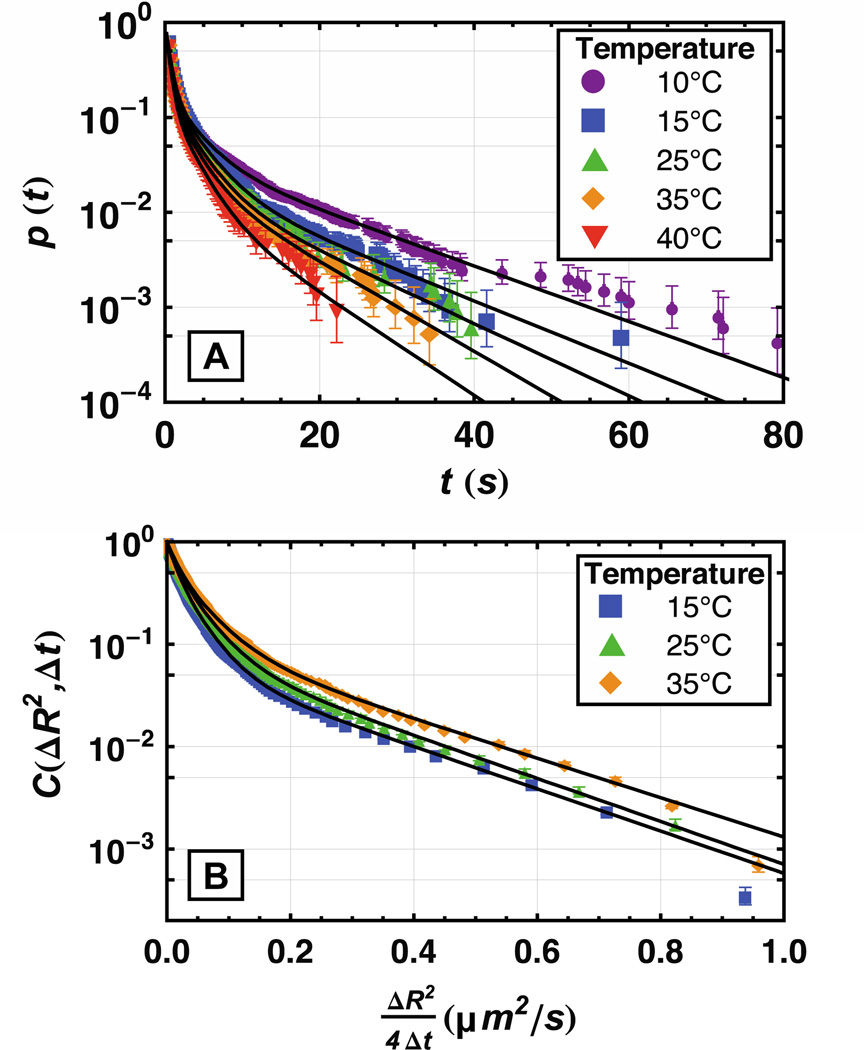
Figure 1.

Semilog plot of cumulative distributions for desorption and diffusion of Fg on fused silica at different temperatures. (A) In the cumulative surface residence time distribution, p(t) is the probability of observing a surface residence time longer than t. On these semilog axes, a single first-order desorption process would appear as straight line with slope equal to the negative of the rate constant. Significant deviations from this behavior are observed at all temperatures. (B) In the cumulative squared-displacement distribution, C(ΔR²,Δt) is the probability of observing a squared-displacement that exceeds ΔR² in a given time window (Δt) where Δt = 0.2 s. When C(ΔR²,Δt) is plotted on a logarithmic scale as a function of ΔR²/(4Δt), random-walk diffusion with a single diffusion coefficient (D) appears as a straight line with slope of −1/D. Multiple diffusive modes are required to describe these data. Reprinted from reference 90 with permission from the Biophysical Society.

Although fluorescence intensity was able to provide insight into aggregation phenomena underlying heterogeneous desorption kinetics in the above studies, the source of heterogeneity remains an open question for each specific system. For example, there may be a finite number of discrete ‘populations’ or a continuum of binding states,^[97] as suggested by the Temkin model of protein adsorption. Heterogeneous behavior may also result from nanoscale spatial variation in the properties of the surface.^[98] Although the adsorption rate was not measured in these SMT studies, it is also reasonable that heterogeneity exists in the adsorption process as well. Indeed, molecular dynamics studies have identified two different approach orientations that lead to different probabilities of successful adsorption events in the interaction between lysozyme and a polyethylene surface.^[99]

It is also possible that protein behavior at the ultra-low surface coverage used in SMT is different than at higher concentrations used for macroscopic measurements. In particular, events that are rare at low concentrations, e.g. interfacial protein-protein collisions, may become common at high concentrations. Generally speaking, it seems plausible that protein-protein interactions may be important at high concentrations, as has been suggested by molecular dynamics (MD) simulations of lysozyme on charged solid surfaces.^[100] The details of this trend, however, may be quite complex. For example, SMT has found fast desorption kinetics for the vast majority of Fg molecules even at higher bulk concentrations, where protein-protein interactions cannot be neglected.^[101] Thus, if desorption occurs rapidly, on average, but there is a heterogeneous distribution of desorption behaviors, it may be that the system contains processes that are relatively rare, but contribute disproportionately to the macroscopic observation. From a mechanistic perspective, therefore, it is important to understand the effect of environmental conditions on all populations.

One might attempt to argue that the only populations of importance are those that dominate the macroscopically observed behavior. From the perspective of understanding the role of environmental conditions in protein layer formation, it is not obvious that the microscopically observable populations can be ignored. For example, imagine a protein ensemble with a common, short-lived population and a rare, long-lived population as described earlier in this section. It may be that the conversion of proteins from the short-lived to the long-lived population is a critical feature of protein layer formation, which cannot be understood without a proper accounting of both populations. Continuing the example, imagine that the long-lived population represents protein aggregates while the short-lived population represents individual proteins. One surface may be better at inducing individual proteins to join aggregates, slowing the apparent desorption rate. With just the average observation, it would be easy to erroneously conclude that the direct protein-surface attraction increased on this surface when in fact the underlying mechanism, involving surface-induced aggregation, is completely different.

3.2 Diffusion

Diffusion is often neglected in models of protein dynamics at solid-liquid interfaces. This choice can be rationalized in terms of the Stokes-Einstein relationship for the diffusion coefficient (D) of a disk straddling an interface:^[102]

$$D=3k_{B}T/[16R({\eta }_1+{\eta }_2)]$$ (4)

Here, k_B is the Boltzmann constant, T is absolute temperature, R is the disk radius and η₁ and η₂ are the viscosities of the media on the different sides of the interface. As the interface in contact with water becomes more viscous, D should decrease and a solid interface, with infinite viscosity, will have D=0. However, Sriram et al. found that D deviates from predictions of equation 4 at high viscosities of the non-aqueous phase.^[103] Physically, this is because protein mobility is no longer dominated by Brownian motion but instead is believed to move through a series of partial or complete detachments from the solid surface that permit lateral translation.^[104] In this case, diffusion behavior is not governed by hydrodynamic effects but rather by energetics of interfacial interactions that determine the rate of detachment.

Macroscopic measurements of interfacial diffusion coefficients, using fluorescence recovery after photobleaching (FRAP)^[105] illustrate why it is tempting to neglect diffusion at the solid-liquid interface. These measurements show that protein diffusion coefficients at air-water interfaces (D ~ 10¹–10² µm²/s),^[106] or on model lipid bilayers in aqueous media (D ~ 10⁰–10¹ µm²/s)^[107] are much larger than at solid-liquid interfaces (D ~ 10⁻³–10⁻² µm²/s).^[108] Importantly, however, interfacial diffusion at solid-liquid interfaces is non-zero. The question then arises, “How low must D be in order to neglect interfacial diffusion?” In the context of protein layer formation, interfacial diffusion is expected to facilitate protein-protein interactions. Consequently, the significance of interfacial diffusion will depend on the average separation between proteins. If the instantaneous protein surface coverage is given by σ (units of molecules / area), then the characteristic time between protein collisions (τ_c) should be of order τ_c ~ (Dσ)⁻¹. In order for proteins to collide prior to desorption, τ_c should be less than the characteristic surface residence time, τ_s. For the short-lived protein population discussed in Section 3.1, τ_s is roughly 1 s. Therefore, assuming the interfacial diffusion coefficients mentioned above, this population will experience significant protein-protein interactions before desorption at surface coverages of σ ~ 10²–10³ molecules/µm². Given typical protein ‘footprints’ (10⁻⁵–10⁻⁴ µm²/molecule)^[21] it is reasonable to expect surface densities for a close-packed monomer of 10⁴–10⁵ molecules/µm². Thus, interfacial diffusion is expected to contribute significantly to protein-protein interactions at a fractional surface coverage as low as 10⁻³.

As was seen in the case of desorption kinetics, recent SMT experiments have brought new perspective to the understanding of interfacial diffusion. For example, it is commonly found that a diffusion model that relies on a single random-walk diffusion coefficient is inadequate to describe the distribution of squared displacements derived from observations of molecular position as a function of time (Figure 1B).^{[91,109–111]} It may be that the distribution of protein-surface interactions that leads to multi-modal desorption kinetics has a similar effect on diffusion, but it is important to note that the two processes are distinct. In particular, desorption depends on the energy landscape when moving normal to the interface while diffusion depends on the corrugation of the surface interaction potential in directions parallel to the interface. For example, a strong surface attraction that is independent of interfacial position (small corrugation) will lead to slow desorption and fast diffusion relative to a weak surface attraction that originates from discrete sites (high corrugation) around the interface.

Regardless of the underlying mechanisms, heterogeneous diffusion has important implications in the context of protein layer formation. Even in cases where the average diffusion coefficient for proteins at the solid-liquid interface is small, heterogeneity allows for the possibility that some proteins will diffuse much more quickly than average. This behavior was observed in separate SMT studies of Fg diffusion on a hydrophobic surface, which found diffusion coefficients between 0.7–1.3 µm²/s, roughly two orders of magnitude faster than the macroscopic observations described above.^[112–113] In order to better illustrate this rapid diffusion, a sample movie obtained in the experiments reported in work by Skaug et al.,^[113] is provided in the Supplementary Material. Fast diffusion is also inferred from macroscopic measurements in which models of FRAP data that account for separate populations of mobile and immobile molecules find D ~ 10⁻¹–10⁰ µm²/s for the mobile fraction.^[114–116] These fast-diffusing proteins may contribute disproportionately to protein-protein interactions but may be overlooked in measurements that report only average apparent diffusion.

As used above, heterogeneous diffusion refers to different behavior when comparing separate proteins. However, heterogeneity can also exist within the same molecule at different times. This scenario is generally referred to as anomalous diffusion,^[117] and surface-bound molecules have been found to exhibit subdiffusive behavior by switching between periods of near-immobilization and mobility with a broad distribution of ‘waiting times’ in the nearly immobile state.^[113,118] Although subdiffusion is often assumed to decrease the ability of a protein to sample its environment, recent simulations have shown that subdiffusion actually increases the probability of finding a nearby target.^[119] Thus at very low surface coverage, surfaces that encourage subdiffusive processes may increase the likelihood of protein-protein interactions in the early stages of layer formation. The extent to which the proposed mechanism is true for any specific system likely depends on whether ‘immobile’ proteins are truly immobile or are allowed to explore small, confined areas, with only the latter expected to improve search efficiency.

The above observations suggest that diffusion is an important feature of interfacial protein dynamics that increases the frequency of protein-protein collisions even at low surface coverage. Basic models of protein adsorption generally neglect interfacial diffusion, and this is a reasonable assumption if protein-protein collisions are essentially hard body interactions. However, the subsequent section will argue that protein-protein attractions are critically important in protein layer formation and thus diffusion must be accounted for. In these cases, surfaces that either promote fast diffusion or encourage efficient subdiffusive search mechanisms may exhibit greater net protein adhesion than surfaces with slower microscopic desorption rates but that hold adsorbed proteins in relatively fixed locations.

3.3 The Role of Protein-Protein Interactions and Surface Relaxation in Long-Lived Species

Macroscopic studies of protein adsorption commonly observe a fraction of molecules that appear ‘irreversibly’ bound whereby excessive rinsing of the surface simply does not remove all protein from the interface.^{[32,120–124]} However, there is still a question of whether adsorption is truly irreversible (i.e. leading to non-equilibrium behavior) or whether this population simply has a characteristic timescale for desorption that is much longer than the experimental observation.^{[78,125–126]} Although for most practical purposes the distinction is inconsequential, as will be discussed below, it is possible that protein denaturation and/or clustering phenomena may be responsible for long-lived protein species. Desorption of denatured protein in monomeric or cluster form could nucleate denaturation and/or aggregation of proteins in solution.^[127–129] For convenience, this work will hereafter refer to this phenomenon as irreversible adsorption with the understanding that this may not strictly be true.

Mechanistically, irreversible binding is often attributed to interfacial ‘relaxation’, which is a general term that may include protein unfolding and/or reorientation of protein relative to the interface. There is ample experimental evidence that the average structure of an adsorbed protein population often becomes increasingly denatured over time.^{[34–35,130–132]} Hydrophobic interactions are generally believed to drive interfacial denaturation, as the Gibbs free energy of unfolding is often related to the ability of an unfolded protein to sequester hydrophobic amino acid side chains away from contact with water.^[133–135] However, hydrophobically-driven denaturation is not always the dominant factor, as Baugh et al. observed a greater degree of spreading of fibronectin (Fn) on hydrophilic, as opposed to hydrophobic, surfaces.^[36] In this case, the ‘spread’ Fn conformation was better able to support cell adhesion and growth, presumably because this conformation presented important peptide sequences in the proper orientation for recognition by integrins on the cell surface. Other studies have also noted an increase in the size of the protein footprint after adsorption,^{[22,136–137]} which may correlate with changes in protein conformation but may also be due to conversion between end-on and side-on configurations in macromolecules with high aspect ratios.^[138–139] The consequence of protein spreading is that total surface coverage at apparent saturation often depends on the rate of adsorption relative to spreading; slower adsorption allows more time for spreading, which decreases the available area for subsequent adsorption.

From a modeling perspective, irreversible binding behavior can be added into basic models of protein adsorption as an additional level of complexity.^{[40,74–76,78,140–145]} More generally, these models can account for multiple different protein ‘states’, that each exhibit different dynamic behavior, with the potential to interconvert between states. Such states may result from different conformations or orientations relative to the surface or other proteins. In addition to distinguishing between qualitatively different protein states, it is also possible to model the effects of different interfacial contact areas in each state.^[49,146] However, it can be difficult to apply these models to experimental data on account of the fact that signatures of reversible and irreversible states, aside from interfacial affinity, are often subtle. For example, while CD and IR signatures can detect changes in secondary structure, tertiary changes, like the Fn spreading described above, can be observed only given a priori knowledge of the conformational change combined with highly specific experimental design to detect it. Even in cases where a distinct signal for conformational change is present, quantitative interpretation can be ambiguous.^[2] For example, a CD signal that shows the α-helix secondary structure decreased relative to random coils could be interpreted as evidence that some fraction of proteins lost all α-helix structure, that all proteins lost a fraction of helical structure, or somewhere between these extremes. Thus, models of multi-state protein behavior are often used to describe protein surface coverage using even more free parameters than are found in equation 3.

Due to the increase in parameters, it is important to note that agreement between models and experimental data does not necessarily justify the underlying assumptions of the models, even though these assumptions are often reasonable. For example, it is often assumed that surface-induced denaturation and conversion to an irreversibly bound state is responsible for a net increase of denatured protein at the interface. However, it is equally reasonable to hypothesize that net accumulation of denatured protein at the interface can result in the preferential adsorption and retention of species that are in states of lower structural stability in solution (i.e. that the surface acts as a ‘collector’ of these species).^[147] In this case, accumulation of denatured protein might be prevented by the addition of stabilizers to bulk solution, while surface-induced denaturation might be addressed by optimization of surface chemistry. Regardless of the mechanism behind irreversible adsorption, the vast body of literature cited here leads to the unambiguous conclusion that distinct protein states often exist on the surface and lead to macroscopic behaviors that cannot be predicted by basic models presented in Section 2.

Until now, this article has focused on the direct interactions between proteins and surfaces. However, there is increasing evidence from experiment, simulation, and theory that protein-protein attractions are important and may also explain irreversible binding behavior. Atomic force, electron, and fluorescence microscopy have been able to visualize cluster formation in different proteins at solid interfaces^{[79,121,148–152]} while simulations^[153–154] and theory^{[49– 51,79]} highlight that attractive interactions between proteins, combined with interfacial diffusion and/or the ability of a protein to adsorb directly into a cluster, are responsible for the appearance of clusters. Although a repulsive component of a protein-protein interaction is expected from the steric interactions combined with the fact that proteins often carry net charges of the same sign, a low Debye length in physiological environments can screen electrostatic repulsion and allow attractive interactions to overcome steric repulsion.^[155–157] Protein-protein attractions may stem from a combination of van der Waals, hydrogen bonding, and hydrophobic interactions between amino acid side chains as well as the peptide backbones of separate proteins. Additionally, the local distribution of positively and negatively charged amino acids may cause strong attraction despite the fact that the net protein charge would suggest repulsion. In addition, strong protein-protein attractions may be inherent in the structure of the protein, as is the case for proteins that form ordered, stable networks (i.e. S-layers) on solid or lipid-coated surfaces and are of increasing interest in nanotechnology applications.^[158–159] The interfacial dynamics of these proteins would make for an interesting comparison with proteins, such as albumin, which exhibit relatively weak protein-protein attractions.

Cluster formation is important in the biofunctionality of an adsorbed protein layer, as attractive protein-protein interactions in clusters may alter protein structure. This phenomenon has important implications for a number of disease states, including Alzheimer’s and Parkinson’s disease, which involve aggregation of mis-folded proteins aggregate into well-organized fibrils. These fibrils grow by a mechanism that involves a combination of protein adsorption and conformational changes.^[13–16]

Regarding the role of clustering in total protein surface coverage, both simulations and macroscopic and microscopic experiments indicate that despite the potential for many different attractive interactions between protein and surface, apparent activation barriers for protein desorption are relatively weak, on the order of a single hydrogen bond.^[160–165] However, SMT studies have shown that aggregated proteins have significantly slower desorption rates than the monomeric species and the apparent activation barrier for desorption increases with aggregation number.^[58,91] Thus, surfaces that promote more frequent protein-protein interactions are expected to lead to clustering and potentially more irreversibly bound protein (Figure 2A,B). More frequent protein-protein collisions result both from faster interfacial diffusion and from slower desorption and/or faster adsorption of irreversibly bound protein that increases the transient surface coverage. Perhaps less appreciated is the potential for the surface to influence the ‘productivity’ of protein-protein collisions (Figure 2C,D). In other words, the collision between two proteins may be more likely to result in a long-lasting association on one surface relative to another. For example, nanostructured polymer surfaces with anisotropic nanoscale topography^[166] are believed to pre-orient Fg monomers and promote the formation of stable clusters.^[101] Another mechanistic hypothesis is that surface interactions may ‘soften’ protein structure without completely denaturing the protein, thereby increasing the propensity for hydrophobically-driven aggregation.

Figure 2.

Indirect effects of environmental conditions on protein-protein interactions. In each example, protein-protein interactions are more important in the scenario shown to the right of the dashed line. The environment can increase the frequency of protein-protein interactions by higher surface coverage due to faster adsorption and/or slower desorption (A) or faster diffusion caused by smaller corrugations in the surface interaction potential (B). The tendency of a protein-protein interaction to result in aggregation can depend on orientation bias due to anisotropic protein-surface interactions (C) or protein denaturation due to strong protein-surface interactions (D).

4. Microscopic Observations Feed Complicated Models of Protein Dynamics

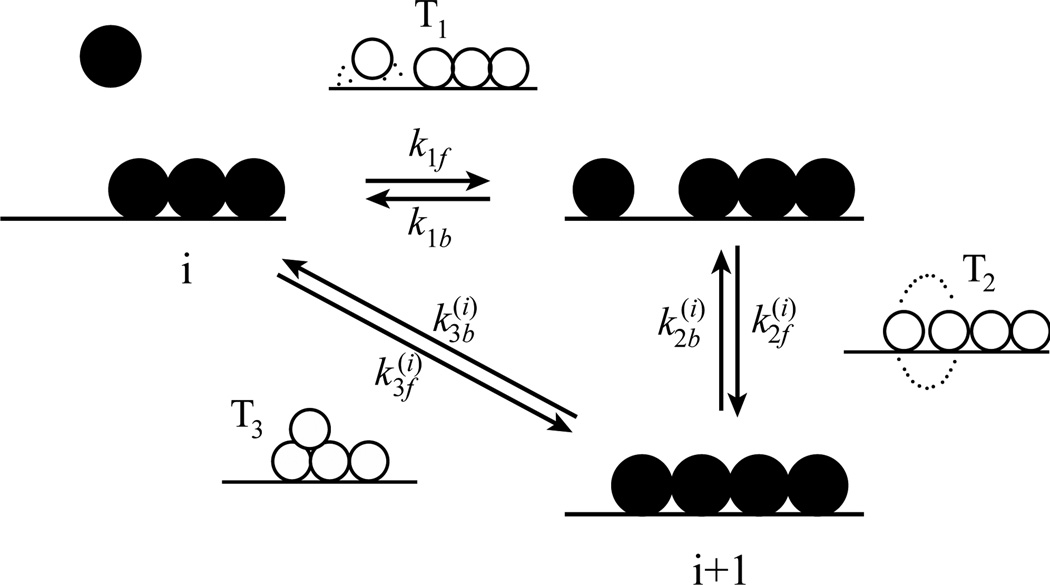
Many of the factors discussed above lead to strong deviations from Langmuir-like protein adsorption behavior predicted in Section 2. In response, Minton derived a more complicated ad hoc kinetic model of protein adsorption that included parameters to describe adsorption and desorption both to/from a monomer state and directly to a cluster state (Figure 3).^[50–51] Dynamic association and dissociation of clusters was also included via interfacial diffusion of monomers, while desorption and interfacial diffusion of clusters was neglected. This model also made reasonable assumptions about the shape and maximum size of clusters and included a description of excluded volume interactions between proteins based on scaled particle theory of mixtures of convex hard particles. After specifying the necessary parameters, the fractional surface coverage could be calculated as a function of time by solving a set of ordinary differential equations. By choosing different parameters, Minton was able to reproduce the qualitative features of various kinetic adsorption experiments, including those that exhibited positive or negative cooperativity as well as those that appeared to be Langmuir-like. Interestingly, “pseudo-Langmuirian” behavior was found under conditions where attractive and repulsive protein-protein balanced in contrast to the assumption of negligible protein-protein interactions in the Langmuir model.

Figure 3.

Schematic depiction of the Minton model. Different reversible pathways include: (1) direct deposition of monomer onto the surface, (2) incorporation of monomer into clusters by interfacial diffusion, and (3) piggyback deposition of monomers directly into clusters. Transition states are shown with open circles for each pathway. Pathways (2) and (3) can occur for clusters with aggregation number i. Reprinted from reference 49 with permission from the Biophysical Society.

Similar to Minton’s model, population-balance models were developed to describe cluster nucleation and growth in epitaxial films^{[43–44,47–48]} or self-assembled monolayers,^[45–46] but have also been applied to interfacial protein behavior.^[167] These models account for adsorption to and from a monomer state, cluster formation by interfacial diffusion of both monomers and larger aggregates, and desorption from both monomers and larger aggregates, but do not allow for cluster dissociation. Analogous population-balance models have been developed for protein aggregation in solution,^[168] and some variations of the solution models allow for dissociation of clusters.^[169] The possibility of protein multilayers can also be accounted for by adapting the approaches of previously developed theoretical models.^{[39,170–174]} In general, proteins that do not aggregate in solution have net repulsive interactions and are therefore expected to reach equilibrium at monolayer coverage because proteins in direct surface contact shield subsequently adsorbing proteins from attractive protein-surface interactions. However, the surface interaction may change the properties of proteins in the adsorbed monolayer, possibly through conformational changes, leading to attractive protein-protein interactions with a second layer of adsorbing proteins. This scenario can lead to a finite equilibrium thickness if the surface-induced protein-protein attraction decreases in layers that are farther from the surface (e.g. if conformational changes induced by protein-protein interactions are less pronounced than those induced by protein-surface interactions). Thus, it is possible to incorporate a wide variety of dynamic processes into a model of interfacial protein behavior at the cost of adding additional parameters.

The success of the models discussed above in predicting observable interfacial protein behavior emphasizes the benefit of including the microscopic phenomena discussed in Section 3. However, applying models containing many parameters to a system that has essentially one directly observable quantity (surface coverage) leads to high uncertainty in the exact value of each parameter. For example, while increased interfacial diffusion could increase cluster formation and consequently the total surface coverage, the same macroscopic phenomenon might also result from stronger protein-protein or protein-surface attractions. Thus, the optimal parameter values obtained in a typical regression scheme may be highly coupled. In principle, this uncertainty can be reduced if additional macroscopic observables, such as average protein secondary structure, can be both measured and predicted by the model and, therefore, used as additional constraints. In practice, however, it may be that observable secondary structure is only weakly related to distinct interfacial states for proteins that undergo important tertiary or quaternary structural changes, or simply reorient relative to the surface. Thus, it seems that the best way to reduce uncertainty is to measure at least some microscopic parameters directly.

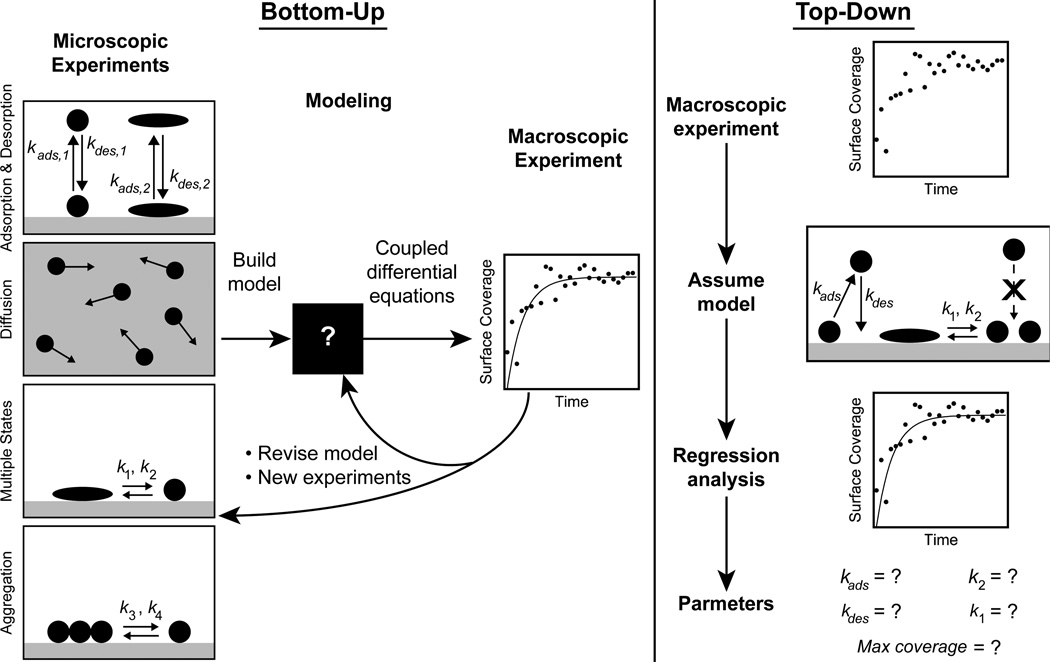
Given that the sophisticated models described above are most useful in combination with microscopic measurements of protein dynamics, it is reasonable to propose a bottom-up approach to understanding interfacial protein behavior. In this approach, microscopic observations are used to specify parameters and refine the underlying assumptions in a complicated model, which then generates predictions of macroscopic observations that are not readily deduced from the individual microscopic behaviors. Discrepancies between macroscopic prediction and observation can then generate hypotheses that are testable by new experiments at the microscopic level; this cycle can be repeated in order to reach consensus between prediction and observation. This approach is illustrated in Figure 4, which also provides contrast with the top-down approach of Section 2.

Figure 4.

Illustration of the bottom-up and top-down approaches to understanding interfacial protein dynamics. In the bottom-up approach (left), microscopic dynamics are observed directly. These observations are used to develop a model that predicts the macroscopic behavior. Comparisons between prediction and macroscopic behavior can suggest refinements to the model and new experiments at the microscopic level. In the top-down approach (right), a model incorporating a small number of dynamic processes is chosen to describe macroscopic experiments. The resulting model fit to the data yields parameters for the microscopic dynamics that depend on a correct initial choice of model.

An important advantage of the bottom-up approach is that models can be made arbitrarily complex as long as the added complexity is based on direct observations. In particular microscopic observations discussed in Section 3 suggest that, in addition to the clustering phenomena included in the population-balance framework, models may benefit from the inclusion of different states on the surface to represent the different conformations and orientations of proteins that lead to different surface affinity and mobility. Parameters to describe the kinetic behavior and relative prevalence of these states can be taken directly from available SMT literature. While it may be possible to directly observe different conformations^[175] or aggregation states^[176] at the single-molecule level, from a practical perspective, these states can be characterized by their dynamic behaviors (e.g. different desorption rates or diffusion coefficients) without fully understanding the molecular structure of each state. This approach would be sufficient for modeling total protein coverage but applications in which protein conformation is important would require greater effort to quantify the conversion rates between each state.

Model simplifications are also justified by microscopic measurements. For example, SMT studies suggest that interfacial diffusion of larger clusters may be reasonably neglected based on observations that diffusion slows rapidly as aggregation number increases.^[58,96] The resulting models would undoubtedly contain many coupled differential equations; however, this is not expected to pose a significant problem for modern computational capabilities. In the bottom-up approach, the system of coupled differential equations would only need to be solved for one set of parameters in order to compare with macroscopic observation. In contrast, to extract parameters from macroscopic observation, the top-down approach would require solving the system of equations $x={\prod }_{i=1}^N{b}_i^N$ times where N is the number of parameters and b_i is the number of variations of the i^th parameter. Obviously this would require substantially more computational effort for even modest values of N and b_i.

Simulations based on molecular dynamics (MD) can also support the bottom-up approach proposed here by testing molecular-level hypotheses that are difficult to address experimentally. A number of force fields and software packages, including AMBER,^[177] CHARMM,^[178] and GROMACS,^[179] have proven useful for simulating the behavior of proteins, peptides and other macromolecules at levels of detail ranging from quantum mechanical to atomistic to coarse grained approaches that treat groups of atoms as a single entity.^[180–181] In the context of protein layer formation, these simulations may provide insight into the physical origin of different ‘states’ that arise perhaps due to surface-induced conformational changes or from anisotropic interactions of various chemical groups on one protein either with the surface or with another macromolecule.^[182–183] Understanding the origin of interfacial interactions can lead to rational design of surfaces that control important dynamic behaviors. While these insights can aid the interpretation of experimental data, it is unlikely that simulations will provide direct quantification of dynamic parameters for use in the bottom-up approach depicted in Figure 4. This limitation stems from the fact that even relatively coarse-grained simulations can only access time scales of 10⁻⁷–10⁻⁶ s whereas the dynamic processes that likely contribute to protein layer formation (adsorption, desorption, protein-protein collisions, conformational change, etc.) can take place over much longer time scales (10⁻¹–10² s). Nevertheless, MD simulations may be used to map the free energy of a protein as a function of position (e.g. distance from the surface). This information can then predict apparent activation energy barriers that control kinetic rate constants, providing some understanding of the physical basis for experimentally observed rates.

5. The Ability of Single-Molecule Tracking to Resolve Microscopic Protein Dynamics

In recent years, SMT measurements have been increasingly used to observe microscopic interfacial protein dynamics. Rather than provide further review of these studies, this article will discuss the strengths and limitations of the technique for providing input to the bottom-up approach described above.

1. Sample size has long been a concern in SMT, as each molecule must be observed and tracked separately from all others; this can require significant computational effort. Recent advances in high throughput tracking methods have increased typical sample sizes by several orders of magnitude to 10⁴–10⁶ molecular trajectories, allowing relatively rare behaviors to be characterized with statistical significance.^[184] However, even a sample size of 10⁶ is still several orders of magnitude below the number of molecules that contribute to macroscopic measurements, making it inevitable that SMT will neglect some rare behaviors. Neglected rare events may or may not be important to the system in question, but this bias should be considered in conclusions drawn from SMT experiments.

2. A common expectation of SMT is that, because the point spread functions of fluorescent objects may not overlap, these experiments are done at ultra low surface coverage such that results are not applicable to higher coverage. While it is true that most SMT experiments are done at low surface coverage, arbitrarily high surface coverage may be studied so long as the surface density of fluorescently labeled objects is low.^[101,167] In other words, objects tracked in SMT can be used as representative probes of their local environment. An interesting application of this idea is to make near-direct measurements of surface coverage in which the number of probe molecules observed on the surface is a known fraction of the total molecules on the surface (equivalent to the fraction of labeled proteins in solution). This measurement will yield an absolute surface coverage without any assumptions about protein size or spectroscopic properties. Of course in order to confidently assert that solution and surface fractions of labeled proteins are equal, the measurement should be repeated with fluorescent dyes with different chemical structure (e.g. cyanine versus Alexa Fluor dyes) to demonstrate that the label does not significantly alter the behavior of the protein.

3. It is now relatively straightforward to use SMT to make direct observations of heterogeneous behavior in diffusion or desorption processes. However, artifacts in these data can result from finite temporal and spatial resolution. Temporally, SMT will neglect processes with characteristic time scales much faster than the minimum required time to observe interfacial positions. Very slow processes, on the other hand, may either exceed the practically observable time window and be neglected or may be very rare, as discussed above. Regarding diffusion, uncertainty in determining instantaneous object position, due both to motion blur and to noise in signal collection, leads to apparent diffusion that is faster than the true diffusion.^{[185– 186]} While this effect becomes increasingly important at higher temporal resolution, data analysis methods have been proposed to extract the true diffusive behavior.^[112] The significance of the artifacts discussed above should be considered on a case-by-case basis when drawing conclusions from SMT data.

4. Quantifying adsorption at the molecular level is not as straightforward as it is for desorption, which is characterized by a surface residence time distribution. For adsorption, the challenge is to distinguish between a ‘collision’ with the surface and the point at which a molecule crosses a free energy barrier to become ‘adsorbed’, and to quantity the fraction of collisions that result in adsorption. One might imagine doing this by setting a minimum surface residence time for a molecule to be considered adsorbed (often limited by the time resolution of the instrument), but this is an arbitrary criterion. In practice, the best strategy might be to extrapolate the measured surface residence time distribution back to zero time in order to determine the theoretical number of adsorbed objects. Furthermore, quantifying the number of protein-surface collisions will require high temporal resolution due to the high diffusion coefficients of proteins in solution (30–80 µm²/s). During typical observation periods (10⁻²–10⁻¹ s) necessary to measure object position in SMT, many objects that collide with the surface and diffuse back into bulk solution will appear to be background noise. However, temporal resolution approaching 10⁻⁵ s has been demonstrated using quantum-dot fluorescent labels that permit high-speed imaging, and similar experimental design may be useful in quantifying adsorption.^[187]

5. The use of single-molecule resonance energy transfer (RET) provides an orthogonal signal to distinguish protein structural changes or protein-protein associations from observations of molecular adsorption, diffusion, and desorption. In RET, energy is transferred nonradiatively from an excited donor fluorophore to a ground-state energy acceptor with an efficiency that depends on separation in the range of 1–10 nm.^[188] Measuring the distance between two points on a single protein can provide information about secondary and tertiary structure while the nanoscale distance between two proteins can be used to identify protein-protein associations such as nonspecific clustering or specific receptor-ligand binding. Indeed, SMT incorporating intramolecular RET has been demonstrated in freely-adsorbing, diffusing, and desorbing DNA molecules.^[189–190] The challenge for translating these methods to the study of interfacial protein behavior is the ability to place fluorescent labels in appropriate places on the protein. Although protein engineering techniques facilitate site-specific labeling, experimental design depends critically on a priori knowledge of the conformational states in question in order to correlate the donor-acceptor distance with conformational change. Such an approach was recently demonstrated in which site-specific fluorescence labeling allowed a conformational change in freely-adsorbing organophosphorous hydrolase to be measured at the single-molecule level.^[175]

Regarding protein-protein associations, labeling donors and acceptors at random sites on separate proteins creates a RET signature that can distinguish unassociated from associated states. Rabe et al. used such a strategy to observe slow spreading kinetics (over several hours) of large BSA clusters on hydrophilic and hydrophobic surfaces.^[191] A similar strategy has been used in SMT to observe highly dynamic, reversible associations between BSA on self-assembled monolayers of poly(ethylene glycol) at low protein surface coverage.^[176] Heterogeneity was observed in the characteristic protein-protein contact times that also correlated positively with RET efficiency, suggesting that larger aggregates were more stable. It therefore seems possible to make crude distinctions between proteins that associate with small versus large aggregates. While a precise description of dynamic behavior as a function of aggregation number is likely beyond the resolution of this technique, the ability to observe reversible protein associations at the single-molecule level can help to specify the association and dissociation rate constants for modeling purposes.

6. Summary and Outlook

Rigorous understanding of protein layer formation at solid-liquid interfaces is challenging simply because many microscopic processes (adsorption, desorption, diffusion, conformational change, aggregation, etc.) contribute in highly-coupled and potentially non-linear ways to relatively few observable macroscopic behaviors such as the time-dependent average surface coverage. Models that seek to connect macroscopic observations to microscopic dynamics that are influenced by the underlying solid surface properties must therefore make assumptions about microscopic processes that are reasonable but unjustified by the agreement between model and data. This top-down approach can lead to erroneous interpretations, both qualitatively and quantitatively, as models based on different assumptions can often explain the data equally well.

In contrast, a bottom-up modeling approach may lead to increased understanding by collecting many direct observations of distinct microscopic dynamic properties to justify a model that can explain macroscopic phenomena, thereby avoiding simplifying assumptions that are difficult to test. An important challenge for this approach is the number of simultaneously existing microstates that may arise due to protein aggregation or different conformations and orientations relative to the surface. Importantly, these distinct microstates will likely exhibit differences in dynamic rate constants for adsorption, desorption, diffusion, etc. Due to the added complexity required to account for each of these microstates, SMT is particularly useful for its ability to quantify heterogeneous interfacial behavior without the need to artificially tether proteins to the surface. As such, the proposed bottom-up approach will greatly benefit from improvements to the SMT approach, both experimentally and in the interpretation of the molecular trajectories that can be obtained. In particular, combining SMT with RET measurements, enabled by site-specific labeling methods, can help to clarify connections between protein structure and dynamic behavior. Additionally, simulations may help to interpret SMT data by identifying the physical origins of heterogeneous microscopic behaviors which will, in turn, lead to mechanistic understanding of the ways in which surface properties influence interfacial protein behavior.

Highlights.

• It is desirable to control interfacial protein dynamics using environmental factors

• Simple models of this process make assumptions that may lead to flawed conclusions

• More realistic models contain many unknown parameters with overlapping effects

• Single-molecule tracking makes direct observations of microscopic protein dynamics

• Bottom-up models combine microscopic observations to make macroscopic predictions