Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jun 3.
Published in final edited form as: J Biomech. 2014 Feb 14;47(8):1899–1903. doi: 10.1016/j.jbiomech.2014.02.011

Atomic Force Microscopy Determination of Young’s Modulus of Bovine Extra-ocular Tendon Fiber Bundles

Lawrence Yoo 1, Jason Reed 6, Andrew Shin 1,2, Joseph L Demer 1,3,4,5
PMCID: PMC4028417  NIHMSID: NIHMS567614  PMID: 24767704

Abstract

Extra-ocular tendons (EOTs) transmit the oculorotary force of the muscles to the eyeball to generate dynamic eye movements and align the eyes, yet the mechanical properties of the EOTs remain undefined. The EOTs are known to be composed of parallel bundles of small fibers whose mechanical properties must be determined in order to characterize the overall behavior of EOTs. The current study aimed to investigate the transverse Young’s modulus of EOT fiber bundles using atomic force microscopy (AFM).

Fresh bovine EOT fiber bundle specimens were maintained under temperature and humidity control, and indented 100 nm by the inverted pyramid tip of an AFM (Veeco Digital Instruments, NY). Ten indentations were conducted for each of 3 different locations of 10 different specimens from each of 6 EOTs, comprising a total of 1,800 indentations. Young’s modulus for each EOT was determined using a Hertzian contact model.

Young’s moduli for fiber bundles from all six EOTs were determined. Mean Young’s moduli for fiber bundles were similar for the six anatomical EOTs: lateral rectus 60.12 ± 2.69 (±SD) MPa, inferior rectus 59.69 ± 5.34 MPa, medial rectus 56.92 ±1.91 MPa, superior rectus 59.66 ±2.64 MPa, inferior oblique 57.7± 1.36 MPa, and superior oblique 59.15± 2.03. Variation in Young’s moduli among the six EOTs was not significant (P > 0.25).

The Young’s modulus of bovine EOT fibers is highly uniform among the six extraocular muscles, suggesting that each EOT is assembled from fiber bundles representing the same biomechanical elements. This uniformity will simplify overall modeling.

Keywords: biomechanics, extra-ocular tendon, orbital mechanics, strabismus

Introduction

Since extra-ocular tendons (EOTs) are manipulated by strabismus surgery for correction of binocular misalignment, it is important to understand their mechanical properties. Although some non-ocular tendon properties have been reported (Maganaris and Paul, 1999, 2002; Reeves et al., 2003), mechanical properties for EOTs have not yet been defined. In the absence of biomechanical data, the best current computational model of the biomechanics of the extraocular muscles and orbital tissues assumes that the EOTs are infinitely stiff (Miller et al., 1999). This obviously unrealistic assumption might cause erroneous simulation results, and highlights the need to obtain actual data on EOTs. Investigators in the field have employed various techniques to accurately determine the biomechanical properties of other orbital tissues, including conventional tensile elongation (Collins et al., 1981; Quaia et al., 2009a; Robinson et al., 1969; Simonsz, 1994; Yoo et al., 2009) and micro/nano indentation (Yoo et al., 2011c; Yoo et al., 2011d) methodologies. Despite studies in some tissues (Boyce et al., 2007; Quaia et al., 2009a; Quaia et al., 2009b; Yoo et al., 2011a; Yoo et al., 2009; Yoo et al., 2011b; Yoo et al., 2011c; Yoo et al., 2011d), however, many material parameters of orbital tissues have yet to be defined.

Atomic force microscopy (AFM) has emerged as a useful nanoindentation tool to determine properties such as the elastic modulus of biological specimens (Brunner et al., 2006; Kunda et al., 2008; Lu et al., 2006; Ludwig et al., 2008). In AFM, fine cantilevers serve as soft nanoindenters, allowing local testing of small and inhomogeneous specimens like cells or tissues (Collinsworth et al., 2002; Cross et al., 2008; Matzke et al., 2001; Pelling et al., 2007; Rotsch et al., 1999; Rotsch and Radmacher, 2000). Most current formulations used to compute mechanical parameters have been based on the Hertz model, as modified to match experimental conditions such as indenter shape or specimen thickness (Lin et al., 2007; Radmacher, 1997). The current project employed AFM to characterize, using the Hertzian theoretical framework, the Young’s modulus of the fiber bundles that comprise the fundamental building blocks of EOTs.

Methods

Specimen Preparation

Bovine specimens were obtained fresh from a local abattoir (Manning Beef LLC, Pico Rivera, CA). Total preparation time including transportation time for specimens averaged 60 ± 15 (SD) minutes. Figure 1 shows an EOT extraction site. All six extraocular tendons were extracted, and cylindrical fiber bundles were extracted from each under an optical dissecting microscope.

Figure 1.

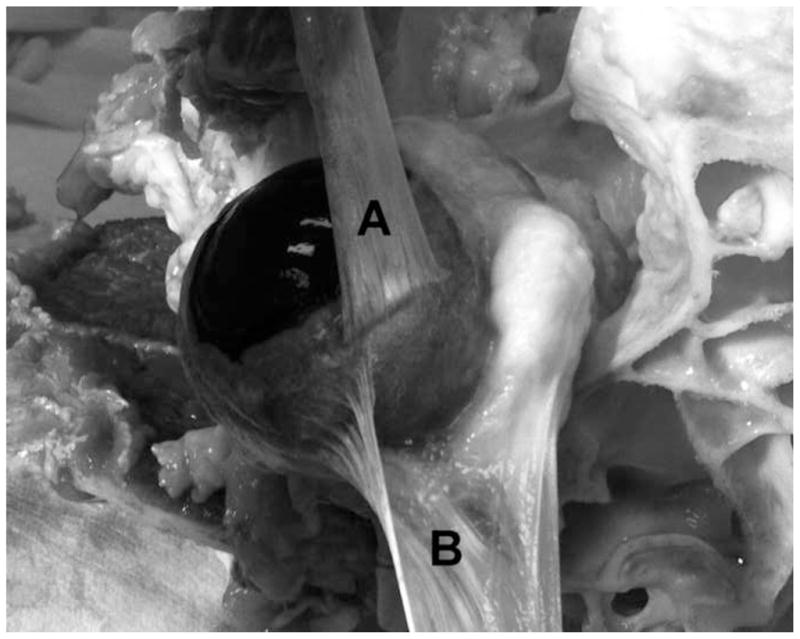
Figure 1

Open in a new tab

Two different bovine EOTs during extraction from a dissected orbit, illustrating their composition from numerous thin, parallel fiber bundles. A. Superior rectus EOT has been reflected anteriorly (upward in the photograph) over the cornea that is to the left. B. Superior oblique EOT has been reflected laterally (downward in the photograph) away from the sclera after fracture of the trochlea at upper right.

Fiber bundles had thickness ranging from 16 to 20 μm and the length ranging from 10 to 15 mm. Figure 2A shows a bovine EOT at low magnification.

Figure 2.

Figure 2

Open in a new tab

A. Bovine lateral rectus EOT showing horizontal grain composed of parallel fiber bundles. B. Extracted EOT fiber bundle contacted by AFM indenter at the tip of triangular cantilever whose shadow appears at right.

In order to avoid substrate effect, the ends and the middle of the extracted EOT fibers were glued to the glass bottom of a Petri dish. Ten fiber bundle specimens were prepared from each of the six anatomical bovine EOTs.

Nano-mechanical analysis of tendon fiber bundles using AFM

Experiments were conducted using a Dimension 5000 Scanning Probe Microscope (Veeco digital instruments, Plainview, NY) in contact mode. The spring constant of the cantilever was determined to be 0.02 Nm−1 by fitting the first resonance of the thermally-actuated spectrum. For distance calibration of the deflection signal, the sharpened silicon nitride cantilever bearing an inverted pyramid tip with 35° side angle was pushed against a glass substrate, for which zero indentation was assumed, to a known distance of 1 μm. Measurements were recorded at 37° C at 100% humidity and 1 Hz rate for 100 nm indentation at three different locations within each specimen. Force–displacement curves were recorded to determine the transverse stiffness (Young’s modulus, E) of tendon fiber bundles.

Hertz Model

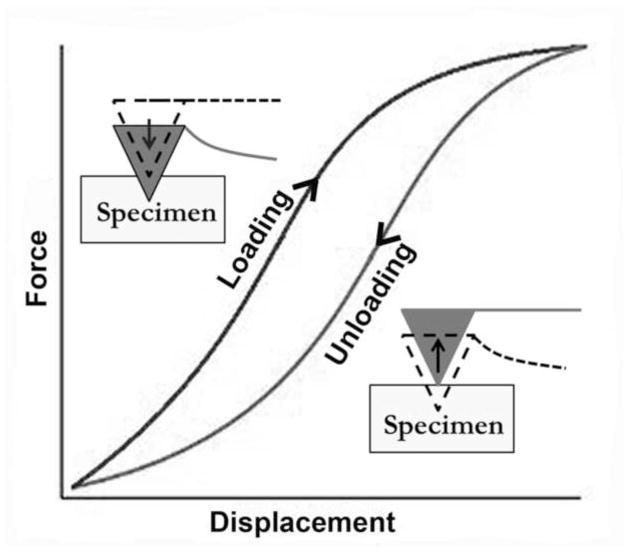
The Hertzian Model approximates the specimen as an isotropic, linear, elastic solid occupying an infinite half space. Furthermore, it is assumed that the indenter is not deformable and that there are no additional interactions between indenter and sample. If these conditions are met, the Young’s modulus (E) of the specimen can be determined. For most biological tissues, the energy delivered by the indenter is not completely returned upon withdrawal, but dissipates because of viscoelastic or plastic behavior that would also appear as the hysteresis difference between loading and unloading regions of the force curve (Figure 3). However, through preliminary experiments it was discovered that EOT fiber bundles exhibited no detectable hysteresis, and thus purely elastic mechanical behavior. Because loading and unloading phases overlapped without a hysteresis loop, it was justifiable to use the Hertzian contact model.

Figure 3.

Figure 3

Open in a new tab

Hypothetical force-displacement curve for viscoelastic soft tissue specimens. Difference between loading and unloading phases represents energy dissipated through viscosity.

Young’s moduli were calculated by converting force–displacement curves into force–indentation curves and fitting with the Hertz model. The Hertz model assumes indentation up to 3% of specimen thickness to be negligible in comparison to sample thickness, so that the substrate does not influence the calculations. The equation relating force, indentation, and Young’s modulus of the specimen is given in Eq.1 (Lin et al., 2007).

F=E1-υ2tanα2δ2 Eq.1

where F is indenting force, δ is indentation distance, E is Young’s modulus of the specimen, ν is the Poisson’s ratio, and α is the side face angle of the pyramidal indenter. More detailed discussion on the calculation and application of this model to mechanical properties of soft tissues can be found in previous publications (Almqvist et al., 2004; Matzke et al., 2001; Rotsch et al., 1997; Rotsch and Radmacher, 2000; Sneddon, 1965). For calculation of elastic behavior, the Poisson’s ratio of the specimen was assumed to be 0.5, as is typical for soft biological material where incompressibility is assumed. Analysis was restricted to low force ranges resulting in shallow indentations (<100 nm) to prevent damage to the specimen surface and to reduce any possible influence from substrate induced effects (Rotsch and Radmacher, 2000; Stolz et al., 2004).

Results

A total of sixty EOT fiber bundle specimens were prepared (10 specimens from each of six EOTs) and three different locations were chosen along each fiber bundle specimen to obtain 10 force-indentation recordings per site. Most of specimens revealed behavior close to linear albeit not perfectly. Because the Hertz model for a pyramidal indenter relates force to the square of indentation distance, fitting to any perfectly linear result produced more errors than fits to nonlinear results. Figure 5 shows samples of the best and worst fits of the model to the results.

Figure 5.

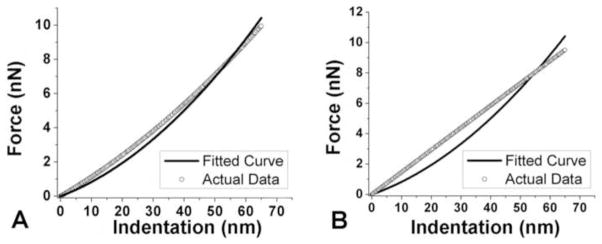
Figure 5

Open in a new tab

A. Best curve fitting to result. B. Worst curve fitting result that occurred when the behavior was purely linear.

After determination of Young’s modulus from curve fitting, values of Young’s modulus was averaged for each EOT fiber bundles and are plotted in Figure. 6.

Figure 6.

Figure 6

Open in a new tab

Mean Young’s modulus of fiber bundles for the 6 anatomical extraocular muscles. (N = 300 measurements each) A. Lateral rectus. B. Inferior rectus. C. Medial rectus. D. Superior rectus. E. Inferior oblique. F. Superior oblique.

Young’s modulus averaged over all fiber bundles from anatomical EOTs was 58.88 ± 3.35. Young’s moduli for the six different anatomical EOTs did not differ significantly as the T-test indicated. (P > 0.25)

Discussion

Nano indentation of EOT fiber bundles analyzed within the Hertzian framework effectively characterized the transverse Young’s modulus, a critical mechanical parameter, for bovine EOT fiber bundles. The authors believe that the present investigation is the first to do so by nano indentation characterization in EOT. The mean transverse Young’s modulus for fiber bundles from lateral, inferior, medial, superior recti, inferior and superior oblique EOTs were computed to be 58.88 ± 3.35 MPa, a value that did not vary significantly according to the anatomical extraocular muscle from which the EOTs were obtained.

Figure 7 shows previously reported Young’s modulus for a wide range of materials (Alonso and Goldmann, 2003; Dimitriadis et al., 2002; Stolz et al., 2004; Wenger et al., 2007). Fibers from EOT have a transverse Young’s modulus between stiff gelatin and protein such as collagen, and significantly higher than for cells or gelatin. Since EOT fiber bundles are comprised mainly of collagen, the observation that the Young’s modulus of EOT fiber bundles is appreciably less than that of collagen implies a more compliant micro-structure. Tendon fibers have been reported to have a helical microstructure that gives arise to volume loss under axial tensile loading (Reese et al., 2010; Rigby et al., 1959). It is also generally accepted that the helical structure of fiber bundles causes the fiber-aligned modulus to be one to two orders of magnitude larger than the transverse modulus (Lynch et al., 2003; Quapp and Weiss, 1998; Yamamoto et al., 2000). The presentation determination of EOT fiber bundle transverse Young’s modulus as one to two orders of magnitude less than the axial modulus of collagen is thus consistent with known properties of non-ocular tendons. The difference between transverse and axial Young’s moduli can result from an endotendinous sheath that provides a stress shielding effect (Yamamoto et al., 2000).

Figure 7.

Figure 7

Open in a new tab

Young’s moduli for various materials [31–34], including EOT fiber bundles.

Unlike other ocular and orbital tissues (Yoo et al., 2009; Yoo et al., 2011d), single fibers from EOT exhibit much higher stiffness and purely elastic, rather than viscoelastic, behavior. From previous investigations on viscoelastic characteristic of orbital/ocular tissues, it was reported that Young’s modulus of most of orbital tissues does not exceed 120kPa (Yoo et al., 2011d). Perhaps the purely elastic behavior of EOT facilitates the extreme eye movements also known as saccades, which are not only the fastest movements achieved by any part of the body, but are regulated by neural commands that appear optimized to minimize the time required to shift from one eye position to the next (Kirchner and Thorpe, 2006). Saccades must be brief because vision during the flight of a saccade is nearly impossible as saccade speed typically ranges from 300°/s to 600°/s; saccade durations range from 20 – 200 ms (Lebedev et al., 1996). Since EOTs are in series with the actuating extraocular muscles, any viscous behavior of EOTs would have the undesirable effect of damping peak saccade acceleration and prolonging the intra-saccadic period of impaired vision. Moderately high EOT stiffness would also be desirable, since elongation under load would dissipate the muscle force required to rotate the eye.

The highly reproducible determination of transverse Young’s modulus of EOT fiber bundles reported in the present study not only gives us an insight to the axial stiffness of EOTs, but also should facilitate quantitative modeling of ocular motor biomechanics. It would be reasonable to model all EOTs similarly, reducing the complexity of models representing interactions among multiple extraocular muscles. Such a representation might ultimately be represented using finite element analysis in a theoretical framework practical for graphical simulation of quasi-static strabismus and its surgical treatment.

The current investigation employed AFM to determine the transverse Young’s modulus of bovine EOT fiber bundles, and to demonstrate that they have negligible viscous properties. As anticipated, the determined value of Young’s modulus for EOT fiber bundles was significantly lower than that of collagen, suggesting that EOT fiber bundles incorporate fine structural features that increase compliance without introducing viscosity. Since the transverse properties of EOTs in macroscopic scale involve multi constituents such as collagen as well as components that comprise connective tissue sheath around the EOTs, the value of Young’s modulus reported in current investigation does not reflect the macroscopic properties of EOTs. However, the value reported in the current study can serve as the low threshold for EOT transverse properties in macroscopic characterization.

Figure 4.

Figure 4

Open in a new tab

Sample graph of loading and unloading phases of lateral rectus EOT. Loading and unloading phases of all EOTs exhibited exactly the same behavior, indicating pure elasticity to the limit of measurement error.

Acknowledgments

Support: Supported by U.S. Public Health Service, National Eye Institute: grants EY08313 and EY00331; and Research to Prevent Blindness. J. Demer is Leonard Apt Professor of Ophthalmology.

The authors acknowledge Manning Beef, LLC, Pico Rivera, CA, for their generous contribution of bovine specimens. We also thank Jose Martinez, Claudia Tamayo, and Ramiro Carlos of Manning Beef for assistance with specimen preparation and Im-Sun Joung for assistance with data processing.

Footnotes

Conflict of Interest Statement

The authors declare that none of them has any financial or personal relationships with people or organizations that can inappropriately influence this work or the conclusions drawn from this investigation.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting galley proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Almqvist N, Bhatia R, Primbs G, Desai N, Banerjee S, Lal R. Elasticity and adhesion force mapping reveals real-time clustering of growth factor receptors and associated changes in local cellular rheological properties. Biophys J. 2004;86:1753–1762. doi: 10.1016/S0006-3495(04)74243-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Alonso JL, Goldmann WH. Feeling the forces: atomic force microscopy in cell biology. Life Sci. 2003;72:2553–2560. doi: 10.1016/s0024-3205(03)00165-6. [DOI] [PubMed] [Google Scholar]
  3. Boyce BL, Jones RE, Nguyen TD, Grazier JM. Stress-controlled viscoelastic tensile response of bovine cornea. J Biomech. 2007;40:2367–2376. doi: 10.1016/j.jbiomech.2006.12.001. [DOI] [PubMed] [Google Scholar]
  4. Brunner CA, Ehrlicher A, Kohlstrunk B, Knebel D, Käs JA, Goegler M. Cell migration through small gaps. Eur Biophys J. 2006;35:713–719. doi: 10.1007/s00249-006-0079-1. [DOI] [PubMed] [Google Scholar]
  5. Collins CC, Carlson MR, Scott AB, Jampolsky A. Extraocular muscle forces in normal human subjects. Invest Ophthalmol Vis Sci. 1981;20:652–664. [PubMed] [Google Scholar]
  6. Collinsworth AM, Zhang S, Kraus WE, Truskey GA. Apparent elastic modulus and hysteresis of skeletal muscle cells throughout differentiation. American Journal of Physiology-Cell Physiology. 2002;283:C1219–C1227. doi: 10.1152/ajpcell.00502.2001. [DOI] [PubMed] [Google Scholar]
  7. Cross SE, Jin YS, Tondre J, Wong R, Rao J, Gimzewski JK. AFM-based analysis of human metastatic cancer cells. Nanotechnology. 2008;19:384003. doi: 10.1088/0957-4484/19/38/384003. [DOI] [PubMed] [Google Scholar]
  8. Dimitriadis EK, Horkay F, Maresca J, Kachar B, Chadwick RS. Determination of Elastic Moduli of Thin Layers of Soft Material Using the Atomic Force Microscope. Biophys J. 2002;82:2798–2810. doi: 10.1016/S0006-3495(02)75620-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kirchner H, Thorpe SJ. Ultra-rapid object detection with saccadic eye movements: Visual processing speed revisited. Vision Res. 2006;46:1762–1776. doi: 10.1016/j.visres.2005.10.002. [DOI] [PubMed] [Google Scholar]
  10. Kunda P, Pelling AE, Liu T, Baum B. Moesin controls cortical rigidity, cell rounding, and spindle morphogenesis during mitosis. Curr Biol. 2008;18:91–101. doi: 10.1016/j.cub.2007.12.051. [DOI] [PubMed] [Google Scholar]
  11. Lebedev S, Van Gelder P, Tsui WH. Square-root relations between main saccadic parameters. Invest Ophthalmol Visual Sci. 1996;37:2750–2758. [PubMed] [Google Scholar]
  12. Lin DC, Dimitriadis EK, Horkay F. Robust strategies for automated AFM force curve analysis-I. Non-adhesive indentation of soft, inhomogeneous materials. J Biomech Eng. 2007;129:430. doi: 10.1115/1.2720924. [DOI] [PubMed] [Google Scholar]
  13. Lu YB, Franze K, Seifert G, Steinhäuser C, Kirchhoff F, Wolburg H, Guck J, Janmey P, Wei EQ, Käs J. Viscoelastic properties of individual glial cells and neurons in the CNS. Proceedings of the National Academy of Sciences. 2006;103:17759–17764. doi: 10.1073/pnas.0606150103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ludwig T, Kirmse R, Poole K, Schwarz US. Probing cellular microenvironments and tissue remodeling by atomic force microscopy. Pflügers Archiv-European Journal of Physiology. 2008;456:29–49. doi: 10.1007/s00424-007-0398-9. [DOI] [PubMed] [Google Scholar]
  15. Lynch HA, Johannessen W, Wu JP, Jawa A, Elliott DM. Effect of fiber orientation and strain rate on the nonlinear uniaxial tensile material Properties of Tendon. J Biomech Eng. 2003;125:726–731. doi: 10.1115/1.1614819. [DOI] [PubMed] [Google Scholar]
  16. Maganaris CN, Paul JP. In vivo human tendon mechanical properties. The Journal of physiology. 1999;521:307–313. doi: 10.1111/j.1469-7793.1999.00307.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Maganaris CN, Paul JP. Tensile properties of the in vivo human gastrocnemius tendon. J Biomech. 2002;35:1639–1646. doi: 10.1016/s0021-9290(02)00240-3. [DOI] [PubMed] [Google Scholar]
  18. Matzke R, Jacobson K, Radmacher M. Direct, high-resolution measurement of furrow stiffening during division of adherent cells. Nat Cell Biol. 2001;3:607–610. doi: 10.1038/35078583. [DOI] [PubMed] [Google Scholar]
  19. Miller J, Pavlovski D, Shaemeva I. Orbit 1.8 gaze mechanics simulation. San Francisco: Eidactics; 1999. [Google Scholar]
  20. Pelling AE, Dawson DW, Carreon DM, Christiansen JJ, Shen RR, Teitell MA, Gimzewski JK. Distinct contributions of microtubule subtypes to cell membrane shape and stability. Nanomed Nanotechnol Biol Med. 2007;3:43–52. doi: 10.1016/j.nano.2006.11.006. [DOI] [PubMed] [Google Scholar]
  21. Quaia C, Ying HS, Nichols AM, Optican LM. The viscoelastic properties of passive eye muscle in primates. I: static forces and step responses. PLoS ONE. 2009a;4:e4850. doi: 10.1371/journal.pone.0004850. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Quaia C, Ying HS, Optican LM. The viscoelastic properties of passive eye muscle in primates. II: testing the quasi-linear theory. PLoS ONE. 2009b;4:e6480. doi: 10.1371/journal.pone.0006480. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Quapp K, Weiss J. Material characterization of human medial collateral ligament. J Biomech Eng. 1998;120:757–763. doi: 10.1115/1.2834890. [DOI] [PubMed] [Google Scholar]
  24. Radmacher M. Measuring the elastic properties of biological samples with the AFM. Engineering in Medicine and Biology Magazine, IEEE. 1997;16:47–57. doi: 10.1109/51.582176. [DOI] [PubMed] [Google Scholar]
  25. Reese SP, Maas SA, Weiss JA. Micromechanical models of helical superstructures in ligament and tendon fibers predict large Poisson's ratios. J Biomech. 2010;43:1394–1400. doi: 10.1016/j.jbiomech.2010.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Reeves ND, Maganaris CN, Narici MV. Effect of strength training on human patella tendon mechanical properties of older individuals. The Journal of physiology. 2003;548:971–981. doi: 10.1113/jphysiol.2002.035576. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Rigby BJ, Hirai N, Spikes JD, Eyring H. The mechanical properties of rat tail tendon. The Journal of general physiology. 1959;43:265–283. doi: 10.1085/jgp.43.2.265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Robinson DA, O'Meara DM, Scott AB, Collins CC. Mechanical components of human eye movement. J Appl Physiol. 1969;26:548–553. doi: 10.1152/jappl.1969.26.5.548. [DOI] [PubMed] [Google Scholar]
  29. Rotsch C, Braet F, Wisse E, Radmacher M. AFM imaging and elasticity measurements on living rat liver macrophages. Cell Biol Int. 1997;21:685–696. doi: 10.1006/cbir.1997.0213. [DOI] [PubMed] [Google Scholar]
  30. Rotsch C, Jacobson K, Radmacher M. Dimensional and mechanical dynamics of active and stable edges in motile fibroblasts investigated by using atomic force microscopy. Proceedings of the National Academy of Sciences. 1999;96:921–926. doi: 10.1073/pnas.96.3.921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Rotsch C, Radmacher M. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study. Biophys J. 2000;78:520–535. doi: 10.1016/S0006-3495(00)76614-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Simonsz HJ. Force-length recording of eye muscles during local anesthesia surgery in 32 strabismus patients. Strabismus. 1994;2:197–218. doi: 10.3109/09273979409035475. [DOI] [PubMed] [Google Scholar]
  33. Sneddon IN. The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. IJES. 1965;3:47–57. [Google Scholar]
  34. Stolz M, Raiteri R, Daniels A, VanLandingham M, Baschong WUA. Dynamic elastic modulus of porcine articular cartilage determined at two different levels of tissue organization by indentation-type atomic force microscopy. Biophys J. 2004;86:3269–3283. doi: 10.1016/S0006-3495(04)74375-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wenger MPE, Bozec L, Horton MA, Mesquida P. Mechanical Properties of Collagen Fibrils. Biophys J. 2007;93:1255–1263. doi: 10.1529/biophysj.106.103192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Yamamoto E, Hayashi K, Yamamoto N. Effects of stress shielding on the transverse mechanical properties of rabbit patellar tendons. J Biomech Eng. 2000;122:608–614. doi: 10.1115/1.1319660. [DOI] [PubMed] [Google Scholar]
  37. Yoo L, Gupta V, Lee C, Kavehpore P, Demer J. Viscoelastic properties of bovine orbital connective tissue and fat: constitutive models. Biomechanics and Modeling in Mechanobiology. 2011a;10:901–914. doi: 10.1007/s10237-010-0281-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yoo L, Kim H, Gupta V, Demer JL. Quasilinear viscoelastic behavior of bovine extraocular muscle tissue. Invest Ophthalmol Visual Sci. 2009;50:3721–3728. doi: 10.1167/iovs.08-3245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Yoo L, Kim H, Shin A, Gupta V, Demer JL. Creep behavior of passive bovine extraocular muscle. Journal of Biomedicine and Biotechnology. 2011b;2011 doi: 10.1155/2011/526705. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Yoo L, Reed J, Gimzewski JK, Demer JL. Mechanical interferometry imaging for creep modeling of the cornea. Invest Ophthalmol Vis Sci. 2011c;52:8420–8424. doi: 10.1167/iovs.11-7911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Yoo L, Reed J, Shin A, Kung J, Gimzewski JK, Poukens V, Goldberg RA, Mancini R, Taban M, Moy R, Demer JL. Characterization of ocular tissues using micro-indentation and Hertzian viscoelastic models. Invest Ophthalmol Vis Sci. 2011d doi: 10.1167/iovs.10-6867. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES