The cleverSuite approach for protein characterization: predictions of structural properties, solubility, chaperone requirements and RNA-binding abilities

Abstract

Motivation: The recent shift towards high-throughput screening is posing new challenges for the interpretation of experimental results. Here we propose the cleverSuite approach for large-scale characterization of protein groups.

Description: The central part of the cleverSuite is the cleverMachine (CM), an algorithm that performs statistics on protein sequences by comparing their physico-chemical propensities. The second element is called cleverClassifier and builds on top of the models generated by the CM to allow classification of new datasets.

Results: We applied the cleverSuite to predict secondary structure properties, solubility, chaperone requirements and RNA-binding abilities. Using cross-validation and independent datasets, the cleverSuite reproduces experimental findings with great accuracy and provides models that can be used for future investigations.

Availability: The intuitive interface for dataset exploration, analysis and prediction is available at http://s.tartaglialab.com/clever_suite.

Contact: gian.tartaglia@crg.es

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Due to the latest advances in technology, a large number of sequences have been deposited into databases (Harrow et al., 2012; Wang et al., 2012) and computational methods are being developed for their analysis and interpretation (Bailey et al., 2009; Dinkel et al., 2013). Some algorithms require per-case configuration (Buchan et al., 2013) or lack intuitive interface (Rost, 1996), which prohibits diffusion among non-computational scientists.

Experimental scales encoding physico-chemical properties are useful to retrieve basic information on protein sequences (Wilkins et al., 1999) and to predict features associated with protein folding (Gao et al., 2010; Tartaglia and Vendruscolo, 2010), aggregation (Fernandez-Escamilla et al., 2004; Tartaglia et al., 2008) and molecular interactions (Cirillo et al., 2013; Muppirala et al., 2011). For instance, the Zyggregator method predicts aggregation propensity using a combination of physico-chemical properties including secondary structure, solvent accessibility, hydrophobicity and polarity (Tartaglia and Vendruscolo, 2008). Similarly, the SVMprot algorithm exploits amino acid properties to predict protein families annotated in Pfam (Cai et al., 2003). Indeed, experimental scales can be employed to investigate large-scale properties of proteomes and identify common features (Hlevnjak et al., 2012; Zanzoni et al., 2013) but no systematic approach has been attempted so far to provide a general-purpose algorithm. We aim to provide researchers with an intuitive and statistically robust method to characterize protein groups exploiting the information contained in primary structure. Our premise is that the user should be able to make multiple hypotheses on the training sets and build models that others can test. As a general-purpose universal optimization is theoretically impossible (Ho and Pepyne, 2002), our strategy is to build a class of predictors that are specific for the individual problems. We pay particular attention to derive unbiased models because over-fitting of internal parameters can undermine the general applicability of algorithms (Hawkins, 2004; Tartaglia et al., 2004).

Our approach, the cleverSuite, provides a series of easy-to-use, configuration-free tools with interactive graphical interface. The central part of the suite is the cleverMachine (CM), an algorithm to characterize protein datasets. CM does not require external fitting parameters and returns multiple physico-chemical properties ranked by their significance. Relevant properties are merged together to provide coherent and consistent classification, allowing complex feature analysis. The second element of our suite is the cleverClassifier (CC) that builds on top of results generated by the CM to allow classification of protein datasets using state of the art machine-learning approaches (Pedregosa et al., 2011). CM and CC algorithms are freely available at http://s.tartaglialab.com/page/clever_suite.

We illustrate the powerfulness of our approach by making predictions of several protein features, including structural disorder (Sickmeier et al., 2007), solubility (Niwa et al., 2009), chaperone interactions (Calloni et al., 2012; Kerner et al., 2005) and RNA-binding abilities (Baltz et al., 2012; Castello et al., 2012). CM and CC models that are available for consultation at: http://s.tartaglialab.com/clever_community.

2 METHODS

2.1 The cleverMachine

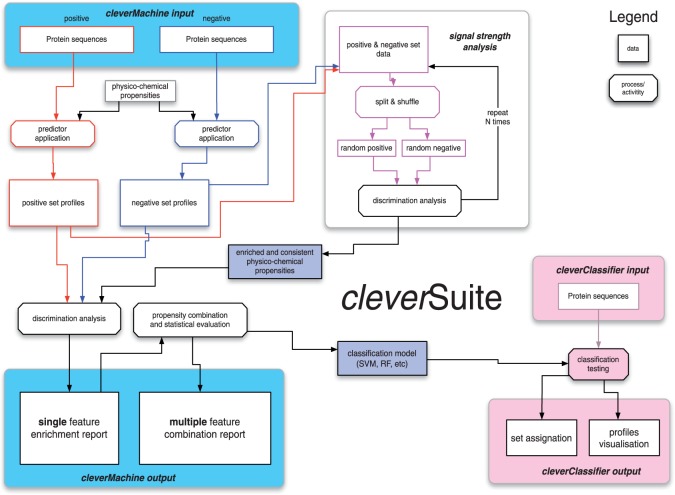
The algorithm evaluates relative difference in physico-chemical properties between two provided datasets. The first dataset is considered to be positive (P) and the second negative (N). The operations of the algorithm consist of multiple stages (Fig. 1).

Fig. 1.

The cleverSuite algorithm. The CM estimates the ability of physico-chemical properties to discriminate two input datasets. The statistical analysis gives information about individual property coverages and strength with respect to randomized sets. An exhaustive property-combination search is performed to assess the significance of the datasets separation. The CC uses the models generated by CM to classify new datasets to either the positive or negative set. Individual physico-chemical profiles are reported along with the discrimination statistics

2.1.1 Data generation

The raw information is extracted from protein sequences using experimental physico-chemical propensities. Our curated database contains 80 physico-chemical propensities, derived from experimental data [e.g. hydrophobicity (Black and Mould, 1991; Bull and Breese, 1974; Fauchere and Pliska, 1983)] and statistics on computational tools. Physico-chemical propensities are organized into groups based on higher level properties (Fig. 2 and Supplementry Fig. S1). At present, we use eight classes (hydrophobicity, alpha-helix, beta-sheet, disorder, burial, aggregation, membrane and nucleic acid-binding propensities), but additional descriptors are allowed (see Section 2.3). For a given propensity, each protein sequence is scanned using a sliding window, moved one residue at a time, starting from the N-terminus (protein profile). The size of the sliding window is set to 7 amino acids to allow best discrimination between alpha helix (hydrogen bonding in the range 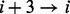and 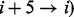and beta sheet (strands between 3–10 amino acids) elements, but it can be modified.

Fig. 2.

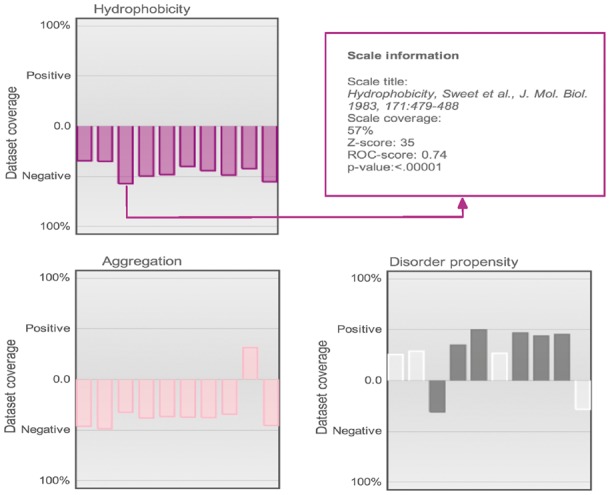
Grouped property view. Example of properties grouped by class assignment and color (each property is described by 10 predictors). The E.coli solubility analysis is used as illustrative case: soluble proteins (positive case) are more disordered and less hydrophobic/aggregation prone. Low-significance properties (Z-score < Z_th; P > 0.01; Section 2) are devoid of color. In the webserver, this view is interactive and shows information about each scale after clicking (see also Supplementary Fig. S1)

2.1.2 Signal detection

For each property, we count how many proteins from one dataset have profiles enriched with respect to the other dataset:

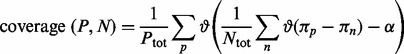(1)

In Equation (1), 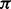is the signal extracted from the protein profile, the counter 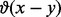is 1 if 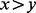and 0 otherwise 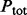and and 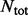are the total number of sequences in P and N datasets. The internal parameter 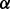is a cut-off used in the counting (see Section 2.1.6). The coverage is calculated for all proteins from both datasets and individual scale enrichments (i.e. fractions of P and N that can be discriminated) are calculated. For each physico-chemical propensity, the algorithm estimates the area under the receiver operating characteristics curve (AUC). In the five cases reported in this article, AUC and 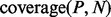show more than 0.85 correlation (Fig. 3 and Supplementary Fig. S2). As AUC is cut-off independent, the high correlation indicates that 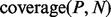depends only weakly on 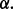It is important to mention that the ROC analysis is not defined in multiple dimensions (Li and Fine, 2008), while different physico-chemical properties can be combined into an overall coverage. Coverage of 50% indicates that half of the dataset is differentially enriched (expectation for a random set is 25% corresponding to 0.5 of AUC; Fig. 3 and Supplementary Fig. S2).

Fig. 3.

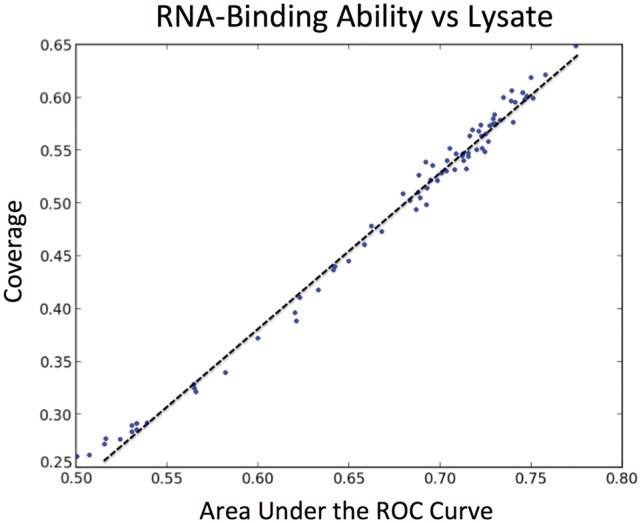
Correlation between coverage and AUC. For the five cases presented in this study, AUC and coverage of individual physico-chemical properties show a correlation r > 0.85. In this example, we use human RNA-binding proteins (compared with lysate; r = 0.95)

2.1.3 Properties selection and combination

To calculate the significance of each physico-chemical property, P and N are merged together and shuffled sets matching P and N in size are extracted. The procedure is repeated R times. For each of the randomized dataset pairs, we estimate the coverage. Information from the random dataset discrimination is used to rank properties significance using Z-scores and their associated P-values (Supplementary Fig. S3). Properties not meeting the criteria Z-score > Z_th and P-value < 0.01 are excluded from the analysis. Using 500 random sets, we observe that optimal values are Z_th = 6 and R = 15. To check consistencies among predictors of the same physico-chemical propensity, we group the properties by higher level features and also highlight the ones that pass the selection criteria (Fig. 2 and Supplementary Fig. S1). For each combination of properties ranging from 1 to 5 (∼10⁷ alternatives), the overall coverage (union of individual coverages) is calculated and the best-performing set is selected (Fig. 4). We observe that some physico-chemical properties are correlated. Nevertheless, since the algorithm selects only the most discriminative combination of properties, correlation does not represent a limitation. In fact, if two properties produce overlapping lists of proteins, their combination creates smaller coverage compared to scales that are more different.

Fig. 4.

Scale combinations and statistics. (A) Relationship between the number of combined scales and the coverages for both positive (blue bars) and negative (green bars) datasets. (B) Statistics for each scale combination and its individual members. In the webserver, click-through the combination titles reveals scales contained and detailed statistics (three-scale combination is shown; the E.coli solubility analysis is used as example). This view is used to summarize results of both CM and CC

2.1.4 Model generation

In order to identify the best model for further set classification, the algorithm evaluates combination of scales with multiple machine learning methodologies. The selected classifiers include random forests, support vector machine, nearest neighbour and adaptive boosting algorithms (Pedregosa et al., 2011). To avoid set size bias, we perform multiple equal size samplings from each of the datasets. Moreover, we perform 10-fold cross-validation with each of the models to select the best performing (highest accuracy) algorithm.

2.2 The cleverClassifier

The main goal is the set-wide assignment of query X to either P or N set from the reference submission (Fig. 1). The prediction is carried out using the best model evaluated on reference data. CD-HIT (Fu et al., 2012) algorithm is employed to detect set sequence similarity of X with respect to reference. If the similarity exceeds 10%, the value is reported to the user. Random sets generated with the same AA composition as the reference sets are employed to estimate signal strength, which is defined as the difference between performance of set X (i.e. fraction of cases that can be classified) and random sets. Signal strength ranges between 0 (no enrichment) to 0.5 (strong signal) (Supplementary Tables S1 and S2). For each of the entries from dataset X, individual physico-chemical profiles (Supplementary Fig. S4) are reported together with element assignment to either P or N. Moreover, for each individual prediction we estimate prediction strength using consensus from cross-validation models.

2.3 Additional features

(i) Custom scales: if the ‘expert mode’ option is selected in the webserver, the user can submit up to 10 amino acid scales for CM calculations. As CM employs 10 scales for each physico-chemical group (e.g. hydrophobicity) we suggest a similar approach for the choice of additional scales. Custom scales do not need to be normalized.

(ii) Derived scale: at every run, CM produces an ad hoc scale derived from the input sets (‘expert mode’). The scale is measured by considering the frequency of each amino acid in both sets P and N:

(2)

In Equation (2), amino acid frequencies are normalized: 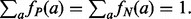The derived scale can be used in CC runs (see (i) above).

(iii) Adaptive threshold: the optimal cut-off 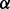corresponds to the highest coverage with respect to shuffled sets:

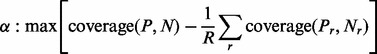(3)

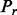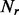The number of shuffled sets and is 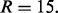If the ‘expert mode’ option is selected, the algorithm optimizes 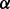for the input sets. In the ‘normal run’ mode, the cut-off is 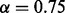(Supplementary Fig. S5).

(iv) Peak detection: the coverage can be computed using (a) the average of physico-chemical profiles or (b) regions that deviate more than one standard deviation from the average score. Average score and standard deviation are estimated from the distribution of profiles (considering both positive and negative sets). The use of a threshold, previously implemented for the calculation of aggregation properties (Tartaglia and Vendruscolo, 2008), introduces a sequence-position dependency in the calculation of profiles.

3 RESULTS

A sketch describing CM and CC workflow is presented in Figure 1. The goal of the CM algorithm is to discriminate between two protein sets. A number of properties, including hydrophobicity, alpha-helical, beta-sheet, disorder, burial, aggregation, membrane and nucleic acid-binding propensities, are employed to build physicochemical ‘profiles’. The physico-chemical properties are combined together to identify similarities and differences between the two sets. Once the discriminating properties are characterized, CM generates a model, which is employed by CC to classify new datasets. As shown in the examples below, we tested CM and CC performances on protein features such as secondary structure, structural disorder, solubility, chaperone requirements and RNA-binding ability (Supplementary Table S1). Unless otherwise stated, we always remove overlap between training and test sets using CD-HIT with default cut-off set for sequence similarity (Fu et al., 2012).

3.1 Alpha-helix versus beta-sheet proteins

In this first introductory example, we trained CM to distinguish between alpha-helical and beta-sheet proteins. The PDB database (Bernstein et al., 1977) was used to retrieve protein structures, STRIDE (Heinig and Frishman, 2004) was applied to analyse alpha-helical and beta-sheet content and CD-HIT (Fu et al., 2012) was employed to filter out sequences with >50% identity. After sequence redundancy removal, the alpha-helical set consisted of 277 proteins adopting >80% of alpha-helical conformation while the beta-sheet set was comprised of 191 proteins containing >60% of beta-sheet content. Sequences coding for alpha-helical structures were used to build the positive set, while the negative set consisted of beta-sheet proteins.

3.1.1 Performances

In striking agreement with structural classification, we found that even a single physico-chemical scale of alpha-helical propensity (Deléage and Roux, 1987) is able to discriminate 98% of the two sets with a 99.0% accuracy and 100% precision (Table 1). Hence, CM shows ideal performances in separating alpha-helical and beta-sheet proteins. All alpha-helical scales (Burgess et al., 1974; Chou and Fasman, 1978; Kanehisa and Tsong, 1980) showed consistent enrichment in the positive set, while the beta propensity scales displayed significant enrichment in the negative set (the signal is strong with respect to permutated input sets with P-value < 0.01) (Chou and Fasman, 1978; Deléage and Roux; Kanehisa and Tsong, 1980; Levitt, 1978; Prabhakaran, 1990).

Table 1.

cleverSuite performances

	cleverSuite			Reference
	ACCa (%)	TPRb (%)	TNRb (%)	Method	TPRc (%)	TNRc (%)
Alpha-beta	97.9	90.4	93.2	RePROF	92.6	72.0
Disorder	86.1	84.5	73.6	FoldIndex	62.9	64.7
Solubility	89.8	84.7	60.5	PROSO II	78.5	74.0
Chaperones	81.6	75.4	60.0	Limbo	100.0	22.5
mRNA	84.3	72.9	79.2	RNApred	82.5	52.8

^aA 10-fold cross-validation accuracy for CM models (ACC is accuracy).

^bIndependent validation performances for CC.

^cPerformance comparison with algorithms reported in literature. TPR (true positive rate) and TNR (true negative rate) are calculated on the same sets used to validate CC. Links to full results are given in Supplementary Table S1.

3.1.2 Cross-validation

Through a 10-fold cross-validation on both sets, our CM showed accuracy of 97.9% (Table 1). When compared to random sets, the signal strength was 0.5 (Supplementary Table S2). CM selected AdaBoost (Pedregosa et al., 2011) classifier as the best performing algorithm for this calculation.

3.1.3 Independent validations

We downloaded alpha/beta proteins from SCOP (Andreeva et al., 2008). After redundancy removal (CD-HIT 50), the alpha-helical set consisted of 176 proteins adopting >80% of alpha-helical conformation while the beta-sheet set was comprised of 79 proteins containing >60% of beta-sheet content. Our predictions showed accuracy of 90.4% for alpha-helical (positive set) and 93.2% for beta-sheet (negative set) assignments (Table 1). The testing sets achieved separation from random of 0.4 (alpha-helix) and 0.4 (beta-sheet). On the same datasets, the RePROF (Rost, 1996) algorithm yielded accuracies of 92.6% (alpha-helical proteins) and 72.1% (beta-sheet proteins; Table 1 and Supplementary Material). As an additional test we used NetSurfP (Petersen et al., 2009) that achieved accuracy of 96% (alpha-helical proteins) and 64% (beta-sheet proteins).

3.2 Structural disorder

It has been shown that natively unfolded proteins are implicated in cellular regulation, signalling and assembly of macromolecular complexes (Dunker et al., 2002). Absence of native structure has functional implications for complex organisms (Koonin et al., 2002). In fact, higher eukaryotes show larger amount of intrinsically disordered proteins with respect to prokaryotes (Tartaglia et al., 2005). We applied our algorithm to intrinsically disordered proteins [positive set containing 630 proteins from DisProt (Sickmeier et al., 2007)] and structured proteins [negative set containing 3347 proteins from SCOP (Andreeva et al., 2008)].

3.2.1 Performances

CM identifies disorder as the most discriminative physico-chemical property: TOP-IDB and DisProt cover respectively 65.5% and 61.0% (Campen et al., 2008; Sickmeier et al., 2007). We found that disordered proteins are more hydrophilic and soluble. Indeed, the coverage is 50% for hydrophobicity [corresponding to 0.7 of AUC (Eisenberg et al., 1984)], 45% for aggregation (Tartaglia and Vendruscolo, 2010) and 42% for burial (Harpaz et al., 1994). The CM achieves optimal performances by combining the scales for disorder (Sickmeier et al., 2007), hydrophobicity (Eisenberg et al., 1984), burial (Harpaz et al., 1994), aggregation (Tartaglia and Vendruscolo, 2010) and alpha-helix (Kanehisa and Tsong, 1980) (sensitivity of 0.9 and false positive rate of 0.07).

3.2.2 Cross-validation

Through a 10-fold cross-validation on both sets, our CM showed accuracy of 86.7% (Table 1). When compared to random sets, the signal strength was 0.4 (Supplementary Table S2). The best performing classifier for this case was Extremely Randomized Trees (Pedregosa et al., 2011), a variant of the Random Forest ensemble classifier.

3.2.3 Independent validations

As a positive set we used a database of yeast prions that are enriched in structural disorder [27 entries after sequence redundancy removal (Alberti et al., 2009)]. The negative set was comprised of a manually curated database of structured proteins whose folded native state has been studied in vitro [44 entries after sequence redundancy removal (Tartaglia and Vendruscolo, 2010)]. Our predictions showed accuracy of 84.5% for prions and 73.6% for structured proteins (Table 1). The testing sets achieved separation from random of 0.4 (prions) and 0.2 (structured proteins). On the same datasets, the FoldIndex (Prilusky et al., 2005) algorithm yielded accuracies of 62.9% (prions) and 64.7% (structured proteins; Table 1 and Supplementary Material). In addition, we employed NetSurfP (Petersen et al., 2009) and observed accuracies of 88.8% (prions) and 63.7% (structured proteins).

3.3 Solubility

A number of proteins such as fragile X mental retardation protein FMRP, TAR–DNA-binding protein 43 TDP43, fused in sarcoma FUS and prions have a strong propensity to aggregate into amyloid fibrils (Cirillo et al., 2013). Hence, prediction of protein solubility is fundamental to understand functional (e.g. RNA-binding) and dysfunctional (e.g. aggregated) states. To build a predictor of protein solubility, we took advantage of a study in which the solubility of 70% of Escherichia coli proteins was experimentally measured using an in vivo translation system (Niwa et al., 2009). In this analysis, we ranked proteins by their solubility and used top (1000 soluble proteins) and bottom (1000 insoluble proteins) elements as the positive and negative sets (Agostini et al., 2012).

3.3.1 Performances

In agreement with experimental evidence (Niwa et al., 2009), we found that hydrophobicity (Fauchere and Pliska, 1983; Sweet and Eisenberg, 1983) (coverage of 54–57%), aggregation (Conchillo-Solé et al., 2007) (coverage of 49%) and burial (Wertz and Scheraga, 1978) (coverage of 58%) propensities are depleted in the positive set while disorder (Campen et al., 2008) (coverage of 50%) and alpha-helix (Kanehisa and Tsong, 1980) (coverage of 41%) propensities are enriched (Fig. 2 and Supplementary Fig. S2). By selecting the scales for disorder (Bhaskaran and Ponnuswamy, 1988; Monné et al., 1999), burial (Argos et al., 1982; Chothia, 1975) and alpha-helix (Burgess et al., 1974) the algorithm reported optimal performances associated with sensitivity of 0.96 and false positive rate of 0.07 (Fig. 4).

3.3.2 Cross-validation

Through a 10-fold cross-validation on both sets, our CM showed accuracy of 89.7% (Table 1). When compared to random sets, the signal strength was 0.5 (Supplementary Table S2). In this case, Random Forest classifier (Pedregosa et al., 2011) was selected as the best performing.

3.3.3 Independent validations

As positive set we used proteins whose folding kinetics and thermodynamics have been studied in vitro [71 non-redundant entries (Tartaglia and Vendruscolo, 2010)]. The negative set contained proteins requiring molecular chaperones to fold into native structure [81 entries (Kerner et al., 2005)]. Our predictions showed accuracy of 84.7% for the positive set and 60.5% for the negative. The testing achieved separation from random of 0.5 (soluble proteins) and 0.1 (insoluble proteins). On the same datasets, PROSO II (Smialowski et al., 2012) algorithm yielded accuracies of 78.5% (positive set) and 74% (negative set; Table 1; Supplementary Material).

3.4 Chaperone requirements

Hsp70, the major stress-induced heat shock protein, facilitates substrate folding into native state (Calloni et al., 2012; Hartl and Hayer-Hartl, 2002) and is able to associate with AU-rich transcripts (Kishor et al., 2013; Zimmer et al., 2001). Mass spectrometry experiments show that E.coli DnaK interacts with proteins lacking strong hydrophobic core or exposing regions that are buried in the native state. In our analysis, the positive set was composed of proteins that require DnaK/GroEL to fold properly (109 sequences) and the negative set consisted of independently folding proteins [39 sequences (Kerner et al., 2005)].

3.4.1 Performances

Our results show strong agreement with experimental findings, with proteins in the positive set having low hydrophobic propensity [43% coverage (Eisenberg et al., 1984)] but high burial propensity [68% coverage (Rose et al., 1985)], which is consistent with the observation that lack of a hydrophobic core prevents from folding into native state (Tartaglia et al., 2010). In agreement with experimental evidence (Zimmer et al., 2001), we found that the positive set is enriched in proteins binding to nucleic acids (Zimmer et al., 2001; Calloni et al., 2012; Kishor et al., 2013). By automatically combining the scales for nucleic acid binding (Lewis et al., 2011), burial (Argos et al., 1982; Rose et al., 1985), membrane (Argos et al., 1982) and hydrophobicity (Eisenberg et al., 1984) propensities, CM achieved a sensitivity of 0.91 and false positive rate of 0.08.

3.4.2 Cross-validation

Through a 10-fold cross-validation we find that CM has accuracy of 81.6% and separation from random of 0.3 (Table 1 and Supplementary Table S2). The best performance was achieved with the AdaBoost (Pedregosa et al., 2011) classification algorithm.

3.4.3 Independent validations

The positive validation set was comprised of proteins requiring chaperones to fold (81 entries) (Kerner et al., 2005) while the negative validation was a manually curated dataset of independently-folding proteins [71 non-redundant entries (Tartaglia and Vendruscolo, 2010)]. The independent sets achieved accuracies of 75.4% for chaperone-dependent set and 60% for independently folding proteins. The testing sets achieved separations from random of 0.2 (chaperone-dependent and -independent set). To compare our performance to existing methods, we used Limbo (Van Durme et al., 2009) to predict DnaK-binding affinity of protein peptides. The method classified 100% of the positive set as chaperone-dependent (the accuracy was 96% on the positive training set), and it achieved 22.5% assignation accuracy on the independently folding dataset (Table 1 and Supplementary Material).

3.5 RNA-binding abilities

Recent technological advances have made it possible to discover that number of proteins have RNA-binding ability (Riley and Steitz, 2013). We focused on RNA-interacting proteins (715 entries) detected with UV cCL and PAR-CL protocols on proliferating HeLa cells and compared them with the cell lysate [2831 entries after sequence redundancy removal (Castello et al., 2012)].

3.5.1 Performances

The single property analysis revealed a strong and consistent RNA-binding property of the dataset: RNA-binding scales (Castello et al., 2012; Lewis et al., 2011; Terribilini et al., 2006) cover between 62–65%. Moreover, it has been observed that protein disorder is an important feature for RNA-binding proteins (Bellay et al., 2011; Cirillo et al., 2014). In agreement with this result, we found a significant enrichment in disorder propensities (Bhaskaran and Ponnuswamy, 1988; Campen et al., 2008). CM automatically selects the scales for RNA binding (Castello et al., 2012; Lewis et al., 2011), disorder (Campen et al., 2008; Isogai et al., 1980) and aggregation propensities (Tartaglia et al., 2008) achieving a sensitivity of 0.91 and false positive rate of 0.07 on the entire dataset.

3.5.2 Cross-validation

A 10-fold cross-validation on both datasets yielded accuracy of 84.3% and separation from random of 0.5 (Table 1 and Supplementary Table S2). The Extremely Randomised Tree classifier (Pedregosa et al., 2011) was selected as the best performing algorithm for this case.

3.5.3 Independent validations

The positive set contained proteins identified as RNA-binding using quantitative proteomics (Baltz et al., 2012). We removed any overlap between training and test sets using CD-HIT (Fu et al., 2012), leaving the positive set size to 86 entries. The negative validation contained 250 not nucleic acid binding proteins (Shazman and Mandel-Gutfreund, 2008). Our predictions showed accuracy of 72.9% for the mRNA-binding set and 79.2% for the negative validation. The separation from internal random dataset was respectively 0.5 and 0.1 for the positive and negative testing sets. Using the same data as for CC validation, the RNApred (Kumar et al., 2011) achieved accuracy of 82.5% for the positive set and 52.8% for the negative validation (Table 1; Supplementary Material).

4 DISCUSSION

The cleverSuite provides a novel and unique approach for both characterization and classification of protein groups. In striking agreement with experimental evidence, we reported accurate predictions of protein solubility in E.coli (Niwa et al., 2009), RNA-binding ability in H. Sapiens (Castello et al., 2012), structural disorder (Sickmeier et al., 2007) and chaperone requirements (Kerner et al., 2005). Our performances are comparable to other algorithms that were built to predict specific protein features. In agreement with previous observations, we found that physicochemical propensities linked to structural disorder and are relevant for RNA-binding, chaperone requirement and solubility (Agostini et al., 2012; Calloni et al., 2012; Cirillo et al., 2014), which very well captures the central role of natively unfolded proteins in higher eukaryotes (Babu et al., 2011). This observation is further supported by direct comparison of H.sapiens and E.coli proteomes, which shows enrichment in hydrophobicity and aggregation propensity for E.coli and structural disorder for H.sapiens (all links to results are provided in Supplementary Table S1).

Our findings suggest that the cleverSuite is an ideal tool to analyse the outcome of large-scale experiments. As shown in the examples, the algorithm can be applied to very diverse types of cases to allow a fine classification of protein features (Table 1). Future plans include incorporation of more properties and alternative ways to extract the signal from protein profiles. At present, the choice of propensity scales is mainly based on their previous use but custom scales are allowed in the webserver. We would like to note that our approach is not restricted to propensity scales and that any function mapping a primary structure into a profile could be interfaced with the algorithm. In next version, we are planning to implement the projection of profiles onto orthonormal bases, which should improve our performances.

In the CM each physico-chemical property is described by same number of propensity scales (eight groups containing 10 scales each; Fig. 2 and Supplementary Fig. S3), which guarantees that there is not over-representation of a particular property. We stress that the algorithm is built in a way that only non-correlated scales are selected for the analysis. In fact, if two scales discriminate the same set of proteins, their combination together would result in a smaller coverage compared to non-correlated scales. The CM can compute up to 10 millions associations of propensities (i.e. five scales out of 80 groups) to find the optimal combination, which is computationally expensive but ensures an impartial and exhaustive search. For this reason, the calculations have been parallelized to complete the analysis in short time, even when the input sets are large. We could have used other algorithms instead of the exhaustive search, but our focus is the simple and clear interpretation of scale contributions, which is not possible through more complex approaches.

We base our approach on the assumption that the algorithm works optimally if the system is able to select its predictors without external intervention (Wolpert, 2002). Similarly to what has been done to rationalize the determinants of protein aggregation (Chiti et al., 2003), the cleverSuite identifies the most relevant properties for a specific problem with the main differences being that: (i) fitting parameters are avoided and (ii) features are selected from a large pool of physico-chemical characteristics. Notably, the method allows the user to choose the reference set, which is strategic to circumvent the problem of the lack of negative cases in literature (Smialowski et al., 2010).

Although other useful tools are available to analyse protein features (Hall et al., 2009; Rao et al., 2011), we did not find any general-purpose method to discriminate datasets using parameter-free combinations of physico-chemical characteristics and we hope that our efforts will inspire future studies in the field. In conclusion, the cleverSuites offers an easy-to-use interface, accessible to a wide range of experimental and computational scientists.

Submissions are by default private, however, if a user wishes to share an analysis result or a classifier, there is an option to publish links on the ‘featured results’ page (http://s.tartaglialab.com/clever_community, maintained by the authors).