Micro-bias and macro-performance

Abstract

We use agent-based modeling to investigate the effect of conservatism and partisanship on the efficiency with which large populations solve the density classification task – a paradigmatic problem for information aggregation and consensus building. We find that conservative agents enhance the populations’ ability to efficiently solve the density classification task despite large levels of noise in the system. In contrast, we find that the presence of even a small fraction of partisans holding the minority position will result in deadlock or a consensus on an incorrect answer. Our results provide a possible explanation for the emergence of conservatism and suggest that even low levels of partisanship can lead to significant social costs.

1 Introduction

Many practical and scientific problems require the collaboration of groups of experts, with different expertise and background. Remarkably, it turns out that large groups of cooperative agents are extremely adept at finding efficient strategies for solving such problems [1,2]; the development of the scientific method within the physical sciences or the development of entire suites of computer software by the open source movement [3] being perhaps two of the most notable instances [4]. Indeed, even loosely structured groups have demonstrated an ability to coordinate and find innovative solutions to complex problems.

In the corporate world, several companies – including IBM, HP and various consulting companies – have used “the wisdom of the crowd” principle as the justification for the creation of knowledge communities, the so-called “Communities of Practice,” which have enabled organizations to spawn new ideas for products and services [5]. Other companies, such as Intel, Eli Lilly, and Procter & Gamble, which created company-sponsored closed knowledge networks, are now opening them to outsiders [6].

Recognizing that knowledge exists not merely in the members of the network but in the networks themselves – that is, in the members and in their interactions – naturally leads to the question of what characterizes successful communities and what measures could be taken to improve the ability of groups and organizations to innovate. Previous work investigated the importance of group diversity [7,8], team formation [9], and the structure of the interaction network [10–14]. Here, we focus instead on the effect of micro-level strategies on macro-level performance.

Recent work demonstrates that under quite general conditions, well-intentioned and completely trusting agents can efficiently solve information aggregation and coordination tasks [11]. We investigate how changes in the intention and trust level of agents affects the efficiency of solving such tasks by considering three types of agents: naives, conservatives and partisans. Naive agents are well-intentioned and completely trusting. Conservative agents are well-intentioned but not completely trusting. Partisan agents are neither well-intentioned nor completely trusting.

Remarkably, we find that conservative agents, despite slowing the information aggregation and coordination process, actually enhance the populations’ ability to efficiently solve these tasks under large levels of noise. In contrast, we find that even a small fraction of partisans holding the minority position will result in deadlock or a consensus on an incorrect answer. Significantly, only by completely disregarding partisan opinions, can the population recover its original ability to solve the task.

2 The model

We use here the density classification task, a model of decentralized collective problem-solving [15], to quantitatively investigate information aggregation and coordination. The density classification task is completed successfully if (i) all agents converge to the same state within a determined time period, and (ii) that consensual state was the majority state in the initial configuration.

Before proceeding, let us explain the reasons why the density classification task is a good paradigm for the type of problems into which we aim to gain insight. Consider a population of agents tackling a problem in which there is a large uncertainty and for which no agent will be able, by herself, to demonstrate that a particular solution is correct. If one assumes that all agents are well-intentioned, that is, that they want to find a good solution to the problem, then it is plausible to assume that the answer reached by a specific agent “contains” a good answer distorted by some noise. Under these conditions, an efficient strategy is to aggregate the answers from all agents, as information aggregation cancels the distorting component of the individual answers. However, in many situations a centralized structure may not be practical or desirable because it is too inefficient, too costly, or because it would be difficult to secure an unbiased central authority. For these reasons, decentralized strategies may be preferable or even the only ones feasible.

2.1 The agents

We consider a population of N agents. For simplicity, and without loss of generality. The state of each agent is a binary variable a_j ∈ {−1, 1} that represents the answer to a stated problem. Updating occurs using Boolean functions. As we indicated earlier, agents can hold various types of intentions. Specifically, well-intentioned agents have a bias b_j toward their present state b_j = a_j(t), while “partisan” agents have a bias toward a particular state, for example, b_j = −1. Naive and conservative agents are thus not biased for or against either state per se, they merely prefer whatever answer they currently hold. While all three types of agents may change their state in response to peer pressure, a partisan agent will defect back to his preferred state if peer pressure decreases below a threshold value.

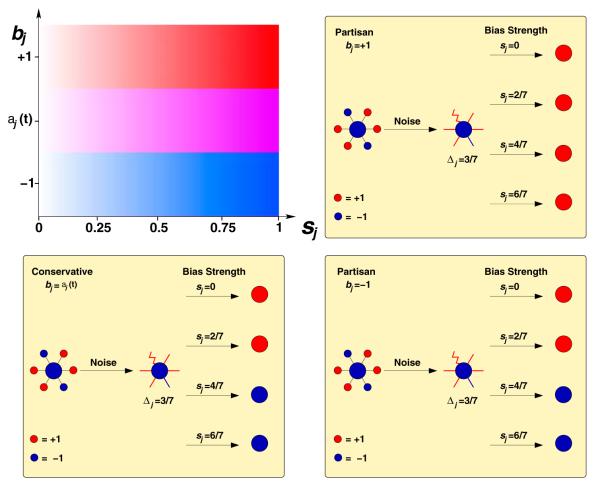
Both conservative and partisan agents can have different levels of trust on their neighbors, that is, different thresholds for responding to peer pressure. We define the “strength” s_j ∈ [0, 1] of agent j’s “conviction” as the threshold that must be exceed by Δ_j(t) – which is the difference between the fraction of majority and minority positions among agent j’s neighbor – for agent j to change states. If s_j = 0, then the agent is completely trusting, that is, naive, whereas if s_j = 1, the agent is completely distrusting and thus will never change his answer (Fig. 1).

Fig. 1.

Illustration of the different agent strategies. The strategy followed by an agent j is characterized by two parameters: b_j, which indicates the agent’s bias, and s_j, which quantifies the strength of the bias. b_j ∈ {a_j (t),−1, 1}, whereas s_j ∈ [0, 1]. Well-intentioned agents (whether naive or conservative) have b_j = a_j(t), whereas partisan agents have b_j = ±1. If s_j = 0, agents are completely trusting. As s_j increases, the level of distrust increases, so that, for s_j = 1, agents will freeze once they attain their preferred state.

Formally, one can write the update rule for agents with naive, conservative, or partisan strategies as:

$$a_j(t+1)=\{\begin{array}{cc}+1\hfill & {\Delta }_j\left(t\right)>-b_j{s}_j\hfill \\ a_j\left(t\right)\hfill & {\Delta }_j\left(t\right)=-b_j{s}_j\hfill \\ -1\hfill & {\Delta }_j\left(t\right)<-b_j{s}_j\hfill \end{array}\phantom{\}}$$ (1)

where Δ_j(t) is defined as:

$${\Delta }_j\left(t\right)=\frac{1}{1+k_j}\left(a_3\left(t\right)+\sum _{l=1}^{k_j}{\tilde{a}}_l^j\left(t\right)\right).$$ (2)

Here, k_j is the number of neighbors of agent j and ${\tilde{a}}_l^j\left(t\right)$ is the perceived state of neighbor l by agent j at time t, which may differ from a_l(t) due to noise [11]. We implement the effect of noise by picking with probability η a value for ${\tilde{a}}_l^j\left(t\right)$ that is drawn with equal probability from {−1, 1}. If η = 0, then ${\tilde{a}}_l^j\left(t\right)=a_l\left(t\right)$, whereas for η = 1, ${\tilde{a}}_l^j\left(t\right)$ is a random variable. Figure 1 illustrates the response of each type of agent to different signals.

The model we study is, on the surface, quite similar to the voter model which has been widely used to study social dynamics and opinion formation [10,12,14]. A significant difference, however, is that whereas in the voter model the agent picks a single neighbor at random and adopts its neighbor’s state, the model we use is more similar to that of an Ising model with zero temperature Glauber dynamics, in which at each step the agent tries to align with some local field exerted by the neighbors and herself. This subtle difference leads the two models to quite distinct dynamics.

Tessone and Toral [16] have recently studied opinion formation in a model in which agents have preference toward a specific opinion with a variety of strengths. Each agent follows the simple majority of their neighbors to update her state taking into account her bias. The authors find that the system responds more efficiently to external forcing if the agents are diverse, that is if each agent has a different bias strength. In here, however, we focus on the effect of opinion-bias on consensus formation without external forcing.

2.2 Network topology

A large body of literature demonstrates that social networks have complex topologies [17], and yet have common features [18,19]. We build a network following the model proposed by Watts and Strogatz [20,21], which, despite its simplicity, captures two important properties of social networks: local cliquishness and the small-world property. We implement the Watts and Strogatz model as follows. First, we create an ordered network by placing the agents on the nodes of a one-dimensional lattice with periodic boundary conditions. Then, we connect each agent to its k nearest neighbors in the lattice. Next, with probability p, we rewire each of the links in the network by redirecting a link to a randomly selected agent in the lattice. By varying the value of p, the network topology changes from the ordered one-dimensional lattice (p = 0) to a random graph (p = 1). We verified that our results are robust to changes in p as long as the network has a small-world topology, which for N = 401 occurs for p ≥ 0.1 (Supporting Online Material). In this study, we investigate populations of N = 401 agents placed on a one-dimensional ring lattice where each agent has k = 6 neighbors. To implement a small-world topology we rewire each connection with probability p = 0.15. Recent research demonstrates that, under these conditions, the naive heuristic enables the efficient convergence of the system to the correct consensus [11,22]. This finding is similar to what has been reported for the voter model. Specifically, studies of the voter model on complex topologies have shown that finite systems convergence faster to a consensus in small-world networks than in regular lattices in one dimension and that this effect is independent of the degree distribution [10,12,14].

3 Results

3.1 Effect of conservatism

We first consider the effect of conservative agents on the efficiency of the system (see Appendix A for definition of efficiency). Let’s assume that the system has both naive and conservative agents present, and that the fraction of agents using conservative strategies is f_c. The characteristics of the population are then described by the distribution

$$P(b_j,s_j)={\delta }_{b_j,a_j\left(t\right)}{P}_s\left(S_j\right).$$ (3)

For simplicity, we set s_j = s > 0 for the conservative agents and s_j = 0 for the naive agents. Thus,

$$P_s\left(S_j\right)=(1-f_c)\delta (s_j-0)+f_c\delta (S_j-S).$$ (4)

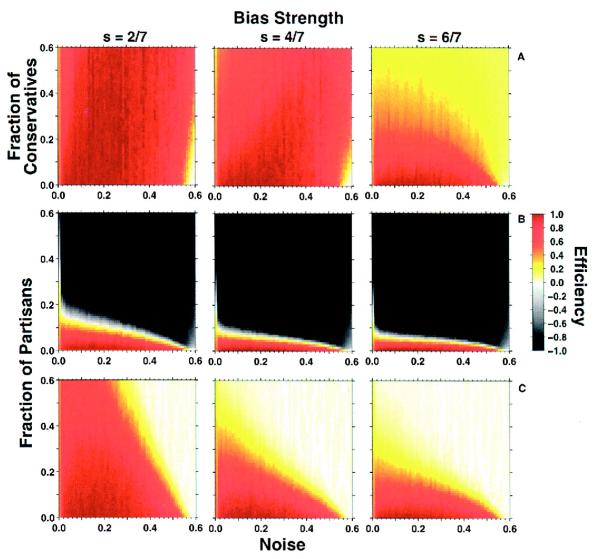
We study three values for the bias strength: s = 2/7, 4/7, and 6/7 (Fig. 2A). For s = 2/7 and s = 4/7, the system completes the density classification task with extraordinary efficiency. Indeed, increasing f_c results in greater efficiencies for high noise levels, which can be explained if one considers the stabilizing effect of conservative agents on the dynamics.

Fig. 2.

Efficiency of a population of distributed autonomous agents in completing the density classification task as a function of noise intensity and: (A) the fraction of conservative agents, (B) the fraction of partisan agents holding the minority state, and (C) the total fraction of partisan agents in the population whose preferred states are equally distributed between majority and minority states. We show results for three bias strengths, s = 2/7, 4/7, and 6/7. Our results suggest that (i) conservatism can be beneficial because it enhances the ability of the population to efficiently solve the density classification task for grater noise levels (panel A); (ii) partisanship can completely cancel the efficiency of a population in solving the task, even if a small fraction of partisans (f_p ≥ 0.15) is present (Panel B). Panel (C) shows how having partisans toward both answers leads to deadlock, especially at high noise levels for which the population as a whole will be evenly split between the two states.

In order to further characterize the effect of conservative agents on the system’s efficiency, we next investigate how the time needed for the system to reach the steady state depends on f_c (Fig. 3 and Supporting Online Material). We find that the “convergence time” grows quite rapidly with the fraction of conservatives in the system. In particular, for f_c > 0.3 the system can no longer reach the steady state within 2N time steps.

Fig. 3.

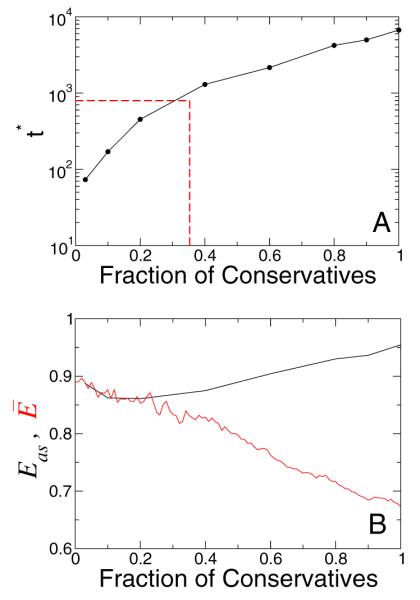
Effect of conservatism on attaining the steady state. (A) Time for a population to reach the stationary state as a function of the fraction of conservatives. (B) Comparison of the asymptotic efficiency (E_as), that is the efficiency in the stationary state, and the efficiency E attained after 2N time steps as a function of the fraction of conservatives. Note that for f_c > 0.3, the system cannot reach the stationary state in the 2N time steps used in the simulations.

These two findings suggest that a population of agents trying to optimize strategies in order to reach maximum efficiency must balance the greater accuracy of the system in completing the task for larger noise levels afforded by larger fractions of conservative agents with the rapidly increasing convergence time as f_c increases.

3.2 Effect of partisanship

We next consider the effect of partisan agents on the efficiency of the system. Let’s assume that the system now has both naive and partisan agents present, and that the fraction of agents using partisan strategies is f_p. Because partisan agents can have bias toward two distinct answers, we consider two scenarios. In the first scenario, all partisan agents have a bias toward “−1”, that is, they prefer the incorrect answer to the density classification task the population is trying to complete¹. If s_j = s > 0, then the characteristics of the population in this scenario are described by the distribution

$$P(b_j,S_j)=(1-f_p)\delta (S_j-0){\delta }_{b_j,a_j\left(t\right)}+f_p\delta (S_j-S){\delta }_{b_j,-1}.$$ (5)

We again study three values for the bias strength: s = 2/7, 4/7, and 6/7. Our results reveal that even when partisan agents have a small bias strength s = 2/7, and therefore, yield to peer pressure easily, f_p ≥ 0.15 is enough to overcome the initial majority and lead the population to converge to the incorrect answer (Fig. 2B).

In the second scenario, we consider a balanced distribution of partisans with f_p/2 agents partisan toward answer “1” and f_p/2 agents partisan toward answer “−1” (Fig. 2C). For η < 0.4 and f_p < 0.3, we find that the strength of the initial majority is able to drive the population to a consensus on the correct answer. However, if either the noise level or the fraction of partisans increases, the population settles into a deadlock. One could naively expect that in the high bias strength case the results for partisans and conservatives should be identical. In both systems, conservatives and partisans alike are frozen in their preferred state. In the system with conservatives, the distribution of preferred states is exactly the same as the distribution of initial states, which is that 57% of agents prefer state “1”. However, in the system with partisans, the distribution of preferred states is such that 50% of the agents prefer state “1”. Therefore, even though the distribution of initial states is 57%, all partisans will switch to their preferred state because of the high bias strength. As a consequence, in the regions of lowest efficiency, there is a difference in efficiency between the results for conservatives and the results for partisans.

The effect of strongly biased partisans in opinion formation, that is those partisans that never change opinion, has also been studied in the context of the voter model [23,24] showing that only one partisan is enough to significantly slow down consensus formation and that, in regular lattices and complete graphs, when an equal number of partisans P of each opinion is present, the efficiency of the system in the steady state is Gaussian distributed with zero mean and variance $\propto 1\sqrt{(}P)$. Thus for large systems, a vanishing fraction of partisans is necessary to put the system in deadlock and prevent consensus from happening. Such finding is consistent with our results. However, since we consider that partisans are biased but can change state, our model shows that, in the presence of noise, the population can actually reach consensus when there are large fractions of partisans.

3.3 Effect of distrust

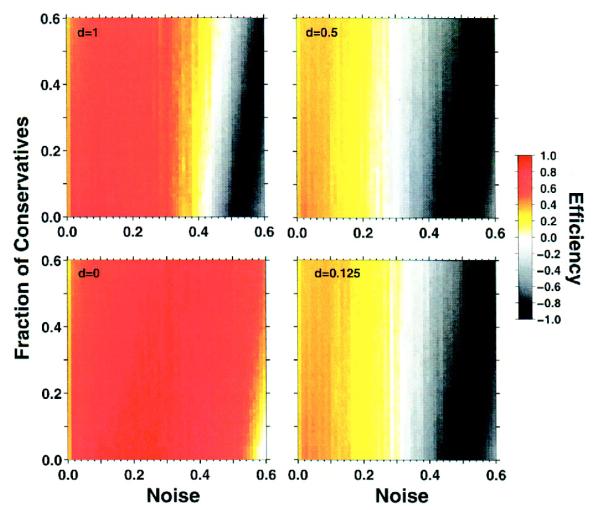
Because partisanship appears to remove a population’s ability to reach consensus on the correct answer, we next investigate possible ways to counter the effect of partisan agents. A plausible strategy for non-partisan agents is to “discount” the signal of partisan agents. We thus define a discount parameter d ∈ [0, 1] with which non-partisans weigh the information held by partisan agents. As demonstrated by a recent study [25], we must also enable partisan agents to discount the signals of both non-partisan and opposing partisan agents with at least the same discount rate.

Surprisingly, we find that the increased distrust among agents actually has a deleterious effect on the efficiency of the system in solving the density classification task (Fig. 5). The reason for this apparently counter-intuitive result is that s_j = s > 0 for partisans, so that when d ≤ 0.5, partisan agents discount the answer of non-partisan agents to such an extent that they will never abandon their preferred answer. In fact, only for d = 0 is a system containing partisan agents able to efficiently complete the density classification task.

Fig. 5.

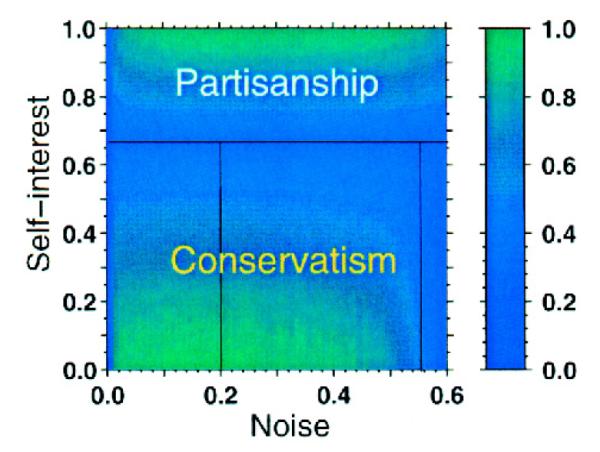
Strategy evolvability.We show the utility function U of an agent as a function of his self-interest I_j and the noise level η, where $U_j\equiv I_j\frac{N_{-}}{N}+(1-I_j)E^{\ast }\left(\eta \right)=(1-\frac{3I}{2})E^{\ast }\left(\eta \right)+\frac{I}{2}$. We show results for populations with a 10% of non-naive agents (see Figs. 2A and 2B), that is, for each set of values {I_j, η}, we select the combination {b_j, s_j} whose efficiency E*(η) maximizes U. In the diagram, we also show that the specific combination {b_j, s_j} that maximizes U defines well separated regions of how different strategies can be optimal for different self-interest and noise levels. Significantly, an agent will choose to be partisan if I_j > 2/3, regardless of the value of η.

4 Discussion

Common experience demonstrates the existence of partisanship within groups of any kind. One possible interpretation for partisanship is a strong a priori belief that a certain answer is correct. Alternatively, one may consider the case where agents have personal interests that may in fact differ from the “common good.” In this case individual decision rules, such as the degree of partisanship, can be interpreted as the solution to a maximization problem at the individual level. We model this question by assigning to a set of rational agents an idiosyncratic utility function that each agent tries to maximize, while the rest of the agents use the naive strategy. The interesting case is the one in which the agent’s self-interest comes from answer “−1” being adopted while the “common good” comes from “1” being adopted. A utility function for the rational agents is:

$$\begin{array}{cc}\hfill U_j& \equiv I_j\frac{N_{-}}{N}+(1-I_j)E\hfill \\ \hfill & =\left(1-\frac{3I_j}{2}\right)E+\frac{I_j}{2},\hfill \end{array}$$ (6)

where I_j is the degree to which the agent values his own “self-interest over the common good.” If I > 2/3, the agent’s utility is maximized by minimizing E. Thus, if an agent has I > 2/3 the optimal individual strategy is partisanship with s = 1. If I ≤ 2/3, then the optimal strategy depends on the strength of the noise (Fig. 4); the stronger the noise, the more conservative the agents should be.

Fig. 4.

Effect of selective distrust. We consider a system in which well-intentioned agents take partial consideration of partisan agents’ opinions and vice-versa. The discount parameter d quantifies the weight a well-intentioned agent assigns to the opinion of a partisan agent. We consider a population with a fraction f_c of conservative agents and 5% of partisan agents, both of them with bias strength s = 2/7, and 5% of population being partisans to the minority opinion. We show the efficiency of the population as a function of f_c and of noise. For d > 0.5, partisans may converge to the positive state if a qualified majority of their neighbors are already in that state. In such case, the population can still attain a relatively high efficiency for a wide range of parameter values. In contrast, when 0 < d ≤ 0.5, partisans are unlikely to change states even when all their neighbors are in the opposite state. In such conditions, the small fraction of partisans acts as a constant bias toward the negative state, resulting in a drastic reduction of the population’s efficiency. Only for d = 0, that is when the two groups, well-intentioned and partisan agents, completely disregard each other does the system recover the ability to efficiently solve the density classification task.

These findings thus provide a possible explanation for the emergence of conservatism and partisanship as mechanisms to maximize individual rather than collective advantage. The question then arises of how one can reconcile the advantage of self-interest with the evolution toward cooperative societies. The answer is that for individual decisions to serve common good, societies must develop and adopt norms that regulate self-interest [26,27]. Importantly, only in the presence of norms and the “metanorms” that support their enforcement [26], will individuals adopt strategies that lead toward cooperation and better social outcomes.

Our findings for the effect of partisan agents on the efficiency with which the system completes the density classification task are striking. Even a small fraction of partisans can completely erase the efficiency of the system. It is not difficult to envision the consequences of this result on our daily lives. Democratic societies face many situations in which “difficult” decisions must be made [28–36]. Moreover, the ability of policy makers to reach timely decisions on difficult matters clearly increases when a strategy has broad support. Reaching such broad consensus, unfortunately, is unlikely to occur if partisan agents are present. Sadly, partisanship is the rational individual strategy if there are no norms against it.

Appendix A

For concreteness, and without loss of generality, we assign a 57% probability to state “1” in the initial configuration of the system. By setting p = 0.57, we avoid finite size effects (Supporting Online Material). We then define the instantaneous efficiency of the coordination process as

$$\epsilon \left(t\right)\equiv \frac{N_{+}\left(t\right)-N_{-}\left(t\right)}{N},$$ (A.1)

where N₊ is the number of agents that are in state “1” and N₋ is the number of agents that are in state “−1”. For each realization, we allow the system to evolve for 2N time steps. In order to ensure that the strategies used by the agents are scalable, we let the system evolve for a number of time steps proportional to the number of agents in the system N. We define the efficiency $\stackrel{‒}{\epsilon }$ of a single realization as

$$\stackrel{‒}{\epsilon }\equiv \frac{1}{r}\sum _{t=2N-\tau }^{2N}\epsilon \left(t\right)$$ (A.2)

setting τ = N/4. The efficiency E for a given set of parameter values is the average of $\stackrel{‒}{\epsilon }$ over 1000 realizations. Crutchfield and Mitchell [15] allowed the system to converge to a point where all the agents have the same state, and a realization is considered to be successful provided the converged state is the same as the majority state. Instead of requiring that the system reaches consensus, we focus on the steady state configuration reached by the system.