Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 May 22;4:5035. doi: 10.1038/srep05035

Brittle to Ductile Transition in Densified Silica Glass

Fenglin Yuan 1, Liping Huang 1,a
PMCID: PMC4030258  PMID: 24849328

Abstract

Current understanding of the brittleness of glass is limited by our poor understanding and control over the microscopic structure. In this study, we used a pressure quenching route to tune the structure of silica glass in a controllable manner, and observed a systematic increase in ductility in samples quenched under increasingly higher pressure. The brittle to ductile transition in densified silica glass can be attributed to the critical role of 5-fold Si coordination defects (bonded to 5 O neighbors) in facilitating shear deformation and in dissipating energy by converting back to the 4-fold coordination state during deformation. As an archetypal glass former and one of the most abundant minerals in the Earth's crest, a fundamental understanding of the microscopic structure underpinning the ductility of silica glass will not only pave the way toward rational design of strong glasses, but also advance our knowledge of the geological processes in the Earth's interior.

Silica glass (a-silica), owing to its low atomic packing density, can be permanently densified to a large extent (>20%) by static cold compression at room temperature1,2, shock compression3 or by pressure quenching from melt4. Extensive experimental and computational studies have been conducted to understand the structure and properties of a-silica under static cold compression at room temperature5,6,7,8,9,10,11,12,13,14,15,16,17,18,19. Raman spectra of shock-retrieved a-silica (experienced peak pressures of 52 GPa and temperatures of 3000 K) show substantial differences from those of a statically cold compressed sample3. This indicates that the compression mechanisms in a-silica at low temperature seem to be different from those at high temperature, which may be closely related to the compression mechanisms in the melt. This view was supported by NMR studies in silicate glasses quenched from melts under high pressure, in which appreciable amount of 5- and 6-fold coordinated Si was identified, while only 4-fold Si atoms were observed in normally melt-quenched samples20,21,22,23. Our previous study showed that elastic properties of a-silica can be tuned by the pressure quenching route in a controllable manner4. It is the goal of this work to systematically study the plastic deformation mechanisms of pressure-quenched a-silica. Direct probing the microscopic changes associated with the plastic deformation in glass is a formidable challenge for experiment2. Here we resorted to large-scale molecular dynamics (MD) simulation in this study, which has an advantage over experiment in that it can provide atomistic-level structural details associated with the plastic deformation during mechanical tests.

A modified BKS potential24,25 implemented in the LAMMPS26 package was used to prepare a series of pressure-quenched a-silica samples (details can be found in the Methods part and in Supporting Information (SI)). Densified a-silica samples are labeled by the pressure applied during the quenching process for convenience. In this study, we investigated the deformation mechanisms of densified a-silica using three large-scale mechanical tests (i.e., uniaxial tension test, V-crack tension test and nanoindentation test) at the same homologous temperature of 0.1 Tf (fictive temperature, defined and calculated in SI). The structural origins responsible for the enhanced ductility in densified a-silica were attributed to 5-fold Si coordination defects formed during the pressure quenching process. The amount of 5-fold Si coordination defects can be controlled by the quenching pressure, which in turn determines the deformation modes of densified a-silica. As an archetypal glass-former and one of the most abundant minerals in the Earth's crust, a fundamental understanding of the microscopic structure underpinning the ductility of a-silica will not only pave the way toward the rational design of strong glasses27,28,29,30,31,32, but also shed light on the geochemical and geophysical processes in the Earth's interior7,8,33,34,35.

Results

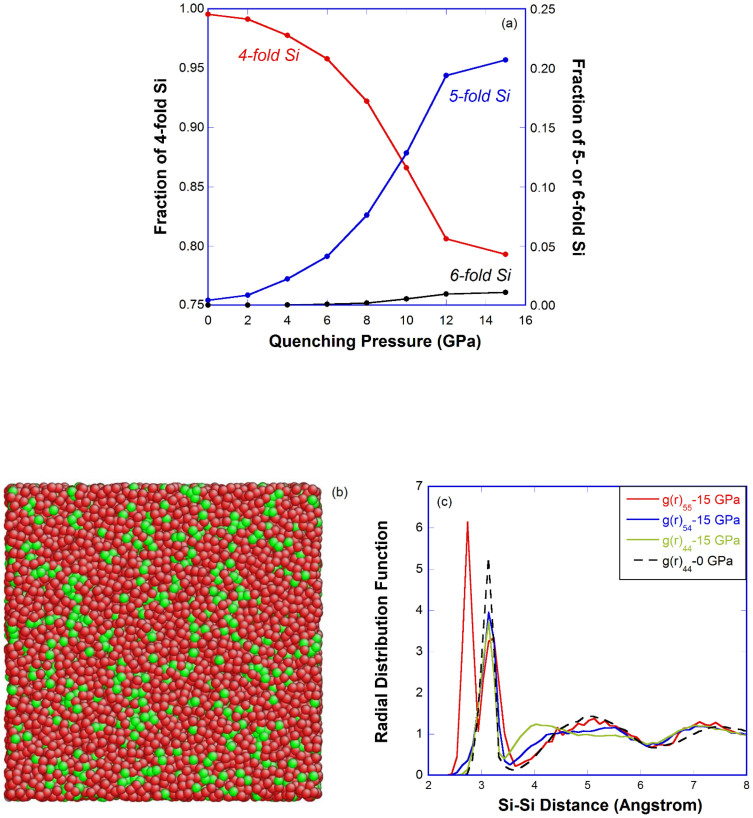
A range of constant hydrostatic pressures were applied during the melt-quenching process to prepare a series of densified samples4. Upon pressure release at 0.1 Tf, Fig. 1(a) shows that the fraction of 5-fold Si atoms steadily increases with the quenching pressure (more than 20% in the 15 GPa sample), which constitute the major coordination defects in densified a-silica. There is only ~1% 6-fold Si coordination defects in the 15 GPa sample, which indicates that silica melt/glass seems to compress differently from the crystalline counterparts under pressure where the coordination number of Si changes from 4 to 636. Distribution of the 4- and 5-fold Si in the 15 GPa sample is shown in Fig. 1(b), indicating a tendency of cluster formation in 5-fold Si atoms. Radial distribution functions of the 4-fold and 5-fold Si in the 0 GPa and 15 GPa sample in Fig. 1(c) confirm that some of the 5-fold Si atoms tend to stay closer together, indicated by the inner g(r)55 peak below 3 Å. Clusters of 5-fold Si atoms are uniformly distributed throughout the sample, which may correspond to the high density regions in the original silica melt37.

Figure 1. Coordination defects in pressure-quenched a-silica.

Figure 1

Open in a new tab

(a) Fraction of 4-, 5- and 6-fold Si versus quenching pressure; (b) Configuration of two types of Si atoms (red: 4-fold, green: 5-fold) in the 15 GPa sample, O atoms are omitted for clarity; (c) Si-Si radial distribution function of 4-fold and 5-fold Si atoms in the 0 GPa and 15 GPa sample (represented by the subscript 4 and 5 in g(r), respectively).

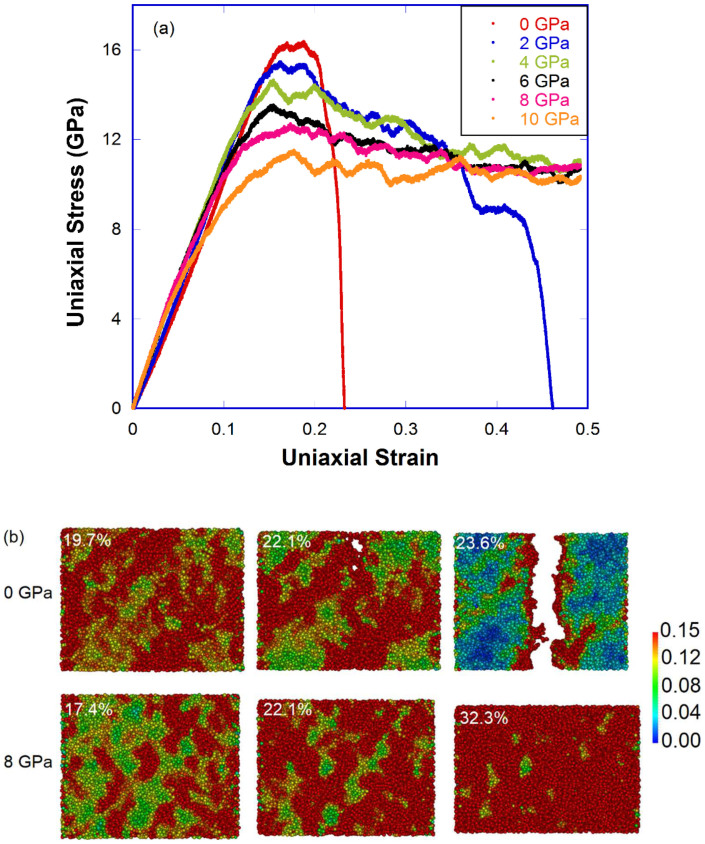
To investigate the deformation mechanisms of densified a-silica, we first carried out uniaxial tension tests in as-quenched samples (0, 2, 4, 6, 8, 10, 12 and 15 GPa). To avoid the system size effect as reported in our previous study38, dimensions of samples for uniaxial tension tests have been properly chosen (see Table. S2). In Fig. 2(a), a clear brittle to ductile transition can be found in samples quenched under pressures of 2 to 4 GPa. The 0 GPa sample (i.e., pristine a-silica) displays a clear brittle fracture behavior, consistent with observations from previous experiments39,40 and simulations38,41,42. Above 4 GPa, all densified samples don't fracture even up to 50% uniaxial strain, indicating a typical ductile behavior. A local shear strain analysis43 was performed at selected tensile states during uniaxial tension tests for the 0 GPa and 8 GPa sample (see Fig. 2(b)). In general, a higher local shear strain value (i.e., more reddish) means that a local cluster has been heavily shear deformed. For the 0 GPa sample, void formation and crack propagation mechanism can be envisaged from the local shear strain mapping in Fig. 2(b). Voids probably form in heavily sheared regions due to decohesion resulted from local heating44 or due to heterogeneous nanoscale cavitations45. In contrast, for the 8 GPa sample, despite a large portion of the sample is heavily shear deformed, no such voids form, implying that void formation has a higher activation energy than shear deformation in densified a-silica.

Figure 2. Deformation of pressure-quenched a-silica during uniaxial tension test.

Figure 2

Open in a new tab

(a) Stress-strain curves of uniaxial tension test for pressure-quenched samples (0, 2, 4, 6, 8 and 10 GPa); (b) Local shear strain mapping of uniaxial tension test for the 0 GPa (top) and 8 GPa (bottom) sample.

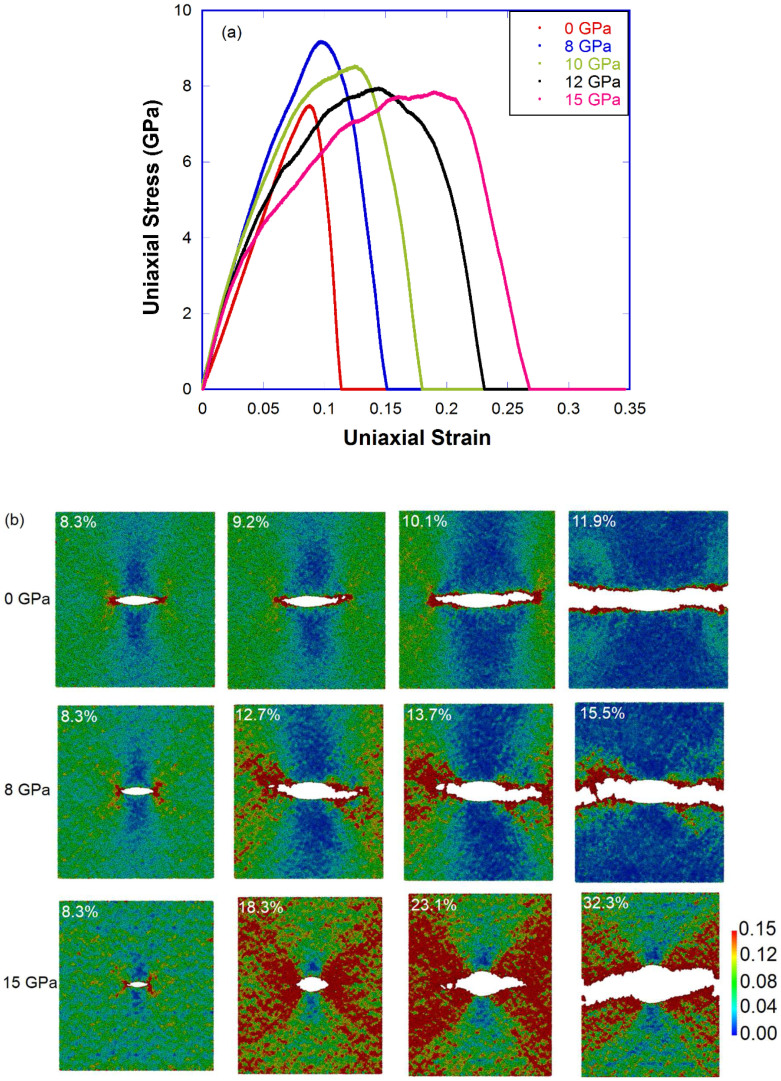
To study the resistance of densified a-silica to propagation of pre-existing cracks, we carried out a series of V-crack tension tests in the 0, 8, 10, 12 and 15 GPa samples. Fig. 3 shows that with increasing quenching pressure, samples display more and more plastic deformation before fracture, evidenced by shear banding and crack blunting. The strain at fracture or fracture strain, as an indicator of ductility, increases from 10.5% to 24.1% when the quenching pressure increases from 0 to 15 GPa (see Fig. S13). For all samples, pre-existing cracks always induce stress concentration around crack tip regions and can serve as nucleation sites for new voids. However, for the 0 GPa sample, the crack never blunts, and the void formation and coalesce phenomena at crack tip, although regarded as indication of nanoscale ductility46, would not lead to a macroscopic ductile behavior due to high crack propagation speed and localized void formation very close to the crack tip40,47. For densified samples, the crack substantially blunts before propagating together with extensive shear flow events (as evidenced by the local shear strain mapping in the 15 GPa sample in Fig. 3(b)). As seen in Fig. S12, the fracture surface is very smooth for the 0 GPa sample, similar to Guin and Wiederhorn's AFM results47; it becomes increasingly rougher with the increase of quenching pressure. The fracture surface roughness is 7.6, 20.2 and 33.3 Å for the 0, 8 and 15 GPa sample, respectively, another signature of enhanced ductility in densified samples.

Figure 3. Deformation of pressure-quenched a-silica during V-crack tension test.

Figure 3

Open in a new tab

(a) Stress-strain curves of V-crack tension test for pressure-quenched samples (0, 8, 10, 12 and 15 GPa); (b) Local shear strain mapping of V-crack tension test for the 0 GPa (upper), 8 GPa (middle) and 15 GPa (bottom) sample.

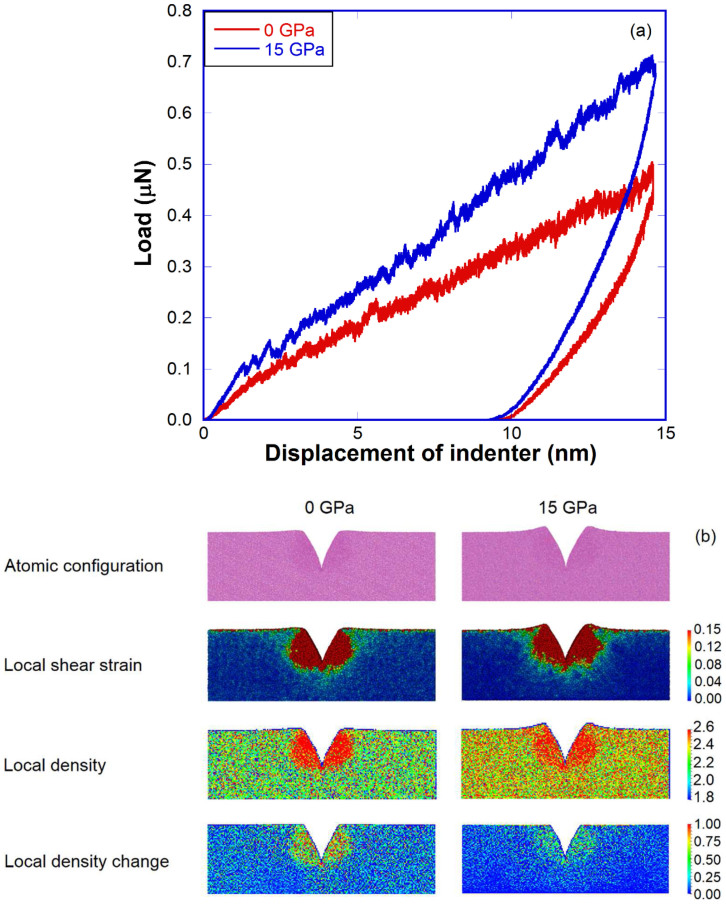
In addition, nanoindentation tests in the 0 GPa and 15 GPa sample were performed using a V-shaped nanoindenter with a round tip. Load-displacement curves of the two nanoindentation tests are plotted in Fig. 4(a) and configuration snapshots after a full unloading of the indenter are compared in Fig. 4(b). As seen in Fig. 4(a), the densified a-silica (i.e., the 15 GPa sample) definitely has a higher contact elastic modulus and nano-hardness than the pristine a-silica (i.e., the 0 GPa sample). The serrated stress drops in the plastic region (after ~1.0 nm indentation depth) can be attributed to permanent local rearrangements (e.g., shear flow events48). By comparing the after-unloading snapshots, the densified a-silica shows much more pile-up than the pristine one in Fig. 4(b). It can be seen in Fig. 4(b) that the densified a-silica tends to deform predominantly through shear flow instead of permanent densification under sharp contact loading. The shear flow under nanoindentation leads to more pile-up after unloading, in excellent agreement with Rouxel et al. 's experimental observations in densified a-silica obtained from static cold compression at room temperature2. While in the pristine a-silica, permanent densification is the dominant deformation mode under indentation due to its low atomic packing density (Fig. 4(b)), consistent with Yoshida's experimental observations49.

Figure 4. Deformation of pressure-quenched a-silica during nanoindentation test.

Figure 4

Open in a new tab

(a) Load-displacement curves of nanoindentation test for the 0 GPa and 15 GPa sample; (b) Atomic configuration (first row), local shear strain (second row), local density (third row) and local density change mapping under indenter (fourth row) after nanoindentation test for the 0 GPa and 15 GPa sample.

Discussion

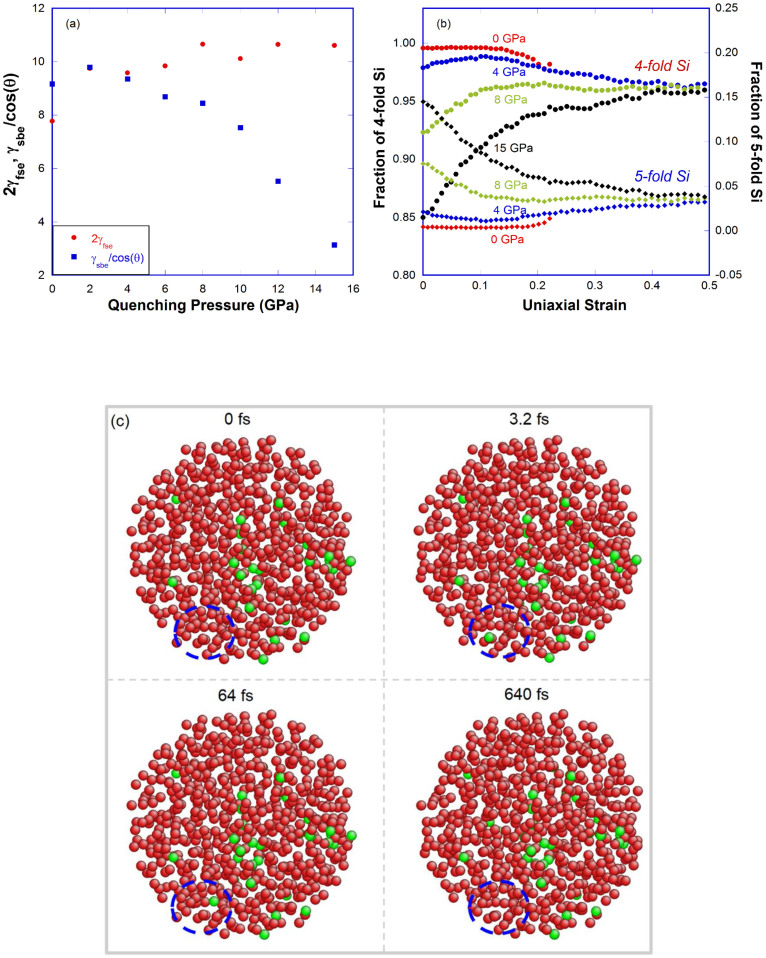
A simple model based on the competition between two fracture mechanisms, namely “shear banding” versus “cleavage”, is used (more details in SI) to understand the brittle to ductile transition in the densified a-silica from the energy point of view. The fracture energy for the cleavage mode is 2γfse × A and for the shear banding mode is γsbe / cos(θ) × A, where A is the cross section area perpendicular to the tensile axis, γfse is fracture surface energy per unit area, θ is the shear band angle and taken as 45° for simplicity in this study, and γsbe is shear banding energy per unit area (assuming the thickness of shear bands in uniaxial tension test and pure shear test are the same, see SI). Since the cross section A is the same for two different fracture modes, the net comparison is between 2γfse and γsbe / cos(θ). If 2γfse > γsbe/cos(θ), shear banding fracture will dominate; otherwise, cleavage mode will be more feasible. The crossover of the two energies in Fig. 5(a) around 2–4 GPa implies the fracture mode changes from cleavage to shear flow, consistent with the trend observed in Fig. 2(a).

Figure 5. Origins of the enhanced ductility in densified a-silica.

Figure 5

Open in a new tab

(a) Fracture surface energy and shear banding energy of a-silica versus quenching pressure; (b) Fraction of 4- and 5-fold Si as a function of strain during uniaxial tension test for densified samples (0, 4, 8 and 15 GPa). (c) Snapshots of the 8 GPa sample at different times at 35% strain in the uniaxial tension test. Note: red for 4-fold Si, green for 5-fold Si, O atoms are omitted for clarity. Inside the dashed circle, two 5-fold Si atoms appear then disappear, indicating the migration of 5-fold Si atoms inside the sample while maintaining a constant population as seen in (b).

In MD simulations, we can directly observe the dynamic evolution of the 5-fold coordination defects during large-scale mechanical tests. The fraction of the 4- and 5-fold Si atoms in uniaxial tension tests are plotted for the 0, 4, 8 and 15 GPa samples in Fig. 5(b) and very different behaviors can observed in samples with different amount of 5-fold Si coordination defects after the pressure quenching process. For the 0 GPa sample with negligible amount of 5-fold Si, it exhibits a clear brittle fracture at the maximum stress. For samples densified above 8 GPa, the 5-fold Si converts back to the 4-fold coordination state upon initial uniaxial tension, which gives the steady decrease in the first region in Fig. 5(b), then approaching a constant population of ~4% at larger strains. In the 4 GPa sample, the initial population of the 5-fold Si coordination defects is about 4%, which decreases slightly upon uniaxial tension then approaches the steady state as others. It is very interesting to see in Fig. 5(b) that as long as a sample has enough 5-fold coordination defects to start with, it can reach a steady flow state as shown in Fig. 2(b). This converging behavior is very similar to what was observed in simple shear tests of model metallic glasses50. The easiness of shear flow in densified a-silica as evidenced in all three mechanical tests can be attributed to a less rigid local environment associated with 5-fold Si coordination defects, more amenable to local shear deformation as compared with the 4-fold coordination state as shown in Fig. S20–S21.

Fig. 5(b) also shows that the coordination state conversion in densified a-silica provides a new deformation mode besides the bond stretching upon uniaxial tension. Fig. S23–25 further demonstrate that the conversion from the 5-fold (dense packing) to the 4-fold (loose packing) state provides additional mechanism for energy dissipation in densified a-silica. To some extent, the two-level deformation mechanism in densified a-silica is similar to that in polymers: untwining the network chains before bonds in the network are stretched. In the pristine a-silica, the dominant energy dissipation mechanism upon expansion is simply to stretch bonds, leading to earlier bond rupture and cavitation.

5-fold Si coordination defects have been shown to be responsible for the diffusivity maximum in silicate melts51, and proposed as one of the possible transition states for the high-temperature growth of quartz from glass52. Previous cold-compression study of a-silica in MD simulation by Liang et al. also showed that 5-fold Si coordination defects enhance local rebonding and relaxation, and therefore plasticity (densification) beyond the elastic limit53. Liang et al. further proposed that 5-fold Si-activated diffusion is responsible for the minimum yield strength around 10 GPa observed in mechanical strength measurements in a-silica27. Fig. 5(c) shows that 5-fold Si atoms are migrating but maintaining a constant population during the flow state of the uniaxial tension test in Fig. 2(b). This indicates that 5-fold Si atoms act like “catalyst” for shear flow events or “plasticity carrier” analogous to the liquid-like component in amorphous Si proposed by Demkowicz and Argon54, therefore playing an indispensable role in the enhanced ductility in densified a-silica. The negligible amount of 6-fold coordination defects observed in our pressure-quenched samples indicates that octahedral units such as those proposed by Stolper and Ahrens7 do not play an important role in the enhanced ductility in densified a-silica.

In conclusion, densified a-silica prepared by the pressure-quenching route displays enhanced ductility evidenced by three large-scale mechanical tests: uniaxial tension test, V-crack tension test and nanoindentation test. Intrinsic fracture reflected by uniaxial tension test shifts from a brittle to a ductile mode as the quenching pressure increases and a simple model based on the cleavage and the shear banding fracture successfully explains the crossover in samples quenched under 2 ~ 4 GPa. Ductility of densified a-silica in the presence of V-shaped crack shows significant increase indicated by extensive shear banding and obvious crack blunting. There is much more pile-up under nanoindentation in densified a-silica, indicating an easy activation of shear flow under indentation. Structural origins of the enhanced ductility in densified a-silica can be attributed to 5-fold Si coordination defects, which serve as “plasticity carrier” to promote shear flow and provide additional means for energy dissipation by converting back to the 4-fold coordination state. Our study shows that the pressure quenching route may provide a novel way to quench the 5-fold Si coordination defects, giving rise to enhanced ductility in densified a-silica.

Methods

Classical molecular dynamics (MD) simulations were conducted in the LAMMPS package26 (http://lammps.sandia.gov/) using a modified version of the BKS potential24 with a short range cutoff of 0.55 nm and a long-range Columbic cutoff of 1.0 nm. Previous studies have shown that this modified BKS potential can reproduce both bulk and surface properties of silica glass25,38. The Columbic interaction was calculated via the Ewald summation technique with a relative precision of 10−5 in force. The Velocity-Verlet algorithm with a time step of 1.6 fs was used for integrating the equations of motion and the Nose-Hoover thermostat55,56 and barostat57 were used to control the system temperature and pressure when necessary.

A constant hydrostatic pressure was applied during the melt-quenching process (cooling rate of 10 K/ps), providing an additional driving force to densify the glass sample. The pressure ramping and releasing rates during the pressure quenching process were fixed at 0.125 GPa/ps. The dimensions of pressure-quenched samples after pressure-release are listed in Table. S1 and used in uniaxial tension tests. For V-crack tension tests and nanoindentation tests, they were duplicated in the x and y axis for multiple times. Periodic boundary conditions (PBCs) were applied in all directions unless stated otherwise (e.g., in nanoindentation test). All mechanical tests were carried out at the same homologous temperature 0.1 Tf (fictive temperature) to get rid of the temperature effect on the brittle to ductile transition observed in our previous study38.

Author Contributions

L.H. designed the research, F.Y. carried out the simulations. Both L.H. and F.Y. performed the data analysis and wrote the manuscript.

Supplementary Material

Supplementary Information

Supporting Information for 'Brittle to Ductile Transition in Densified Silica Glass'

srep05035-s1.pdf (2.1MB, pdf)

Acknowledgments

This work was supported by the National Science Foundation under Grant No. DMR-0907076 and DMR-1105238. The authors thank Drs. Y. Shi, M. Tomozawa, T. Rouxel, J. Kieffer and J. C. Mauro for stimulating discussions. Some of the simulations were carried out on supercomputers at the Center for Computational Innovations (CCI) at RPI.

References

  1. Rouxel T., Ji H., Hammouda T. & Moréac A. Poisson's ratio and the densification of glass under high pressure. Phys. Rev. Lett. 100, 225501 (2008). [DOI] [PubMed] [Google Scholar]
  2. Rouxel T., Ji H., Guin J., Augereau F. & Ruffle B. Indentation deformation mechanism in glass: Densification versus shear flow. J. Appl. Phys. 107, 094903 (2010). [Google Scholar]
  3. Tschauner O. et al. Shock-synthesized glassy and solid silica: Intermediates between four- and six-fold coordination. High Press. Res. 24, 471–479 (2004). [Google Scholar]
  4. Huang L. & Kieffer J. Anomalous thermomechanical properties and laser-induced densification of vitreous silica. Appl. Phys. Lett. 89, 141915 (2006). [Google Scholar]
  5. Grimsditch M. Polymorphism in amorphous SiO2. Phys. Rev. Lett. 52, 2379–2381 (1984). [Google Scholar]
  6. Hemley R., Mao H., Bell P. & Mysen B. Raman-spectroscopy of SiO2 glass at high-pressure. Phys. Rev. Lett. 57, 747–750 (1986). [DOI] [PubMed] [Google Scholar]
  7. Stolper E. & Ahrens T. On the nature of pressure-induced coordination changes in silicate melts and glasses. Geophys. Res. Lett. 14, 1231–1233 (1987). [Google Scholar]
  8. Williams Q. & Jeanloz R. Spectroscopic evidence for pressure-induced coordination changes in silicate-glasses and melts. Science 239, 902–905 (1988). [DOI] [PubMed] [Google Scholar]
  9. Meade C., Hemley R. & Mao H. High-pressure X-ray-diffraction of SiO2 glass. Phys. Rev. Lett. 69, 1387–1390 (1992). [DOI] [PubMed] [Google Scholar]
  10. Sato T. & Funamori N. Sixfold-coordinated amorphous polymorph of SiO2 under high pressure. Phys. Rev. Lett. 101, 255502 (2008). [DOI] [PubMed] [Google Scholar]
  11. Fukui H., Kanzaki M., Hiraoka N. & Cai Y. Q. Coordination environment of silicon in silica glass up to 74 GPa: An x-ray Raman scattering study at the silicon L edge. Phys. Rev. B 78, 012203 (2008). [Google Scholar]
  12. Horbach J. Molecular dynamics computer simulation of amorphous silica under high pressure. J. Phys. Condens. Matter 20, 244118 (2008). [Google Scholar]
  13. Benmore C. J. et al. Structural and topological changes in silica glass at pressure. Phys. Rev. B 81, 054105 (2010). [Google Scholar]
  14. Murakami M. & Bass J. D. Spectroscopic evidence for ultrahigh-pressure polymorphism in SiO2 glass. Phys. Rev. Lett. 104, 025504 (2010). [DOI] [PubMed] [Google Scholar]
  15. Sato T. & Funamori N. High-pressure structural transformation of SiO2 glass up to 100 GPa. Phys. Rev. B 82, 184102 (2010). [Google Scholar]
  16. Tangney P. & Scandolo S. An ab initio parametrized interatomic force field for silica. J. Chem. Phys. 117, 8898–8904 (2002). [Google Scholar]
  17. Wu M., Liang Y., Jiang J.-Z. & Tse J. S. Structure and properties of dense silica glass. Sci. Rep. 2, 398 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Mantisi B., Tanguy A., Kermouche G. & Barthel E. Atomistic response of a model silica glass under shear and pressure. Eur. Phys. J. B 85, 304 (2012). [Google Scholar]
  19. Shi Y., Luo J., Yuan F. & Huang L. Intrinsic ductility of glassy solids. J. Appl. Phys. 115, 043528 (2014). [Google Scholar]
  20. Xue X., Stebbins J., Kanzaki M. & Tronnes R. Silicon coordination and speciation changes in a silicate liquid at high-pressures. Science 245, 962–964 (1989). [DOI] [PubMed] [Google Scholar]
  21. Stebbins J. & Mcmillan P. Five- and six-coordinated Si in K2Si4O9 glass quenched from 1.9 GPa and 1200°C. Am. Mineral. 74, 965–968 (1989). [Google Scholar]
  22. Stebbins J. NMR evidence for 5-coordinated silicon in a silicate glass at atmospheric-pressure. Nature 351, 638–639 (1991). [Google Scholar]
  23. Stebbins J. F. & Poe B. T. Pentacoordinate silicon in high-pressure crystalline and glassy phases of calcium disilicate (CaSi2O5). Geophys. Res. Lett. 26, 2521–2523 (1999). [Google Scholar]
  24. Vollmayr K., Kob W. & Binder K. Cooling-rate effects in amorphous silica: A computer-simulation study. Phys. Rev. B 54, 15808–15827 (1996). [DOI] [PubMed] [Google Scholar]
  25. Roder A., Kob W. & Binder K. Structure and dynamics of amorphous silica surfaces. J. Chem. Phys. 114, 7602–7614 (2001). [Google Scholar]
  26. Plimpton S. Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 117, 1–19 (1995). [Google Scholar]
  27. Meade C. & Jeanloz R. Effect of a coordination change on the strength of amorphous SiO2. Science 241, 1072–1074 (1988). [DOI] [PubMed] [Google Scholar]
  28. Liu Y. H. et al. Super plastic bulk metallic glasses at room temperature. Science 315, 1385–1388 (2007). [DOI] [PubMed] [Google Scholar]
  29. Demetriou M. D. et al. A damage-tolerant glass. Nat. Mater. 10, 123–128 (2011). [DOI] [PubMed] [Google Scholar]
  30. Wisitsorasak A. & Wolynes P. G. On the strength of glasses. Proc. Natl. Acad. Sci. U. S. A. 109, 16068–16072 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Kumar G., Neibecker P., Liu Y. H. & Schroers J. Critical fictive temperature for plasticity in metallic glasses. Nat. Commun. 4, 1536 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sarac B. & Schroers J. Designing tensile ductility in metallic glasses. Nat. Commun. 4, 2158 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Jeanloz R. Easy transformations in glasses. Nature 332, 207–207 (1988). [Google Scholar]
  34. Lee S. K. et al. X-ray Raman scattering study of MgSiO3 glass at high pressure: Implication for triclustered MgSiO3 melt in Earth's mantle. Proc. Natl. Acad. Sci. U. S. A. 105, 7925–7929 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Murakami M. & Bass J. D. Evidence of denser MgSiO3 glass above 133 gigapascal (GPa) and implications for remnants of ultradense silicate melt from a deep magma ocean. Proc. Natl. Acad. Sci. U. S. A. 108, 17286–17289 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Huang L., Durandurdu M. & Kieffer J. Transformation pathways of silica under high pressure. Nat. Mater. 5, 977–981 (2006). [DOI] [PubMed] [Google Scholar]
  37. Saika-Voivod I., Sciortino F. & Poole P. Fragile-to-strong crossover and polyamorphism in liquid silica: changes in liquid structure. Philos. Mag. 84, 1437–1445 (2004). [Google Scholar]
  38. Yuan F. & Huang L. Molecular dynamics simulation of amorphous silica under uniaxial tension: From bulk to nanowire. J. Non-Cryst. Solids 358, 3481–3487 (2012). [Google Scholar]
  39. Guilloteau E., Charrue H. & Creuzet F. The direct observation of the core region of a propagating fracture crack in glass. Europhys. Lett. 34, 549–553 (1996). [Google Scholar]
  40. Celarie F. et al. Glass breaks like metal, but at the nanometer scale. Phys. Rev. Lett. 90, 075504 (2003). [DOI] [PubMed] [Google Scholar]
  41. Pedone A., Malavasi G., Menziani M. C., Segre U. & Cormack A. N. Molecular dynamics studies of stress-strain behavior of silica glass under a tensile load. Chem. Mater. 20, 4356–4366 (2008). [Google Scholar]
  42. Muralidharan K., Simmons J. H., Deymier P. A. & Runge K. Molecular dynamics studies of brittle fracture in vitreous silica: Review and recent progress. J. Non-Cryst. Solids 351, 1532–1542 (2005). [Google Scholar]
  43. Falk M. L. & Langer J. S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 57, 7192–7205 (1998). [Google Scholar]
  44. Rodney D., Tanguy A. & Vandembroucq D. Modeling the mechanics of amorphous solids at different length scale and time scale. Model. Simul. Mater. Sci. Eng. 19, 083001 (2011). [Google Scholar]
  45. Guan P., Lu S., Spector M. J. B., Valavala P. K. & Falk M. L. Cavitation in amorphous solids. Phys. Rev. Lett. 110, 185502 (2013). [DOI] [PubMed] [Google Scholar]
  46. Chen Y.-C. et al. Interaction of voids and nanoductility in silica glass. Phys. Rev. Lett. 99, 155506 (2007). [DOI] [PubMed] [Google Scholar]
  47. Guin J.-P. & Wiederhorn S. M. Fracture of Silicate Glasses: Ductile or Brittle? Phys. Rev. Lett. 92, 215502 (2004). [DOI] [PubMed] [Google Scholar]
  48. Shi Y. & Falk M. Stress-induced structural transformation and shear banding during simulated nanoindentation of a metallic glass. Acta Mater. 55, 4317–4324 (2007). [Google Scholar]
  49. Yoshida S., Sangleboeuf J.-C. & Rouxel T. Quantitative evaluation of indentation-induced densification in glass. J. Mater. Res. 20, 3404–3412 (2005). [Google Scholar]
  50. Albano F. & Falk M. L. Shear softening and structure in a simulated three-dimensional binary glass. J. Chem. Phys. 122, 154508 (2005). [DOI] [PubMed] [Google Scholar]
  51. Angell C., Cheeseman P. & Tamaddon S. Pressure enhancement of ion mobilities in liquid silicates from computer-simulation studies to 800-Kilobars. Science 218, 885–887 (1982). [DOI] [PubMed] [Google Scholar]
  52. Aziz M. J., Circone S. & Agee C. B. Vanishing atomic migration barrier in SiO2. Nature 390, 596–599 (1997). [Google Scholar]
  53. Liang Y., Miranda C. R. & Scandolo S. Mechanical strength and coordination defects in compressed silica glass: Molecular dynamics simulations. Phys. Rev. B 75, 024205 (2007). [Google Scholar]
  54. Demkowicz M. J. & Argon A. S. High-density liquidlike component faciliates plastic flow in a model amorphous silicon system. Phys. Rev. Lett. 93, 025505 (2004). [DOI] [PubMed] [Google Scholar]
  55. Nose S. A molecular-dynamics method for simulations in the canonical ensemble. Mol. Phys. 52, 255–268 (1984). [Google Scholar]
  56. Nose S. A unified formulation of the constant temperature molecular-dynamics methods. J. Chem. Phys. 81, 511–519 (1984). [Google Scholar]
  57. Shinoda W., Shiga M. & Mikami M. Rapid estimation of elastic constants by molecular dynamics simulation under constant stress. Phys. Rev. B 69, 134103 (2004). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supporting Information for 'Brittle to Ductile Transition in Densified Silica Glass'

srep05035-s1.pdf (2.1MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES