Nonrandom Clusters of Palindromes in Herpesvirus Genomes

Abstract

Palindromes are symmetrical words of DNA in the sense that they read exactly the same as their reverse complementary sequences. Representing the occurrences of palindromes in a DNA molecule as points on the unit interval, the scan statistics can be used to identify regions of unusually high concentration of palindromes. These regions have been associated with the replication origins on a few herpesviruses in previous studies. However, the use of scan statistics requires the assumption that the points representing the palindromes are independently and uniformly distributed on the unit interval. In this paper, we provide a mathematical basis for this assumption by showing that in randomly generated DNA sequences, the occurrences of palindromes can be approximated by a Poisson process. An easily computable upper bound on the Wasserstein distance between the palindrome process and the Poisson process is obtained. This bound is then used as a guide to choose an optimal palindrome length in the analysis of a collection of 16 herpesvirus genomes. Regions harboring significant palindrome clusters are identified and compared to known locations of replication origins. This analysis brings out a few interesting extensions of the scan statistics that can help formulate an algorithm for more accurate prediction of replication origins.

1. INTRODUCTION

DNA palindromes are words from the nucleotide base alphabet $\mathcal{A}=\{A,C,G,T\}$ that are symmetrical in the sense that they read exactly the same as their complementary sequences in the reverse direction (see Fig. 1(a)). A DNA palindrome is necessarily even in length because the middle base in any odd-length nucleotide string cannot be identical to its complement. Palindromes are involved in a variety of biological processes. For example, the recognition sites for bacterial restriction enzymes to cut foreign DNA are mostly palindromic (Waterman, 1995, Chapter 2). Palindromes also play important roles in gene regulation and DNA replication processes (Wagner, 1991, Chapters 6, 12, 18; Kornberg and Baker, 1992, Chapter 1). It appears that palindromes have to do with DNA–protein binding. The local two-fold symmetry created by the palindrome provides a binding site for DNA-binding proteins which are often dimeric in structure. Such double binding markedly increases the strength and specificity of the binding interaction (Creighton, 1993, Chapter 8).

FIG. 1.

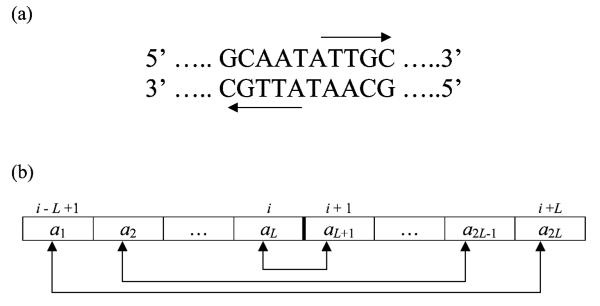
DNA palindrome. (a) This is a palindromic nucleotide sequence on the two complementary strands of DNA which are always read in opposite directions from the 5′ end to the 3′ end as shown by the arrows. The displayed segment reads exactly the same on both strands. (b) On each strand, the first base of the palindrome is complementary to the last, the second to the second last, and so on. This is a schematic representation of such complementary pairing between the bases in a 2L-palindrome centered at base i.

The herpesvirus family includes some of the well-known pathogenic viruses such as herpes simplex, varicella-zoster, Epstein-Barr, and cytomegalovirus. Some of these viruses are believed to pose major risks in immunosuppressive posttransplantation therapies, while others have been associated with life-threatening diseases such as AIDS and various cancers (Bennett et al., 2001; Biswas et al., 2001; Labrecque et al., 1995; Vital et al., 1995). A number of the animal herpesviruses are of agricultural concern. For example, the alcelaphine herpesvirus 1, indigenous to the wildebeest, is a causative agent of the fatal lymphoproliferative disease malignant catarrhal fever in cattle and deer (Bridgen, 1991).

Replication origins are places on the DNA molecules where replication processes are initiated. As DNA replication is the central step in the reproduction of many viruses, understanding the molecular mechanisms involved in DNA replication is of great importance in developing strategies to control the growth and spread of viruses (Delecluse and Hammerschmidt, 2000). For Epstein-Barr virus, one of these replication origins has been shown to associate with cellular proteins that regulate the initiation of DNA synthesis in human cells (Sugden, 2002). This suggests that these replication origins are also important locations for studying possible mechanisms of infecting human host cells. Knowledge of the locations of these replication origins will enhance the development of antiviral agents by blocking viral DNA replication or by interfering with the infection process.

As replication origins in DNA are considered major sites for regulating genome replication in general, labor-intensive laboratory procedures have been used to search for replication origins in various organisms (e.g., see Hamzeh, 1990; Zhu, 1998; Newlon and Theis, 2002). With the increasing availability of genomic DNA sequence data, the value of using computational methods to predict likely locations of replication origins before the experimental search has already been recognized although no prediction scheme that works for all DNA in general is available to date. The success of the computational prediction depends critically on the observation of the characterizing patterns in the nucleotide sequence around the replication origins of the particular kind of organisms under study. For example, the algorithm of Salzberg et al. (1998) predicted the replication origins for a number of bacterial and archaeal genomes based on the finding of seven-base and eight-base oligomers whose orientation is preferentially skewed around the replication origins. However, as pointed out by the authors, this algorithm is not suited for DNA molecules, like those in many viruses and their eukaryotic hosts, where multiple replication origins exist. In those cases, one would need to rely on other relevant sequence patterns to locate the replication origins.

The existence of high concentrations of palindromes in proximity of the replication origins of herpesviruses has been reported in some early studies (Weller et al., 1985; Reisman et al., 1985; Masse et al., 1992). This phenomenon is generally attributed to the fact that initiation of DNA replication typically requires an assembly of enzymes such as the helicases to locally unwind the helical structure of DNA and pull apart the two complementary strands. Furthermore, Masse et al. (1992) have demonstrated that by looking for palindrome clusters, among other features such as clusters of close repeats and close inversions on the nucleotide sequence, likely regions containing replication origins can be predicted.

Leung et al. (1994) describe how a statistical criterion, based on the scan statistics (Glaz, 1989; Dembo and Karlin, 1992), is developed for identifying nonrandom palindrome clusters by modeling the occurrences of palindromes in the genome as points randomly sampled from the unit interval according to the uniform distribution. Despite the fact that the criterion worked well for the cytomegalovirus genome sequence used for illustration in that article, the authors point out that the assumption of uniform distribution of palindromes has not yet been mathematically justified. In this paper, we shall justify this claim under the model that the nucleotide sequence is generated as a sequence of independent and identically distributed (i.i.d.) random variables.

The second, and more important, aim of this paper is to analyze a collection of herpesvirus genome sequences for nonrandom palindrome clusters and examine their connections with replication origins. Table 1 presents the collection of herpesvirus genomes to be analyzed. The dataset comprises all the complete genome sequences of the herpesvirus family downloaded from GenBank at the NCBI website in June 2001. Listed along with each virus name in the table are an abbreviation that will be used throughout this paper, its accession number in the GenBank database, its genome sequence length in number of bases, and the relative frequencies of the four nucleotide bases in the genome. The experimentally confirmed replication origins among the viruses in this dataset will help us assess the palindrome-based algorithm and suggest directions for improving the rate of successful prediction.

Table 1.

The List of Herpesvirus Genomes to be Analyzed

Name	Abbrev.	Accession	Length	Base composition
Alcelaphine herpesvirus 1	AHV1	NC_002531	130608	(.27, .24, .22, .26)
Ateline herpesvirus 3	AtHV3	NC_001987	108409	(.32, .19, .17, .31)
Bovine herpesvirus 1.1	BHV1	NC_001847	135301	(.14, .36, .37, .14)
Equine herpesvirus 1	EHV1	NC_001491	150223	(.22, .29, .28, .22)
Equine herpesvirus 4	EHV4	NC_001844	145597	(.25, .25, .25, .25)
Gallid herpesvirus 1	MDV2	NC_002530	110637	(.24, .25, .25, .25)
Gallid herpesvirus 2	MDV	NC_002229	138675	(.28, .22, .21, .29)
Human herpesvirus 1	HSV1	NC_001806	152261	(.16, .34, .34, .16)
Human herpesvirus 2	HSV2	NC_001798	154746	(.15, .35, .35, .15)
Human herpesvirus 3	VZV	NC_001348	124884	(.27, .23, .23, .27)
Human herpesvirus 4	EBV	NC_001345	172281	(.20, .30, .29, .20)
Human herpesvirus 5	HCMV	NC_001347	229354	(.22, .28, .29, .21)
Human herpesvirus 6	HHV6	NC_001664	159321	(.29, .22, .21, .29)
Human herpesvirus 7	HHV7	NC_001716	144861	(.32, .18, .17, .32)
Ictalurid herpesvirus	CCV1	NC_001493	134226	(.21, .28, .28, .22)
Saimiriine herpesvirus 2	HVS2	NC_001350	112930	(.33, .18, .16, .32)

It would be of interest to ask whether our algorithm, developed for the herpesviruses, can be applied to identify replication origins in other organisms, or even to identify other functionally important regions, such as regulatory sites. While one would not anticipate that palindrome clusters will be the universal characterizing sequence pattern for all kinds of organisms and all types of functional sites, existence of palindrome clusters may serve as one possible criterion for these general purposes. For example, we have already noted that this approach adds to the skewed-oligomers method described by Salzberg et al. (1998) because it is not limited to DNA molecules with single replication origins. It is our hope that it will contribute to a general prediction tool that can be broadly applied to various domains of the tree of life.

The organization of the paper is as follows: Section 2 formulates the random process representing the palindrome occurrences on a nucleotide sequence and introduces the Wasserstein distance for measuring the difference between the palindrome process and the Poisson process. Using a general mathematical Poisson process approximation theorem, we derive an explicitly computable upper bound for this distance which approaches zero under suitable conditions. Section 3 briefly reviews how the scan statistics are used to identify nonrandom clusters of palindromes, treating them as points randomly sampled from a uniform distribution. The significant palindrome clusters obtained from the herpesviruses are presented in Section 4 where their association with replication origins is also discussed. We conclude with a few remarks about future works towards a more accurate replication origin prediction scheme in Section 5.

2. DISTRIBUTION OF PALINDROMES ON RANDOM DNA SEQUENCES

In this section, we shall see that if a DNA genome is assumed to be a sequence of nucleotide bases generated as i.i.d. random variables taking values A,C,G,T with probabilities p_A,p_C,p_G,p_T, respectively, the occurrences of palindromes above a certain minimal length can be approximated by a Poisson process. This is achieved by deriving an upper bound for the Wasserstein distance, also called the d₂ metric (Barbour et al., 1992, Chapter 10), between the palindrome process and the Poisson process. Under suitable conditions, this Wasserstein distance dwindles to 0 as the sequence length increases indefinitely. Before these results can be stated, we need to first make precise the notion of the palindrome process and explain the concept of the Wasserstein distance.

2.1. The palindrome process and Wasserstein distance

Due to the complementary base pairing, it is often sufficient to represent DNA as a single nucleotide sequence. Any segment of the nucleotide sequence consisting of 2L bases will be a palindrome if its first base and its 2Lth base form a complementary pair, and so do its second and (2L − 1)st bases, the third and (2L − 2)nd, … , up to the Lth and (L + 1)st bases in the center of the segment (Fig. 1(b)). Using the center of the palindrome to indicate its position, we say that a palindrome of length 2L occurs at position i of the sequence if the bases i − j + 1 and i + j are complementary to each other for j = 1, … , L. This characterization does not preclude the possibility that a palindrome of length 2L may be extended to a longer length if the complementary pairing continues on for j > L. In this paper, it will be understood that the term “palindrome of length 2L” actually means “palindrome of length 2L or more.” For short, we shall just refer to it as a 2L-palindrome. If there are multiple 2L-palindromes centered at the same position of the sequence, only the longest one will be counted.

Because it is impossible for a nucleotide sequence of length M to have any 2L-palindrome centered at positions 1, … , L − 1 and M − L + 1, … , M, we shall represent the occurrences of palindromes as a random process on $\frac{1}{n},\frac{2}{n},\dots ,\frac{n}{n}$, where n = M − 2L + 1. The palindrome process is defined as

$$\Xi =\sum _{i=1}^n{\mathit{I}}_i{\delta }_{i∕n}.$$

Here I_i is the indicator random variable for the occurrence of a 2L-palindrome centered at base i + L − 1 of the DNA sequence and δ_i/n denotes the unit point mass at i/n. In this definition, the DNA segment H of length 2L spanning bases i, … , i + L − 1, i + L, … , i + 2L − 1 is associated with the indicator I_i and the unit point mass at $\frac{i}{n}$. For brevity, we shall say that the DNA segment H is positioned at i for the rest of the paper.

In an i.i.d. random nucleotide sequence, the success probability for the random variable I_i is

$$p_i=P({\mathit{I}}_i=1)=1-P(I_i=0)={\theta }^L,$$ (1)

with θ = 2(p_Ap_T + p_Cp_G), and the expected number of palindromes is

$$\lambda =\sum _{i=1}^n{p}_i=n{\theta }^L.$$ (2)

Because palindromes occurring close to each other overlap, the I_i’s are locally dependent. The neighborhood of dependence of I_i is

$$A_i=\{1\le j\le n:\mid j-i\mid <2L\}.$$ (3)

For all j outside of A_i, I_i and I_j are independent of each other.

We want to approximate the palindrome process Ξ defined on the n equally spaced discrete points $\frac{1}{n},\frac{2}{n},\dots ,\frac{n}{n}$ in [0, 1] by the Poisson process Z_λ with intensity λ on the continuous interval [0, 1]. In a number of DNA related studies (e.g., Arratia et al., 1990, 1996; Reinert et al., 2000; Reinert and Schbath, 1998; Schbath, 1995), the differences between two random processes are quantified by the total variation distance d_TV between them. However, as explained in Chapter 10 of Barbour et al. (1992), the total variation distance is too strong to be useful for point processes like Ξ and Z_λ. Indeed,

$$d_{\mathit{TV}}\left(\mathcal{L}\right(\Xi ),\mathcal{L}(Z_{\lambda }\left)\right)=\underset{A}{\sup }\mid P(\Xi \in A)-P(Z_{\lambda }\in A)\mid$$

where the supremum is taken over all measurable subsets¹ of $\mathcal{Y}$ where

$$\mathcal{Y}=\left\{\sum _{i=1}^n{\delta }_{x_i}:n\ge 0,x_i\in [0,1]\right\}$$

is often called the configuration space of [0, 1]. From this, it can be shown that

$$d_{\mathit{TV}}\left(\mathcal{L}\right(\Xi ),\mathcal{L}(Z_{\lambda }\left)\right)=1∕2\underset{-1\le f\le 1}{\sup }\mid \mathit{Ef}\left(\Xi \right)-\mathit{Ef}\left(Z_{\lambda }\right)\mid$$

which always equals 1 because Ξ has support only in {i/n : 1 ≤ i ≤ n} whereas Z_λ has no points in {i/n : 1 ≤ i ≤ n} with probability 1.

Unlike d_TV , the Wasserstein distance, also called the d₂ metric, is less sensitive to small changes in the positions of points. It is more suitable for our purpose of measuring the discrepancy between the palindrome process and the Poisson process. Essentially, the Wasserstein distance between two point processes X and Y is the supremum of all expected differences between X and Y under test functions f that do not fluctuate too vigorously on the configuration space of [0, 1] with respect to the d₁ metric explained below. These test functions are called Lipschitz functions. We give a concise explanation of the Wasserstein distance below. A more detailed description can be found in Barbour et al. (1992, Chapter 10, Section 2).

The Wasserstein distance between two point processes X and Y is defined as

$$d_2\left(\mathcal{L}\right(X),\mathcal{L}(Y\left)\right)=\sup \{\mid \mathit{Ef}(X)-\mathit{Ef}(Y)\mid :{\Vert f\Vert }_{\mathrm{Lip}\left(\mathcal{Y}\right)}\le 1\}$$

where $f:\mathcal{Y}\to \mathbf{R}$ and

$${\Vert f\Vert }_{\mathrm{Lip}\left(\mathcal{Y}\right)}=\sup \left\{\frac{\mid f\left({\xi }_1\right)-f\left({\xi }_2\right)\mid }{d_1({\xi }_1,{\xi }_2)}:{\xi }_1\ne {\xi }_2\in \mathcal{Y}\right\}.$$

Here, d₁(ξ₁, ξ₂) denotes the distance between two configurations ξ₁ = (y₁₁, … , y_1m1) and ξ₂ = (y₂₁, … , y_2m2). It is defined to be 1 if ξ₁ and ξ₂ have different numbers of points in [0, 1] and is defined to be the average distance between ξ₁ and ξ₂ under the closest matching if they have the same number of points. More precisely,

$$d_1({\xi }_i,{\xi }_2)=\{\begin{array}{cc}1\hfill & \text{if}{m}_1\ne m_2\hfill \\ \min \{1∕m\sum _{i=1}^m\mid y_{1i}-y_{2\pi \left(i\right)}\mid \}\hfill & \text{if}{m}_1=m_2\hfill \end{array}\phantom{\}}$$

where the minimum is taken over all permutations π of (1, 2, … , m) with m being the common value of m₁ and m₂. Since our point processes are defined on [0, 1], without loss of generality, we can assume that y₁₁ ≤ y₁₂ ≤ … ≤ y_1m1 and y₂₁ ≤ y₂₂ ≤ … ≤ y_2m2. Then, when m₁ = m₂ = m,

$$d_1({\xi }_1,{\xi }_2)=\frac{1}{m}\sum _{i=1}^m\mid y_{1i}-y_{2i}\mid .$$

The above simplified expression for d₁(ξ₁, ξ₂) will be formally proved as Proposition 3 in the appendix.

With this background, we present the following general theorem giving an upper bound for the Wasserstein distance between a point process Ξ and the Poisson process Z_λ. We will use the following notations. Let I₁, … , I_n be indicator random variables with P(I_i = 1) = 1 − P (I_i = 0) = p_i, and p_ij = P(I_i = I_j = 1) for 1 ≤ i, j ≤ n. For each i, I_i has a neighborhood of dependence A_i which is a collection of those indices j such that I_j may be dependent on I_i. Define a random point process

$$\Xi =\sum _{i=1}^n{I}_i{\delta }_{i∕n}$$

where δ_i/n denotes the unit point mass at i/n. We also define the point processes

$$V_i=\sum _{j\notin A_i}{\mathit{I}}_j{\delta }_{j∕n}\text{and}{V}_{\mathit{ij}}=\sum _{k\notin A_i\cup A_j}{\mathit{I}}_k{\delta }_{k∕n}.$$

We let

$$\mid V_i\mid =\sum _{j\notin A_i}{\mathit{I}}_j\text{and}\mid V_{\mathit{ij}}\mid =\sum _{k\notin A_i\cup A_j}{I}_k$$

denote the number of points in these processes.

Theorem 1

Let Z_λ denote the Poisson process on [0, 1] with intensity $\lambda ={\sum }_{i=1}^n{p}_i$. Assume (I_j, j ∉ A_i) is independent of I_i and (I_k, k ∉ A_i ⋃ A_j) is independent of (I_i, I_j) for all i, j. Then we have

$$d_2\left(\mathcal{L}\right(\Xi ),\mathcal{L}(Z_{\lambda }\left)\right)\le \left[\frac{5}{\lambda }+3\underset{\begin{array}{c}\hfill 1\le i\le n\hfill \\ \hfill j\in A_i\backslash \left\{i\right\}\hfill \end{array}}{\sup }E\left(\frac{1}{\mid V_{\mathit{ij}}\mid +1}\right)\right](b_1+b_2)+\frac{1}{2n}$$ (4)

where

$$b_1=\sum _{i=1}^n\sum _{j\in A_i}{p}_i{p}_j$$

is the sum of products of the probabilities of observing 2L-palindromes at positions i and j within the neighborhood of dependence of each other and

$$b_2=\sum _{i=1}^n\sum _{j\in A_i\backslash \left\{i\right\}}{p}_{\mathit{ij}}$$

is the sum of probabilities of observing overlapping 2L-palindromes at both positions i and j (∉ i) within the neighborhood of dependence of each other.

The proof of this theorem, given in the appendix, is based on an adaptation of Stein’s method (1972) for the Poisson process setting. We shall now examine how to use Theorem 1 to obtain a Poisson limit for the palindrome process. With long sequences, n is large, making the last term in the above bound negligible. We have noted in Equations (1) and (2) that for any i, p_i = θ^L, giving λ = nθ^L. It is also easy to see from (3) that in the palindrome process Ξ, the neighborhood of dependence of I_i can stretch in either the forward or backward direction from base i for at most only 2L − 1 bases. This implies

$$b_1\le n(4L-1){\theta }^{2L}.$$ (5)

To obtain an explicit upper bound for the Wasserstein distance between Ξ and Z_λ, two things remain to be done. First, we need to examine the b₂ term which involves the probabilities of overlapping palindromes. Second, we need to work out a uniform upper bound for $E\left(\frac{1}{\mid V_{\mathit{ij}}\mid +1}\right)$ which is independent of i, j.

The b₂ term comprises the probabilities p_ij of observing overlapping 2L-palindromes at positions i and j that are no more than 2L − 1 bases apart. For example, the sequence ATCGATCG contains a 6-palindrome centered at position i = 3 overlapping with another 6-palindrome centered at position j = 5. The following proposition expresses the overlapping probability p_ij in terms of the base probabilities p_A, p_C, p_G, and p_T, the length parameter L, and the distance h = ∣i − j∣ between the centers of the two palindromes.

Proposition 1 (probability of overlapping palindromes)

Let h = ∣i − j∣ > 0. If h < 2L, the probability p_ij of having overlapping palindromes at both positions i and j are given by the following.

Case (a): L ≤ h ≤ 2L − 1. We have

$$p_{\mathit{ij}}={\theta }^{2(h-L)}{\left[p_A{p}_T\right(p_A+p_T)+p_C{p}_G(p_C+p_G\left)\right]}^{2L-h}.$$

Case (b): 0 < h < L. Here we let L = qh + r and consider two subcases according to how big the remainder r is in relation to h.

Subcase (b1): 0 ≤ r < (h + 1)/2.

$$\begin{array}{cc}\hfill p_{\mathit{ij}}=& {\left[2\right({\left(p_A{p}_T\right)}^{q+1}+{\left(p_C{p}_G\right)}^{q+1}\left)\right]}^{2r}\hfill \\ \hfill & \cdot {\left[{\left(p_A{p}_T\right)}^q\right(p_A+p_T)+{\left(p_C{p}_G\right)}^q(p_C+p_G\left)\right]}^{h-2r}.\hfill \end{array}$$

Subcase (b2): (h + 1)/2 ≤ r < h.

$$\begin{array}{cc}\hfill p_{\mathit{ij}}=& {\left[2\right({\left(p_A{p}_T\right)}^{q+1}+{\left(p_C{p}_G\right)}^{q+1}\left)\right]}^{2(h-r)}\hfill \\ \hfill & \cdot {\left[{\left(p_A{p}_T\right)}^{q+1}\right(p_A+p_T)+{\left(p_C{p}_G\right)}^{q+1}(p_C+p_G\left)\right]}^{2r-h}.\hfill \end{array}$$

Proof

Without loss of generality, we can assume i < j < 2L + i. Let H_i and H_j denote the DNA segments of length 2L positioned at i and j, respectively. Because of their overlap, H_i and H_j must share a common subsegment of length 2L − h at the right end of H_i and the left end of H_j. Throughout the proof, we shall use a’ to denote the complement of base a (e.g., A’ = T), w’ to denote the inverse complement of word w, and P(w) to denote the probability for w (e.g., if w = (ATC), then P(w) = p_Ap_Tp_C). We discuss the cases separately.

Case (a)

Let w = (a₁, … , a_2L−h) denote the common subsegment. For both H_i and H_j to be palindromes, we must have the arrangement as shown in Fig. 2(a). At the left end of H_i and the right end of H_j, the sequence must be w’. The center portions of H_i and H_j must be 2(h − L)-palindromes denoted, respectively, by (u’, u) and (v, v’). The probability of this arrangement is

$$p_{\mathit{ij}}={\theta }^{2(h-L)}\sum _{\mathbf{w}}\mathit{P}\left(\mathbf{w}\right)\mathit{P}{\left({\mathbf{w}}^{\prime }\right)}^2$$

where the sum is taken over all possible DNA words w of length 2L − h. Writing out P(w) in terms of the base probabilities, we have

$$\begin{array}{cc}\hfill p_{\mathit{ij}}=& {\theta }^{2(h-L)}\sum _{a_1,\dots ,a_{2L-h}\in \mathcal{A}}\left(p_{a_1}{p}_{a_1^{\prime }}^2\right)\cdots \left(p_{a_{2L-h}}{p}_{a_{2L-h}^{\prime }}^2\right)\hfill \\ \hfill =& {\theta }^{2(h-L)}{\left[\sum _{a\in \mathcal{A}}{p}_a{p}_{a^{\prime }}^2\right]}^{2L-h}\hfill \\ \hfill =& {\theta }^{2(h-L)}{\left[p_A{p}_T\right(p_A+p_T)+p_C{p}_G(p_C+p_G\left)\right]}^{2L-h}\hfill \end{array}$$

where a is summed over the four bases in the alphabet $\mathcal{A}$.

FIG. 2.

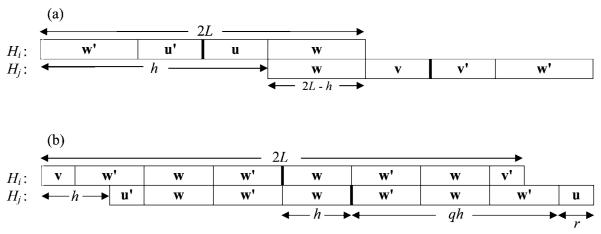
Overlapping palindromes. (a) When L ≤ h ≤ 2L − 1, the DNA segments H_i and H_j must have this structure for both of them to be 2L-palindromes centered at positions i and j, respectively. The center position of each segment is represented by a bold vertical bar. (b) Similarly, this displays the structures of H_i and H_j for both of them to be palindromes when 0 < h < L. In this illustration, q = 3.

Case (b)

This time, let w = (a₁, … , a_h) denote the first h bases to the right of the center of H_i and to the left of the center of H_j. Let u = (a₁, … , a_r) and v = (a_h−r+1, … , a_h), respectively, stand for the first and last r bases of w. Figure 2(b) displays the necessary structure in H_i and H_j for both of them to be palindromes when q = 3. In general, the probability of such arrangements can be computed as

$$p_{ij}=\{\begin{array}{cc}\sum _{\mathbf{w}}{\left[\mathit{P}\right(\mathbf{w}\left)\right]}^q{\left[\mathit{P}\right({\mathbf{w}}^{\prime }\left)\right]}^{q+1}\mathit{P}\left(\mathbf{u}\right)\mathit{P}\left(\mathbf{v}\right)\hfill & \text{when}q\text{is ood},\hfill \\ \sum _{\mathbf{w}}{\left[\mathit{P}\right({\mathbf{w}}^{\prime }\left)\right]}^q{\left[\mathit{P}\right(\mathbf{w}\left)\right]}^{q+1}\mathit{P}\left({\mathbf{u}}^{\prime }\right)\mathit{P}\left({\mathbf{v}}^{\prime }\right)\hfill & \text{when}q\text{is even}.\hfill \end{array}\phantom{\}}$$

Subcase (b1)

$0\le \mathit{r}<\frac{h+1}{2}$. If q is odd,

$$\begin{array}{cc}\hfill p_{\mathit{ij}}=& {\left[\sum _{a\in \mathcal{A}}{\left(p_a{p}_{a^{\prime }}\right)}^{q+1}\right]}^{2r}{\left[\sum _{a\in \mathcal{A}}{p}_{a^{\prime }}{\left(p_a{p}_{a^{\prime }}\right)}^q\right]}^{h-2r}\hfill \\ \hfill =& {\left[2\right({\left(p_A{p}_T\right)}^{q+1}+{\left(p_C{p}_G\right)}^{q+1}\left)\right]}^{2r}{\left[{\left(p_A{p}_T\right)}^q\right(p_A+p_T)+{\left(p_C{p}_G\right)}^q(p_C+p_G\left)\right]}^{h-2r}.\hfill \end{array}$$

If q is even, the calculation is exactly the same except a and a’ need to be swapped, reducing to the same expression in terms of the base probabilities.

Subcase (b2)

$\frac{h+1}{2}\le \mathit{r}<\mathit{h}$.

$$p_{\mathit{ij}}={\left[\sum _{a\in \mathcal{A}}{\left(p_a{p}_{a^{\prime }}\right)}^{q+1}\right]}^{2(h-r)}{\left[\sum _{a\in \mathcal{A}}{p}_a{\left(p_a{p}_{a^{\prime }}\right)}^{q+1}\right]}^{2r-h}$$

when q is odd. Just like subcase (b1), a and a’ need to be swapped when q is even. Either way, the expression reduces to

$${\left[2\right({\left(p_A{p}_T\right)}^{q+1}+{\left(p_C{p}_G\right)}^{q+1}\left)\right]}^{2(h-r)}{\left[{\left(p_A{p}_T\right)}^{q+1}\right(p_A+p_T)+{\left(p_C{p}_G\right)}^{q+1}(p_C+p_G\left)\right]}^{2r-h}.$$

The following two lemmas will facilitate proving that the palindrome process approaches a Poisson limit under the equal complementary probability (ECP) assumption of p_A = p_T and p_C = p_G.

Lemma 1

Under the ECP assumption, p_ij ≤ θ^3L/2 for 1 ≤ i ≠ j ≤ n.

Proof

When j ∉ A_i, the inequality is trivially true because I_i and I_j are independent and p_ij = p_ip_j = θ^2L. We therefore only need to look at those p_ij’s with ∣j − i∣ < 2L. The calculations needed involve expressions of the form (0.5 − x)^l + x^l where x = P_G = P_C is a number between 0 and 0.5 and l is a positive integer. We note the following elementary algebraic properties:

A. 1/8 ≤ (0.5 − x)² + x² ≤ 1/4 (i.e., 1/4 ≤ θ ≤ 1/2).

B. If α > β ≥ 0, then

$${(0.5-x)}^{\alpha }+x^{\alpha }\le [{(0.5-x)}^{\beta }+x^{\beta }][{(0.5-x)}^{\alpha -\beta }+x^{\alpha -\beta }].$$

It follows that for any positive integer q

$${(0.5-x)}^{2q}+x^{2q}\le {[{(0.5-x)}^2+x^2]}^q$$

and

$${(0.5-x)}^{2q+1}+x^{2q+1}\le 0.5{[{(0.5-x)}^2+x^2]}^q.$$

In Case (a), L ≤ h ≤ 2L − 1. Here

$$\begin{array}{cc}\hfill p_{\mathit{ij}}=& {\left\{2\right[{(0.5-x)}^2+x^2\left]\right\}}^{2(h-L)}{\left\{2\right[{(0.5-x)}^3+x^3\left]\right\}}^{2L-h}\hfill \\ \hfill \le & 2^h{[{(0.5-x)}^2+x^2]}^{2(h-L)}{\left\{0.5\right[{(0.5-x)}^2+x^2\left]\right\}}^{2L-h}\left(\text{property B}\right)\hfill \\ \hfill =& 2^{2(h-L)}{[{(0.5-x)}^2+x^2]}^h.\hfill \end{array}$$

With θ^L = 2^L[(0.5 − x)² + x²]^L, we have

$$\frac{p_{\mathit{ij}}}{{\theta }^{3L∕2}}\le \frac{2^{2(h-L)}{[{(0.5-x)}^2+x^2]}^{h-L}}{2^{3L∕2}{[{(0.5-x)}^2+x^2]}^{L∕2}}.$$

This ratio is ≤ 1 because the numerator is ≤ 1 while the denominator is ≥ 1 by property A noted above. Similar calculations lead to

$$\frac{p_{\mathit{ij}}}{{\theta }^{3L∕2}}\le \frac{2^{2r}{[{(0.5-x)}^2+x^2]}^r}{2^{3L∕2}{[{(0.5-x)}^2+x^2]}^{L∕2}}.$$

for Subcase (b1) and

$$\frac{p_{\mathit{ij}}}{{\theta }^{3L∕2}}\le \frac{2^{2(h-r)}{[{(0.5-x)}^2+x^2]}^{(h-r)}}{2^{3L∕2}{[{(0.5-x)}^2+x^2]}^{L∕2}}$$

for Subcase (b2). Both of these ratios are ≤ 1 again because of property A.

Remark on Lemma 1

Although not directly relevant to the analysis in this paper, it is of interest to point out that calculations similar to those in Lemma 1 will also show that if p_A = p_T and p_C = p_G, p_ij ≥ p_ip_j = θ^2L. Equality is obtained when one of the following special situations occur: Either all four probabilities are equal to 1/4, or one pair of probabilities is equal to 0 while the other pair is equal to 0.5. These equalities have been obtained by Ghosh and Godbole (1996). Other than these special cases, we now see that under the ECP assumption, I_i and I_j are nonnegatively correlated indicator random variables. Furthermore, we have carried out quite extensive computations, and the results indicate that the positive correlation between I_i and I_j holds even without the ECP assumption. We have yet to prove it analytically though. This positive correlation essentially says that when a palindrome occurs, it enhances the probability of having another palindrome occurring nearby that overlaps with it.

Lemma 2

Assuming ECP, then for 1 ≤ i ≤ n and j ∈ A_i, we have

$$E\left(\frac{1}{1+\mid V_{\mathit{ij}}\mid }\right)\le \frac{7}{\lambda }$$ (6)

provided that 4 ≤ L ≤ n/500.

Proof

Notice that ∣V_ij∣ = ∑_k∈Ai⋃Aj I_k, which is of the form ∑_k∈Γij I_k. For simplicity, we suppress the notational dependence of Γ_ij on i, j and write

$$W=\mid V_{\mathit{ij}}\mid =\sum _{k\in \Gamma }{\mathit{I}}_k,\mu =E\left(W\right),\text{and}{\sigma }^2=\mathrm{var}\left(W\right).$$

Lemma 3.1 from Brown et al. (2000) states that for any random variable X ≥ 1,

$$E\left(\frac{1}{X}\right)\le \frac{1+\kappa ∕2+\sqrt{\kappa (1+\kappa ∕4)}}{E\left(X\right)}$$ (7)

where κ = Var (X)/E(X). Here, we let X = 1 + W. Then

$$\kappa =\frac{\mathrm{Var}\left(X\right)}{E\left(X\right)}=\frac{{\sigma }^2}{1+\mu }\le \frac{{\sigma }^2}{\mu }.$$

For k, l ∈ Γ. where ∣k − l∣ ≥ 2L, I_k and I_l are independent. So we have

$$\begin{array}{cc}\hfill {\sigma }^2=& \sum _{k\in \Gamma }{\theta }^L(1-{\theta }^L)+\sum _{k\in \Gamma }\sum _{l\in A_k,l\ne k}\mathrm{Cov}({\mathit{I}}_k,{\mathit{I}}_l)\hfill \\ \hfill \le & \mid \Gamma \mid {\theta }^L(1-{\theta }^L)+2(2L-1)\mid \Gamma \mid {\theta }^{3L∕2}\hfill \\ \hfill \le & \mid \Gamma \mid {\theta }^L(1-{\theta }^L+4L{\theta }^{L∕2})\text{from Lemma}1\hfill \\ \hfill \le & 5\mu \text{as}L{\theta }^{L∕2}\le 1\text{for}L\ge 4.\hfill \end{array}$$

Consequently, κ ≤ 5. We observe that the upper bound on E(1/X) in (7) is an increasing function in κ. Replacing κ by 5 yields

$$E\left(\frac{1}{1+\mid V_{\mathit{ij}}\mid }\right)\le \frac{1+5∕2+\sqrt{5(1+5∕4)}}{E(\mid V_{\mathit{ij}}\mid )}\le \frac{6.86}{[1-4(2L-1)∕n]\lambda }\le \frac{7}{\lambda }.$$

The middle inequality comes from the fact that

$$E(\mid V_{\mathit{ij}}\mid )=\sum _{k\notin A_i\cup A_j}E\left({\mathit{I}}_k\right)\ge [n-4(2L-1\left)\right]{\theta }^L=[1-4(2L-1)∕n]\lambda .$$

The last inequality follows from L ≤ n/500.

2.2. Poisson limit for the palindrome process

We shall make use of Lemmas 1 and 2 in conjunction with Theorem 1 to prove the following proposition stating that the palindrome process approaches a Poisson process in the limit under suitable conditions. This is done by showing that the Wasserstein distance between Ξ and Z_λ can be made arbitrarily small provided that n → ∞ and L grows at a suitable rate proportional to log n.

Proposition 2

Assume ECP and suppose that n, L → ∞ in such a way that nθ^L = λ, where λ ≥ 1/32 is a fixed positive constant, then

$$d_2\left(\mathcal{L}\right(\Xi ),\mathcal{L}(Z_{\lambda }\left)\right)\le \mathit{cL}{\theta }^{L∕2}\to 0$$

where c is an absolute constant no greater than 131.

Proof

First note that the condition 4 ≤ L ≤ n/500 in Lemma 2 is easily satisfied when n and L become large with nθ^L = λ. This condition will continue to be assumed true. It has been pointed out in (5) that b₁ ≤ n(4L − 1)θ^2L ≤ 4Lλθ^L. From Lemma 1, it follows that b₂ ≤ n(4L − 2)θ^3L/2 ≤ 4Lθ^L/2λ. Combining the two inequalities gives

$$d_1+b_2\le 4L\lambda {\theta }^{L∕2}(1+{\theta }^{L∕2})\le 5L\lambda {\theta }^{L∕2}$$ (8)

because θ^L/2 ≤ (1/2)^L/2 ≤ 0.25 for L ≥ 4. From Lemma 2, it follows that

$$\frac{5}{\lambda }+3\sup E\left(\frac{1}{\mid V_{\mathit{ij}}\mid +1}\right)\le \frac{26}{\lambda }$$ (9)

where the supremum is taken over 1 ≤ i ≤ n, j ∈ A_i \ {i}. Combining Inequalities (8) and (9), we see that first term in the upper bound for the Wasserstein distance in Theorem 1 is less than 130Lθ^L/2. It can be verified that the second term 1/(2n) ≤ Lθ^L/2 when λ ≥ 1/32. Putting the two terms together gives

$$d_2\left(\mathcal{L}\right(\Xi ),\mathcal{L}(Z_{\lambda }\left)\right)\le 131L{\theta }^{L∕2}.$$

Furthermore, as nθ^L = λ, L must be growing at the rate log n, and hence

$$L{\theta }^{L∕2}\le c^{\prime }\sqrt{\lambda }\log n∕\sqrt{n}\to 0.$$

2.3. Remarks on various assumptions in Proposition 2

Various assumptions and constraints have been made in order to prove the result in Proposition 2. How restrictive are these assumptions? Are they satisfied, at least to a reasonable extent, by the actual viral genome DNA data? We shall discuss these questions in the following remarks.

Remark 1. The ECP assumption

It should be noted that the ECP assumption is sufficient but not necessary for obtaining the Poisson process limit. The proofs of Lemma 2 and Proposition 2 require only the inequality p_ij ≤ θ^3L/2, which can be computationally verified to hold for many base frequencies that do not satisfy the ECP assumption (e.g., p_A = 0.1, p_C = 0.2, p_G = 0.3, p_T = 0.4). In those cases, the palindrome process still approaches a limiting Poisson process.

Intuitively, the ECP assumption is quite believable, and it has been used in a number of genomic or chromosomal DNA sequence analysis studies (e.g., Burge et al., 1992; Karlin et al., 1993). Looking at the base composition of the herpesviruses in Table 1, we see that the relative frequencies of A and T are quite close to each other, and so are those of C and G. It is tempting to believe in the ECP assumption.

To examine this more objectively, one can turn to the Bayesian information criterion (BIC). For each genome, we compare the saturated multinomial model where the bases are generated with probabilities (p_A, p_C, p_G, p_T) summing to 1 against the ECP model with the extra condition that p_A = p_T and p_C = p_G. As summarized in Tavaré and Giddings (1989), the BIC of a model D can be computed by

$$\mathrm{BIC}\left(D\right)=-2l+k\log M$$

where M is the sequence length, k is the number of free parameters in model D (k = 3 in the saturated model and k = 1 in the ECP model), and

$$l=\sum _{a\in \mathcal{A}}n\left(a\right)\log {\widehat{p}}_a$$

is the log likelihood for the data, with n(a) representing the count of base a in the sequence and ${\widehat{p}}_a$ the maximum likelihood estimate of the base probability p_a. In the saturated model, ${\widehat{p}}_a$ is the relative frequency of a. In the ECP model, ${\widehat{p}}_a$ is the averaged relative frequency of a and a’. When comparing two statistical models, the model with smaller BIC is considered superior.

It turns out from the BIC that in 8 out of the 16 herpesviruses in our dataset, the ECP model is preferred hence justifying the ECP assumption for their DNA sequences. For the rest of the viruses, we do not have such a nice statistical justification. Fortunately, one can computationally verify, by working out the values of p_ij and θ, that the inequality in Lemma 1 remains true for those base probabilities estimated from each of the 16 viruses, ascertaining the Poisson process limit for the palindrome process in each genome as explained above.

Remark 2. Restrictions on n, L, and λ

We have also posed the restriction of 4 ≤ L ≤ n/500 and λ ≥ 1/32 in Lemma 2 and Proposition 2. These restrictions offer no difficulty at all to our application. In each of the herpesviruses to be analyzed, n is of the order 10⁵ and θ is close to 1/4. The values of L of interest are in the range of 4–8. One can easily verify that in each case, these requirements on n, L, and λ are satisfied.

Remark 3. The constant c

The constant c in Proposition 2 can be made much smaller than 131 in most cases of practical interest in DNA sequence analysis. The θ value calculated from real DNA base frequencies are usually close to 1/4 rather than 1/2, making the upper bound in (8) quite close to 4.25Lλθ^L/2 and the upper bound in (9) close to 17/λ. This will reduce the constant c to about 73. There are places in Theorem 1 and Lemma 1 where the bounds can be made tighter also. However, since the main goal of Proposition 2 is to give a Poisson limit for the palindromes process, the actual value of c is not of great concern.

Remark 4. Can the Poisson limit approximate the palindrome process in real DNA?

Proposition 2 gives only an asymptotic result stating that the palindrome process will approach a Poisson process in the limit. In the proof of Proposition 2, it was further shown that the rate of convergence is of the order log $n∕\sqrt{n}$. As this result is to serve as the basis of approximating the palindrome process in a real DNA sequence which is finite in length, one would naturally have to ask how large n and L have to be in order to make the Poisson process a good approximation of the palindrome process. Since the d₂ distance has not been previously applied to any practical setting, at this point there is no firm basis for a reliable assessment of how good the approximation is. However, we refer to a previous work of Leung et al. (1994) where the Poisson approximation was demonstrated to be reasonable by Q-Q plots for the cytomegalovirus genome with n = 229,354 and L = 5. The d₂ distance calculated for this case is 0.1644 (see Table 2). In our application to the herpesvirus genome coming up in Section 4, we shall use this value of the d₂ distance as a benchmark to pick values of the parameter L for the given genome lengths and compositions.

Table 2.

Values of Lθ^L/2 at L = 4, 5, 6, 7, 8

Virus	L = 4	L = 5	L = 6	L = 7	L = 8
AHV1	0.2523	0.1580	0.0950	0.0556	0.0318
AtHV3	0.2867	0.1854	0.1151	0.0695	0.0411
BHV1	0.3605	0.2469	0.1624	0.1038	0.0650
EHV1	0.2586	0.1630	0.0986	0.0580	0.0334
EHV4	0.2500	0.1563	0.0938	0.0547	0.0313
MDV2	0.2500	0.1562	0.0937	0.0547	0.0312
MDV	0.2600	0.1641	0.0994	0.0586	0.0338
HSV1	0.3213	0.2138	0.1366	0.0848	0.0516
HSV2	0.3400	0.2295	0.1487	0.0937	0.0578
VZV	0.2531	0.1587	0.0955	0.0559	0.0320
EBV	0.2700	0.1720	0.1052	0.0626	0.0365
HCMV	0.2603	0.1644	0.0996	0.0587	0.0339
HHV6	0.2615	0.1653	0.1003	0.0592	0.0342
HHV7	0.2948	0.1920	0.1200	0.0730	0.0434
CCV1	0.2577	0.1623	0.0981	0.0577	0.0332
HVS2	0.2997	0.1960	0.1231	0.0751	0.0449

Remark 5. The i.i.d. sequence model

Proposition 2 is proved only for a random nucleotide sequence generated as i.i.d. random variables. While in many studies it has been pointed out that this i.i.d. sequence model does not fit well with real DNA sequences, the model is still frequently used for deriving statistical criteria to evaluate whether certain observed sequence patterns are unlikely to be observed simply by chance, mostly because of the difficulty in deriving analytical results with more elaborate models. It is also because of this limitation that the i.i.d. model is used to derive Proposition 2. The assumption of independent bases is rather hard to relax. However, one may consider allowing the base probabilities p_A, p_C, p_G, p_T to vary from one region of the sequence to another so that the local base frequencies are better reflected in the model. Indeed, there is evidence indicating that base frequencies change from one region of the genome to another. For example, Mrazrek and Karlin (1998) report a change of base preference in some herpesvirus replication origins from having more G’s than C’s on one side of the origin to having more C’s than G’s on the other. Because of the possibility of fluctuation of palindrome probabilities due to these changes in base composition, we have checked the regions around all the known replication origins in our dataset to see whether there are base compositional differences substantial enough to cause the θ value to become significantly different from that estimated from other segments of similar lengths sampled from the rest of the genome. The result in every case shows no significant difference. We have therefore chosen to simply use a value of θ estimated by the overall base frequencies in the entire genome for our analysis.

3. USE OF THE SCAN STATISTICS TO LOCATE PALINDROME CLUSTERS

In light of the mathematical result of the previous section, we can justifiably make the assumption that the midpoints of the 2L-palindromes are distributed like the events of a Poisson process on the unit interval. It then follows from the properties of a Poisson process that if the total number of 2L-palindromes is known, say, m, then these m points are distributed in the same way as m i.i.d. uniform random variables on (0, 1) (Karlin and Taylor, 1981, Chapter 4).

For a set of points X₁, … , X_m distributed independently and uniformly over the unit interval (0, 1), the traditional scan statistic N_w = max_1≤i≤m N_w(i), where 0 < w < 1 is a prescribed window length and N_w(i) is the number of points in the interval [X_(i), X_(i) + w), is a generalized likelihood ratio test statistic that has been shown to be most powerful among a class of statistics to test against the clustering alternative (Naus, 1965). More recently, Dembo and Karlin (1992) define the r-scan statistic A_r to be the minimal cumulative lengths of r consecutive distances between the ordered statistics X_{(1), … , X(m)}. Formally, let S_i denote the distance between the ordered ith and (i + 1)st points, i.e., S_i = X_(i+1) − X_(i), i = 1, … , m − 1. For any fixed integer r between 1 and m − 1, the r-scan is A_r = min{A_r(i), i = 1, … , m − r} where $A_r\left(i\right)={\sum }_{j=i}^{i+r-1}{S}_j$, i = 1, … , m − r Both the traditional and the r-scan statistics are used quite extensively in DNA sequence analysis (see Glaz et al., 2001, Chapter 6).

These two scan statistics are essentially equivalent. Consider the event {N_w(i) ≥ r + 1 for i = 1, … , m − r, which says that there are at least r + 1 points contained in the window [X_(i), X_(i) + w). This is equivalent to the event {A_r(i) < w} which says that there are at least r adjoining spacings, starting at X_(i), whose cumulative length is less than w. See Fig. 3 for illustration with r = 3. We therefore have a simple duality relationship between N_w and A_r:

$$\mathit{P}(N_w\ge r+1)=\mathit{P}(A_r<w).$$ (10)

If either of the above probabilities is too small (say, < 0.05), then a cluster of at least r points in a window of length w is statistically significant.

FIG. 3.

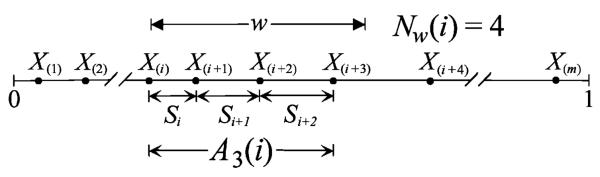
The w- and r-scan statistics. The equivalence of the events {N_w ≥ r + 1} and {A_r < w} is illustrated with r = 3.

There is a very simple asymptotic approximation for the distribution of A_r (Cressie, 1977; Dembo and Karlin, 1992): For any x > 0,

$$\underset{m\to \infty }{\lim }\mathit{P}(A_r\le \frac{x}{m^{1+1∕r}})=e^{-x^r∕r^{!}}.$$

When m is large, it yields the following approximation:

$$\mathit{P}(A_r\le w)\approx 1-\exp \left(\frac{-m^{r+1}{w}^r}{r^{!}}\right).$$ (11)

Leung et al. (1994) make use of Equation (11) to identify nonrandom palindrome clusters for the HCMV but they observe that in some cases the approximate probabilities so computed have rather large discrepancies when compared with simulated probabilities such as those obtained by Glaz (1989). It is therefore not advisable to routinely apply this approximation to evaluate the statistical significance of palindrome clusters without first considering whether the desired accuracy can be achieved.

Leung and Yamashita (1999) review a few other Poisson type approximations to the distribution of the scan statistics with special interest in their accuracy when used on data from the palindrome occurrences in seven herpes genomes which is part of our dataset in the present paper. Their simulation results show that the compound Poisson distribution put forth by Glaz et al. (1994) based on a result of Roos (1993) produces the best approximation to A_r. We have, therefore, adopted their result to evaluate the statistical significance of palindrome clusters for the genomes in our dataset. Explicitly, this approximation is

$$\mathit{P}(A_r\le w)\approx 1-\exp \{-(m-r\left)\pi \right(1-p+p^r(r+p-\mathit{rp})\left)\right\},$$ (12)

where π = Q₁, p = 1 − Q₂/Q₁, with

$$Q_1=\sum _{j=1}^{m}B(j;m,w),$$ (13)

$$Q_2=\sum _{j=1}^m{(-1)}^{r+j}B(j;m,w),$$ (14)

and $B(j;m,w)=\left(\begin{array}{c}\hfill m\hfill \\ \hfill j\hfill \end{array}\right)w^j{(1-w)}^{m-j}$. The approximation in (12) is used in the next section to assess the statistical significance of the r-clusters of palindromes observed in the herpesvirus genomes.

4. PALINDROME CLUSTERS IN HERPESVIRUS GENOMES

4.1. Choosing L

Our study of palindromes is motivated by their association with replication origins. In HCMV, the replication origin “oriLyt” is successfully located by a significant cluster of palindromes with L = 5 using the r-scan statistic The name “oriLyt” is designated to the origin of replication where DNA replication is initiated during the lytic phase of the virus life cycle. A detailed explanation of the terminology as well as the methodology is given in the article of Leung et al. (1994). The choice of L = 5 turns out to be crucial for the successful detection of the oriLyt. When the analysis is done with L = 4, too many statistically significant clusters were detected over very diverse regions of the genome. With L = 6, no significant palindrome cluster was detected at all. This indicates that the choice of L can be quite influential on the success rate of predicting a replication origin. Too small a value of L degrades the specificity while too large a value reduces the sensitivity of this method of replication origin prediction. However, apart from the knowledge that L should increase like the logarithm of the sequence length for the palindrome process to approach the Poisson limit, we do not have any guideline on what is the best length of palindromes one should examine.

We have therefore set up our algorithm in such a way that L is a parameter in the program so that its value can be easily reset by the user. The prediction accuracy is tested on our dataset with L = 4, 5, 6, 7, and 8. L = 5 is found to work best for many of the genomes, but there are several exceptions. For example, choosing L = 5 for BHV1 produced 17 significant palindrome clusters, only two of which are close to replication origins. Increasing L to 6 reduces the number of significant clusters to five, which is a more acceptable number. This is at first somewhat surprising because the BHV1 genome is much shorter than that of HCMV. On closer examination, we notice that BHV1 has a much higher C/G content than all the other genomes, yielding a higher θ, which affects the palindrome probability.

In using the scan statistics to detect palindrome clusters, the choice of L should be made so that the overall palindrome process can be approximated reasonably by a Poisson process on one hand, but it should still allow the unusual palindrome clusters to be detected on the other hand. Proposition 2 tells us that the Wasserstein distance between the palindrome process and the Poisson process is bounded above by a quantity proportional to Lθ^L/2, which depends on the base frequencies as well as L. Table 2 contains the values of Lθ^L/2 computed at L = 4, 5, 6, 7, 8 for the base frequencies of the 16 herpesvirus genomes. If we use the value of Lθ^L/2 with L = 5 for HCMV as a benchmark (that is, for each virus, we choose L such that Lθ^L/2 is closest to 0.1644), L is chosen to be 5 for most of the viruses with the exceptions of BHV1, HSV1, and HSV2 whose genomes are more C/G rich than the others. For these three viruses, L = 6 is the closest choice. The entries corresponding to the chosen L are bold-printed in Table 2.

Eventually, we hope to be able to formulate a criterion of choosing L for each genome that has a biological basis on the type of genome structure under analysis. However, this can be achieved only if we have a larger database of experimentally confirmed replication origins. For now, our hope is that by reporting these regions of significant palindrome clusters, we will be able to facilitate the experimentation to expand this database, which will in turn help improve the prediction scheme.

4.2. The palindrome clusters and replication origins

Having chosen L, we have a computer program, which is a simple adaptation of an algorithm of Leung et al. (1991), to examine each of the herpes genome nucleotide sequences and find all 2L-palindromes. It should be noted that we choose to use this particular program mainly because we have easy access to it and there are other programs for finding palindromes available in standard sequence analysis packages such as EMBOSS (Rice et al., 2000). Only the nonredundant 2L-palindromes are used for the analysis. That is, if one palindrome is completely contained in a longer one, the shorter palindrome will be discarded. The S-Plus functions developed by Leung and Yamashita (1999), based on the compound Poisson approximation to the r-scans described in Section 3, are then applied to examine the palindrome locations and identify all the nonrandom (r + 1)-clusters with r ranging from 1 to 15. Table 3 shows the spans of all the significant clusters found in HCMV, where the span of a cluster is the range of bases starting at the beginning position of the first palindrome in the cluster to the ending position of the last palindrome in the cluster. Not surprisingly, the spans of many of these clusters overlap one another. To reduce redundancy, we go through the list of clusters and join them to become one if their spans overlap. After this joining process, typically only a few nonoverlapping regions of a genome emerge. Each region contains one or more significant clusters. Table 4 lists all the regions found from the herpesvirus genomes.

Table 3.

Segments of the HCMV Genome Spanned by Significant r + 1-Clusters

r	Clusters
1	None
2	None
3	92701–92792
4	92526–92718, 92569–92756, 92643–92792, 92701–92868, 195029–195227, 195109–195268
5	92526–92756, 92569–92792, 92643–92868, 195029–195268
6	92526–92792, 92569–92868, 92643–93119
7	91953–92792, 92526–9286, 92569–93119, 92643–93260, 92701–93520, 92709–93610 AU1
8	91635–92792, 91953–92868, 92526–93119, 92569–93260, 92643–93520, 92701–93610
9	91490–92792, 91635–92868, 91953–93119, 92526–93260, 92569–93520, 92643–93610, 92701–94183
10	91490–92868, 91635–93119, 91953–93260, 92526–93520, 92569–93610, 92643–94183
11	90759–92868, 91490–93119, 91635–93260, 91953–93520, 92526–93610, 92569–94183
12	90251–92868, 90759–93119, 91490–93260, 91635–93520, 91953–93610, 92526–94183
13	90251–93119, 90759–93260, 91490–93520, 91635–93610, 91953–94183
14	89585–93119, 90251–93260, 90759–93520, 91490–93610, 91635–94183
15	89585–93260, 90251–93520, 90759–93610, 91490–94183

Table 4.

Regions of the Herpesvirus Genomes Containing Significant Clusters

Genome	Region	Palindrome	Feature
BHV1	77155–77168	3
	102895–106948	22
	113462–113636	5	1.75 mua from Ori
	124582–124756	5	1.61 mu from Ori
	131268–135221	21
EHV1	115125–119094	17	Overlaps transcriptional regulator
	144064–148033	17	Overlaps transcriptional regulator
EHV4	None
HSV1	None
HSV2	None
VZV	None
EBV	6772–11675	19	Contains OriP
	49460–54858	25	Contains OriLyt
HCMV	89585–94183	19	Contains OriLyt
	195029–195268	8	Enhancer element
HHV6	None
HHV7	120758–124422	16
AHV1	113456–113759	5
ATHV3	95350–100098	17
MDV2	93143–93243	4
	109331–110590	8
MDV	None
CCV1	None
HVS2	None

^aHere, mu stands for a map unit, which is 1% of the genome length. The distance is calculated from the midpoint of the cluster region to the midpoint of the closest replication origin.

Although our ultimate goal is to eventually make use of palindrome clusters to help predict the likely locations of replication origins, it must be recognized that at this stage, it is not yet possible to achieve much prediction accuracy. There are two main problems. First, the prediction procedure must also include information about clusters of close repeats and inversions which are also known to be characteristics of replication origins. A close repeat (respectively, inversion) is a segment of DNA with an exact (respectively, inverted complementary) copy of itself present in close vicinity, say, within 150 bases. A palindrome is actually a special case of close inversion because it is a segment of DNA followed immediately by its inverted complement. The statistical assessments of clusters for close repeats and inversions still need to be developed. Second, reports on confirmed location of replication origins is relatively scarce. We hope that the findings of the palindrome clusters in this paper will be helpful towards the experimental determination of more replication origins so that more information is available for prediction accuracy testing in the future.

Nevertheless, even with limited information, it is still of interest to examine the correspondence between these significant palindrome clusters and the actual confirmed locations of the replication origins. From various sources like the annotations in the GenBank file of these sequences and the references therein, plus published genetic maps and other biomedical articles (Farrel, 1993; Masse et al., 1992; McGeoch and Schaffer, 1993; Baumann et al., 1989), we are able to compile a list of replication origins in 10 of the 16 herpesviruses. These include one herpesvirus hosted in the cow, two in the horse, and seven in humans. It is not surprising that these viruses have been studied more than the others because of their agricultural and medical importance. The location of those origins are displayed in Table 5, and we also indicate them in the last column of Table 4 whenever they are close (within 2% of the genome length) to one of the regions found to contain significant clusters.

Table 5.

Location of Replication Origins in Ten Herpesviruses

Virus	Replication origins
BHV1	111080–111300(OriS), 126918–127138(OriS)
EHV1	126187–126338
EHV4	73900–73919(OriL), 119462–119481(OriS), 138568–138587(OriS)
HSV1	62475(OriL), 131999(OriS), 146235(OriS)
HSV2	62930(OriL), 132760(OriS), 148981(OriS)
VZV	110087–110350, 119547–119810
EBV	7315–9312(OriP), 52589–53581(OriLyt)
HCMV	92270–93715(OriLyt)
HHV6	67617–67993(OriLyt)
HHV7	66685–67298

While we see some agreements between palindrome cluster regions and replication origins in BHV1, EBV, and HCMV, many clusters regions have not been found to contain replication origins. There are two possibilities. First, there may be a replication origin which has not yet been experimentally located so that it is not documented in the biomedical literature. Second, a cluster region may correspond to a regulatory site rather than a replication origin. For example, the region 195029–195268 in HCMV is actually an enhancer element (Weston, 1988).

We also note that among the 19 replication origins compiled in Table 5, only five of them have palindrome clusters in their proximity. Palindrome clusters by themselves, therefore, will not be sufficient in terms of replication origin prediction. This is not unexpected because the sequence features of close repeat and inversion still need to be incorporated into the prediction scheme. Indeed, for the 14 replication origin sequences which do not contain any palindrome clusters, we further analyze the sequence structure around them using the program developed by Leung et al. (1991). Highly noticeable close repeats or inversions are found in all of these sequences, with only one exception.

The one exception is the oriL in the herpes Simplex I (HSV1) virus. This replication origin, located at position 62475 of the genome, is not identified by any significant palindrome clusters, nor does it have any unusual clusters of close repeats and inversions in its proximity. Instead, it has a perfect palindrome of length 144 stretching from base 62404 to base 62547. This means that it is possible to have a replication origin sequence with a highly unusual palindrome, yet our method has failed to identify it because it contains only a single long palindrome instead of a cluster of shorter ones. Upon further examination for long palindromes in the other genomes in our dataset, we find that the two replication origins of the chicken pox virus (VZV) located at bases 110087–110350 and 119547–119810 also contain two palindromes of length 36 from base 110194 to 110229 and 119668 to 119703. Again, despite the presence of a long palindrome, no significant palindrome cluster is detected.

These observations suggest the necessity of a generalization of our method of identifying palindrome clusters to take the length of the palindrome into consideration. Presently, we represent the occurrence of a palindrome by a point placed at its center. These points are considered equally as events in a Poisson process. Hence, the 144 bp palindrome carries the same weight as a 10 bp palindrome and counts as only one point. Suppose that we weigh the palindromes proportional to their lengths; then the 144 bp palindrome would count as 14 points and be deemed a significant cluster by itself. The idea of letting weights be given to events in a point process is encompassed in the theory of marked point process where each point is attached with a real-valued random variable called a mark. The Wasserstein distance between the new palindrome process and the appropriate marked Poisson process, as well as the distribution of the scan statistics will need to be developed. Such extension of the present model is under way. Together with the future incorporation of close repeats and inversions, we anticipate that a more accurate and efficient prediction scheme for replication origins can be established.

For the time being, the nonrandom palindrome clusters located by the method in this paper can be used for prioritizing which segments of DNA should be experimentally tested for replication origins first. Among the 10 herpesvirus genomes in Table 5, 12 nonrandom palindrome clusters have been identified of which 5 (over 40%) are in proximity of replication origins. One would, therefore, expect that for those herpesviruses where no replication origins have yet been identified, the chance of finding a replication origin in a segment of about 5% the length of the genome around a palindrome cluster would be much better than that of a random genome segment of similar length. We believe that, like the work of Masse et al. (1992) on HCMV, a good initial choice of genome segments for testing can expedite the experimental search for replication origins.

5. CONCLUDING REMARKS

In this paper, we have focused our analysis on herpesvirus genomes. We shall be conducting a broader analysis on other families of double-stranded DNA viruses such as the adenoviruses and papillomaviruses to gain more insight into the relationship between palindrome clusters and replication origins in other viral genomes. Moreover, we would like to point out that palindrome clusters may also be associated with the other biologically relevant functional sites (e.g., enhancer elements, transcriptional regulators as indicated in Table 4). The general statistical criterion for significant palindrome clusters will allow exploratory studies of such possible associations to be undertaken. The computer programs, implemented in C and S-Plus, for locating statistically significant clusters of palindromes using scan statistics will be accessible from the web page www.bioinformatics.utep.edu/mleung so that interested readers can adapt them for other applications.

Recently, predictions for various biological features, such as CpG islands and coding regions on the genome sequence, have been accomplished using hidden Markov models. We expect that the hidden Markov model approach can also be useful for prediction of replication origins. The difficulty, at least for now, is insufficient known replication origins that can be used for estimation of the model parameters. In cases where data is scanty, it has been suggested (Durbin et al., 1998) that Bayesian estimation should be used instead of maximum likelihood estimation. In this regard, the knowledge gained from understanding the connection between clusters of palindromes and repeats can be useful for choosing reasonable prior distributions for the model parameters.

It is a well known fact that nucleotide sequences in real DNA molecules do not fit well with the model of i.i.d. random variables (Philips et al., 1987; Prum et al., 1995; Leung et al., 1996; just to name a few). Preferably a Markov model of order at least 3 should be used. This motivates the need to generalize Theorem 1 to a Markov chain context. Even from a purely mathematical point of view, such a generalization is an interesting problem worthy of in depth investigation. Once more, this illustrates that the interaction between mathematical and biological research will prove fruitful for the advancement of both sciences.

APPENDIX: TECHNICAL PROOFS

Proposition 3

Let Γ = [0, 1] with metric d(x, y) = ∣x − y∣. If ${\xi }_1={\sum }_{i=1}^m{\delta }_{t_i}$ with 0 ≤ t₁ ≤ ⋯ ≤ t_m ≤ 1 and ${\xi }_2={\sum }_{i=1}^m{\delta }_{s_i}$ with 0 ≤ s₁ ≤ ⋯ ≤ s_m ≤ 1, then

$$\sum _{i=1}^m\mid t_i-s_i\mid \le \sum _{i=1}^m\mid t_i-s_{\pi \left(i\right)}\mid$$ (15)

for all permutations π of (1, ⋯ , m), and hence

$$d_1({\xi }_1,{\xi }_2)=\frac{1}{m}\sum _{i=1}^m\mid t_i-s_i\mid .$$

Proof

We use mathematical induction to prove the claim. Suppose first that m = 2. Without loss of generality, we may assume t₁ = min{t₁, t₂, s₁, s₂}. Then it suffices to consider the following three cases.

(i) t₂ ≥ s₂, then

$$\mid t_1-s_1\mid +\mid t_2-s_2\mid =s_1-t_1+t_2-s_2\le \mid t_1-s_2\mid +\mid t_2-s_1\mid$$

(ii) s₁ ≤ t₂ < s₂, then

$$\mid t_1-s_1\mid +\mid t_2-s_2\mid =s_1-t_1+s_2-t_2\le \mid t_1-s_2\mid +\mid t_2-s_1\mid$$

(iii) t₂ < s₁, then

$$\mid t_1-s_1\mid +\mid t_2-s_2\mid =s_1-t_1+s_2-t_2=\mid t_1-s_2\mid +\mid t_2-s_1\mid$$

Now, suppose (15) holds for m ≤ k with k ≥ 2; we shall prove it holds for m = k + 1 and all permutations π of (1, ⋯ , k + 1). As a matter of fact, the claim is obvious if π(k + 1) = k + 1. Assume π(k + 1) ≠ k + 1, then follows that

$$\begin{array}{cc}\hfill \sum _{i=1}^{k+1}\mid t_i-s_{\pi \left(i\right)}\mid =& \sum _{i\ne k+1,i\ne {\pi }^{-1}(k+1)}\mid t_i-s_{\pi \left(i\right)}\mid +[\mid t_{k+1}-s_{\pi (k+1)}\mid +\mid t_{{\pi }^{-1}(k+1)}-s_{k+1}\mid ]\hfill \\ \hfill \ge & \sum _{i\ne k+1,i\ne {\pi }^{-1}(k+1)}\mid t_i-s_{\pi \left(i\right)}\mid +\mid t_{{\pi }^{-1}(k+1)}-s_{\pi (k+1)}\mid +\mid t_{k+1}-s_{k+1}\mid \hfill \\ \hfill \ge & \sum _{i=1}^k\mid t_i-s_i\mid +\mid t_{k+1}-s_{k+1}\mid .\hfill \end{array}$$

Proof of Theorem 1

Define a Poisson process, $\tilde{Z}$, on $J≔\{\frac{1}{n},\frac{2}{n},\dots ,\frac{n-1}{n},\frac{n}{n}\}$ as follows:

$$\tilde{Z}=\sum _{i=1}^N{\delta }_{{\zeta }_i}$$

where ζ₁, ζ₂, … are independent random variables uniformly distributed on J and N is a Poisson random variable with mean λ and is independent of the ζ_i’s. For coupling argument below, we need to represent the usual Poisson process on [0, 1] as

$$Z_{\lambda }=\sum _{i=1}^N{\delta }_{{\zeta }_i-U_i∕n}$$

where U_i’s are independent and uniformly distributed on [0, 1]. This can be seen as follows: first we pick a point from J at random and then move it to the left in a uniform manner within a distance 1/n. We shall prove Theorem 1 in two steps: first, we apply a coupling argument to show that

$$d_2\left(\mathcal{L}\right(\tilde{Z}),\mathcal{L}(Z_{\lambda }\left)\right)\le \frac{1-e^{-\lambda }}{2n}.$$

And in the second step, we apply Stein’s method to bound $d_2\left(\mathcal{L}\right(\Xi ),\mathcal{L}(\tilde{Z}\left)\right)$, giving the first two terms in Theorem 1. Then Theorem 1 will follow immediately by the triangle inequality:

$$d_2\left(\mathcal{L}\right(\Xi ),\mathcal{L}(Z_{\lambda }\left)\right)\le d_2\left(\mathcal{L}\right(\Xi ),\mathcal{L}(\tilde{Z}\left)\right)+d_2\left(\mathcal{L}\right(\tilde{Z}),\mathcal{L}(Z_{\lambda }\left)\right).$$

Step 1

We see that,

$$\begin{array}{cc}\hfill d_2\left(\mathcal{L}\right(\tilde{Z}),\mathcal{L}(Z_{\lambda }\left)\right)=& \sup \{\mid \mathit{Eh}(\tilde{Z})-\mathit{Eh}(Z_{\lambda })\mid :{\Vert h\Vert }_{\mathrm{Lip}\left(\mathcal{Y}\right)}\le 1\}\hfill \\ \hfill \le & \sup \{\mid E\mid h(\tilde{Z})-h(Z_{\lambda })\mid :{\Vert h\Vert }_{\mathrm{Lip}\left(\mathcal{Y}\right)}\le 1\}\hfill \\ \hfill \le & {\mathit{Ed}}_1(\tilde{Z},Z_{\lambda })\hfill \\ \hfill =& {\mathit{Ed}}_1\left(\sum _{i=1}^N{\delta }_{{\zeta }_i},\sum _{i=1}^N{\delta }_{{\zeta }_i-U_{i∕n}}\right)\mathit{I}(N\le 1)\hfill \\ \hfill =& E\left[\frac{1}{N}\sum _{i=1}^N\mid {\zeta }_i-({\zeta }_i-U_i∕n)\mid \right]\mathit{I}(N\le 1)\left(\text{by Proposition}3\right)\hfill \\ \hfill =& E\frac{\mathit{I}(N\ge 1)}{\mathit{nN}}\sum _{i=1}^N{U}_i\hfill \\ \hfill =& \frac{P(N\ge 1)}{2n}\text{as}{\mathit{EU}}_i=1∕2\text{and}{U}_i^{\prime }s\text{independent of}N\hfill \\ \hfill =& \frac{1-e^{-\lambda }}{2n}.\hfill \end{array}$$

Step 2

Let $\{{\mathit{I}}_i^{\prime },1\le i\le n\}$ be an independent copy of {I_i, 1 ≤ i ≤ n}. We first derive Stein’s equation (16) follows:

$$\begin{array}{cc}\hfill E\int \left[h\right(\Xi )-h& (\Xi -{\delta }_x)\left]\Xi \right(\mathit{dx})\hfill \\ \hfill =& \sum _{i=1}^n{\mathit{EI}}_i\left[\mathit{h}\right(\Xi )-\mathit{h}(\Xi -{\delta }_{i∕n})-h({\mathit{V}}_i+{\delta }_{i∕n})+\mathit{h}({\mathit{V}}_i\left)\right]+\sum _{i=1}^n{\mathit{EI}}_i\left[\mathit{h}\right({\mathit{V}}_i+{\delta }_{i∕n})-\mathit{h}({\mathit{V}}_i\left)\right]\hfill \\ \hfill =& \sum _{i=1}^n{\mathit{EI}}_i\left[\mathit{h}\right(\Xi )-\mathit{h}(\Xi -{\delta }_{i∕n})-h({\mathit{V}}_i+{\delta }_{i∕n})+\mathit{h}({\mathit{V}}_i\left)\right]+\sum _{i=1}^n{\mathit{EI}}_i^{\prime }\left[\mathit{h}\right({\mathit{V}}_i+{\delta }_{i∕n})-\mathit{h}({\mathit{V}}_i\left)\right]\hfill \\ \hfill =& \sum _{i=1}^n{\mathit{EI}}_i\left[\mathit{h}\right(\Xi )-h(\Xi -{\delta }_{i∕n})-\mathit{h}({\mathit{V}}_i+{\delta }_{i∕n})+\mathit{h}({\mathit{V}}_i\left)\right]\hfill \\ \hfill & -\sum _{i=1}^n{\mathit{EI}}_i^{\prime }\left[\mathit{h}\right(\Xi +{\delta }_{i∕n})-\mathit{h}(\Xi )-\mathit{h}({\mathit{V}}_i+{\delta }_{i∕n})+\mathit{h}({\mathit{V}}_i\left)\right]\hfill \\ \hfill & +\sum _{i=1}^n{\mathit{EI}}_i^{\prime }\left[\mathit{h}\right(\Xi +{\delta }_{i∕n})-\mathit{h}(\Xi \left)\right]\hfill \\ \hfill & ={\mathit{R}}_1\left(h\right)-{\mathit{R}}_2\left(h\right)+\mathit{E}\int \left[\mathit{h}\right(\Xi +{\delta }_x)-\mathit{h}(\Xi \left)\right]\tilde{\lambda }\left(\mathit{dx}\right)\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & \tilde{\lambda }\left(\mathit{dx}\right)=\sum _{i=1}^n{p}_i{\delta }_{i∕n}\left(\mathit{dx}\right),\hfill \\ \hfill & {\mathit{R}}_1\left(\mathit{h}\right)=\sum _{i=1}^n{\mathit{EI}}_i\left[\mathit{h}\right(\Xi )-\mathit{h}(\Xi -{\delta }_{i∕n})-\mathit{h}({\mathit{V}}_i+{\delta }_{i∕n})+\mathit{h}({\mathit{V}}_i\left)\right],\hfill \end{array}$$

and

$${\mathit{R}}_2\left(\mathit{h}\right)=\sum _{i=1}^n{\mathit{EI}}_i^{\prime }\left[\mathit{h}\right(\Xi +{\delta }_{i∕n})-\mathit{h}(\Xi )-\mathit{h}({\mathit{V}}_i+{\delta }_{i∕n})+\mathit{h}({\mathit{V}}_i\left)\right].$$

Hence, we have derived Stein’s identity,

$$E\int \left[\mathit{h}\right(\Xi +{\delta }_x)-\mathit{h}(\Xi \left)\right]\tilde{\lambda }\left(\mathit{dx}\right)+E\int \left[\mathit{h}\right(\Xi -{\delta }_x)-\mathit{h}(\Xi \left)\right]\Xi \left(\mathit{dx}\right)=-{\mathit{R}}_1\left(\mathit{h}\right)+{\mathit{R}}_2\left(\mathit{h}\right).$$

Consider Stein’s equation:

$$\int \left[\mathit{h}\right(\xi +{\delta }_x)-\mathit{h}(\xi \left)\right]\tilde{\lambda }\left(\mathit{dx}\right)+\int \left[\mathit{h}\right(\xi -{\delta }_x)-\mathit{h}(\xi \left)\right]\xi \left(\mathit{dx}\right)=f\left(\xi \right)-\int \mathit{fd}\pi$$ (16)

where ${\Vert f\Vert }_{\mathrm{Lip}\left(\mathcal{Y}\right)}\le 1$ and $\pi =\mathcal{L}\left(\tilde{Z}\right)$.

We need a from Brown and Xia (2001, Theorem 5.1) which gives a nonuniform bound on the solution of Stein’s equation: Suppose f satisfies ${\Vert f\Vert }_{\mathrm{Lip}\left(\mathcal{Y}\right)}\le 1$ and h_f is the solution to Stein’s equation; then we have

$$\mid {\mathit{h}}_f(\xi +{\delta }_x+{\delta }_y)-{\mathit{h}}_f(\xi +{\delta }_x)-{\mathit{h}}_f(\xi -{\delta }_y)+{\mathit{h}}_f\left(\xi \right)\mid \le \frac{5}{\lambda }+\frac{3}{\mid \xi \mid +1}$$ (17)

where ∣ξ∣ denotes the number of points in the configuration ξ.

Back to the proof of Theorem 1. We have

$$\mathit{Ef}\left(\Xi \right)-\mathit{Ef}\left(\tilde{Z}\right)=-{\mathit{R}}_1\left({\mathit{h}}_f\right)+{\mathit{R}}_2\left({\mathit{h}}_f\right)$$

where

$$\begin{array}{cc}\hfill \mid {\mathit{R}}_1\left({\mathit{h}}_f\right)\mid \le & \sum _{i=1}^n{\mathit{EI}}_i\mid {\mathit{h}}_f(\Xi -{\mathit{h}}_f(\Xi -{\delta }_{i∕n})-{\mathit{h}}_f({\mathit{V}}_i+{\delta }_{i∕n})+{\mathit{h}}_f({\mathit{V}}_i)\mid \hfill \\ \hfill \le & \sum _{i=1}^n{\mathit{EI}}_i\sum _{j\in A_i,j\ne i}{\mathit{I}}_j\left[\frac{5}{\lambda }+\frac{3}{1+\mid {\mathit{V}}_i\mid }\right]\hfill \\ \hfill \le & \sum _{i=1}^n\sum _{j\in A_i,j\ne i}{\mathit{EI}}_i{\mathit{I}}_j\left[\frac{5}{\lambda }+\frac{3}{1+\mid {\mathit{V}}_{\mathit{ij}}\mid }\right]\hfill \\ \hfill =& \sum _{i=1}^n\sum _{j\in A_i,j\ne i}{p}_{\mathit{ij}}E\left[\frac{5}{\lambda }+\frac{3}{1+\mid {\mathit{V}}_{\mathit{ij}}\mid }\right].\hfill \end{array}$$

In the second inequality, we write h_f (Ξ) − h_f (Ξ − δ_i/n) − h_f (V_i + δ_i/n) + h_f (V_i) as a telescoping sum and apply (17). Similarly,

$$\begin{array}{cc}\hfill \mid {\mathit{R}}_2\left({\mathit{h}}_f\right)\mid \le & \sum _{i=1}^n{p}_i\mathit{E}\mid {\mathit{h}}_f(\Xi +{\delta }_{i∕n})-{\mathit{h}}_f\left(\Xi \right)-{\mathit{h}}_f({\mathit{V}}_i+{\delta }_{i∕n})+{\mathit{h}}_f\left({\mathit{V}}_i\right)\mid \hfill \\ \hfill \le & \sum _{i=1}^n\mathit{pi}\sum _{j\in A_i,j\ne i}{\mathit{EI}}_j\left[\frac{5}{\lambda }+\frac{3}{1+\mid {\mathit{V}}_i\mid }\right]\hfill \\ \hfill \le & \sum _{i=1}^n\sum _{j\in A_i,j\ne i}{p}_i{p}_j\mathit{E}\left[\frac{5}{\lambda }+\frac{3}{1+\mid {\mathit{V}}_{\mathit{ij}}\mid }\right]\hfill \end{array}$$

Combining the bounds on the error terms R₁(h_f) and R₂(h_f) which are independent of f, we take the supremum over all f with ${\Vert f\Vert }_{\mathrm{Lip}\left(\mathcal{Y}\right)}\le 1$ to get the d₂ distance. This completes the proof of Theorem 1.

Remark

Theorem 1 has been extended by Chen and Xia (2004) using Palm theory to a more general setting with wider applicability.