Multilevel sparse functional principal component analysis

Abstract

We consider analysis of sparsely sampled multilevel functional data, where the basic observational unit is a function and data have a natural hierarchy of basic units. An example is when functions are recorded at multiple visits for each subject. Multilevel functional principal component analysis (MFPCA; Di et al. 2009) was proposed for such data when functions are densely recorded. Here we consider the case when functions are sparsely sampled and may contain only a few observations per function. We exploit the multilevel structure of covariance operators and achieve data reduction by principal component decompositions at both between and within subject levels. We address inherent methodological differences in the sparse sampling context to: 1) estimate the covariance operators; 2) estimate the functional principal component scores; 3) predict the underlying curves. Through simulations the proposed method is able to discover dominating modes of variations and reconstruct underlying curves well even in sparse settings. Our approach is illustrated by two applications, the Sleep Heart Health Study and eBay auctions.

1. Introduction

Motivated by modern scientific studies, functional data analysis (FDA; Ramsay & Silverman, 2005) is becoming a popular and important area of research. The basic unit of functional data is a function, curve or image, typically high-dimensional, and the aim of FDA is to understand variations in a sample of functions. Functional principal component analysis (FPCA) plays a central role in FDA, and thus we briefly review the most recent developments in this area. The fundamental aims of FPCA are to capture the principal directions of variation and to reduce dimensionality. Besides discussion in Ramsay & Silverman (2005), other relevant research in FPCA includes Ramsay & Dalzell (1991), Silverman (1996), James et al. (2000), and Yao et al. (2005), while important theoretical results can be found in Hall & Hosseini-Nasab (2006).

The standard FPCA methodology was designed for a sample of densely recorded independent functions. Its scope was extended in two directions later. First, it was extended to sparse functional/longitudinal data (Yao et al., 2005; Muller, 2005). Sparsity is the characteristic of the sampling scheme that leads to a small number of observations per function and a dense collection of sampling points across all curves. Traditionally, these data were treated as longitudinal data (see Diggle et al., 2002) and analyzed using parametric or semi-parametric models. The functional approach views them as sparse and noisy realizations of an underlying smooth process and aims to study the modes of variations of the process. Second, it was extended to functional data with a hierarchical structure, which led to multilevel functional principal component analysis (MFPCA; Di et al., 2009). In this paper, we propose methods for a sample of sparsely recorded functions with hierarchical structure, and discuss issues arising from both sparsity and multilevel structure.

Our research was motivated by two applications, the Sleep Heart Health Study (SHHS) and online auctions from eBay.com. The SHHS is a multi-center cohort study of sleep and its impacts on health outcomes. A detailed description of the SHHS can be found in Quan et al. (1997) and Crainiceanu et al. (2009a). Between 1995 and 1997, 6,441 participants were recruited and underwent in-home polysomnograms (PSGs). A PSG is a quasi-continuous multi-channel recording of physiological signals acquired during sleep that include two surface electroencephalograms (EEG). Between 1999 and 2003, a second SHHS follow-up visit was undertaken on 3,201 participants (47.8% of baseline cohort) and included a repat PSG as well as other measurements on sleep habits and other health status variables. The sleep EEG percent δ-power series of the SHHS data is one of the main outcome variables. The data include a function of time in 30-second intervals per subject per visit, with each function has approximately 960 data points in an 8-hour interval of sleep. For this analysis, we conducted the analysis of sparsified data where each function is sub-sampled at a random set of time points, and compared this to full analysis of the dense data.

Our second application originates from online auctions, which are challenging because they involve user-generated data: sellers decide when to post an auction, and bidders decide when to place bids. This can result in individual auctions that have extremely sparse observations, especially during the early parts of the auction. In fact, well-documented bidding strategies such as early bidding or last-minute bidding cause “bidding-draughts” (Bapna et al., 2004; Shmueli et al., 2007; Jank & Shmueli, 2007) during the middle, leaving the auction with barely any observations at all. Peng & Müller (2008), Liu & Müller (2009), Jank et al. (2010) and Reithinger et al. (2008) studied analysis of dynamics of such sparse auction data Here, we study bidding records of 843 digital camera auctions that were listed on eBay between April, 2007, and January, 2008. These auctions were on 515 types of digital cameras, from 233 distinct sellers. On average, there were 11 bids per auction. The timing of the bids was irregular and often sparse: some auctions contained as many as 56 bids, while others included as few as 1-2 bids. In this application we are particularly interested in investigating the pattern of variation of an auction's bidding path and decomposing it into components that are attributable to the product and components attributable to the bidding process.

The remainder of this paper is organized as follows. Section 2 introduces Multilevel Functional Principal Component Analysis (MFPCA) for sparse data. Section 3 provides mathematical details for predicting the principal component scores and curves. Section 4 describes extensive simulation studies for realistic settings. Section 5 describes applications of our methodology to the SHHS data and eBay auction data. Section 6 includes some discussion.

2. MFPCA for sparsely sampled functions

In this section, we briefly review the MFPCA technique proposed by Di et al. (2009), and then discuss and address methodological issues arising from sparsity.

2.1. MFPCA: review

The MFPCA was designed to capture dominant modes of variations and reduce dimensions for multilevel functional data. This method decomposes the total functional variation into between and within subject variations via functional analysis of variance (FANOVA), and conducts principal component analysis at both levels. More precisely, letting Y_ij(t) denote the observed function for subject i at visit j, the two way FANOVA decomposes the total variation as

$$Y_{ij}\left(t\right)=\mu \left(t\right)+{\eta }_j\left(t\right)+Z_i\left(t\right)+W_{ij}\left(t\right)+{∊}_{ij}\left(t\right),$$ (1)

where μ(t) and η(t) are fixed functional effects that represent the overall mean function and visit-specific shifts, respectively, Z_i(t) and W_ij(t) are the subject-specific and visit-specific deviations, respectively, and ε_ij(t) is measurement error process with mean 0 and variance σ². The level 1 and 2 processes, Z_i(t) and W_ij(t), are assumed to be centered stochastic processes that are uncorrelated with each other. The idea of MFPCA is to decompose both Z_i(t) and W_ij(t) using the Karhunen-Loève (KL) expansions (Karhunen, 1947; Loève, 1945; Ramsay & Silverman, 2005), i.e., $Z_i\left(t\right)={\sum }_{k=1}^{N_1}{\xi }_{ik}{\varphi }_k^{\left(1\right)}\left(t\right)$ , $W_{ij}\left(t\right)={\sum }_{l=1}^{N_2}{\zeta }_{ijl}{\varphi }_l^{\left(2\right)}\left(t\right)$ where ${\varphi }_k^{\left(1\right)}\left(t\right)$ and ${\varphi }_l^{\left(2\right)}\left(t\right)$ are level 1 and level 2 eigenfunctions, respectively, and ξ_ik and ζ_ijl are mean zero random variables called principal component scores. The variances of ξ_ik and ζ_ijl , ${\lambda }_k^{\left(1\right)}$ and ${\lambda }_l^{\left(2\right)}$ , respectively, are the level 1 and 2 eigenvalues that characterize the magnitude of variation in the direction of the corresponding eigenfunctions. The number of principal components at level 1 and 2, N₁ and N₂, could be either finite integers or ∞. Combining model (1) with the KL expansions, one obtains the MFPCA model

$$Y_{ij}\left(t\right)=\mu \left(t\right)+{\eta }_j\left(t\right)+\sum _{k=1}^{N_1}{\xi }_{ik}{\varphi }_k^{\left(1\right)}\left(t\right)+\sum _{l=1}^{N_2}{\zeta }_{ijl}{\varphi }_l^{\left(2\right)}\left(t\right)+{∊}_{ij}\left(t\right).$$ (2)

The MFPCA reduces high dimensional hierarchical functional data {Y_i1 (t), ··· , Y_ini (t)} into the low dimensional principal component score vectors, including subject level (level 1) scores ξ = (ξ_i, ···, ξ_iN1) and subject/visit level (level 2) scores ζ_ij = (ζ_ij1 ···, ζ_ijN2). while retaining most information contained in the data. The detailed interpretation of this model is discussed in Di et al. (2009).

Equation (1) introduces FANOVA in full generality without details about the sampling design for t_ijs. The set of sampling points {t_ijs : s = 1, 2, ··· , T_ij} for subject i at visit j can be dense or sparse, regular or irregular, depending on the application. Although Di et al. (2009) discussed potential difficulties with sparse designs, they focused on densely and regularly recorded functional data. In the following, we will discuss and address new problems raised by the sparse sampling design. This will lead to methods that are related to but markedly different from MFPCA.

2.2. Estimating eigenvalues and eigenfunctions

Throughout the paper, we assume sparse and irregular grid points. More precisely, for each subject and visit, the number of grid points T_ij is relatively small, and the set of grid points {t_ijs : s = 1, 2, ··· , T_ij} is a random sample of $\mathcal{T}$. We also assume that the sets of grid points are different across subjects and visits and that the collection of grid points over all subjects and visits is a dense subset of $\mathcal{T}$.

The first step of MFPCA is to estimate the eigenvalues and eigenfunctions. This can be done by the method of moments and eigen-analysis for dense functional data, but smoothing is needed for sparse functional data. Let K_B(s,t) = cov{Z_i(s), Z_i(t) } be the covariance function for level 1 processes (“between” covariance), K_w(s,t) = cov{W_ij(s), W_ij(t)} be the covariance function for level 2 processes (“within”). The total covariance function K_T(s, t) contains three sources of variation, that is, K_T(s, t) = K_B(s, t) + K_T(s, t) + σ²/(t = s). One can easily verify that E{Y_ij(t)} = μ(t) + η_j(t), cov{Y_ij(s), Y_ij(t)} = K_B(s, t) + K_w(s, t) + σ²/(t = s), and cov{Y_ij(s), Y_ik(t)} = K_B(s, t). These results suggest the following convenient algorithm to estimate the eigenvalues and eigenfunctions.

Because functions were sparsely sampled over irregular grid points, scatter plot smoothing will be used repeatedly to estimate the underlying mean functions and covariance kernels.

Sparse MFPCA Algorithm

Step 1. Apply scatter plot smoothing using pairs {(t_ijs, Y_ij(t_ijs)) : i = 1,···,n;j = 1,···,n_i;s = 1,···,T_ij} to obtain an estimate of μ(t), $\widehat{\mu }\left(t\right)$. and apply scatter plot smoothing using pairs $\{(t_{ijs},Y_{ij}\left(t_{ijs}\right)):i=1,\dots ,n;j=1,\dots ,n_i;s=1,\dots ,T_{ij}\}$ to obtain an estimate of η_j, ${\widehat{\eta }}_j\left(t\right)$;

Step 2. Estimate K̂_B(s, t) by bivariate smoothing of all products $\{Y_{i{j}_1}\left(t_{i{j}_{1}s}\right)-\widehat{\mu }\left(t_{i{j}_{1}s}\right)-{\widehat{\eta }}_{j_1}\left(t_{i{j}_{1}s}\right)\}\{Y_{i{j}_2}\left(t_{i{j}_{2}r}\right)-\widehat{\mu }\left(t_{i{j}_{2}r}\right)-{\widehat{\eta }}_{j_2}\left(t_{i{j}_{2}r}\right)\}$ with respect to $(t_{i{j}_{1}s},t_{i{j}_{2}r})$ for all i,j₁,j₂, r and s with j₁ ≠ j₂;

Step 3. Estimate K̂_T(s, t) by bivariate smoothing of all products $\{Y_{ij}\left(t_{ijs}\right)-\widehat{\mu }\left(t_{ijs}\right)-{\widehat{\eta }}_j\left(t_{ijs}\right)\}\{Y_{ij}\left(t_{ijr}\right)-\widehat{\mu }\left(t_{ijr}\right)-{\widehat{\eta }}_j\left(t_{i{j}_{2}r}\right)\}$ with respect to (t_ijs, t_ijr) for all i,j, r,swith r ≠ s, and set K̂_W(s, t) = K̂_T(s, t) - K̂_W(s, t);

Step 4. Use eigen-analysis on K̂_B(s, t) to obtain ${\widehat{\lambda }}_k^{\left(1\right)}$, ${\widehat{\varphi }}_k^{\left(1\right)}\left(t\right)$: use eigenanalysis on K̂_W(s, t) to obtain ${\widehat{\lambda }}_l^{\left(2\right)}$, ${\widehat{\varphi }}_l^{\left(2\right)}\left(t\right)$.

Step 5. Estimate the nugget variance σ² by smoothing ${\{Y_{ij}\left(t_{ijs}\right)-\widehat{\mu }\left(t_{ijs}\right)-{\widehat{\eta }}_j\left(t_{ijs}\right)\}}^2-{\widehat{K}}_T(t_{ijs},t_{ijs})$ with respect to t_ijs for all possible i,j,s.

For univariate and bivariate smoothing we use penalized spline smoothing (Ruppert et al., 2003) with the smoothing parameter estimated via restricted maximum likelihood (REML). This technique has been implemented in statistical packages, such as the “SemiPar” package in R. Cross validation (CV) or generalized cross validation (GCV) could also be used. Alternatively, one can also use local polynomial smoothing Fan & Gijbels (1996) with cross validation to choose the smoothing parameter. In Step 3, the diagonal elements (when s = r) are dropped when estimating the total covariance K_T(s, t), because they are contaminated by measurement error. In contrast, diagonal elements are included when estimating the between covariance K_B(s, t).

In Step 4, one needs to determine the dimensions of level 1 and 2 spaces, namely, N₁ and N₂, respectively. Although they are allowed to be ∞ in theory, in practice a low dimensional principal component space suffices to approximate the functional space. We will discuss this issue in more details later.

2.3. Principal component scores

Once the fixed functional effects μ(t), η_ij(t), the eigenvalues ${\lambda }_k^{\left(1\right)}$, ${\lambda }_l^{\left(2\right)}$ and the eigenfunctions ${\varphi }_k^{\left(1\right)}\left(t\right)$, ${\varphi }_l^{\left(2\right)}\left(t\right)$ are estimated, the MFPCA model can be re-written as a linear mixed model

$$\{\begin{array}{c}{Y}_{ijs}=\mu \left(t_{ijs}\right)+{\eta }_j\left(t_{ijs}\right)+\sum _{k=1}^{N_1}{\xi }_{ik}{\varphi }_k^{\left(1\right)}\left(t_{ijs}\right)+\sum _{l=1}^{N_2}{\zeta }_{ijl}{\varphi }_l^{\left(2\right)}\left(t_{ijs}\right)+{∊}_{ijs}\hfill \\ {\xi }_{ik}\sim N\{0,{\lambda }_k^{\left(1\right)}\},{\zeta }_{ijl}\sim N\{0,{\lambda }_l^{\left(2\right)}\},{∊}_{ijs}\sim N(0,{\sigma }^2),\hfill \end{array}\phantom{\}}$$ (3)

where Y_ijs := Y_ij(t_ijs) and ε_ijs = ε_ij(t_ijs). The random effects ξ_ik and ζ_ijl are principal component scores that we are trying to estimate. Thus, one could use the mixed model inferential machinery to estimate the scores, for example, using the best linear unbiased prediction (BLUP). The BLUP gives point estimates of the scores, and one could also construct their 95% confidence intervals.

Note that the subject-specific effect, Z_i(t), and the visit-specific effect, W_ij(t), are linear functions of the random effects ξ_ik and ζ_ijl respectively. Thus, Z_i(t), W_ij(t) and their variability can be estimated directly from the BLUP formulas for the random effects. The BLUPs of Z_i(t) and W_ij(t) are shrinkage estimators, which automatically combine information from different visits of the same subject and across subjects. More information is borrowed when the measurement error variance, σ, is large and when the number of observations at the subject level is small.

2.4. Choosing the dimensions N₁ and N₂

Two popular methods for estimating the dimension of the functional space in the single level case are cross validation (Rice & Silverman, 1991) and Akaike's Information Criterion (or AIC, as in Yao et al., 2005). These methods can be generalized to the multilevel setting. For example, one could use the leave-one-subject-out cross validation criterion to select the number of dimensions. Define the cross validation score as

$$CV(N_1,N_2)=\sum _{i=1}^n\sum _{j=1}^{n_i}\sum _{s=1}^{T_{ij}}{\{Y_{ij}\left(t_{ijs}\right)-{\widehat{Y}}_{ij}^{(-i),N_1,N_2}\left(t_{ijs}\right)\}}^2,$$

where ${\widehat{Y}}_{ij}^{(-1),N_1,N_2}\left(t_{ijs}\right)$ is the predicted curve for subject i at visit j, computed after removing the data from subject i. The estimated number of dimensions N₁ and N₂ are the arguments that minimize CV(N₁,N₂). In practice, the leave-one-subject-out cross validation method may be too computationally intensive, and an m-fold cross validation can serve as a fast alternative. This method divides the subjects into m groups, and the prediction error for the m^th group is calculated by fitting a model using the data from other groups. The number of dimensions are chosen as those that minimize the total prediction error. Similar criteria could be designed for leave-visits-out.

One could also use a fast method. More precisely, let P₁ and P₂ be two thresholds and define

$$N_1=\min \{k:{\rho }_k^{\left(1\right)}\ge P_1,{\lambda }_k^{\left(1\right)}<P_2\},N_2=\min \{k:{\rho }_k^{\left(2\right)}\ge P_1,{\lambda }_k^{\left(2\right)}<P_2\},$$

where ${\rho }_k^{\left(j\right)}=({\lambda }_1^{\left(j\right)}+\dots +{\lambda }_k^{\left(j\right)})∕({\lambda }_1^{\left(j\right)}+\dots +{\lambda }_k^{\left(j\right)}+\cdots )$, j = 1,2, is the proportion of variation explained by the first k principal components at level j. Intuitively, this method chooses the number of dimension at each level to be the smallest integer k such that the first k components explain more than P₁ of the total variation while any component after the k^th explains less than P₂ of the variation. To use this method, the thresholds P₁ and P₂ need to be carefully tuned using simulation studies or cross validations. In practice, we found that P₁ = 90% and P₂ = 5% often work well.

2.5. Iterative procedure to improve accuracy

Initial estimates of the mean functions and eigenfunctions via smoothing are typically accurate in the dense functional data, and less accurate for the sparse data. To improve estimation accuracy, one may adopt an iterative procedure, which iterates between updating fixed effects (mean, eigenfunctions and eigenvalues) and principal component scores.

Iterative Sparse MFPCA Algorithm

Step 1. Obtain initial estimates, ${\widehat{\mu }}^0\left(t\right)$ , ${\widehat{\eta }}_j^0\left(t\right)$, ${\widehat{\lambda }}_k^{\left(1\right),0}$, ${\widehat{\lambda }}_l^{\left(2\right),0}$, ${\widehat{\varphi }}_k^{\left(1\right),0}\left(t\right)$, ${\widehat{\varphi }}_l^{\left(2\right),0}\left(t\right)$ and ${\widehat{\sigma }}^{2,0}$ for all j,k,l, using the sparse MFPCA algorithm described in Section 2.2; estimate principal component scores, ${\widehat{\xi }}_i^0$, and ${\widehat{\zeta }}_i^0$, using formulas that will be described in Section 3;

Step 2. Apply Steps 1–2 of the sparse MFPCA algorithm on $Y_{ij}\left(t_{ijs}\right)-{\sum }_{k=1}^{N_1}{\widehat{\xi }}_{ik}^0{\widehat{\varphi }}_k^{\left(1\right),0}\left(t_{ijs}\right)-{\sum }_{l=1}^{N_2}{\widehat{\zeta }}_{ijl}^0{\widehat{\varphi }}_l^{\left(2\right),0}\left(t_{ijs}\right)$ and obtain updated mean functions ${\widehat{\mu }}^1\left(t\right)$ and ${\widehat{\eta }}_j^1\left(t\right)$;

Step 3. Apply Steps 3–6 of the sparse MFPCA algorithm on $Y_{ij}\left(t_{ijs}\right)-{\sum }_{k=1}^{N_1}{\widehat{\xi }}_{ik}^0{\widehat{\varphi }}_k^{\left(1\right),0}\left(t_{ijs}\right)-{\sum }_{l=1}^{N_2}{\widehat{\zeta }}_{ijl}^0{\widehat{\varphi }}_l^{\left(2\right),0}\left(t_{ijs}\right)$, and obtain updated eigenvalues ${\widehat{\lambda }}_k^{\left(1\right),1}$, ${\widehat{\lambda }}_l^{\left(2\right),1}$, eigenfunctions ${\widehat{\varphi }}_k^{\left(1\right),1}\left(t\right)$, ${\widehat{\varphi }}_l^{\left(2\right),1}\left(t\right)$ and ${\widehat{\sigma }}^{2,1}$ for all j,k,l;

Step 4. Update principal component scores, ${\widehat{\xi }}_i^1$ and ${\widehat{\zeta }}_i^1$, based on the new estimates from Steps 2–3;

Step 5. Stop if certain criteria are met. Otherwise, set ${\widehat{\mu }}^1\left(t\right)$, ${\widehat{\eta }}_j^1\left(t\right)$, ${\widehat{\lambda }}_k^{\left(1\right),1}$, ${\widehat{\lambda }}_l^{\left(2\right),1}$, ${\widehat{\varphi }}_k^{\left(1\right),1}\left(t\right)$, ${\widehat{\varphi }}_l^{\left(2\right),1}\left(t\right)$, ${\widehat{\xi }}_i^1$ and ${\widehat{\zeta }}_i^1$ as initial estimates and repeat Step –5 until the algorithm converges.

One reasonable set of the stopping criteria could be $\Vert {\widehat{\mu }}^1\left(t\right)-{\widehat{\mu }}^0\left(t\right)\Vert <{\epsilon }_1$, $\Vert {\widehat{\eta }}_j^1\left(t\right)-{\widehat{\eta }}_j^0\left(t\right)\Vert <{\epsilon }_1$, $\Vert {\widehat{\varphi }}_k^{\left(1\right),1}\left(t\right)-{\widehat{\varphi }}_k^{\left(1\right),0}\left(t\right)\Vert <{\epsilon }_1$, $\Vert {\widehat{\varphi }}_l^{\left(2\right),1}\left(t\right)-{\widehat{\varphi }}_l^{\left(2\right),0}\left(t\right)\Vert <{\epsilon }_1$, $\mid {\widehat{\lambda }}_k^{\left(1\right),1}-{\widehat{\lambda }}_k^{\left(1\right),0}\mid {\epsilon }_2$, and $\mid {\widehat{\lambda }}_l^{\left(2\right),1}-{\widehat{\lambda }}_l^{\left(2\right),0}\mid <{\epsilon }_2$, for all j, k and l, where ε₁> 0 and ε₂ > 0 are small pre-specified thresholds.

3. Prediction of principal component scores and curves

This section provides BLUP calculation results for principal component scores and function prediction at various levels. Some heavy notation is unavoidable, but results are crucial for the implementation of our quick algorithms.

3.1. Prediction of principal component scores

We introduce some notations before presenting the formulas for the principal component scores. Let ξ_i = (ξ_i1,ξ_i2,···,ξ_iN₁)^T be an N₁ × 1 vector, ζ_ij = (ζ_ij1,ζ_ij2,···,ζ_ijN₂)^T be an N₂ × 1 vector, ${\zeta }_i={({\zeta }_{i1}^T,{\zeta }_{i2}^T.\cdots ,{\zeta }_{i{n}_i}^T)}^T$ be an (N₂n_i) × 1 vector, Y_ij = (Y_ij1,···,Y_ijTij) be a Y_ij × 1 vector, t_ij = (t_ij1,···,t_ijTij) be a T_ij × l vector, $Y_i={(Y_{i1}^T,\cdots ,Y_{i{n}_i}^T)}^T$ be a (Σ_iT_ij × 1 vector. Calculations will be done conditionally on μ(t), η(t), ${\lambda }_k^{\left(1\right)}$, ${\lambda }_l^{\left(2\right)}$ and ${\varphi }_k^{\left(1\right)}\left(t\right)$ and ${\varphi }_l^{\left(2\right)}\left(t\right)$, which can be estimated using methods described in the previous sections. It is straightforward to evaluate these functions at observed grid points, i.e, μ_ij = {μ(t_ij1),..., μ(t_ijTij) }^T, ${\mu }_i={({\mu }_{ij}^T,\cdots ,{\mu }_{i{n}_i}^T)}^T$, η_ij = {η(t_ij1),..., η(t_ijTij) }^T, η_ij = (η_ij^T,···,η^T_ini)|^T, ${\eta }_i={({\eta }_{ij}^T,\cdots ,{\eta }_{i{n}_i}^T)}^T$, ${\varphi }_{k,ij}^{\left(1\right)}={\{{\varphi }_k^{\left(1\right)}\left(t_{ij1}\right),\cdots ,{\varphi }_k^{\left(1\right)}\left(t_{ij{T}_{ij}}\right)\}}^T$ and ${\varphi }_{l,ij}^{\left(2\right)}={\{{\varphi }_l^{\left(2\right)}\left(t_{ij1}\right),\cdots ,{\varphi }_l^{\left(2\right)}\left(t_{ij{T}_{ij}}\right)\}}^T$. Let ${\Phi }_{ij}^{\left(1\right)}$ denote a T_ij × N₁ matrix whose ^th column is given by ${\varphi }_{k,ij}^{\left(1\right)}$, ${\Phi }_{ij}^{\left(2\right)}$ denote a T_ij × N₂ matrix whose I^th column is given by ${\varphi }_{l,ij}^{\left(2\right)}$,Λ⁽¹⁾ denote an N₁ × N₁ diagonal matrix with diagonal elements (${\lambda }_1^{\left(1\right)},\cdots ,{\lambda }_{N_1}^{\left(1\right)}$) and Λ⁽²⁾ denote an N₂ × N₂ diagonal matrix with diagonal elements (${\lambda }_1^{\left(2\right)},\cdots ,{\lambda }_{N_2}^{\left(2\right)}$). The following proposition gives the point estimates and variance for the principal component scores.

Proposition 1. Under the MFPCA model (3), the best linear unbiased prediction for principal component scores (${\xi }_i^T$, ${\zeta }_i^T$) has the following form,

$$\left(\begin{array}{c}\hfill {\widehat{\xi }}_i\hfill \\ \hfill {\widehat{\zeta }}_i\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathit{A}}_i\hfill \\ \hfill {\mathit{B}}_i\hfill \end{array}\right){\Sigma }_i^{-1}({\mathit{Y}}_i-{\mu }_i-{\eta }_i),$$ (4)

and their covariance matrix, $\mathrm{cov}\{({\widehat{\xi }}_i^T-{\xi }_i^T,{\widehat{\zeta }}_i^T-{\zeta }_i^T)\mid Y_i\}$, is given by

$$\left(\begin{array}{cc}\hfill {\Lambda }^{\left(1\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Lambda }^{\left(2\right)}\otimes {\mathit{I}}_{n_i\times n_i}\hfill \end{array}\right)-\left(\begin{array}{c}\hfill {\mathit{A}}_i\hfill \\ \hfill {\mathit{B}}_i\hfill \end{array}\right){\Sigma }_i^{-1}({\mathit{A}}_i^T,{\mathit{B}}_i^T),$$ (5)

where ⊗ denotes the Kronecker product, A_i := cov(ξ_i, Y_i) is an N₁ × Σ_jT_ij) matrix, B_i := cov(ζ_i, Y_i) is an N_2ni × Σ_jT_ij) matrix and Σ_i := cov(Y_i) is a $\left({\sum }_j{T}_{ij}\right)\times \left({\sum }_j{T}_{ij}\right)$ matrix. The matrix A_i has the form ${\mathit{A}}_i=({\Lambda }^{\left(1\right)}{\Phi }_{i1}^{{\left(1\right)}^T},{\Lambda }^{\left(1\right)}{\Phi }_{i2}^{{\left(1\right)}^T},\cdots ,{\Lambda }^{\left(1\right)}{\Phi }_{i{n}_i}^{{\left(1\right)}^T})$, and B_i, is a block diagonal matrix with diagonal elements $\{{\Lambda }^{\left(2\right)}{\Phi }_{i1}^{{\left(2\right)}^T},{\Lambda }^{\left(2\right)}{\Phi }_{i2}^{{\left(2\right)}^T},\cdots ,{\Lambda }^{\left(2\right)}{\Phi }_{i{n}_i}^{{\left(2\right)}^T}\}$. Let Σ_i,jk := cov(Y_ij, Y_ik) be the (j,k) block of Σ_i, with size T_ij × T_ik. When j = k,

$${\Sigma }_{i,jj}={\Phi }_{ij}^{\left(1\right)}{\Lambda }^{\left(1\right)}{\Phi }_{ij}^{{\left(1\right)}^T}+{\Phi }_{ij}^{\left(2\right)}{\Lambda }^{\left(2\right)}{\Phi }_{ij}^{{\left(2\right)}^T}+{\sigma }^2{\mathit{I}}_{T_{ij}\times T_{ij}},$$

where I_Tij × T_ij is an identity matrix, and when j ≠ k, ${\Sigma }_{i,j,k}={\Phi }_{ij}^{\left(1\right)}{\Lambda }^{\left(1\right)}{\Phi }_{ik}^{{\left(1\right)}^T}$ .

Equation (4) provides the best prediction of the principal component scores under the Gaussian assumptions, and the best linear prediction otherwise. Thus, the Gaussian assumptions in model (3) can be relaxed. Crainiceanu et al. (2009b) also provides formulae for the BLUPs of the principal component scores. Their results are applicable to balanced and dense designs only, i.e. to cases when each function is measured at exactly the same set of grid points; the formulae in Proposition 1 are applicable both for balanced and unbalanced designs. When data are balanced and dense, the results in Crainiceanu et al. (2009b) are preferable because they avoid inverting large matrices. Otherwise, one should use results in Proposition 1.

Once estimates of principal component scores are obtained, they can be used in further analysis either as outcome or predictor variables. For example, Di et al. (2009) explored the distribution of subject specific principal component scores in different sex and age groups. Di et al. (2009) and Crainiceanu et al. (2009b) considered generalized multilevel functional regression, which modeled principal component scores as predictors for health outcomes, such as hypertension. These analyses can be extended to the sparse case.

3.2. Prediction of functional effects

Our approach for sparsely recorded functions allows estimation of the covariance structure of the population of functions at various levels; it also provides a simple algorithm for predicting subject-level or subject/visit-level curves. This process intrinsically borrows information both across subjects and across visits within-subjects, and yields surprisingly accurate predictions; see our simulation results in Section 4 and data analysis in Section 5 for demonstration. The following Proposition provides the formulas for prediction of various functions and their confidence intervals. Results are derived based on the MFPCA model (3) and Proposition 1.

Proposition 2. Let ${\Phi }^{\left(1\right)}\left(t\right)≔{\{{\varphi }_1^{\left(1\right)}\left(t\right),{\varphi }_2^{\left(1\right)}\left(t\right),\cdots ,{\varphi }_{N_1}^{\left(1\right)}\left(t\right)\}}^T$ and ${\Phi }^{\left(2\right)}\left(t\right)≔{\{{\varphi }_1^{\left(2\right)}\left(t\right),{\varphi }_2^{\left(2\right)}\left(t\right),\cdots ,{\varphi }_{N_2}^{\left(2\right)}\left(t\right)\}}^T$. Under the MFPCA model (3), the best linear unbiased prediction for the subject-specific curve, Z_i(t), is given by

$${\widehat{Z}}_i\left(t\right)={\Phi }^{\left(1\right)}{\left(t\right)}^T{\widehat{\xi }}_i={\Phi }^{\left(1\right)}{\left(t\right)}^T{\mathit{A}}_i{\Sigma }_i^{-1}({\mathit{Y}}_i-{\mu }_i-{\eta }_i),$$

with variance, $\mathrm{var}\{{\widehat{Z}}_i\left(t\right)-Z_i\left(t\right)\mid Y_i\}={\Phi }^{\left(1\right)}{\left(t\right)}^T({\Lambda }^{\left(1\right)}-{\mathit{A}}_i{\Sigma }_i^{-1}{\mathit{A}}_i^T){\Phi }^{\left(1\right)}\left(t\right)$. The best linear unbiased prediction for the visit-specific curve, W_ij(t), is given by

$${\widehat{W}}_{ij}\left(t\right)={\Phi }^{\left(2\right)}{\left(t\right)}^T{\widehat{\zeta }}_{ij}={\Phi }^{\left(2\right)}{\left(t\right)}^T{\mathit{H}}_j{\mathit{B}}_i{\Sigma }_i^{-1}({\mathit{Y}}_i-{\mu }_i-{\eta }_i),$$

with variance, $\mathrm{var}\{{\widehat{W}}_{ij}\left(t\right)-W_{ij}\left(t\right)\mid Y_i\}={\Phi }^{\left(2\right)}{\left(t\right)}^T({\Lambda }^{\left(2\right)}\otimes I_{n_i\theta n_i}-H_j{B}_i{\Sigma }_i^{-1}{A}_i^T{H}_j^T){\Phi }^{\left(2\right)}\left(t\right)$, where the matrix $H_j=(H_{j,1},\cdots ,H_{j,n_i})$ is N₂ × (N₂n_i) with H_j,k = I_N2 × N₂ if j = k and H_j,k = 0 otherwise. The individual curve Y_ij(t) can be predicted by ${\widehat{Y}}_{ij}\left(t\right)=\widehat{\mu }\left(t\right)+{\widehat{\eta }}_j\left(t\right)+{\widehat{Z}}_i\left(t\right)+{\widehat{W}}_{ij}\left(t\right)$, with variance, $\mathrm{var}\{{\widehat{Y}}_{ij}\left(t\right)-Y_{ij}\left(t\right)\mid Y_i\}$, estimated by

$$\Phi {\left(t\right)}^T{\mathit{G}}_j\left\{\left(\begin{array}{cc}\hfill {\Lambda }^{\left(1\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Lambda }^{\left(2\right)}\otimes {\mathit{I}}_{n_i\times n_i}\hfill \end{array}\right)-\left(\begin{array}{c}\hfill {\mathit{A}}_i\hfill \\ \hfill {\mathit{B}}_i\hfill \end{array}\right){\Sigma }_i^{-1}({\mathit{A}}_i^T,{\mathit{B}}_i^T)\right\}{\mathit{G}}_j^T\Phi \left(t\right),$$

where G_j = (I_N1 × N₁) and $\Phi \left(t\right)={({\Phi }^{\left(1\right)}{\left(t\right)}^T,{\Phi }^{\left(2\right)}{\left(t\right)}^T)}^T$.

Proofs of Proposition 1 and 2 can be obtained by BLUP calculations (see, e.g., Ruppert et al., 2003) for general linear mixed models, and are omitted. This is a two-step procedure, first estimating in the fixed functional effects μ(t) and (η_j(t), eigenvalues ${\lambda }_k^{\left(1\right)}$ and ${\lambda }_l^{\left(2\right)}$ eigenfunctions ${\varphi }_k^{\left(1\right)}\left(t\right)$ and ${\varphi }_k^{\left(2\right)}\left(t\right)$ and variance σ², and then plugging in these estimators in the BLUP estimation. Note that similar to (Yao et al., 2005), the variance formulas in Proposition 1 and 2 do not account for the uncertainty associated to estimating the quantities in the first step. Goldsmith et al. (2013) proposed bootstrap based procedures to obtain corrected confidence bands for functional data using principal components, and their approach can be adopted to estimate the total variation.

4. Simulations

To evaluate finite sample performance, we conducted simulation studies under a variety of settings. The data was generated from a true model used in Di et al. (2009), except that the curves are sampled on a sparse set of grid points.

More precisely, the true model is the MFPCA model with with ${\xi }_{ik}\sim N(0,{\lambda }_k^{\left(1\right)})$, ${\zeta }_{ijl}\sim N(0,{\lambda }_l^{\left(2\right)})$, ${∊}_{ij}\left(t_{ijm}\right)\sim N(0,{\sigma }^2)$ and (t_ijm : m = 1, 2,···, T_ij) is a set of grid points in the interval [0,1]. The set of grid points are generated uniformly in the interval [0,1], and are different across subjects and visits. For simplicity, we assume that the number of visits are the same across subjects and that the number of grid points per curve are the same across subjects and visits, i.e., n_i = J and T_ij = N for i = 1,···, n;j = 1,···, n_i, although our methods apply to the case of varying n_i, and T_ij easily. The true mean function is μ(t) = 8t(l - t). The true eigenvalues are ${\lambda }_k^{\left(1\right)}={0.5}^{k-1}$ and ${\lambda }_l^{\left(2\right)}={0.5}^{l-1}$, k, l = 1, 2, 3,4, with eigenfunctions ${\varphi }_k^{\left(1\right)}\left(t\right)=\{\sqrt{2}\sin \left(2\pi t\right),\sqrt{2}\cos \left(2\pi t\right),\sqrt{2}\sin \left(4\pi t\right),\sqrt{2}\cos \left(4\pi t\right)\}$ at Level 1 and ${\varphi }_1^{\left(2\right)}\left(t\right)=1$, ${\varphi }_2^{\left(2\right)}\left(t\right)=\sqrt{3}(2t-1)$, ${\varphi }_3^{\left(2\right)}\left(t\right)=\sqrt{5}(6t^2-6t+1)$, ${\varphi }_4^{\left(2\right)}\left(t\right)=\sqrt{7}(20t^3-30t^2+12t-1)$ Level 2.

We considered several scenarios corresponding to various choices of n, N and σ², and simulated 1,000 data sets for each scenario. We considered n = 100, 200, 300 subjects, J = 2 visits per subject, N = 3,6, 9,12 measurements per function, and magnitude of noise σ = 0.01,0.5,1,2. Due to space limitations, we report results for a few scenarios, and present the others in the supplementary file.

We found that the estimation accuracy of eigenvalues and eigenfunctions increases with the number of subjects n, the number of visits J, and the number of grid points N. With n = 100 subjects and J = 2 visits, the first two components at both levels can be recovered well when N = 3; more precisely, the shapes of estimated eigenfunctions approximate well the true eigenfunctions and the estimated eigenvalues are close to their true values. When the number of grid points increases to N = 9, all four principal components at both levels can be estimated well. Table 1 reports the root mean square errors (RMSE) for eigenvalues and root integrated mean square errors for eigenfunctions in various simulation settings. More details on these results can be found in the supplementary file.

Table 1.

Root (integrated) mean square errors for eigenvalues and eigenfunctions in simulations. Simulation settings vary according to sample size (n = 100, 200, 300) and the number of grid points per function (N = 3, 6, 9, 12). In simulations, the first four principal components (PC) at both levels were compared to their underlying true counterparts. Root mean square errors and root integrated mean square errors are used to measure estimation accuracy for eigenvalues and eigenfunctions, respectively.

n	N	Eigenvalues				Eigenfunctions
		PC 1	PC 2	PC 3	PC 4	PC 1	PC 2	PC 3	PC 4
Level 1
100	3	0.25	0.39	0.69	1.16	0.45	0.66	1.03	1.07
100	6	0.29	0.36	0.76	1.26	0.56	0.81	1.00	1.21
100	9	0.19	0.25	0.35	0.48	0.38	0.54	0.83	0.98
100	12	0.21	0.26	0.36	0.54	0.42	0.66	0.85	1.08
200	3	0.18	0.22	0.26	0.36	0.34	0.48	0.73	0.92
200	6	0.19	0.23	0.30	0.41	0.35	0.56	0.76	0.97
300	3	0.17	0.20	0.23	0.31	0.32	0.46	0.66	0.87
Level 2
100	3	0.14	0.18	0.28	0.36	0.25	0.37	0.67	0.90
100	6	0.15	0.21	0.30	0.42	0.31	0.51	0.71	0.95
100	9	0.15	0.23	0.45	0.64	0.27	0.39	0.81	0.98
100	12	0.17	0.25	0.37	0.64	0.36	0.62	0.83	1.06
200	3	0.12	0.16	0.39	0.50	0.21	0.30	0.67	0.90
200	6	0.14	0.22	0.32	0.51	0.30	0.53	0.74	0.97
300	3	0.09	0.10	0.16	0.20	0.15	0.21	0.33	0.51

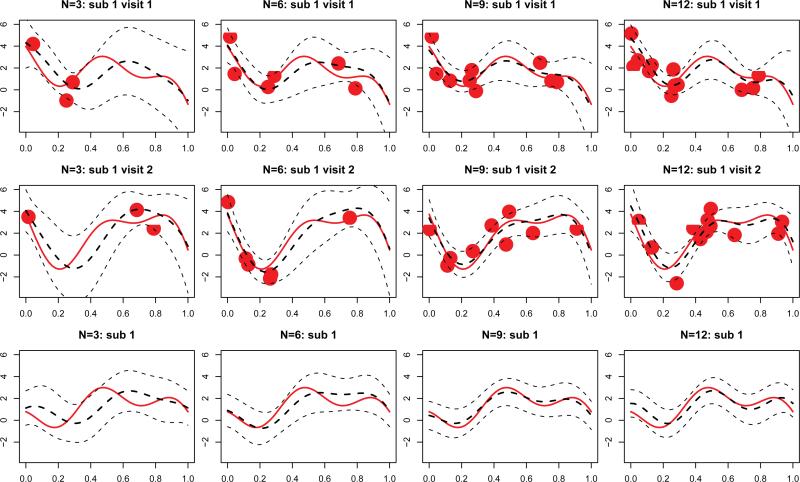
We also evaluated the finite sample performance of predictions of subject and subject/visit level curves. We discuss our results for the case when n = 200, J = 2 with different levels of noise level, σ, and number of observations per visit, N. Figure 1 shows predictions for subject- and visit-specific curves for the first subject under various scenarios. In the sparsest case, N = 3, the BLUPs can still capture the rough shape of the curve, the confidence bands are relatively wide because of the large amount of uncertainty, but cover the true curve in most cases. For example, the predicted curve corresponding to subject 1 visit 2 (first panel in the middle row) identifies a local minimum at t = 0.2, even though there are no observations around the area. This is probably due to the additional information provided by the data for the same subject at visit 1 (first panel in the top row). The bottom row shows results for subject-specific curve, Z₁(t), indicating that the BLUP estimates captures the major trend, though misses some of the details. When the number of grid points increases, predictions of both individual curves and subject specific curves improve. When N = 9, these predictions are already very close to the true curves.

Figure 1.

Prediction of curves for the first subject, in simulation setting with n = 200 subjects, J = 2 visits per subject, N = 3,6,9,12 grid points per curve and noise variance σ² = 1. Different columns correspond to different levels of sparsity, with the number of grid points varying from 3 to 12. The first and second rows show predictions of subject/visit specific curves, at visit 1 and 2, respectively. In these subfigures, red solid lines correspond to the true underlying curves, Y_ij(t), and red dots are observed sparse data, Y_ij(t_ijs). The thick black dashed lines are the predictions of curves, ${\widehat{Y}}_{ij}\left(t\right)$, and thin black dashed lines give their 95% pointwise confidence bands. The third row display subject level curves, Z_i(t), and their predictions ${\widehat{Z}}_i\left(t\right)$.

In summary, the sparse MFPCA algorithm is able to capture dominating modes of variations at both levels for sparse data, in a typical setting with hundreds of subjects and a few visits per subject. Predictions of curves via BLUPs also perform very well in finite samples.

5. Applications

5.1. SHHS

We now illustrate the use of sparse MFPCA on the SHHS data. The data contains dense EEG series for 3201 subjects at two visits per subject. Di et al. (2009) analyzed the full SHHS data using the MFPCA methodology and extracted dominant modes of variations at both between and within subject levels. To illustrate the comparison between dense and sparse analysis, we take a sparse random sample of the SHHS data even though the true data is dense. More precisely, for each subject and each visit, we take a random sample of N data points from the sleep EEG δ-power time series. We perform analysis with N=3, 6, 12, 24 observations per visit and compare the results using the proposed sparse MFPCA method on the sub-sampled sparse data with those using the MFPCA method on the full data set. This will provide insights into the performance of our method and build confidence into using these methods even when N is small. The analysis based on the full data (henceforth denoted “full analysis”) provides a “gold standard”, which can be compared with the analysis based on sparse data. The sparse MFPCA analyses with increased number of observations, N, will further illustrate how much information is gained at different level of sparsity, in realistic settings.

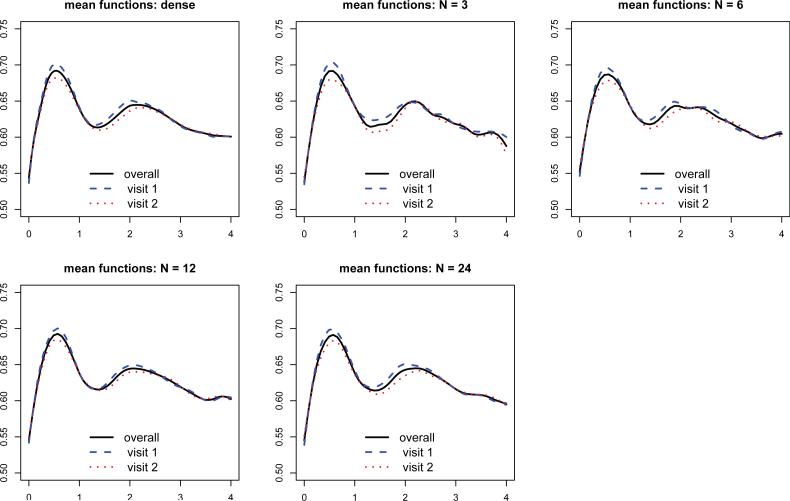
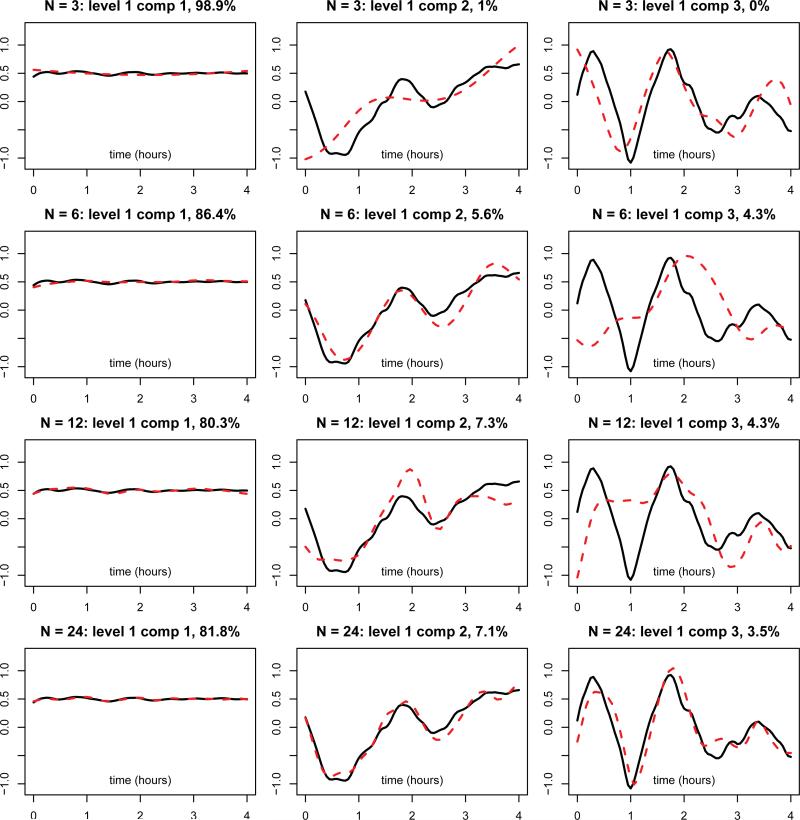
Figure 2 displays the estimated mean functions, including the overall mean function and visit specific mean functions, in the dense case and four different sparse cases. Even with N=3, the estimated mean functions are similar to those from the full analysis. By borrowing information from 3201 subjects, the sparse MFPCA captures the trend of mean functions well and correctly identifies peaks and valleys, compared to those from the full analysis. When the number of grid points increases to 6, 12 and 24, the estimated mean functions become indistinguishable from the full analysis. Table 2 displays estimated eigenvalues and Figure 3 shows estimated eigenfunctions at the subject level (level 1). The dashed lines represent eigenfunctions estimated from the dense analysis, while solid lines correspond to estimated eigenfunctions from the sparse analysis. The first principal components were recovered very well in each case, even when N = 3. The shapes of the second and third components are roughly captured with 3 grid points, and get closer to those from full analysis as N increases. When N = 24, all components agree well with their full analysis counterparts. For the visit level (level 2), similar results are observed and the details are reported in the supplementary file. Similar patterns can be observed for eigenvalues and percent variance explained. The surprisingly good performance on estimation mean functions and eigenvalues is due to the ability of sparse MFPCA to borrow information over all subjects and visits.

Figure 2.

Estimated mean functions from MFPCA for the SHHS data: dense and sparse cases. The upper left panel shows estimated mean functions from the full analysis using dense data. The four remaining panels correspond to results from sparse cases, with the number of grid points per curve N = 3, 6,12, 24, respectively. In each subfigure, solid lines correspond to overall mean functions, $\widehat{\mu }\left(t\right)$, while dashed and dotted lines represent visit specific mean functions, $\widehat{\mu }\left(t\right)+{\widehat{\eta }}_j\left(t\right)$, at visit 1 and 2, respectively.

Table 2.

Estimated eigenvalues (first three components at level 1 and first five components at level 2) for SHHS, from dense and four sparse cases. “Percent” means percentage of variation explained by the corresponding to the principal component, relative to the total variation at the corresponding level. “N” is the number of grid points per function, and reflects levels of sparsity.

		Level 1			Level 2
		PC 1	PC 2	PC 3	PC 1	PC 2	PC 3	PC 4	PC 5
dense	eigenvalue	1.30	0.10	0.10	1.30	0.80	0.70	0.60	0.60
	percent	80.80	7.60	3.30	21.80	12.80	12.50	10.90	9.60
N = 3	eigenvalue	1.20	0.00	0.00	1.30	0.70	0.50	0.50	0.40
	percent	98.90	1.10	0.00	34.00	18.50	14.40	13.20	10.30
N = 6	eigenvalue	1.30	0.10	0.10	1.30	0.80	0.60	0.60	0.40
	percent	86.40	5.60	4.30	27.40	15.60	13.50	11.80	9.10
N = 12	eigenvalue	1.30	0.10	0.10	1.30	0.80	0.70	0.60	0.50
	percent	80.30	7.30	4.30	24.60	14.70	13.80	11.50	9.40
N = 24	eigenvalue	1.30	0.10	0.10	1.30	0.80	0.70	0.70	0.50
	percent	81.80	7.10	3.50	23.60	13.80	13.40	12.10	9.70

Figure 3.

Estimated eigenfunctions (first three components at level 1) from MFPCA for the SHHS data: dense and sparse cases. The four rows correspond to different levels of sparsity, with the number of grid points per function N = 3, 6,12, 24, respectively. The three columns represent the first three principal components, respectively. In each subfigure, solid black lines correspond to estimates from the dense case, while dashed red lines represent estimates from sparse cases.

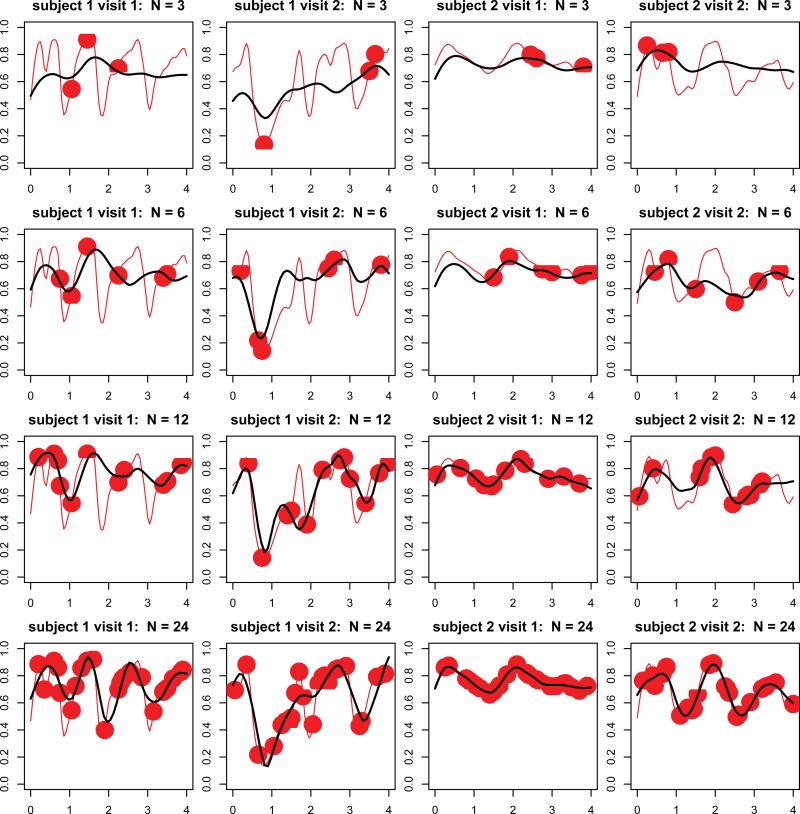
We next evaluate predictions in each of the four sparse scenarios, and illustrate the results on the first two subjects in Figure 4. The thick solid lines are predictions using sparse MFPCA methods on sparse data, while the thin solid lines are smooth estimates of the functions using the full data set. The dots are the actual sampled points. With N = 3 (first row of panels), predictions of curves can only capture the rough trend and miss refined features such as peaks and valleys, even though mean functions and eigenfunctions can be recovered well. This is not surprising, because a lot of subject-specific information loss should be expected. When the number of sampled points increases (next rows of panels), the sparse MFPCA method estimates more detailed features.

Figure 4.

Prediction of sleep EEG curves for the first two subjects from the SHHS. The first and second columns correspond to visit 1 and 2 for the first subject, respectively. The third and fourth columns correspond to visit 1 and 2 for the second subject, respectively. Different rows represent different levels of sparsity, with the number of grid points N varying from 3 to 12. In each subfigure, red lines represent smoothed sleep EEG curves, while red dots are sparsified data at certain level of sparsity. Black lines are predictions of sleep EEG curves from the MFPCA model.

To summarize, the sparse MFPCA methods can estimate the mean and principal component functions well even with sparse samples, provided that there are many subjects. The prediction accuracy greatly depends on the amount of available information, or equivalently, the level of sparsity. One can expect to recover a rough trend with few grid points, but more observations are needed to estimate detailed features, if those features exist.

5.2. eBay auction data

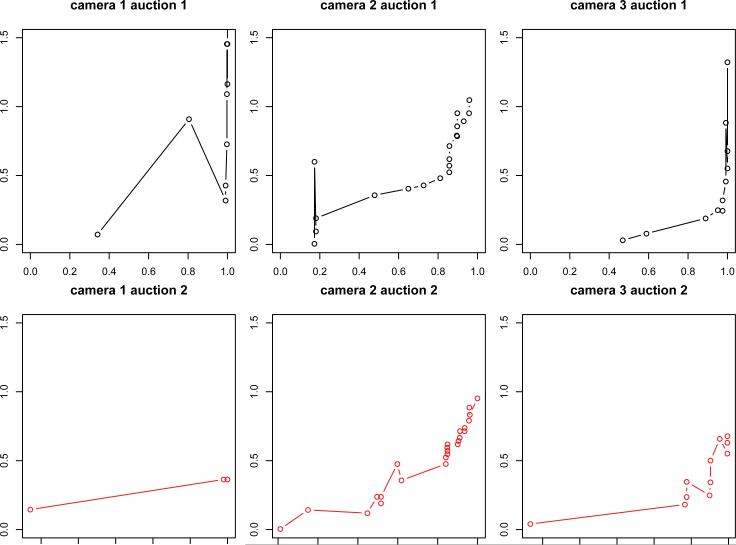
In this subsection, we analyzed a subset of our online auction data that consist of 40 pairs of auctions of digital cameras. Every pair contains two auctions of exactly the same camera, so any observed differences in the auction outcome must be due to differences in the seller or the bidding process. Figure 5 displays the raw auction data for the first three cameras. Auction time is normalized to to [0,1], where t = 0 and t = 1 correspond to the beginning and end of an auction, respectively. We also re-scale the y-axis (“pricep=”) to the average final price so that all auctions are comparable with respect to an item's value. Figure 5 shows that some auctions include as few as 3 bids, while others have as many as 20 – 30 bids. The bid-timing is irregular and unbalanced – often it is quite sparse at the beginning and middle phases of the auction but rather dense towards the end. We point out that the bids in Figure 5 are not monotonically increasing as would be expected from an ascending auction. The reason lies in eBay's proxy bidding system (explained in details in the online supplementary file).

Figure 5.

Auction trajectories for three digital cameras with two auctions per camera. The “x” axis represents normalized bidding time with range t ε [0,1], and the “Y” axis corresponds to re-scaled bidding prices. The two subfigures in each column show two auctions from a specific type of digital camera.

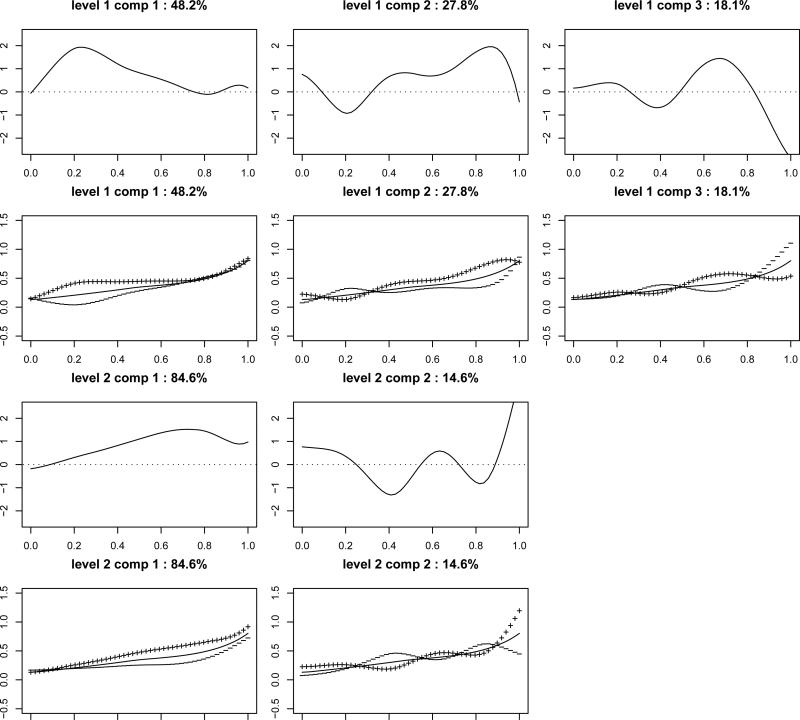
We look at level 1 and level 2 principal components, which extract dominating modes of variations at the between and within camera level, respectively. Eigenvalues and Eigenfunctions are shown in Table 3 and Figure 6, respectively. Based on Table 3, level 1 and 2 explain 35.9% and 64.1% of the total variation, respectively. Thus, there is substantial amount of variation at both levels.

Table 3.

Estimated eigenvalues from eBay auction data. Level 1 and 2 correspond to between camera and within camera variations, respectively. “% var” means percentage of variance explained by corresponding components, while “cum. % var” means cumulative percentage of variance explained by current and prior components.

Level 1				Level 2
(Proportion explained: 35.9%)				(Proportion explained: 64.1%)
Component	1	2	3	1	2
eigenvalue (×10–3)	6.2	3.6	2.3	19.4	3.4
% var	48.2	27.8	18.1	84.6	14.6
cum. % var	48.2	76.0	94.1	84.6	99.2

Figure 6.

Estimated eigenfunctions at level 1 (Rows 1-2) and level 2 (Rows 3-4). In Row 1 and 3, the solid lines represent estimated eigenfunctions. In Row 2 and 4, solid lines represent the overall mean function μ(t), and the lines indicated by “+” and “-” are mean function plus or minus a multiple of ${\varphi }_1^{\left(1\right)}\left(t\right)$, respectively. Namely, “+” represents $\mu \left(t\right)+c{\varphi }_1^{\left(1\right)}\left(t\right)$, and “-” represents $\mu \left(t\right)+c{\varphi }_1^{\left(1\right)}\left(t\right)$ for some constant c.

Next, we look at estimated eigenfunctions at both levels, which capture modes of variations across different cameras and across auctions within the same camera. In Figure 6, the first row show the shapes of three leading eigenfunctions at Level 1, $\{{\varphi }_1^{\left(1\right)}\left(t\right),{\varphi }_2^{\left(1\right)}\left(t\right),{\varphi }_3^{\left(1\right)}\left(t\right)\}$, while the second row display the types of variations resulting from them. The first eigenfunction (PCI) is mostly positive, indicating that auctions loading positively (negatively) on this component will always have higher (lower) values than average. Its magnitude is small at the beginning, increases and reaches maximum around t=0.2, then gradually decreases to 0 around t=0.8, and is close to 0 after t=0.8. The price for an auction loading positively on PC1 (the “+” line in Row 2 Column 1) increases rapidly at the beginning, almost flattens in the middle phase and increases somewhat towards the end, while an auction with a negative loading on PCI ((the “-” line in Row 2 Column 1)) has prices flat at the beginning but increasing after t=0.2. This component explains 48.2% of variation at the between camera level. In the auction context, this PC suggests that while price (or more precisely, willingness to pay) increases over the course of auctions, there is significant variation in bidder's valuations during the early auction stages. This is in line with earlier research that has documented that the early auction phase is often swamped with “bargain hunters.” The second principal component that explains 27.8% of variation characterizes mostly the variation at the later parts (t = 0.4 to t = 0.95) of auctions. This is in line with auctions that experience different early- and late-stage dynamics (Jank & Shmueli, 2007). One can interpret other eigenfunctions in a similar manner. The third and fourth row of Figure 6 show the shapes of two leading eigenfunctions at Level 2, e.g., with camera level. More detailed explanations of the auction application can be found at the online supplementary file.

Our analysis allows one to partition bidders’ willingness to pay into temporally different segments. In fact, level 1 analysis shows that early differences in willingness to pay can be attributed mostly to product differences. Our level 2 analysis suggests that bidders uncertainty about the valuation is largest during mid- to late-auction.

6. Discussion

We considered sparsely sampled multilevel functional data, and proposed a sparse MFPCA methodology for such data. We incorporated smoothing to deal with sparsity. Simulation studies show that our methods perform well. In an application to the SHHS, we compared the full analysis with sparse analysis under different levels of sparsity. The results show that the sparse MFPCA methodology works well in extracting the principal components, while prediction accuracy of functions depends on the level of sparsity. We also applied our methods to auction data from eBay and identified interesting bidding patterns Di et al. (2009) is the first attempt to generalize FPCA to multilevel functional data, and the current paper further extends its scope to sparsely sampled hierarchical functions. To the best of our knowledge this is the first FPCA based approach for sparsely sampled functional data. The proposed sparse MFPCA not only helps understand modes of variation at different levels but also reduces dimension for further analysis.

Multilevel functional data analysis is a rich research area motivated by an explosion of studies that generate functional data sets. The explosion is mainly due to improved technologies that generate new type of data sets. There are few directions for future methodological development. First, it would be interesting to extend the generalized multilevel functional regression Crainiceanu et al. (2009b) to the sparse case. Second, more efficient methods for estimating eigenvalues and eigenfunctions (e.g., generalizations of James et al., 2000; Peng & Paul, 2009) can be extended to the multilevel functional data. Another direction is to consider non-FPCA based methods, e.g., extensions of wavelet-based functional mixed models Morris et al. (2003) and Morris & Carroll (2006).