Abstract
Establishing meaningful relationships between cellular structure and function requires accurate morphological reconstructions. In particular, there is an unmet need for high quality surface reconstructions to model subcellular and synaptic interactions among neurons at nanometer resolution. We address this need with VolRoverN, a software package that produces accurate, efficient, and automated 3D surface reconstructions from stacked 2D contour tracings. While many techniques and tools have been developed in the past for 3D visualization of cellular structure, the reconstructions from VolRoverN meet specific quality criteria that are important for dynamical simulations. These criteria include manifoldness, water-tightness, lack of self- and object-object-intersections, and geometric accuracy. These enhanced surface reconstructions are readily extensible to any cell type (including glia) and are used here on complex spiny dendrites and axons from mature rat hippocampal area CA1. Both spatially realistic surface reconstructions and reduced skeletonizations are produced and formatted by VolRoverN for easy input into analysis software packages for neurophysiological simulations at multiple spatial and temporal scales ranging from ion electro-diffusion to electrical cable models.
Introduction
Brains are richly structured at the cellular and subcellular level as evidenced by the diversity in form of synapses, the compartmentalization of synaptic spines on dendrites, the intricate branching of dendrites and axons, and the complex inter-digitation of glial processes [1, 2]. Clinical findings reveal dramatic disruption in the structure and subcellular composition under a variety of neuropathies [3–8]. Recent advances in imaging are beginning to provide access to an unprecedented amount of structural data from serial section electron microscopy (EM) at nanometer resolution [9–16]. A number of software packages have been developed to support three-dimensional reconstruction from EM images (RECONSTRUCT™ [17, 18], TrakEM2 [19], ilastik [20], NeRV [21], NeuroTrace [22], KNOSSOS [23, 24]); however, their surface representations were developed primarily for rapid visualization and are insufficient to serve as a framework for dynamical simulations.
Any algorithm for reconstruction of brain geometry from serial sections must confront the challenge posed by structures that are smaller than section thickness (~45 nm) [25]. Objects within the thickness of the section can be obscured by overlapping structures in the projected EM image. Consequently, ambiguous geometries arise in the reconstruction of fine structure that is undersampled by the image data and incorrectly represented by extracted contours, frequently yielding 3D objects that are nonphysiological, e.g. with aberrant holes in the surface or erroneous connections between cells.
VolRoverN is a new software package that accepts as input the contour tracings from existing software tools, and automatically generates reconstructions that are physiologically plausible and formatted for easy input into other software tools for simulation of neuronal or other cellular dynamics. VolRoverN makes implementations of published algorithms available to practitioners in an intuitive, comprehensive interface, easing the task of model generation. We describe the functionality of VolRoverN, including accurate 3D surface reconstructions from manual contour tracings and production of derivative skeletonizations from these reconstructions. We enumerate common errors in surface reconstruction and demonstrate VolRoverN’s ability to produce error-free, quality reconstructions.
Functionality
VolRoverN is freely downloadable at http://cvcweb.ices.utexas.edu. It is currently available on the Mac OS X platform, and we anticipate release for Linux and Windows platforms. With the VolRoverN download is a sample dataset with contours and images of 8 axons and 2 dendrites in the CA1 region of the hippocampus. All images in this paper were produced using this dataset. A shared data repository will also be available where users of VolRoverN can share images, traces, 3D meshes, and simulation files for NEURON and MCell.
VolRoverN accepts RECONSTRUCT™ and TrakEM2 contour tracings as input. In the case of TrakEM2, the tracings are pixel-based and are automatically converted to polygonal representation by VolRoverN. Aligned and segmented images can also be imported into VolRoverN for visualization purposes.
The software first fits a triangulated surface to contours such that the contours are exactly interpolated and the surface meets important quality criteria. We list and show examples of violations of these criteria in Fig 1. Properties of quality reconstructions include water-tightness, manifoldness, lack of intersections, quality (close to equilateral) triangles, and geometric accuracy. With the surface mesh in place the user can make geometric queries, such as surface area and volume of a spine head. Further, VolRoverN provides tools to create derivative models, including 1D cable models. The various models can be saved in standard file formats, including Wavefront obj, OFF, ele/node, MDL (MCell), and HOC (NEURON).
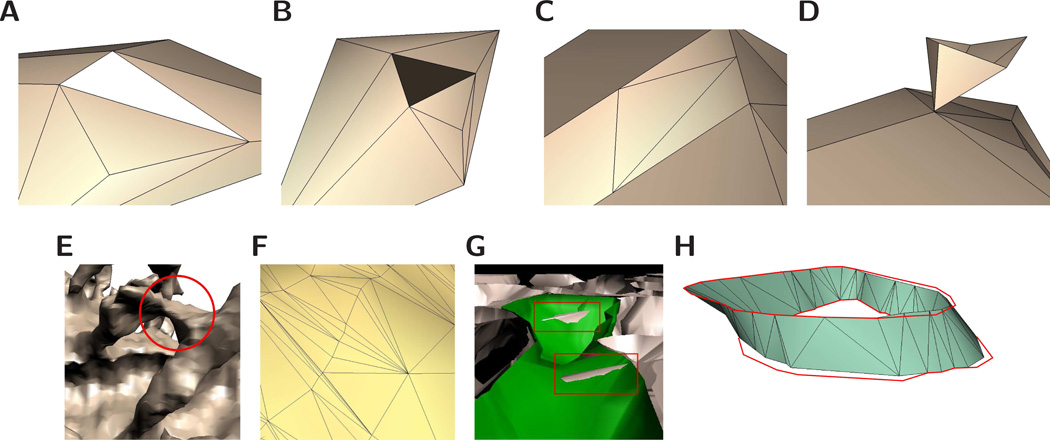
Figure 1.
Requirements for quality surface models. The illustrations demonstrate errors commonly encountered in morphological reconstructions of neurons. (A) Surface models should be water-tight, or free of holes. (B) A normal vector is associated with each facet in a mesh representation, and all facets should be consistently oriented. (C) Vertices should not be coincident with edges of other facets. (D) A surface is manifold if an arbitrarily small piece of the surface is a topological disk. In this example the point at which the two surfaces meet is not a topological disk. (E) In this example, two spine heads are erroneously joined during the reconstruction process. Meshes should be topologically consistent with the physical specimen they are approximating. (F) In a mesh representation, the facets (most commonly triangles) should be of good quality. In the case of a triangle, one definition of quality is that the ratios of edge lengths are close to one, or the triangle is close to equilateral. (G) A very common error in existing neuropil reconstruction methods is object-object intersections. Also common are triangle intersections within the same object. (H) Surface reconstructions should interpolate, or pass exactly through, the original contour tracings. The figure shows an example of error in interpolation. Both VolRoverN and marching cubes are error-free in that they exactly interpolate the contours.
VolRoverN shares a code base with the related software package VolRover 2.0 [26] which performs image processing, reconstruction and visualization of single particle and tomographic cryo-EM and includes 3DEM molecular ultra-structure identification and quasi-atomistic model-based refinement. As such, VolRoverN and VolRover 2.0 have similar look and feel, but the tools included in VolRoverN are appropriate primarily for neuronal modeling.
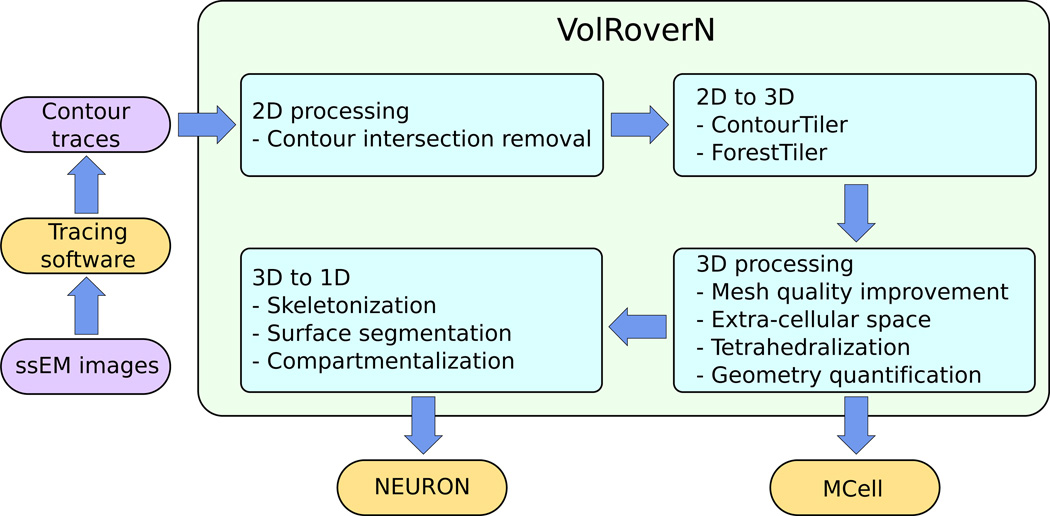
VolRoverN has 4 steps in producing models suitable for analysis (Fig 2). 1) Process 2D input. 2) Fit a 3D triangulated surface to the contours. 3) Process the 3D surface meshes, which includes improvement of the mesh. 4) Reduce the mesh to a 1D cable model. We now discuss each of these steps.
Figure 2.
A high-level look at VolRoverN’s functionality. There are four main phases: 2D processing, 2D to 3D reconstruction, 3D processing, and 3D to 1D reduction.
2D processing
Contour intersection removal
Contours are given as closed, simple polygons. Contours may be nested, as is the case with surface dimples and organelles. Each contour has a label that corresponds to a unique neuronal process, for example “axon16” or “dendrite3”. Manually-traced contours can accidentally intersect each other and these overlaps must be removed. VolRoverN has an automatic intersection removal algorithm [27] (Fig 3) that not only ensures that contours don’t intersect each other, but has an optional feature of guaranteeing a minimum separation distance [28]. The 2D intersection removal algorithm is purely geometric and does not take the EM images into consideration.
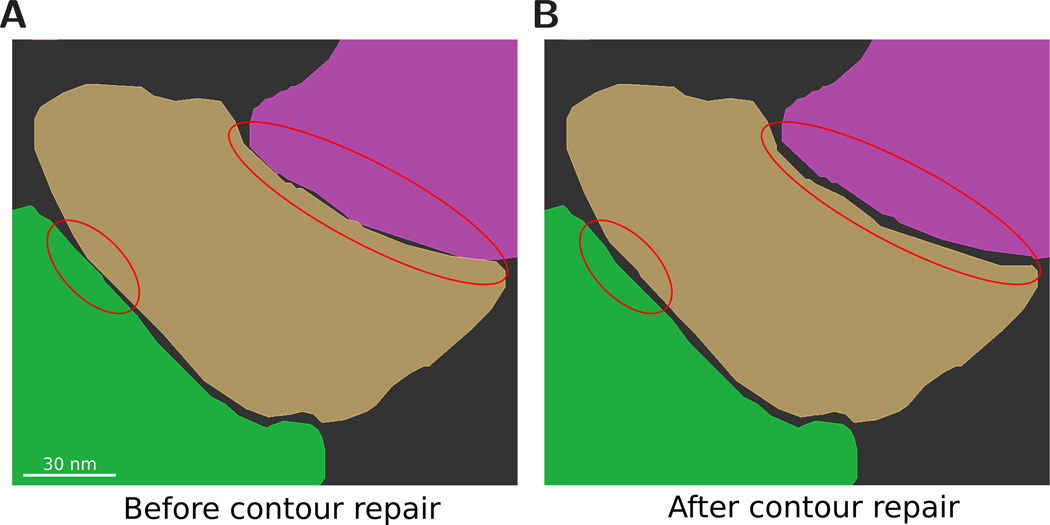
Figure 3.
2D curation. Because components are usually traced independently of each other, intersection errors can occur. (A) A number of intersections and close approaches can be seen between contours. (B) The intersections have been removed and a specific contour spacing is enforced.
2D to 3D
ContourTiler
VolRoverN has a 2D image and contour display called the Section Viewer (Fig 4A) that enables navigation through sections while inspecting contours. The Section Viewer and 3D Viewer are linked: imagery and semi-transparent contours can be visualized in the 3D view alongside surface meshes and volumes (Figs 4B and 4C). VolRoverN includes a tool called ContourTiler [27, 29] that fits a triangulated surface to a set of 2D polygonal contours derived from EM images. We call these triangles “tiles”. Three attributes of neuronal data make reconstruction non-trivial: (1) ssEM data is highly anisotropic. In-plane pixel resolution is usually about 2–5 nm, whereas spacing between sections is usually 45–70 nm. (2) Neurons are tortuous, with frequent twists and branching. (3) Neuronal processes are tightly packed. These three attributes make reconstruction of intersection-free surface meshes especially difficult for such complex morphologies. Other cell types, such as glia, can have similarly complex surfaces.
Figure 4.
Reconstruction from 2D contours. (A) Input to VolRoverN is a set of 2D polygonal traces, or contours, derived from EM images. (B) Software embedded in VolRoverN called ContourTiler fits a triangulated surface to each set of contours to produce a 3D surface model. (C) Multiple components are combined using ForestTiler such that they are free of intersections.
ContourTiler matches adjacent contours with identical labels and fits a surface between them. Matching is commonly referred to as the correspondence problem, i.e., whether two contours with identical labels in adjacent sections should be connected topologically. The correspondence problem is difficult and many methods have been used to solve it, including user consensus [23] and machine learning [30]. Our algorithm uses a simple heuristic, that of matching contours from adjacent sections together if their projections onto the plane intersect, which results in sensitivity to image registration quality. Our heuristic can also result in errors when small contours that are oriented obliquely to the image plane have grey boundaries that are difficult to trace, which may result in corresponding contours that don’t overlap. We anticipate incorporating more sophisticated correspondence predicates in the future.
Our tiling algorithm requires that the contours have no intersections, which is taken care of in our 2D contour intersection removal step. In addition, the contours are assumed to be registered, or aligned. Registration is typically done using the EM images [31] and the resulting 2D transformations are applied to the contours. An important property of our reconstruction approach is that the reconstructed surface exactly interpolates the input contours, so no error in the original section planes is introduced.
ForestTiler
ContourTiler produces a surface for each individual object. These surfaces are then combined together into a single geometry file that contains all of the objects. When the section spacing is very large, as is the case with anisotropic data, combining object meshes yields many object-object intersections. Most solutions to the intersection problem are primarily used with reconstruction algorithms that tend not to preserve correct topology in tightly-packed data [32]. We have implemented an algorithm called ForestTiler [27] that removes intersections in a way that preserves the interpolation property of the original reconstruction. In addition, similar to 2D contour curation, the user can specify a minimum separation distance δ, which corrects the reconstruction of unknown regions (between sections) to more closely match empirically determined extracellular spacings [28]. ForestTiler does not take membrane junctions into account, but a small value for distance δ may be specified to preserve very close spacing.
3D processing
Mesh quality improvement
VolRoverN includes a suite of tools to produce meshes with good quality triangles, i.e. triangles that are close to equilateral. The first tool is decimation, which uses the QSlim algorithm [33] to reduce the number of triangles. QSlim is an edge-collapse algorithm that is popular because of its speed and robustness. We then use the geometric-flow mesh improvement algorithm of Zhang et al [34, 35] that produces a surface mesh with triangles of good aspect ratio (Figs 5A–5B). The mesh improvement algorithm can be iteratively applied for increasing triangle quality. Quality improved meshes are not guaranteed to meet the contour interpolation property. VolRoverN also has mesh repair utilities (Figs 5C–5D) to repair errors such as holes, non-manifoldness and self-intersections. Non-manifoldness and self-intersections are repaired by automatic removal of offending triangles. Resulting gaps are then closed using our hole-filling tool, which uses an ear-clipping algorithm [36]. Our mesh repair utilities are general and can be applied to problematic meshes from other reconstruction software packages. Simplification, improvement, and mesh fixing are intended to be applied as follows:
Simplification
Improvement
Repair
Improvement
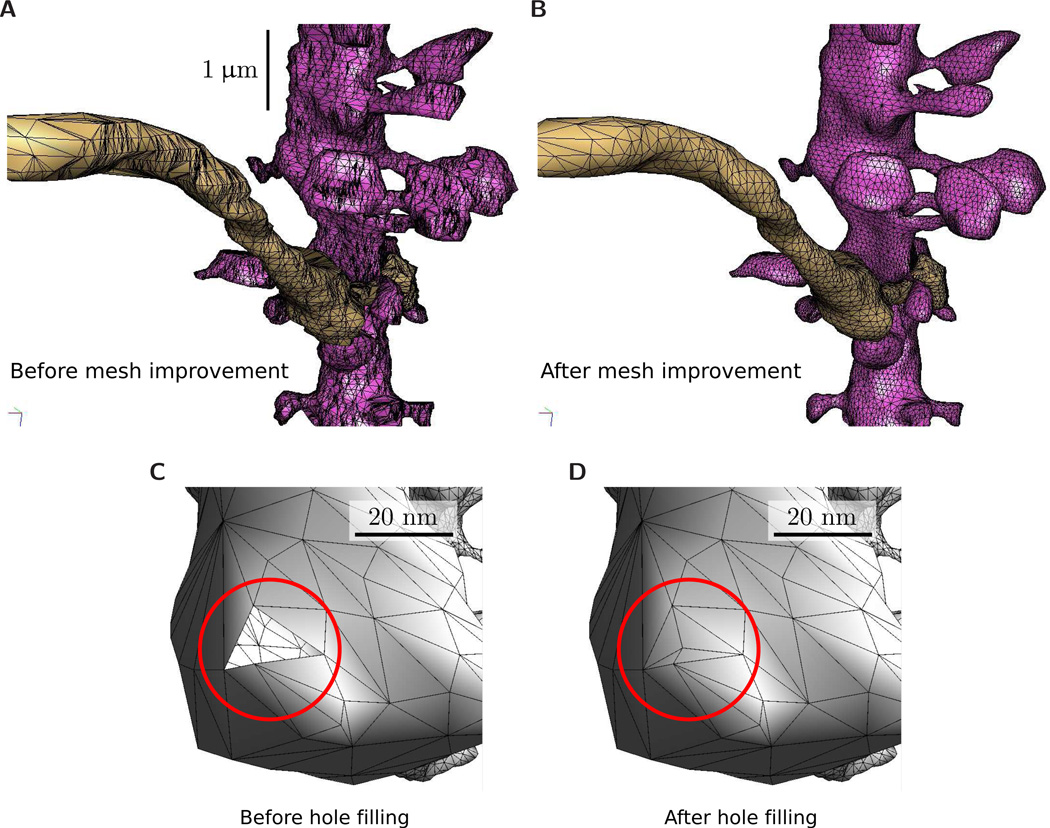
Figure 5.
Mesh improvement. (A) The original reconstructed triangulation of a dendrite and axon. The horizontal bands in the surface mesh reflect the separation between EM images of thin tissue sections. (B) The reconstruction after decimation and smoothing. The final triangulation has fewer than half the triangles as the original and the triangles have far better aspect ratio. (C) Repair utilities in VolRoverN include manifold correction and hole filling. The figure shows a hole outlined in red.(D) After hole filling. The before/after ratio of total mesh surface area in this example was 32.7/32.8, for a total hole surface area of 0.3%.
Repair is generally more effective if the model has already been simplified and improved. It is often best to finish with the improvement step as repair can introduce poor quality triangles.
Complementary space and tetrahedralization
A feature of VolRoverN is automatic complementary space (CS) generation outside (and complementary) to water-tight surface meshes and inside a bounded region of interest. The user is able to define a bounding box and the CS tool constructs a closed polyhedron with faces consisting of portions of the surface meshes and the bounding box (Fig 6). The CS polyhedron converges to a model of extra-cellular space (ECS) when the input surface meshes are a complete description of cells within a bounding box. Models of ECS have been used in reaction-diffusion simulations [28, 37].
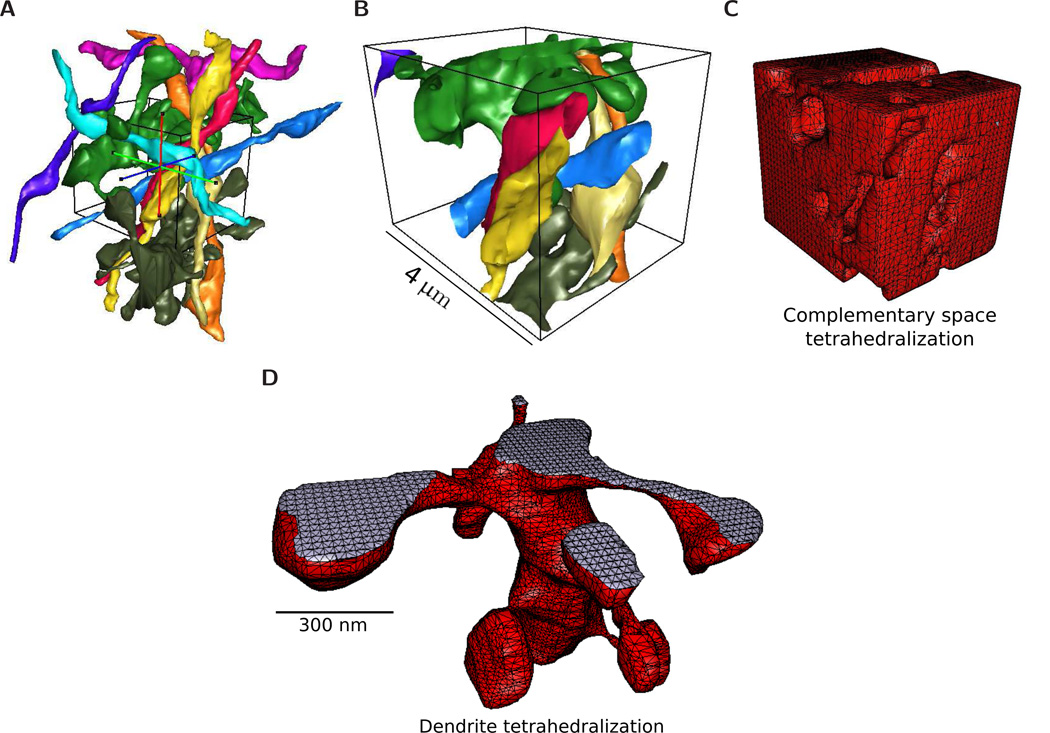
Figure 6.
VolRoverN utilities. (B) A bounding box is placed around the surface meshes in an area of interest. (B) The surfaces are clipped at the bounding box. (C) VolRoverN’s ECS and tetrahedralization tools create a volumetric model of complementary space. (D) Tetrahedralization of a dendrite using VolRoverN’s tetrahedralization tool.
VolRoverN also has the capability of tetrahedralizing surface meshes [38–40] (Fig 6D). This uses an adaptive subdivision meshing algorithm contained in a library from our Level Set Boundary-Interior-Exterior (LBIE) software package [41]. Tetrahedra are exported in RAW and ele/node formats for ease of import into simulation packages such as STEPS [42].
Comparison to other surface reconstructions
Standard algorithms such as marching cubes, which is used in most popular contouring software packages [19–21], yield large numbers of intersections between objects when the objects are tightly packed (Fig 7). Additionally, marching cubes produces blocky reconstructions with poor geometric accuracy due to its lack of interpolation between contours. This is especially evident with neuronal EM images that are highly anisotropic. Our algorithm resolves both problems, producing surface meshes that are intersection-free and linearly interpolated between contours.
Figure 7.
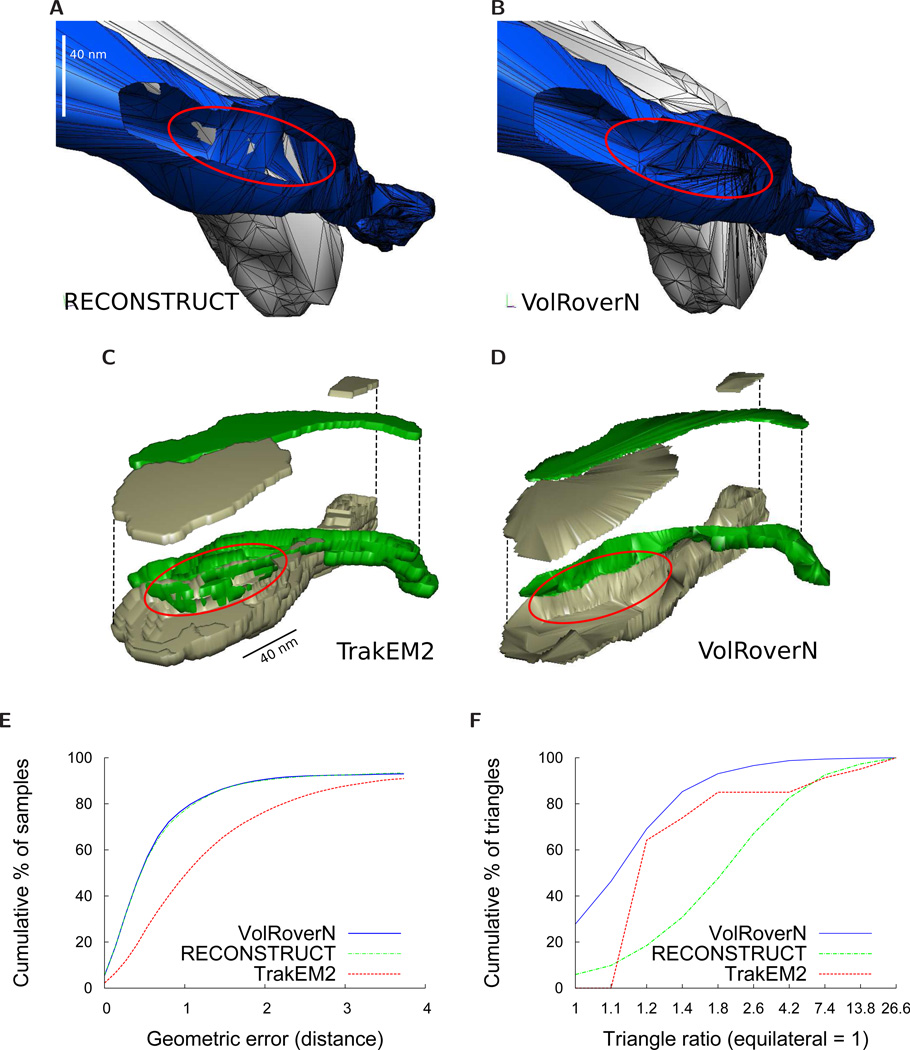
Comparisons with RECONSTRUCT™ and TrakEM2. (A)-(B) Comparison between RECONSTRUCT™ (Boissonnat) and VolRoverN surfaces using axons a001 and a020 from the sample dataset. Part of a020 is cut out to see the interior intersections. The RECONSTRUCT™ surfaces yield a large number of intersections between objects. Output from ForestTiler is intersection-free. (C)-(D) Comparison between TrakEM2 and VolRoverN surfaces. A portion of two axons are reconstructed with ImageJ’s marching cubes implementation (resample=1, no smoothing) and the top is lifted to reveal the interior. Marching cubes yields numerous intersections between objects. Output from ForestTiler is intersection-free. (E) Geometric error measured as distance from a reconstruction to a C1-continuous approximating surface. This is a cumulative plot of percentage of sample points within a given error. 100,000 sample points were taken. VolRoverN and RECONSTRUCT™ have far less geometric error than TrakEM2. To create the C1-continuous surface SC1, we randomly choose 4 adjacent, non-bifurcating contours (called c1, c2, c3, and c4) and fit cubic B-splines to each of them using a least-squares fit. We then join the contours together with interpolating cubic curves, forming a patch that is C1-continuous everywhere between c1 and c2. The data used in this test are from axon a001 between slices 115 and 118. (F) Comparison of quality of triangles between the three reconstruction methods. We define triangle ratio as rc/2ri where rc is the circumradius and ri is the inradius of a triangle. The ideal triangle ratio is 1. The plot is a cumulative percentage of triangles below a given ratio.
Here we compare ContourTiler with the implementation of marching cubes found in TrakEM2 (ImageJ) [19, 43] and the Boissonnat algorithm implemented in the RECONSTRUCT™ software [44]. We compared object-object intersections and geometric accuracy, as well as water-tightness and manifoldness. Other important surface mesh qualities (oriented normals, regularity, topological correctness, and contour interpolation) are met by all three algorithms. We reconstructed the 8 axons and 2 dendrites in the sample dataset distributed with VolRoverN using both RECONSTRUCT™ and VolRoverN and compared the results by quantifying the most common errors of those described in Fig 1. Figs 7A–7D show reconstruction of two axons in close proximity (a001 and a020 from the sample dataset) using the three reconstruction methods. VolRoverN meshes are free of intersections between multiple objects, in contrast to surfaces produced by the marching cubes and the Boissonnat algorithms. The Boissonnat and marching cubes representations yield a large number of intersections, whereas the VolRoverN surfaces are entirely free of intersections because VolRoverN meshes are guaranteed to have a user-specified minimum spacing between objects. Meshes produced by VolRoverN interpolate, or pass exactly through, the input contours. To quantify surface error in regions between contours we compared surfaces produced by VolRoverN and the other two algorithms to a C1-continuous surface fitted to the contours. The distribution of errors is reported in Fig 7E and shows that VolRoverN’s reconstructions are geometrically very similar to the RECONSTRUCT™ implementation of the Boissonnat algorithm, both of which are closer to a smooth approximation than marching cubes.
Triangle quality is another important measure of how successful a simulation will likely be in terms of error convergence [45]. Figure 7F illustrates how VolRoverN outperforms both other methods in terms of triangle aspect ratio (ratio of the circumradius to twice the inradius).
Using VolRoverN output in simulations
3D to 1D skeletonization and surface segmentation
Cable model simulation requires 1D skeleton models of neurons. Cable models are typically created with neurite tracing software, but VolRoverN utilizes surface meshes to generate 1D models automatically. VolRoverN decomposes the mesh into cylindrical chunks using an algorithm that first finds a skeleton of the surface mesh (Fig 8A) using an iterative Laplace contraction algorithm [46]. The skeletonization algorithm induces a surface segmentation as a side effect. The segmentation is not perfect, so VolRoverN performs operations to repair and smooth the segmentation, resulting in regions such as those shown in Fig 8B. Each of these regions is approximated with a 1D segment with length and diameter (and thereby volume and surface area) properties. These segments are typically conceptualized as generalized cylinders. Our decomposition algorithm preserves volume, that is, the sum of all cylindrical region volumes equals the volume of the polyhedron. VolRoverN reports surface area and volume of regions of a reconstructed object. After surface segmentation, the user can discover geometric measurements of segments (e.g. Fig 8B) by clicking on the region.
Figure 8.
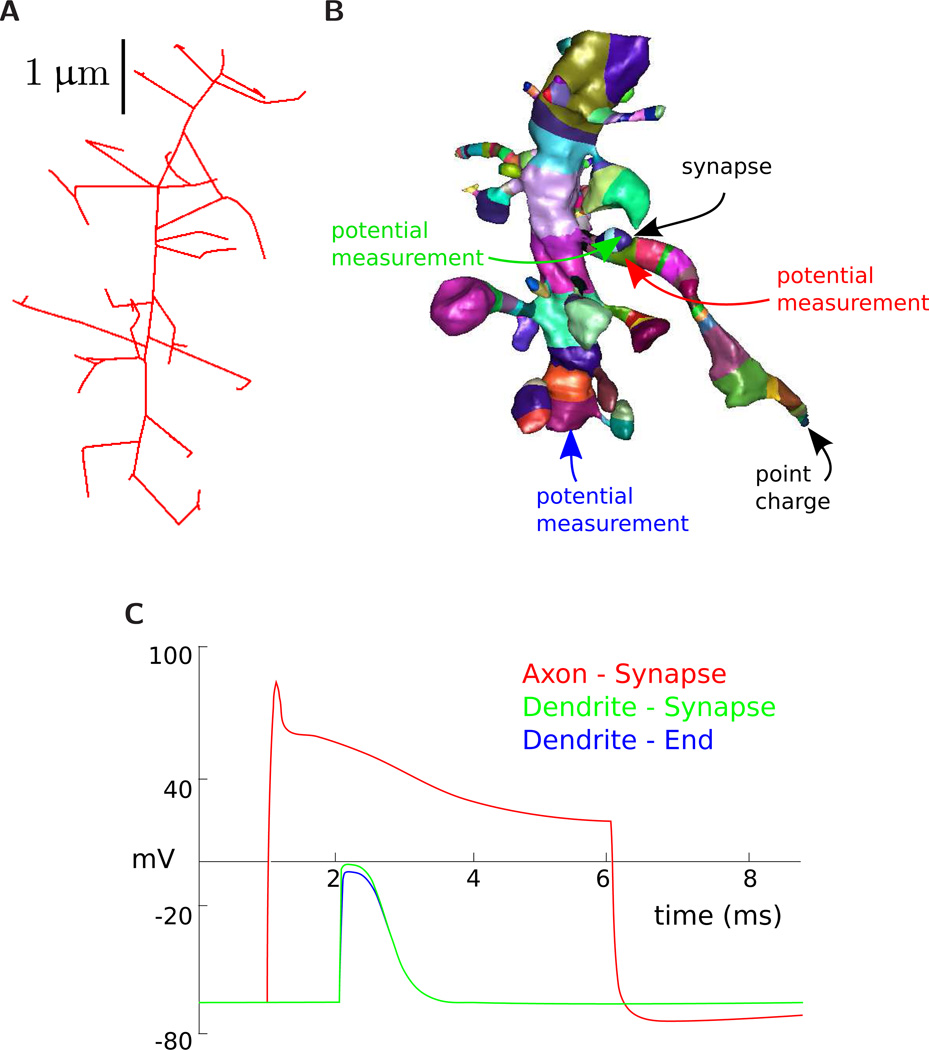
Multi-compartment model generation. Our surface segmentation first skeletonizes the mesh (A), which induces a segmentation (B). Each segment is in a different color in the figure. After correction, the segmentation can be used to produce surface area/volume statistics of different regions as well as labeling different regions for ion diffusion studies. This graphic shows a simple cable model simulation. The compartmentalized versions of the axon and dendrite are input to NEURON. A synapse with a threshold and delay is added between the dendrite and axon and a point charge is placed at the end of the axon. Three potential measurements are made over time. Arrow colors correspond the potential measurements reported in the NEURON simulation graph in figure (C).
NEURON
VolRoverN’s skeletonization tools are used to automatically reduce the surface representation to a multicompartmental cable model and simulate ion channel-driven dynamics of membrane voltage in NEURON [47]. NEURON is a simulation software that implements multi-compartment models of electrical signaling based on cable theory (Fig 8C). VolRoverN outputs to a NEURON HOC file, which contains length and diameter properties for each region as well as connection properties defining their topological connectedness. The output HOC file also contains a skeleton simulation function. As reduction to 1D includes a coarsening of resolution, we expect NEURON simulation results to be similar regardless of reconstruction algorithm used.
MCell
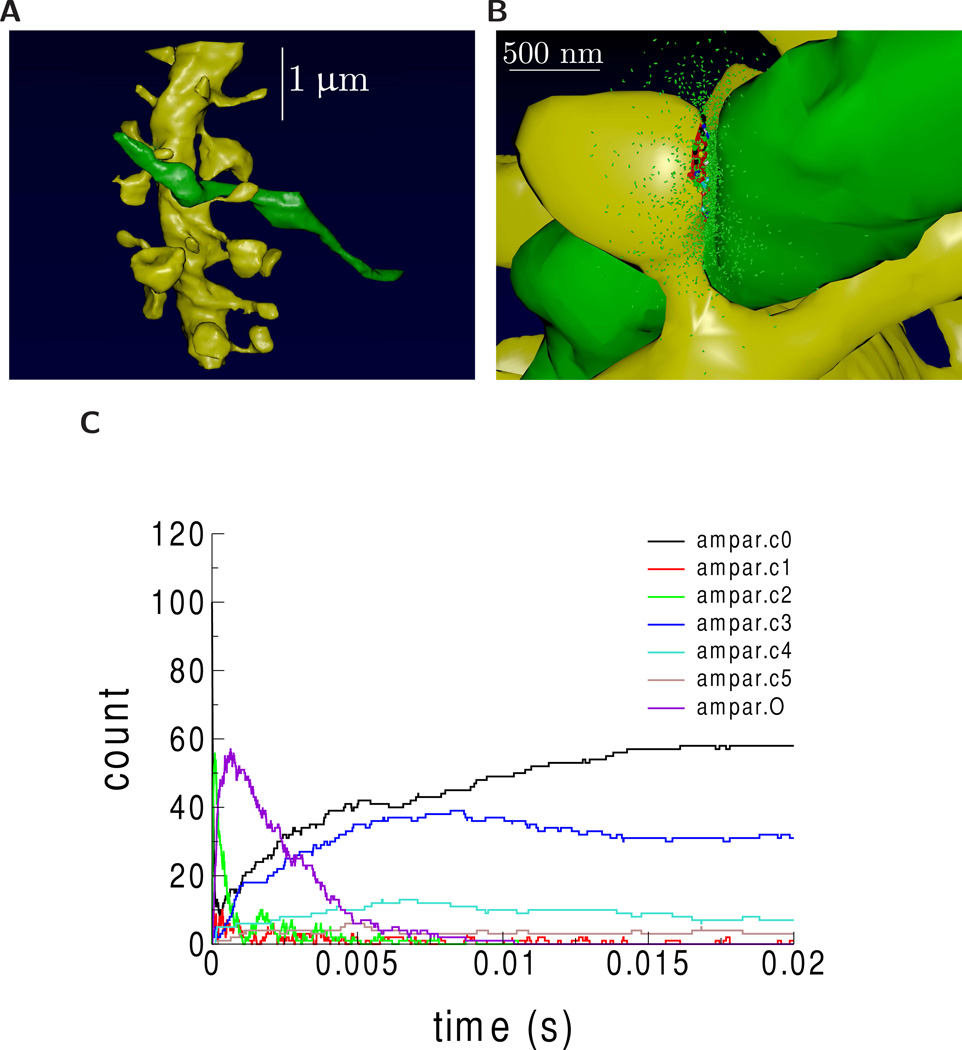
VolRoverN also enables MCell simulations. MCell [48, 49] is a software package that simulates multi-ion species reaction-diffusion usingMonte Carlo algorithms over geometrically complex domains. VolRoverN’s ForestTiler and mesh improvement tools were used to generate surface triangulations of an individual axon and dendrite in the VolRoverN sample (Fig 9A). The MCell export tool in VolRoverN writes a given surface mesh to an MCell MDL file. As noted, these meshes are required to be water-tight, manifold, and free of self-intersections which can be repaired, if necessary, using VolRoverN’s mesh repair utilities. A complete physiological simulation study was set up with the CellBlender software package (http://www.mcell.org) using the MCell MDL geometry files. The geometric analysis tools in CellBlender confirmed that the imported MDL meshes were of computational quality for use in simulations. CellBlender was then used to generate and run an MCell simulation of glutamatergic synaptic transmission at a synapse between the axon and dendrite (Fig 9B). Fig 9C shows the time course of activation of synaptic receptors by diffusing neurotransmitter molecules released at the synapse.
Figure 9.
MCell reaction/diffusion simulation of synaptic transmission from generated model. Generated meshes of axon (green) and dendrite (yellow) were imported into CellBlender to create an MCell simulation from the meshes. Images were rendered using CellBlender. (A) The axon and dendrite. (B) Visualization of synaptic transmission 100 microseconds after release of 2000 molecules of the neurotransmitter glutamate (small green ellipsoids). 10 NMDA receptors (NMDAR) and 100 AMPA receptors (AMPAR) were placed at the synaptic contact area between the axon and dendrite (small red patch of membrane on the dendrite). Color indicates state of activation of the receptors. At 100 microseconds, the glutamate has started to bind and activate some receptors and has started to spill out of the synaptic cleft space into the surrounding volume. (C) Time course of activation of AMPARs. AMPAR can be in 7 states: c0 (unbound state), c1 (one glutamate bound), c2 (two glutamate bound), c3 (one glutamate bound, desensitized state 1), c4 (two glutamate bound desensitized state 2), c5 (two glutamate bound, desensitized state 3), and O (two glutamate bound, ion channel open).
Direct comparison of MCell simulations using VolRoverN, Boissonnat, and marching cubes models has not been informative because reaction-diffusion simulations such as MCell require geometric consistency. Meshes with errors are rejected outright with an error message. As shown in Figs 7A and 7C Boissonnat and marching cubes models have large numbers of intersections between objects, causing attempted simulations to fail.
Volume rendering and isocontour visualization
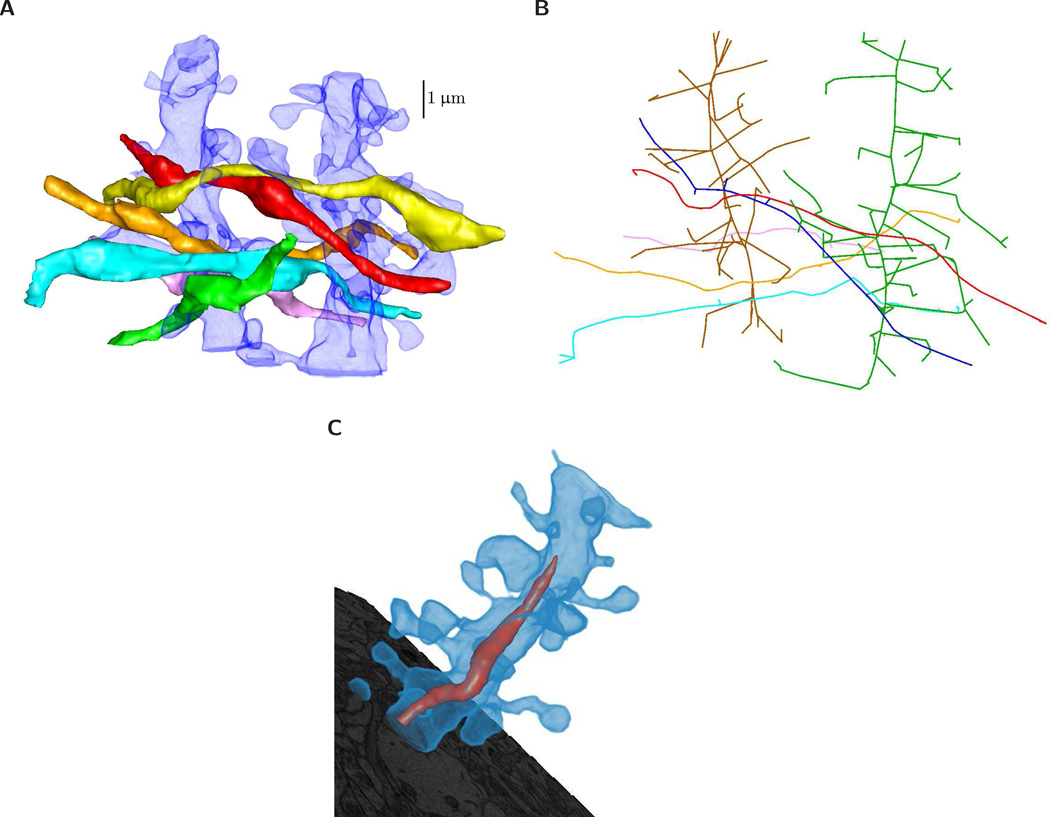
VolRoverN’s volume rendering capabilities and isocontour visualization tools enable interactive visual exploration of topology and geometry. Volume renderings include the capacity to illustrate numerous objects of varying color and transparencies (Fig 10A) which can also be illustrated as NEURON-ready skeletons (Fig 10B) and include intracellular organelles (Fig 10C).
Figure 10.
Volume rendering with geometry rendering. (A) Axons rendered with semi-transparent dendrites. (B) A view of a skeletonization of all axons and dendrites in the sample dataset. Skeletons can be saved in OFF and raw file formats. (C) A dendrite is rendered with semi-transparent volume rendering to reveal mitochondria. ForestTiler naturally supports nested components.
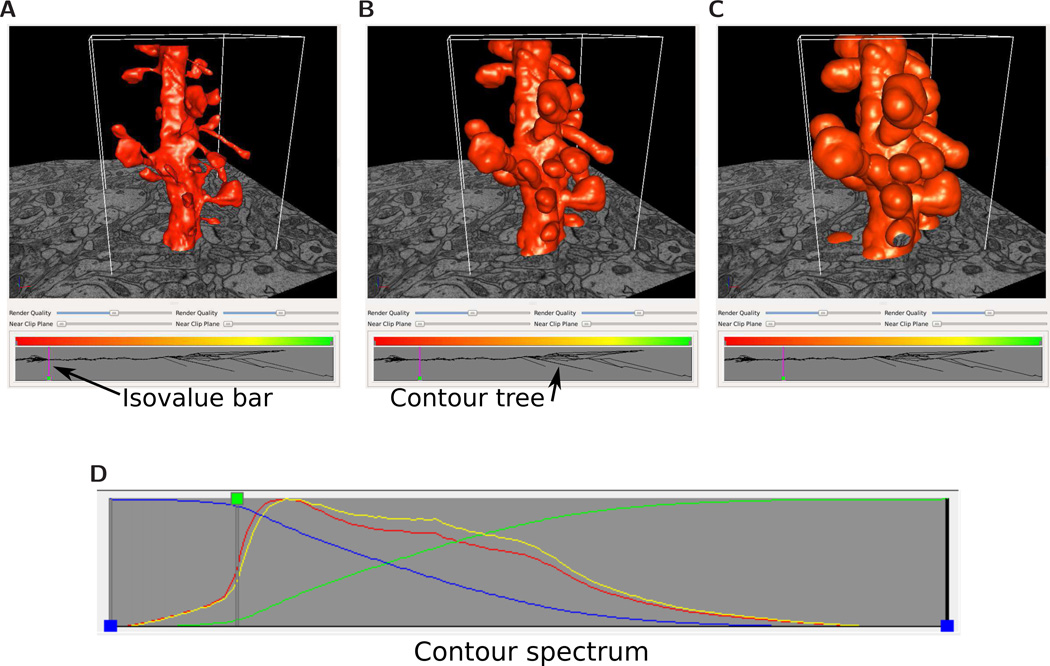
The signed distance function (SDF) in VolRoverN is a tool that produces a volume of scalar values (a volumetric scalar field) representing the distance from a surface. SDF, together with VolRoverN’s volume rendering capabilities (Fig 10) and isocontour visualization tools, enables interactive visual exploration of topology and geometry of isosurfaces (also called level sets) at various isovalues (level-set values) of the magnitude of the SDF . VolRoverN volume renders scalar fields (stored in HDF5 format) and geometries together and seamlessly. The transfer function tool supports both color and transparency ramps across the spectrum of level-set values in a volume and is used to color and achieve see-through translucency. The fast isocontour visualization [50] capability within VolRoverN enables interactive visual exploration of volumetric scalar fields through rendering of isosurfaces generated for distinct isovalues. Fast isocontour visualization when applied to SDF of input surfaces of complicated topology and geometry, provides for a quick visual surface exploration of the topological and geometric complexity (Fig 11). SDF fields of surfaces produced by ForestTiler can be examined for changes in their level-set topology and geometry. Fast isocontour visualization also provides a means to explore visually the results of function fields produced in simulations. A supporting topological visualization tool is the contour tree [51, 52] where branching reveals the splitting of level sets across the entire range of level-set values (Figs 11A–11C). The contour spectrum [53] plot gives additional insight, showing signature curves representing the variation of isosurface properties such as area, volume and gradient (normal) magnitude across isovalues (Fig 11D). The spectrum plot helps quickly locate isovalues where the isosurface properties become critical (e.g. maximum, minimum, etc.).
Figure 11.
Isosurfaces of a signed distance scalar field generated from a triangulated surface model of a dendrite, and at different isovalues. Isosurfaces are computed from surface geometries and are useful in characterizing object shape. The contour tree at bottom shows the topological branching structure of the isosurface. The vertical line in the contour tree shows the isovalue of the surface relative to the tree. (A) is close to the true surface, as at that isovalue the contour tree is a confluence of branches into one. (B) and (C) are isosurfaces at progressively larger absolute distance values. By convention, negative distance values indicate points outside the object, while positive values are for points inside. (D) The contour spectrum tool’s signature properties plot window. Four attribute curves are shown: surface area (red); min volume (green); max volume (blue); gradient weighted surface area (yellow). The green isovalue node is at an isovalue for which surface area and gradient weighted surface area curves are close to their respective maximum values, which usually occurs near the zero isovalue. The×axis represents distance from the original surface. Each curve is normalized with respect to the y axis.
Scalability and performance
The algorithms used in VolRoverN are scalable. Our reconstruction method linearly interpolates between sections, so only two sections need be stored in memory at one time, thus the memory requirements remain static with increasing stack size. Memory also remains static with increasing image resolution since the reconstruction algorithm uses exclusively geometric contours and not the original images. However, memory requirements do increase with larger numbers of contours per image (such as would be the case with greater image footprints), but memory goes up proportionally to the number of contours. The fact that the VolRoverN reconstruction algorithm operates only on pairs of sections makes it an excellent candidate for parallelization, a feature for future development.
ForestTiler and associated mesh improvement tools in VolRoverN are efficient. We tested reconstruction time on the sample dataset, which consists of portions of 8 axons and 2 dendrites with a combined 129.32 µm2 surface area, 8.44 µm3 volume and 204,906 triangles. Reconstruction took 6 minutes and 40 seconds on a Linux Kubuntu workstation with Intel Xeon 3.20 GHz quad core CPU and 4 GB of memory. Decimation, triangle improvement and mesh fixing tools took an additional 56 seconds.
Discussion
VolRoverN plays a complementary role in the set of neuronal morphology software. It provides tools to enhance geometric understanding of 2D tracings and offers an alternative method of skeletonizing neurites. VolRoverN also fills a critical gap, in that it produces meshes that are manifold, geometrically accurate, water-tight, and free of intersections. Before now, producing such reconstructions required a large amount of manual work, but VolRoverN’s powerful tools greatly reduce the amount of time and domain knowledge required to prepare reconstructions for geometric analysis. Reconstructions serve as substrate for dynamical simulation of cellular activity.
VolRoverN accepts geometric contours as input. Thus, success in quality reconstruction is at least partly dependent on the quality of the contours produced using other software tools. This is largely mitigated by visual proofing tools in tracing software [17–19]. However, if surface reconstruction from VolRoverN reveals errors in the contour tracings then the user can revert back to the original tracing software for contour repair at well-identified locations.
Representations of the cell surface enable simulations using 3D boundary element methods (BEM) such as combined Monte Carlo simulation of particle diffusion and kinetic state-based modeling of protein dynamics at the microsecond time scale by MCell [28,37]. 3D finite element method (FEM) simulations [54] of electro-diffusion with multi-species continuum concentrations are enabled by decomposing a reconstruction into a collection of small volumes. Also, by approximating neuronal geometry as a collection of cylindrical compartments each aligned to segments of the geometry [55], and modeling ionic conductance in each compartment with coupled differential equations, one arrives at the traditional cable simulation of electrical signals in the brain at the millisecond scale, as supported by simulation software such as NEURON [47]. Deriving these geometric representations of brain structure from a single source (surface meshes) facilitates future multi-scale simulations via coupled MCell, FEM and NEURON models.
Third-party libraries
VolRoverN uses several third-party software libraries. The reconstruction tools use CGAL [56] and QSlim [33]. Rendering is done using OpenGL and the interface uses the cross-platform GUI package QT.
Data sources
Data used in the figures is from hippocampal area CA1 of a postnatal day 77, perfusion-fixed, male rat [57,58]. All images are ssEM with 2 nm in-plane and 45 nm out-of-plane resolution. Image size is 4K × 4K pixels. The dataset is available as a sample with download of VolRoverN. All rendered figures in this paper were produced using VolRoverN except plots (prepared by gnuplot) and the MCell simulation which used CellBlender (Figs 9A and 9B).
Information sharing
VolRoverN binaries, a tutorial, and a sample dataset are freely downloadable at http://cvcweb.ices.utexas.edu. Source code is freely available at the same link for non-profit institutions. We anticipate the future addition of a public data repository on the same page for images, traces, 3D meshes, and simulation files.
Acknowledgments
We thank the anonymous reviewers for their many constructive comments that greatly improved the manuscript. Jose Rivera, Josef Spacek, Deborah Watson, Michael Chirillo and John Mendenhall assisted in various phases of this work. This work of CB, JE, ED was funded in part by NIH contracts R01-EB00487, R01-GM074258, and a grant from the UT-Portugal colab project. Work by TJS was supported by NSF grant EMI9822, that of DJ by NIH grants, MH048432 and MH094838 and of KH by NIH grants NS074644, NS21184, and the Texas Emerging Technologies Fund.
References
- 1.Sorra KE, Harris KM. Overview on the structure, composition, function, development, and plasticity of hippocampal dendritic spines. Hippocampus. 2000;10:501–511. doi: 10.1002/1098-1063(2000)10:5<501::AID-HIPO1>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 2.Andersen P, Morris R, Amaral D, Bliss T, O’Keefe J. The hippocampus book. USA: Oxford University Press; 2006. [Google Scholar]
- 3.Fiala J, Spacek J, Harris K. Dendritic spine pathology: cause or consequence of neurological disorders? Brain Research Reviews. 2002;39:29–54. doi: 10.1016/s0165-0173(02)00158-3. [DOI] [PubMed] [Google Scholar]
- 4.Ramćrez OA, Couve A. The endoplasmic reticulum and protein trafficking in dendrites and axons. Trends in cell biology. 2011;21:219–227. doi: 10.1016/j.tcb.2010.12.003. [DOI] [PubMed] [Google Scholar]
- 5.Liu M, Duggan J, Salt TE, Cordeiro MF. Dendritic changes in visual pathways in glaucoma and other neurodegenerative conditions. Experimental eye research. 2011;92:244–250. doi: 10.1016/j.exer.2011.01.014. [DOI] [PubMed] [Google Scholar]
- 6.De Rubeis S, Fernández E, Buzzi A, Di Marino D, Bagni C. Synaptic Plasticity. Springer; 2012. Molecular and cellular aspects of mental retardation in the fragile×syndrome: from gene mutation/s to spine dysmorphogenesis; pp. 517–551. [DOI] [PubMed] [Google Scholar]
- 7.van Spronsen M, Hoogenraad CC. Synapse pathology in psychiatric and neurologic disease. Current neurology and neuroscience reports. 2010;10:207–214. doi: 10.1007/s11910-010-0104-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kuwajima M, Spacek J, Harris KM. Beyond counts and shapes: Studying pathology of dendritic spines in the context of the surrounding neuropil through serial section electron microscopy. Neuroscience. 2012 doi: 10.1016/j.neuroscience.2012.04.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Denk W, Horstmann H. Serial block-face scanning electron microscopy to reconstruct three- dimensional tissue nanostructure. PLoS Biol. 2004;2:e329. doi: 10.1371/journal.pbio.0020329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hayworth K, Kasthuri N, Schalek R, Lichtman J. Automating the collection of ultrathin serial sections for large volume tem reconstructions. Microsc Microanal. 2006;12:86–87. [Google Scholar]
- 11.Knott G, Marchman H, Wall D, Lich B. Serial section scanning electron microscopy of adult brain tissue using focused ion beam milling. The Journal of Neuroscience. 2008;28:2959–2964. doi: 10.1523/JNEUROSCI.3189-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bock DD, Lee WCA, Kerlin AM, Andermann ML, Hood G, et al. Network anatomy and in vivo physiology of visual cortical neurons. Nature. 2011;471:177–182. doi: 10.1038/nature09802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kuwajima M, Mendenhall JM, Lindsey LF, Harris KM. Automated transmission-mode scan- ning electron microscopy (tsem) for large volume analysis at nanoscale resolution. PloS one. 2013;8:e59573. doi: 10.1371/journal.pone.0059573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kleinfeld D, Bharioke A, Blinder P, Bock D, Briggman KL, et al. Large-scale automated histology in the pursuit of connectomes. The Journal of Neuroscience. 2011;31:16125–16138. doi: 10.1523/JNEUROSCI.4077-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Briggman KL, Bock DD. Volume electron microscopy for neuronal circuit reconstruction. Current opinion in neurobiology. 2012;22:154–161. doi: 10.1016/j.conb.2011.10.022. [DOI] [PubMed] [Google Scholar]
- 16.Helmstaedter M, Mitra PP. Computational methods and challenges for large-scale circuit mapping. Current Opinion in Neurobiology. 2012;22:162–169. doi: 10.1016/j.conb.2011.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fiala J. Reconstruct: a free editor for serial section microscopy. Journal of Microscopy. 2005;218:52–61. doi: 10.1111/j.1365-2818.2005.01466.x. [DOI] [PubMed] [Google Scholar]
- 18.Lu J, Fiala J, Lichtman J. Semi-automated reconstruction of neural processes from large numbers of fluorescence images. PLoS One. 2009;4:5655. doi: 10.1371/journal.pone.0005655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cardona A, Saalfeld S, Schindelin J, Arganda-Carreras I, Preibisch S, et al. TrakEM2 software for neural circuit reconstruction. PLoS One. 2012;7:e38011. doi: 10.1371/journal.pone.0038011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sommer C, Straehle C, Koethe U, Hamprecht FA. ilastik: Interactive learning and segmen- tation toolkit. 8th IEEE International Symposium on Biomedical Imaging (ISBI 2011); 2011. pp. 230–233. [Google Scholar]
- 21.Jurrus E, Watanabe S, Giuly RJ, Paiva AR, Ellisman MH, et al. Semi-automated neuron boundary detection and nonbranching process segmentation in electron microscopy images. Neuroinformatics. 2012:1–25. doi: 10.1007/s12021-012-9149-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jeong W, Beyer J, Hadwiger M, Blue R, Law C, et al. Ssecrett and neurotrace: interactive visualization and analysis tools for large-scale neuroscience data sets. IEEE Computer Graphics and Applications. 2010;30:58. doi: 10.1109/MCG.2010.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Helmstaedter M, Briggman K, Denk W. High-accuracy neurite reconstruction for high- throughput neuroanatomy. Nature Neuroscience. 2011;14:1081–1088. doi: 10.1038/nn.2868. [DOI] [PubMed] [Google Scholar]
- 24.Briggman KL, Helmstaedter M, Denk W. Wiring specificity in the direction-selectivity circuit of the retina. Nature. 2011;471:183–188. doi: 10.1038/nature09818. [DOI] [PubMed] [Google Scholar]
- 25.Harris KM, Perry E, Bourne J, Feinberg M, Ostroff L, et al. Uniform serial sectioning for transmission electron microscopy. The Journal of neuroscience. 2006;26:12101–12103. doi: 10.1523/JNEUROSCI.3994-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang Q, Bettadapura R, Bajaj C. Macromolecular structure modeling from 3D EM using VolRover 2.0. Biopolymers. 2012;97:709–731. doi: 10.1002/bip.22052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Edwards J, Bajaj C. Topologically correct reconstruction of tortuous contour forests. Computer-Aided Design. 2011;43:1296–1306. doi: 10.1016/j.cad.2011.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kinney JP, Spacek J, Bartol TM, Bajaj CL, Harris KM, et al. Extracellular sheets and tunnels modulate glutamate diffusion in hippocampal neuropil. Journal of Comparative Neurology. 2013;521:448–464. doi: 10.1002/cne.23181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bajaj C, Coyle E, Lin K. Arbitrary topology shape reconstruction from planar cross sections. Graphical Models and Image Processing. 1996;58:524–543. [Google Scholar]
- 30.Chklovskii DB, Vitaladevuni S, Scheffer LK. Semi-automated reconstruction of neural circuits using electron microscopy. Current opinion in neurobiology. 2010;20:667–675. doi: 10.1016/j.conb.2010.08.002. [DOI] [PubMed] [Google Scholar]
- 31.Saalfeld S, Fetter R, Cardona A, Tomancak P. Elastic volume reconstruction from series of ultra-thin microscopy sections. Nature Methods. 2012;9:717–720. doi: 10.1038/nmeth.2072. [DOI] [PubMed] [Google Scholar]
- 32.Turk G, O’Brien J. SIG- GRAPH’99. 1999. Shape transformation using variational implicit functions; pp. 335–342. [Google Scholar]
- 33.Qslim Garland M. http://mgarland.org/software/qslim.html.
- 34.Zhang Y, Bajaj C, Sohn B. 3D finite element meshing from imaging data. The Special Issue of Computer Methods in Applied Mechanics and Engineering (CMAME) on Unstructured Mesh Generation. 2005;194:5083–5106. doi: 10.1016/j.cma.2004.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhang Y, Bajaj C, Xu G. Surface smoothing and quality improvement of quadrilat- eral/hexahedral meshes with geometric flow. Communications in Numerical Methods in Engineering. 2009;25:1–18. doi: 10.1002/cnm.1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.O’Rourke J. Computational Geometry in C. Cambridge University Press. 1994. [Google Scholar]
- 37.Kinney J. Ph.D. thesis. San Diego: University of California; 2009. Investigation of neurotransmitter diffusion in three-dimensional reconstructions of hippocampal neuropil. [Google Scholar]
- 38.Bajaj C, Coyle E, Lin K. Computer Methods in Applied Mechanics and Engineering. 1999. Tetrahedral meshes from planar cross sections; pp. 31–52. [Google Scholar]
- 39.Zhang Y, Bajaj C. Adaptive and quality quadrilateral/hexahedral meshing from volumetric data. Computer methods in applied mechanics and engineering. 2006;195:942–960. doi: 10.1016/j.cma.2005.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang Y, Hughes TJ, Bajaj CL. An automatic 3d mesh generation method for domains with multiple materials. Computer Methods in Applied Mechanics and Engineering (CMAME) 2010;199:405–415. doi: 10.1016/j.cma.2009.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.CVC. LBIE: Level set boundary interior and exterior mesher. http://cvcweb.ices.utexas.edu/cvcwp/?page_id=103.
- 42.Hepburn I, Chen W, Wils S, De Schutter E. STEPS: efficient simulation of stochastic reaction- diffusion models in realistic morphologies. BMC Syst Biol. 2012;6 doi: 10.1186/1752-0509-6-36. 1752-0509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Schmid B, Schindelin J, Cardona A, Longair M, Heisenberg M. A high-level 3d visualization api for java and imagej. BMC bioinformatics. 2010;11:274. doi: 10.1186/1471-2105-11-274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Boissonnat J, Geiger B. Three-dimensional reconstruction of complex shapes based on the Delaunay triangulation. Proceedings of SPIE. 1992;ume 964:964–975. [Google Scholar]
- 45.Shewchuk J. What is a good linear finite element? interpolation, conditioning, anisotropy, and quality measures (preprint) University of California at Berkeley; 2002. [Google Scholar]
- 46.Au OKC, Tai CL, Chu HK, Cohen-Or D, Lee TY. Skeleton extraction by mesh contraction. ACM Transactions on Graphics. 2008;27:44, 1–10. [Google Scholar]
- 47.Carnevale N, Hines M. The NEURON Book. Cambridge, UK: Cambridge University; 2006. [Google Scholar]
- 48.Stiles JR, Bartol TM, et al. Computational neuroscience: Realistic modeling for experimentalists. Boca Raton, FL: CRC Press; 2001. Monte carlo methods for simulating realistic synaptic microphys- iology using mcell; pp. 87–128. [Google Scholar]
- 49.Kerr R, Bartol T, Kaminsky B, Dittrich M, Chang J, et al. Fast Monte Carlo simulation methods for biological reaction-diffusion systems in solution and on surfaces. SIAM Journal on Scientific Computing. 2008;30:3126. doi: 10.1137/070692017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bajaj C, Pascucci V, Schikore D. Proceedings of the 1996 symposium on Volume visualization. IEEE Press; 1996. Fast isocontouring for improved interactivity; pp. 39–46. [Google Scholar]
- 51.Carr H, Snoeyink J, Axen U. Proceedings of the eleventh annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics; 2000. Computing contour trees in all dimensions; pp. 918–926. [Google Scholar]
- 52.Zhang X, Bajaj CL, Kwon B, Dolinsky TJ, Nielsen JE, et al. Application of new multiresolution methods for the comparison of biomolecular electrostatic properties in the absence of global structural similarity. Multiscale Modeling & Simulation. 2006;5:1196–1213. doi: 10.1137/050647670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bajaj C, Pascucci V, Schikore D. The contour spectrum. Proceedings of the 8th conference on Visualization’97; IEEE Computer Society Press; 1997. pp. 167–173. [Google Scholar]
- 54.Bajaj C, Bettadapura R, Lei N, Mollere A, Peng C, et al. Constructing A-spline weight func- tions for stable WEB-spline finite element methods. Proceedings of the 14th ACM Symposium on Solid and Physical Modeling; ACM; 2010. pp. 153–158. [Google Scholar]
- 55.Lindsay K, Rosenberg J, Tucker G. From maxwell’s equations to the cable equation and beyond. Progress in Biophysics and Molecular Biology. 2004;85:71–116. doi: 10.1016/j.pbiomolbio.2003.08.001. [DOI] [PubMed] [Google Scholar]
- 56.Cgal. Computational Geometry Algorithms Library. http://www.cgal.org.
- 57.Harris K, Stevens J. Dendritic spines of CA 1 pyramidal cells in the rat hippocampus: serial electron microscopy with reference to their biophysical characteristics. The Journal of Neuroscience. 1989;9:2982. doi: 10.1523/JNEUROSCI.09-08-02982.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mishchenko Y, Hu T, Spacek J, Mendenhall J, Harris K, et al. Ultrastructural analysis of hippocampal neuropil from the connectomics perspective. Neuron. 2010;67:1009–1020. doi: 10.1016/j.neuron.2010.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]