Initial steps of inactivation at the K⁺ channel selectivity filter

Significance

C-type inactivation represents a key process that governs cellular K⁺ channel activity. Although C-type inactivation seems to be inextricably linked with dissociation of K⁺ from the channel’s pore, the structural connection between K⁺ dissociation and initiation of C-type inactivation has been unclear. Here, we combine electrophysiology and molecular simulation of MthK, a prototypical K⁺ channel of known structure, to determine relations between K⁺ dissociation and entry into the inactivated state. We find that Ca²⁺ can bind to a site in the pore favored by outward movement of K⁺. K⁺ subsequently dissociates, favoring a conformational change to the inactivated state. This study, thus, establishes a direct link between K⁺ dissociation and initiation of C-type inactivation.

Abstract

K⁺ efflux through K⁺ channels can be controlled by C-type inactivation, which is thought to arise from a conformational change near the channel’s selectivity filter. Inactivation is modulated by ion binding near the selectivity filter; however, the molecular forces that initiate inactivation remain unclear. We probe these driving forces by electrophysiology and molecular simulation of MthK, a prototypical K⁺ channel. Either Mg²⁺ or Ca²⁺ can reduce K⁺ efflux through MthK channels. However, Ca²⁺, but not Mg²⁺, can enhance entry to the inactivated state. Molecular simulations illustrate that, in the MthK pore, Ca²⁺ ions can partially dehydrate, enabling selective accessibility of Ca²⁺ to a site at the entry to the selectivity filter. Ca²⁺ binding at the site interacts with K⁺ ions in the selectivity filter, facilitating a conformational change within the filter and subsequent inactivation. These results support an ionic mechanism that precedes changes in channel conformation to initiate inactivation.

Potassium (K⁺) channels are activated and opened by a variety of stimuli, including ligand binding and transmembrane voltage, to enable K⁺ efflux and thus, modulate physiological processes related to electrical excitability, such as regulation of action potential firing, smooth muscle contraction, and hormone secretion (1). In addition, many K⁺ channels are further controlled by a gating phenomenon known as C-type inactivation, in which K⁺ conduction is stopped, despite the continued presence of an activating stimulus (2). The mechanisms underlying C-type inactivation in voltage-gated K⁺ channels (Kv channels) are linked to both intracellular and extracellular permeant ion concentrations, and several lines of evidence have suggested that C-type inactivation is associated with a conformational change near the external mouth of the K⁺ channel pore (i.e., at the canonical K⁺ channel selectivity filter) (3–11).

In Shaker Kv channels, C-type inactivation is known to be enhanced and recovery from inactivation is slowed by impermeant cations accessing the cytoplasmic side of the channel (5, 6, 10). Enhancement of inactivation by these cations suggests a working hypothesis, in which the impermeant ion prevents refilling of the selectivity filter with K⁺ (6). Thus, K⁺ presumably dissociates from the filter to the external solution, and this vacancy leaves the filter susceptible to a conformational change that underlies the nonconducting, inactivated state. However, the physical basis for the relation between ion movements and C-type inactivation as well as the structural underpinnings of the mechanism remain unclear.

Here, we use divalent metal cations (Mg²⁺, Ca²⁺, and Sr²⁺) as probes of inactivation mechanisms in MthK, a model K⁺ channel of known structure (Fig. 1) (12–14). Specifically, we analyze conduction and gating of single MthK channels by electrophysiology combined with analysis of ion and protein movements by molecular simulation. Our electrophysiological experiments indicate that, although each of these divalent metal ions can reduce the size of single channel currents, only Ca²⁺ and Sr²⁺ can enhance inactivation, whereas Mg²⁺ does not. Using molecular simulation and potential of mean force (PMF) calculations, we find that Ca²⁺, but not Mg²⁺, can shed its hydration shell waters to access a site, termed S5, at the entry to the channel’s selectivity filter (Fig. 1C) after displacement of K⁺ ions to the extracellular side of the channel. Subsequent dissociation of a K⁺ ion from the filter, in turn, favors a conformational change within the selectivity filter, contributing to enhanced inactivation. These results support a working hypothesis that directly relates dissociation of K⁺ with a structural change in the selectivity filter to initiate inactivation of K⁺ channels.

Fig. 1.

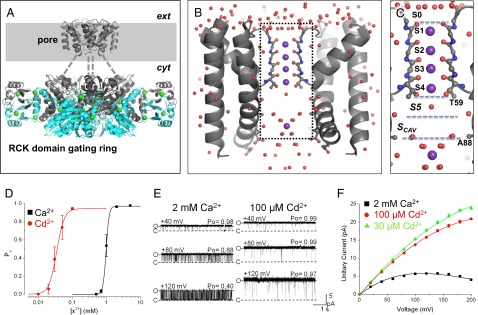
Structure and activation properties of MthK. (A) Presumed biological structure of MthK shown as a Cα-trace [Protein Data Bank (PDB) ID code 3RBZ]. The channel consists of a transmembrane pore domain tethered to a ring of RCK domains, which mediate channel activation by cytoplasmic Ca²⁺ (green spheres). The gray-shaded region represents the presumed plasma membrane; dashed lines represent the linker region between the pore and RCK gating ring that is unresolved in the crystal structure. (B) High-resolution structure of the MthK pore domain, with the selectivity filter shown in ball and stick representation (PDB ID code 3LDC). Subunits in the front and back have been removed for clear visualization of the conduction pathway (inside dashed rectangle), with K⁺ ions shown as purple spheres and ordered water molecules shown as red spheres. (C) –Magnified view of the MthK conduction pathway (boxed region in B) with potential ion binding sites (S0–S_cav) indicated. (D) Po vs. [Ca²⁺] (black symbols) and [Cd²⁺] (red symbols) from currents recorded at −100 mV. MthK activation requires ∼20-fold lower [Cd²⁺] compared with [Ca²⁺]. Curves represent fits with a Hill equation with the following parameters: EC₅₀ = 1.0 mM and n_H = 9.5 for Ca²⁺; EC₅₀ = 49 μM and n_H = 8.4 for Cd²⁺. (E) Representative single channel currents from reconstituted MthK at depolarized voltages with 200 mM KCl at both sides of the membrane and Ca²⁺ or Cd²⁺ at the cytoplasmic side of the channel as indicated. Cd²⁺ can fully activate MthK at concentrations that produce much less fast blockade than Ca²⁺. O and C indicate open and closed current levels, respectively. (F) Unitary current vs. voltage for MthK channels activated with 30 and 100 μM Cd²⁺ (green and red, respectively) and 2 mM Ca²⁺ (black). Smooth curves are drawn for display only; 100 μM Cd²⁺ results in nominal levels of fast blockade, yielding large outward current.

Results

Rapid Blockade of MthK Channels by Cytoplasmic Divalent Cations.

MthK channels can be activated through binding of Ca²⁺ to the channel’s cytoplasmic domain (Fig. 1). However, Ca²⁺ can also apparently enter the pore of the channel to produce a rapid blockade of outward K⁺ current (12, 14–18). To avoid potential confounds arising from blocking effects of Ca²⁺, we used Cd²⁺ as an alternative agonist to activate MthK channels in our experiments (19–21). Fig. 1 D and E illustrates that, under the conditions of our experiments, 100 μM Cd²⁺ was sufficient to activate MthK channels to a mean Po > 0.95 (measured at −100 mV), which is equivalent to the mean Po with 2 mM Ca²⁺. In contrast, 100 μM Cd²⁺ yielded much less reduction in outward current than 2 mM Ca²⁺ (Fig. 1 E and F). For example, outward K⁺ current measured at +100 mV with 100 μM Cd²⁺ was 13.7 ± 0.2 pA compared with 5.7 ± 0.1 pA with 2 mM Ca²⁺.

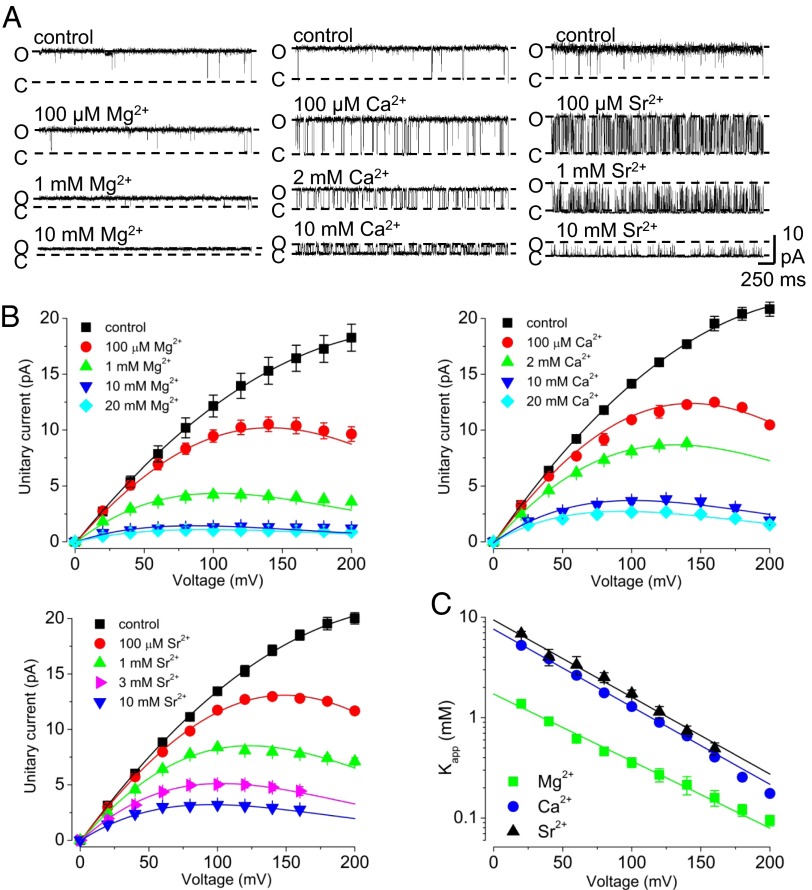
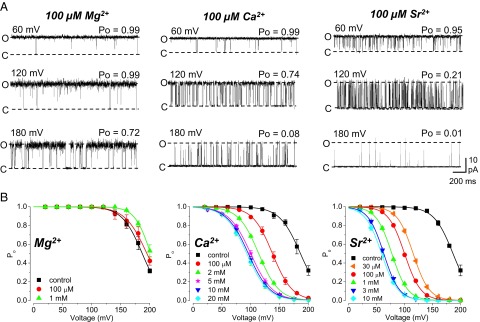
Using 100 μM Cd²⁺ to fully activate MthK channels, we observe that Mg²⁺, Ca²⁺, and Sr²⁺, applied to the cytoplasmic side of the channel, reduced outward current in a voltage-dependent manner (Fig. 2). We quantified current blockade by Mg²⁺, Ca²⁺, and Sr²⁺ using the Woodhull equilibrium block model, which yields estimates of zδ (the effective fraction of the transmembrane electric field traversed by the charged blocker) and K_app(0) (the apparent 0 mV dissociation constant of the blocking ion) (22). Interestingly, the estimated zδ-values were similar for each of the blocking ions (zδ = 0.43 ± 0.03, 0.45 ± 0.03, and 0.45 ± 0.02 e₀ for Mg²⁺, Ca²⁺, and Sr²⁺, respectively) (Fig. 2C). If we assume that each of these divalent cations elicits fast blockade of the outward K⁺ current by acting at one site, then these similar zδ-values are consistent with Mg²⁺, Ca²⁺, and Sr²⁺ blocking at the same site within the MthK pore. In contrast to their similar estimated zδ-values, the K_app(0) for each ion followed the sequence Mg²⁺ < Ca²⁺ < Sr²⁺ [K_app(0) = 1.9 ± 0.1, 7.6 ± 0.4, and 9.4 ± 0.7 mM for Mg²⁺, Ca²⁺, and Sr²⁺, respectively] (Fig. 2C). Thus, if these ions block at a single common site, then Mg²⁺ seems to bind to the site with a greater affinity than the larger divalent ions Ca²⁺ and Sr²⁺.

Fig. 2.

Rapid blockade of MthK channels by cytoplasmic divalent cations. (A) Representative currents at 120 mV with the indicated concentrations of divalent cation. In these experiments and subsequent experiments, channels are activated using 100 μM Cd²⁺, and control indicates recordings and results obtained without the addition of Mg²⁺, Ca²⁺, or Sr²⁺. (B) Unitary current amplitude vs. voltage over a range of [Mg²⁺], [Ca²⁺], and [Sr²⁺] as indicated. Smooth curves are drawn for display only. (C) K_app(V) vs. voltage for experiments with Mg²⁺, Ca²⁺, and Sr²⁺. Fractional current (relative to amplitude without added divalent) was measured over a range of depolarized voltages and fitted with Hill equations to estimate K_app(V). K_app(V) vs. voltage relations values were fit with an equilibrium block model, K_app(V) = K_app(0)exp(−zδVF/RT), to estimate K_app(0) and zδ. The similar zδ-values of ∼0.45 e₀ for [Mg²⁺]_i, [Ca²⁺]_i, and [Sr²⁺]_i suggest that the fast blocking site for these ions is at the same location in the conduction pathway, whereas the estimated K_app(0) values are consistent with a lower apparent affinity of Sr²⁺ and Ca²⁺ compared with Mg²⁺.

Ca²⁺ and Sr²⁺, but Not Mg²⁺, Enhance Gating into an Inactivated State.

In previous experiments, MthK channels activated by Ca²⁺ were found to spend increased time in a nonconducting or inactivated state with increasing depolarization (18, 23). However, with Cd²⁺ activation, entry into the inactivated state occurs at more depolarizing voltages compared with gating in the presence of Ca²⁺ (Fig. 1E).

Because Ca²⁺ both facilitates inactivation and leads to fast blockade of MthK, we wondered whether inactivation and fast blockade occur through Ca²⁺ binding at a single inactivation/blocking site. If inactivation and fast blockade occur through a single site, then based on the observation that Mg²⁺ is a more potent fast blocker than Ca²⁺ (Fig. 2), one might predict that Mg²⁺ would facilitate inactivation even more potently than Ca²⁺. To test this possibility, we measured Po in the presence of Mg²⁺ over a range of voltages (Fig. 3A, Left). In contrast to the effects of Ca²⁺, we observe that inactivation was not enhanced with increasing [Mg²⁺] over the range of 100 μM to 1 mM (Fig. 3B, Left). However, inactivation was enhanced with increasing [Sr²⁺] (even more potently than Ca²⁺) (Fig. 3B, Center and Right). Because increasing [Mg²⁺] does not facilitate entry into the inactivated state as observed with Ca²⁺ and Sr²⁺, these results indicate clearly that fast blockade on its own is not correlated with inactivation and that inactivation does not occur by divalent cations binding to the fast blocking site. The results further suggest that inactivation can occur at strongly depolarized voltages without the addition of either Ca²⁺ or Sr²⁺ (Fig. 3B, Left).

Fig. 3.

Effects of divalent ions on inactivation in MthK. (A) Representative currents with 100 μM Mg²⁺, Ca²⁺, and Sr²⁺ over a range of voltages. Ca²⁺ and Sr²⁺ facilitate entry to an inactivated state at depolarized voltages. (B) Po vs. voltage in the presence of Mg²⁺, Ca²⁺, or Sr²⁺ at the indicated concentrations; curves represent fits with a Boltzmann equation. Increasing [Mg²⁺] has nominal effects on Po compared with increasing [Ca²⁺] or [Sr²⁺], consistent with the idea that Ca²⁺ and Sr²⁺ enhance entry to an inactivated state by acting at a site that is inaccessible to Mg²⁺.

The observation that inactivation occurs in strongly depolarized MthK channels without added Ca²⁺ or Sr²⁺ (Fig. 3) suggests that inactivation does not correspond to discrete events of Ca²⁺ blockade (18, 23). However, it could also be argued that low levels of Ca²⁺ present in these solutions might lead to discrete events of Ca²⁺ blockade, which become more frequent at depolarized voltages. We tested this possibility in two ways. First, we performed experiments using recording solutions, in which contaminating divalents were first sequestered using Chelex-100 resin (details are provided in Methods). Briefly, the Chelex-100 resin is expected to reduce the low levels of contaminating Ca²⁺ in our 200 mM KCl-based solutions to <0.5 μM (24); after removal of the Chelex-100 resin by filtration, 100 μM CdCl₂ is added to the solution. Second, we performed experiments in bath solutions using KF substituted for KCl. Because CaF₂ forms a tight complex that is very poorly soluble in water (K_sp for CaF₂ = 3.5 × 10⁻¹¹), F⁻ greatly lowers free [Ca²⁺] in these solutions, such that the effective free [Ca²⁺] can be considered <20 nM; Cd²⁺, however, does not form an insoluble complex with F⁻ (K_sp for CdF₂ = 6.4 × 10⁻³) and is free to bind and activate the channel (25, 26).

We observed that channels entered the inactivated state in either the Chelex-100–treated 200 mM KCl solutions or KF-based solutions (`1A). In addition, we observed that, with nominal Ca²⁺, KF-based solutions lowering [K⁺] at the external side of the channel from 200 to 5 mM resulted in an ∼70 mV leftward shift in the V_1/2 for steady-state inactivation (V_1/2 = 170 ± 2.1 mV with 200 mM 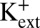; 96 ± 3.5 mV with 5 mM 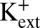), which was observed previously in MthK channels using KCl-based solutions (18). Together, these results suggest that entry into the inactivated state arises from a gating mechanism that does not strictly require Ca²⁺ and responds to lowering external [K⁺] similar to slow inactivation observed in Shaker Kv channels (3, 9).

To rule out the possibility that entry into the nonconducting, inactivated state arises from Cd²⁺, we reasoned that if 100 μM Cd²⁺ promoted gating into the inactivated state, then reducing [Cd²⁺] to 30 μM should lead to higher Po at 200 mV compared with that observed with 100 μM Cd²⁺. In contrast, we observe that lowering the [Cd²⁺] to 30 μM leads to overall lower Po compared with 100 μM Cd²⁺ (Fig. S1B). Together with the results obtained in nominally Ca²⁺-free solutions, these experiments suggest that gating in the inactivated state does not strictly arise from either Cd²⁺ or from levels of contaminant Ca²⁺.

Molecular Simulations at 0 mV Suggest the Locations of Ion Binding Sites in the Pore.

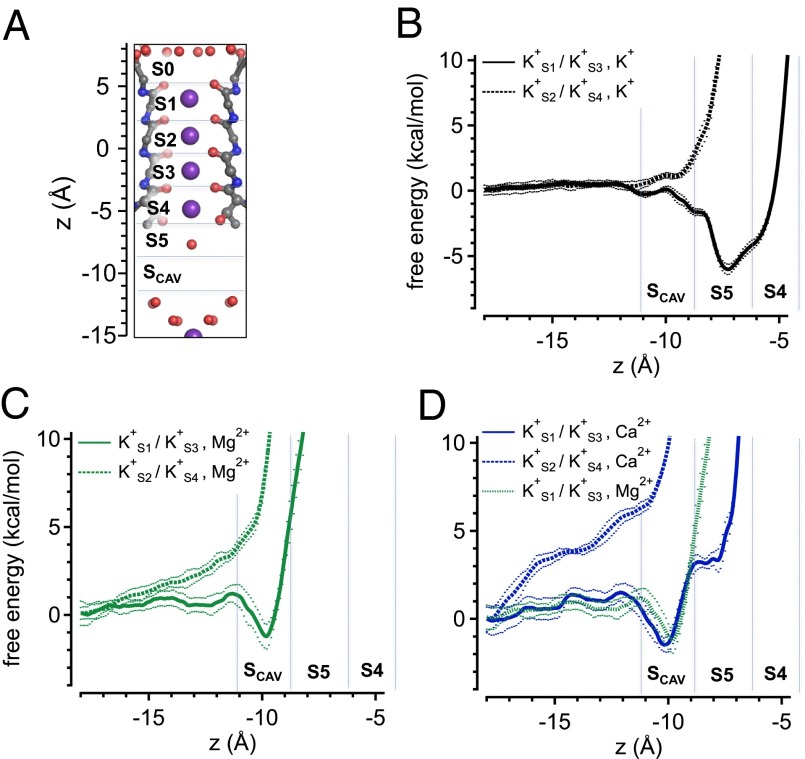
We next sought to determine why inactivation at depolarized voltages might be effectively enhanced by Ca²⁺ but immune to Mg²⁺. To examine this mechanism further, we performed atomistic simulations of the MthK pore containing two K⁺ ions at defined positions in the selectivity filter (either S1 and S3 or S2 and S4) and a cation (K⁺, Mg²⁺, or Ca²⁺) initially in the cavity of the pore. The free energies of each ion at positions along the length of the cavity were estimated through calculation of the PMF; thus, the positions of energy minima (i.e., wells) would correspond to potential binding pockets for ions, and energy maxima correspond to barriers impeding ion access.

Initially, we performed simulations with a transmembrane voltage of 0 mV, reasoning that these simulations should reveal the positions of energy wells and barriers attributable to interactions between the channel protein, ions, and water, whereas additional experiments (see below) might further reveal effects of depolarizing voltage on free energy profiles. In simulations at 0 mV with K⁺ ions in the S1/S3 positions, an additional K⁺ ion in the cavity can occupy one of two largely overlapping energy wells that correspond to two microscopically adjacent sites on either side of the threshold of the selectivity filter (Fig. 4 A and B, solid curve). At one site, termed S5 (located at approximately z = −7.5 Å), a partially hydrated K⁺ ion is coordinated by the oxygen atoms from the side chain hydroxyl groups of T59 (in each subunit); this Thr residue forms part of the highly conserved K⁺ channel signature sequence (TVGYG) (27). The adjacent energy well, appearing as a shoulder to the right of the S5 energy well, is located at the S4 site within the selectivity filter (approximately z = −5.5 Å). The relatively small (1–2 kcal/mol) energy barrier for K⁺ movement from S5 to S4 under these conditions is consistent with a permeation mechanism in which a K⁺ ion moves from the cavity region to S4, where it may subsequently drive outward movement of K⁺ ions at S3 and S1, similar to the knockon permeation mechanism suggested for the K⁺ channel KcsA (28, 29). In contrast, with K⁺ ions in the S2/S4 positions (Fig. 4B, dashed curve), a K⁺ ion in the cavity occupies no substantial energy well and encounters a steep energy barrier impeding access to the S5 site. This result implies that the S2/S4 K⁺ ions can destabilize ion binding in the MthK cavity and are obliged to translocate (i.e., to S1/S3) as a new ion approaches the selectivity filter.

Fig. 4.

Free energies of ions in the MthK pore based on PMF calculations. (A) Structure of the MthK selectivity filter (PDB ID code 3LDC) with potential ion binding sites S0–S_cav indicated. The axis at the left indicates distance (z) relative to the center of mass of the selectivity filter. (B–D) Free energies for K⁺, Mg²⁺, and Ca²⁺ ions in the cavity region, respectively, plotted as a function of ion position along the central axis of the pore. Vertical dashed lines indicate approximate boundaries of potential ion binding sites. Simulations were performed with K⁺ ions at S1 and S3 (solid curves) or S2 and S4 (dashed curves) at 0 mV. These results suggest that either Mg²⁺ or Ca²⁺ can occupy an energy well near −10 Å (S_cav), whereas Ca²⁺ may further access the S5 position (near −7.5 Å) at the entrance to the filter. Dotted curves indicate ± SD (Methods).

In contrast to K⁺, Mg²⁺ can occupy an energy well within the cavity of the pore (z = −10 Å), termed S_cav, and encounters a strong energy barrier (>10 kcal/mol) impeding its movement to the S5 position, with K⁺ ions at S1/S3 (Fig. 4C, solid green curve). With K⁺ ions at S2/S4, Mg²⁺ encounters a steep energy barrier, impeding its approach to either S_cav or S5. These observations are consistent with the idea that, when in the cavity, Mg²⁺ interacts with K⁺ ions in the selectivity filter but is unlikely to either occupy a binding site at S5 or enter the filter. In contrast, a Ca²⁺ ion can occupy the energy well corresponding to S_cav and could also potentially move beyond S_cav to the S5 position, encountering a moderate energy barrier of ∼4 kcal/mol under the conditions of this simulation, with K⁺ ions in S1/S3 (Fig. 4D).

Because both Ca²⁺ and Mg²⁺ can produce a fast blockade of outward K⁺ current (i.e., reduced conductance) that displays a relatively weak voltage dependence (Fig. 2), these simulations seem consistent with the idea that the S_cav site, which corresponds to an energy well common to both Ca²⁺ and Mg²⁺, underlies fast blockade (Discussion). However, movement to the S5 site seems possible for Ca²⁺ but not Mg²⁺. This difference may begin to explain the differential effects of Ca²⁺ vs. Mg²⁺ on entry to the inactivated state.

Voltage-Driven Outward Movement of K⁺ Ions Can Stabilize Ca²⁺ Binding at the Threshold of the Selectivity Filter.

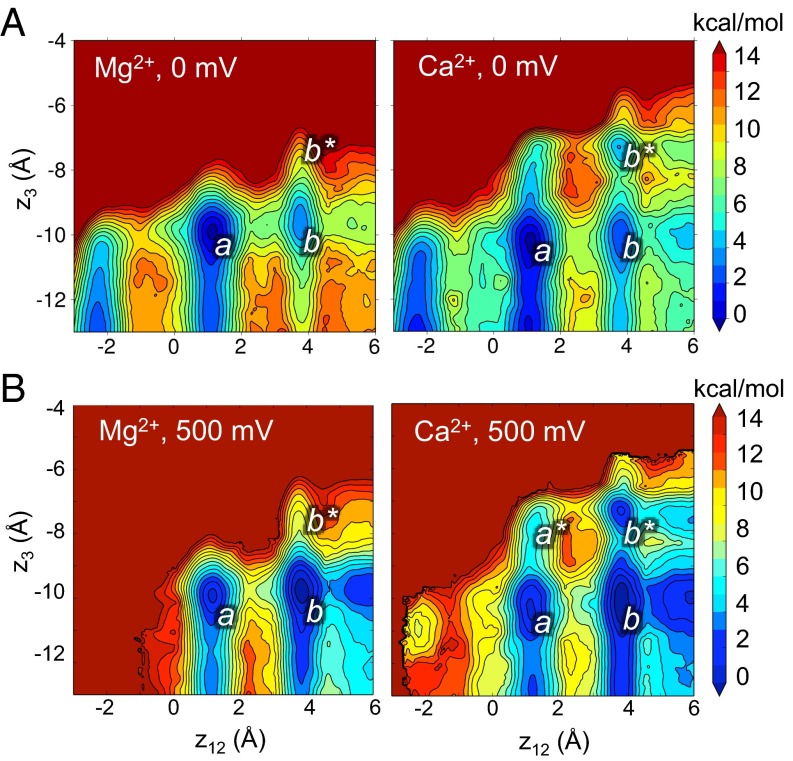
The PMF calculations in Fig. 4 illustrate the free energies of Mg²⁺ and Ca²⁺ ions with K⁺ ions at fixed positions in the filter. To further explore the energetic relations among these ion configurations, we performed 2D PMF calculations, which provide information on the energy landscape as a function of K⁺ and divalent ion locations along the pore axis. In the 2D PMF contour plots (Fig. 5), the combined reaction coordinate z₁₂ represents the positions of K⁺ ions in the filter (calculated as the center of mass of pairs of K⁺ ions relative to the center of mass of the selectivity filter backbone) (29), and z₃ represents the position of the Ca²⁺ or Mg²⁺ ion as indicated.

Fig. 5.

Energetic relations among ion binding configurations in the MthK pore. (A) Free energy of ion configurations as a function of K⁺ ion positions (z₁₂) and Ca²⁺ or Mg²⁺ (z₃) from simulations performed at 0 mV. Ca²⁺, but not Mg²⁺, occupies an energy well located at S5 (z₃ = −7.5 Å; indicated by b*), with K⁺ ions driven to the extracellular end of the selectivity filter (z₁₂ = 3.5 Å). Colors correspond to free energies (in kilocalories per mol) as indicated in the scale bar on the right. (B) Free energy of ion configurations from simulations performed with 500 mV depolarizing voltage. Depolarization drives K⁺ ions to the extracellular end of the filter (z₁₂ = 3.5 Å) and permits Ca²⁺ to bind more stably at S5. In A and B, z₁₂ corresponds to the center of mass of pairs of K⁺ ions in the filter relative to the center of mass of the selectivity filter; z₃ represents the position of the Ca²⁺ or Mg²⁺ ion (as indicated) relative to the center of mass of the selectivity filter.

Fig. 5A indicates that, at 0 mV, Mg²⁺ (Fig. 5A, Left) does not occupy an energy well beyond z₃ = −10 Å (corresponding to the S_cav position in Fig. 4A) and that occupancy of Mg²⁺ at the S_cav position leads to relative stabilization of K⁺ ions centered on the S1/S3 positions (z₁₂ = 1.5 Å) (indicated by a in Fig. 5A), with an additional, shallow energy well centered on the S0/S2 position (z₁₂ = 3.5 Å) (indicated by b in Fig. 5A). In contrast, Ca²⁺ (Fig. 5A, Right) occupies a clearly defined energy well at z₃ = −7.5 Å, corresponding to the S5 position with K⁺ ions to the external end of the selectivity filter (z₁₂ = 3.5 Å) (indicated by b* in Fig. 5A, right). The PMF shows that the movement of Ca²⁺ from the S_cav to the S5 position is most favorable after outward movement of K⁺ ions. This idea is indicated by the relatively low energy pathway from a to b to b* compared with a direct pathway from a to b* without entering b.

Entry into the inactivated state in MthK is favored by depolarization (Fig. 3) (18, 23). To determine the impact of depolarization on movement of Mg²⁺, Ca²⁺, and K⁺ in MthK, we performed additional 2D PMF calculations with a transmembrane voltage of 500 mV (Fig. 5B). Although this voltage is stronger than the depolarization typically applied in our electrophysiological experiments, our goal here was to identify the relative impact of voltage on energy wells corresponding to ion binding sites in the pore. In the presence of Mg²⁺, depolarization drove K⁺ ions to the extracellular end of the selectivity (on average), resulting in deeper energy well at position b relative to a, although movement of Mg²⁺ beyond the S_cav position was essentially unaffected. In contrast, depolarization resulted in outward displacement of K⁺ ions with Ca²⁺ at either S_cav or S5 (at positions b and b*) and seemed to permit slight stabilization of Ca²⁺ at the S5 position with K⁺ ions centered on the S1/S3 positions (position a*). However, the lowest energy pathway of a to b to b* persists even with stronger depolarization, relative to the pathway of a to a* to b*. This result suggests that, in terms of MthK inactivation, the predominant effect of voltage is to drive K⁺ outward. This outward K⁺ movement is permissive for binding of Ca²⁺ at the S5 position, which in turn, could attenuate access of K⁺ from the cytoplasmic end of the pore and prevent replenishing of the pore with K⁺.

To further illustrate the impact of K⁺, Mg²⁺, and Ca²⁺ on the distribution of K⁺ ions in the selectivity filter, we performed additional simulations by restraining these ions within their respective energy wells in the MthK pore (K⁺ and Ca²⁺ in S5 and Mg²⁺ in S_cav at 0 mV) (Fig. S2). We observe that occupancy of Mg²⁺ at the S_cav position leads to likely stabilization of K⁺ ions centered on the S1/S3 positions (z₁₂ = 1.5 Å), with additional shallow energy wells centered on the S2/S4 and S0/S2 positions (z₁₂ = −2 and 3.5 Å, respectively) (Fig. S2, green line). In contrast, a K⁺ ion at S5 leads to a bias of ions within the filter to the extracellular end, which is indicated by a shallower energy well at z₁₂ = −2 Å (by ∼4 kcal/mol) and a slightly deeper energy well at z₁₂ = 3.5 Å (−2 kcal/mol compared with Mg²⁺) (Fig. S2, black line). A Ca²⁺ ion at S5, in turn, leads to an even stronger bias to the extracellular end, with the energy well at z₁₂ = −2 Å replaced by an energy barrier of >10 kcal/mol, and an even deeper energy well at z₁₂ = 3.5 Å (−6 kcal/mol compared with Mg²⁺) (Fig. S2, blue line). Thus, both K⁺ and Ca²⁺ have the effect of stabilizing K⁺ ions to the extracellular end of the selectivity filter. However, whereas a K⁺ ion can move beyond S5 to drive K⁺ permeation to the extracellular side, a Ca²⁺ ion is unlikely to move beyond S5 deeper into the selectivity filter. Thus, Ca²⁺ occupancy at S5 favors the outward movement of K⁺, preceding its own dissociation from S5 to the cytoplasmic side of the channel.

Geometry of the S5 Site Favors Access by Ca²⁺ over Mg²⁺.

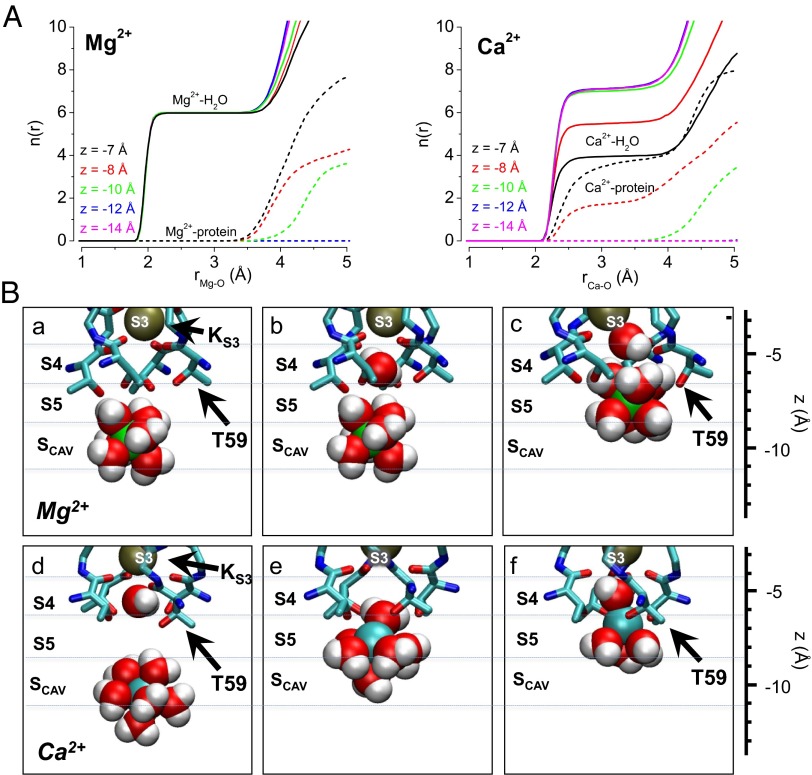
To further understand the basis for selection of Ca²⁺ over Mg²⁺ at the S5 site and coordination of these ions in the MthK pore, we quantified the number of oxygen ligands provided by water and protein atoms in our simulations as a function of Mg²⁺ or Ca²⁺ position in the pore. The results illustrate that Mg²⁺ remains hydrated with six water molecules while it resides in the pore and in contrast, that Ca²⁺ is hydrated with a maximum of seven water molecules at more shallow positions in the pore (z < −10 Å) and progressively dehydrates, exchanging three to four water molecules for protein oxygen atoms as it moves to the S5 position (Fig. 6A).

Fig. 6.

Structural basis for Ca²⁺ access and binding at the S5 site. (A) Number of oxygen atoms within radius r [n(r)] of (Left) Mg²⁺ and (Right) Ca²⁺; n(r) is shown separately for water and protein oxygen (solid and dashed lines, respectively), and each curve represents the relative position of the ion along the central axis of the MthK pore (z). These data show that Mg²⁺ remains hydrated with up to six water molecules at these positions in the MthK pore (coordination distance between 2 and 3.5 Å), whereas Ca²⁺ can exchange three to four water molecules for protein oxygen as it approaches the S5 site (z between −7 and −8 Å). (B) Representative snapshots from MthK pore simulations with (a–c) Mg²⁺ (green spheres) and (d–f) Ca²⁺ (cyan spheres) with nearby water molecules (red spheres, oxygen; white spheres, hydrogen) and selectivity filter atoms (shown as sticks with side chain of Thr-59 indicated by black arrows). These snapshots illustrate that the energy barrier impeding Mg²⁺ access to S5 arises primarily from its strong interaction with hydration shell water molecules, which leads to overall steric hindrance by selectivity filter atoms (c), whereas Ca²⁺ exchanges its hydration shell water molecules in favor of the hydroxyl side chains of T59 (f).

Hydration and coordination of Mg²⁺ and Ca²⁺ near the selectivity filter are illustrated in a series of snapshots from our simulations (Fig. 6B). An Mg²⁺ ion at the S_cav position is fully hydrated by six water molecules (Fig. 6 B, a and b). When an Mg²⁺ ion reaches the S5 position, it is energetically very unfavorable for the ion to exchange its hydration shell waters for protein oxygen atoms, and occupancy of S5 by the fully hydrated ion leads to distortion of the protein structure (Fig. 6 B, c). In contrast, Ca²⁺ can shed up to three hydration shell water molecules as it moves from S_cav to S5 (Fig. 6 B, d–f) with a relatively small net energetic cost (the energetics corresponding to these ion configurations are illustrated in Fig. 4 C, solid curve and D, solid curve). Together, these results suggest that Ca²⁺ likely gains access to the S5 site owing to the favorable energetics of exchanging hydration shell water molecules in the context of the geometry of the S5 site.

Ion Dissociation from the Selectivity Filter Favors a Conformational Change That Can Break the Permeation Cycle.

Our electrophysiological and in silico results are consistent with the idea that Ca²⁺ can access the S5 site at the threshold of the selectivity filter, where it drives K⁺ ions to the extracellular side to potentially dissociate into the bulk extracellular solution (Figs. 3–5). In addition, transitions to the inactivated state are facilitated by strong depolarization in the nominal absence of Ca²⁺ as well as lowered external [K⁺] (Fig. S1) (5, 6, 18). To determine the possible relation between ion movements and entry into the inactivated state, we analyzed the structure of the selectivity filter during simulations in different ionic conditions. We reasoned that conditions that mimic those conditions that favor inactivation could reveal structural changes that underlie interruptions in K⁺ conduction or increased barriers to permeation.

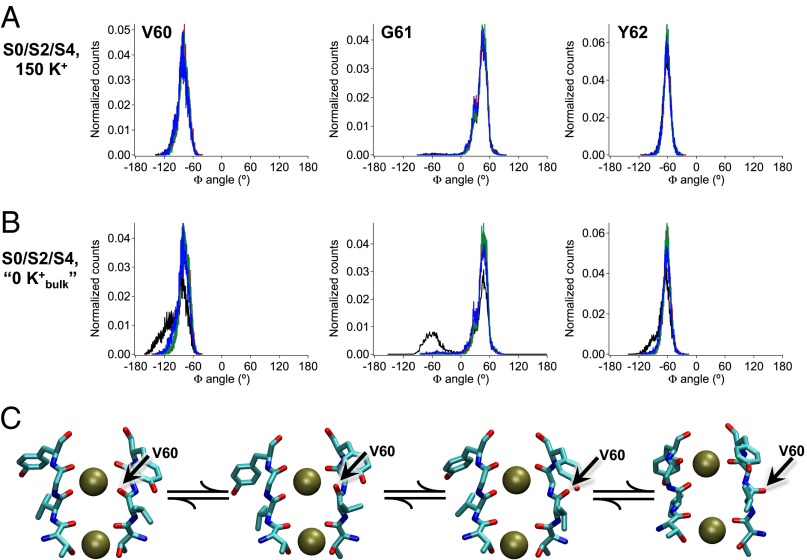
In simulations initiated with K⁺ ions at the S2 and S4 positions in the selectivity filter and 150 mM K⁺ in the bulk solution, we observe that dihedral (Φ) angles for filter residues remain stable about their canonical positions (Fig. 6A). This result is not unexpected; in electrophysiological experiments with MthK in the presence of 200 mM external K⁺, no apparent inactivation is observed without strong depolarization (Fig. 3) (18). Interestingly, in these simulations, a K⁺ ion from the bulk external solution is observed to stably occupy a site at the external mouth of the selectivity filter, termed S0 (29). Because lowering external [K⁺] facilitates entry to the inactivated state, we designed additional simulations to mimic these electrophysiological experiments (termed 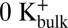) (Methods). The results (Fig. 7B) suggest that, under conditions in which the K⁺ ion at the S0 position rapidly dissociates to the external bulk solution, the peptide linkage between residues Val-60 and Gly-61 in one of four subunits is observed to rearrange between its canonical position and an alternative inverted (rotated) position (Fig. 7C). Histograms of Φ-angles determined from these simulations indicate a rotation of around 110° for the Φ-angle of Gly-61, corresponding to a rotation of the carbonyl oxygen of Val-60 away from the central axis of the selectivity filter. This distorted selectivity filter conformation, which was previously observed in simulations of the KcsA K⁺ channel, is known to underlie a nonconducting state of the filter (30). Thus, dissociation of a K⁺ ion from the extracellular end of the MthK selectivity filter is correlated with a conformational change in the filter that underlies a nonconducting state. Rotation of the Val-60 carbonyl oxygen is also observed in simulations with K⁺ ions initially at the S1 and S3 sites (Fig. S3).

Fig. 7.

K⁺ dissociation facilitates a conformational change in the MthK selectivity filter. (A) Histograms of Φ-angles for the indicated residue sampled during molecular simulations. Each channel subunit is represented by a different color (black, red, green, and blue). With K⁺ occupying the S0/S2/S4 positions, all carbonyl oxygen atoms face the central axis of the pore (in canonical positions) over the entire simulation. Thus, the Φ-angles for each residue are centered around single peaks. (B) With K⁺ ions initially occupying the S0/S2/S4 positions but a force applied to repel binding of K⁺ ions coming from the bulk 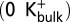(Methods), the S0 K⁺ ion dissociates from the channel, and a conformational change occurs, leading primarily to a 110° rotation of the Val-60 carbonyl oxygen in one of four subunits (black). Thus, for one of the subunits, the Φ-angles determining the position of the Val-60 carbonyl oxygen and its adjacent residues are distributed bimodally, with one peak corresponding to the canonical position and one peak corresponding to the rotated (flipped) position (black lines). (C) Series of selectivity filter snapshots from simulations illustrating rotation of the Val-60 backbone carbonyl (indicated by arrows). Selectivity filter segments from two of four subunits are shown side by side, with K⁺ ions at S2 and S4 shown as dark green spheres.

The relation between the Val-60 carbonyl rotation and dissociation of ion from the selectivity filter led us to hypothesize that the canonical state of the selectivity filter is favored in conditions where three ions are associated with the selectivity filter, whereas the energy barrier preventing carbonyl rotation is reduced in conditions where two ions are associated with the filter. Three-ion states correspond to the simulations in Fig. 7A (S0/S2/S4) and Fig. S3A (S1/S3/S5); two-ion states are reached in simulations using the 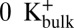constraint (Fig. 7B and Fig. S3B) and could be reached in electrophysiological experiments with low external [K⁺] (Fig. S1A).

To determine the impact of ion occupancy on the energetics of Val-60 carbonyl rotation, we performed PMF calculations of the Φ-angle with the filter in three-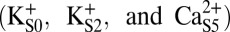 or two-ion states 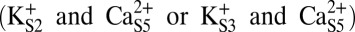. Fig. 8A illustrates that, in the three-ion state, the canonical state (Φ_Gly-61 ∼ 45°) is favored by >5 kcal/mol over the rotated state (Φ_Gly-61 ∼ −75°) and strongly favored by >10 kcal/mol over any additional rotations. In contrast, Fig. 8B shows that dissociation of K⁺ from S0 resulting in the two-ion state 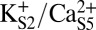can potentially lower the energy barrier for rotation (by ∼2 kcal/mol), and in the two-ion state, 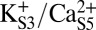(Fig. 8C), the canonical and rotated states are effectively equivalent in terms of free energy. Potential impacts of K⁺ ion dissociation on selectivity filter structure are further illustrated through plots of ion position and selectivity filter Φ-angles as a function of time in Fig. S4.

Fig. 8.

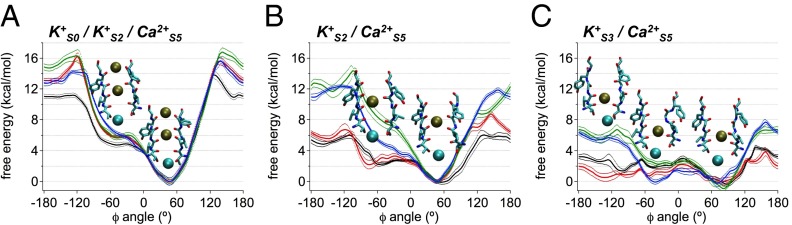
Free energy of a conformational change in the MthK selectivity filter with different ion configurations. Free energy plotted as a function of the Φ-angle of Gly-61. Each curve is determined for a single MthK subunit in four independent simulations, in which three of four subunits in the pore are constrained to have the canonical Gly-61 Φ-angle (45°). Curves are shown as means ± SDs. (A) In the three-ion state, 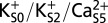, an energy barrier of ∼5 kcal/mol hinders rotation of the Val-60 carbonyl much beyond the canonical position. This energy barrier is attenuated in the two-ion states (B) 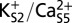and (C) .

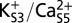Discussion

Inactivation in MthK displays properties in common with C-type inactivation in Kv channels, notably modulation by external [K⁺] and other permeant ions (3, 5, 6, 18). In Kv channels, impermeant ions, such as quaternary ammonium derivatives, as well as the poorly permeant ion Cs⁺ applied to the cytoplasmic side of the channel were found to increase the rate of inactivation. This observation is consistent with a mechanism in which dissociation of K⁺, coupled with impeded refilling of the pore, facilitates subsequent inactivation (5, 6). Although the energetics of pore blockade by divalent cations have been described using empirical models, in which the charged blocking ion competes with permeant K⁺ (31, 32), the structural bases of interactions between specific blocking ions and the pores of K⁺ channels have not been well-understood.

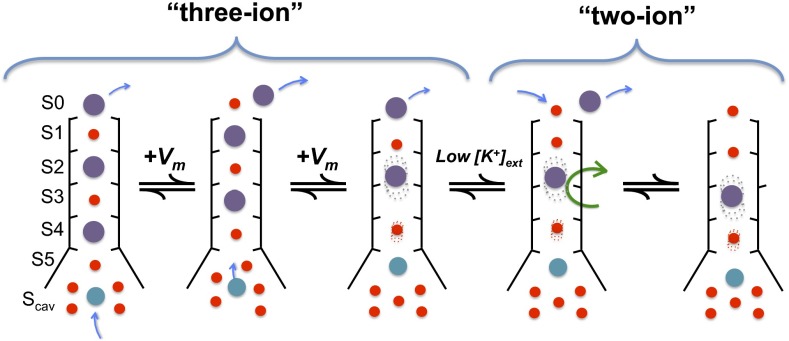
Whereas the MthK channel can apparently accommodate up to three K⁺ ions in the vicinity of its selectivity filter (at positions S0/S2/S4 or S1/S3/S5), strong depolarization and low external [K⁺] can contribute to outward movement of K⁺ ions and limit rebinding of K⁺ from the external side of the selectivity filter, respectively (Figs. 3–5 and Fig. S1) (18). This K⁺ dissociation can result in a state with only two ions in the vicinity of the selectivity filter. We observe that this configuration is permissive for rotation of a filter-lining carbonyl group (of Val-60) (Figs. 7 and 8), which in turn, can raise an energy barrier to prevent K⁺ permeation (28–30). Our electrophysiological and computational results are consistent with a working hypothesis, in which Ca²⁺ (but not Mg²⁺), by preventing refilling of the pore with K⁺, can stabilize ion configurations in the selectivity filter that favor transitions to a nonconducting, inactivated state (Fig. 9).

Fig. 9.

Working hypothesis of initial steps in MthK inactivation. Schematic diagram of the MthK selectivity filter in a series of different ion occupancy states. From the state (far left) with K⁺ ions occupying the S0/S2/S4 positions (purple spheres), one Ca²⁺ (cyan sphere) occupies the S_cav position. Depolarization drives the K⁺ ions outward in register as Ca²⁺ moves to the S5 position. Lowered extracellular [K⁺] drives the filter from the three-ion states to the two-ion states by lowering the probability of K⁺ rebinding after its dissociation from S0. In the final step (far right), carbonyl rotation occurs (indicated by the green arrow), leading to inactivation.

The distinct effects of Ca²⁺ and Mg²⁺ on MthK inactivation can be mainly attributed to differences in the interactions of these ions with their hydration shell water molecules. Ca²⁺, which has a larger atomic radius than Mg²⁺ but identical charge, exchanges waters of hydration in favor of protein oxygen more readily than Mg²⁺ (33). It is the partial dehydration of Ca²⁺ that permits its access to the S5 position, which in turn, impacts selectivity filter occupancy. Computational studies estimate the ion–water lifetime correlation function for Ca²⁺-first hydration shell waters to be 18 ps, indicating an exchange rate ∼10 times faster than that of Mg²⁺ (228 ps) (34). This slow exchange rate in the case of Mg²⁺ contributes to the high free energy barrier preventing binding to S5. It is worth noting that divalent ions might induce important polarization of their ligands, which is likely not well-captured by classical force fields as used in our simulations (35). Nevertheless, we believe the calculated binding free energy difference between Ca²⁺ and Mg²⁺ remains meaningful, notably because the ions here interact mainly with water molecules (and the chemically similar hydroxyl group of threonine side chains), for which the polarization effects are implicitly included, at least partially, as ions were parameterized to reproduce properties in solution (36).

Crystallographic, electrophysiological, and in silico studies of inactivation in the KcsA K⁺ channel underscore the importance of pore helix side chains in the inactivation process (37–40). Specifically, hydrogen bond interactions involving the Glu-71 and Asp-80 side chains in KcsA provide a substantial driving force to promote inactivation, although other factors are likely to contribute. Interestingly, whereas Glu-71 seems to be critical for inactivation in KcsA, the acidic side chain at this position is not highly conserved among other inactivating K⁺ channels, including either Shaker or MthK. In its place, both Shaker and MthK contain Val (Val-55 in MthK and Val-438 in Shaker), which has a branched hydrophobic side chain that cannot form hydrogen bonds. Therefore, although Glu-71 clearly facilitates and stabilizes the inactivated state in KcsA, a model to account for C-type inactivation as observed in Shaker would need to incorporate additional or alternative driving forces. These driving forces might include the ion effects addressed above.

Both fast blockade and inactivation of MthK display voltage dependence, which must arise from movement of charged particles across the transmembrane electric field (Figs. 2 and 3). If fast blockade arises from a divalent ion (Mg²⁺ or Ca²⁺) reaching the S_cav site, which appears to be substantially outside of the transmembrane electric field (41), then the observed zδ-value of ∼0.42–0.45 e₀ observed with fast blockade by Mg²⁺, Ca²⁺, or Sr²⁺ must arise primarily from coupling between the movement of a divalent ion to the S_cav site with either net movement of one K⁺ ion nearly halfway through the selectivity filter (e.g., from S_cav to S3) or more likely, movement of two K⁺ ions some shorter distance through the filter (e.g., from S4/S2 to S3/S1) (42, 43). These hypothetical coupled divalent/K⁺ movements are consistent with the interactions between Mg²⁺ and K⁺ in our PMF calculations (Figs. 4 and 5). Similarly, steady-state inactivation of MthK in either the presence or the nominal absence of Ca²⁺ or Sr²⁺ can be described by a Boltzmann equation with a zδ-value of ∼1.3 e₀ (Fig. 3) (18, 23). Because the electrical distance between S_cav and S5 also appears to be relatively small, then the voltage dependence of inactivation must, similarly, arise primarily from net movement of at least two K⁺ ions through two positions in the selectivity filter (e.g., from S4/S2 to S2/S0). These hypothetical Ca²⁺/K⁺ movements are consistent with the interactions between Ca²⁺ and K⁺ that were suggested in our PMF calculations (Figs. 4 and 5).

Although our results suggest that the coupling of ion movements within the pore and dissociation of K⁺ within the selectivity filter of MthK are linked to changes in filter conformation, C-type inactivation is likely to be a complex process that is controlled by many chemical driving forces, including interactions among side chains that determine selectivity filter structure (30, 37, 38, 44). Clearly, a complete understanding of inactivation and other forms of gating at the K⁺ channel selectivity filter will require additional determination of energetic relationships among these processes.

Methods

Channel Purification and Reconstitution.

MthK was expressed, purified, and reconstituted into proteoliposomes as described previously (15, 17). Proteoliposomes were composed of Escherichia coli lipids (Avanti) that were rapidly frozen in liquid N₂ and stored at −80 °C until use. Protein concentrations in proteoliposomes ranged from 5 to 25 μg protein/mg lipid.

Electrophysiology.

Recordings were obtained using planar lipid bilayers of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine:1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (POPE:POPG) (3:1) in a horizontal bilayer chamber. Unless otherwise specified, solution in the cis (top) chamber contained 200 mM KCl and 10 mM Hepes (pH 7.0). Solution in the trans (bottom) chamber contained 200 mM KCl, 10 mM Hepes (pH 8.1), 100 µM Cd²⁺, and the specified concentration of different divalent cations. Within each bilayer, multiple solution changes were performed using a gravity-fed perfusion system. To ensure completeness of solution changes, the trans chamber was washed with a minimum of 10 mL (∼10 chamber volumes) solution before recording under a given set of conditions.

Single channel currents were amplified using a Dagan PC-ONE patch clamp amplifier with low-pass filtering to give a final effective filtering of 333 Hz (dead time of 0.538 ms) and sampled by computer at a rate of 50 kHz. Currents were analyzed by measuring durations of channel openings and closings at each current level by 50% threshold analysis using pClamp 9.2. These measurements were used to calculate NPo as

in which i is the open level and Pi is probability of opening at that level. The mean single channel open probability (Po) is obtained by dividing NPo by N, which is the number of channels in the bilayer, determined by recording under conditions where the maximum level of channel opening can be observed. The voltage dependence of Po was described by the Boltzmann equation,

in which Pomax is the maximal Po, zδ is the effective gating valence (in units of electronic charge, e₀), V_1/2 is the voltage at half-maximal Po, k_B is Boltzmann constant, and T is temperature. For data where Po at a given voltage was described as a function of divalent cation concentration (like with Ca²⁺ and Cd²⁺ in Fig. 1D), data were fitted with a Hill equation,

in which [X²⁺] is the divalent cation concentration, EC₅₀ is the [X²⁺] required to reach half-maximal Po, and n_H is the fitted Hill coefficient. Single channel current amplitudes were quantified by plotting all-points histograms of current levels for a given voltage and subtracting the mean closed level from the mean open level. Fast blockade of unitary current was quantified by first estimating the divalent ion concentration (i.e., Mg²⁺, Ca²⁺, or Sr²⁺) yielding 50% current at several voltages, using

in which [B] is the divalent (blocker) concentration, K_app is the blocker concentration required to reduce the unitary current to 50% of its amplitude in absence of blocker (at a given voltage), and I/I₀ is the fractional unitary current amplitude. Estimated K_app values at each voltage were used to estimate K_app at 0 mV and the voltage dependence (zδ) of K_app by fitting with the Woodhull equilibrium blockade model (22):

in which V is the transmembrane voltage, F is Faraday’s constant, R is the gas constant, and T is absolute temperature. Data points (e.g., Po and mean interval durations) are presented as means ± SEMs of three to five observations for each data point, and collectively, they represent data from a total of 48 different bilayers.

Molecular Dynamics Simulations.

Molecular dynamics simulations were performed using the MthK pore structure in high [K⁺] (Protein Data Bank ID code 1LDC) (13) using methods described previously (45). Briefly, molecular systems were assembled using the CHARMM-GUI web service (46) using a protocol developed by Woolf and Roux (47). The channel protein, with its symmetry axis aligned along the z axis, was embedded in a lipid bilayer of dipalmitoyl-phosphatidylcholine molecules. The number of ions in the bulk was adjusted to reproduce experimental ionic concentrations (150 mM KCl) and obtain electrical neutrality. The molecular system contained about 59,170 atoms total. All calculations were performed using the CHARMM software version c34 (48) using the all-atom potential energy function PARAM27 for protein and phospholipids and the TIP3P potential for water molecules (49, 50). Parameters for K⁺, Ca²⁺, and Mg²⁺ ions were as provided by PARAM27, with an additional NBFIX correction applied to K⁺–carbonyl oxygen pair interactions (51). Periodic boundaries conditions were applied, and long-range electrostatic interactions were treated by the particle mesh Ewald algorithm (52). The molecular systems were equilibrated for about 300 ps with decreasing harmonic restraints applied to the protein atoms, the pore ions, and the water molecules localized in the P loop and the filter. All trajectories were generated with a time step of 2 fs at constant normal pressure (1 atm) controlled by an extended Lagrangian algorithm and constant temperature (323 K) using a Nosé–Hoover thermostat (53–55).

The 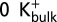condition (Fig. 7B and Fig. S3), mimicking a low concentration of external K⁺, was created by applying to all K⁺, except those K⁺ already present in the filter, a repulsive potential to disfavor the ions from reaching S0. Ions entering a sphere of 15-Å radius, centered 3 Å below the center of mass of the selectivity filter, were subjected to a harmonic potential with a force constant of 5 kcal/mol⋅A². The transmembrane voltage was modeled by the application of a constant electric field along the z axis, with the potential difference of 500 mV taken between the extremities of the simulation cell (56).

PMF and Radial Distribution Calculations.

PMF calculations were performed according to the umbrella sampling approach using a self-learning adaptive scheme for the 2D PMFs (57). Reaction coordinates involving a single ion (z and z₃) were defined as the distance along the pore axis between the ion and the center of mass of the selectivity filter. The reaction coordinate z₁₂, used in Fig. 5 and Fig. S2, was defined as the distance along the pore axis between the center of the mass of pairs of K⁺ ions in the selectivity filter and the center of the mass of the selectivity filter protein atoms. Independent simulations of 1 ns were performed every 0.5 Å along the reaction coordinates using a biasing harmonic potential with a force constant of 20 kcal/mol⋅Ų. The PMF calculations on the Φ-angle of Gly-61 were performed for one subunit at a time. Windows separated by 15° were sampled for 1 ns with a harmonic restraint of 20 kcal/mol·rad². The corresponding dihedral angles of the three subunits not subjected to the PMF calculations were restrained to Φ = 45°, with a force constant of 5 kcal/mol·rad². The ions were restrained to their binding sites with a force constant of 20 kcal/mol·Å². All calculations were unbiased using the weighted histogram analysis method (58).

For each PMF calculation, the sampling was split into 10 intervals of 100 ps, and a PMF was calculated independently for each interval. After comparison of these 10:00 PMFs, only the last 500 ps of sampling were considered for the final PMF calculation, considering the first 500 ps as equilibration. The SE given in all 1D PMFs is the SD calculated using the independent PMFs of the last five intervals and the total PMF as the average. The relative free energy between each of five interval PMFs and the average PMF was beforehand adjusted to minimize the rmsd between the two PMFs.

The number of coordinating ligands, n(r), was calculated by counting the number of coordinating atoms within concentric spherical shells with a thickness of 0.04 Å and radius r centered on the targeted ion as described previously (45).