The quantum world differs from our classical experience in many ways. Perhaps most curious is the phenomenon of quantum entanglement, where measuring the state of one particle can instantaneously define the state of another, even though the second particle is arbitrarily distant. For much of the 20th century, it was debated whether entanglement really exists. The issue was quantified by Bell’s formulation of the Bell inequality (1), and the subsequent flurry of experiments by Clauser, Aspect, and others, demonstrating that quantum entanglement was real (2–4). All of these early tests were applied to systems where the measured state of one particle can only take one of two values, but such systems are not representative of the wider world. In PNAS, Krenn et al. derive a new entanglement test for systems where the measured state can take on one of many values (Fig. 1) (5). The authors apply their test to the spatial structure (i.e., state) of two separated photons. Krenn et al. confirmed that the photons are entangled over at least 100 of these spatial states. This large number of states allows entanglement in higher dimensions, which can increase both the security of communication and the efficiency of computing protocols (6).
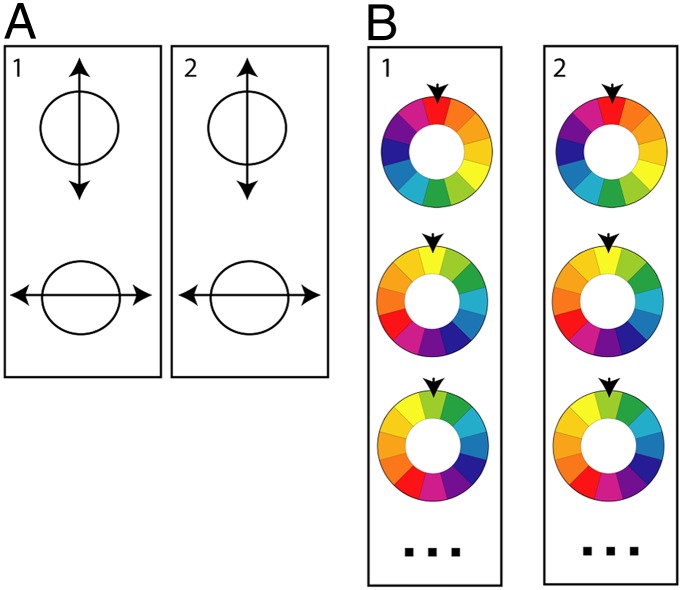
Fig. 1.
Two separate systems, 1 and 2, are said to be entangled if the properties of 1 and 2 cannot be defined independent of each other. Entanglement gives rise to correlations, regardless of the distance between 1 and 2. (A) In a 2D space, such as polarization (which can only be vertical or horizontal), individual measurement results on each system are random, but always correlated. Each system is in a superposition of the horizontal and vertical polarizations (B) In higher dimensions, one can imagine spinning a color wheel. When individually examined, the color where the wheel stops is random, but always the same for 1 and 2. Each system is in a superposition of the many colors in the wheel.
The first experimental tests to reveal entanglement were based upon the measurement of the polarization of a bipartite system consisting of two separate photons. The polarizations of the individual photons were found to be correlated with each other regardless of the photons’ separation. Equally important is that the correlations were present regardless of the choice of measurement basis (e.g., whether the polarizers were measuring horizontal-vertical or left-right circular polarizations) (2–4). In terms of dimensionality, studies of entanglement measuring polarization are relatively easy to characterize. Because polarization can take only one of two values, each photon can be considered as a discrete two-state system, referred to as a “qubit.” Hence, what the first experimental tests demonstrated was the bipartite entanglement of qubits (2–4).
A richer playground for exploring both practical and fundamental aspects of entanglement is provided by entangled states that are more complicated. For example, a collection of N qubits [e.g., a row of trapped ions (7)] can be in any one of 2N possible states, and can be used for communication protocols, such as quantum secret sharing (8). Studies of nonlocality with multiple particles are interesting; just for the case of three qubits, one can show a stronger conflict between the predictions of quantum mechanics and local realism (9). However, at least for photonic experiments, there are few practical sources of more than two entangled photons. If one is restricted to bipartite entanglement, increasing the complexity requires measuring photon properties that can take on d values (where d > 2).
Measuring properties other than polarization is beneficial for increasing the dimension of the entanglement. For quantum cryptography, a higher dimension means more information that can be encoded (10), more security against eavesdroppers (11), and better resilience to noise (12). It has been shown that working with higher dimensions can simplify quantum logic, perhaps pointing to deeper aspects of entanglement that we have yet to explore (13). High-dimensional entanglement is most easily observed in photons. Nowadays, the photon pairs are generated in the process of spontaneous parametric down-conversion (SPDC). Here, a pump photon interacts with a nonlinear crystal, resulting in the creation of two lower-energy photons endowed with various properties exhibiting correlations. Properties, such as frequency and spatial mode, are theoretically unbounded in their dimensionality. The benefits of high-dimensional entanglement are therefore accessible in principle, although challenges remain. One of the most difficult challenges is to certify that high-dimensional entanglement is present in the system. The problem amounts to answering these two questions: (i) Is the system entangled? (ii) If it is entangled, over how many dimensions: that is, what is d?
The most obvious and rigorous way to determine whether a system is entangled is to determine the entangled state through an approach called quantum state tomography (14). However, for this tomography, the number of measurements required scales as ∼d4, making the method impractical for higher dimensions. In the regime where Krenn et al. are working, quantum state tomography would require ∼100 million individual measurements! Moreover, although not often said, it is necessary to assume the dimensionality in advance of performing the tomography itself. Defining the dimensionality may be straightforward for photon polarization, where d = 2, but not for other degrees of freedom. The dimensionality of spatial states of photons [the property exploited by Krenn et al.(5)] is theoretically unbounded, but depends on various experimental parameters, such as the geometry of the photon generation and detection scheme (15).
Fortunately, knowledge of the quantum state is not necessary to determine whether a system is entangled or not. The Bell inequality was formulated to show that quantum mechanics is at odds with a classical picture of nature, but its violation also implies entanglement. Although the first demonstrations were made with pairs of qubits, the approach of the Bell inequality has been extended to bipartite multistate systems in the Collins–Gisin–Linden–Massar–Popescu (CGLMP) inequality (16). In this case, for an arbitrary dimension d, the number of measurements scales as ∼d2, and experimental violations for as high as d = 11 have been shown for the spatial modes of photons (17). Moreover, at least for small values of d, the amount with which the (d × d)-state system violates the CGLMP inequality puts a lower bound on d without any assumptions regarding the form of the quantum state (18), hence simultaneously certifying both the presence of entanglement and the dimensionality of the system.
It is conventional to think that to verify the entanglement between two d-state particles, one needs to calculate and measure states that are superpositions of all those belonging to the state space of each individual particle. This approach is the case for both quantum state tomography and demonstrations of Bell (and CGLMP) inequality violations. It is not impossible, but as discussed above becomes time consuming and, hence, nontrivial as d increases. Krenn et al. (5) show that by assuming the entangled state is perfectly correlated, the number of measurements required can be greatly reduced. In fact, the authors’ measurements are only performed within the various 2D subspaces of the total state space of the individual particle, making their method experimentally feasible.
The criterion for entanglement that Krenn et al. (5) use is based on the perfect correlation and anticorrelation of the particles. Within the 2D subspace, they measure states that are theoretically perfectly correlated and perfectly anticorrelated (i.e., the visibilities are theoretically equal to 1). The authors then derive a metric, W, from these visibilities, which can be optimized for a particular d, thus giving a lower bound on the dimensionality of the entanglement. If their observed value of W exceeds the bound Wd for a particular d, then an individual particle can take on any of (d + 1) possible states, and the entanglement is over (d + 1) × (d + 1) dimensions.
Krenn et al. (5) apply their method to photon pairs generated via SPDC, measuring the photons’ transverse spatial modes. More specifically, they use the Laguerre–Gaussian family of modes to define their measurement
Krenn et al. have shown that if one is only interested in knowing the dimensionality of the entangled state, ∼200,000 measurements are enough.
states. The Laguerre–Gaussian states are characterized by two quantum numbers, one of which is associated with the orbital angular momentum of the photons, and the other with the radial intensity structure of the light field. Correlations in both these quantum numbers have been investigated previously (19, 20), meaning that the conservation of orbital angular momentum in SPDC has been rigorously tested. Hence, their assumption of perfect correlation in establishing the bound is physically sound.* In practice, there are no perfect correlations but, as the authors point out, any imperfection only decreases the observed value of their criterion thus keeping their bound valid.
The authors investigated the correlation of 186 modes. They measured states belonging to the various 2D subspaces consisting of the 186 × 186- space. They obtained an experimental value of W > W100, indicating that the dimensionality of the spatial mode of the individual photons is at least 100. Thus, Krenn et al. (5) have shown that if one is only interested in knowing the dimensionality of the entangled state, ∼200,000 measurements are enough, and this is much smaller than the ∼100,000,000 measurements required for full knowledge of a (100 × 100)-entangled state.
We are now in an era where high-dimensional entanglement can be routinely generated in the laboratory. The creation of a (100 × 100)-dimensional entangled state with photons is a testament to the technological advances that have been made by various groups worldwide. However, characterization and verification of high-dimensional entanglement has remained a difficult and time-consuming task. The work of Krenn et al. (5) is a significant step toward overcoming these difficulties because they provide a practical tool for quantifying the dimensionality in high-dimensional entanglement. Their development hopefully takes the field closer to our common goal of fully exploiting the advantages that high-dimensional entanglement has to offer, in understanding fundamental issues and in improving communication and computation protocols.
Supplementary Material
Footnotes
The authors declare no conflict of interest.
See companion article on page 6243.
*The authors assume that the state 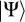 is of the form
is of the form 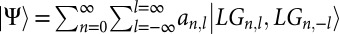 where
where 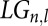 refers to a Laguerre–Gaussian mode of quantum numbers n and l, and al are complex coefficients.
refers to a Laguerre–Gaussian mode of quantum numbers n and l, and al are complex coefficients.
References
- 1.Bell JS. On the problem of hidden variables in quantum mechanics. Rev Mod Phys. 1966;38(3):447–452. [Google Scholar]
- 2.Freedman SJ, Clauser JF. Experimental test of local hidden-variable theories. Phys Rev Lett. 1969;28(14):938–941. [Google Scholar]
- 3.Aspect A, Grangier P, Roger G. Experimental tests of tealistic local theories via Bell's theorem. Phys Rev Lett. 1981;47(7):460–463. [Google Scholar]
- 4.Genovese M. Research on hidden variable theories: A review of recent progresses. Phys Rep. 2005;413(6):319–396. [Google Scholar]
- 5.Krenn M, et al. Generation and confirmation of a (100 × 100)-dimensional entangled quantum system. Proc Natl Acad Sci USA. 2014;111:6243–6247. doi: 10.1073/pnas.1402365111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Franke-Arnold S, Garri A, Trepps N. High dimensional quantum entanglement. Eur Phys J D. 2013;67:104. [Google Scholar]
- 7.Hillery M, Bužek V, Berthiaume A. Quantum secret sharing. Phys Rev A. 1999;59(3):1829–1834. [Google Scholar]
- 8.Cirac JI, Zoller P. Quantum computations with cold trapped ions. Phys Rev Lett. 1995;74(20):4091–4094. doi: 10.1103/PhysRevLett.74.4091. [DOI] [PubMed] [Google Scholar]
- 9.Greenberger DM, Horne MA, Shimony A, Zeilinger A. Bell’s theorem without inequalities. Am J Phys. 1990;58(12):1131–1143. [Google Scholar]
- 10.Walborn SP, Lemelle DS, Almeida MP, Ribeiro PH. Quantum key distribution with higher-order alphabets using spatially encoded qudits. Phys Rev Lett. 2006;96(9):090501. doi: 10.1103/PhysRevLett.96.090501. [DOI] [PubMed] [Google Scholar]
- 11.Durt T, Kaszlikowski D, Chen JL, Kwek LC. Security of quantum key distributions with entangled qudits. Phys Rev A. 2004;69(3):032313. [Google Scholar]
- 12.Almeida ML, Pironio S, Barrett J, Tóth G, Acín A. Noise robustness of the nonlocality of entangled quantum states. Phys Rev Lett. 2007;99(4):040403. doi: 10.1103/PhysRevLett.99.040403. [DOI] [PubMed] [Google Scholar]
- 13.Lanyon BP, et al. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nat Phys. 2009;5(4):134–140. [Google Scholar]
- 14.Thew RT, Nemoto K, White AG, Munro WJ. Qudit quantum-state tomography. Phys Rev A. 2002;66:012303. [Google Scholar]
- 15.Miatto FM, et al. Bounds and optimisation of orbital angular momentum band-widths within parametric down-conversion systems. Eur Phys J D. 2012;66:178. [Google Scholar]
- 16.Collins D, Gisin N, Linden N, Massar S, Popescu S. Bell inequalities for arbitrarily high-dimensional systems. Phys Rev Lett. 2002;88(4):040404. doi: 10.1103/PhysRevLett.88.040404. [DOI] [PubMed] [Google Scholar]
- 17.Dada A, Leach J, Buller G, Padgett MJ, Andersson E. Experimental high-dimensional two-photon entanglement and violations of generalized Bell inequalities. Nat Phys. 2011;7:677–680. [Google Scholar]
- 18.Brunner N, et al. Testing the dimension of Hilbert spaces. Phys Rev Lett. 2008;100(21):210503. doi: 10.1103/PhysRevLett.100.210503. [DOI] [PubMed] [Google Scholar]
- 19.Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature. 2001;412(6844):313–316. doi: 10.1038/35085529. [DOI] [PubMed] [Google Scholar]
- 20.Salakhutdinov VD, Eliel ER, Löffler W. Full-field quantum correlations of spatially entangled photons. Phys Rev Lett. 2012;108(17):173604. doi: 10.1103/PhysRevLett.108.173604. [DOI] [PubMed] [Google Scholar]