Bayesian inference for an emerging arboreal epidemic in the presence of control

Significance

Fast-moving and destructive emerging epidemics are seldom left to run their course because of the imperative to control further spread. Contemporaneous control measures, however, greatly complicate the characterization of the disease transmission process and the extraction of the epidemiological parameters of interest. The spread of Huanglongbing on orchard scales is used as a case study for modeling an emerging epidemic in the presence of control. We show that even with missing and censored data, and with seasonal and host age dependencies, it is possible to infer the parameters of a fully spatiotemporal stochastic model of disease spread. The value of the fitted model is to provide an engine for simulation studies of the costs and benefits of proposed disease control strategies.

Abstract

The spread of Huanglongbing through citrus groves is used as a case study for modeling an emerging epidemic in the presence of a control. Specifically, the spread of the disease is modeled as a susceptible-exposed-infectious-detected-removed epidemic, where the exposure and infectious times are not observed, detection times are censored, removal times are known, and the disease is spreading through a heterogeneous host population with trees of different age and susceptibility. We show that it is possible to characterize the disease transmission process under these conditions. Two innovations in our work are (i) accounting for control measures via time dependence of the infectious process and (ii) including seasonal and host age effects in the model of the latent period. By estimating parameters in different subregions of a large commercially cultivated orchard, we establish a temporal pattern of invasion, host age dependence of the dispersal parameters, and a close to linear relationship between primary and secondary infectious rates. The model can be used to simulate Huanglongbing epidemics to assess economic costs and potential benefits of putative control scenarios.

Under the threat of an emerging epidemic, it is imperative to estimate the key epidemiological parameters to predict the likelihood and extent of further spread, as well as to quantify the effectiveness of different strategies for disease control. In recent years, there has been an increasing emphasis on the use of spatiotemporal dynamical models to represent the dispersal and transmission processes of epidemics (1–4). Such models have an advantage over analyses that simply look at spatiotemporal associations in that inferences can be related directly to the underlying processes.

The parameters for dynamical models are often estimated, however, from relatively limited and imprecise data. The data are limited because many disease events, for example, exposed or infectious status, are unobservable, and the data are imprecise because even observable events, such as symptom detection, are typically censored in time. In this context, Bayesian inference, supported by modern computational methods, is particularly tractable, and is increasingly the approach of choice (1, 5–9).

There are several additional challenges in estimating the key epidemiological parameters for a previously unknown, emerging pathogen. For example, the patterns of spread used to estimate the dispersal and transmission parameters may also reflect the impacts of disease or vector control measures. Allowance for such measures, often applied empirically to manage an emerging pathogen, requires inferences to be made about the effects of control on pathogen spread and disease expression. Furthermore, there is likely to be unknown heterogeneity in the susceptibility of the host population through which the epidemic is spreading. There may also be a need to include seasonal forcing in the model and any effect of vector population dynamics. The host pathogen introduced in the next section exemplifies all these issues.

Case study: Huanglongbing

Huanglongbing (HLB), also known as Citrus Greening, is the most destructive citrus pathosystem worldwide (10). It causes severe chlorosis of foliage and dieback, leading to tree death in some cases, and is associated with fruit drop as well as misshapen, discolored, and ill-flavored fruit. There is no known source of resistance to HLB within commercial citrus cultivars or genetically accessible citrus relatives, and there is no known commercially viable cure for an infected tree. In the last decade, HLB has inflicted increasingly severe economic losses on growers in some of the world’s key citrus-growing areas (10).

HLB is associated with three bacteria (11): Candidatus Liberibacter asiaticus (Las), Candidatus Liberibacter africanus (Laf), and Candidatus Liberibacter americanus (Lam). In the western hemisphere, Las is now the most prevalent type. The major vector of HLB is the Asian citrus psyllid (ACP), Diaphorina citri. During feeding, Las-carrying psyllids pass the bacteria into the vascular system of a tree. There, the bacteria multiply and become increasingly distributed, although not uniformly, throughout the tree. Subsequently, a proportion of psyllids feeding on Las+ sites on the tree become Las carriers, completing the loop of the host-vector-pathogen system. Las appears to have minimal impact on ACP.

The timeline of HLB in citrus is measured in years, with dependence on age and variety of tree (10, 12, 13). Once symptoms are evident, they become increasingly severe, and the commercial value of the infected tree rapidly diminishes. Of major concern, however, is the long incubation period of infection, which is between 6 mo and 3 y. As a consequence, visual inspection is not a reliable method to assess the health of a tree, and although the cryptic period appears to be only of order several months, it is clear an epidemic can be underway well before symptoms are first seen.

ACP were first identified in the US state of Florida, in the coastal regions near Miami, in 1998, and HLB was first detected in 2005 (10). Subsequently, ACP reached the commercially important citrus-growing regions of central Florida. HLB has been endemic there since 2005, resulting in huge losses for growers due to crop loss and the costs of detection efforts, control measures, and tree removals and replantings.

The aim of this work is to provide and fit a phenomenological model of the tree-to-tree spread of HLB on orchard scales while accounting for contemporaneous control measures. Such a model can then be used as the engine for simulations of HLB epidemics to assess the economic costs and potential benefits of putative control strategies. We used an extensive dataset, collected by Southern Gardens Citrus, relating to more than a quarter of a million trees in the Southern Gardens plantation in south Florida. In particular, observational sweeps for symptomatic trees, conducted over the course of several years, give a series of spatial “snapshots” of the progress of the epidemic. We propose a spatially explicit, stochastic susceptible-exposed-infectious-detected-removed (SEIDR) model and carry out Bayesian estimation of the model parameters. Specifically, we ask the following questions. Can the disease transmission process be characterized in the presence of control measures? If so, can we identify details of the latent period, including possible seasonality? What are the primary and secondary rates of infection? What is the range of secondary infection? Are there host age dependencies in the epidemiological parameters?

The estimation of dispersal and transmission parameters for stochastic models from spatial snapshots of disease has attracted previous attention (14–18); indeed, likelihood estimation of dispersal parameters from successive snapshots for a continuous time stochastic model was first applied (14) to citrus tristeza disease in plantations. The current analysis is based on subsequent Markov chain Monte Carlo (MCMC) methods developed in refs. 15–17. The novelty of the current work lies in model comparison and inference for data from successive snapshots subject to interference by disease control strategies, variable host age, and periodic environmental forcing. A vital feature of the approach is the ability to handle latent and censored data.

Methods and Results

Data.

Southern Gardens is a commercial citrus plantation consisting of ∼4,900 ha of contiguous citrus plantings, located about 36 km south of Clewiston, Florida. The Southern Gardens dataset concerns more than 250,000 trees in a rectangular region of 180 contiguous blocks. Apart from its northeast corner, the region under consideration is surrounded by further blocks of citrus. The east-west dimension of the region is 3.5 km; the north-south dimension is 2.4 km. The blocks are arranged in six east-west rows of 30 blocks, with each block typically containing around 1,500 trees arranged in 14 north-south rows. The spacing between trees along rows is between 3 and 4 m; the spacing between rows is ∼8 m; and the typical spacing between blocks is 25 m.

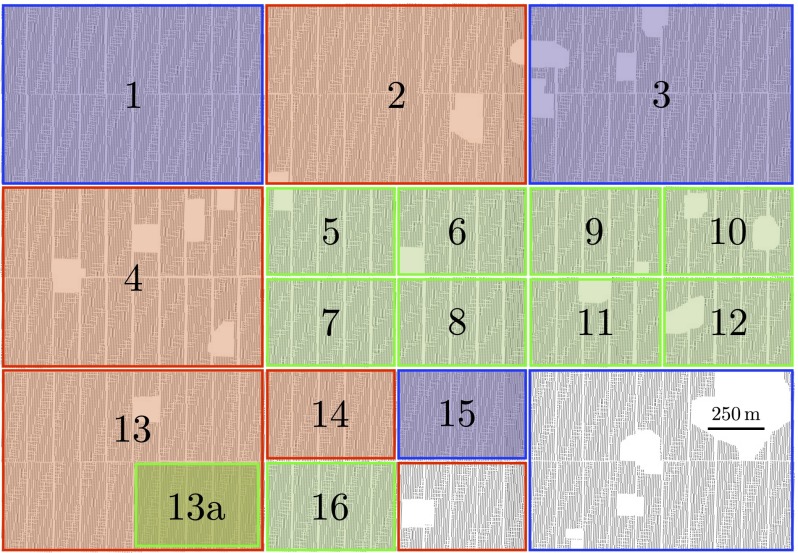
The blocks are all sweet orange, Citrus sinesis (L.) Osbeck, of two scion cultivars Hamlin and Valencia in nearly equal proportion, and grafted on a mixture of four rootstocks: Cleopatra mandarin, Citrus reshni Hort. Ex Tan; Swingle citrumelo, Citrus paradisi Macf. × Poncirus trifoliata (L.) Raf.; Carrizo citrange, Citrus sinensis (L.) Osbeck) × Poncirus trifoliata (L.) Raf.; and Volk, Citrus volkameriana Tan & Pasq. Of the 180 blocks, 103 were planted in 1988 or 1989, and 77 were planted in 1999 or 2001–2003. Thus, the blocks naturally split into old and young blocks. The layout of the blocks is shown in Fig. 1.

Fig. 1.

Layout of the Southern Gardens dataset with subregions used to estimate epidemic parameters. Green indicates blocks planted after 1998; blue indicates blocks planted before 1998; red indicates a subregion of mixed age; subregions in which the model could not be fit reliably are gray.

Four sweeps for symptomatic trees were made through the blocks between November 2005 and July 2007, with each sweep taking approximately 3 mo to complete. The spread of HLB during the four sweeps is shown in SI Text. The epidemic first becomes apparent in young trees in the east and then spreads both westward and to older trees. More than 27,000 trees were found to be symptomatic. Symptomatic trees were fully enumerated using a differential global positioning system and tagged for subsequent removal. In most blocks, there was a sharp increase in detections in either the second or third observation cycle, followed by a decrease in detections in the fourth cycle. Symptomatic means HLB symptoms are readily apparent to visual inspection by trained and experienced personnel. Given the skill of the inspectors in detecting symptoms, the false-negative rate is small, and we take it to be zero. The false-positive rate is also small: PCR analysis of clippings taken from a random subsample of trees deemed to be symptomatic confirmed detection in 98% of cases.

These data therefore describe the presence of HLB symptoms but they do not account for cryptic or latent infection. Specifically, the dataset comprises censored symptomatic times and removal times, with times of transition to exposed and infectious classes unobserved. Data on the locations of host trees not exhibiting symptoms of HLB were inferred from a secondary dataset of block-by-block information and from satellite images. The secondary dataset gives tree count and plant date for each block, and the satellite images show where trees were and were not planted. Combined with the geometrical regularity of the orchard, this allows us to reconstruct reliably the locations of trees never seen to be symptomatic.

During the observational period, in addition to the removal of symptomatic trees, a spray program was initiated to control psyllid numbers in both the region under observation and the surrounding areas. The spray program was sufficiently intensive that most psyllids were eradicated by the end of 2006. Given the available data on the spraying schedule and psyllid trap counts, we estimate that the density of psyllids decreased linearly to zero during the course of 2006. Accounting for the control program is a crucial component in our modeling of the epidemic.

Modeling Approach.

We model the spread of HLB on orchard scales as a spatially explicit, stochastic SEIDR epidemic in a fixed population of trees, where S denotes susceptible, E denotes exposed, I denotes infectious but not yet detectable, D denotes detectable or symptomatic, and R denotes removed. This compartmental model therefore gives a phenomenological description of the host-vector-pathogen system. In what follows, 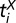is used to denote the time at which tree i enters class X. The key components of the model are the process of the exposure to HLB and the distribution of the latent period of the disease in the trees. These two components are the main innovations of our work. A primary, external source of infection is required to seed the epidemic, whereas secondary infection is mediated by a distance-dependent dispersal kernel. We consider both exponential and power law forms for the kernel. In addition, the rates of primary and secondary infection are allowed to be time dependent to account for control of the vector. The latent period is known to depend on the age of the tree at exposure. Furthermore, exploratory analysis of the data suggested a seasonal component, and we consider a variety of models to account for this. We also compare these with models without seasonality. Two assumptions of our model are that the primary infection is homogeneous in space, and the dispersal kernel is isotropic. Although these assumptions are usually considered reasonable on orchard scales, there is evidence of edge effects in the Southern Gardens dataset (Discussion).

Initial Time.

Let 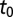denote the time the first infected psyllids arrive in a particular subregion. In other words, 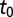marks the onset of infectious challenge or, equivalently, the start time of the epidemic. In the absence of psyllid trap data from the earliest times, becomes a model parameter to be estimated.

Modeling Exposure to Infection.

For a vectored disease, to say a tree is infectious is to say it is transmitting inoculum to the vector. The rate at which inoculum is transmitted is proportional to the density of noninfected vectors in the vicinity of the infectious tree. On the other hand, the rate at which a tree becomes exposed is proportional to the density of infected vectors in its vicinity. In the absence of specific data on the spatial and temporal dependence of the densities of infected and noninfected psyllids—only a time sequence of spatially averaged total psyllid counts is available—it is necessary to make a number of approximations to model exposure.

A summary of the full analysis carried out in SI Text is as follows: we account for psyllid control in Southern Gardens by estimating the relative psyllid density as a piecewise linear function

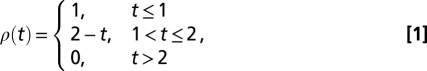where t is measured in years and 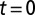corresponds to the start of 2005. Then the instantaneous rate of infection at time t for susceptible tree i is written as

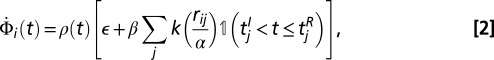where is the indicator function that returns 1 when its argument is true and 0 otherwise. The function 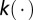represents an isotropic dispersal kernel—isotropic because 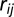is the Euclidean distance between tree i and tree j—and we consider decaying exponential models, , and power law models expressed in the form 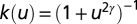. The parameters to be estimated are the primary or external rate of infection ε, the secondary rate of infection β, and the dispersal length scale α.

Modeling the Latent Period.

It is useful to think of the latent period as a time to failure. Modeling the latent period then amounts to specifying a hazard rate 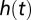, which gives rise to the probability density function for the infection time given the exposed time: 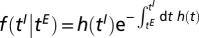. We suppose a tree moves from the exposed class to the infectious class independently of other trees but that the transition rate depends on intrinsic properties of the tree and has a seasonal component. We use an age-dependent hazard rate with yearly oscillations

where 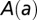is the amplitude fixed by a combination of in-orchard and in-nursery observations, and a is the age of the tree when it became exposed. We call this the cyclic model. The cyclic model can be easily made much more flexible without sacrificing analytic tractability: both the period and phase of the oscillation can be changed and an overall positive constant can be added to the hazard rate. (This last change might be appropriate in regions of less marked seasonality, for example.) In what follows, we also consider the effect of 6-mo oscillations.

We also compare the cyclic model with three alternative models for the latent period: (i) the exponential model is the default model in many epidemiological applications: a constant hazard rate 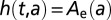, leading to an exponentially-distributed latent period; (ii) the gamma model posits a gamma-distributed latent period, , corresponding to a hazard rate that starts at zero, grows and then tends to 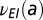; it has no cyclic behavior; and (iii) the cyclic Weibull model has a hazard rate 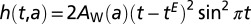; this incorporates seasonality but with an amplitude that starts at zero and increases indefinitely.

The motivation for the gamma and cyclic Weibull models is to capture in-nursery observations of a hazard rate that is initially small and then increases. The parameter values for the cyclic model and the three alternative models in three age categories are given in Table 1.

Table 1.

Parameters for the cyclic, exponential, gamma, and cyclic Weibull models for the latent period

Age (y)	A (y−1)	Ae 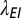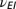(y−1)		(y−1)	AW (y−1)
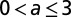	2.4	2.4	12	15	4.6
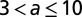	1.1	1.1	14	8	0.43
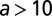	0.8	0.8	10	4	0.17

Note that in the Southern Gardens dataset, there were no trees in the age range of 0–3 y.

Modeling the Cryptic Period.

The times for the cryptic period, which measures the time from initiation of infectiousness to the detection of visible symptoms, are taken to be gamma distributed, 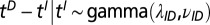, with parameters fixed by in-nursery observations. Specifically, we use 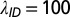and . Note that when combined with the cyclic model for the latent period transition, this suggests a peak in detections in the autumn months.

We do not attempt to estimate the latent period and cryptic period parameters. It has previously been noted (19) that the issue of identifiability arises in epidemiological models with unobserved compartments. This problem is further aggravated by the use of uninformative priors.

Parameter Estimation.

We adopt a Bayesian approach to parameter estimation. We use data augmentation (15–17) and reversible-jump (20) MCMC techniques, with uninformative exponential priors, to obtain, after a burn-in period, a joint posterior density for the parameters 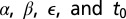. The technical details are provided in SI Text.

Estimation in Subregions.

Model parameters were estimated in 16 subregions of the Southern Gardens dataset. Carrying out separate analyses of the data over disjoint subregions enables investigation of the spatial dependence of the parameters—notably, the initial time —and ensures estimation via MCMC remains computationally feasible. The choice of subregions was motivated by the need to balance the competing requirements that the number of symptomatic trees in a subregion was sufficiently large to obtain reliable parameter estimates and that the subregion was small to afford reasonable spatial resolution of the epidemic in Southern Gardens. Ideally, subregions would comprise either young or old trees, but unavoidably some subregions are of mixed age. The mixed-age subregions, however, do provide a check of robustness of the model: typically, their inferred parameters interpolate between those for young and old subregions. The subregions are shown in Fig. 1. The smaller subregions consist of 7,000–8,000 trees; the larger subregions consist of 25,000–30,000 trees.

Temporal Pattern of Invasion.

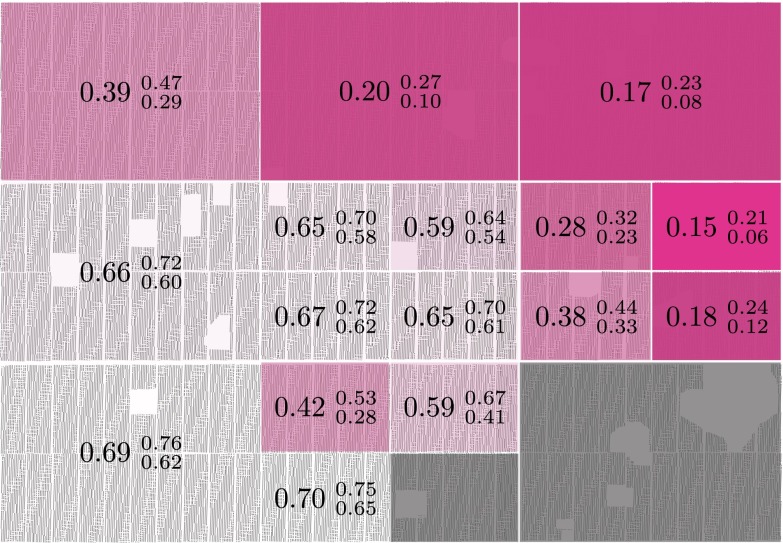
The posterior estimates for 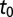by subregion are summarized in Fig. 2. Although it was not possible to estimate 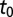in the southeast corner, there is a clear east-to-west spread of the disease. Note that the old blocks tend to have earlier values of the start time even though HLB is first clearly evident in young blocks, because of the shorter latent period for young trees. Furthermore, 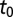is not correlated with the first detection time in each subregion.

Fig. 2.

Estimated epidemic start time by subregion in years from the start of 2005. The large number in each subregion is the mean posterior value for 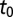and the smaller numbers give the 95% credible interval. The transparency of the pink shading is linearly proportional to the mean value of .

Age Dependence of the Dispersal and Transmission Parameters.

The dependence of the dispersal and transmission parameters on age can only be interpreted in an averaged sense. Consider the impact of infectious tree j on susceptible tree i: age dependence means the rate of secondary transmission, β, for example, depends on the ages of both trees and varies during the interval 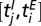, where of course both 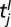and 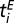are unknown. As a consequence, the imputed value of β will be the average over all pairwise interactions and over time. In addition, there is some uncertainty in the age in which trees were planted out in the orchard. Thus, there is an intrinsic uncertainty in specifying a quantity like 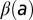, and the same argument applies to 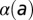and 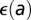. Nevertheless, a reasonable proxy for age is the average age of trees in the subregion of interest at the start of the epidemic. Note that the uncertainty in the inferred value of 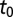is small in comparison with the intrinsic uncertainty. In the boxplots below, the subregions are color-coded by age: young (green), old (blue), and mixed (red).

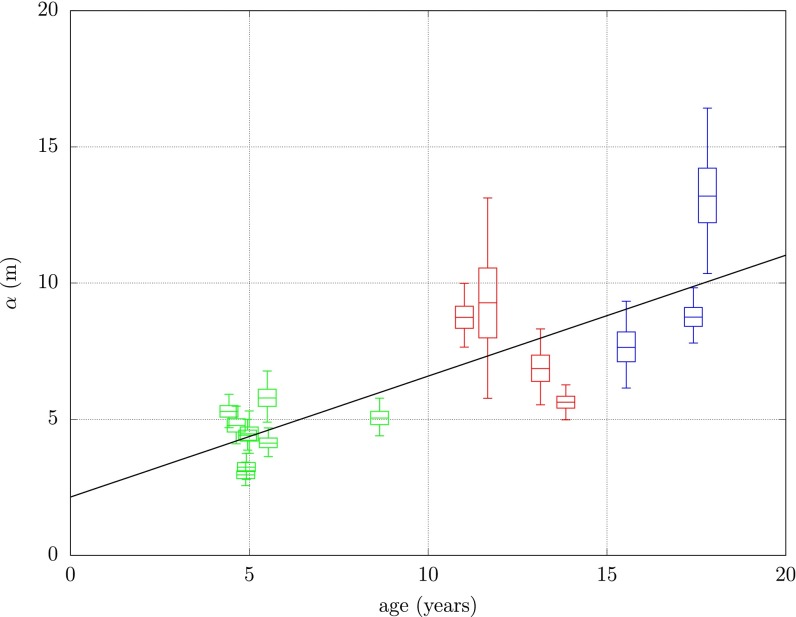
The length scale of the dispersal kernel, shown in Fig. 3, grows approximately linearly with the age of the trees in the subregion. More precisely, a linear model for the mean posterior length scale, 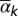, in terms of the average age of the kth subregion, 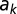, is

Fig. 3.

Length scale of the dispersal kernel, α, by average age of subregion at estimated epidemic start time. The line in black is the linear model fitted to the mean length scale in terms of the mean age.

where c and m are, respectively, the intercept and slope terms, and 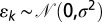is a Normal error term capturing between-subregion variability. Standard analysis shows 67% of the variation in the mean length scale is explained by the linear trend, and the distribution of residuals is consistent with the modeled error with 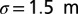. One explanation as to why this linear relationship should hold is that psyllids prefer the new growth and open structure of young trees to the mature and tight canopy structure of old trees. Consequently, psyllids travel further in old-aged subregions.

The age dependence of the secondary and primary rates of infection is shown in SI Text. Both infection rates tend to decrease with age, and there appears to be rather sharp behavioral difference between subregions less than 8 y old and those more than 8 y old. We attribute this to the fact that 8 y is the approximate age at which tree canopies begin to touch and intermingle along rows. Before this age, host canopies are isolated. The conclusion is that tight canopies are a barrier to infection, in the sense that infection rates are reduced. This reduction is partially offset, however, by the fact that the dispersal kernel length scale is increased. Note that canopies are not allowed to intermingle across rows; this implies that the actual dispersal kernel in old-aged subregions will be anisotropic.

Linear Relationship Between Primary and Secondary Infectious Rates.

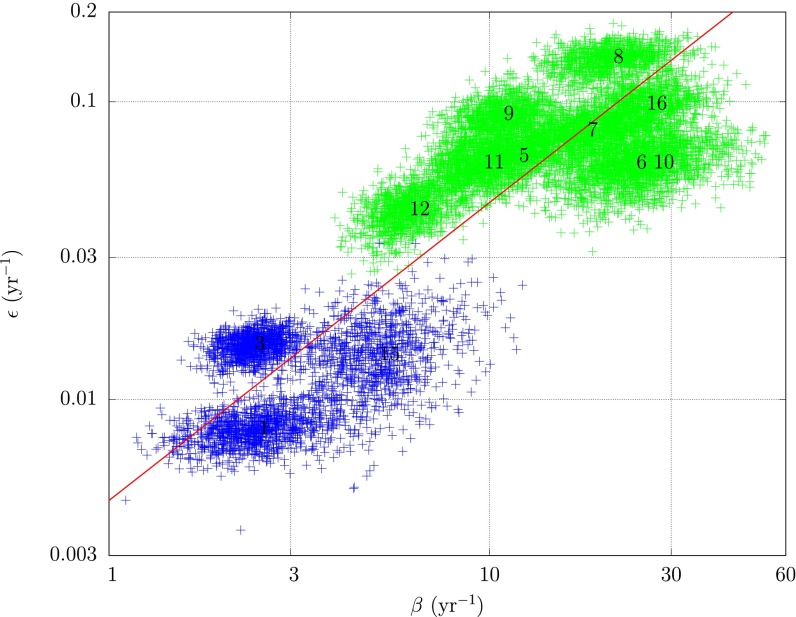
A log-log plot of the infection rates is shown in Fig. 4. The clustering about the 45° line suggests that the ratio of primary and secondary infection rates is roughly constant across subregions. To make this statement more rigorous, we first note that the marginal posterior distributions for and 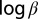are well approximated by a Normal distribution in each subregion. We are then justified in fitting a linear model to the infection rates across subregions

Fig. 4.

A log-log plot of primary rate of infection, ε, vs. secondary rate of infection, β; 1,000 draws from the posteriors for 12 subregions are shown. Subregions less (more) than 8 y old are shown in green (blue). Mean parameter values for each subregion are labeled by subregion number. The clustering about the 45° line shown in red shows 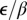is roughly constant across subregions.

where 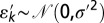. Standard analysis shows 77% of the observed variation is explained by the linear trend, and the distribution of residuals is consistent with the modeled error with 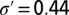. The 95% CI for the slope 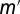is [0.52, 1.18]. The fact this interval contains 1 supports the contention that the ratio 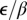is invariant over subregions. We show in SI Text that the observed invariance can be understood as a consequence of certain biological and physical assumptions concerning the exposure process. Note that subregions with both young and old trees have been omitted because psyllid density is likely to be uneven in these cases.

Model Checking and Model Comparison.

To carry out model checking and model comparison, we focus on subregion 13a. This subregion was chosen because the course of the epidemic was the most consistent with the assumptions of homogeneity of primary infection and isotropy of the dispersal kernel. The subregion comprises five blocks and 7,700 trees.

We compare eight different models, a model being specified by a choice of dispersal kernel and latent period model: (a) exponential kernel plus cyclic model with yearly oscillations; (b) exponential kernel plus exponential latent period; (c) Cauchy kernel (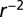 power law kernel) plus yearly cyclic model; (d) exponential kernel plus gamma model; (e) 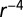power law kernel plus yearly cyclic model; (f) exponential kernel plus cyclic Weibull model; (g) 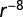power law kernel plus yearly cyclic model; and (h) exponential kernel plus twice-yearly cyclic model.

We fit each model using reversible jump MCMC with data augmentation. From the resulting joint posterior for 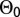, we randomly drew 100 parameter sets and simulated epidemics using the Selke algorithm. We then compared the temporal and spatial structure of simulated outcomes with those of the actual outcome. Specifically, we considered the counts of symptomatic trees in each of the four sweeps and the two-point spatial correlation of all symptomatic trees observed up to and including the final sweep.

The counts of symptomatic trees are shown in SI Text. Only in models a and c are all actual counts well within the distribution of simulated counts. Model d, the only model that favors a long latent period, is completely ruled out.

The two-point correlation function we use is a modified Moran’s I statistic for presence-absence data and is detailed in SI Text. Each model gives correlation functions that are consistent with the vanishing of the observed correlation function for r > 80 m. Conversely, only model a accommodates the observed correlation function for r > 80 m. Models e and g fit reasonably well except for a lack of power in the range of 30–40 m. Once again, model d appears to be completely ruled out.

Model c gives widely varying outcomes in terms of counts of symptomatic trees and spatial correlation. The reason for this is that the favored dispersal length scale is close to zero (SI Text), essentially implying external infection alone is responsible for disease transmission. We consider this model to be highly implausible from a biological viewpoint.

Discussion

When faced with a fast-moving and destructive emerging epidemic, there is often a conflict between the need to observe the epidemic to estimate the key epidemiological parameters and the need to deploy control measures to contain the epidemic (21). We used the spread of HLB on orchard scales as a case study to test the feasibility of estimating parameters for models of an emerging epidemic that is subject to perturbation by control. Using just four censored successive snapshots of disease, we demonstrated that the disease transmission process can be characterized despite contemporaneous control measures. The statistical analyses have yielded previously unidentified aspects of the epidemiology of HLB. Our analyses were able to establish the temporal pattern of invasion, including the likely sequence of invasion through uneven aged groves of citrus. The analyses successfully demonstrated how dispersal and transmission parameters for HLB varied with host age and supported seasonal changes in host susceptibility. We also confirmed a linear relationship between primary infection of citrus by HLB, driven by inoculum arriving from outside the study area, and secondary infection from tree to tree within the groves.

Our analyses demonstrated the power of computational methods to extract these insights about disease spread through a spatially and temporally heterogeneous environment despite the high degree of censoring present in the observations. Given the severity of the challenge to extract meaningful and consistent results, we commend the use of these statistical methods to aid understanding of other pathosystems of similar complexity and scale. Although this paper is focused on demonstrating the robustness of the methodology for estimation, the power of the parameterized epidemiological models to predict the likely future of epidemics is shown in SI Text. The parametized models may also be used to compare the effectiveness of alternative control strategies. The use of the model to predict future outcomes of disease spread, as well as the effectiveness of control, together with the consistency of results, for example, with respect to the effects of host age, all provide means to check the longer-term value of the deductions from the model.

Two of the principal innovations within the general strategy for model fitting in our work are modeling time dependence in a vectored disease due to control of the vector, and incorporating seasonal and host age effects during the latent period. Recent work by Chiyaka et al. (22) has also incorporated seasonal forcing into a model for HLB spread within trees. Chiyaka et al. also modeled the dynamics of vector infection on a single tree. Here we treated the tree as the unit of interest within large populations of 7,000–30,000 trees, for which we inferred transmission and important dispersal parameters from censored maps of disease spread. There is scope in future research to assess the potential to use within-tree dynamics to assess the dynamics of the force of infection on individual trees for tree-to-tree spread.

The models used in the current analysis of HLB assume homogeneous distribution of primary infections. This assumption could easily be dropped to allow for a directional or spatially decaying source of external infection, when there is evidence for such effects. The models also assume isotropic secondary infection. By assuming isotropic spread, our estimates have utility by setting an upper bound for the worst case scenario for unimpeded spread of HLB. Future research will address anisotropic secondary infection to test for differences in transmission rates along and between rows and for edge effects, where vectors congregate, for example, along trees at the edge of a grove.