Abstract
We examine the distribution and structure of human genetic diversity for 710 individuals representing 31 populations from Africa, East Asia, Europe, and India using 100 Alu insertion polymorphisms from all 22 autosomes. Alu diversity is highest in Africans (0.349) and lowest in Europeans (0.297). Alu insertion frequency is lowest in Africans (0.463) and higher in Indians (0.544), E. Asians (0.557), and Europeans (0.559). Large genetic distances are observed among African populations and between African and non-African populations. The root of a neighbor-joining network is located closest to the African populations. These findings are consistent with an African origin of modern humans and with a bottleneck effect in the human populations that left Africa to colonize the rest of the world. Genetic distances among all pairs of populations show a significant product-moment correlation with geographic distances (r = 0.69, P < 0.00001). FST, the proportion of genetic diversity attributable to population subdivision is 0.141 for Africans/E. Asians/Europeans, 0.047 for E. Asians/Indians/Europeans, and 0.090 for all 31 populations. Resampling analyses show that ∼50 Alu polymorphisms are sufficient to obtain accurate and reliable genetic distance estimates. These analyses also demonstrate that markers with higher FST values have greater resolving power and produce more consistent genetic distance estimates.
The study of human genetic variation provides opportunities to examine population history and genetic structure. From early work characterizing blood groups and protein polymorphisms, the field has progressed to include studies of mtDNA (Cann et al. 1987; Vigilant et al. 1991; Stoneking and Soodyall 1996; Ingman et al. 2000; Bamshad et al. 2001), Y-chromosome variation (Hammer et al. 1998; Seielstad et al. 1999; Forster et al. 2000), genome-wide polymorphic autosomal microsatellite variation (Bowcock et al. 1994; Deka et al. 1995; Goldstein et al. 1995; Jorde et al. 1997; Perez-Lezaun et al. 1997) and single-nucleotide variation (Sachidanandam et al. 2001; Stephens et al. 2001; Gabriel et al. 2002; Marth et al. 2003). Assessing individual and population level variation is becoming commonplace for gene mapping, association analysis for complex traits, and analysis of population history (Jorde et al. 2000; Risma et al. 2002; Tang et al. 2002; Yu et al. 2002). Although the distribution and organization of human genetic variation bears directly upon the diverse fields of linkage and association mapping, haplotype and recombination studies, and human evolutionary history, its assessment remains incomplete.
Alu insertion elements are the most abundant class of short interspersed elements (SINEs) in the human genome, numbering >1 million per haploid genome (Rubin et al. 1980; International Human Genome Consortium 2001). Alu elements are dimeric 300-bp sequences that propagate by retroposition into new chromosomal locations, probably by using a target-site primed mechanism (Vanin 1985; Weiner et al. 1986; Eickbush 1992; Luan et al. 1993; Feng et al. 1996; Jurka 1997; Esnault et al. 2000; Kajikawa and Okada 2002). Germline and somatic Alu retroposition is ongoing, and de novo insertions into genes are responsible for cases of neurofibromatosis type-1, Apert syndrome, and various cancers (Wallace et al. 1991; Miki et al. 1996; Deininger and Batzer 1999; Oldridge et al. 1999). Members of the Y, Ya5, Ya8, Yb8, Yb9, Yc1, Yc2, and Yd subfamilies all produce new Alu insertions that are polymorphic in the human population (Batzer and Deininger 1991, 2002; Batzer et al. 1995; Carroll et al. 2001; Roy-Engel et al. 2001; Xing et al. 2003).
Alu insertion polymorphisms and other SINE elements are robust markers for evolutionary and phylogenetic studies because they have a unique mutational mechanism, an absence of back mutation, and a lack of recurrent forward mutation (Okada 1991; Batzer et al. 1994; Hamdi et al. 1999; Roy-Engel et al. 2001). Aspecific Alu insertion and nearby flanking sequence will be identical by descent in all individuals in whom they occur (Batzer et al. 1994). Thus, sets of related chromosome regions marked by an Alu insertion event can be distinguished from a pool of ancestral chromosomes that lack the element. These features give each locus genetic polarity that allows the independent assignment of an ancestral state and a root for phylogenetic analyses.
Previous studies of human genetic variation have utilized polymorphic Alu insertions to gain insight into population history. Studies using multiple Alu loci or a single Alu locus with flanking markers show high African diversity and a greater effective population size for Africans (Batzer et al. 1994; Stoneking et al. 1997; Tishkoff et al. 1998; Watkins et al. 2001). When a large number of Alu elements are analyzed, individuals can usually be classified according to their continent of origin (Bamshad et al. 2003). Alu insertions are also useful for resolving genetic relationships in more limited locales such as NW Africa and the Caucasus region (Comas et al. 2000; Nasidze et al. 2001). Here, we examine population variation using 100 Alu insertion polymorphisms. Most of these Alu elements are recently identified insertions from the human genome sequence (Carroll et al. 2001; Roy-Engel et al. 2001) and are examined in broadly dispersed world populations for the first time.
RESULTS
For the 31 world populations (Fig. 1) combined, Alu insertion frequencies for the 100 loci are distributed from 0.001–0.999. The average Alu insertion frequencies for four major human population groups are similar among E. Asians (0.557), Indians (0.544), and Europeans (0.559), but lower in Africans (0.463). Alu gene diversity is higher in Africans than in E. Asians, Indians, and Europeans (Table 1).
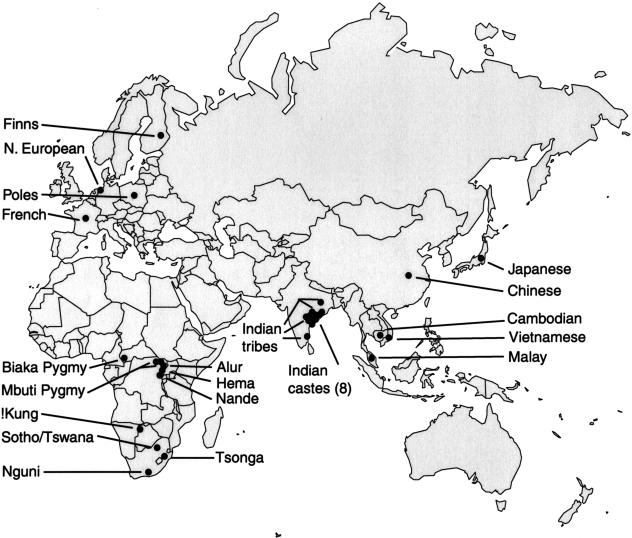
Figure 1.
A map showing the locations of the 31 populations sampled in the study.
Table 1.
Alu Diversity for Major Groups and 31 Populations
| Alu diversity | |
|---|---|
| Africans | 0.3487 |
| (0.3189-0.3785) | |
| Alur | 0.3544 |
| Biaka Pygmy | 0.3073 |
| Hema | 0.3503 |
| !Kung | 0.3390 |
| Mbuti Pygmy (Coriell) | 0.3221 |
| Mbuti Pygmy | 0.3135 |
| Nande | 0.3393 |
| Nguni | 0.3445 |
| Sotho/Tswana | 0.3411 |
| Tsonga | 0.3510 |
| E. Asians | 0.3104 |
| (0.2729-0.3480) | |
| Cambodian | 0.2947 |
| Chinese | 0.3178 |
| Japanese | 0.3064 |
| Malay | 0.3256 |
| Vietnamese | 0.2965 |
| Europeans | 0.2973 |
| (0.2616-0.3331) | |
| Finns | 0.2927 |
| French | 0.3009 |
| N. European | 0.2964 |
| Poles | 0.2798 |
| Indians | 0.3159 |
| (0.2803-0.3514) | |
| Brahmin | 0.3128 |
| Irula | 0.3068 |
| Kapu | 0.3117 |
| Khonda Dora | 0.3050 |
| Kshatriya | 0.3031 |
| Madiga | 0.3103 |
| Mala | 0.3113 |
| Maria Gond | 0.3029 |
| Relli | 0.3220 |
| Santal | 0.3007 |
| Vysya | 0.2993 |
| Yadava | 0.3127 |
(95% CI in parentheses)
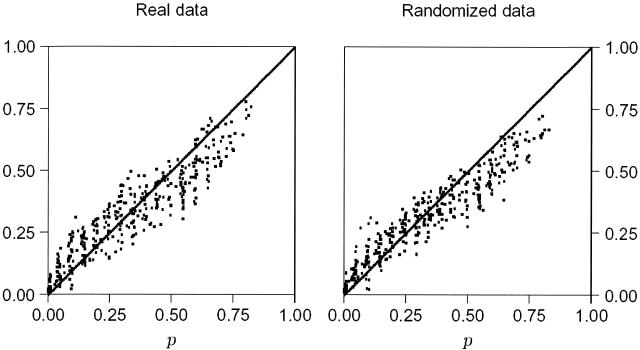
We tested Hardy-Weinberg equilibrium (HWE) in each of the 100 loci in 31 regional populations. The left panel of Figure 2 shows the cumulative distribution of the 3100 P-values corresponding to each deviation (F) from HWE. If these loci departed from HWE ratios because of sampling effects alone, we would expect to find P ≤ 0.05 at 5% of samples, P ≤ 0.10 at 10%, and so on. The points in the panel should fall along the 45° line. The scatter of points is centered about this line in the left half of the graph, but falls below it on the right, suggesting a deficit of samples with large P.
Figure 2.
The cumulative distribution of P-values measuring significance of deviation from Hardy-Weinberg expectation. The cumulative frequency of P-values is plotted against each value of P for 100 Alu loci and 31 populations (left) and for 100 loci with the same allele frequencies but randomly assigned genotypes (right).
In expecting the points to fall along the line, however, we are assuming that P is uniformly distributed over the interval between 0 and 1. But, in fact, the distribution of P is discrete, reflecting the discrete number of values that F can take given the count of “+” (insert present) and “-” (insert absent) alleles in any sample. To test the hypothesis that a discrete distribution of F accounts for the deficit of large P values, we repeated the analysis using artificial data generated by randomly reassigning alleles to genotypes while maintaining the counts of the “+” and “-” alleles in each sample. The results (Fig. 2, right) show the pattern expected under the hypothesis of HWE. The left and right panels are indistinguishable. Thus, the observed deficit of samples with large P values is consistent with the expected distribution of F and shows that these data are in HWE.
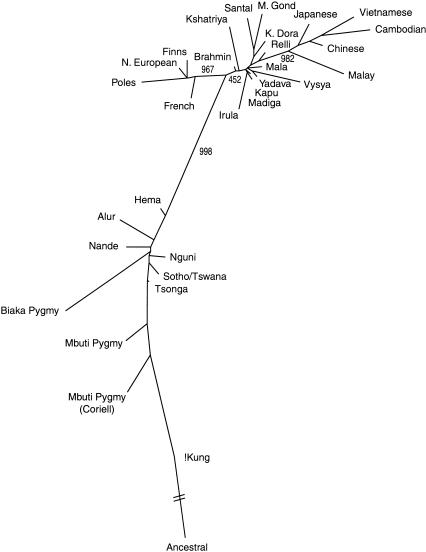
The genetic distance estimates reported here are based on Nei's D method (Nei 1987). These estimates are highly similar to those produced by alternative methods (squared Euclidean, Cavalli-Sforza's chord measure, and Reynold's distance), with all distance matrix correlations exceeding 0.985 (P < 0.0001) for our data. The genetic distances between Africans and the non-African groups are significantly larger than those among E. Asians, Europeans, and Indians (Table 2). In a neighbor-joining network, African, E. Asian, and European populations form distinct clusters, with bootstrap values of 99.8%, 98.2%, and 96.7%, respectively (Fig. 3). The South Indian caste and tribal populations are located in the same portion of the network, between the European and E. Asian clusters. The boot-strap value for a branch that includes the Indian populations with the E. Asian populations is only 45.2%, which reflects the fact that the genetic distance between the Indian and E. Asian population groups is almost identical to the genetic distance between the Indian and European population groups (Table 2).
Table 2.
Genetic Distances Between Africans, E. Asians, Europeans, and Indians
| African | E. Asian | European | |
|---|---|---|---|
| E. Asian | 0.1049 (0.0757-0.1341) | ||
| European | 0.0883 (0.0622-0.1144) | 0.0384 (0.0227-0.0541) | |
| Indian | 0.0785 (0.0554-0.1016) | 0.0203 (0.0130-0.0276) | 0.0201 (0.0140-0.0262) |
(95% CI in parentheses)
Figure 3.
A neighbor-joining network on the basis of 100 Alu insertion polymorphisms. The network is rooted using a hypothetical ancestral group that lacks the Alu insertions at each locus. Bootstrap values are shown for major branches.
The overall topology of the network shows similarity to the geographic distribution of these populations. The network is rooted by an ancestral outgroup that was created using an Alu insertion frequency of 0 for each locus. The actual genetic distance between the hypothetical root and any African population is smaller than the distance between the root and any non-African population. In the non-African cluster, three tribal Indian groups (Maria Gond, Santal, and Khonda Dora) have smaller pairwise genetic distances from the root than do the other populations. As suggested by the network, the average genetic distance among populations within each major group is higher for Africans (0.044) than for E. Asians (0.033), Europeans (0.018), or Indians (0.019).
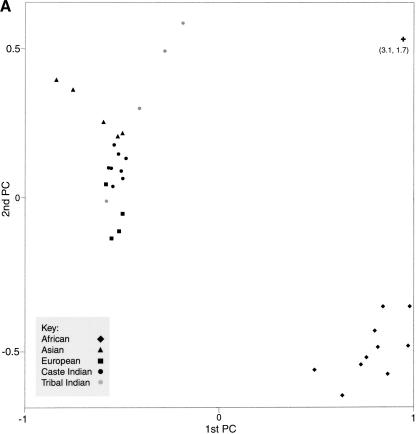
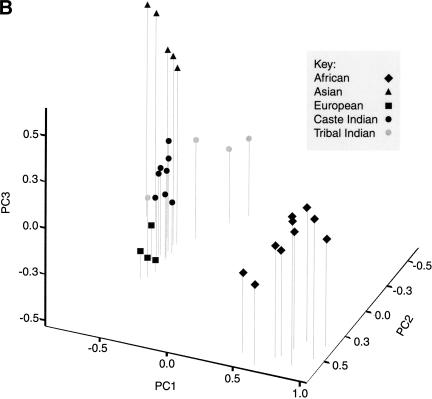
Principal components analysis of genetic distance estimates provides an alternative means of examining interpopulation relationships. An advantage of this method is that is does not impose a bifurcating structure on population relationships. Atwo-dimensional principal components plot of the 31 populations (Fig. 4A) demonstrates clustering of the African, E. Asian, and European populations, with the Indian caste populations located between the E. Asian and European populations (as in the network in Fig. 3). The African and non-African populations are well separated by the first component, which accounts for 51% of the variance in the genetic distance matrix. European, Indian caste, and E. Asian populations show a west-to-east gradient along the second component (16% of the variance). Three of the four tribal Indian groups diverge from the other Eurasians, and this divergence is toward the hypothetical ancestral population when the location of the root is included. It is interesting that the latter pattern is not readily apparent in the network shown in Figure 3 but becomes clear in the principal components plot and by examination of the actual pairwise genetic distances.
Figure 4.
(A) A plot of the first two principal components of a genetic distance matrix estimated for 31 populations. The hypothetical ancestral, or root population is also shown on the graph, although the actual coordinates of this population on the first two principal components (shown in parentheses below the symbol) place it well off the graph. (B) A plot of the first three principal components of the genetic distance matrix. The length of each line below the symbol represents the coordinate of each population on the third component.
Additional detail is provided by plotting the first two principal components against the third component in a three-dimensional graph (Fig. 4B). The third component, which accounts for 6% of the variance of the genetic distance matrix, resolves the Eurasian populations into three clusters (European, Indian caste and tribal, and E. Asian).
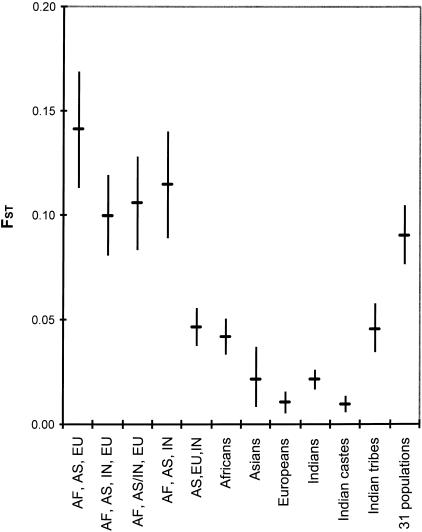
To quantify the amount of Alu genetic diversity that occurs between different human populations, FST was calculated for several population groupings (Fig. 5). The largest FST occurs for the traditional continental comparison of Africans, E. Asians, and Europeans (14.1%), but FST decreases to 10.0% when Indians are included as a fourth geographic group. Combining the Indian and E. Asian populations and comparing them with Europeans and Africans produces a similar result (FST = 10.6%). Comparing only the three non-African population groups produces a significantly lower FST of 4.7%. Using all 31 populations as the units of subdivision yields an FST of 9.0%. As expected, the FST values obtained within each of the geographic regions of India, E. Asia, Europe, and Africa demonstrate lower levels of population differentiation (FST = 0.010 to 0.042). All values of FST are significantly different from zero (P < 0.025). Ahierarchical analysis of molecular variance (AMOVA) using the 4 major groups and 31 populations indicates that 9.6% of variation occurs among groups, 1.9% occurs among populations within groups, and 88.6% occurs within populations. The among-group variation estimate of 9.6% obtained using AMOVA is highly similar to the four-group FST value of 10.0% obtained using the GDA program (see Methods).
Figure 5.
FST for world populations. FST estimates with 95% confidence intervals are shown for comparisons between major groups of Africans (AF), E. Asians (AS), Europeans (EU), and Indians (IN), for populations within the major groups, and for all 31 populations.
To test the hypothesis that genetic distance derived from the 100 Alu insertion polymorphisms is correlated with the geographic distance between populations, we examined these two variables using Mantel matrix comparisons and regression analysis. Comparison of geographic and genetic distance matrices for all 31 populations produces a highly significant product-moment correlation of 0.6918 (P < 0.00001). Linear regression analysis yields a predicted best line with a slope of 9.5 × 10-6/km. This indicates an increase in genetic distance of ∼0.095 +/- 0.009 per 1000 km. Nei's formula measures distances as -ln (I), in which I is the gene identity between populations, standardizing by the geometric mean of gene identity within regions. Thus, converting to identity within this range, the regression predicts a decrease of ∼1% genetic identity per 1000 km of geographic distance.
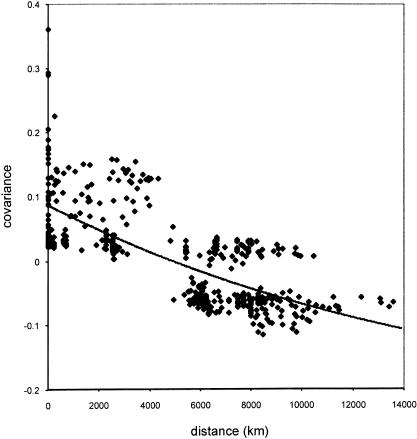
The Malécot model of isolation by distance was used to further test the relationship between genetic and geographic distances. This model takes the general form, ϕ(d) = ae-bd, in which ϕ(d) is the probability of genetic identity by descent for two randomly chosen individuals located distance d apart, and a and b are parameters estimated by nonlinear regression. Parameter a measures local kinship (i.e., genetic identity between individuals in the same population), and parameter b measures the rate of decline of genetic identity with geographic distance. This form of the Malécot model assumes that the population is distributed uniformly along a line. Model fitting produced regression parameters of local kinship (a) = 0.33970 and rate of decline (b) = 0.00006. Scalar adjustment for fitting negative covariance values (see Methods) yields a final curve with a y-intercept (parameter a) of 0.086 (Fig. 6). Both linear and nonlinear regression models used in our analyses capture ∼50% of the variance in the data (R2 = 0.479 and 0.520, respectively).
Figure 6.
Relationship between geographic and genetic distance. Great circle distances (in kilometers) are plotted against the covariance of allele frequencies for 31 populations. A nonlinear regression line based on a one-dimensional Malécot model is fit to the data.
The Malécot model can accommodate two-dimensional migration by modifying the isolation-by-distance equation as follows: ϕ(d) = ae-bdd-1/2. Application of this version of the model produced a poor fit (R2 = 0.228), which can be explained by the fact that the model assumes uniform migration in both dimensions. As shown in Figures 3 and 4, most of the variation in the genetic distance data occurs along a single dimension, so it is expected that a one-dimensional model would provide a better fit to the data.
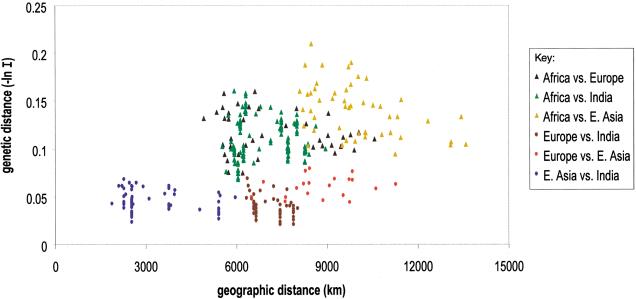
Additional insights are gained by separating the genetic versus geographic distance comparison into two components, distances between populations from different major groups and distances between populations from the same major group. Aplot of this relationship reveals interesting features of population structure not apparent from the regression analyses (Fig. 7). Pairwise comparison between populations from different major groups (Africa, E. Asia, India, and Europe) produces a significant positive correlation of 0.4660 (P < 0.0002). African versus non-African comparisons yield high geographic and genetic distances (triangles). African versus European and African versus Indian comparisons have overlapping ranges for geographic and genetic distances. The highest values for geographic and genetic distances occur for the African versus E. Asian comparisons. In contrast, the non-African comparisons (circles) have a wide geographic distribution (∼2000 to ∼12,000 km) but low, relatively uniform genetic distances (0.0202–0.0788). Almost all of the genetic distances comparing Eurasian populations are less than those of Africans versus Eurasians. Considered alone, there is little correlation between geographic and genetic distance in Eurasia. The pairwise comparisons between populations within each of the major groups of Africa, E. Asia, Europe, and India revealed lower, nonsignificant correlations.
Figure 7.
Geographic distance is plotted against genetic distance measured as the negative log of Nei's identity for pairwise comparisons between population groups from Africa, E. Asia, Europe, and India. The six possible comparison groups are color coded. Comparisons using Africans are triangles and Eurasians are circles.
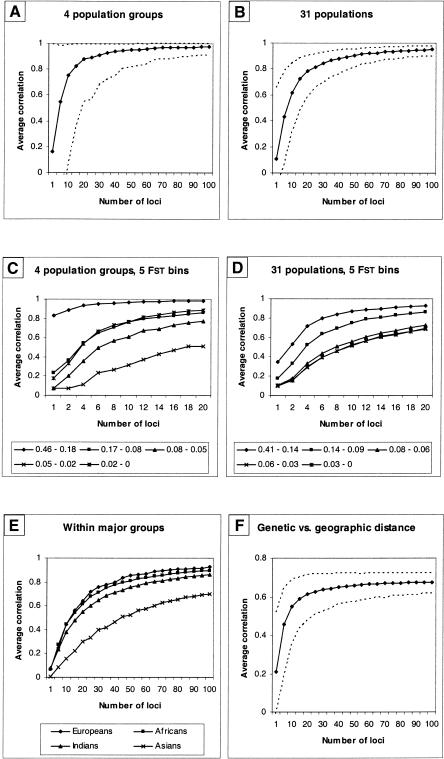
Using a strategy in which loci are randomly resampled, we assessed the consistency of genetic distance estimates as a function of the number of Alu insertion polymorphisms analyzed (Fig. 8). The correlation between pairs of genetic distance matrices based on randomly resampled loci rises rapidly with increasing numbers of Alu polymorphisms and achieves 95% of its maximum value when 35 loci are sampled for the 4 major population groups. Atotal of 51 loci are required to reach this level of correlation when 31 populations are analyzed (Fig. 8A,B). Higher correlations are achieved more rapidly using Alu markers with FST values in the upper 20th and 40th percentiles of all markers (Fig. 8C,D). Loci were separated into five quintiles ordered by FST value, and a correlation was estimated between a distance matrix on the basis of all 100 loci and a matrix on the basis of the loci in each FST quintile. The highest correlation, 0.95, was obtained using the matrix on the basis of the upper FST quintile, and the correlations decreased gradually with the lower quintiles (0.90, 0.66, 0.74, and 0.50 for the second, third, fourth, and fifth quintiles, respectively). For populations within the 4 major groups, Europeans, Africans, and Indians are similar in the number of loci needed to produce high correlations, whereas E. Asian populations show lower correlations even with 100 Alu markers (Fig. 8E).
Figure 8.
Average correlations between genetic distance matrices for increasing numbers of resampled Alu loci. (A) Four major geographic groups of Africa, Asia, Europe, and India; (B) 31 populations; (C) the 4 major groups with Alu loci sorted into 5 FST bins (actual FST values are indicated); (D) 31 populations and 5 FST bins; (E) correlations for populations within each of the 4 major geographic groups; (F) the correlation between genetics distance matrices and geographic distance for 31 populations. All points represent mean values from 1000 product-moment correlations. Broken lines indicate the 95% confidence interval.
We also used a resampling approach to assess consistency of the correlation between genetic and geographic distance. Genetic distance estimates attain 95% of the maximum correlation with geographic distance when 50 loci are used (Fig. 8F). The use of additional polymorphic Alu loci reduces the 95% confidence intervals about the correlation estimates considerably.
DISCUSSION
The genetic distance patterns using 100 Alu insertion polymorphisms show three major trends. First, the genetic distances between a hypothetical ancestral population lacking Alu insertions are smaller for African populations than for non-frican populations. Second, the genetic distances between African populations and non-African populations are large relative to distances between non-African populations. Third, the average genetic distance among populations within Africa is large relative to those among populations of Asia, Europe, or India. The latter result is similar to a recent finding based on extensive DNA resequencing (Yu et al. 2002). Because these results are based on a large number of individuals and many autosomal Alu insertion polymorphisms scattered throughout the genome, the genetic distance trends observed here are unlikely to be greatly influenced by sampling error.
The genetic inferences made here are in accord with an earlier study of 35 Alu loci (Watkins et al. 2001), but show higher statistical support for the inferred population relationships. For analyses of populations such as these, highly consistent estimates of genetic distance should require ∼50 Alu insertion polymorphisms. Greater consistency can be achieved by selecting loci with high FST values, but it should be borne in mind that this applies only to genetic distance results. Selection of loci on the basis of FST values could lead to biases in other applications (e.g., estimating the dates of demographic events).
Average Alu diversity is highest in Africa and lower in the other major population groups. The lowest diversity occurs in European populations. Among the 31 populations, 7 of the 10 African populations have the highest values for Alu heterozygosity, and the African populations with lower diversity are Pygmy populations. The diversity trends using 100 Alu insertion polymorphisms are, in general, consistent with studies using smaller numbers of Alu loci (Batzer et al. 1994; Stoneking et al. 1997; Watkins et al. 2001) and other molecular marker systems including autosomal microsatellites (Jorde et al. 1997; Jin et al. 2000), autosomal sequence variation (Tishkoff et al. 1996; Nickerson et al. 2000; Yu et al. 2002) Y-microsatellites (Seielstad et al. 1999), mtDNA(Merriwether et al. 1991; Jorde et al. 2000), and protein markers (Nei and Livshits 1989).
FST results suggest that Alu diversity between populations is highest for continental groups that are separated by large geographic distances, such as Africa, Asia, and Europe. The reduction in FST observed when Indians are included is consistent with previous work showing both Asian and European affinities in South Indian populations (Bamshad et al. 2001). FST is influenced by the number of populations analyzed and by the way in which individual populations are defined and sampled (Jorde 1980; Urbanek et al. 1996). Thus, caution is warranted in the interpretation of this statistic. The FST estimate of 9.0% using the 31 individual populations is likely to be the most unbiased. Other groupings, however, can yield insight into how human genetic variation is apportioned. Our results indicate that a major proportion of the intercontinental FST value is contributed by the African populations. The between-population variance for all E. Asian, Indian, and European populations is relatively low and not significantly different from the between-population variance within Africa alone. The observed patterns of between-population differentiation are consistent with a bottleneck or a successive series of bottleneck events that have reduced genetic diversity among non-African populations and may have coincided with emigration from Africa (Harpending and Rogers 2000; Jorde et al. 2000; Reich et al. 2001).
The large sample of Indian populations allowed us to examine eight Indian caste groups and four endogamous south Indian tribal populations. The Indian castes from the state of Andhra Pradesh show low between-group differences that are probably attributable, in part, to low geographic distances between groups. The tribal Indian groups show relatively high between-group differentiation that probably can be attributed to reproductive isolation and drift, consistent with previous studies of such populations (Das et al. 1996).
The distribution of Alu insertion polymorphisms reveals a consistent trend of higher average insertion frequencies in non-African populations. A recent survey of 2000 database-ascertained insertion/deletion polymorphisms also shows a pattern of higher ancestral allele frequencies in African populations (Weber et al. 2002). One explanation for this trend may be simple ascertainment bias. Most of the Alu insertions were identified using overlapping BAC sequences thought to be derived primarily from non-African samples (International Human Genome Consortium 2001; Weber et al. 2002). Several arguments against simple ascertainment bias accounting entirely for this pattern have been discussed previously for 35 Alu loci (Watkins et al. 2001). Simulations and in-depth statistical analyses suggest that, although present, simple ascertainment bias cannot explain the 20% difference in the averaged African versus non-African Alu insertion frequencies (A.R. Rogers, W.S. Watkins, C.T. Ostler, M.J. Bamshad, J.A. Walker, M.A. Batzer, and L.B. Jorde, in prep.). An alternative, direct (but labor-intensive) approach for addressing the issue would be to ascertain a set of Alu insertion polymorphisms from a panel of African-derived genomic libraries, which could then be genotyped in a world-wide panel of human DNA samples. The results could provide important information for future studies that utilize any type of polymorphism identified solely by database mining approaches.
The correlation observed between genetic and geographic distances suggests that geographic separation of populations has contributed substantially to the observed genetic distances between human populations, as has been seen with numerous other studies (Cavalli-Sforza et al. 1994). A negative exponential correlation between genetic and geographic distance is predicted theoretically (Malecot 1948; Kimura and Weiss 1964). Using the Malécot model, our data produced a large estimate of parameter a (0.086) and small estimate of parameter b (0.00006), substantially lower than estimates from local populations separated by smaller geographic distances (for review, see Jorde 1980). The shallow rate of decline of genetic distance suggested by these findings may reflect a relatively sudden, widespread geographic dispersion of a small subset of modern humans leaving Africa to populate Europe and Asia. Although extensive gene flow throughout Eurasia could also produce this result, the estimate of an effective Pleistocene population size of 10,000 breeding individuals makes the latter scenario improbable (Harpending et al. 1998).
Polymorphism age may influence the pattern of geographic and genetic differentiation observed in this study. A large percentage (∼90 %) of these Alu insertion polymorphisms have insertion allele frequencies greater than 0.10 and are likely to represent older polymorphisms that may predate the out-of-Africa expansion estimated to have occurred 156,000 years ago (Goldstein et al. 1995). Older polymorphisms may provide limited resolution of recent population history. The most prominent feature of the genetic distances in this study is the split between sub-Saharan African and non-African populations. This pattern highlights the human migration from Africa, which is likely to be one of the oldest major events in human evolutionary history (Cavalli-Sforza et al. 1994; Goldstein et al. 1995).
Young, population-specific Alu insertions polymorphisms, low-frequency SNPs, and rapidly mutating STRs may provide better resolution of more recent population events (e.g., the African Bantu expansion or recent migrations into the Indian subcontinent). Such genetic markers may produce significant correlations between geographic and genetic distances within continents or limited geographic regions. Using 60 STRs typed in 15 of the 31 populations examined here, Eller found a significant positive correlation for genetic and geographic distance in Africa (0.62), Eurasia (0.88), and the world (0.60), but not within Asia or Europe alone (Eller 1999).
Additional populations from other world regions including Northern Africa, Central Asia, extreme Southeast Asia, and the original populations of the Western Hemisphere will be required to fully understand the extent of human genetic variation. The 31 populations from 4 major world regions examined here show a pattern of decreasing genetic diversity moving away from an ancestral African origin. The amount of genetic variation distributed between populations is quite low, no more than 15% of the total genetic variance, even for major groups separated by large geographic distances. Low diversity, higher Alu insertion frequencies, and small genetic distances between European and Asian populations that are separated by large geographic distances suggest that a bottleneck has eliminated a great deal of ancestral genetic diversity.
METHODS
Samples
The human population samples used for this study have been described previously, and their locations are shown on a geopolitical Mercator projection of the Eastern Hemisphere (see Fig. 1; Jorde et al. 1995; Bamshad et al. 1998; Watkins et al. 1999; Bamshad et al. 2001). Briefly, the population groups and their sample sizes are Africans (152)—Alur (12), Biaka Pygmy (5), Hema (18), Coriell Mbuti Pygmy (5), a second sample of Mbuti Pygmy from the Democratic Republic of the Congo (33), Nande (17), Nguni (14), Sotho/Tswana (22), !Kung (San) (15), Tsonga (14); E. Asians (75)—Cambodian (12), Chinese (17), Japanese (17), Malay (6), Vietnamese (9), mixed E. Asian ancestry (14); Europeans (118)—Northern Europeans (68), French (20), Poles (10), Finns (20); Subcontinent Indians (365)—Brahmin (60), Kshatriya (11), Vysya (10), Kapu (58), Yadava (53), Relli (19), Mala (26), Madiga (29), Irula (34), Khonda Dora (27), Maria Gond (22), and Santal (16). Lymphocyte DNA was extracted from whole blood or cell lines using standard phenol/chloroform extraction procedures or a Puregene (Genecodes) DNA extraction kit. Samples were collected under institutionally approved internal review board protocols with informed consent.
Human-specific Alu insertion polymorphisms were identified from the available human genome sequence with BLAST using sequences specific to the Ya5, Yb8, Yb9, and Yc1 subfamilies (Carroll et al. 2001; Roy-Engel et al. 2001). Locus-specific primers were designed from unique flanking sequence using the PRIMER3 program to produce amplicons with allele sizes between 90 and 900 bp. Atotal of 614 Alu insertions demonstrated human-specific variation in a panel of 20 African Americans, 20 Greenland natives, 20 Egyptians, and 20 Europeans (Carroll et al. 2001; Roy-Engel et al. 2001). Asubset of 100 polymorphic Alu loci was selected and typed by PCR using standard 3-step conditions as described previously (Watkins et al. 2001). The 100 Alu insertion polymorphisms are distributed broadly over all 22 autosomes, and these insertions were absent from the genomes of several nonhuman primates that included common chimpanzee, pygmy chimpanzee, and gorilla.
Genotyping
Afew of the loci in our initial genotyping exhibited departures from HWE for some populations that may have been produced by difficulties in genotyping Alu insertions. Three Alu genotyping issues and how we addressed them are described below.
First, errors can result when a set of PCR primers amplifies more than one locus. If amplification products from paralogs produce products of similar size, there will be an apparent excess of heterozygotes. To address this problem, we tested each set of primers against the draft sequence of the Human Genome Project (HGP) using the BLAST search tool. For several loci, we also performed a PCR-based analysis of human/rodent monochromosomal hybrid cell-line DNA panels, as reported previously (Carroll et al 2001, Roy-Engel et al, 2001). Additionally, we redesigned primers and/or selected Alu insertion polymorphisms to ensure that each pair of primers amplified a single locus. Second, errors can also result from preferential amplification of the noninsertion allele in heterozygotes for some loci. If an Alu insertion product falls below the limit of visibility in our genotyping assay, heterozygotes could be mistaken for homozygotes. We dealt with this problem by redesigning primer sets and repeating amplifications that appeared problematic. Athird source of error may result from polymorphic variation of the template if it occurs at the 3′ ultimate or penultimate bases of the primer sequence. Such mutations may prevent or reduce amplification of one allele, causing some heterozygotes to be scored as homozygotes. We developed a statistical model to investigate this issue. For this model, an Alu locus is analogous to the ABO genetic system, with a null Alu allele being the O allele. This model improved the fit of genotype frequencies in only 2 of the 100 loci in our data set. Thus, it seems unlikely that this problem influences our results.
Data Analysis
Alu insertion frequencies for each population were determined by gene counting. HWE was tested for each locus in populations of Africans, E. Asians, Europeans, and Indians using Fisher's exact test. Atotal of 17 of 400 tests (3, 7, 1, and 6 for Africans, E. Asian, Europeans, and Indians, respectively) were significant (P < 0.05). This number is less than would be expected by chance alone. Individual populations were also tested for deviation from HWE. To evaluate HWE in the 31 populations, we compared the genotype frequencies within our sample against their expectations under HWE. At each locus and in each population in our sample, we measured the deviation from HWE by F = (JO - JE)/(1 - JE), in which JO is the observed homozygosity, and JE is the expected homozygosity under HWE, given the number of copies of the “+” and “-” alleles in the sample. With 31 regional populations and 100 loci, we can calculate 3100 separate values of F and their associated P values. The distribution of F is unimodal, with a mode near zero, as expected under HWE. We used a randomization procedure to test the significance of the difference between each estimate of F and 0.
Unbiased estimates of heterozygosity (h) were calculated as h = (n/n - 1)(1
- 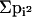 ), in which n is
the sample size and pi is the frequency of the ith allele. Genetic
distances between populations, on the basis of an infinite alleles model of
evolution, were calculated using DISPAN
(Ota 1993) or the GENDIST
(Felsenstein 1993) program,
and neighbor-joining trees were constructed using NEIGHBOR
(Felsenstein 1993). Branch
support for the population tree was assessed by bootstrap resampling using
SEQBOOT and CONSENSE. Two-level FST calculations were performed
using the Genetic Data Analysis (GDA) software package
(Weir 1996;
Lewis and Zaykin 2000).
Hierarchical analysis of molecular variance (AMOVA) was performed with the
Arlequin software package (Excoffier et
al. 1992; Schneider et al.
2000). Both GDA and Arlequin use a variance components approach to
estimate population structure statistics, but there are differences in the
ways in which missing data and bias corrections are handled. For details, see
Weir (1996), Excoffier (1992),
and Schneider et al. (2000).
Principal components were extracted from genetic distance matrices using the
MATFIT program (Lalouel
1973).
), in which n is
the sample size and pi is the frequency of the ith allele. Genetic
distances between populations, on the basis of an infinite alleles model of
evolution, were calculated using DISPAN
(Ota 1993) or the GENDIST
(Felsenstein 1993) program,
and neighbor-joining trees were constructed using NEIGHBOR
(Felsenstein 1993). Branch
support for the population tree was assessed by bootstrap resampling using
SEQBOOT and CONSENSE. Two-level FST calculations were performed
using the Genetic Data Analysis (GDA) software package
(Weir 1996;
Lewis and Zaykin 2000).
Hierarchical analysis of molecular variance (AMOVA) was performed with the
Arlequin software package (Excoffier et
al. 1992; Schneider et al.
2000). Both GDA and Arlequin use a variance components approach to
estimate population structure statistics, but there are differences in the
ways in which missing data and bias corrections are handled. For details, see
Weir (1996), Excoffier (1992),
and Schneider et al. (2000).
Principal components were extracted from genetic distance matrices using the
MATFIT program (Lalouel
1973).
Product-moment correlations and significance levels between genetic distance matrices or between genetic and geographic distance matrices were estimated by matrix randomization (Smouse et al. 1986). To estimate the correlation between genetic distance matrices and its confidence interval, data sets for a given number of Alu polymorphisms were created by random resampling of loci with replacement. For a given number of loci, 2000 individual genetic distance matrices were calculated from 2000 random loci sets, yielding 1000 product-moment correlations between pairs of matrices. A mean correlation and its 95% empirical confidence intervals were calculated. For comparisons of Alu polymorphsisms on the basis of FST, loci were sorted by FST into 5 bins of 20 loci, from which resampling was performed.
Geographic distances between pairs of populations were calculated as great circle distances on the basis of the approximate latitude and longitude of each of the 31 populations. The eight caste populations of Andhra Pradesh were all collected from the same region and have small between-group distances. Geographic distances were compared with standard genetic distances (as described above) or to the covariance of allele frequencies between populations. An R matrix of covariance (rij) was calculated as rij = [(pi - P)(pj - P)]/[P(1 - P)], in which pi and pj are the frequencies of the Alu insertion at a given locus in populations i and j, and P is the mean insertion frequency for that locus in all populations (Harpending and Jenkins 1973). The resulting R matrices are averaged over all loci.
The relationship between genetic and geographic distance was evaluated using linear and nonlinear regression analyses. Aone-dimensional Malécot model was fitted to the data: ϕ(d) = ae-bd, in which ϕ(d) is estimated as the genetic covariance (rij), d is geographic distance between each pair of populations, and a (local kinship) and b (rate of decline of kinship with geographic distance) are estimated by nonlinear regression. Aportion of the covariance estimates will be more dissimilar than average, yielding negative values. Curve fitting for the negative covariance values that occur at large geographic distances thus requires the addition of a scalar to ae-bd, specified as 1/(4Nem + 1) (Harpending 1973; Workman et al. 1973). Avalue of 10,000 was used for Ne (effective population size), and m (systematic pressure) was estimated as a parameter in the nonlinear regression. The estimated value of m was 0.0000737, yielding a scalar value of 0.253. All parameter estimation was performed using the SPSS software package.
Acknowledgments
We thank the many study participants and collaborators that have contributed to this work including samples sent by J.M. Naiad, B.B. Rao, T. Jenkins, J. Kidd, K. Kidd, and H. Soodyall. We also thank C. Ricker, J. Hawks, and H. Harpending for helpful contributions. Additionally, we thank the anonymous referees for their useful comments. This work is supported by National Institutes of Health Grants GM-59290 and RR-00064, Louisiana Board of Regents Millennium Trust Health Excellence Fund HEF (2000-05)-05, (2000-05)-01, (2001-06)-02, and National Science Foundation grants SBR-9514733, SBR-9512178, SBR-9818215, BCS-0218338, and BCS-0218370.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.894603.
Footnotes
Article published online before print in June 2003.
[Supplemental material is available online at www.genome.org. The following individuals kindly provided reagents, samples, or unpublished information as indicated in the paper: J.M. Naiad, B.B. Rao, T. Jenkins, J. Kidd, K. Kidd, and H. Soodyall.]
References
- Bamshad, M., Kivisild, T., Watkins, W.S., Dixon, M.E., Ricker, C.E., Rao, B.B., Naiad, J.M., Prasad, B.V., Reddy, P.G., Rasanayagam, A., et al. 2001. Genetic evidence on the origins of Indian caste populations. Genome Res. 11: 994-1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bamshad, M.J., Watkins, W.S., Dixon, M.E., Jorde, L.B., Rao, B.B., Naiad, J.M., Prasad, B.V., Rasanayagam, A., and Hammer, M.F. 1998. Female gene flow stratifies Hindu castes. Nature 395: 651-652. [DOI] [PubMed] [Google Scholar]
- Bamshad, M.J., Wooding, S., Watkins, W.S., Ostler, C.T., Batzer, M.A., and Jorde, L.B. 2003. Human population genetic structure and group membership. Am. J. Hum. Genet. 72: 578-579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batzer, M.A. and Deininger, P.L. 1991. A human-specific subfamily of Alu sequences. Genomics 9: 481-487. [DOI] [PubMed] [Google Scholar]
- Batzer, M.A. and Deininger, P.L. 2002. Alu repeats and human genomic diversity. Nat. Rev. Genet. 3: 370-379. [DOI] [PubMed] [Google Scholar]
- Batzer, M.A., Stoneking, M., Alegria-Hartman, M., Bazan, H., Kass, D.H., Shaikh, T.H., Novick, G.E., Ioannou, P.A., Scheer, W.D., Herrera, R.J., et al. 1994. African origin of human-specific polymorphic Alu insertions. Proc. Natl. Acad. Sci. 91: 12288-12292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batzer, M.A., Rubin, C.M., Hellmann-Blumberg, U., Alegria-Hartman, M., Leeflang, E.P., Stern, J.D., Bazan, H.A., Shaikh, T.H., Deininger, P.L., and Schmid, C.W. 1995. Dispersion and insertion polymorphism in two small subfamilies of recently amplified human Alu repeats. J. Mol. Biol. 247: 418-427. [DOI] [PubMed] [Google Scholar]
- Bowcock, A.M., Ruiz-Linares, A., Tomfohrde, J., Minch, E., Kidd, J.R., and Cavalli-Sforza, L.L. 1994. High resolution of human evolutionary trees with polymorphic microsatellites. Nature 368: 455-457. [DOI] [PubMed] [Google Scholar]
- Cann, R.L., Stoneking, M., and Wilson, A.C. 1987. Mitochondrial DNA and human evolution. Nature 325: 31-36. [DOI] [PubMed] [Google Scholar]
- Carroll, M.L., Roy-Engel, A.M., Nguyen, S.V., Salem, A.H., Vogel, E., Vincent, B., Myers, J., Ahmad, Z., Nguyen, L., Sammarco, M., et al. 2001. Large-scale analysis of the Alu Ya5 and Yb8 subfamilies and their contribution to human genomic diversity. J. Mol. Biol. 311: 17-40. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza, L.L., Menozzi, P., and Piazza, A. 1994. The history and geography of human genes. Princeton University Press, Princeton, NJ.
- Comas, D., Calafell, F., Benchemsi, N., Helal, A., Lefranc, G., Stoneking, M., Batzer, M.A., Bertranpetit, J., and Sajantila, A. 2000. Alu insertion polymorphisms in NW Africa and the Iberian Peninsula: Evidence for a strong genetic boundary through the Gibraltar Straits. Hum. Genet. 107: 312-319. [DOI] [PubMed] [Google Scholar]
- Das, K., Malhotra, K.C., Mukherjee, B.N., Walter, H., Majumder, P.P., and Papiha, S.S. 1996. Population structure and genetic differentiation among 16 tribal populations of central India. Hum. Biol. 68: 679-705. [PubMed] [Google Scholar]
- Deininger, P.L. and Batzer, M.A. 1999. Alu repeats and human disease. Mol. Genet. Metab. 67: 183-193. [DOI] [PubMed] [Google Scholar]
- Deka, R., Jin, L., Shriver, M.D., Yu, L.M., DeCroo, S., Hundrieser, J., Bunker, C.H., Ferrell, R.E., and Chakraborty, R. 1995. Population genetics of dinucleotide (dC-dA)n.(dG-dT)n polymorphisms in world populations. Am. J. Hum. Genet. 56: 461-474. [PMC free article] [PubMed] [Google Scholar]
- Eickbush, T.H. 1992. Transposing without ends: The non-LTR retrotransposable elements. New Biol. 4: 430-440. [PubMed] [Google Scholar]
- Eller, E. 1999. Population substructure and isolation by distance in three continental regions. Am. J. Phys. Anthropol. 108: 147-159. [DOI] [PubMed] [Google Scholar]
- Esnault, C., Maestre, J., and Heidmann, T. 2000. Human LINE retrotransposons generate processed pseudogenes. Nat. Genet. 24: 363-367. [DOI] [PubMed] [Google Scholar]
- Excoffier, L., Smouse, P., and Quattro, J. 1992. Analysis of molecular variance inferred from metric distances among DNA haplotypes: Application to human mitochondrial DNA restriction data. Genetics 131: 479-491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein, J. 1993. PHYLIP (Phylogeny Inference Package) version 3.5c. Distributed by the author. Department of Genetics, University of Washington, Seattle, WA.
- Feng, Q., Moran, J.V., Kazazian Jr., H.H., and Boeke, J.D. 1996. Human L1 retrotransposon encodes a conserved endonuclease required for retrotransposition. Cell 87: 905-916. [DOI] [PubMed] [Google Scholar]
- Forster, P., Rohl, A., Lunnemann, P., Brinkmann, C., Zerjal, T., Tyler-Smith, C., and Brinkmann, B. 2000. Ashort tandem repeat-based phylogeny for the human Y chromosome. Am. J. Hum. Genet. 67: 182-196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel, S.B., Schaffner, S.F., Nguyen, H., Moore, J.M, Roy, J., Blumenstiel, B., Higgins, J., DeFelice, M., Lochner, A., Faggart, M., et al. 2002. The structure of haplotype blocks in the human genome. Science 296: 2225-2229. [DOI] [PubMed] [Google Scholar]
- Goldstein, D.B., Ruiz Linares, A., Cavalli-Sforza, L.L., and Feldman, M.W. 1995. Genetic absolute dating based on microsatellites and the origin of modern humans. Proc. Natl. Acad. Sci. 92: 6723-6727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamdi, H., Nishio, H., Zielinski, R., and Dugaiczyk, A. 1999. Origin and phylogenetic distribution of Alu DNA repeats: Irreversible events in the evolution of primates. J. Mol. Biol. 289: 861-871. [DOI] [PubMed] [Google Scholar]
- Hammer, M.F., Karafet, T., Rasanayagam, A., Wood, E.T., Altheide, T.K., Jenkins, T., Griffiths, R.C., Templeton, A.R., and Zegura, S.L. 1998. Out of Africa and back again: Nested cladistic analysis of human Y chromosome variation. Mol. Biol. Evol. 15: 427-441. [DOI] [PubMed] [Google Scholar]
- Harpending, H. 1973. Inference in population structure studies. Am. J. Hum. Genet. 23: 536-538. [PMC free article] [PubMed] [Google Scholar]
- Harpending, H. and Jenkins, T. 1973. Genetic distance among Southern African populations. In Methods and theories of anthropological genetics. (eds. M.H. Crawford and P.L. Workman), pp. 177-199. University of New Mexico Press, Albuquerque, NM.
- Harpending, H. and Rogers, A. 2000. Genetic perspectives on human origins and differentiation. Annu. Rev. Genomics Hum. Genet. 1: 361-385. [DOI] [PubMed] [Google Scholar]
- Harpending, H.C., Batzer, M.A., Gurven, M., Jorde, L.B., Rogers, A.R., and Sherry, S.T. 1998. Genetic traces of ancient demography. Proc. Natl. Acad. Sci. 95: 1961-1967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingman, M., Kaessmann, H., Paabo, S., and Gyllensten, U. 2000. Mitochondrial genome variation and the origin of modern humans. Nature 408: 708-713. [DOI] [PubMed] [Google Scholar]
- International Human Genome Consortium. 2001. Initial sequencing and analysis of the human genome. Nature 409: 860-921. [DOI] [PubMed] [Google Scholar]
- Jin, L., Baskett, M.L., Cavalli-Sforza, L.L., Zhivotovsky, L.A., Feldman, M.W., and Rosenberg, N.A. 2000. Microsatellite evolution in modern humans: Acomparison of two data sets from the same populations. Ann. Hum. Genet. 64: 117-134. [DOI] [PubMed] [Google Scholar]
- Jorde, L. 1980. The genetic structure of human populations: A review. In Current developments in anthropological genetics (eds. J. Mielke and M. Crawford), pp. 135-208. Plenum, New York.
- Jorde, L.B., Bamshad, M.J., Watkins, W.S., Zenger, R., Fraley, A.E., Krakowiak, P.A., Carpenter, K.D., Soodyall, H., Jenkins, T., and Rogers, A.R. 1995. Origins and affinities of modern humans: A comparison of mitochondrial and nuclear genetic data. Am. J. Hum. Genet. 57: 523-538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorde, L.B., Rogers, A.R., Bamshad, M., Watkins, W.S., Krakowiak, P., Sung, S., Kere, J., and Harpending, H.C. 1997. Microsatellite diversity and the demographic history of modern humans. Proc. Natl. Acad. Sci. 94: 3100-3103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorde, L.B., Watkins, W.S., Bamshad, M.J., Dixon, M.E., Ricker, C.E., Seielstad, M.T., and Batzer, M.A. 2000. The distribution of human genetic diversity: Acomparison of mitochondrial, autosomal, and Y-chromosome data. Am. J. Hum. Genet. 66: 979-988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurka, J. 1997. Sequence patterns indicate an enzymatic involvement in integration of mammalian retroposons. Proc. Natl. Acad. Sci. 94: 1872-1877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kajikawa, M. and Okada, N. 2002. LINEs mobilize SINEs in the eel through a shared 3′ sequence. Cell 111: 433-444. [DOI] [PubMed] [Google Scholar]
- Kimura, M. and Weiss, G.H. 1964. The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics 46: 561-576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lalouel, J.M. 1973. Topology of population structure. In Genetic structure of populations (ed. N.E. Morton), pp. 139-149. University Press of Hawaii, Honolulu, HI.
- Lewis, P.O. and Zaykin, D. 2000. Genetic Data Analysis: Computer program for the analysis of allelic data. Distributed by the author, Department of Ecology and Evolution, University of Connecticut, Storrs, CT.
- Luan, D.D., Korman, M.H., Jakubczak, J.L., and Eickbush, T.H. 1993. Reverse transcription of R2Bm RNA is primed by a nick at the chromosomal target site: Amechanism for non-LTR retrotransposition. Cell 72: 595-605. [DOI] [PubMed] [Google Scholar]
- Malecot, G. 1948. Les Mathematiques de l'Heredite, Masson, Paris (translated as The Mathemetics of Heredity (1969). Freeman, San Francisco, CA.
- Marth, G., Schuler, G. Yeh, R., Davenport, R., Agarwala, R., Church, D., Wheelan, S., Baker, J., Ward, M., Kholodov, M., et al. 2003. Sequence variations in the public human genome data reflect a bottlenecked population history. Proc. Natl. Acad. Sci. 100: 376-381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merriwether, D.A., Clark, A.G., Ballinger, S.W., Schurr, T.G., Soodyall, H., Jenkins, T., Sherry, S.T., and Wallace, D.C. 1991. The structure of human mitochondrial DNA variation. J. Mol. Evol. 33: 543-555. [DOI] [PubMed] [Google Scholar]
- Miki, Y., Katagiri, T., Kasumi, F., Yoshimoto, T., and Nakamura, Y. 1996. Mutation analysis in the BRCA2 gene in primary breast cancers. Nat. Genet. 13: 245-247. [DOI] [PubMed] [Google Scholar]
- Nasidze, I., Risch, G.M., Robichaux, M., Sherry, S.T., Batzer, M.A., and Stoneking, M. 2001. Alu insertion polymorphisms and the genetic structure of human populations from the Caucasus. Eur. J. Hum. Genet. 9: 267-272. [DOI] [PubMed] [Google Scholar]
- Nei, M. 1987. Molecular evolutionary genetics. Columbia University Press, New York.
- Nei, M. and Livshits, G. 1989. Genetic relationships of Europeans, Asians and Africans and the origin of modern Homo sapiens. Hum. Hered. 39: 276-281. [DOI] [PubMed] [Google Scholar]
- Nickerson, D.A., Taylor, S.L., Fullerton, S.M., Weiss, K.M., Clark, A.G., Stengard, J.H., Salomaa, V., Boerwinkle, E., and Sing, C.F. 2000. Sequence diversity and large-scale typing of SNPs in the human apolipoprotein E gene. Genome Res. 10: 1532-1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okada, N. 1991. SINEs. Curr. Opin. Genet. Dev. 1: 498-504. [DOI] [PubMed] [Google Scholar]
- Oldridge, M., Zackai, E.H., McDonald-McGinn, D.M., Iseki, S., Morriss-Kay, G.M., Twigg, S.R., Johnson, D., Wall, S.A., Jiang, W., Theda, C., et al. 1999. De novo alu-element insertions in FGFR2 identify a distinct pathological basis for Apert syndrome. Am. J. Hum. Genet. 64: 446-461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ota, T. 1993. Dispan: Genetic distance and phylogenetic analysis. Pennsylvania State University, University Park, PA.
- Perez-Lezaun, A., Calafell, F., Mateu, E., Comas, D., Ruiz-Pacheco, R., and Bertranpetit, J. 1997. Microsatellite variation and the differentiation of modern humans. Hum. Genet. 99: 1-7. [DOI] [PubMed] [Google Scholar]
- Reich, D.E., Cargill, M., Bolk, S., Ireland, J., Sabeti, P.C., Richter, D.J., Lavery, T., Kouyoumjian, R., Farhadian, S.F., Ward, R., et al. 2001. Linkage disequilibrium in the human genome. Nature 411: 199-204. [DOI] [PubMed] [Google Scholar]
- Risma, K.A., Wang, N., Andrews, R.P., Cunningham, C.M., Ericksen, M.B., Bernstein, J.A., Chakraborty, R., and Hershey, G.K. 2002. V75R576 IL-4 receptor α is associated with allergic asthma and enhanced IL-4 receptor function. J. Immunol. 169: 1604-1610. [DOI] [PubMed] [Google Scholar]
- Roy-Engel, A.M., Carroll, M.L., Vogel, E., Garber, R.K., Nguyen, S.V., Salem, A.H., Batzer, M.A., and Deininger, P.L. 2001. Alu insertion polymorphisms for the study of human genomic diversity. Genetics 159: 279-290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin, C.M., Houck, C.M., Deininger, P.L., Freidmann, T., and Schmid, C.W. 1980. Partial nucleotide sequence of the 300-nucleotide interspersed repeated human DNA sequences. Nature 284: 372-374. [DOI] [PubMed] [Google Scholar]
- Sachidanandam, R., Weissman, D., Schmidt, S.C., Kakol, J.M., Stein, L.D., Marth, G., Sherry, S., Mullikin, J.C., Mortimore, B.J., Willey, D.L., et al. 2001. Amap of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 409: 928-933. [DOI] [PubMed] [Google Scholar]
- Schneider, S., Kueffer, J.M., Roesslie, D., and Excoffier, L. 2000. Arlequin: A software for population genetic data analysis. University of Geneva, Geneva.
- Seielstad, M., Bekele, E., Ibrahim, M., Toure, A., and Traore, M. 1999. Aview of modern human origins from Y chromosome microsatellite variation. Genome Res. 9: 558-567. [PMC free article] [PubMed] [Google Scholar]
- Smouse, P.E., Long, J.C., and Sokal, R.R. 1986. Multiple regression and correlation extensions of the Mantel test of matrix correspondence. System. Zool. 35: 627-632. [Google Scholar]
- Stephens, J.C., Schneider, J.A., Tanguay, D.A., Choi, J., Acharya, T., Stanley, S.E., Jiang, R., Messer, C.J., Chew, A., Han, J.H., et al. 2001. Haplotype variation and linkage disequilibrium in 313 human genes. Science 293: 489-493. [DOI] [PubMed] [Google Scholar]
- Stoneking, M. and Soodyall, H. 1996. Human evolution and the mitochondrial genome. Curr. Opin. Genet. Dev. 6: 731-736. [DOI] [PubMed] [Google Scholar]
- Stoneking, M., Fontius, J.J., Clifford, S.L., Soodyall, H., Arcot, S.S., Saha, N., Jenkins, T., Tahir, M.A., Deininger, P.L., and Batzer, M.A. 1997. Alu insertion polymorphisms and human evolution: Evidence for a larger population size in Africa. Genome Res. 7: 1061-1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang, K., Ngoi, S.M., Gwee, P.C., Chua, J.M., Lee, E.J., Chong, S.S., and Lee, C.G. 2002. Distinct haplotype profiles and strong linkage disequilibrium at the MDR1 multidrug transporter gene locus in three ethnic Asian populations. Pharmacogenetics 12: 437-450. [DOI] [PubMed] [Google Scholar]
- Tishkoff, S.A., Dietzsch, E., Speed, W., Pakstis, A.J., Kidd, J.R., Cheung, K., Bonne-Tamir, B., Santachiara-Benerecetti, A.S., Moral, P., and Krings, M. 1996. Global patterns of linkage disequilibrium at the CD4 locus and modern human origins. Science 271: 1380-1387. [DOI] [PubMed] [Google Scholar]
- Tishkoff, S.A., Goldman, A., Calafell, F., Speed, W.C., Deinard, A.S., Bonne-Tamir, B., Kidd, J.R., Pakstis, A.J., Jenkins, T., and Kidd, K.K. 1998. Aglobal haplotype analysis of the myotonic dystrophy locus: Implications for the evolution of modern humans and for the origin of myotonic dystrophy mutations. Am. J. Hum. Genet. 62: 1389-1402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urbanek, M., Goldman, D., and Long, J.C. 1996. The apportionment of dinucleotide diversity in Native Americans and Europeans: A new approach to measuring gene identity reveals asymmetric patterns of divergence. Mol. Biol. Evol. 13: 943-953. [DOI] [PubMed] [Google Scholar]
- Vanin, E.F. 1985. Processed pseudogenes: Characteristics and evolution. Annu. Rev. Genet. 19: 253-272. [DOI] [PubMed] [Google Scholar]
- Vigilant, L., Stoneking, M., Harpending, H., Hawkes, K., and Wilson, A.C. 1991. African populations and the evolution of human mitochondrial DNA. Science 253: 1503-1507. [DOI] [PubMed] [Google Scholar]
- Wallace, M.R., Andersen, L.B., Saulino, A.M., Gregory, P.E., Glover, T.W., and Collins, F.S. 1991. Ade novo Alu insertion results in neurofibromatosis type 1. Nature 353: 864-866. [DOI] [PubMed] [Google Scholar]
- Watkins, W.S., Bamshad, M., Dixon, M.E., Bhaskara Rao, B., Naiad, J.M., Reddy, P.G., Prasad, B.V., Das, P.K., Reddy, P.C., Gai, P.B., et al. 1999. Multiple origins of the mtDNA 9-bp deletion in populations of South India. Am. J. Phys. Anthropol. 109: 147-158. [DOI] [PubMed] [Google Scholar]
- Watkins, W.S., Ricker, C.E., Bamshad, M.J., Carroll, M.L., Nguyen, S.V., Batzer, M.A., Harpending, H.C., Rogers, A.R., and Jorde, L.B. 2001. Patterns of ancestral human diversity: An analysis of Alu-insertion and restriction-site polymorphisms. Am. J. Hum. Genet. 68: 738-752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber, J.L., David, D., Heil, J., Fan, Y., Zhao, C., and Marth, G. 2002. Human diallelic insertion/deletion polymorphisms. Am. J. Hum. Genet. 71: 854-862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner, A.M., Deininger, P.L., and Efstratiadis, A. 1986. Nonviral retroposons: Genes, pseudogenes, and transposable elements generated by the reverse flow of genetic information. Annu. Rev. Biochem. 55: 631-661. [DOI] [PubMed] [Google Scholar]
- Weir, B.S. 1996. Genetic Data Analysis II. Sinauer, Sunderland, MA.
- Workman, P.L., Harpending, H., Lalouel, J.M., Lynch, C., Niswander, J.D., and Singleton, R. 1973. Population studies on southwestern Indian tribes VI. In Genetic structure of populations (ed. N.E. Morton), pp. 166-194. University Press of Hawaii, Honolulu, HI.
- Xing, J., Salem, A.H., Hedges, D., Kilroy, G.E., Watkins, W.S., Schienman, J.E., Stewart, C.B., Jurka, J., Jorde, L.B., and Batzer, M.A. 2003. Comprehensive analysis of two Yd subfamilies. J. Mol. Evol. (in press). [DOI] [PubMed]
- Yu, N., Chen, F.C., Ota, S., Jorde, L.B., Pamilo, P., Patthy, L., Ramsay, M., Jenkins, T., Shyue, S.K., and Li, W.H. 2002. Larger genetic differences within africans than between africans and eurasians. Genetics 161: 269-274. [DOI] [PMC free article] [PubMed] [Google Scholar]