Signal Processing and Flagellar Motor Switching During Phototaxis of Halobacterium salinarum

Abstract

Prokaryotic taxis, the active search of motile cells for the best environmental conditions, is one of the paradigms for signal transduction. The search algorithm implemented by the cellular biochemistry modulates the probability of switching the rotational direction of the flagellar motor, a nanomachine that propels prokaryotic cells. On the basis of the well-known biochemical mechanisms of chemotaxis in Escherichia coli, kinetic modeling of the events leading from chemoreceptor activation by ligand binding to the motility response has been performed with great success. In contrast to Escherichia coli, Halobacterium salinarum, in addition, responds to visible light, which is sensed through specific photoreceptors of different wavelength sensitivity (phototaxis). Light stimuli of defined intensity and time course can be controlled precisely, which facilitates input-output measurements used for system analysis of the molecular network connecting the sensory receptors to the flagellar motor switch. Here, we analyze the response of halobacterial cells to single and double-pulse light stimuli and present the first kinetic model for prokaryotic cells that couples the signal-transduction pathway with the flagellar motor switch. Modeling based on experimental data supports the current biochemical model of halobacterial phototaxis. Moreover, the simulations demonstrate that motor switching occurs through subsequent rate-limiting steps, which are both under sensory control, suggesting that two signals may be involved in halobacterial phototaxis.

Halobacterium salinarum cells swim back and forth by switching the rotational sense of their flagellar bundle, which is composed of 5-10 flagellar filaments (Alam and Oesterhelt 1984). Without exogenous stimulus, spontaneous reversals of the swimming direction occur randomly on the time scale of tens of seconds. Stimulation with UV or blue light shortens the average duration of the current run by inducing the next switching event earlier, whereas an increase of orange light intensity prolongs the straight swimming period by transiently suppressing spontaneous motor switching (Hildebrand and Schimz 1985). Excited cells adapt to the incident light intensity and resume their spontaneous behavior within the time period of one motor-switching event (Hildebrand and Schimz 1985). The interplay of excitation and adaptation makes the cells accumulate at those sites of their habitat that provide the best environmental conditions.

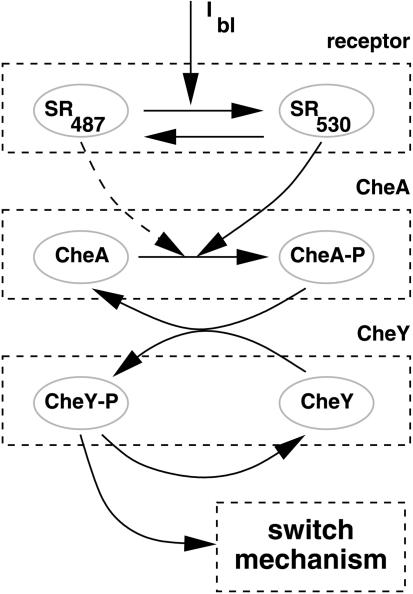
Light sensing occurs through sensory rhodopsins, transmembrane photoreceptors that are associated physically with their specific signal transducers, which are homologous in sequence, structure, and function to the eubacterial methyl-accepting chemotaxis proteins, but lack an extracellular ligand-binding domain (Hoff et al. 1997, and references therein; Gordeliy et al. 2002). Sensory rhodopsin I (SRI) is the receptor specific for orange and UV light; sensory rhodopsin II (SRII) senses blue light. Photo-isomerization of the retinal chromophore of a sensory rhodopsin molecule by a single photon, and subsequent reisomerization in a light-independent reaction produces a transient conformational change of the protein moiety embedding the chromophore that is transmitted to the corresponding transducer molecule HtrI or HtrII (halobacterial transducer of rhodopsin), respectively (for review, see Hoff et al. 1997). The conformational state of the receptor-transducer complex is then relayed to the flagellar motor switch by modulating the activity of the autophosphorylating kinase CheA, which phosphorylates the CheY protein required for flagellar motor switching (Rudolph and Oesterhelt 1995, 1996; Rudolph et al. 1995). Sensory adaptation is mediated by methylation and demethylation of the transducers, which resets the signaling activity to that of the unstimulated state (Alam et al. 1989; Spudich et al. 1989; Nordmann et al. 1994).

Whereas the molecules involved in photoreception and signal transduction are well studied, the dynamic behavior of these individual components regarding excitation, amplification, and adaptation during sensing and response still is speculative. This is especially true with respect to the dynamic behavior of the switch complex of the flagellar motor apparatus that is used as readout of input-output measurements. Halobacterial genome projects have revealed that, for the proteins which compose the flagellar motor and its switch complex in Escherichia coli, no homologs with significant sequence similarity are present in Halobacterium, whereas the signaling molecules of the two-component system are conserved (Ng et al. 2000; D. Oesterhelt, unpubl.). This suggests that the biochemistry of motor switching might be different in both species.

Because it is easy to control light stimuli in intensity, time, and space, stimulus-response relationships can be measured precisely on a single-cell level and can be used to probe structure and dynamics of the molecular network that mediates phototaxis.

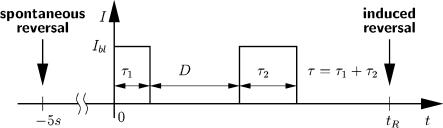
At room temperature, halobacterial cells observed with nonactinic infrared light spontaneously reverse their swimming direction on a time scale of tens of seconds (on average once every 43 sec at 21°C). When challenged with a short blue-light pulse, motor switching can already occur 1 sec after stimulus onset, suggesting that a switching signal can be formed rapidly (Marwan and Oesterhelt 1987). The time elapsing after pulse delivery until the response occurs depends on the intensity of the pulse, suggesting that the rate of signal formation increases with the number of activated receptor-transducer complexes. If the intensity of the stimulus pulse is low, the cellular response becomes a stochastic event (Marwan et al. 1988). One and the same cell then will not respond to each pulse delivered, and the probability that a response will occur depends on the stimulus strength (Marwan and Oesterhelt 1987). Intensity dependence of the response time of single cells was used to determine the time course of the formation of the switching signal by double-pulse experiments, in which the second pulse was used to probe the amount of signal produced in response to the first pulse. These experiments revealed that formation of the switching signal is proportional to the number of activated sensory rhodopsin molecules and that it occurs on the time scale of the response time (Marwan and Oesterhelt 1987). The response to single and double pulses of blue light can be described by an equation linking the response time t_R (the time interval elapsing from the beginning of the stimulus until motor switching) to the various parameters of the stimulation program:

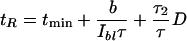1

in which t_R is the average response time, I_bl is the intensity of the blue light stimulus, and b is an empirical constant accounting for the light sensitivity of the cells. The time profile of stimulation is shown in Figure 1. At saturating light intensity, the response time adopts a minimal value of t_R = t_min 1 sec. Below the saturation level, it is reciprocally proportional to the light exposure of the total pulse [I_bl(τ₁+ τ₂)]. The third term of the equation describes the cellular response to double-pulse stimulation. The response time is proportional to the dark interval D, which separates the two pulses, and it is also proportional to the ratio of the duration of the second pulse τ₂ and the total of both pulses τ.

Figure 1.

Time profile of a stimulus program used in double-pulse experiments.

A mechanism in which activated photoreceptor molecules cause the catalytic formation of the switching signal, whatsoever its chemical identity might be, was proposed by Marwan and Oesterhelt (1987). Starting from this mechanism, we developed a kinetic model that reproduces the experimental findings to a satisfying grade.

RESULTS

On the basis of experimental results on double-pulse stimulation and on the molecular data that are currently available, we aimed at identifying a dynamical mathematical model for sensory excitation including the process of motor switching. Because the probabilities for spontaneous, as well as for stimulated motor switching are very similar (if not identical) during CW and CCW motor rotation; our model does not discriminate between the alternative rotational modes. All models are based on ordinary differential equations, and the reaction rates are calculated by the law of mass action.

We started with a most simple model composed of known biochemical elements of the signaling pathway (basic model; see below). The basic model, however, could not explain the experimental observations because it does not include any decision-making step that determines the time point of the reversal. Therefore, this simple kinetic model was step-by-step made more complex (model a) until the simulations perfectly fitted to equation 1 (model b). Finally, the signal-oriented model b could be translated into a molecular model (model c), which perfectly simulates the response of halobacterial cells to double-pulse stimulation programs as well as their spontaneous motor switching behavior. In the following, we describe the individual models with respect to the kinetic constraints imposed by the response of halobacterial cells to double-pulse stimulation with blue light.

Basic Model

The basic model considers only the first steps of the signal-transduction chain mediating the excitation process. Processes due to adaptation are neglected because the cellular response time to the double pulses is shorter than the time period for adaptation. The basic model pathway consists of the sensory rhodopsin-transducer complex and the autophosphorylating kinase CheA, which phosphorylates CheY by catalytic transfer of the phosphoryl group. CheY-P finally acts as the switching signal (Fig. 2).

Figure 2.

Simple basic model accounting for the first steps of a two-component system type signal cascade.

Starting from the basic model, we investigated different models for the dynamic behavior of the switch put under photosensory control through CheY-P. The kinetic parameters of the receptor and the number of receptor complexes are known and were incorporated into the basic model and in the other models derived thereof. All other parameters were determined by fitting the simulation results to the calculated values of equation 1.

Model a

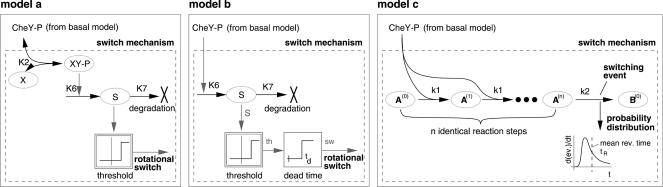
Spontaneous, as well as light-controlled motor switching could occur by continuous formation of the switch signal until a certain threshold is reached. The slope of the ramp-like time course of the concentration of the switching signal would determine the response time accordingly.

At saturating light intensities, the minimal response time (in average) does not decline beyond a minimal duration of 1 sec. It has been demonstrated experimentally that this saturation phenomenon is caused by light-independent downstream events rather than by light saturation of the photoreceptors (Marwan and Oesterhelt 1987). The minimal time is already reached, even at a photon exposure, which only activates approximately half of the sensory rhodopsin II molecules. It cannot be further reduced by a second pulse given at a time when most of the photoreceptor molecules activated by the first pulse have already recovered (Marwan and Oesterhelt 1987). Therefore, we had to include a light-independent, rate-limiting step (reaction k2) that precedes the decision making step (threshold) in a first version of the switch model (Fig. 3, model a). Before all the photoreceptors are activated, most of X is already bound to CheY-P. Because XYP mediates the formation of the switching signal S, the process cannot be accelerated any more by further increasing the light intensity. X is a hypothetical molecule, that, for example, could be fumarate, which has been shown to be a switch factor (Marwan et al. 1990).

Figure 3.

Different mathematical models for the dynamical switch behavior. In model c dissociation of bound CheY from the subunits of the switch complex is so slow that it is neglected in the simulation.

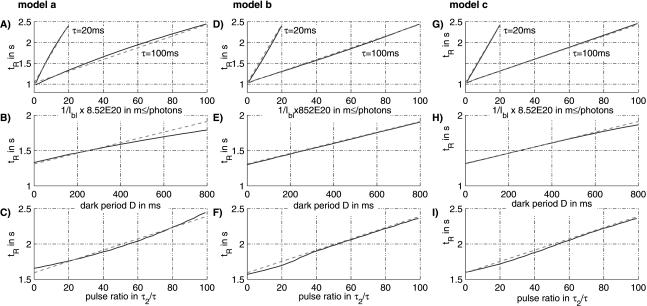
When compared with the experimental results, the curves for the single-pulse experiment show a reasonable good fit with the calculated values, although the simulated curves are slightly bent (Fig. 4A,B,C). A significant difference between simulation and the stimulus dependence of the cellular response as predicted by equation 1 exists for experiment B (variation of the dark period): The mathematical description predicts a slope of τ₂/τ = 3/4, which is much smaller in the simulation results. This deviation in the simulation is caused by the fact that the photons delivered during the second pulse, according to the model, are less effective than the photons delivered by the first pulse, as the signaling cascade to some extent is saturated by depletion of X. However, equation 1 claims a linear correlation. The deviation between simulation and cellular response as predicted by the equation in experiment C (variable ratio of the duration of the second pulse and the total pulse time) is only minor, but the curve is bent down in its middle part. The difference of the response time for τ₂ = 0 and τ₂ = τ is equal to the duration of the dark period D = 800 msec, as predicted by the equation. The relatively low values in the middle again refer to the nonlinear saturation effect.

Figure 4.

Simulation results (solid lines) of the models a, b, and c as compared with the mathematical equation (broken lines) describing the cellular response to double-pulse stimuli. In all panels shown, the reaction time t_R is plotted against various parameters. (A,D,G) A single light pulse with 20 or 100 msec duration and variable intensity is applied to the cells. The value of the reciprocal intensity is given on the abscissa. (B,E,H) Double pulses are applied with a duration of the first pulse of τ₁ = 25 msec and of the second pulse of τ₂ = 75 msec, whereas the dark time between the two pulses is varied. (C,F,I) Results of double-pulse experiments with a constant total duration of τ = 100 msec, a dark period of D = 800 msec and variable ratio of the two pulses.

Model b

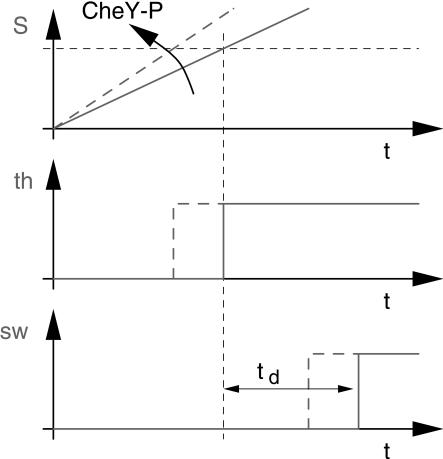
In model a, motor switching occurs without delay when the switching signal exceeds a critical level. Because there are no known biochemical correlates to the intermediates X and S introduced downstream of CheY-P by model a, and because model a does not even reproduce the experimental results in a perfect way, we included the dynamics of motor switching into the overall process. Thereby, we avoided introducing any additional soluble factors downstream of CheY-P as far as possible. In this second try (model b), we implemented an intrinsic dead time that delays the decision of the preceding threshold to account for t_min instead of assuming a step that limits the formation of the switching signal (Fig. 3, model b). In model b, CheY-P directly controls the formation of the switching signal S, which is totally depleted at the beginning of a simulated run interval. After reaching the threshold, the actual switching event is delayed by a constant dead time t_d (Fig. 5).

Figure 5.

Time course of the cellular concentration of the switching signal according to signal-oriented model b. Because the degradation of S is negligible, S can be regarded as an integrator for CheY-P. The threshold signal th indicates when S has reached the threshold level. This triggers a constant dead time, t_d, after which the actual switching is taking place, indicated by the signal, sw.

Because this model does not contain a rate-limiting step (apart from the limited number of receptor molecules), the plots show a linear correlation for all experiments (Fig. 4D,E,F). All results for the model fit precisely to the values from the formula.

Model c

In the models a and b, motor switching is triggered by threshold crossing of the switching signal S without providing a kinetic model for the switching mechanism. Model b results in a good agreement with the experimental data; therefore, we now describe the signal formation, the decision-making step, and the delay of model b by biochemical reactions instead of mathematical functions to obtain model c. In model b, the formation of the switching signal S is catalyzed by CheY-P and is degraded again in a first-order reaction. However, the parameter optimization resulted in a negligible value for the degradation constant, therefore, from the cybernetic point of view, the formation of S can be regarded as an ideal integrator of the signal CheY-P. If the integrator reaches a certain level, the threshold flips and triggers the constant dead time. After this constant delay, the switching process occurs. Although the simulations of model b match very well with the formula, it is just a description of the average behavior of a large number of cells equivalent to a large number of experiments with a single cell. It cannot give a predication of the distribution of reversals in a population of cells. Therefore, it seemed obvious to include the switching process of the flagellar motor into the kinetic model for the photosensory control of phototaxis by putting the individual steps of the models for spontaneous motor switching under the control of the switching signal. The four-state model (Marwan and Oesterhelt 1987), when put under the control of CheY-P, did not reproduce the experimental results with a sufficiently high fidelity (simulation results not shown). Duke et al. (2001) described an elegant and attractive allosteric model of a ring of 34 FliM protein subunits in an E. coli flagellar motor-switch complex. By simulating their model, we found that the probability distribution of a switching event cannot describe the experimentally observed low probability directly after a preceding switching event found in Halobacterium (Fig. 6). In contrast, a model with a chain of multiple simple reactions (Fig. 3, model c) similar to that proposed by Naber (1997) yielded excellent results.

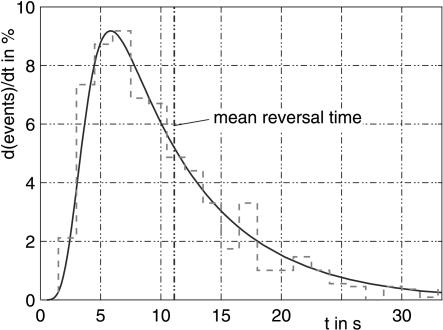
Figure 6.

Distribution of spontaneous motor reversals at 34°C. (Solid line) Simulation; (dotted line) measured values. Experimental data taken from Marwan and Oesterhelt (1987).

Analogous to the mentioned models, not only the average response time can be derived from this model, but also the time-dependent probability of a switching event (transitions from A⁽ⁿ⁾ to B⁽⁰⁾). This probability distribution was already measured for unstimulated, spontaneous reversals. Therefore, we first fitted the parameters k1 and k2 of the switch model to the distribution of spontaneous reversals. We also tried several numbers of steps of the reaction chain and obtained good results for n = 7 CheYP-dependent reactions. Figure 6 shows the simulation results and the experimental data for spontaneous events in the dark at 34°C. These data are reproduced very well (the parameter k1, k2, and n were fitted manually. Naber identified his model to be comprised of n = 16 steps).

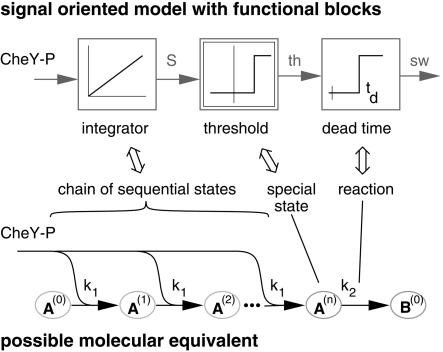
The first n reactions of the switch model are responsible for the low-switching probability within the first seconds after the last reversal and for its steep increase thereafter. The last reaction, k2, is much slower than the preceding ones and dominates the decay shown in the probability distribution in Figure 6. According to model b, the first step of the switch dynamic has to act like an integrator for the switch signal CheY-P. A sequence of equal reactions of CheY-P with the switch-complex acts in the first approximation as an integrator (Fig. 7) and is additionally consistent with the model proposed by Naber (1997). Each step in this chain of reactions changes the state of the switch complex. The switch complex spontaneously undergoes subsequent steps to finally reach state A⁽ⁿ⁾. State A⁽ⁱ⁾ can be interpreted as a fraction of cells in an experiment that has been modified i times. Alternatively, it can be regarded as the probability of a single cell being modified i times. Thus, the time course of the reaction rate for the transition from A⁽ⁿ⁾ to B⁽⁰⁾ can be regarded as the probability distribution of the switching event, although modeled with ordinary differential equations.

Figure 7.

Correlation between the signal-oriented model b, describing the average behavior of the cells and the molecular model c, describing the individual behavior within a population of cells.

The integrating behavior of this reaction chain would be exact if the chain of subsequent reactions consisted of an infinite number of reactions, otherwise, it can be regarded as an approximation. The corresponding value of the single integrator can be calculated approximately from the reaction chain by evaluating the weighted mean of the sequence of states (equation 2), what can be interpreted as the degree of modification.

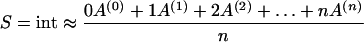2

This means that a single integrator can approximately describe the average behavior of a sequence of modifications. Thereby, however, the information about the probability distribution of the modifications is lost.

Homologous to the reaching of a certain threshold in models a and b, the reaching of a certain state of modification can represent the threshold behavior in the molecular model c. Consequently, in this model, only cells in state A⁽ⁿ⁾ can perform the next step, that is, the actual switching (Fig. 7).

The last functional unit of model b is a delay for a constant time. In a first order reaction with a constant reaction rate constant, each single reaction will be performed at a random time point. However, on average, a reaction will occur after a certain duration after reaching the preceding state (in this case, A⁽ⁿ⁾). In this respect, an observed dead time can be due to a first order reaction, if only the average behavior of the cells is considered.

The mean duration of the transition from state A⁽⁰⁾ to A⁽ⁿ⁾ in model c is approximately equal to the time when the integrator (represented by the switch molecule S) reaches the threshold in model b. Similarly, the mean duration of the transition A⁽ⁿ⁾ to B⁽⁰⁾ can mimic a dead time. Because both parts of the model in this system are characterized by a nonretroactive behavior, they can be connected in series without altering their behavior. Consequently, the mean reversal time is the sum of both mean durations of the transitions A⁽⁰⁾ to A⁽ⁿ⁾ and A⁽ⁿ⁾ to B⁽⁰⁾. Thus, model b is an approximation of the average behavior of model c (Fig. 7).

At the very beginning of the simulation, A⁽⁰⁾ is 1, whereas A^(1...n) and B⁽⁰⁾ are 0, representing the state of the switching complex directly after a switching event. Depending on the switching signal CheY-P, the cells will pass through the succeeding states to A⁽ⁿ⁾ faster or slower. The transition of A⁽ⁿ⁾ to B⁽⁰⁾ then represents the next switching event. This model describes only one swimming interval, the model for the following interval would result in an analogous transition from B⁽⁰⁾ via B⁽ⁿ⁾ to A⁽⁰⁾.

This model has been used with the same model parameters for the pulse experiments with the following exceptions:

• The reaction rate constants of reactions k1 and k2 have been adapted to the temperature of 21°C instead of 34°C (Marwan and Oesterhelt 1987).

• The reaction rate of k2 had to be significantly higher for stimulated cells than for simulating spontaneous reversals, because stimulation with blue light not only accelerates the increase, but also the decrease of the probability distribution. By optimization, k2 was fitted to a 28 times higher value than for spontaneous reversals, and left constant for all simulations of responses to blue light pulses. For possible biochemical mechanisms for adjusting k2, see the Discussion section.

The main difference between our model and the model of Naber (1997) is the fact that in Naber's model, only the last reaction step (which would be k2 in our model) is modified by the stimulus, whereas the first steps are not influenced. In our model, however, the first steps are accelerated by blue-light exposure through CheY-P, and the reaction rate constant of the last step (k2) was assigned a constant value, although it is significantly higher than in the spontaneous case.

The free parameters of the basic model have been fitted to the calculated values of the formula, leading to very good results (Fig. 4G,H). One difference in comparison to model b is most obvious; the simulation-results of experiment B (variable dark period) flattens for dark periods greater than 600 msec. For larger values of the dark period, the curve converges to a constant value of 2.15 sec, the same value as if only the first pulse was applied. In model b, in which the average cell is regarded, an immediate transition of the constant slope to the constant value can be observed. In contrast, in model c, which describes a population of cells, a smooth transition occurs (simulations not shown). The beginning of this transition can be seen in the flattening of the curve at dark periods >600 msec.

DISCUSSION

We present a mathematical model that allows quantitative explanation of the response of halobacterial cells to single and double-pulse stimuli of blue light. Components of the model were the sensory rhodopsin-transducer complex, the histidine kinase CheA and the response regulator CheY. Phosphorylated CheY causes the flagellar motor to switch its rotational sense during chemo- or phototaxis. Simulation of a simple model consisting of these few elements confirmed our previous finding that light-independent rate-limiting steps downstream of the photocatalytically formed switching signal (CheY-P) must be postulated (Marwan and Oesterhelt 1987). Moreover, by simulation of the previously suggested kinetic model for light-induced formation of the switching signal (CheY-P) triggering the change of the rotational sense at a critical concentration (threshold crossing), we now found that additional steps are required to quantitatively simulate the experimental data. Obviously, such rate-limiting steps may be due to conformational transitions in the subunits of the switching complex that occur when the rotational sense of the flagellar motor is reversed. By direct coupling of CheY-P to the four-state model of the switch (Marwan and Oesterhelt 1987), the response of halobacterial cells to double-pulse stimuli could not be simulated without significant deviation from the experimental results. Therefore, we replaced the four-state model of the switch by a functionally similar behaving, but mechanistically different model, suggested by Naber (1997), in which the individual subunits subsequently undergo transitions in a switching signal-dependent manner.

The model of motor switching implemented in our simulations assumes two rate-limiting steps. In the first step, the subunits of the switch complex are activated by binding a switching signal, while the motor continues rotating in its current sense. The subsequent binding reactions act like a technical integrator of the switching signal. A sequence of binding reactions modifies the state of the switch complex from zero to n bindings. The number of modifications can be regarded as the state of the integrator. A chain of subsequent modifications is an important principle of realizing an integrating behavior in nature. One of various examples is known in chemotaxis; the multiple methylation of the transducers in the adaptational process, which serves as an integrator in an integral feedback loop (Yi et al. 2000).

When some, many, most, or (as assumed by the model) all of the subunits have been activated, a major conformational rearrangement, that is, motor switching (change of the rotational sense), occurs with a constant probability per unit of time (a first order kinetics). Photocatalytic signal formation including sensory rhodopsin, transducer, CheA, and CheY, together with the modified model of the motor switch, perfectly simulate the experimental results considered. In addition, the model of the switch almost perfectly mimics the probability distribution of spontaneous motor switching. However, to simulate spontaneous switching, it was necessary to lower the rate constant for the conformational change (k2) 28-fold. This is an important finding. It means that activation of the signaling pathway by blue light increases both the rate of the first and the rate of the second step. In fact, Hildebrand and Schimz (1985) show clearly that both the rise and the decay of frequency distributions of run-length intervals are under sensory control in cells exposed to repellent or attractant light stimuli.

How can the model of spontaneous motor switching and that of the response to double-pulse stimulation be translated into a molecular mechanism? If the signal that sequentially activates the subunits of the switching complex was CheY-P, then there are two principally different options of how the rate constant k2, which defines the probability for the conformational change, could be directly or indirectly under sensory control.

One possibility is that the switching reaction with rate constant k2⁽ⁱ⁾ can occur at different states A⁽ⁱ⁾ with an increasing transition probability for an increasing number of subunits with bound CheY-P. Let us assume that, in the absence of stimulation, there is a low steady-state level of CheY-P bound to the subunits of the switch complex, setting the value of k2⁽ⁱ⁾ low. In an attractant-stimulated cell, the concentration of CheY-P, and hence, the number of subunits with bound CheY-P, would be even lower, resulting in a correspondingly low probability (k2⁽ⁱ⁾) for the conformational change of the motor-switch complex. In cells, which in response to repellent light, reverse with a higher probability per unit of time as compared with attracted stimulated or nonstimulated cells, the steady-state level of subunits with bound CheY-P would assume a high value, which increases k2⁽ⁱ⁾ accordingly to achieve a higher value as used in our simulation. Making the binding of CheY-P to the motor subunits reversible would include such a mechanism into our model of motor switching.

An alternative biochemical mechanism could be that motor switching is controlled by two switching signals, one binding to the subunits of the switch complex, the other mediating switching of the activated subunits. In fact, biochemical evidence in favor of a two-signal hypothesis exists. The first step could be binding of CheY-P to the subunits, the second step (k2) could be controlled by the cellular concentration of fumarate or vice versa. Fumarate has been shown to be a switch factor in Halobacterium (Marwan et al. 1990) and in Escherichia coli (Barak and Eisenbach 1992). In Halobacterium, it has been shown that the cellular concentration of fumarate is under sensory control of the sensory rhodopsin-transducer complexes, and that there is considerable amplification (in terms of fumarate molecules released per activated sensory rhodopsin; Montrone et al. 1993). In E. coli, it was shown (1) that motor switching requires fumarate (Barak and Eisenbach 1992), (2) that the probability of motor switching depends on the cellular fumarate concentration, even in the presence of nonphosphorylatable CheY (Montrone et al. 1996, 1998), (3) that the cellular fumarate level regulates motor switching at low temperatures, even in complete absence of CheY (Prasad et al. 1998), and (4) that fumarate acts by lowering the free-energy difference between clockwise and counterclockwise states of the motor (Prasad et al. 1998). However, the molecular mechanism of how fumarate interacts with the switch complex and the biochemical mechanism of the sensory control of its cytoplasmic concentration in Halobacterium is unclear at present.

How can the kinetic models of the switch and its sensory control by blue light provided in this work be used to support or disprove the two-signal hypothesis? If switching is triggered by CheY-P and fumarate through a mechanism of two signals that facilitate two subsequent steps, then the response kinetics of cells with altered cytoplasmic levels of fumarate or CheY should change as predicted by the model. In addition, we aim at explaining effects like the refractory period following a switching event. Repellent stimuli during this time led to a probability distribution of motor reversals that splits into two clearly separated populations (Krohs 1995).

We conclude that modeling approaches, combined with experimental work, can gain insight into the molecular mechanism of flagellar motor switching, which, due to its complexity, is still enigmatic in all prokaryotic organisms.

METHODS

Modeling

The models have been set up with the modeling tool PROMOT in a modularly structured way using an abstract and general modeling methodology (Ginkel et al. 2003). Elementary modeling objects representing elementary molecular functional units (like storages and reactions) are aggregated to higher structured modules that can be further connected to more complex models. PROMOT is developed at the Max-Planck-Institute for Dynamics of Complex Technical Systems in Magdeburg, Germany. Model parameters can be found as Supplemental research data online at www.genome.org and http://www.mpi-magdeburg.mpg.de/people/torsten/swich_models.html.

Simulation

For simulation of the final model, PROMOT forms a compact DAE (differential algebraic equations) that is coded in FORTRAN and can be further processed in the simulation environment DIVA. DIVA (Mohl et al. 1997) is also developed at the MPI in Magdeburg. It provides several numerical methods, for example, different solvers for nonlinear equations, different DAE integrators, and parameter optimization algorithms. For the simulations in this work, a LIMEX algorithm has been used.

All simulations of the experiments start from a stationary state that is reached after sufficient long integration without a stimulus. As an exception, the initial values for the switching mechanisms are set to S = 0, A⁽⁰⁾ = 1, A ^(1...7) = 0, B⁽⁰⁾ = 0.

Optimization

The unknown parameters of the models have been fitted to equation 1 instead of the underlying experimental results. This procedure has been chosen to achieve consistent conditions for all three experiments that have been made on different days. Halobacterium salinarum cells may exhibit slightly different light sensitivity from day to day, resulting in a small variation of the parameters of the equation (t_min and b) for experiments performed on different days. Approximately nine single points out of these experiments were chosen, and the values for the reversal time were calculated with equation 1 with constant parameters t_min and b. The deviation of the simulation results and the equation were minimized by DIVA with an optimization routine that works with an evolutionary algorithm. This algorithm starts with random sets of parameters (in a given range) and tries to imitate the mechanisms of evolution. Hereby, the main mechanism is that one generation of parameters has children who inherit their values with random mutations. Only the fittest (best) sets of parameters survive and build the next generation. This algorithm can search for the optimum in a broader parameter space than gradient-driven optimization routines, and has the possibility to get out of local minima due to the random changes of the parameter values. This makes it ideal for models of highly nonlinear biological processes.