Abstract
Vertebrate pre-mRNA transcripts contain many sequences that resemble splice sites on the basis of agreement to the consensus,yet these more numerous false splice sites are usually completely ignored by the cellular splicing machinery. Even at the level of exon definition,pseudo exons defined by such false splices sites outnumber real exons by an order of magnitude. We used a support vector machine to discover sequence information that could be used to distinguish real exons from pseudo exons. This machine learning tool led to the definition of potential branch points,an extended polypyrimidine tract,and C-rich and TG-rich motifs in a region limited to 50 nt upstream of constitutively spliced exons. C-rich sequences were also found in a region extending to 80 nt downstream of exons,along with G-triplet motifs. In addition,it was shown that combinations of three bases within the splice donor consensus sequence were more effective than consensus values in distinguishing real from pseudo splice sites; two-way base combinations were optimal for distinguishing 3′ splice sites. These data also suggest that interactions between two or more of these elements may contribute to exon recognition,and provide candidate sequences for assessment as intronic splicing enhancers.
In higher eukaryotes, most protein-coding genes are mosaics of exons and introns: The exons contain the protein coding information but are interspersed with larger intervening sequences of no known physiological functions called introns. The introns are removed from the gene transcripts in a process known as pre-mRNA splicing (Reed 2000). Splicing is mediated by the spliceosome, a large complex of over 100 proteins and five RNA molecules (Hartmuth et al. 2002; Jurica et al. 2002; Rappsilber et al. 2002; Zhou et al. 2002). Intron removal takes place in two transesterification steps. The first involves cleavage at the upstream end of the intron accompanied by the ligation of the 5′ end of the intron to the 2′ hydroxyl group of an adenosine residue about 20 to 30 nt from the downstream end of the intron; this branch point results in a lariat structure. In the second step, cleavage at the downstream end of the intron is accompanied by ligation of the two exons. The freed lariat goes on to be degraded. These chemical steps can take place before transcription has been completed (Kessler et al. 1993; Bauren and Wieslander 1994).
Before these chemical transformations can take place, the two ends of the intron must be identified by the splicing machinery. This identification must be precise and orderly so as to insure the production of a functional messenger RNA. Although splice sites are usually recognized unambiguously, there is a large class of exceptions in which alternative splice sites can be recognized. All possible modes of alternative splicing have been observed (e.g., alternative 5′ splice sites, alternative 3′ splice sites, exon skipping, etc.), resulting in two or more protein products specified by the same gene. As more and more mRNA molecules have been analyzed, the proportion of genes recognized to give rise to alternatively spliced products has increased to over 60% (Graveley 2001). Nevertheless, because typically only one or a few of the exons in a gene are subject to alternative splicing, the great majority of exons remain constitutively spliced.
In this study, we applied a computational approach to the problem of splice site recognition, but restricted ourselves to a consideration of constitutive splicing only. The most obvious identifiers of splice sites are the distinctive sequence elements at the ends of the introns, the integrity of which is necessary for splicing. Almost universally conserved are a GT dinucleotide at the 5′ end and an AG at the 3′ end of each intron (the DNA version of all sequences will be used here). A consensus sequence extends the 5′ splice site (donor) to the 9-mer (C or A)AG GTRAGT and the 3′ splice site (acceptor) to the 15-mer Y10NCAG G (the nonpolar terms donor and acceptor will be used here to avoid confusion as we switch focus between exons and introns). The degree of conservation of a particular base at these additional positions varies from 35% to 80%, and only a small minority of splice sites contain a perfect match to the consensus. Due to the degeneracy of the splice site consensus sequences and the large size of introns, it is possible to find many candidate sequences that match the consensuses as well or better than real splice site sequences. These pseudo sites far outnumber the real sites, yet they are successfully ignored by the splicing machinery (Sun and Chasin 2000).
The pairing of splice sites may be a factor in their recognition, and there is considerable evidence that interaction of splice sites across the exon, rather than the intron, is important for splice site recognition (Berget 1995). The designation of the exon rather than the intron as the primary target of recognition is termed exon definition, and is supported by two types of evidence. The concept emerged from biochemical experiments in which the provision of a splice site downstream of the second exon in a two-exon pre-mRNA was seen to greatly enhance splicing of the upstream intron in a cell-free splicing system (Robberson et al. 1990). Genetic evidence comes from the analysis of splice site mutations: mutations in the splice site residues at either end of an exon result more often than not in the skipping of the entire exon; that is, the unmutated end of the affected exon is also spoiled for splicing. Many examples of this sort have been seen either among multiple mutations in a single gene (Carothers et al. 1993; O'Neill et al. 1998) or in a survey of single splicing mutations in many genes associated with human genetic disease (Krawczak et al. 1992).
Exon definition can be used as a further criterion for proper splice site choice: Coupled with the observations that most internal exons are between 50 and 250 nt long, we can define pseudo exons as stretches of intron within these limits that are bounded by pseudo splice sites. However, this restraint does not do much to remove false sites from consideration. In our previous analysis of the human hprt gene, pseudo exons outnumbered real exons by an order of magnitude (Sun and Chasin 2000). Thus there must be additional sequence information that distinguishes real splice sites from pseudo splices or real exons from pseudo exons.
Splicing enhancer sequences have been proposed to fill this role. These sequences were originally discovered as short purine-rich exonic stretches that were necessary for the inclusion of alternatively spliced exons (Watakabe et al. 1993). Subsequent work showed that effective sequences could also be pyrimidine-rich or AC-rich (Tian and Kole 1995; Coulter et al. 1997), although purine-rich sequences still predominate (Ladd and Cooper 2002). More recently, in vitro or in vivo selection experiments have produced a large number of sequences that can act as enhancers when introduced into alternatively spliced or otherwise debilitated exons, and these show specificity for interactions with particular protein splicing factors (Liu et al. 1998, 2000; Schaal and Maniatis 1999b). Although tested in alternative splicing systems, exonic enhancer sequences have been readily found in constitutively spliced exons (Schaal and Maniatis 1999a). Moreover, it has long been recognized that mutations within exons in sites other than the splice consensus sequences can impair splicing (Reed and Maniatis 1986). However, the degeneracy of the exonic splicing enhancer sequences that have emerged from these studies makes it difficult to see how this information can be used to distinguish real exons from pseudo exons, because enhancer-like sequences abound within introns and within pseudo exons (X.H-F. Zhang and L.A. Chasin, unpubl.).
Additional information that specifies real splice sites could involve: (1) a distinction between real enhancers and pseudo enhancers; (2) enhancer sequences not yet identified; (3) silencer sequences that repress the use of pseudo splice sites; (4) subtle differences in splice site sequences; (5) specific interactions among these elements. These possibilities are not mutually exclusive. The recognition of these elements is difficult because the active sequences may be located at variable distances from the relevant splice sites, they may be represented by a heterogeneous family of sequences, and they may represent variable sequence solutions for the formation of specific structures that are the actual targets of recognition. In the face of these difficulties, we have undertaken a computational approach to this question based on machine learning.
We asked whether a machine-learning classifier could learn to distinguish between the real exons and pseudo exons we have defined above, and we used support vector machines (SVMs) for this purpose. SVMs have been used extensively in text classification and image recognition (Cortes and Vapnik 1995; Joachims 1998), and have been applied to protein sequence classification (Jaakkola et al. 1999; Leslie et al. 2002) and to discrimination tasks in nucleic acid sequences such as translation initiation site recognition (Zien et al. 2000). SVMs are state-of-the-art classifiers that have shown excellent empirical performance in prediction tasks and have strong theoretical justification (Vapnik 1998).
Our basic strategy was to identify sequence features that allow an SVM to distinguish real from pseudo exons, and then to apply statistical tests to the sequences that emerged to determine whether they are specifically associated with exons. We limited ourselves to constitutively spliced internal exons. We trained SVMs by providing positive and negative examples (real vs. pseudo exons) and features we believed could be available to the cellular splicing machinery of the cell: the individual sequences comprising the acceptor and donor splice site consensus and the occurrences of k-mers in intronic flanking sequences. Sequences in exon bodies present a special problem of interpretation, because they harbor a variety of signals that distinguish them from introns but that may have no relevance for splicing. The most obvious of these is protein coding information, but signals for mRNA transport, stability, and localization are also undoubtedly present. These readily discernible differences confound the identification of splicing-specific signals. For this reason we have deferred a detailed examination of exon sequences in this work, concentrating instead on the splice sites and their intronic flanks.
We found sequence elements in 50-nt windows upstream and downstream of exons that are associated with exons, and we found sequence elements that are avoided by these regions. In addition, an SVM revealed combinations of bases within donor site sequences that provide a sharper distinction between real and pseudo sites than do the consensus values. The functionality of these associations can now be tested in molecular genetic experiments. Although it was not our intention to produce an algorithm for gene finding, the results reported here may be of some use toward that end.
RESULTS
The Real Exon and the Pseudo Exon Databases
A total of 25,229 internal exons were collected from 3917 genes (see Methods) in the Exon Intron Database (EID) of Saxonov et al. (2000). From this set we limited ourselves to 5753 exons that were not known to be alternatively spliced, that were flanked by completely sequenced introns, and that were between 50 and 250 nt long. From the same set of genes, we established a data set of 9246 pseudo exons, sequences that have the appearance of exons in that they have the same size limits and must have consensus values (see Methods) higher than 78 for donor sites (5′ splice sites) and 75 for acceptor sites (3′ splice sites). Real exons have median consensus values of 82 for donor sites and 80 for acceptors. The cited limits would eliminate about 25% of real exons. In addition, pseudo exons had to be at least 100 nt away from the closest real exon. We left branch points as a feature that might be defined by our analysis. The pseudo exon data set provides a control set to help us discover functional sequence elements, both those needed to define an exon and potentially those that repress splicing of pseudo exons.
In addition to the sequences from EID, we generated 15,000 real exons and 25,000 pseudo exons for use as a final test set from 1853 full-length human genes (all different from those in the EID) collected by aligning mRNA sequences from GenBank to genomic sequences from the human genome database (see Methods).
Use of Support Vector Machine to Discriminate Exons From Pseudo Exons
We trained a support vector machine classifier (SVM) on a training set of true and pseudo exons in order to learn a classification rule that can discriminate between them. Each input sequence is represented by a vector of sequence-based features, scored as either present (1) or absent (0) in the sequence. The features used are short sequences (k-mers) from the exon flanks and exon body and combinations of bases within the splice site (see Methods). The learned prediction rule is evaluated on a test set of examples unseen during training. By training on features from different regions of the sequence (flanks, body, and splice sites) and evaluating SVM performance, we can determine which regions are most useful for discrimination. We can also examine the trained SVM classifier to see which individual sequence features are most discriminative and whether they are positively or negatively weighted (indicative of true or pseudo exons).
The trained SVM determines a ranking of test examples by their the discriminant values. Varying the threshold for the discriminant scores yields a plot of the rate of true positives as a function of the rate of false positives, resulting in a “receiver operating curve” for the test set. We evaluate classification performance using the receiver operating characteristic (ROC) score, which is the area under this curve. Perfect ranking of true positives above false positive gives an ROC score of 1, whereas a random classifier has an expected ROC score close to 0.5.
We trained the SVM on a set of ∼3000 real exons and a like number of pseudo exons and then reported the ROC score on an untouched set of ∼2000 of each. Statistical analyses of sequence-based features were then carried out on yet another untouched set of ∼15,000 real and pseudo exons.
Contribution of Different Components to the Discrimination of Exons From Pseudo Exons
We divided exons and their flanks into five nonoverlapping components: upstream flanks, acceptor splice sites [3′ splice sites including the polypyrimidine tract (PPT)], exon bodies, donor splice sites (5′ splice sites), and downstream flanks. The flank and exon sequences were defined as starting beyond the splice site sequences themselves (i.e., not starting exactly at the exon/intron boundary). These were taken to be -14 for the upstream flank and +6 for the downstream flank, numbers being relative to the intron-exon boundary. Although the length of the flank was varied in many experiments, 50 nt was used in most experiments reported here (unless otherwise indicated). Thus the upstream flanks extended from -64 to -15, the downstream flank from +7 to +56, and the exons from +2 to -4. We then used an SVM to evaluate the information contained in the sequences of these components, as described below.
Splice Site Sequences
Although both real exons and pseudo exons comprise sequences with similar consensus values, they differ in the particular arrangement of bases that underlie these scores. To test the idea that pseudo exons may host different internal base combinations, we used position-dependent base combinations as features for an SVM, assessing up to seven base combinations in the donor sites (excluding the GT) and up to 13 in the acceptor sites (excluding the AG). Combinations of three bases proved to be optimal for donor sites, whereas two-way base combinations were best for acceptor sites. Using both sites simultaneously, an ROC score of 0.907 was achieved, indicating that there was a substantial difference in base combinations between real sites and pseudo sites (Table 1). Leaving out either site significantly compromised the results (Table 1). This result suggests that the particular arrangement of bases in the splice site plays a large role in its recognition. However, we note that the real exons were not subjected to filtering by consensus score, unlike pseudo exons, which had to have a donor consensus value of at least 78. To control for this possible bias in the case of donor sites, we eliminated the low-scoring (donor consensus value < 78) real sites so that the real and pseudo sets had the same score range. The SVM using donor-site base combinations alone achieved an ROC of 0.822, only slightly lower than the value of 0.837 obtained when the real set included the low-scoring sites (Table 1). However, even though the real and pseudo sites now shared the same threshold, the distribution of their scores was different. Pseudo exons tend to have more scores near the cut-off (78 for donor and 75 for acceptor sites), whereas real exons in this range have a peak around a median value of 85.6. We therefore ran another experiment that eliminated the consensus value as a filter altogether. We collected from introns any 9-mer with GT at the fourth and fifth positions as the negative data set (870,000) that was within 50 to 250 nt downstream of any AG. The positive data set included all real donor sites (3000). We obtained ROC values of 0.951 using consensus values and 0.977 for SVM using three-way donor base combinations. The higher ROC values are due to the fact that we are using a very large and poor set of sequences as pseudo exons in this case. We conclude that the three-way combinations are as good or better than consensus values as a criterion for distinguishing real from pseudo donor sites.
Table 1.
SVM Peformance in Distinguishing Real From Pseudo Exons
|
Flanks
|
Splice sites
|
|||||
|---|---|---|---|---|---|---|
| US | DS | 3′ | 5′ | Exon body | ROC | Specificitya |
| CVb | 0.609 | 0.484 | ||||
| + | - | - | - | - | 0.791 | 0.638 |
| - | + | - | - | - | 0.784 | 0.618 |
| + | + | - | - | - | 0.855 | 0.695 |
| - | - | + | - | - | 0.823 | 0.672 |
| - | - | - | + | - | 0.837 | 0.698 |
| - | - | + | + | - | 0.907 | 0.777 |
| + | + | + | + | - | 0.932 | 0.825 |
| - | - | - | - | + | 0.946 | 0.841 |
| + | + | - | - | + | 0.984 | 0.956 |
| - | - | + | + | + | 0.987 | 0.964 |
| + | + | + | + | + | 0.991 | 0.976 |
Performances are indexed by ROC values and specificity. Each row is an SVM test. ROC values were measured in untouched sets of ∼2200 real and ∼2300 pseudo exons. The first five columns indicate the components used by SVM. US, upstream; DS, downstream; TP, true positive; FN, false negative; FP, false positive; SE, sensitivity; SP, specificity.
Specificity = TP/(TP + FP) at a sensitivity (SE = TP/(TP + FN)) of 0.90
The SVM classified on the basis of the acceptor and the donor consensus values
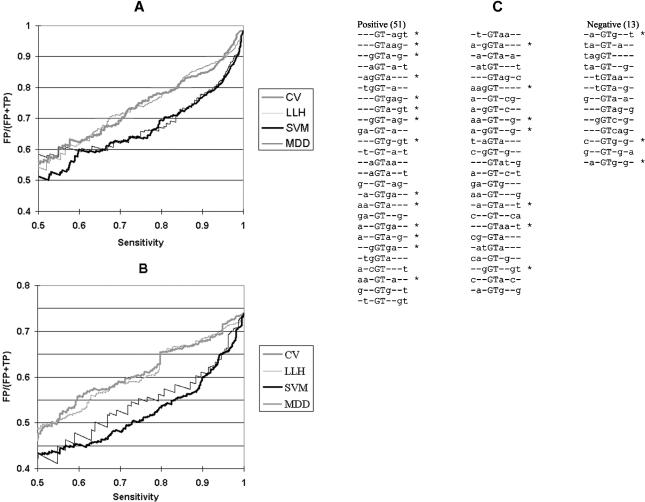
To compare the consensus value and the three-way combinations more sensitively, we plotted the false positive rate, FP/(TP+FP), as a function of sensitivity. The use of consensus values produced about twice as many false positives at almost all sensitivity levels than did an SVM using three-way base combinations, whether performed on the set of pseudo donor sites chosen only on the basis of GT (Fig. 1A) or on the set with a minimum consensus value of 78 (Fig. 1B). As shown in Figure 1, similar results were obtained whether we computed consensus values by adding the probabilities at each position (CV: Shapiro and Senapathy 1987) or by calculating the log likelihood (LLH; Rogan et al. 1998). We also compared the SVM results to the maximum dependence decomposition (MDD) method, which is based on two-way base combinations (Burge and Karlin 1997, as implemented by G. Yeo and C. Burge at http://genes.mit.edu/burgelab/maxent/Xmaxentscan_scoreseq.html). The two methods performed similarly on pseudo donor sites built around any GT, but the SVM performed better on the selected set of pseudo sites with consensus value scores greater than 78 (Fig. 1B). These results support the idea that a substantial proportion of pseudo splice sites host unfavorable base combinations, and they suggest that three-way base combinations could be more predictive of the quality of donor sites than consensus value.
Figure 1.
Three-way combinations of bases within the splice donor site. (A,B) False positive rate as a function of sensitivity in discriminating real and pseudo exon donor sites. Systematic variation of the threshold resulted in the different sensitivities. Classifying scores were from SVM (heavy black lines); multiple dependence decomposition (MDD, light black lines); consensus value (CV) calculated according to Shapiro and Senapathy (1987; heavy gray lines); and consensus values calculated by the log likelihood method (LLH, light gray lines). (A) The data set contained all of the real exons. Pseudo exons were defined as containing a simple GT as a potential donor site (no consensus value filter). (B) The data set contained all of the real exons. Pseudo exons were defined as having consensus values of at least 78. (C) Three-way combinations weighted most highly by SVM in distinguishing real from pseudo exons. The training set consisted of approximately 3400 real exons and 3200 pseudo exons, all of which exhibited donor site consensus values of at least 78. Positive and negative weights are listed separately, in descending weight order (absolute value). Asterisks denote agreements to the consensus. These 64 combinations allow SVM to perform at 92% of the accuracy achieved with the full set.
Flanks
If there are some general enhancers in the flanks of real exons or repressors in the flanks of pseudo exons, then their presence may be detectable by differences in oligomer composition. We examined the performance of an SVM using occurrences of oligomers from 4 to 7 nt long in each flank as features, and explored flank lengths from 50 to 400 nt beyond the splice sites. The optimum result was achieved using pentamers or tetramers and 50-nt flanks with a degree-2 polynomial kernel, which implicitly uses pairs as well as individual features (see Methods). The ROC value using pentamers was 0.855 (Table 1). Leaving out either of the flanks or using a linear kernel significantly compromised performance, and the use of longer oligomers (6- or 7-nt), slightly decreased the ROC value (data not shown). Extending both flanks to 100 nt did not improve the SVM performance, and when the flanks were extended above 200 nt the result was substantially worse (data not shown). We concluded that there is distinctive sequence information in flanks of exons, and this information involves both upstream and downstream 50-100-nt flanks. It should be noted that although splice site sequence information was not used in examining the contribution of the flanks, the very definition of a flank does require a topological designation of a potential splice site.
Exon Bodies
As with the flanks, we used an SVM to differentiate real and pseudo exons solely on the basis of their exon body oligomers. Hexamers yielded the highest ROC score (0.947) by a slight margin, but we present the results for pentamers for consistency with the flank data. A statistical differentiation of exon bodies from their intronic contexts is not difficult and has been used extensively in gene-finding algorithms (e.g., Burge and Karlin 1997). However, exon bodies are filled with information for translation, mRNA transport, and mRNA stability. For this reason, it is difficult to know how much of the distinctiveness of exon sequences reflects splicing information.
Combining Features
SVM performance improved when more than one type of feature was used. Addition of flank sequences to splice sites increased the ROC value from 0.907 to 0.932, a high value achieved in the absence of exon body information. The inclusion of all three feature types increased the performance of SVM to 0.993 (Table 1), close to the maximum achievable. An analysis of the relative contributions of the different classes of features can be found in the online Supplemental material, available at www.genome.org. Varying the original parameters for the number of positions in the splice site sequence and the length of oligomers in the flanks did not improve the combined SVM performance.
The effectiveness of the SVM in discriminating between real and pseudo exons using only flank and splice site information (ROC = 0.932) could in part be due to the presence of highly repeated sequences in or near pseudo exons but not real exons. To evaluate this contribution, we used RepeatMasker (Smit and Green 2002) to eliminate highly repeated sequences from our data sets. Of a set of 9246 pseudo exons (including 400 nt of flank) subjected to this filter, 4912 remained in the data set as repeat-free sequences. Using this repeat-free data set, we repeated the training and testing using splice site and flank information (no exon bodies); performance was not affected by the removal of repeats (ROC = 0.931). SVM also performed equally well (ROC = 0.933) with these features using a data set of real exons that had been purged of those with low consensus values (< 78), ruling out the possibility that these real exons were being distinguished by their low scores.
Exon Prediction
To evaluate how these features could help predict real exons in a gene sequence, we chose eight genes that were not in our training set and generated a list of 1225 potential exons. The splice consensus values used were just low enough to capture all 37 real exons in these genes. We then used an SVM to predict the real internal exons. Inclusion of information from several combinations of components for SVM greatly cut down the number of pseudo exons. The inclusion of flank information reduced the number of pseudo exons by a factor of 2 to 3 (Table 2, rows 4 and 5), reinforcing the idea that flanks can be important in exon recognition. Under conditions in which 95% of the real exons were recognized, inclusion of all sequence information reduced the number of pseudo exons from 1188 to 53, representing a reduction in the noise-to-signal ratio from 34 to 1.5.
Table 2.
Exon Prediction Using SVM
|
True positives detected
|
|||||
|---|---|---|---|---|---|
| Splice sites | Flanks | Exon bodies | 32/37 | 35/37 | 37/37 |
| — | — | — | 1225 | 1225 | 1225 |
| — | + | — | 164 | 259 | 668 |
| — | — | + | 108 | 232 | 383 |
| + | — | + | 58 | 111 | 180 |
| + | + | + | 19 | 53 | 90 |
Eight human genes (3—42 42- kb, average 13- kb) were scanned for potential exons using criteria relaxed enough to capture all 37 real internal exons (acceptor and donor splice site scores of 70, lengths from 18 to 300 nt); 1225 pseudo exons were thus generated. SVM was asked to classify the candidates as real or pseudo exons. The weights given to various SVM components were varied, resulting in different degrees of success in recognizing the 37 real internal exons. The number of false positives (pseudo exons) chosen as real exons is shown for the inclusion of splice site sequence, flank sequence, and/or exon sequence information. Note that no reading frame information was included.
We thought it would be interesting to compare the performance described above to that of a full-fledged gene finding program, Genscan. Presented with the eight complete gene sequences, Genscan found all but one real exon (97% sensitivity) and chose only one pseudo exon, compared to the 53 out of 1188 that the SVM found in the binary classification setting (using all sequence features). To test whether gene structure information used by Genscan was responsible for this better performance, we re-ran Genscan using the same input that was used for the SVM: lists of real exons and pseudo exons with 50-nt flanks. In this case, Genscan missed 10 of the 37 exons (73% sensitivity) but chose none of the 1188 pseudo exons, even when run with the most permissive parameters. (For comparison, at the same 73% sensitivity level, the SVM approach using all sequence features retained nine pseudo exons.) The comparison is imperfect, because our SVM was purposely trained to recognize pseudo exons with higher CV scores and because the training sets of the two methods were different. We did not try to improve performance of the SVM as an exon predictor, because our focus was on identifying factors that could play a mechanistic role. However, in addition to suggesting splicing-related sequence features, we believe that the SVM approach described here could potentially be used to improve the performance of gene-finding programs.
Identification of Sequences Used to Distinguish Real Exons
To extract discriminative features, we carried out a systematic recursive feature selection (RFE) on the training set. In this procedure, the SVM was recursively retrained using only the top half of the features that were used in the previous run (see Methods). We continued these feature elimination runs as long as the ROC value remained within 90% of that produced by the original full feature set.
Donor Site Three-Way Combinations
Out of 1340 initial three-way donor combinations present in the data, a total of 64 three-way base combinations sufficed for an effective classification (ROC of 0.809 vs. 0.837) comparing real and pseudo exons with a consensus value of at least 78 (the top 75% of real exons). The list of top contributors included 51 positively and 13 negatively weighted combinations (Fig. 1C). About half of the positive combinations (21/51) represent the consensus sequence, and these were the most highly weighted combinations. For the most part the weighting follows the difference in prevalence of these combinations in the real versus the pseudo set (data not shown). However, the negatives include a similar proportion of consensus combinations (3/13), and there are some exceptional combinations that do not follow a simple prevalence discriminator. For example, g--GT-ag-, ga-GT--g-, and ga-GT-a--all are fairly abundant among real exons (11% to 13%) but are even more abundant among pseudo exons (14% to 15%), yet were assigned weights that were in the top quarter among positives. Because the SVM score is a weighted sum of all possible three-way combinations, it could be that these particular combinations, although prevalent in pseudo exons, are associated with other (unfavorable) combinations within the same pseudo splice site sequence.
Acceptor Site Two-Way Base Combinations
We extracted high-scoring two-way base combinations from the SVM results of a comparison of real and pseudo exons having a minimum acceptor site consensus value of 75. The inclusion of 128 two-way base combinations was sufficient to maintain the effectiveness of this type of information (ROC = 0.805 vs. 0.844 for all 1248 possible two-way combinations). Of these, 49 had positive and 79 had negative weights. The G+C content was three times as high in the positive set (74/98) compared to the negative set (35/158). Among the positive combinations, two sequences of adjacent bases stood out: four AA and three CG dinucleotides were present, a number several times higher than the 0.5 expected on a random basis in this set and found among pseudo exons. This difference prompted us to examine the overall frequency of these dinucleotides in 10-nt PPTs (i.e., the -14 to -5 region upstream of real exons, 15,896 examined) of the large untouched test set. AA occurred 2.3 times more frequently than expected based on the consensus matrix. Analysis of the CG frequency is complicated by the fact that this dinucleotide is about one-fifth the expected value in the genome in general. In PPTs, it is present at a higher level, about one-quarter of expectation. A more useful indicator of CG abundance is its fourfold greater frequency with real exons (0.093 per PPT) compared to pseudo exons (0.024 per pseudo PPT). It appears that AA and CG are characteristic of many PPTs.
Among negatively weighted combinations, AG was overrepresented, and this dinucleotide is indeed rare in PPTs, at only 13% of its expected value. The scarcity of AG has been noted previously in the region between the branch point and the acceptor site (Zhang 1998), and can be understood as representing the avoidance of a competitor for the real splice site. TA was another dinucleotide overrepresented in the negatively weighted set, and it is modestly underrepresented in PPTs at 75% of its predicted value. Again, because the SVM is examining all two-way combinations in every sequence, the TA may be an indirect indicator of more distinctive (and of course more complex) combinations.
Finally, we noted that among the 13 positions examined, position -4 was included at a frequency (in 21 of 256 possible two-way combinations) close to the average for all positions. In the consensus sequence, this position is N: it is just as likely to be represented by any of four bases. This result raises the possibility that position -4 may play a role in splice site recognition despite its lack of calculated information content.
Flanks
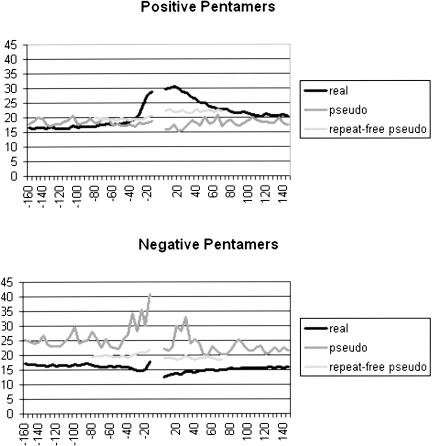
We used the SVM recursively to extract the top features found in 50-nt upstream and downstream flanks. An SVM was initially presented with all possible pentamers, 1024 for each flank; the highest scorers were chosen without regard to the flank in which they resided. The number of pentamers could be reduced to 256, one-eighth of the original number, without greatly compromising the effectiveness of SVM in using flank information exclusively to distinguish real from pseudo exons (ROC = 0.827 compared to the original 0.855 using all 2048 pentamers). These top pentamers were first divided into two categories: those with positive weights, being either associated with real exons and/or disassociated with pseudo exons, and those with negative weights, with the converse associations. These pentamers were then further divided according to their origin in the upstream or downstream flank, resulting in four groups of pentamers: 62 upstream positives, 61 downstream positives, 65 upstream negatives, and 68 downstream negatives.
To determine whether these top rated pentamers were limited to particular regions in the exon flanks, we plotted the sum of the weights of the 256 top-rated pentamers found in 5-nt windows upstream and downstream of real exons. As can be seen in Figure 2, there is a pronounced peak for these summed weights proximal to the exon on each side. On the downstream side, there is a peak about 15 nt from the exon with a decrease to background levels at +80 nt. The upstream distribution is much more constrained, extending only to -40 nt. Because we only compared 50-nt windows with the SVM, we did not make use of the finer (5-nt) positional information revealed in Figure 2. Future applications of SVMs may be able to use this information to advantage.
Figure 2.
Distribution around exons of pentamer weights assigned by SVM. The top 256 pentamers were divided into four groups according to their origins (downstream or upstream) and signs of their weights (positive or negative). For each group, the SVM weights assigned to each pentamer were summed for pentamers that started in nonoverlapping windows of 5 nt on either side of 15,000 real exons, 24,000 pseudo exons, and 12,000 repeat-free pseudo exons. Values for upstream pentamers only are shown on the left and for downstream pentamers only on the right (i.e., values derived from exclusively upstream pentamers are not plotted on the downstream side and vice versa). Top: positively-weighted pentamers; bottom: negatively-weighted pentamers
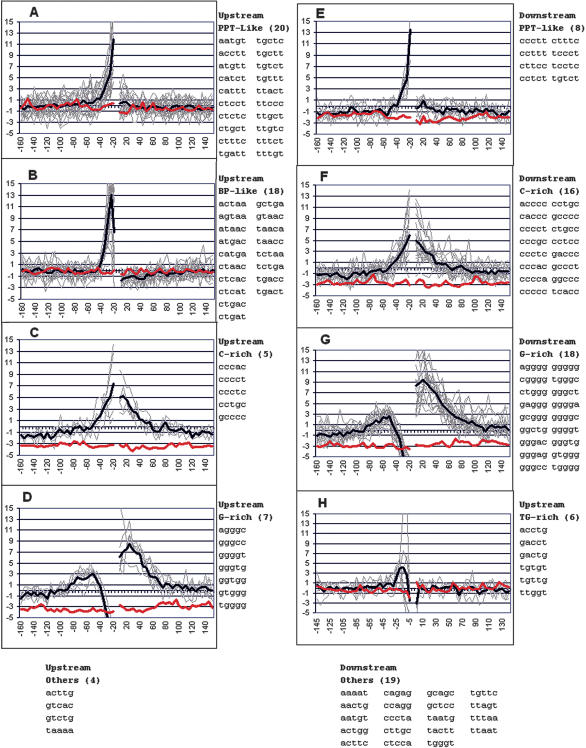
We next examined the prevalence of the individual pentamers within the regions 150 nt upstream and downstream of the splice site sequences (from -165 to +156). For each pentamer in each position bin of 5 nt (e.g., -15 to -20), a z-score was calculated as a measure of the representation of the pentamer beyond that expected by chance (see Methods). Thus, each pentamer was associated with a vector composed of a set of z-scores, representing its frequency profile around exons. These vectors were then clustered hierarchically and further grouped using a self-organizing map (SOM; http://gepas.bioinfo.cnio.es/cgi-bin/somtree). By this means, pentamers having similar positional profiles were clustered together. Remarkably, almost all of the pentamers in each cluster showed a high degree of sequence similarity despite the fact that the clustering procedure took no account of the actual sequences (Fig. 3). Two additional groups were comprised of pentamers that showed no significant positional preference (Fig. 3, bottom panels). Many of these clusters represented known splicing elements, but some were novel. We describe each pentamer cluster below.
Figure 3.
Grouping and distribution of the top positively scoring flanking pentamers. A subset of 121 positively weighted pentamers that contributed most to the ability of SVM to distinguish real from pseudo exons were grouped according to their similar positional distributions of their prevalence around exons, as measured by a z-score (see text). Z-scores with an absolute value greater than 2 have a P-value of less than 0.05. Values were summed for pentamers starting in windows of 5 nt starting just upstream of the acceptor site (-15) and just downstream of the donor site (+7); an exception is panel H, in which upstream windows up to the exon (-1) are shown. Light gray lines represent individual pentamers listed on the right; the heavy dark line is the average. The red line shows the average for the distribution of these pentamers around pseudo exons. Pentamers in each flank were treated separately for extraction from SVM and for clustering. However, their prevalence is shown both upstream and downstream of the exons regardless of their origin.
Pyrimidine-Rich Sequences
One of the largest clusters of positive pentamers consisted of pyrimidine-rich sequences. Almost all had four or five pyrimidines and originated in the upstream flank (Fig. 3A). The prevalence of these pentamers peaked at a position just upstream of the PPT and declined monotonically with increasing distance from the exon. We had defined our acceptor sites as having a PPT of 10 nt, but this limit was rather arbitrary, as the tract often extends further upstream (Penotti 1991). The distribution of pyrimidine-rich pentamers undoubtedly reflects this extended PPT. Thus these sequences are probably more appropriately considered part of the polypyrimidine tract that defines the acceptor site rather than “flank” information of a different type. The red line in each distribution chart depicts the average distribution of the pentamer cluster in the pseudo exon set. In all cases, the pseudo exon distribution is relatively flat compared to that of the real exons. Moreover, it is often consistently lower than the flat regions of the real exons. We interpreted this decrement as due to the presence of highly repeated sequences present in the pseudo exon class but rare in the real exons flanks. If a particular pentamer is not highly represented in repeat sequences, its prevalence overall will decrease by default, because about half of the pseudo exons overlap with repeats. When repeat-free pseudo exons were examined, the background prevalence increased (data not shown) to match the background of real exons, defined as the prevalence in regions more than 100 nt from the splice sites.
Pyrimidine-rich pentamers were also found among downstream sequences, but the prevalence of these pentamers there is not higher than expected by chance (Fig. 3E). Their lower prevalence among pseudo exons explains why they were highly weighted by SVM. Note that these sequences are also prevalent in the upstream flank; indeed two of the eight pentamers that originated downstream have identical counterparts among the upstream pentamers. It should be remembered that upstream and downstream pentamers constituted separate features for the SVM, and the flanks were not constrained to contribute equally to the final set.
The pentamers were clustered on the basis of similar positional distributions, not sequences. Thus, three of the pentamers in this “pyrimidine-rich” cluster are not actually pyrimidine-rich: AATGT, TGATT, and ATGTT. They might be better placed in a cluster of branch point-like sequence with a similar but distinct distribution, described below.
Branch Point-Like Sequences
A second cluster of pentamers in upstream flanks resembled the YNYTRAY branch point consensus sequence (Green 1991): the 18 members of this class define a consensus of CTRAC. This pentamer cluster peaks in the window from -20 to -24, and reaches background levels at -40 (Fig. 3B). This distribution is similar to that of known branch points (Harris and Senapathy 1990). Although the prevalence of the branch point consensus is only slightly overrepresented upstream of real exons (Harris and Senapathy 1990), the SVM was able to designate these sequences as important signals. This result serves as a sort of internal control for important flank sequences that validates the assignment of the additional sequences described below.
G-Rich Sequences
A large cluster of downstream pentamers were G-rich, and all but one of the 18 members include a G-triplet. These sequences show a broad distribution stretching as far as 90 nt downstream of the donor site sequence (Fig. 3G). G-rich pentamers were also detected upstream of the exon, from positions -40 to -84, but these were much fewer and less prevalent than the downstream sequences (Fig. 3D). The dearth of G-rich sequences from -15 to -40 is simply a reflection of the extended polypyrimidine tract. The abundance of G-rich sequences near the ends of intron has been noted previously (Nussinov 1988; Engelbrecht et al. 1992). The pseudo exons show no increased prevalence of these sequences.
C-Rich Sequences
Although also pyrimidine-rich, C-rich sequences emerged as a class distinct from polypyrimidines in their distribution, in that they were found downstream (Fig. 3F) as well as upstream of the exons (Fig. 3C). The distinctiveness of this class from general pyrimidine-rich sequences can be seen by comparing the downstream distributions in Figures 3F and 3E. Most of these sequences (12 of 16) included a C-triplet, and their heightened prevalence extended to 36 nt downstream of the donor site sequence. The upstream C-rich sequences were fewer, and each sequence had an exact counterpart downstream. As expected, the upstream sequences overlapped with the extended polypyrimidine tract, but they exhibited a broader distribution (cf. Figs. 3C, 3A).
TG-Rich Sequences
Five of six pentamers that clustered just upstream of the PPT position contained the dinucleotide TG. Although this cluster presented the lowest z-scores, there is a significant peak just upstream of the exon. In Figure 3H, the prevalence of these pentamers is plotted to include the PPT, so that it can be seen that the distribution of these pentamers is not that of pyrimidine-rich sequences.
Other Positive Sequences
Of the 121 positive pentamers, 29 did not fall into a common cluster. These sequences are shown in the bottom panels in Figure 3. Although diverse, these sequences remain candidates for intronic splicing enhancers and are being further investigated.
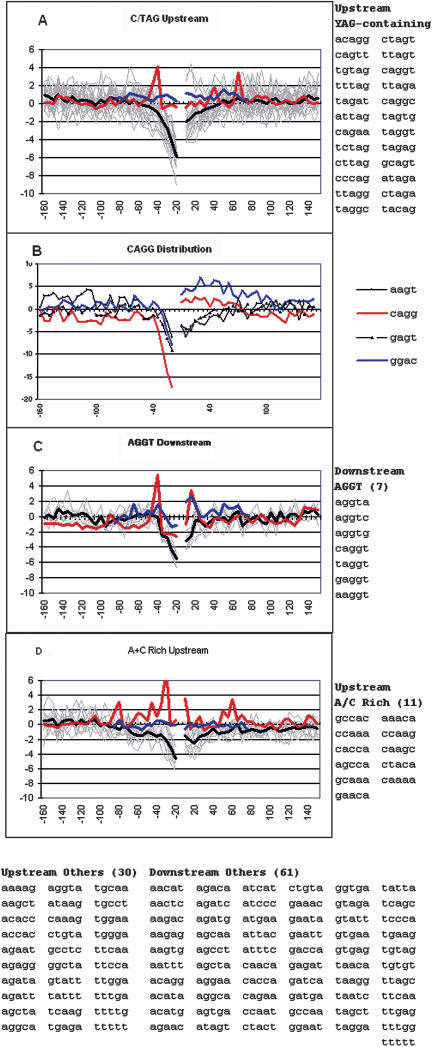
Negative Sequences
The 140 negatively weighted sequences that were extracted are more difficult to interpret, as they could represent highly repeated sequences present only in the pseudo exon set or simply mirrors of positive sequence concentrations. An example of the latter could be purine-rich pentamers that are negatively associated with upstream flanks simply because there is a predominance of pyrimidines there (the extended PPT). Nevertheless, we found the distribution of some negatively correlating sequences interesting. One cluster of pentamers exhibited a relative scarcity in the immediate upstream flank and contained YAG (Y = C or T) as a common motif (Fig. 4A). The frequency of these pentamers was also below expectations in the downstream flank, but this difference was of borderline significance. Interestingly, these pentamers exhibited sharp peaks of prevalence rather than scarcity in the flanks of pseudo exons (red line in Fig. 4A). These pseudo exon peaks disappeared when highly repeated sequences were removed from the data set (blue line in Fig. 4A). Because YAG represents part of the acceptor splice site consensus sequence (CAG G), we measured the distribution of this tetramer in exon flanks. As can be seen in Figure 4B, CAGG shows an even more extreme scarcity than YAG. This underrepresentation (compared to all possible tetramers) is not simply due to purine content, because the reverse sequence, GGAC, exhibits a much weaker negative correlation (peak z-score of -8 vs. -17); indeed, tetramers containing AG but bordered by bases with the poorest agreement to the consensus (AAGT and GAGT) do not show an underrepresentation beyond that displayed by a purine-rich tetramer (Fig. 4B). Thus there seems to be a lack of a full consensus splicing site sequence rather than the lack of a simple AG in this region. It is reasonable to think that an ectopic CAGG that could act as a competitor for the real splice site has been selected against.
Figure 4.
Grouping and distribution of the top negatively scoring flanking pentamers. A subset of 140 pentamers that contributed most with a negative weight to the ability of SVM to distinguish real from pseudo exons were grouped according to their similar positional distributions of their prevalence around exons, as measured by a z-score (see text). Zscores with an absolute value greater than 2 have a P-value of less than 0.05. (A,C,D) Light gray lines represent individual pentamers listed to the right; the heavy dark line is the average. The red line shows the average for the distribution of these pentamers around pseudo exons; the blue line shows this average for repeat-free pseudo exons. Pentamers in each flank were treated separately for extraction from SVM and for clustering. However, their prevalence is shown both upstream and downstream of the exons regardless of their origin. (D) Distribution of the acceptor splice consensus sequence CAGG and related tetramers.
We also found evidence for the avoidance of competitor donor splice site sequences. A group of seven pentamers containing the sequence AGGT was found to be scarcer than expected downstream of the donor splice site (Fig. 4C). These four bases straddle the splice site in the donor consensus sequence. Their scarcity upstream of the exon as well can be explained by their purine-rich character or their resemblance to an acceptor AG. The avoidance of downstream GT can also be seen in the distribution of tetramers shown in Figure 4B.
A third group that emerged from the negative data based on distributional similarity consisted of pentamers rich in A and C (at least four of five). These 11 sequences are scarce both upstream and downstream of the splice sites (Fig. 4D). Although they are moderately purine-rich as a group (62%), their underrepresentation on either side of the exon and their emergence as sequences highly weighted by the SVM suggests that they may have a negative influence on splicing.
Population of Exons Flanks by Positive Pentamers
The z-scores shown in Figures 3 and 4 provide a reliable assessment of the concentration of pentamers in exon flanks, but they do not measure the number of exons that harbor these sequences. A survey of the 50-nt flanks showed that in general, positive pentamers were more frequent among real exons than among randomly chosen intronic 50-mers and less frequent among pseudo exons (see online Supplemental material).
DISCUSSION
Our aim in this work was to discover information used by the cell to recognize splice sites. Toward this end we used pseudo exons as a foil to help sort out signals from noise in a computational analysis of human genomic sequences. Pseudo exons also served as a control set for evaluating the significance of potential splicing signal sequences. We excluded reading frame information in our analysis, making the assumption that this information was not available in the cell nucleus. An SVM was effectively trained by comparing these two sets and was able to reveal topological and sequence information associated with real signals. In this initial analysis, our representation of sequences depended on oligomer composition, base combinations and distance constraints, but one can imagine other types of input that could be useful, such as longer but mismatched oligomers and RNA structural information. Similarly, more narrowly defined pseudo sets could be used, such as alternative versus constitutive exons, weak versus strong exons, etc. For instance, we found that an SVM can distinguish pseudo exons even if they are comprised of dicodon sequences similar to those found in real exons (see online Supplemental material). This strategy, that is, the definition of a set of pseudo signals highly similar to the real signals and the use of an SVM to find differences between the pseudo and real sets, may also be usefully applied to define other genomic signals, most notably the sequence elements that distinguish real promoter/enhancers from more numerous false sites.
Highly repeated sequences such as SINES and LINES make up about half of the human genome but do not generally overlap with real exons, and some are even excluded from flanking regions (Majewski and Ott 2002; X.H-F. Zhang and L.A. Chasin, unpubl.). In contrast, repeats were present in about half of our pseudo exons. We did not exclude them, reasoning that the question of why pseudo exons in repeats are not spliced is as valid a question as why pseudo exons in unique sequences are not spliced. However, the inclusion of repeats brings with it the danger that some of the sequences we have associated with splicing or nonsplicing are indirect indicators of the real signals, being fellow travelers within the repeats. Future analyses should allow us to distinguish such indirect associations.
Machine learning via an SVM achieved an ROC of 0.99 for real versus pseudo exon recognition, or if we take one value from the ROC curve, a specificity (true positives found/all predicted) of 0.95 at a sensitivity (true positives found/real exons) of 0.95. When applied as a predictor of internal exons in a test set of eight genes under more demanding conditions (a pseudo exon to real exon ratio of 33 to 1 and exons as small as 18 nt), SVM yielded a specificity of 0.63 at a sensitivity of 0.85. These latter values are close to the average for six gene predictor programs tested by Rogic et al. (2001) for internal exons, notwithstanding the fact that we did not optimize SVM for general exon prediction (e.g., consensus values less than 78) and did not include any reading frame information.
Splice Site Sequences
Although both real exons and pseudo exons comprise sequences with similar consensus values, they differ in the particular arrangement of bases that underlie these scores. Two-way combinatorial information has been used previously to search for exons, as in the maximal dependence decomposition of 5′ splice sites in Genscan (Burge and Karlin 1997). Here we found that three-way combinations for donor sites and two-way combinations for acceptor sites were effective for discrimination. Indeed, the use of three-way base combinations as a criterion for donor site identification proved to be superior to consensus values in predicting real exons (Fig. 1). These data provide a new additional or alternative standard by which to judge the strength or weakness of potential splice sites, especially donor sites. For example, we described a double mutation of the dihydrofolate reductase gene intron 5 donor site (AGG/gtcagt) that had an improved consensus score (80.8) compared to the wild type (AGA/gtaagt, 79.6) yet spliced exon 5 with only 3% efficiency (Carothers et al. 1993). Its consensus value increased from the 35th to the 41st percentile from wild type to mutant, whereas its three-way value score dropped from the 81st to the 10th percentile, consistent with its poor splicing phenotype. For those wishing to use this three-way donor site data for exon prediction, we include a normalized list of scores in the online Supplemental material.
The two-way combinations in the acceptor site sequence represent simpler associations, but they nevertheless revealed some interesting relationships. In the positive set of two-way combinations, purines represented 67% of the relevant bases, whereas their frequency in 10-nt PPTs is only 20%. Why would the SVM find purines as a positive way to differentiate real from pseudo exons? The stretch of pyrimidines upstream of the acceptor splicing site is termed the polypyrimidine tract, but in reality it is usually punctuated with one or two purines: 88% of the real exons in our data set contain at least one purine in the 10-nt region from -14 to -5. To produce a positive weighting factor, purines could be playing either a positive role or a neutral role. In the latter case, the SVM would be detecting neutral combinations associated with real exons as opposed to deleterious combinations associated with pseudo exons. There is no evidence that purines play a positive role in the PPT: studies in which the PPT was varied either by design (Roscigno et al. 1993; Coolidge et al. 1997) or by iterative selection (Buvoli et al. 1997; Lund et al. 2000) pointed to pyrimidines as being the sole or at least the key recognition elements for a PPT. Similarly, a purine-free consensus was derived for sequences selected for binding to the PPT-binding protein U2AF65 (Singh et al. 1995). Although a positive role cannot be ruled out, we favor the second explanation, that some purine combinations are particularly benign, and it is these that are noticed by the SVM.
Position -4 in the acceptor site is occupied approximately equally by each of the four bases in most surveys of real exons. Thus one might assume that this position contains no general information with respect to splicing and would not be used by an SVM as a discriminator between real and pseudo splice sites. Contrary to this expectation, position -4 was included among highly rated combinations at a frequency comparable to that of the other 12 positions (8%). Because this raises the possibility of a role of position -4 in splicing, we sought other tests of this idea. CpGs occur in introns at 1/5 of the expectation based on the frequency of C and of G, but in exons this ratio increases to 1/2, presumably due to functional selection. The underrepresentation of CpGs at position -4 is 0.36, suggesting some functionality. As a second test we compared position -4 conservation among 7600 pairs of orthologous mouse and human exons. The base at position -4 was 64% conserved, a level no less than the PPT as a whole (61%). For comparison, position -3 is 77% conserved, whereas positions around -100 are only 40% conserved. These two tests support the SVM result suggesting that the base at position -4 is functional in at least some cases.
Flanking Sequences
A key conclusion of this work is that regions bordering the splice site sequences from about -40 to +80 contain information that could be used for splice site recognition. Majewski and Ott (2002) also concluded that exon flanks may contain sequences important for splicing on the basis of a nonrandom distribution of k-mers. Extraction of pentamer sequences that contributed most to the performance of the SVM and clustering them according to their position relative to the exon revealed both expected and novel sequence classes in these regions.
One class that might have been expected comprised pyrimidine-rich pentamers just upstream of the -14 border that we defined as the limit of the PPT. Although the information content of the upstream flank falls off beyond this position, a nonrandom distribution favoring pyrimidines remains detectable out to -27 (Penotti 1991; Stephens and Schneider 1992). We found a nonrandom (P < 0.05) distribution of these pentamers extended to position -34. As pseudo exons were only selected to have a PPT out to -14, it is understandable that these sequences stood out. However, this group of 28 alone could not achieve a high degree of distinction between real and pseudo exons. A group representing possible branch point sequences was also found upstream of the real exons, peaking at a position near -22, distinct from that of the pyrimidine-rich pentamers. The consensus provided by this select group of pentamers was CTRAC, and the two corresponding pentamers displayed the highest z-scores in this region. This sequence agrees with the TACTAAC sequence complementary to the 5′ end of U2 snRNA and represents a subset of the YNYTRAY consensus defined by (relatively few) experimentally established branch points.
The SVM identified G-triplets as a major class of flanking sequence associated with real exons. It was noted previously that G-triplets are more abundant near the 5′ ends of introns and to a lesser extent at the 3′ ends (Nussinov 1988; Engelbrecht et al. 1992; Lim and Burge 2001; Majewski and Ott 2002). Despite the abundance of G-triplets at both ends of the intron, the SVM made use of these sequences mainly downstream of the exon, suggesting that G-triplets act as enhancers that target an upstream 5′ splice site and not the 3′ splice site. Indeed, McCollough and Berget (1997, 2000) showed that G-triplets can bind U1 snRNP to enhance splicing at upstream donor sites in a short intron. Carlo et al. (1996) defined a more extended G-rich sequence (GGGGCUG) that could act as an intronic enhancer for very short exons by binding SF1 (Carlo et al. 2000). All three pentamers defined by this 7-nt sequence are found among those extracted as most important for the SVM (Fig. 3), suggesting that this enhancer element may be used more generally.
C-rich pentamers were especially distinctive downstream of the exon, where they did not overlap with a PPT. C-rich sequences have been noted previously but within exons, apparently associated with the acceptor site (Nussinov 1988), or as elements that enhance the splicing of small introns in Drosophila (Kennedy and Berget 1997). Their emergence here suggests a role as a more general intronic enhancer element. Similarly, the concentration of TG-rich pentamers in a region between the branch point and the PPT suggest these pentamers as candidate enhancing elements.
Negatively Weighted Sequences
Groups of pentamers weighted negatively represented sequences that were relatively scarce in real exon flanks compared to pseudo exons. These included sequences corresponding to the consensuses immediately bordering the sites of splicing, CAGG and AGGT for the acceptor and donor sites, respectively. The ambiguity presented by such competitors may not be tolerated. A third type of negative sequence was AC-rich. AC-rich sequences have previously been associated with exonic splicing enhancers (Coulter et al. 1997) rather than silencers, but this is hardly a discrepancy, because the locations are different, and in any case pentamers are undoubtedly only rough representations of complete functional elements.
It is noteworthy that the negative sequences identified here were not highly overrepresented in the pseudo exon set. Such a result might have been anticipated if a major mechanism for the distinction between real and pseudo exons involved silencing of the latter. We previously raised this possibility on the basis of finding that sequences that could inhibit splicing when inserted into an exon were quite common in the human genome (Fairbrother and Chasin 2000). There was some evidence in the present study for such repressive elements in pseudo exons, but they were associated with highly repeated sequences, as indicated by the red line peaks in Figure 4. Thus a repressive mechanism remains a possibility for that large class of pseudo exons associated with repeats.
Other Flanking Sequences
There remained many pentamers that shared neither a common distribution nor a common sequence motif. These sequences may represent a heterogeneous group of splicing enhancer or silencer sequences. Further analysis may help to classify exons according to distinctive enhancer elements.
METHODS
Construction of Real Exon and Pseudo Exon Databases
Databases
The essential features of the collected pseudo exon sequences are described in Results; details are available as online Supplemental material. The consensus score (CV) used to filter real and pseudo exons is based on a position-specific weighted matrix and was calculated essentially according to the method of Shapiro and Senapathy (1987). The best possible score is 100 and the worst is 0. The median CV for real exons is 82 for donor and 80 for acceptor sites.
For SVM training we used approximately 3000 randomly chosen real exons and a similar number of pseudo exons. A test set consisted of approximately 2000 sequences of each type that were never used for testing. Statistics were gathered on a third set of approximately 15,000 sequences of each type that were not used for training or for testing.
SVM Classifiers
Support vector machines (SVMs) are examples of machine learning classifiers; that is, they are used to learn a binary classification rule from labeled (positive and negative) training data. Given feature representations of the training sequences and their labels (true or pseudo), the SVM solves an optimization problem to learn a linear decision function, f(x) = 〈w, x〉 + b where w is the normal vector to the linear decision boundary and x is the feature vector representation of an input sequence. Once the SVM is trained, predictions can be made on a test sequence (represented by x) by predicting positive if f(x) > T for a given threshold, negative otherwise.
Data Division for SVM Classification
The real exons and pseudo exons derived from the EID were randomly divided into two sets. The working set was comprised of approximately 60% of the real exons and 33% of the pseudo exons; their numbers were roughly equal. A test set contained the remainder of the real EID exons and a like number of randomly chosen pseudo exons. The working set was used for training and cross-validation, and the test set was used for evaluation only.
K-mer Features for SVM Experiments
In order to train an SVM classifier, input sequences must be represented by fixed length feature vectors.
For the upstream and downstream flanks and exon bodies, the features we use are occurrences of k-length contiguous subsequences (“k-mers”). That is, we represent sequences by a sparse vector Φ(x) = (φa(x))a=a1,a2...ak, where each choice a = a1,a2...ak of k nucleotides corresponds to a coordinate and the feature φa(x) is 1 if the k-mer a occurs in the sequence x, 0 otherwise. The total number of features is 4k, but since most features are 0 for a given sequence, the vector can be represented in a space-efficient way. Similar representations have been used for SVM protein classification (Leslie et al. 2002), but in this case features were counts of k-mers occurring with mismatches in the input sequences, and the feature vectors were represented implicitly through use of a kernel function (Cristianini and Shawe-Taylor 2000).
Base Combination Features for SVM Experiments
Donor and acceptor sites and pseudo sites were represented by all possible t-way combinations of positions internal to the splice site of the exon or pseudo exon, excluding the nearly universal GT and AG dinucleotides, and all choices of t nucleotides in these positions. For example, if a donor site contains an “A” at position +3, a “G” at position +4, and a “G” at position +5, its value for the feature (3:A,4:G,5:G) is 1. Combinations that do not occur have the feature value 0. For three-way combinations, there are 35 × 64 features (seven choose three combinations of positions multiplied by possible choices of nucleotides for each combination). A similar representation has been used for SVM recognition of peptide cleavage sites (Vert 2002), except that a weighted contribution of t-way combinations for all choices of t was implicitly used, again implemented through a kernel function.
Combining Different Types of Features
Splice site features (t-way combinations) and flank and exon features (k-mers) were combined by concatenating the feature vectors and then using a degree-2 polynomial kernel; that is, we use the kernel function K(x,y) = (〈x,y〉 + c)2 in place of the standard inner product for SVM training and testing. This kernel amounts to implicitly using all pairs of the original features as features for the SVM (taking products of original feature values to obtain the new feature values).
SVM Package and Cross-Validation
We used the GIST SVM package written by William S. Noble (Univ. of Washington) for all SVM experiments. The latest version of the software is publicly available at www.cs.columbia.edu/compbio. We used the command line parameters “-normalize -diagfactor 0.1”, which are default settings in the latest version. Different settings were evaluated using fivefold cross-validation. Feature representations were directly generated using our own Perl scripts. The output was evaluated by the “score-svm-results” script provided in the software.
Real Exon Prediction
Eight multi-exon (> four exons) genes that contain 37 internal real exons were randomly chosen from the untouched data set (AB051901, AF037438, AF041428, AF261937, AF338439, AJ301616, U91328, M26434). The subsequences in these eight genes that satisfy the following criteria were extracted as exon candidates. First, these sequences had to be flanked by an upstream 15-mer whose acceptor site matrix agreement score is greater than 70 and a downstream 9-mer whose donor site matrix agreement score is greater than 70. These lower limits were chosen so as to capture all real exons. Second, the sequences had to be between 18 nt and 250 nt in length. These sequences were allowed to overlap with each other. By this means, 1225 exon candidates were selected, including the 37 real internal exons. We then used SVMs that had been trained on the training data set described above to predict which candidates were real. SVMs assigned a weight to each candidate. By taking different thresholds for this weight, different numbers of true positive (real exons predicted as real) and false positive (pseudo exons predicted as real) were determined.
Recursive Feature Selection
In the SVM solution, the normal vector to the hyperplane decision boundary is defined by
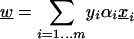 |
1 |
where xi are the training feature vectors, yi = ±1 are the labels, and αi are the learned weights. The coordinates of the vector w can be used to rank the importance of features: If a coordinate |wj| is large in absolute value, then the jth feature is important for SVM; the sign of wj shows whether it is indicative of positive or negative examples. In standard recursive feature elimination (RFE), one trains an SVM, uses the ranking induced by the wj to eliminate the bottom half of the features, and recursively retrains on the smaller feature set.
In our feature selection setting, we are concatenating k-mer feature vectors for the upstream and downstream flanks and then using a degree-2 polynomial kernel to combine both sources of information. We can no longer easily compute w, because we are implicitly using a nonlinear feature mapping. However, we can use the learned SVM weights αi to compute vectors wup and wdown using equation (1) with the k-mer feature vectors for the upstream and downstream flanks, respectively. Now we can eliminate the bottom half of the features for each flank separately and retrain on the smaller feature set. This procedure approximates RFE in our setting. The recursive process was ended when the ROC score for the SVM on an untouched test set fell below 90% of the original ROC score (obtained using the full feature set).
Comparisons Between Three-Way Base Combinations and Consensus Values
The first comparison was carried out between all real exons in the test set versus pseudo exons defined by any 50- to 250-nt sequences between an AG and a GT. The second comparison was made between real exons whose donor site consensus values were greater than 78 and pseudo exons defined in the previous section. In both comparisons, an SVM weight was computed for three-way combinations in donor sites in each sequence as an alternative classifier to consensus value. The discriminative strengths of SVM and consensus values were measured by continuously increasing the thresholds (from lowest to highest) of SVM weights or consensus value, and recording the false positive error rate, FP/(TP+FP), for each threshold in each case.
Statistics of the Top Two-Way Base Combinations in Acceptor Sites
A minimum of 128 two-way base combinations were necessary to maintain the performance of SVM at a level greater than ROC = 0.80. These features comprised 256 individual bases and were divided into two groups according to the signs of their weights. G+C and purine contents were counted at the individual base level in either group, respectively. For dinucleotides (the two bases occupying adjacent positions), such as AA, CG, and AG, the rough expectations of their frequencies in this list of 128 were calculated according to the formula (12/1248) * 128 = 1.2, where the 12 is the number of adjacent position pairs possible among the 13 positions, 1248 is the number of all possible two-way combinations, and 128 is the length of the list. For a dinucleotide to be positive, the expectation is roughly 1.2 * (49/128) = 0.5, where the 49 is the number of positive features in the list.
To further prove the importance of some dinucleotides, we compared their frequencies in real acceptor sites with two different types of expectations. Expectations based on the consensus were made by assuming independence between adjacent positions and multiplying the possibilities of getting the two bases at neighboring positions. Expectations based on pseudo exons were made by counting the frequencies of the dinucleotides in the set of 24,000 pseudo exons. The actual frequencies of these dinucleotides in real exons were computed in the set of 15,000 real exons.
Distribution of Top Pentamer Weights in Flanks
The top 256 features extracted as described in the previous section were divided into four groups according to their origins (downstream or upstream) and signs of their weights (positive or negative). For each group, we examined the pentamers' weight distribution around the 15,000 untouched real exons. We took sliding 5-bp windows from -150 to 150 and summed the SVM weights of the top pentamers that occurred in each window. The resulting distributions were plotted in Figure 3.
Analyses of Top Pentamers
The frequencies of the top-scoring pentamers in flanks were calculated for 5-bp sliding windows. The frequencies in each window were then compared to the background frequencies of these pentamers. For each pentamer in each window, a z-score was calculated by
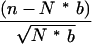 |
where n is the number of occurrences of the pentamer in the bin, N is the total number of all pentamers in the bin, and b is the background frequency of the pentamer taken from a set of 15,878 entire introns. Thus each pentamer is associated with a vector comprised of a set of z-scores representing the prevalence of that pentamer at different positions around the exons. We clustered the top pentamers according to a self-organizing map (http://gepas.bioinfo.cnio.es/cgi-bin/somtree) and then grouped clusters with similar sequences. The distributions of the pentamers in each group were plotted in Figures 3 and 4.
Acknowledgments
We thank Harmen Bussmaker for valuable comments and for reading the manuscript. L.C. was supported by funds from Columbia University. C.L. was supported by an Award in Informatics from the PhRMA Foundation and by NIH grant LM07276-02. X.Z. is a predoctoral Faculty Fellow of Columbia University.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1679003.
Footnotes
[Supplemental material is available online at www.genome.org.]
References
- Bauren, G. and Wieslander, L. 1994. Splicing of Balbiani ring 1 gene pre-mRNA occurs simultaneously with transcription. Cell 76: 183-192. [DOI] [PubMed] [Google Scholar]
- Berget, S.M. 1995. Exon recognition in vertebrate splicing. J. Biol. Chem. 270: 2411-2414. [DOI] [PubMed] [Google Scholar]
- Burge, C. and Karlin, S. 1997. Prediction of complete gene structures in human genomic DNA. J. Mol. Biol. 268: 78-94. [DOI] [PubMed] [Google Scholar]
- Buvoli, M., Mayer, S.A., and Patton, J.G. 1997. Functional crosstalk between exon enhancers, polypyrimidine tracts, and branchpoint sequences. EMBO J. 16: 7174-7183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlo, T., Sterner, D.A., and Berget, S.M. 1996. An intron splicing enhancer containing a G-rich repeat facilitates inclusion of a vertebrate micro-exon. RNA 2: 342-353. [PMC free article] [PubMed] [Google Scholar]
- Carlo, T., Sierra, R., and Berget, S.M. 2000. A 5′ splice site-proximal enhancer binds SF1 and activates exon bridging of a microexon. Mol. Cell. Biol. 20: 3988-3995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carothers, A.M., Urlaub, G., Grunberger, D., and Chasin, L.A. 1993. Splicing mutants and their second-site suppressors at the dihydrofolate reductase locus in Chinese hamster ovary cells. Mol. Cell. Biol. 13: 5085-5098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coolidge, C.J., Seely, R.J., and Patton, J.G. 1997. Functional analysis of the polypyrimidine tract in pre-mRNA splicing. Nucleic Acids Res. 25: 888-896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortes, C. and Vapnik, V.N. 1995. Support-vector networks. Mach. Learn. 20: 273-297. [Google Scholar]
- Coulter, L.R., Landree, M.A., and Cooper, T.A. 1997. Identification of a new class of exonic splicing enhancers by in vivo selection. Mol. Cell. Biol. 17: 2143-2150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cristianini, N. and Shawe-Taylor, J. 2000. An introduction to support vector machines. Cambridge University Press, Cambridge, UK.
- Engelbrecht, J., Knudsen, S., and Brunak, S. 1992. G+C-rich tract in 5′ end of human introns. J. Mol. Biol. 227: 108-113. [DOI] [PubMed] [Google Scholar]
- Fairbrother, W.G. and Chasin, L.A. 2000. Human genomic sequences that inhibit splicing. Mol. Cell. Biol. 20: 6816-6825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graveley, B.R. 2001. Alternative splicing: Increasing diversity in the proteomic world. Trends Genet. 17: 100-107. [DOI] [PubMed] [Google Scholar]
- Green, M.R. 1991. Biochemical mechanisms of constitutive and regulated pre-mRNA splicing. Annu. Rev. Cell Biol. 7: 559-599. [DOI] [PubMed] [Google Scholar]
- Harris, N.L. and Senapathy, P. 1990. Distribution and consensus of branch point signals in eukaryotic genes: A computerized statistical analysis. Nucleic Acids Res. 18: 3015-3019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmuth, K., Urlaub, H., Vornlocher, H.P., Will, C.L., Gentzel, M., Wilm, M., and Luhrmann, R. 2002. Protein composition of human prespliceosomes isolated by a tobramycin affinity-selection method. Proc. Natl. Acad. Sci. 99: 16719-16724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaakkola, T., Diekhans, M., and Haussler, D. 1999. Using the Fisher kernel method to detect remote protein homologies. In Proceedings of the Seventh International Conference on Intelligent Systems for Molecular Biology, pp. 149-158, AAAI Press, Menlo Park, CA. [PubMed]
- Joachims, T. 1998. Text categorization with support vector machines: Learning with many relevant features. In Tenth European Conference on Mach. Learn., pp. 137-142, Springer Verlag, New York.
- Jurica, M.S., Licklider, L.J., Gygi, S.R., Grigorieff, N., and Moore, M.J. 2002. Purification and characterization of native spliceosomes suitable for three-dimensional structural analysis. RNA 8: 426-439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy, C.F. and Berget, S.M. 1997. Pyrimidine tracts between the 5′ splice site and branch point facilitate splicing and recognition of a small Drosophila intron. Mol. Cell. Biol. 17: 2774-2780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessler, O., Jiang, Y., and Chasin, L.A. 1993. Order of intron removal during splicing of endogenous adenine phosphoribosyltransferase and dihydrofolate reductase pre-mRNA. Mol. Cell. Biol. 13: 6211-6222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krawczak, M., Reiss, J., and Cooper, D.N. 1992. The mutational spectrum of single base-pair substitutions in mRNA splice junctions of human genes: Causes and consequences. Hum. Genet. 90: 41-54. [DOI] [PubMed] [Google Scholar]
- Ladd, A.N. and Cooper, T.A. 2002. Finding signals that regulate alternative splicing in the post-genomic era. Genome Biol. 3: 0008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leslie, C., Eskin, E., Westo, J., and Noble, W.S. 2002. Mismatch string kernels for SVM protein classification. In Neural information processing systems, pp. (in press).
- Lim, L.P. and Burge, C.B. 2001. A computational analysis of sequence features involved in recognition of short introns. Proc. Natl. Acad. Sci. 98: 11193-11198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, H.X., Zhang, M., and Krainer, A.R. 1998. Identification of functional exonic splicing enhancer motifs recognized by individual SR proteins. Genes & Dev. 12: 1998-2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, H.X., Chew, S.L., Cartegni, L., Zhang, M.Q., and Krainer, A.R. 2000. Exonic splicing enhancer motif recognized by human SC35 under splicing conditions. Mol. Cell. Biol. 20: 1063-1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lund, M., Tange, T.O., Dyhr-Mikkelsen, H., Hansen, J., and Kjems, J. 2000. Characterization of human RNA splice signals by iterative functional selection of splice sites. RNA 6: 528-544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majewski, J. and Ott, J. 2002. Distribution and characterization of regulatory elements in the human genome. Genome Res. 12: 1827-1836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullough, A.J. and Berget, S.M. 1997. G triplets located throughout a class of small vertebrate introns enforce intron borders and regulate splice site selection. Mol. Cell. Biol. 17: 4562-4571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCullough, A.J. and Berget, S.M. 2000. An intronic splicing enhancer binds U1 snRNPs to enhance splicing and select 5′ splice sites. Mol. Cell. Biol. 20: 9225-9235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nussinov, R. 1988. Conserved quartets near 5′ intron junctions in primate nuclear pre-mRNA. J. Theor. Biol. 133: 73-84. [DOI] [PubMed] [Google Scholar]
- O'Neill, J.P., Rogan, P.K., Cariello, N., and Nicklas, J.A. 1998. Mutations that alter RNA splicing of the human HPRT gene: A review of the spectrum. Mutat. Res. 411: 179-214. [DOI] [PubMed] [Google Scholar]
- Penotti, F.E. 1991. Human pre-mRNA splicing signals. J. Theor. Biol. 150: 385-420. [DOI] [PubMed] [Google Scholar]
- Rappsilber, J., Ryder, U., Lamond, A.I., and Mann, M. 2002. Large-scale proteomic analysis of the human spliceosome. Genome Res. 12: 1231-1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed, R. 2000. Mechanisms of fidelity in pre-mRNA splicing. Curr. Opin. Cell Biol. 12: 340-345. [DOI] [PubMed] [Google Scholar]
- Reed, R. and Maniatis, T. 1986. A role for exon sequences and splice-site proximity in splice-site selection. Cell 46: 681-690. [DOI] [PubMed] [Google Scholar]
- Robberson, B.L., Cote, G.J., and Berget, S.M. 1990. Exon definition may facilitate splice site selection in RNAs with multiple exons. Mol. Cell. Biol. 10: 84-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogan, P.K., Faux, B.M. and Schneider, T.D. 1998. Information analysis of human splice site mutations. Hum. Mutat. 12: 153-171. [DOI] [PubMed] [Google Scholar]
- Rogic, S., Mackworth, A.K., and Ouellette, F.B. 2001. Evaluation of gene-finding programs on mammalian sequences. Genome Res. 11: 817-832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roscigno, R.F., Weiner, M., and Garcia-Blanco, M.A. 1993. A mutational analysis of the polypyrimidine tract of introns. Effects of sequence differences in pyrimidine tracts on splicing. J. Biol. Chem. 268: 11222-11229. [PubMed] [Google Scholar]
- Saxonov, S., Daizadeh, I., Fedorov, A., and Gilbert, W. 2000. EID: The Exon-Intron Database—An exhaustive database of protein-coding intron-containing genes. Nucleic Acids Res. 28: 185-190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaal, T.D. and Maniatis, T. 1999a. Multiple distinct splicing enhancers in the protein-coding sequences of a constitutively spliced pre-mRNA. Mol. Cell. Biol. 19: 261-273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaal, T.D. and Maniatis, T. 1999b. Selection and characterization of pre-mRNA splicing enhancers: Identification of novel SR protein-specific enhancer sequences. Mol. Cell. Biol. 19: 1705-1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro, M.B. and Senapathy, P. 1987. RNA splice junctions of different classes of eukaryotes: Sequence statistics and functional implications in gene expression. Nucleic Acids Res. 15: 7155-7174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh, R., Valcarcel, J., and Green, M.R. 1995. Distinct binding specificities and functions of higher eukaryotic polypyrimidine tract-binding proteins. Science 268: 1173-1176. [DOI] [PubMed] [Google Scholar]
- Smit, A.F.A. and Green, P. 2002. RepeatMasker. http://ftp.genome.washington.edu/RM/RepeatMasker.html.
- Stephens, R.M. and Schneider, T.D. 1992. Features of spliceosome evolution and function inferred from an analysis of the information at human splice sites. J. Mol. Biol. 228: 1124-1136. [DOI] [PubMed] [Google Scholar]
- Sun, H. and Chasin, L.A. 2000. Multiple splicing defects in an intronic false exon. Mol. Cell. Biol. 20: 6414-6425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian, H. and Kole, R. 1995. Selection of novel exon recognition elements from a pool of random sequences. Mol. Cell. Biol. 15: 6291-6298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vapnik, V.N. 1998. Statistical learning theory. Wiley, Chicester, UK.
- Vert, J.-P. 2002. Support vector machine prediction of signal peptide cleavage site using a new class of kernels for strings. In Proceedings of the Pacific Symposium on Biocomputing, pp. 649-660, World Scientific, Singapore. [DOI] [PubMed]
- Watakabe, A., Tanaka, K., and Shimura, Y. 1993. The role of exon sequences in splice site selection. Genes & Dev. 7: 407-418. [DOI] [PubMed] [Google Scholar]
- Zhang, M.Q. 1998. Statistical features of human exons and their flanking regions. Hum. Mol. Genet. 7: 919-932. [DOI] [PubMed] [Google Scholar]
- Zhou, Z., Licklider, L.J., Gygi, S.P., and Reed, R. 2002. Comprehensive proteomic analysis of the human spliceosome. Nature 419: 182-185. [DOI] [PubMed] [Google Scholar]
- Zien, A., Ratsch, G., Mika, S., Scholkopf, B., Lemmen, C., Smola, A., Lengauer, T., and Muller, K.R. 2000. Engineering support vector machine kernels that recognize translation initiation sites. Bioinformatics 16: 799-807. [DOI] [PubMed] [Google Scholar]
WEB SITE REFERENCES
- http://genes.mit.edu/burgelab/maxent/Xmaxentscan_scoreseq.html; maximum entrophy modeling of short sequence motifs by G. Yeo and C.B. Burge. [DOI] [PubMed]
- http://gepas.bioinfo.cnio.es/cgi-bin/somtree; combining hierarchical clustering and self-organizing maps by J. Herrero and J. Dopazo. [DOI] [PubMed]
- www.cs.columbia.edu/compbio; Computational Biology Group at Columbia.