Predictive performance of microarray gene signatures: impact of tumor heterogeneity and multiple mechanisms of drug resistance

Abstract

Gene signatures have failed to predict responses to breast cancer therapy in patients to date. In this study, we used bioinformatic methods to explore the hypothesis that the existence of multiple drug resistance mechanisms in different patients may limit the power of gene signatures to predict responses to therapy. Additionally, we explored whether sub-stratification of resistant cases could improve performance. Gene expression profiles from 1,550 breast cancers analyzed with the same microarray platform were retrieved from publicly available sources. Gene expression changes were introduced in cases defined as sensitive or resistant to a hypothetical therapy. In the resistant group, up to five different mechanisms of drug resistance causing distinct or overlapping gene expression changes were generated bioinformatically, and their impact on sensitivity, specificity and predictive values of the signatures was investigated. We found that increasing the number of resistance mechanisms corresponding to different gene expression changes weakened the performance of the predictive signatures generated, even if the resistance-induced changes in gene expression were sufficiently strong and informative. Performance was also affected by cohort composition and the proportion of sensitive versus resistant cases or resistant cases that were mechanistically distinct. It was possible to improve response prediction by sub-stratifying chemotherapy-resistant cases from actual datasets (non-bioinformatically-perturbed datasets), and by using outliers to model multiple resistance mechanisms. Our work supports the hypothesis that the presence of multiple resistance mechanisms to a given therapy in patients limits the ability of gene signatures to make clinically-useful predictions.

INTRODUCTION

Current approaches for microarray-based gene expression profiling analysis have been effective in generating gene signatures that accurately identify simple and/or overtly dominant phenotypes associated with marked transcriptomic characteristics (e.g. between estrogen receptor (ER)-positive and ER-negative breast cancers)(1-4). It has led to the development of a molecular classification of breast cancer with prognostic implications, and of prognostic gene signatures(3,5-7), both of which also identify subgroups of breast cancers with different sensitivity to chemotherapy, seemly irrespective of the chemotherapy agent(s) used(8-10). The prognostic and predictive power of these tests has been shown to be primarily attributable to their ability to assess the expression levels of ER- and proliferation-related genes(1,4,11,12).

The development of gene signatures predictive of response to specific therapeutic agents and/or combinatorial therapies has proven challenging(1). The ability of gene signatures to predict complex biological phenomena appears to be limited, and some biological endpoints have been shown to be inherently difficult to predict regardless of the study design and bioinformatics methods employed(2,13,14). The predictive signatures generated thus far have either not been validated in subsequent studies or offered limited predictive value in addition to that provided by standard clinico-pathological parameters(1,4,15-17). This limited success in the development of predictive signatures can be attributed to biological phenomena and technical issues, including pharmacokinetics variability that may not be entirely captured by expression profiling of primary tumors (reviewed in (18)), weakly informative features (i.e. limited difference in gene expression levels between sensitive and resistant cases)(2,13), small sample size and/or limited proportion (<10%) of tumors displaying informative gene expression changes(2,13), and the observation that resistance/sensitivity to a given therapeutic agent often involve low-level expression differences in a modest number of genes(17).

Resistance to a given therapeutic agent may be caused by multiple mechanisms underpinned by distinct genetic/epigenetic aberrations (i.e. convergent phenotypes)(19,20). For instance, resistance to small molecule inhibitors targeting EGFR in lung adenocarcinomas harboring EGFR mutations has been shown to be caused by EGFR gatekeeper mutations, MET gene amplification and conversion from adenocarcinoma to small cell lung cancer(21), multiple mechanisms of resistance to Trastuzumab have been described in vitro and in vivo, including loss of PTEN, PIK3CA mutations, over-expression of IGF-1R or MUC4, and HER2-p95 expression(22,23), and resistance to Poly(ADP) Ribose Polymerase (PARP) inhibitors in BRCA1 and BRCA2 mutation carriers with breast and ovarian cancer may be caused by BRCA1 or BRCA2 intragenic deletions or revertant mutations, P-glycoprotein overexpression and 53BP1 loss of expression (reviewed in (24)). These convergent phenotypes pose a challenge for the development of predictive signatures, as tumors with different resistance mechanisms may display either completely different or only partially overlapping gene expression patterns(4,17,25), and conventional methods of genome-wide microarray analysis may only be able to identify genes significantly altered in the majority of therapy-resistant or sensitive tumors in a given dataset(25).

In studies aiming to derive gene expression predictors of response, resistant samples have been treated as a single, homogeneous group without the knowledge of the underlying mechanisms of resistance(25). Hence, we sought to determine the impact of the existence of multiple mechanisms of resistance to a hypothetical therapeutic agent (or combinatorial therapy) on the performance of predictive gene signatures. We bioinformatically spiked-in a breast cancer gene expression dataset (n=1,550) with resistance-associated expression changes to a hypothetical drug (or combinatorial therapy) and demonstrated that the existence of multiple mechanisms of resistance has a deleterious impact on the performance of predictive gene signatures. Furthermore, we assessed in actual datasets of breast cancer patients who underwent neoadjuvant chemotherapy whether sub-stratification of the chemotherapy-resistant cases improved the performance of the predictive signatures generated.

MATERIAL AND METHODS

Dataset and generation of spiked-in datasets

We selected nine breast cancer gene expression datasets generated on the Affymetrix U133a2 platform comprising 1,550 cases from Haibe-Kains et al.(26). The datasets CAL (ArrayExpress: E-TABM-158), EORTC10994 (Gene Expression Omnibus (GEO): GSE1561), MSK (GEO: GSE2603), VDX (GEO: GSE2034, GSE5327), MAINZ (GEO: GSE11121), TRANSBIG (GEO: GSE7390), MDA4 (http://bioinformatics.mdanderson.org/pubdata.html), NCCS (GEO: GSE5364), and MAQC2 (GEO: GSE20194) were downloaded from http://compbio.dfci.harvard.edu/pubs/sbtpaper/. This platform had the largest number of cases (n=1,550) analyzed on any single expression array platform in this collection of datasets. We obtained normalized microarray-based gene-expression data from the above public repository, and to account for batch/source effects, we re-normalized the merged dataset with ComBat(27). The resulting merged dataset showed no signs of bias resulting from batch effects (data not shown). Next, we generated bioinformatically perturbed datasets using this merged dataset by spiking in arbitrarily-selected resistance-associated gene expression changes (i.e. adding specific expression values to genes selected to constitute the gene expression patterns of resistance) to a hypothetical drug or combinatorial therapy (Fig. 1). Using this approach, we have defined bioinformatically the genes associated with resistance to the hypothetical drug or combinatorial therapy, and the cases classified as resistant or sensitive. Sensitive cases to the hypothetical therapeutic agent (s%) were randomly selected at varying proportions ranging from 5% to 50%. The remaining resistant cases (1-s%) were subdivided into 1, 2, 3, 4 or 5 resistant groups (n) on the basis of their hypothetical mechanisms of resistance, where 1/n of the cases were randomly allocated into having the n^th resistance mechanism. For presentation purposes, the ‘ideal’ and ‘clinically-realistic’ prevalence of resistant cases were 50% (i.e. maximal statistical power) and 90%, respectively(28). Resistance-associated gene expression changes were ‘spiked-in’ by adding v (v=0.5, 1.0 or 1.5) to the Log₂-expression value of 100 randomly selected probes (i.e. features), whereby 0.5 (1.4-fold), 1.0 (2.0-fold) and 1.5 (2.8-fold) were considered ‘weak’, ‘optimal’ and ‘strong’ gene expression changes in the context of microarray-based signature generation, respectively(13). For each combination of s, v and n, we repeated the perturbation steps to generate 100 bioinformatically-perturbed datasets. Using the same methods, we also simulated datasets for other scenarios. First, we generated 200 iterations where there were 2, 3, 4 or 5 resistance mechanisms (n), for which the proportions of resistant cases driven by a pre-determined number of resistance mechanisms (i.e. 2, 3, 4 or 5) were randomly allocated (e.g. in a dataset where 50% of cases were resistant to a given therapeutic agent and there were two resistance mechanisms, the proportions of cases driven by mechanism 1 or 2 were randomly allocated). Second, we generated 200 iterations where there were 2, 3, 4 or 5 resistance mechanisms (n), for which the proportions of resistant cases were identical in the training and test sets, however, the proportion of cases driven by a given mechanism of resistance was randomly and independently allocated for the training and test sets. Third, we generated 100 iterations where there were 2, 3, 4 or 5 resistance mechanisms (n) with overlapping changes in gene expression, such that the overlap (o%, o%=0%, 1%, 5%, 10%, 20%, 50% or 90%) of the 100 spiked-in genes was identical for each of the n mechanisms and that the remaining 1-o% genes were randomly selected and mutually exclusive.

Figure 1. Schematic representation of the study design.

Perturbed datasets were generated using microarray-based gene expression profiles of 1,550 breast cancer cases analyzed with the Affymetrix U133a2 platform. We assumed that s% of the cases were therapy sensitive (grey boxes), while the remaining 1-s% were therapy resistant (colored boxes). Within the 1-s% resistant cases, we further assumed that there were n resistance mechanisms, where the resistant cases were randomly allocated into the n^th resistance mechanism (colored boxes). For illustration purposes, we assumed up to three resistance mechanisms (i.e. n=1, 2 or 3). Each resistance mechanism was represented by adding v (v=0.5, 1.0 or 1.5) to the Log2-expression value of 100 randomly selected, but not necessarily mutually exclusive, probes (black boxes). Predictive signature models were derived by ranking the features (probes) by t-tests using the CMA package. The top 100 features were then used as the predictive gene signature for diagonal linear discriminant analysis (DLDA) or supervised principal components (superPC) classification. Validation of the predictive gene signature was performed by stratified 3-fold Monte-Carlo cross-validation, repeated 50 iterations. Comparing the predicted and actual classes, we calculated the area under curve of receiver operating characteristic curves, sensitivity, specificity, accuracy, positive predictive value and negative predictive for each predictive gene signature. For each combination of variables, we repeated the spiking-in and classification up to 200 times.

Predictive signature model building

As with most signatures predictive of response to a given therapeutic agent or combinatorial therapy reported to date, we have employed a linear model, diagonal linear discriminant analysis (DLDA), using the “Classification for MicroArrays” (CMA) package(29). t-test was employed to rank the features based on their ability to distinguish sensitive and resistant cases. The top 100 features were then used as the predictive signature for DLDA. In addition, we generated predictive signatures by supervised principal component analysis using the “superPC” package(30). Feature selection was performed by ranking the features using Wald score. The top 100 features were selected as the gene predictive signature, the optimal number of principal components (up to 3) was selected by cross-validation of the training set and a predictive signature was defined by superPC. For both DLDA and superPC, validation of the predictive signatures was performed by 50 iterations of 3-fold Monte-Carlo cross-validation (MCCV), stratified to preserve the proportions of the different groups of sensitive and resistant cases. Semi-stratified 3-fold MCCV was performed when only the sensitive to resistant ratio had to be preserved but not the proportion of cases driven by a given mechanism of resistance between training and test sets.

For each analysis performed, as performance indicators, we measured the area under curve (AUC) of the receiver operating characteristic (ROC) curves, sensitivity, specificity, accuracy, positive predictive value (PPV) and negative predictive value (NPV) by taking the median of the MCCV repeats, and selected distributions for illustrative purposes.

Statistical methods

We performed two types of statistical analyses. First, we performed a trend test to calculate the statistical significance of the linear slope fitted to the logits of the AUCs (y – dependent values), the logits of the AUCs being inverse variance weighed and the independent values set to the integers 1,2,3,4 or 5 or 1,2,3 or 4 depending on the number of data points. This test is used to calculate the statistical significance of increasing the number of resistance mechanisms. Second, if confidence intervals (CIs) touch or do not overlap, the significance level satisfies p<0.05. Standard errors for differences were calculated by dividing the difference between the confidence limits and the mean by 1.96. If the two standard errors are se₁ and se₂, then the standard error of the difference is $\sqrt{s{e_1}^2+s{e_2}^2}$ and the difference between the means is 2(se₁ + se₂), hence the p-value can be calculated from $z=\frac{2(s{e}_1+s{e}_2)}{\sqrt{s{e_1}^2+s{e_2}^2}}$. We have tested the results for a range of values and observed that the p-values satisfy p<0.05. For example, se1=0.01, se2=0.01, seDiff=0.014, Diff=0.0392 and z=2.77186 result in a p= 0.005573725, se1=0.01, se2=0.1, seDiff=0.1, Diff=0.2156 and z=2.1453 result in a p=0.031928854, and se1=0.2, se2=0.15, seDiff=0.25, Diff=0.686 and z=2.744 result in a p=0.006069554. On this basis, this rule was employed to define statistically significant differences between different classifiers generated.

Predictive signature performance using actual breast cancer datasets

To assess the impact of multiple resistance subgroups on predictive signature performance, we employed two actual (i.e. non-bioinformatically perturbed) breast cancer datasets obtained from patients undergoing neoadjuvant taxane-anthracycline-based chemotherapy (i.e. GSE25055 and GSE25065). GSE25055 was used as the training dataset and GSE25065 was employed as the test (i.e. validation) dataset. Normalized gene expression data from these studies were obtained from Hatzis et al. (31). Data were re-normalized using ComBat(27) to account for batch/source effects. To avoid the impact of proliferation-related genes on the ability to define chemotherapy response predictors, only ER-negative breast cancers were included in the analysis, as these consistently display high levels of proliferation-related genes(1). GSE25055 comprises 129 ER-negative breast cancers, of which 34.9% evolved to pathologic complete response (pCR), and GSE25065 comprises 68 ER-negative breast cancers, of which 33.8% evolved to pCR. Predictive signatures were derived using pCR as a surrogate for sensitivity to the chemotherapy regimen. Performance was determined in the ER-negative cases (n=129 training set, pCR rate 34.9%) by selecting features using either t-tests comparing all sensitive vs resistant cases (‘standard t-test’), a modified Cancer Outlier Profiling Analysis (mCOPA) method(32,33), or a mixed linear model and mCOPA approach (80% and 20% of features derived using the standard t-test and mCOPA, respectively; ‘Mixed (20% mCOPA)’). To investigate the impact of clinical parameters as other potential sources of heterogeneity, we further defined the performance of predictive signatures using a mixed approach where features were derived from age-related signatures (80% and 20% of features derived using standard t-test and age-related signatures, respectively; ‘Mixed (20% age)’), nodal status (80% and 20% of features derived using standard t-test and nodal status-related signatures, respectively; ‘Mixed (20% nodal status)’) and tumor size-related signatures (80% and 20% of features derived using standard t-test and tumor size-related signatures, respectively; ‘Mixed (20% tumor size)’; see below). For a direct comparison, the 80% of features selected by t-test were kept constant in all mixed approaches.

To select features by modified COPA, we used the implementation of mCOPA as described by Wang et al (33) with further modifications. Briefly, COPA transformation was performed on normalized expression values. Using the COPA-transformed scores, we defined over-expressed resistant outliers as features greater than the 75^th percentile plus 1.5 times the inter-quartile value of the sensitive cases and under-expressed resistant outliers as features less than the 25^th percentile minus the inter-quartile value of the sensitive, as originally described. Only candidate features that did not have sensitive outliers in the same direction (either up-regulated or down-regulated) as the resistant outliers and had at least 5% of the resistant cases as outliers were included. Furthermore, only candidate features that displayed at least a 2-fold difference between the mean expression of the resistant outliers and the mean expression of the sensitive cases were included. Using the same approach, candidate features using sensitive outliers were also identified by comparing the sensitive cases to the resistant cases. The features up- and down-regulated in the resistant cases and those up- and down-regulated in the sensitive cases were combined and ranked by the difference in expression between the outliers and the control group (i.e. the resistant outliers vs the sensitive cases and vice-versa) in decreasing order.

To select features associated with age, the cohort was stratified according to age at diagnosis (≤45 vs >45 years of age). Features were selected using t-tests comparing all sensitive vs resistant cases within each sub-cohort of the training set, and selected features were merged from the individual sub-cohorts by ranking according to the t-statistics. Feature selection based on nodal status (N0 vs N1/2/3) and tumor size (T0/1 vs T2/3) was performed in the same manner.

For ‘standard t-test’ and ‘mCOPA’ signatures, the top 100 genes were selected as the gene signature for superPC classification(30). In the mixed approaches, to overcome the potential overlap of predictive genes identified by t-test and mCOPA or by t-test and the methods employed for signature generation using the clinical parameters, the 100 genes that compose the final signature were selected by iteratively adding one feature at a time such that the proportion of genes not shared by the two sources of features was maintained. Validation of the predictive signatures was performed by leave-one-out cross-validation (LOOCV) of the training set. A separate approach was employed, whereby signatures were generated as described above using GSE25055 as the training dataset, and validated using ER-negative samples from GSE25065 (n=68 test set, pCR rate 33.8%) as the validation dataset. At no point, signatures were generated using the validation dataset GSE25065. For each analysis performed, we measured the accuracy, sensitivity, specificity, PPV and NPV.

The R scripts and codes employed for the analyses described are available as a Supplementary file.

RESULTS

The number of distinct resistance mechanisms impacts on the performance of predictive gene signatures

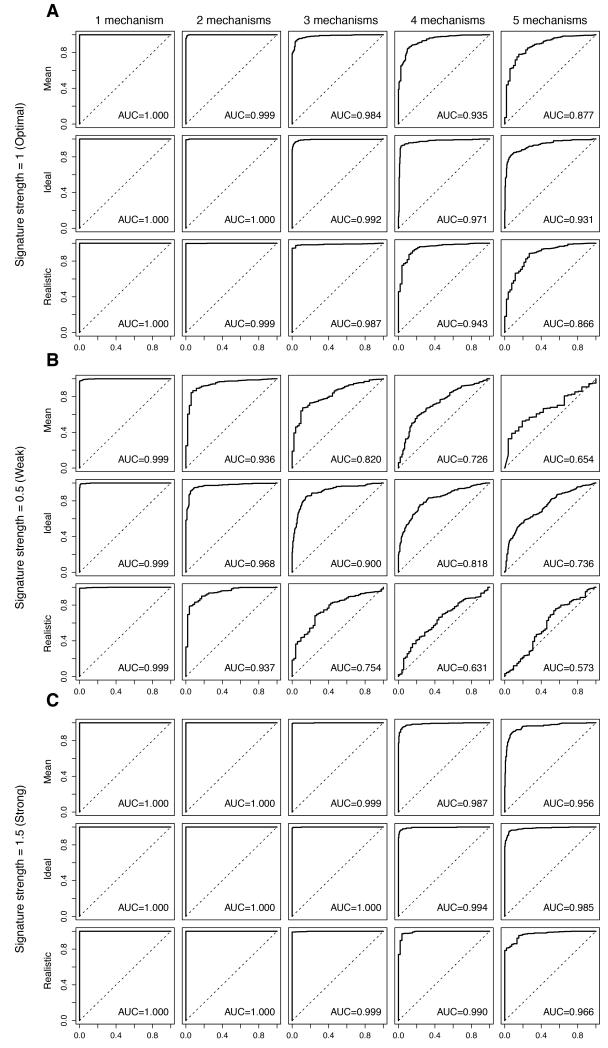
In a scenario where distinct and equally prevalent mechanisms of resistance would result in optimal (i.e. 2-fold) gene expression changes whose overlap is not different from that caused by chance (i.e. random but not necessarily mutually exclusive), increasing the number of resistance mechanisms significantly reduced the performance of the predictive signatures (Fig. 2, Table 1, Supplementary Table S1). In an ideal setting (i.e. 50% resistant cases), an increase in the number of resistance mechanisms resulted in a statistically significant trend of decreasing AUCs (p<0.0001). Employing a more realistic clinical estimate (i.e. 90% of resistant cases(28)), similar findings were obtained (Fig. 2A, Table 1), and an increase in the number of resistance mechanisms from 1 to 5 also resulted in significant trend of decreasing AUCs (p<0.0001). Increasing the proportion of resistant cases from the ideal to the clinically-realistic settings (i.e. from 50% to 90%) did not have a significant impact on trends of AUCs (p>0.05) at optimal signature strength (i.e. ≥2-fold).

Figure 2. Impact of multiple mechanisms of resistance on the performance of the predictive signatures.

Perturbed datasets in which s% (s%=5%, 10%, 20%, 30%, 40% or 50%) of the cases were designated to be therapy sensitive were generated. Within the 1-s% resistant cases, we allocated the cases randomly into n (n=1, 2, 3, 4, 5) equally sized groups of resistance mechanisms. For each n^th resistance mechanism, 100 genes were randomly selected as the “true” gene expression changes and were spiked-in by v (v=0.5, 1, 1.5). For each combination of s, n and v, we repeated the spiking and classification 100 times. Representative receiver operating characteristic (ROC) curves and the mean area under curve (AUC) for the cases are shown, where the Log₂-expression of the 100-gene “true” gene expression changes were spiked-in by 1 (A, labeled “Signature strength=1 (Optimal)”), 0.5 (B, labeled “Signature strength=0.5 (Weak)”) and 1.5 (C, labeled “Signature strength=1.5 (Strong)”). Within each of A, B and C, (top row, labeled “Mean”) simulations for 1-s%=50%, 60%, 70%, 80%, 90% or 95%, (middle row, labeled “Ideal”) simulations for an optimal setting where 1-s%=50% and (bottom row, labeled “Realistic”) simulations for a clinically-realistic setting where 1-s%=90% are shown. Within each row, the representative ROCs for (from left) n=1 (“1 mechanism”), n=2 (“2 mechanisms”), n=3 (“3 mechanisms”), n=4 (“4 mechanisms”), n=5 (“5 mechanisms”) groups of distinct resistance mechanisms are shown.

Table 1.

Impact of distinct mechanisms of resistance on the area under the curve (AUC) of receiver operating characteristic (ROC) curves derived with the predictive gene signatures generated.

Proportion of resistant cases	Optimal signature (2.0-fold)					p-value for trend
	Number of resistance mechanisms
	1	2	3	4	5
0.5*	1.000 (1.000-1.000)	1.000 (0.999-1.000)	0.992 (0.987-0.997)	0.971 (0.955-0.983)	0.931 (0.886-0.955)	< 0.0001
0.6	1.000 (1.000-1.000)	0.999 (0.997-1.000)	0.992 (0.985-0.996)	0.966 (0.943-0.980)	0.930 (0.882-0.954)	< 0.0001
0.7	1.000 (1.000-1.000)	1.000 (0.998-1.000)	0.991 (0.977-0.996)	0.967 (0.933-0.980)	0.927 (0.888-0.953)	< 0.0001
0.8	1.000 (1.000-1.000)	1.000 (0.998-1.000)	0.990 (0.974-0.996)	0.963 (0.933-0.980)	0.920 (0.870-0.947)	< 0.0001
0.9**	1.000 (1.000-1.000)	0.999 (0.998-1.000)	0.987 (0.967-0.995)	0.943 (0.898-0.967)	0.866 (0.786-0.919)	< 0.0001
0.95	1.000 (1.000-1.000)	0.999 (0.994-1.000)	0.951 (0.864-0.987)	0.803 (0.728-0.881)	0.687 (0.619-0.754)	< 0.0001

Proportion of resistant cases	Weak signature (1.4-fold)					p-value for trend
	Number of resistance mechanisms
	1	2	3	4	5
0.5*	0.999 (0.996-1.000)	0.968 (0.935-0.982)	0.900 (0.844-0.936)	0.818 (0.762-0.855)	0.736 (0.689-0.784)	< 0.0001
0.6	0.999 (0.996-1.000)	0.970 (0.949-0.984)	0.892 (0.843-0.925)	0.812 (0.747-0.855)	0.729 (0.682-0.771)	< 0.0001
0.7	0.999 (0.996-1.000)	0.967 (0.944-0.982)	0.895 (0.845-0.921)	0.797 (0.738-0.839)	0.708 (0.659-0.754)	< 0.0001
0.8	0.999 (0.996-1.000)	0.965 (0.933-0.986)	0.872 (0.810-0.909)	0.746 (0.692-0.784)	0.653 (0.619-0.689)	< 0.0001
0.9**	0.999 (0.994-1.000)	0.937 (0.883-0.968)	0.754 (0.692-0.820)	0.631 (0.581-0.686)	0.573 (0.527-0.612)	< 0.0001
0.95	0.998 (0.990-1.000)	0.808 (0.703-0.886)	0.610 (0.550-0.685)	0.550 (0.502-0.606)	0.526 (0.463-0.583)	< 0.0001

Proportion of resistant cases	Strong signature (2.8-fold)					p-value for trend
	Number of resistance mechanisms
	1	2	3	4	5
0.5*	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (0.998-1.000)	0.994 (0.984-0.998)	0.985 (0.970-0.994)	0.002
0.6	1.000 (1.000-1.000)	1.000 (1.000-1.000)	0.999 (0.996-1.000)	0.995 (0.987-0.998)	0.982 (0.963-0.991)	0.0006
0.7	1.000 (1.000-1.000)	1.000 (1.000-1.000)	0.999 (0.998-1.000)	0.994 (0.983-0.998)	0.979 (0.958-0.989)	0.0006
0.8	1.000 (1.000-1.000)	1.000 (1.000-1.000)	0.999 (0.997-1.000)	0.993 (0.976-0.997)	0.977 (0.953-0.989)	< 0.0001
0.9**	1.000 (1.000-1.000)	1.000 (1.000-1.000)	0.999 (0.996-1.000)	0.990 (0.975-0.997)	0.966 (0.925-0.985)	0.0006
0.95	1.000 (1.000-1.000)	1.000 (1.000-1.000)	0.997 (0.991-1.000)	0.959 (0.893-0.988)	0.850 (0.757-0.929)	< 0.0001

Perturbed datasets in which s% (s%=5%, 10%, 20%, 30%, 40% or 50%) of the cases were designated to be therapy sensitive were generated. Within the 1-s% resistant cases, we allocated the cases randomly into n (n=1, 2, 3, 4, 5) equally-sized groups of resistance mechanisms. For each nth resistance mechanism, 100 genes were randomly selected as the “true” gene expression changes and were spiked-in by v (v=0.5,1,1.5). Classification was performed using diagonal linear discriminant analysis (DLDA). For each combination of s, n and v, we repeated the spiking and classification 100 times. The mean value with the 95% confidence intervals in parentheses of the AUC of ROCs for each combination of s, n and v are shown. For v=1, 0.5, 1.5, the sections are labeled “Optimal signature (2-fold)”, “Weak signature (1.4-fold)” and “Strong signature (2.8-fold)” respectively. The last column depicts the p-values for the trend tests as the number of resistance mechanisms is increased from 1 to 5 for a given s%.

^*ideal setting;

^**clinically-realistic estimate

Gene expression changes associated with sensitivity or resistance to a given therapeutic intervention have been shown often to be weaker than 2.0-fold(13). Hence, by using a clinically-relevant ‘weak’ signature (i.e. an increase of 0.5 on the Log₂-expression or 1.4-fold, Fig. 2B, Table 1, Supplementary Table S1), we observed that the deteriorating effect of the increase in the number of equally prevalent resistance mechanisms was even more pronounced. The trends of decreasing AUCs as the number of mechanisms of resistance increased from 1 to 5 in the ideal setting (50% sensitive cases) and the realistic clinical estimate (10% sensitive cases) were both significant (p<0.0001), as was the difference between them (p<0.0001; Fig. 2B, Table 1). The impact of multiple mechanisms of resistance on the performance of the predictive signatures was less pronounced but still statistically significant when the signature was strong (i.e. 2.8-fold, equivalent to an increase of 1.5 on the Log₂-expression scale; ‘strong’, Fig. 2C, Table 1, Supplementary Table S1).

Consistent with the notion that 2-fold expression changes are optimal(13), we observed that reducing the signature strength from 2-fold to 1.4-fold significantly decreased the performance of the predictive gene signature for any given proportion of resistant cases (p<0.0001, Supplementary Table S2), whereas a 2-fold to 2.8-fold increase did not result in a significant improvement (p>0.05, Supplementary Table S2), except for when 95% of the cases were therapy-resistant.

When the same analysis was repeated using superPC as the classifier, similar results were obtained (Supplementary Tables S3, S4), however DLDA performed better than superPC, particularly when the proportion of sensitive cases was low and when >3 mechanisms of resistance were present; hence, the remaining analyses performed employed DLDA for signature generation.

We also investigated scenarios where the different mechanisms of resistance had an uneven and randomly determined prevalence, but identical distributions in the training and test sets. As observed when each resistance mechanism was equally distributed in the resistant population, increasing the number of unevenly distributed resistance mechanisms reduced the AUCs. Given the wider confidence intervals due to the randomly determined prevalence of each resistance mechanism, the trends in AUC reduction were only significant when ‘weak’ changes in gene expression were employed (Supplementary Fig. S1, Supplementary Table S5).

Taken together, these results suggest that the existence of multiple mechanisms of resistance has a negative impact on the performance of predictive signatures.

The proportion of different mechanisms of resistance in training and test sets influences signature performance

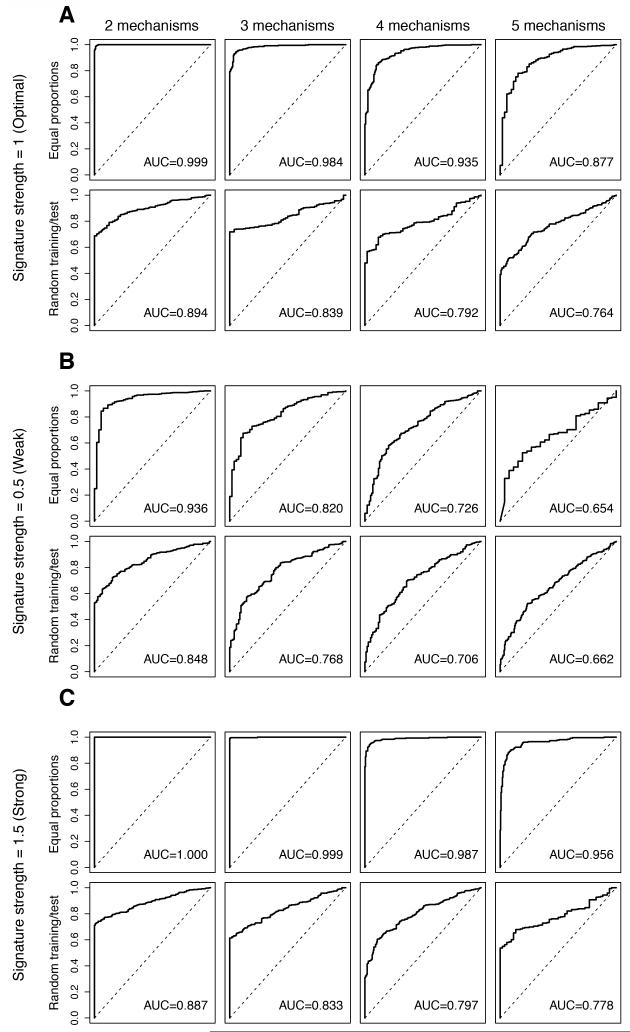
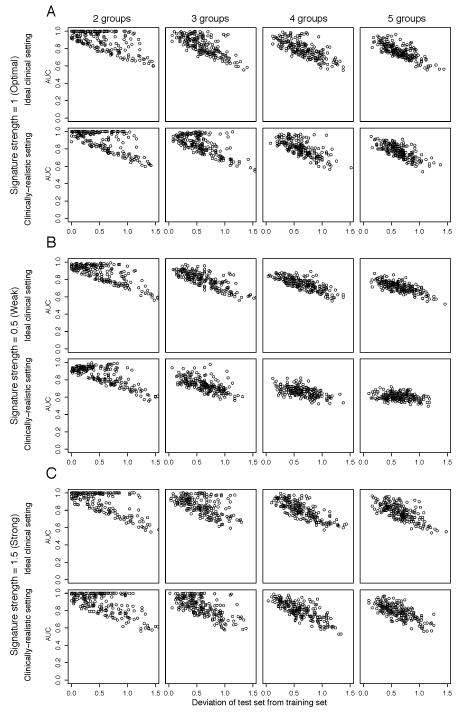
To investigate whether differences in the prevalence of distinct resistance mechanisms between the training and test datasets affect the performance of predictive gene signatures, the training and test datasets were spiked-in with similar proportions of resistant cases, but the proportions of resistant cases driven by each mechanism in the two datasets were randomly and independently allocated. In this scenario, the mean AUCs were consistently lower when the prevalence of each resistance mechanism varied between the training and test set than when the different resistance mechanisms had similar prevalence in the training and test sets irrespective of the strength of gene expression changes and proportion of resistant cases (Fig. 3, Supplementary Table S6). Analysis of the deviation of the proportion of each resistance mechanism in the test set from the training set revealed a systematic decrease in the AUCs as the differences between the proportions of each resistance mechanism in training and test datasets increased, irrespective of signature strength and the number of resistance mechanisms (Fig. 4, Supplementary Fig. S2). Hence, the performance of predictive signatures is affected by varying proportions of resistance mechanisms in the training and test datasets.

Figure 3. Impact of varying proportions of resistance mechanisms within the resistant groups of the training and test sets on the performance of the predictive gene signature.

Perturbed datasets in which s% (s%=5%, 10%, 20%, 30%, 40% or 50%) of the cases were designated to be therapy sensitive were generated. For “Equal proportions”, within the 1-s% resistant cases, we allocated the cases evenly either into n (n=2, 3, 4, 5) equally sized groups of resistance mechanisms. For “Random training/test”, within the resistant cases, although the total percentage of resistant cases remained the same in training and test sets, the cases were allocated randomly into n (n=2, 3, 4, 5) groups of resistance mechanisms and the case allocation for training and test datasets was performed independently. Furthermore, for each n^th resistance mechanism, 100 genes were randomly selected as the “true” gene expression changes and were spiked-in by v (v=0.5, 1, 1.5). For each combination of s, n and v, we repeated the spiking and classification 100 times for “Equal proportions” and 200 times for “Random training/test”. Representative receiver operating characteristic (ROC) curves and the mean area under curve (AUC) for the cases are shown, where the Log₂-expression of the 100-gene “true” gene expression changes were spiked-in by 1 (A, labeled “Signature strength=1 (Optimal)”), 0.5 (B, labeled “Signature strength=0.5 (Weak)”) and 1.5 (C, labeled “Signature strength=1.5 (Strong)”). Within each of A, B and C, representative ROCs and mean AUCs of “Equal proportions” (top row, labeled “Equal proportions”) and of “Random training/test” (bottom row, labeled “Random training/test”) scenarios are shown. Within each row, the representative ROC curves of 2 to 5 resistance mechanisms are presented from left to right. The AUC values presented are the mean values for n resistance mechanisms.

Figure 4. Comparative impact of multiple unevenly distributed resistance mechanisms with random and independent prevalence in training and test sets on the performance of the predictive gene signatures.

Perturbed datasets in which s% (s%=5%, 10%, 20%, 30%, 40% or 50%) of the cases were designated to be therapy sensitive were generated. Within the resistant 1-s% cases, the cases were allocated randomly into n (n=2, 3, 4, 5) groups of resistance mechanisms and the case allocation for training and test datasets was performed independently, in both test and training sets, the total proportion of resistant cases is identical. For each n^th resistance mechanism, 100 genes were randomly selected as the “true” gene expression changes and were spiked-in by v (v=0.5, 1, 1.5). For each combination of s, n and v, we repeated the spiking and classification 200 times. The performance of the predictive gene signature for each repeat where each data point represents the median of 50 Monte-Carlo Cross Validation (MCCV) repeats. The performance of the predictive gene signature was measured by the area under curve (AUC) of receiver operating characteristic (ROC) curves. For v=1 (A, labeled “Signature strength=1 (Optimal)”), v=0.5 (B, labeled “Signature strength=0.5 (Weak)”) and v=1.5 (C, labeled “Signature strength=1.5 (Strong)”), AUC is plotted against the deviation of the sizes of the distinct resistance mechanism groups in the test dataset from those in the training dataset, calculated as ${\Sigma }_{i=2}^n\mid f_{i,test}-f_{i,train}$ where fi,test is the size of the i^th subgroup in the test set and f_i,train is the size of the i^th subgroup in the training set for (from left) n=2 (labeled “2 groups”), n=3 (labeled “3 groups”), n=4 (labeled “4 groups”) and n=5 (labeled “5 groups”). For each of (A), (B) and (C), AUCs are plotted for the “Ideal clinical setting” (where s%=50%) and for “Clinically-realistic setting” (where s%=10%).

Overlapping changes in gene expression mitigate the impact of the existence of multiple resistance mechanisms

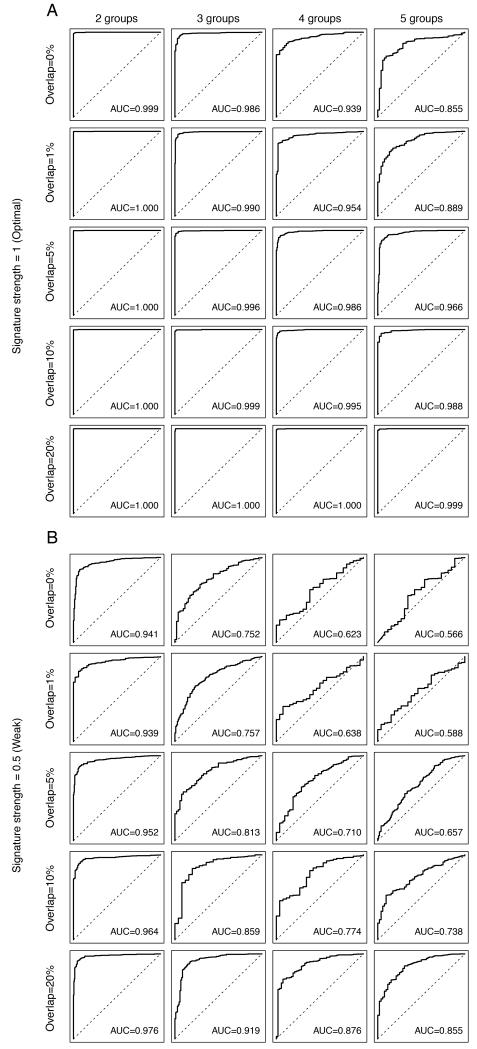
To determine the impact of distinct resistance mechanisms resulting in partially overlapping gene expression changes on the performance of the predictive signatures, we spiked-in resistance-associated gene expression changes for each mechanism that overlapped by up to 90%, and the non-overlapping genes were randomly distributed and mutually exclusive (Fig. 5, Table 2, Supplementary Table S7). Using an optimal signature (i.e. 2-fold change) in the realistic clinical setting (i.e. 10% sensitive cases), an increase in the number of mechanisms of resistance resulted in a significant reduction in signature performance when the overlap genes whose expression was affected by the distinct resistance mechanisms was up to 5% (Table 2, Supplementary Table S7). In this setting, an overlap of 10% of genes whose expression was affected by the distinct resistance mechanisms resulted in a significant increase in the AUC compared to a scenario with no overlap (p-value compared to non-overlapping signatures=0.02, Fig. 5A, Table 2, Supplementary Table S7). When testing weak signatures (i.e. 1.4-fold change), a significant improvement in the AUC was observed with an overlap of just 5% or more of genes whose expression was affected by the distinct resistant mechanisms (p-value compared to non-overlapping signatures=0.0009, Fig. 5B, Table 2, Supplementary Table S7); however, an increase in the number of mechanisms of resistance resulted in a significant reduction in signature performance when the overlap genes whose expression was affected by the distinct resistance mechanisms was up to 20% (Table 2, Supplementary Table S7). When testing strong signatures (i.e. 2.8-fold change), perfect performance was achieved with as few as 5% of overlapping genes between the 5 resistance mechanisms (Table 2, Supplementary Table S7). These simulations suggest that the impact of the existence of multiple mechanisms of resistance in clinically relevant scenarios is mitigated by overlapping changes in gene expression caused by distinct resistance mechanisms.

Figure 5. Impact of the extent of overlapping gene expression changes caused by distinct mechanisms of resistance on the performance of the predictive gene signature.

Perturbed datasets in which s% (s%=5%, 10%, 20%, 30%, 40% or 50%) of the cases were designated to be therapy sensitive were generated. Within the 1-s% resistant cases, we allocated the cases randomly into n (n=2, 3, 4, 5) equally sized groups of resistance mechanisms. For each n^th resistance mechanism, 100 genes were selected as the “true” gene expression changes, of which o% (o%=0%, 1%, 5%, 10%, 20%) of the 100 genes were common to all n mechanisms. The selected genes were then spiked-in by v (v=0.5, 1, 1.5). For each combination of s, n, o and v, we repeated the spiking and classification 100 times. Representative receiver operating characteristic (ROC) curves of the cases where the Log₂-expression of the “true” gene expression changes were spiked-in by 1 (A, labeled “Signature strength=1 (Optimal)”) and 0.5 (B, labeled “Signature strength=0.5 (Weak)”). Within each of A and B, we showed the representative ROCs depicting the mean area under curve (AUC) for simulations where 1-s%=90%, and o%=0% (“Overlap=0%”), o%=1% (“Overlap=1%”), o%=5% (“Overlap=5%”), o%=10% (“Overlap=10%”), o%=20% (“Overlap=20%”)(top to bottom). Within each row, the representative ROCs for n=2 (“2 groups”), n=3 (“3 groups”), n=4 (“4 groups”), n=5 (“5 groups”) groups of resistance mechanisms are shown. The AUC values presented are the mean values for n resistance mechanisms.

Table 2.

Impact of distinct mechanisms of resistance that result in overlapping changes in gene expression on the area under curve (AUC) of receiver operating characteristic (ROC) curves derived with the predictive gene signatures generated.

Optimal signature (2-fold)
Overlap	Number of resistance mechanisms				p-value for trend	p-value compared to non -overlapping signatures
	2	3	4	5
0%	0.999 (0.998-1.000)	0.986 (0.963-0.995)	0.939 (0.884-0.969)	0.855 (0.783-0.905)	< 0.00001	-
1%	1.000 (0.998-1.000)	0.990 (0.972-0.997)	0.954 (0.904-0.984)	0.889 (0.806-0.963)	< 0.00001	> 0.05
5%	1.000 (0.999-1.000)	0.996 (0.987-1.000)	0.986 (0.953-0.998)	0.966 (0.905-0.996)	0.00022	> 0.05
10%	1.000 (0.999-1.000)	0.999 (0.992-1.000)	0.995 (0.981-1.000)	0.988 (0.958-0.999)	> 0.05	0.02
20%	1.000 (1.000-1.000)	1.000 (0.998-1.000)	1.000 (0.997-1.000)	0.999 (0.996-1.000)	> 0.05	< 0.0001
50%	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	N/A	N/A
90%	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	N/A	N/A

Weak signature (1.4-fold)
Overlap	Number of resistance mechanisms				p-value for trend	p-value compared to non -overlapping signatures
	2	3	4	5
0%	0.941 (0.888-0.969)	0.752 (0.674-0.812)	0.623 (0.579-0.670)	0.566 (0.527-0.615)	< 0.0001	-
1%	0.939 (0.877-0.972)	0.757 (0.687-0.823)	0.638 (0.585-0.700)	0.588 (0.534-0.648)	< 0.0001	> 0.05
5%	0.952 (0.892-0.978)	0.813 (0.726-0.878)	0.710 (0.636-0.774)	0.657 (0.593-0.710)	< 0.0001	0.0009
10%	0.964 (0.919-0.987)	0.859 (0.767-0.922)	0.774 (0.695-0.857)	0.738 (0.667-0.819)	< 0.0001	< 0.0001
20%	0.976 (0.945-0.992)	0.919 (0.842-0.969)	0.876 (0.777-0.939)	0.855 (0.767-0.921)	0.0003	< 0.0001
50%	0.994 (0.980-0.999)	0.989 (0.969-0.997)	0.986 (0.964-0.997)	0.986 (0.963-0.997)	> 0.05	< 0.0001
90%	0.998 (0.995-1.000)	0.998 (0.991-1.000)	0.998 (0.990-1.000)	0.998 (0.988-1.000)	> 0.05	< 0.0001

Strong signature (2.8-fold)
Overlap	Number of resistance mechanisms				p-value for trend	p-value compared to non -overlapping signatures
	2	3	4	5
0%	1.000 (1.000-1.000)	0.999 (0.993-1.000)	0.988 (0.962-0.996)	0.960 (0.916-0.984)	< 0.00001	-
1%	1.000 (1.000-1.000)	0.999 (0.997-1.000)	0.994 (0.981-1.000)	0.979 (0.942-0.996)	0.01	> 0.05
5%	1.000 (1.000-1.000)	1.000 (0.999-1.000)	0.999 (0.997-1.000)	0.998 (0.989-1.000)	> 0.05	> 0.05
10%	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (0.999-1.000)	1.000 (0.999-1.000)	> 0.05	> 0.05
20%	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	N/A	N/A
50%	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	N/A	N/A
90%	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	1.000 (1.000-1.000)	N/A	N/A

Perturbed datasets in which s% (s%=5%, 10%, 20%, 30%, 40% or 50%) of the cases were designated to be therapy sensitive were generated. Within the 1-s% resistant cases, we allocated the cases randomly into n (n=2, 3, 4, 5) equally sized groups of resistance mechanisms. For each n^th resistance mechanism, 100 genes were selected as the “true” gene expression changes, of which o% (o%=0%, 1%, 5%, 10%, 20%, 50%, 90%) of the 100 genes were common to all n mechanisms. The selected genes were then spiked-in by v (v=0.5,1,1.5). For each combination of s, n, v and o, we repeated the spiking and classification 100 times. The mean values and 95% confidence intervals of the AUC of ROC curves for each combination of the number of resistance mechanisms (n), the overlap in the gene expression changes ‘spiked-in’ for each resistance mechanism (o) and the signature strength (v), where the proportion of sensitive cases (s) is 10%. “Optimal signature (2-fold)”, “Weak signature (1.4-fold)” and “Strong signature (2.8-fold)” refer to signatures generated with ‘spiked-in’ Log₂ expression values of 1, 0.5 and 1.5, respectively. The column labeled “p-value for trend” shows the p-values for the trend tests as the number of resistance mechanisms is increased from 2 to 5 for a given percentage of overlapping genes o%, where the percentage of sensitive cases (s) is the clinically-realistic estimate of 10%.

Impact of sub-stratification of chemotherapy-resistant breast cancers on predictive signature performance

Without sub-stratification of resistant tumors according to resistance mechanisms, microarrays may not capture gene expression changes associated with resistance mechanisms present only in a small subset of resistant cases(25). Hence, we sought to define whether sub-stratification of resistant cases based on an analysis of outliers would improve the performance of predictive signatures, as suggested by Rottenberg et al.(25). Using gene expression data from a study of predictive signatures of response to taxane-anthracycline-based neoadjuvant chemotherapy(31), we defined subgroups of chemotherapy-resistant breast cancers based on the expression of outliers using mCOPA(32,33). This analysis was restricted to ER-negative breast cancers to avoid the confounding effects of the differences in gene expression, prevalence of pCR (10.5% ER-positive vs 34.5% ER-negative breast cancers (31)) and predictive impact of the expression levels of proliferation-related genes in ER-positive breast cancers(1).

Predictive signatures were derived from features selected using a standard t-test (‘standard t-tests’), a modified COPA (‘mCOPA’), or, to capture both overall and subgroup-specific resistance mechanisms, a mixed mCOPA (20%) and t-test approach (80%; ‘Mixed (20% mCOPA)’) in the training set (n=129). The generated signatures were cross-validated by LOOCV of the training set (n=129), and an increase in the predictive signature performance, in particular the accuracy and sensitivity, was observed for both the mCOPA and mixed mCOPA approaches (e.g. LOOCV, accuracy ‘standard t-tests’ 0.643, ‘mCOPA’ 0.659, ‘Mixed (20% mCOPA)’ 0.705; Supplementary Fig. S3). When these predictive signatures were applied to an independent validation set of taxane-anthracycline-resistant ER-negative breast cancers (n=68), the increase in accuracy and sensitivity, in particular in the ‘Mixed mCOPA’ vs ‘standard t-test’ approaches, was maintained (Supplementary Fig. S3).

We further investigated the impact of other potential sources of heterogeneity, namely age at diagnosis, tumor size and nodal status, on the development and validation of predictive signatures in this breast cancer dataset. To address this, a mixed t-test (80%) and age at diagnosis (20%; ‘Mixed (20% age)’), a mixed t-test (80%) and nodal status (20%; ‘Mixed (20% nodal status)’), and a mixed t-test (80%) and tumor size (20%; ‘Mixed (20% tumor size)’) approach was employed for feature selection in the training set (n=129). In these mixed signatures, only the 20% of features obtained with mCOPA in the ‘Mixed (20% mCOPA)’ approach were replaced with the 20% of features obtained from the age, nodal status and tumor size signatures to generate the respective ‘Mixed (20% age)’, ‘Mixed (20% nodal status)’ and ‘Mixed (20% tumor size)’ signatures, whereas the 80% of features obtained through the “standard t-test” were kept constant. The signatures generated were cross-validated by LOOCV of the training set (n=129). Small numerical increases in the accuracy of all mixed clinical signatures were observed when compared to the ‘standard t-test’ signature, however the highest accuracy was observed with the ‘Mixed (20% mCOPA)’ signature, which takes outliers into account (Supplementary Fig. S3). When these predictive signatures were applied to the validation set (n=68), we observed a similar or reduced prediction accuracy in the ‘Mixed (20% age)’, ‘Mixed (20% nodal status)’ and ‘Mixed (20% tumor size)’ compared to the ‘standard t-test’ approaches, whereas the accuracy of the ‘Mixed (20% mCOPA)’ approach was increased (Supplementary Fig. S3). These observations suggest that the presence of multiple mechanisms of drug resistance in a given cohort may have a greater impact numerically on the accuracy of predictive gene signatures than clinical parameters alone.

Taken together, these results provide evidence to suggest that stratification of resistant breast cancers based on a combination of standard t-tests and the expression of outliers, which may account for the overall and distinct mechanisms of resistance, respectively, improves the accuracy and sensitivity of predictive gene signatures.

DISCUSSION

Here we demonstrate, through bioinformatic modeling of a large breast cancer dataset, that if resistance to a given therapeutic agent or combination therapy is driven by multiple mechanisms that result in distinct gene expression changes, increasing the number of mechanism of resistance has a deleterious impact on the predictive power of gene signatures generated with standard approaches, even when the signal of relevant features is sufficiently informative(13). Our findings demonstrate that not only parameters currently taken into account and controlled for in the design of studies aiming to develop predictive signatures (e.g. ER-status, HER2-status, molecular subtypes), but also the existence of multiple mechanisms of resistance to a given therapeutic agent do have a detrimental impact on the performance of predictive gene signatures if these mechanisms result in non-overlapping gene expression changes. In a way akin to first generation prognostic signatures whose prognostic power is derived from proliferation-related genes which are prognostic in the most common form of breast cancers (i.e. ER-positive/ HER2-negative breast cancer), this study corroborates the observations that microarray-based gene expression profiling preferentially detects a mechanism that is present in the majority of resistant tumors(25). Our results are of clinical importance, as this concept has not been incorporated into the design of studies developing signatures predictive of response to therapeutic agents(4,10) and may provide an explanation for the apparent inability to develop robust and clinically useful breast cancer predictive signatures based on microarray gene expression profiling.

Split-sample approaches and validation of the results in an independent dataset have been widely employed to develop and validate microarray-based signatures(1,34). Although the test datasets are usually designed to represent a population similar to that of the training set, if multiple mechanisms of resistance exist, controlling for their prevalence between the datasets has not been incorporated into the design of previous studies. Here we demonstrate that large deviations in the prevalence of each resistance mechanism between the training and test datasets reduce the performance of the predictive gene signature. Signatures based on different sources of heterogeneity within a cohort of patients (e.g. age and anatomical variables, such as nodal status and tumor size) yielded conflicting results in the LOOCV of the training set and split sample analyses performed; on the other hand, gene expression features obtained from an analysis of outliers, which may recapitulate the existence of multiple mechanisms of resistance(25), consistently provided additional predictive information.

We demonstrate, however, two scenarios in which the deleterious effect of multiple resistance mechanisms may be circumvented. Overlapping changes in gene expression caused by distinct resistance mechanisms partially mitigate their deteriorating impact on the performance of predictive signatures, and sub-stratification of resistant breast cancers on the basis of outliers(25) improved the accuracy of the predictive gene signatures generated.

This study has several limitations. For our simulations, no selection for a specific breast cancer subtype was performed as i) most studies developing therapy-specific predictive signatures included un-stratified breast cancers(4,10,17), ii) the magnitude of changes spiked-in the dataset was sufficiently strong to circumvent the ‘noise’ induced by the inclusion of multiple breast cancer subtypes (data not shown), and iii) statistical power is maximized by including all samples. Although we only spiked-in fixed, positive values (i.e. up-regulation) randomly, in real clinical datasets, components within gene signatures are likely to be correlated, the direction of differential expression is likely to be in both directions and the changes in expression values are likely to vary. We chose this approach to minimize the potential problems related to non-expressed genes and the confounding effect of transcriptional modules. Therefore, our simulation represents the ‘best case scenario’, with strong signal in the informative features, large numbers of informative features in the signatures and large numbers of resistant cases(2,13). Real clinical datasets are unlikely to have features as favorable(13). Although an improvement in predictive signature performance was observed when chemotherapy-resistant breast cancers were sub-stratified using a mixed standard t-test and mCOPA approach, the accuracy of such predictors is still not sufficient for them to be of clinical utility. Finally, given the nature of microarray experiments, we were unable to model the impact of intra-tumor genetic heterogeneity, which is likely to reduce the performance of predictive gene signatures even further(20,35).

From a statistical standpoint, weakly informative features, small sample size and a limited proportion of patients displaying an informative gene expression signature have been shown to have a detrimental effect on the ability of deriving robust predictors(2,4,13,17). Approached purely from a statistical standpoint, the ability to detect an effect will be smaller for weakly informative features because the difference being sought is small. If the sample size is not large then statistical power will necessarily be weak. Lastly if the proportion of patients displaying an informative gene expression signature is small, statistical power will also be reduced. Typically, statistical power is at similar levels, if the proportion of patients displaying an informative gene expression signature is in the range 30%-70%; however it decreases when this proportion is outside the 30%-70% range.

In conclusion, we demonstrate that the presence of multiple mechanisms of resistance to a given therapeutic agent in a patient population has a deleterious impact on the performance of predictive gene signatures. Understanding the diversity of mechanisms of resistance to a given agent or combinatorial therapy, and developing bioinformatic methods taking into account this information, may be required for the successful development of genomic predictors of therapeutic response.

MAJOR FINDINGS: If resistance to a given drug or combinatorial therapy is caused by more than one mechanism, robust and highly accurate predictive gene signatures may not be successfully derived using current bioinformatics approaches, even if the changes in gene expression are strong and informative. The detrimental impact on predictive signature performance by the existence of multiple mechanisms of resistance was found to be maximum when these resulted in distinct patterns of gene expression, but overlapping changes in gene expression mitigated this effect. We propose that the sub-stratification of resistant cancers according to the potential resistance mechanisms may improve the ability to generate clinically useful predictive signatures.

QUICK GUIDE TO EQUATIONS AND ASSUMPTIONS

Spiking in

To generate the bioinformatically perturbed datasets, we spiked-in arbitrarily selected gene expression changes associated with the i^th resistance mechanism (g_i) into a normalized microarray gene expression dataset.

$$X_j=X_{j0}+g_i,j\in P_i$$

where X_j0 is the normalized gene expression of the j^th case and P_i is the set of cases with the i^th resistance mechanism. Resistant cases were arbitrarily selected.

To build the predictive signatures, the following methods were employed:

Diagonal linear discriminant analysis (DLDA)

As the number of features p far exceeds that of the number of cases in microarray gene expression study, we employed the diagonal linear discriminant analysis (DLDA) model, a variant of linear discriminant analysis. The discriminant function to partition the feature space into regions for classes A and B is written as:

$$g\left(x\right)=\sum _{i=0}^p\left(\frac{{\widehat{\mu }}_A\left(x_i\right)-{\widehat{\mu }}_B\left(x_i\right)}{\widehat{\sigma }\left(x_i\right)}\right)\left(\frac{x_i-\widehat{\mu }\left(x_i\right)}{\widehat{\sigma }\left(x_i\right)}\right)$$

Supervised principal component analysis (SuperPC)

Supervised principal component analysis was used as a prediction model as follows:

1. Compute the regression coefficients for each feature using the response variable (i.e. a categorical variable indicating pathological complete response (pCR)).

2. Select the top 100 features and compute the first m principal components.

3. Use these principal components in a regression model to predict response.

Modified cancer profile outlier analysis (mCOPA)

For the generation of signatures based on the expression of outliers, a modified version of the cancer profile outlier analysis (mCOPA) was employed.

First, outliers were identified using the following steps:

1. Normalized expression values were median centered, with the median expression value of each gene set to zero.

2. The median absolute deviation (MAD) was calculated and subsequently scaled to 1 by dividing each gene expression value by its MAD.

3. Genes were ordered according to their percentile scores, and subclassified as ‘over-expressed resistant outliers’ (i.e. features >75^th percentile plus 1.5 times the inter-quartile value of the sensitive cases), ‘under-expressed resistant outliers’ (i.e. features <25^th percentile minus 1.5 times the inter-quartile value of the sensitive cases), ‘over-expressed sensitive outliers’ (i.e. features >75^th percentile plus 1.5 times the inter-quartile value of the resistant cases) and ‘under-expressed sensitive outliers’ (i.e. features <25^th percentile minus 1.5 times the inter-quartile value of the resistant cases).

4. For the selection of outliers for the gene signature building, only candidate features that displayed the following characteristics were included. For the ‘resistant outliers’, i) features that were not found to be outliers with the same directionality in sensitive cases and were present as outliers in ≥5% of the resistant cases were included, and ii) features that displayed at least a 2-fold difference between the mean expression of the resistant outliers and the mean expression of the sensitive cases. For the ‘sensitive outliers’, i) features that were not found to be outliers with the same directionality in resistant cases and were present as outliers in ≥5% of the sensitive cases were included, and ii) features that displayed at least a 2-fold difference between the mean expression of the sensitive outliers and the mean expression of the resistant cases.

After the identification of the outliers, features up- and down-regulated in the resistant cases and those up- and down-regulated in the sensitive cases were combined and ranked in decreasing order by the difference in expression between the outliers and the control group (i.e. the resistant outliers vs the sensitive cases and vice-versa).