Measuring Similarity Between Dynamic Ensembles of Biomolecules

Abstract

Methods for comparing ensembles of biomolecules assess the population overlap between distributions but fail to fully quantify structural similarity. We present a simple and general approach for quantifying population overlap and structural similarity between ensembles. This approach captures improvements in the quality of ensembles determined using increasing input experimental data that go undetected using conventional methods and reveals unexpected similarities between RNA ensembles determined using NMR and molecular dynamics simulations.

There is growing interest in moving beyond a static description of biomolecules towards a dynamic description in terms of conformational ensembles^1–3 in which a biomolecule is represented as a population-weighted distribution of many conformations. Studies indicate that biomolecules employ this broad pool of conformations during folding and when carrying out their biological functions⁴. An ensemble description of biomolecules can also help quantify thermodynamically important conformational entropy⁵ and define a broad range of receptors that can be targeted in drug discovery⁶.

Methods to assess similarity between static structures are well developed and widely used in classifying biomolecules, understanding evolutionary relationships between them, and in predicting their structures and functions⁷. New methods are needed to compare dynamic ensembles of biomolecules^8–10. This is important not only for helping establish dynamics-function relationships⁴, but also in assessing the quality of ensembles determined using experimental and computational methods^{3, 8–10}. Among many approaches for comparing probability distributions¹¹, the Jensen-Shannon Divergence (Ω²)^{8, 9} and S-score (S)¹⁰ have been used to compare dynamic ensembles of biomolecules³. While these approaches provide quantitative information regarding ensemble similarity, particularly with regards to the population overlap between two distributions, they do not quantify the extent of structural similarity for non-overlapping conformations.

For example, based on Ω² or S-score, two very similar yet non-overlapping conformational ensembles (gray and green in Fig. 1a) are measured as having zero similarity. The same level of similarity is assigned to two conformational ensembles that differ much more substantially (gray and magenta ensembles in Fig. 1a). The underlying problem is that non-overlapping conformations in two distributions contribute to Ω² and S in manner independent of the extent of structural similarity (see Methods). Other common measures of similarity or distance between probability distributions suffer from the same limitation including the χ² and the Bhattacharyya distance¹¹. In addition, in application to ensembles, Ω² and S-score are typically reported for an arbitrarily chosen bin size used to describe a given structural variable. However, these measures of similarity are highly dependent on bin size or method used to cluster conformations in an ensemble^8–10. Other approaches for comparing ensembles that involve computing the pairwise RMSD in atomic positions between every pair of conformations in two ensembles (eRMSD)¹² do not capture the population overlap, cannot be generally used to dissect individual structural degrees of freedom, and can be obscured by outliers.

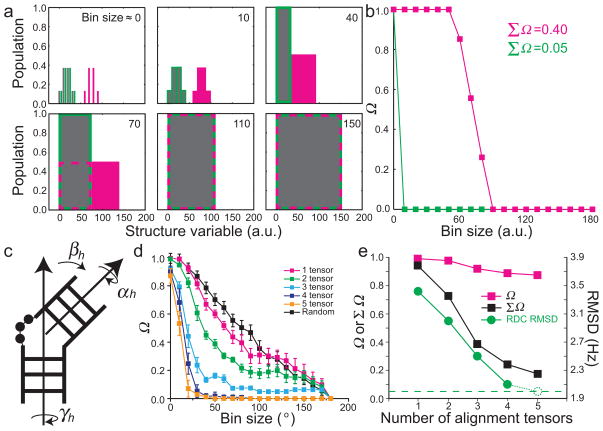
Figure 1. Measuring population overlap and structural similarity between ensembles.

(a) Three discrete ensembles (gray, green, and magenta) described in terms of an arbitrary structural variable are shown as a function of increasing bin size used to build the histogram distribution. Dashed magenta and solid green boxes around the gray ensemble indicate the portion of magenta and green ensemble respectively that are binned together with the gray ensemble. (b) Plots of Ω as a function of increasing bin size comparing the gray vs. green (green line) and gray vs. magenta (magenta line) ensembles. (c) The relative orientation of two helices (or domains) is defined using three Euler angles (α_h, β_h, γ_h). Shown are two RNA helices linked by a trinucleotide bulge. (d) Ω versus bin size comparing the inter-helical angle distributions about a trinucleotide bulge linker between a target ensemble (N=5) and ensembles (N=5) that are selected from the pool randomly (black) or using increasing number of input RDC data sets in SAS selections (color-coded, see inset). The standard deviations of Ω at each bin size over the 50 repetitions of each prediction are shown as error bars (see Methods). (e) The value of Ω at bin size=5° (magenta squares) and ΣΩ (black squares) as a function of number of RDC data sets used in ensemble reconstruction. Also shown is the root-mean-square-deviation (RMSD) in leave-out cross validation in which a constructed ensemble is used to predict a common left out set of RDCs (green circles). The dashed circle represents the optimum RMSD when the left-out data set itself is included in the selection and the flat dashed line denotes the assigned 2 Hz RDC uncertainty.

We developed an approach for simultaneously quantifying population overlap and structural similarity between ensembles. Here, the overlap between two distributions is evaluated using methods such as Ω² and S-score as a function of increasing the bin size used to build the histogram describing a given structural variable, such as a torsion angle or distance. Increasing the bin size effectively reduces the ‘structural resolution’ with which a given structural variable is defined, and thereby increases the probability of binning conformations in two ensembles into common bins (Fig. 1a). Ensembles that differ substantially in structural terms will require larger bin sizes to overlap. We assess overlap using the square root of Ω² because it provides several desirable properties, including being a proven metric^{9, 11}. The value of Ω comparing two ensembles either stays constant (barring statistical noise) or decreases with increasing bin size, and always plateaus at Ω=0 at some bin size cut-off. The plot of Ω (or any other appropriate measure of ensemble similarity) versus bin size then provides a rich 2D description of ensemble similarity that simultaneously captures population overlap and structural similarity, with the latter encoded in the steepness with which Ω drops with bin size (see also Supplementary Fig. 1). The approach readily accommodates outliers, which result in long lasting near zero Ω plateaus, without compromising the ability to detect population overlap and structural similarity in other regions of the ensemble (Supplementary Fig. 2).

The sum of population overlap over all bin sizes (K) normalized relative to values expected for zero overlap (Ω = 1 for all bin sizes) provides a convenient single-value measure of population overlap and structural similarity which we refer to as ΣΩ (w^T, w^P) that ranges between 0 and 1 for perfect and zero similarity, respectively,

$$\mathrm{\sum }\mathrm{\Omega }(w^T,w^P)=\frac{{\mathrm{\sum }}_m\mathrm{\Omega }\left(w_i^T(m),w_i^P(m)\right)}{K}$$ (1)

where { $w_i^T(m)$} and { $w_i^P(m)$} represent the population weights for the i^th bin in ensemble T and P, respectively for a given bin size, m. Note that ΣΩ(w^T, w^P) is also a metric, and therefore symmetric ΣΩ(w^T, w^P) = ΣΩ(w^P, w^T) and equal to zero if and only if two distributions are identical at all bin sizes or {w^T} = {w^P}.

Applying this approach to our previous examples (Fig. 1a), the structurally similar but non-overlapping ensembles (gray and green) start with Ω = 1 for small bin sizes implying zero similarity, but Ω rapidly drops to zero with increasing bin size indicating strong structural similarity (Fig. 1b). The drop in Ω with bin size is far less steep for the structurally more dissimilar ensembles (gray and magenta) (Fig. 1b). ΣΩ is clearly different in the two cases (0.05 and 0.46, Fig. 1b) and captures the structural differences between the two ensembles.

Having the ability to measure ensemble similarity is fundamentally important for testing approaches currently under development for constructing ensembles of biomolecules using experimental data^{1, 2, 13, 14}. A common ensemble construction approach uses ‘Sample and Select’¹⁵ (see Methods) or similar scheme³ to guide selection of conformations from a computationally generated pool and construct ensembles that satisfy experimental data. Methods such as cross-validation^1–3 have been used to show that the quality of constructed ensembles generally improves with increasing input experimental data; however no study has directly quantified the extent or nature of the improvement.

We used our approach to measure the similarity between a known target ensemble (N=5) constructed by randomly selecting five conformations from a pool of ~40,000 conformations and ensembles reconstructed using SAS and up to five independent sets of synthetic residual dipolar couplings (RDCs)^{16, 17} (see Methods). For simplicity, we focused on determining ensembles describing the relative orientation of two chiral domains (in this case A-form RNA helices) as defined using three Euler angles (Fig. 1c). Here, the conformational pool represents the topologically allowed orientations of two A-form helices linked by a trinucleotide bulge¹⁸. As described previously¹⁸, the Cartesian distance between two sets of Euler angles does not provide a faithful measurement of structure similarity and we therefore measure similarity in terms of the amplitude of single axis rotations (see Methods).

The conventional Ω value computed between the target and SAS reconstructed ensemble at the default pool bin size of 5° (see Methods) ranges between 0.87 and 0.99 (Fig. 1d). This implies a very poor level of similarity that is comparable to that observed when comparing the target ensemble with an ensemble (N=5) constructed by randomly selecting conformations from the same pool without guidance from RDC data (Ω=0.99) (Fig. 1d). Moreover, Ω changes insignificantly when increasing the number of RDC data sets used to reconstruct the ensemble (Fig. 1d). Similar results are obtained using other common measures of similarity such as the S-score, χ² (Supplementary Fig. 3) and Bhattacharyya distance (data not shown). These results are at odds with cross-validation analysis (see Methods), which shows substantial improvements in the quality of ensembles determined with increasing RDC data sets as judged based on their ability to predict a common fifth RDC data set that is left out from the ensemble construction. The root-mean-square-deviation (RMSD) between measured and predicted RDCs approaches the assigned RDC uncertainty when using four RDC data sets, implying strong similarity between the target and reconstructed ensembles (Fig. 1e). This improvement in ensemble construction with increasing RDC data sets is perfectly captured when computing Ω as a function of increasing bin size. Ω decreases with increasing bin size and this reduction occurs more rapidly when a larger number of RDC data sets is used in the ensemble construction (Fig. 1d). This decrease is much less steep for the randomly selected ensemble (Fig. 1d) resulting in ΣΩ values that decrease with increasing input RDC data sets, in excellent agreement with the cross-validation results (Fig. 1e). Similarly, our approach captures improvements in the constructed ensembles upon decreasing RDC uncertainty that go undetected based on direct application of Ω (Supplementary Fig. 4).

As a second application, we used our approach to assess the quality of an ensemble determined for the transactivation response element (TAR) RNA (Fig. 2a) from the human immunodeficiency virus type 1 (HIV-1) using molecular dynamics simulations. We previously reported¹⁹ poor agreement (RMSD = 8.6 Hz; experimental uncertainty ~ 2 Hz) between four independent sets of RDCs measured in TAR (Supplementary Fig. 5) and RDCs predicted for a TAR ensemble obtained from an 8.2 μs MD simulation computed on Anton supercomputer using the CHARMM36 force field²⁰. The specific degrees of structural freedom that underlie this disagreement remain unclear and are difficult to resolve given that RDCs report on both local and global aspects of structure^{16, 17}.

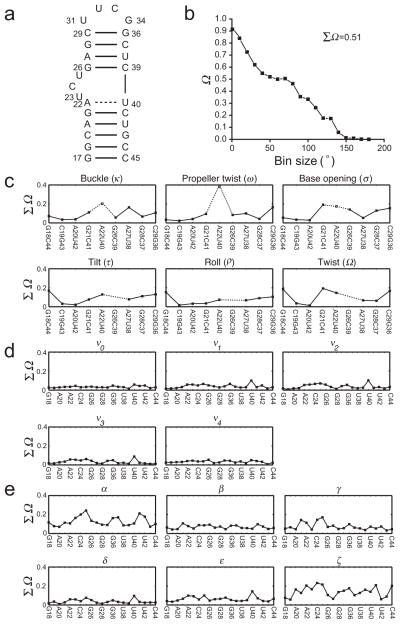
Figure 2. Comparing MD-generated and NMR-RDC selected ensembles of HIV-1 TAR.

(a) Secondary structure of HIV-1 TAR RNA. The highly flexible junction A22-U40 base pair is indicated using a dashed line. (b) Ω versus bin size plots comparing the inter-helical angle distribution in the MD and RDC-selected (N=20) ensembles. The binning is preformed in terms of single-axis rotation amplitudes (see Methods). (c–e) ΣΩ value comparing the distributions of (c) base-pair parameters, (d) sugar and (e) backbone torsion angles between the MD and the RDC selected ensemble. The intra-base-pair parameters for the flexible junction A22-U40 base-pair are shown using open symbols and dashed lines and inter-base-pair parameters are not shown for the junction G26-C39 base-pair because they are ill-defined due to presence of the bulge between G26-C39 and A22-U40.

We previously showed¹⁹ that using the SAS approach, a TAR ensemble that much better satisfies the four sets of RDCs could be constructed from the MD-generated pool (Supplementary Fig. 5). To assess the source of discrepancy between the MD simulation and measured RDCs, we used our approach to directly compare the MD trajectory and the SAS-based RDC-selected ensemble. We observed substantial differences (ΣΩ= 0.51) in the inter-helical angle distributions between the two ensembles (Fig. 2b). This discrepancy alone is expected to affect all RDCs measured in TAR because changes in inter-helical orientation lead to changes in the global structure and overall alignment of the molecule. The observed differences in inter-helical angle distributions are not surprising given that longer simulations are likely needed to properly sample conformational space, and that the TAR inter-helical orientation strongly depends on ionic strength¹⁸.

In contrast, we observed much better agreement for local angle parameters, including base-pair parameters (Fig. 2c, Supplementary Table 1), sugar (Fig. 2d, Supplementary Table 2) and phosphodiester backbone torsion angles (Fig. 2e, Supplementary Table 3) where on average ΣΩ < 0.2. Cases with ΣΩ > 0.3 are rare and tend to be concentrated in the junction A22-U40 base-pair and bulge residues which have previously been shown to be flexible by NMR spin relaxation¹³, and the phosphodiester backbone torsion angles α and ζ which show broad distributions in the MD-ensemble (Supplementary Fig. 6). The deviations in α and ζ at the bulge linker, and in base-pair parameters for residues surrounding the bulge are likely linked to the deviations observed in the inter-helical angle distributions (Fig. 2b). The ability of RDCs to define all the above angles during the SAS selection was confirmed by simulation tests (Supplementary Fig. 7). It is interesting to note that by defining inter-helical orientation and helical parameters, RDCs indirectly help define phosphodiester backbone torsion angles in and around the bulge¹⁹. These results suggest that even though the MD trajectory yields poor agreements with RDCs measured throughout TAR, the main source of disagreement is the inter-helical angle distribution.

In conclusion, we have developed a simple and robust method to measure the similarity between dynamic ensembles that overcomes limitations in conventional methods that primarily capture population overlap at a single bin size and thereby fail to measure structural similarity. The approach can be used in conjunction with many other appropriate metrics for measuring ensemble similarity to compare any structural variable of interest. We anticipate many useful applications of this approach in dynamics-function studies.

Methods

Jensen-Shannon Divergence (Ω²) and S-score

Mathematical expressions for the Jensen-Shannon Divergence (Ω²) and S-score are given by Equations 2 and 3, respectively:

$${\mathrm{\Omega }}^2\left(w_i^T(m),w_i^P(m)\right)=S\left(\frac{w_i^T(m)+w_i^P(m)}{2}\right)-\frac{1}{2}\left[S\left(w_i^T(m)\right)+S\left(W_i^P(m)\right)\right]$$ (2)

$$S\left(w_i^T(m),w_i^P(m)\right)=\frac{1}{2}{\mathrm{\sum }}_{i=1}^N\mid w_i^T(m)-w_i^P(m)\mid$$ (3)

in which { $w_i^T(m)$} and { $w_i^P(m)$} represent the population weights for the i^th bin in ensemble T and P, respectively for a given bin size, m. S(w_i)=−Σw_i(m)log₂w_i(m)) in Equation 2 is the information entropy. Ω² and S vary between 0 and 1 for maximum and minimum similarity, and are equal to zero if and only if $\{w_i^T(m)\}=\{w_i^P(m)\}$. Equations 2 and 3 show that for non-overlapping regions in two distributions, defined as cases in which $\{w_i^T(m)\}=0;\{w_i^P(m)\}\ne 0$ or $\{w_i^T(m)\}\ne 0;\{w_i^P(m)\}=0$, the contribution to Ω² and S is independent of the extent of structural similarity.

Sample and Select (SAS) approach

In the SAS approach^{13, 15, 19}, experimental RDCs are used to guide construction of an ensemble by selecting N conformations from a conformational pool that minimize the following χ² function,

$${\chi }^2={\mathrm{\sum }}_{i=1}^L{(D_i^{\mathit{calc}}-D_i^{\mathit{exp}})}^2/L$$ (4)

in which L is the total number of RDCs used in SAS, $D_i^{\mathit{calc}}$ and $D_i^{\mathit{exp}}$ are calculated and experimentally measured RDCs, respectively. In our implementation of SAS, first an initial ensemble of N conformations is randomly selected from the pool. Then at each step (k) of the selection procedure one conformation in the ensemble is randomly chosen and replaced by a conformation randomly selected from the rest of the pool. The change from step k to k+1 is accepted if χ²(k+1) < χ²(k); if χ²(k+1) ≥ χ²(k) with a probability P=exp((χ²(k)−χ²(k+1))/T), where T is an effective temperature that is linearly decreased using a simulated-annealing scheme¹³. The initial effective temperature is set to sufficiently high so that >99% of the conformations can be replaced and slowly decreased until the acceptance probability is smaller than 10⁻⁵. At each effective temperature, 200,000 steps were implemented followed by a decrease of effective temperature using T_i+1=0.9T_i. A MATLAB script (available from authors upon request) was used to implement this SAS-based ensemble construction.

Evaluating quality of inter-helical ensembles determined with increasing input RDCs

The capability of RDCs to reconstruct inter-helical ensembles using the SAS approach was investigated using synthetic RDC data, using up to five RDC data sets corresponding to five perfectly orthogonal alignment tensors. In these simulations, a given conformation is represented using three inter-helical Euler angles (α_h, β_h, γ_h) describing the relative orientation of the two idealized A-form helices representing the TAR helices connected by a trinucleotide bulge (Fig. 1c). The conformational pool necessary for the SAS selection was generated by using the corresponding topologically allowed space. This space corresponds to all possible inter-helical orientations that satisfy basic steric and connectivity restraints imposed by the bulge¹⁸. The pool was generated using a 5° resolution grid (i.e. each conformation differs from its closest neighbor by a 5° change in one of the three Euler angles). For a trinucleotide bulge, the pool represents ~10% of the total possible inter-helical orientations. A target ensemble containing five distinct conformations (N=5) was then randomly selected from this topologically allowed pool. Five orthogonal alignment tensors arbitrarily fixed on the reference helix were then generated using the Gram-Schmidt procedure²¹. For each of the five alignment tensors, all possible one bond CH RDC were computed for the target ensemble. For each alignment tensor, the RDCs for the five conformations were averaged and error-corrupted assuming 2Hz RDC uncertainty.

The SAS approach was then implemented to select an ensemble of N=5 distinct conformations using one, two, three, four and five sets of input RDCs to guide selection. The target and the predicted ensemble were then compared using similarity measurements including Ω, S-score, χ² and Bhattacharyya distance at various bin sizes as described below. The same process was repeated 50 times and the similarity between target and predicted ensembles were averaged over these 50 comparisons at each bin size. Standard deviation is calculated to estimate the variation in repeated simulations using different numbers of input alignments. The standard deviation is similar across the groups, and small compared to the observed differences between them (Fig. 1d). For the RDC cross validation analysis, ensembles determined using one, two, three and four RDC data sets in the SAS selection were used to predict a fifth RDC data set that was not used in the selection. The resultant RMSD between the RDCs for this fifth data set and values back-calculated from the predicted ensemble was then computed¹⁹.

Binning inter-helical orientations

The Cartesian distance in the Euler space, ((α_hA−α_hB)² + (β_hA−β_hB)² + (γ_hA−γ_hB)²)^1/2 between two sets of Euler angles A and B defining two distinct inter-helical orientations does not provide a measure of structural similarity between the two conformations¹⁸. First, there are inherent degeneracies (α_h′=α_h+180, β_h′=−β_h, γ_h′=γ_h+180; α_h′=α_h−180, β_h′=−β_h, γ_h′=γ_h−180; α_h′=α_h+180, β_h′=−β_h, γ_h′=γ_h−180; α_h′=α_h−180, β_h′=−β_h, γ_h′=γ_h+180) that map several sets of distinct inter-helical Euler angles to the same conformation¹⁸. This problem was overcome by using a restricted grid of Euler angles devoid of any degeneracy¹⁸. Second, even after taking into account the above degeneracy, the Cartesian distance between two sets of Euler angles does not provide a faithful measurement of structural similarity. For example, the Cartesian distances between (0, 0, 0) and (5, 5, 5) is ~9° in the Euler space whereas the two conformations differ by single axis rotation with amplitude ~11°. Likewise, the conformations (5, 5, 0) and (170, −10, 170) differ by a Cartesian distance of ~237° but the two conformations differ by a single axis rotation with amplitude ~25°. More generally, the Cartesian distance between Euler angles can be smaller than, equal to or larger than the actual difference between two conformations. Therefore we used the amplitude of single axis rotation to bin inter-helical orientations together and measure similarity between ensembles¹⁸ (see below).

The binning grid points are constructed by picking a binning origin, defined by minimum value of each of the three Euler angle in the two ensembles upon comparison, and then incrementing each Euler angles by an amount defined by the bin size to cover the entire non-degenerate 3D Euler space. Changing in the binning origin has minimal effects on the resulting analysis (data not shown). Next, the amplitude of a single axis rotation (ω) connecting a given conformation in the ensemble defined by Euler angles (α_h1, β_h1, γ_h1) and a point on the grid (α_h2, β_h2, γ_h2) is computed,

$$R({\alpha }_{h1},{\beta }_{h1},{\gamma }_{h1})=o(x,y,z,\omega )R({\alpha }_{h2},{\beta }_{h2},{\gamma }_{h2})$$ (5)

in which O(x, y, z, ω) represents a single axis rotation about a unit vector (x, y, z) with amplitude (ω). O(x, y, z, ω) can also be expressed by a 3 by 3 matrix in terms of x, y, z and ω

$$o(x,y,z,\omega )=\left(\begin{array}{ccc}\mathit{cos}\omega +x^2(1-\mathit{cos}\omega )& xy(1-\mathit{cos}\omega )-\mathit{zsin}\omega & xz(1-\mathit{cos}\omega )+\mathit{ysin}\omega \\ xy(1-\mathit{cos}\omega )+\mathit{zsin}\omega & \mathit{cos}\omega +y^2(1-\mathit{cos}\omega )& yz(1-\mathit{cos}\omega )-\mathit{xsin}\omega \\ xz(1-\mathit{cos}\omega )-\mathit{ysin}\omega & xy(1-\mathit{cos}\omega )+\mathit{xsin}\omega & \mathit{cos}\omega +z^2(1-\mathit{cos}\omega )\end{array}\right)$$ (6)

And the rotation amplitude ω is given by,

$$\omega =\mathit{arccos}\left(\frac{o_{11}+o_{22}+o_{33}-1}{2}\right)$$ (7)

in which O₁₁, O₂₂ and O₃₃ are the three diagonal elements of O(x, y, z, ω).

In this manner, the amplitude of the single axis rotation connecting a given conformation in an ensemble to every grid point is computed, and the conformation is binned to the grid point that leads to the minimum single axis rotation amplitude ω. The population of each grid point is then calculated to be the number of conformations binned divided by the total number of conformations in the ensemble. In our case, binning of the target and the predicted ensemble led to two population distributions on the same binning grid for a given bin size, and the value of Ω between the two ensembles at the given bin size is then calculated using equation 2. This procedure was repeated as a function of increasing bin size. This analysis was preformed using a MATLAB script that is available from the authors upon request.

Analysis of MD-trajectory-based ensembles

An in-house perl script was used to compute inter-helical angles (α_h, β_h, γ_h) describing the relative orientation of two A-form helices¹⁸. All intra- and inter-base-pair parameters were computed using Curves+ ²² and all the local torsion angles defining the sugar and backbone geometry were computed using an in-house C script. The resulting inter-helical orientations defined by three Euler angles were binned and analyzed as described above. Distributions of base-pair parameters, sugar and backbone torsion angles were directly binned to a binning grid ranging between 5° and 360° with variable increments defined by the bin size. The value of Ω was calculated at each given bin size for each parameter/angle distribution using Equation 2 and the values of ΣΩ are calculated using Equation 1 for distributions of inter-helical orientation, base-pair parameter, sugar, and backbone torsion angles.