Mechanics of DNA packaging in viruses

Abstract

A new generation of single-molecule experiments has opened up the possibility of reexamining many of the fundamental processes of biochemistry and molecular biology from a unique and quantitative perspective. One technique producing a host of intriguing results is the use of optical tweezers to measure the mechanical forces exerted by molecular motors during key processes such as the transcription of DNA or the packing of a viral genome into its capsid. The objective of the current article is to respond to such measurements on viruses and to use the theory of elasticity and a simple model of charge and hydration forces to derive the force required to pack DNA into a viral capsid as a function of the fraction of the viral genome that has been packed. The results are found to be in excellent accord with recent measurements and complement previous theoretical work. Because the packing of DNA in viral capsids occurs under circumstances of high internal pressure, we also compute how much pressure a capsid can sustain without rupture.

In rapid succession over the last several years, a number of new experimental insights into the way DNA in viruses is packaged and ejected have been garnered. For example, the structure of both the portal motor (1) as well as an example of the membrane puncturing device that leads to the delivery of the viral genome have been determined (2). At lower resolution, results of cryo-electron microscopy experiments have revealed the structure of certain viruses at various stages during self-assembly (3) and the ordered arrangements of DNA in concentric circles within viral capsids (4–6). These insights have recently been complemented by single-molecule experiments in which the force exerted by the portal motor is measured during the process of viral packing itself (7).

The problem of DNA packing is intriguing not only on the grounds of sheer geometric crowding, but also because of the recognition that the regions within which DNA is packaged (such as in a viral capsid) have linear dimensions that are comparable to the persistence length of the DNA, resulting in a steep elastic energy cost to be paid to effect such packing. The aim of this article is to take stock of the mechanical forces that come into play during viral packing and to reckon these forces explicitly in closed form in a simple model of DNA elasticity and interactions. These forces are then compared to those measured in fascinating recent single-molecule experiments on such packing (7). Because one of the conclusions to emerge from experiments, as well as models of the energetics of viral packing (8, 9), is that the viral capsid may be under pressures as high as 60 atmospheres, we also estimate the maximum pressure that such a capsid can sustain without rupturing.

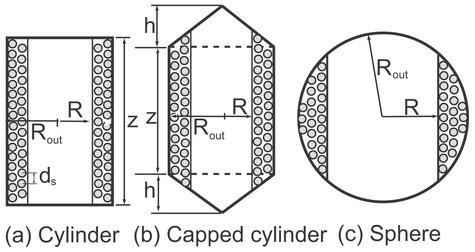
For the purposes of evaluating DNA packing forces, we take our cue from the structural insights into viral packing described above, cognizant, however, that the structural story is likely to be more complicated than the picture adopted here. In particular, we consider three capsid geometries meant to mimic features of real bacteriophage capsids as shown in Fig. 1. Further, we assume that the DNA adopts a configuration we will refer to as an inverse spool that features concentric hoops packed from the outside of the capsid towards the center as shown in Fig. 1. These structural insights are gleaned not only from a variety of different experiments (4–6), but also emerge from theoretical analysis and simulations of viral packing that take into account the relevant competing energies (8, 9).

Fig 1.

Three simplified models of the viral capsid used to illustrate the calculation of the packing energy. These models are a cross-sectional cut through the capsid and the shaded circles represent the strands of DNA that point into and emerge from the page.

In addition to the structural insights that have emerged concerning the ordered arrangements of DNA within viral capsids, there has been enormous progress in assessing the atomic-level structures of the capsids themselves (10). These structures will prove important for our estimates of the critical pressure that such capsids can sustain without rupture. We note that, as can be seen at the Viper website (11), many of the key viral capsids of interest are icosahedral, though the φ29 bacteriophage for which the actual packing forces were measured has a structure more like a capped cylinder (12). Below we evaluate the packing forces and critical rupture stresses for simplified models of both capped cylinders and icosahedral capsids.

The Energetics of Viral Packing

As already elucidated by Riemer and Bloomfield (13) and others (8, 9, 14), the energetics of viral packing is characterized by a number of different factors including: (i) the entropic-spring effect that causes the DNA in solution to adopt a more spread-out configuration than that in the viral capsid, (ii) the energetics of elastic bending that results from inducing curvature in the DNA on a scale that is smaller than the persistence length of ξ_p ≈ 50 nm, and (iii) those factors related to the presence of charge both on the DNA itself and in the surrounding solution. As shown by Riemer and Bloomfield (13), the entropic contribution is smaller by a factor of 10 or more relative to the bending energies and those mediated by the charges on the DNA and the surrounding solution, and hence we make no further reference to it. As a result, just like in earlier work (8, 9, 13), we examine the interplay of elastic and interaction forces, though we neglect surface terms originating from DNA–capsid interactions. Our strategy is to construct analytic estimates of the elastic and interaction energies separately and then to assemble them to obtain a complete estimate of the internal force within the capsid. These analytical results are then compared to measurements made on the φ29 bacteriophage (7).

The estimate that we obtain for the elastic forces associated with viral packing is predicated upon the most naive usage of the linear elastic theory of beams. In particular, we neglect the accumulation of stored elastic energy as a result of twist and concentrate instead only on the contribution of the bending energy. Within this approximation, the elastic energy is given as

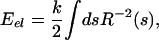where R(s) is the radius of curvature of the DNA at a position on the molecule parametrized by the arclength s, and k = ξ_pk_BT is the flexural rigidity.

Though we imagine the viral DNA to be packed in the form of a helix, from the perspective of our elastic energy functional, the geometry may be thought of as a stacking of hoops of radius R. The key point is that although the actual radius of curvature is given by R(1 + p²/4πR²), where p is the helical pitch, for the geometries of interest here p ≈ 3 nm while R ≈ 20 nm and hence the parameter p²/4πR² ≪ 1 and can be neglected without loss of any important insights. One might worry that at later stages of packing the radius of curvature becomes comparable to the pitch of the helix, but we find that the effect of including the pitch is quantitatively insignificant even in this limit. In light of this approximation the elastic energy can be written as

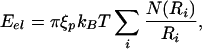where N(R_i) is the number of hoops that are packed at the radius R_i (13). The presence of N(R_i) reflects the fact that because of the shape of the capsid as the radius gets smaller the DNA can pack higher up into the capsid, thus increasing the number of allowed hoops. N(R) for the three capsid geometries considered here is shown in Table 1.

Table 1.

Number of strands at distance R from the central axis (N), the packaged length (L), the bending energy (E_el), and the related force (F_el) for various capsid geometries

Geometry	N(R)	L(R)	Eel(R)	Fel(L)
Cylinder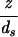
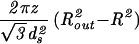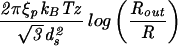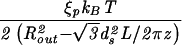Capped cylinder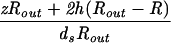
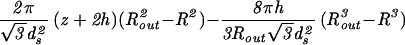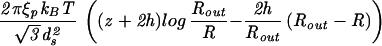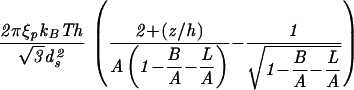Sphere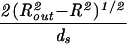

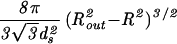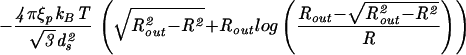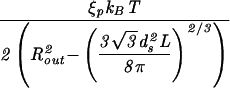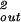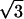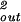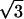The constants A and B for the capped cylinder are given by A = 2π(z + 2h)R/d and B = 8πhR/3d.

To make analytic progress with the expression for the stored elastic energy given above, we convert it into an integral of the form

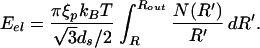The summation ∑_i has been replaced by an integral ∫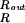[dR′/(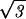d_s/2)] where the integration bounds are the inner and outer radius of the inverse spool, and 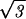d_s/2 is the horizontal spacing between adjacent strands of the DNA packed in a hexagonal array, as shown in Fig. 1. The replacement of the sum by an integral is a quantifiable approximation, the significance of which will be described elsewhere.

The calculation described above will yield the elastic energy in terms of the inner radius (R in Fig. 1) of the packed DNA. On the other hand, for the purposes of comparing with the experiments of Smith et al. (7), we want to express the energy and force in terms of the fraction of the genome packed. The length packed is generally given as

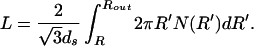With this expression in hand we can solve for R(L) and substitute it into our expression for the energy, yielding E_el(L). The elastic contribution to the packing force as a function of length packed can then be evaluated as F_el(L) = dE_el/dL.

To illustrate how to explicitly reckon the elastic energy we first consider this energy for the simplest (and perhaps unrealistic) case of a cylindrical capsid, with DNA in the inverse spool configuration. Such a geometry may be obtained, for instance, by neglecting the caps of the φ29 virus. In particular, a cylinder (compare Fig. 1a) is characterized by the geometric parameters z (the height) and R_out (the capsid radius). In this case, the number of hoops at a radius R′ is given by N(R′) = z/d_s because the vertical spacing between two adjacent DNA strands is d_s. The corresponding elastic energy obtained by using Eq. 3 is

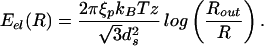From Eq. 4 it follows that the packed length is given by

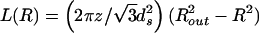or equivalently, R = R_out(1 −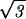dL/2πzR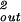)^1/2. The elastic energy may now be rewritten as a function of the packed length of DNA, namely,

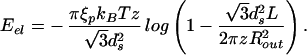This result may be used in turn to compute the force associated with the accumulation of elastic energy. In particular, differentiating the energy obtained above with respect to the length of packed DNA, we find

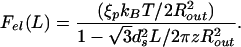Though the algebra is somewhat more involved for other capsid shapes, these same basic steps may be imitated in each case to obtain the elastic contribution to the energy. The results for various geometries are compiled in Table 1.

Thus far, our model does not do justice to all of the competing energies in the problem. In particular, the elastic contributions must be supplemented by interaction terms related to the presence of charges both on the DNA and in the surrounding solution. Measurements (15–17) suggest that the interaction energy per unit length is given by a potential e(d_s), where d_s is the spacing between neighboring strands of the DNA packed in the capsid. The explicit form of this potential depends on the conditions of the solvent. For example, in a solvent that contains only monovalent or divalent cations the potential is purely repulsive, but in a solvent that contains sufficient quantities of trivalent or tetravalent cations there is a preferred spacing between the DNA strands. In the latter case the potential is attractive, if the distance is greater than the preferred spacing, and repulsive if it is smaller. These conclusions are drawn from experiments that make use of osmotic stress to compress DNA in solution (15–17). We note that in the experiments of Smith et al. (7), the conditions are such as to dictate a purely repulsive interaction between adjacent DNA segments, whereas the conditions assumed in the theoretical analysis of Kindt and coworkers (8, 9) result in an repulsive-attractive interaction between neighboring DNA segments. One of the outcomes of the present work is the prediction of substantive measurable effects during the packaging process that depend critically on the ionic character of the solution.

Following Rau et al. (16), e(d_s) is obtained by relating the osmotic pressure to the total energy of a hexagonal array of parallel DNA strands. In the purely repulsive regime the force per unit length between adjacent DNA strands with spacing d_s is

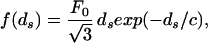where F₀ and c are constants that characterize the strength and decay length of the interaction, respectively. For a repulsive-attractive potential the force is given by

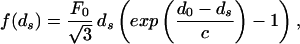where d₀ is the preferred spacing. In what follows we will explicitly treat the purely repulsive regime because we want to make a comparison with the experiments of Smith et al. (7). We note, however, that the methods of analysis carry over entirely to the repulsive-attractive regime, and that the differences between these two regimes suggest interesting new experiments.

We determine the interaction energy by observing that the work per unit length needed to bringing the strands to separation d_s is given by

the factor of 3 accounting for six (times 1/2 to avoid double counting) nearest neighbor DNA strands. According to Parsegian et al. (17) F₀ = 55,000 pN/nm² and c = 0.27 nm are the values of the parameters appropriate for a solution containing 500 mM NaCl at 298 K. The solution in the experiment of Smith et al. (7) is 50 mM Tris⋅HCl buffer (pH 7.8), 50 mM NaCl, 5 mM MgCl₂, conditions that correspond to the repulsive regime. Unfortunately, we are not aware of any direct experimental measurements of the repulsive parameters for the case of interest here. For this reason we view c and F₀ as fitting parameters that we will tune to fit the data from the experiment, though we note that the values of the two parameters obtained from such a fit are entirely consonant with those found by Parsegian et al. (17).

The interaction energy for a circular strand of radius R′ is given by

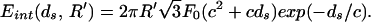The energy spent in bending the same length of DNA to a radius R′ is

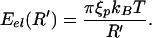It is of interest to compare the magnitudes of these two energies. For d_s = 2.8 nm and R′ = 10 nm the interaction energy is 155 pNnm, while the bending energy is 64 pNnm. They are comparable, and the interplay between these energies determines the geometry of packing, which in turn figures in the total energy (8, 9). As a result, the first step in calculating the total energy is to determine the dependence of the DNA spacing d_s on the length packed. This was computed numerically by Kindt and coworkers (8, 9) though in the context of a solution for which there are attractive interactions between neighboring DNA segments.

To address the question of how d_s varies as a function of the length packed we minimize the total energy of the packed DNA,

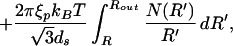where the length packed L is given by the expression

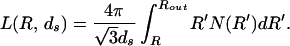Our goal is to find the appropriate d_s for a given L noting that the DNA spacing within capsids, as a function of length of DNA packed, is accessible experimentally (5, 18). We do this by insisting that ∂E/∂d_s = 0 under the constraint that L is constant, being mindful of the fact that N(R′) has explicit d_s dependence. The result of this minimization is:

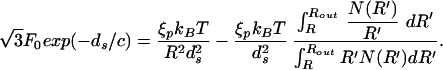Note that this equation depends on the geometry of the capsid through the second term on the right side. Note also that the simultaneous solution of Eq. 16 and Eq. 15 yields d_s and R for a given L. In other words, given the genome length L the value of R and d_s are fixed for given capsid geometry. We call the reader's attention to the fact that in the repulsive-attractive case our analysis goes through except for a slight change of the left side of Eq. 16. For a cylinder N(R) = z/d_s, and Eq. 16 leads to

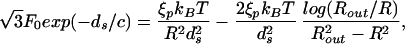while for a sphere this equation reads

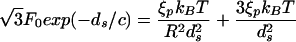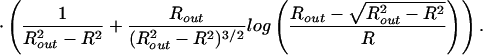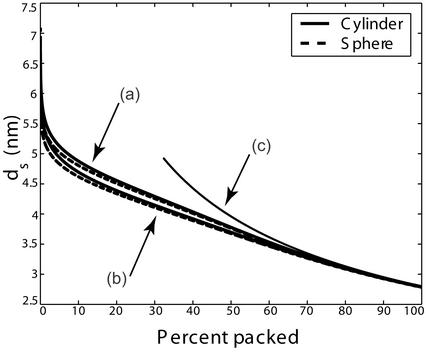
Though these equations can be solved analytically in the small packing fraction limit, over the entire range of packing they have been solved by using the Newton–Raphson method. The resulting spacing as a function of fraction packed is shown for F₀ = 2 × 55,000 pN/nm² and F₀ = 4.1 × 55,000 pN/nm² in Fig. 2. Interestingly, measurements of d_s in fully packed φ29 report a value of 2.75 nm (18), which compares well to the calculated value of 2.79 nm. Moreover, the model predicts interesting dependence of the DNA spacing on the parameter F₀, suggesting that measurements of d_s in viruses for various repulsive solvent conditions would be an interesting test of the ideas presented here.

Fig 2.

Spacing between DNA strands as a function of the percent of genome packed for cylindrical and spherical capsid geometries. We assume repulsive solvent conditions with F₀ = 2 × 55,000 pN/nm² (a) or F₀ = 4.1 × 55,000 pN/nm² (b). The capsid dimensions are chosen so their volumes coincide with the φ29 virus. Curve c is the spacing between strands assuming a uniform packing of the capsid.

Once the DNA spacing as a function of length packed is in hand we can plot the energy E as a function of the length packed. The slope of this curve yields the force as a function of the length packed. The final result is

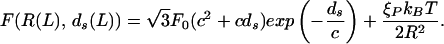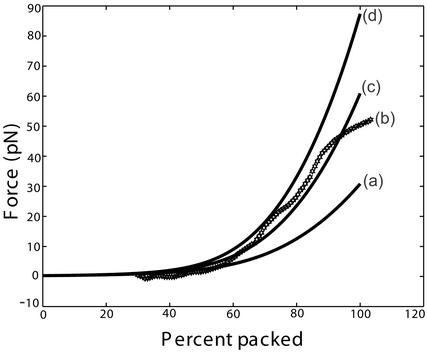
The result of these calculations is shown in Fig. 3. Note that though we show results for a cylindrical model of the capsid, we have also considered the case of capped cylinders and spheres and find that the force is rather insensitive to the capsid geometry. We have used c = 0.27 nm and various multiples of F₀ = 55,000 pN/nm², the value obtained in earlier work in the fully repulsive case. The value of F₀ leading to a best fit to the data of Smith et al. (7) is larger in comparison to the one cited earlier following the work of Parsegian et al. (17). However, this is not surprising because the solvent used in the experiment has a much smaller concentration of cations that should lead to a larger F₀. The value of c is in the range of those suggested by Parsegian et al. and this, too, is expected because the decay length does not vary too much with the solvent concentration. We note that F₀ has the effect of controlling the relative importance of the repulsive and elasticity contributions to the total energy. For the F₀ that is in best accord with the experiments of Smith et al., the late stages of packing are dominated by the repulsion of adjacent strands. This is evident in Fig. 2 because in the late stages of packing the DNA spacing satisfies the scaling d_s ∝ 1/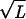 that corresponds to the loosest possible packing. It is interesting to note that this scaling is also evident in data obtained from experiments on deletion mutants of λ-phage DNA (19).

Fig 3.

Force as a function of the percent packed for a cylindrical capsid under purely repulsive solvent conditions. The dimensions of the capsid and the length of genome packed were chosen to correspond to the φ29 phage: R_out = 19.4 nm, z = 37.9 nm, and L = 6.58 μm. Curve b shows the experimental results of Smith et al. (7), while theoretical curves a, c, and d are given by Eq. 19, with F₀ = 2 × 55,000, 4.1 × 55,000, and 6 × 55,000 pN/nm², respectively.

In addition to the mechanics issues concerning the DNA itself, there are intriguing questions related to the response of the capsid as a result of the packing process. Smith et al. (7) speculate that the φ29 capsid is subjected to a pressure of ≈60 atm when fully packed. Similar estimates emerge from the theoretical analysis of Kindt and coworkers (8, 9). Here we obtain an expression for the pressure inside the capsid by using the relation p_i = −∂E/∂V, where E is the total energy of the DNA in the completely filled capsid, and V is the volume of the capsid. Note that p_i and the maximum packing force are not simply related: the former is a measure of the change in total energy of the DNA packed due to a change in volume of the capsid, whereas the latter pertains to the energy change associated with a change in the length of the DNA packed. As discussed in some detail below, in the case of the φ29 virus we find p_i = 60.3 atm, which confirms previous estimates.

For the case of the spherical capsid, differentiating the total energy (Eq. 14) with respect to the volume (V = 4πR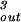/3) while keeping L fixed, leads to:

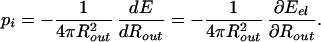The term proportional to ∂E/∂d_s vanishes, because ∂E/∂d_s = 0 is the condition that sets the equilibrium value of the strand separation d_s. Using the result for E_el from Table 1, and the numbers relevant for φ29, R_out = 22.03 nm, d_s = 2.792 nm, and L = 6.584 μm, we obtain the earlier quoted value of 60.3 atm for the internal pressure. Here we approximate the φ29 capsid as a sphere whose radius is set by the volume of the capsid.

As remarked above, our estimate for the internal pressure is insensitive to the strength of the repulsive interactions. This somewhat counterintuitive state of affairs follows from the fact that we have so far neglected the surface contribution to the total energy. Namely, the DNA strands on the surface of the inverse spool are surrounded, on average, by three neighboring strands, as opposed to six in the bulk. This gives a negative contribution to the total energy of −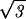F₀(c² + cd_s) exp(−d_s/c)A/2d_s (8, 9), where A is the area of the surface of the inverse spool. For a fully packed spherical capsid A = 4πR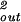, to a good approximation. If we compute the surface contribution to the total energy for the φ29 virus we find that it is about a factor of 10 smaller than the bulk repulsive energy and will have a small effect on the maximum packing force. On the other hand, when estimating the internal pressure, the bulk interaction term makes no contribution while the surface term contributes due to its explicit R_out dependence. Still, for the maximally repulsive conditions we have considered above (ie., F₀ = 6 × 55,000 pN/nm²) the surface energy contribution to the internal pressure is only 2.5 atm.

Given the possibility of high pressures within the fully packed viral capsids, and in light of the fact that such capsids are generally not held together by covalent linkages, it is of interest to examine the maximum pressure sustainable by such a capsid.

Structural Mechanics of Viral Capsids

In the previous section we made an estimate of the pressure in a spherical capsid on the basis of an underlying model for DNA packaging. Presently, we complement that calculation by examining the maximum pressure a capsid can sustain based on the strength of the weak bonds between the proteins that make up the capsid. We do not confine our attention to the φ29 capsid alone; rather our calculation applies to any capsid that is approximately spherical. Our calculational strategy involves two ideas. First, we use continuum mechanics to estimate the stresses within the capsid walls. These stresses are then mapped onto atomic-level forces by appealing to the details of the protein structure of the monomers making up the capsid and a knowledge of the forces that link them. By relating the continuum and atomistic calculations we then determine the maximum sustainable internal pressure.

We imagine the capsid to be a hollow sphere loaded by a pressure p_i from inside and a pressure p_o from the outside. The inner and outer radii are R_i and R_o, respectively. As a representative example, bacteriophage GA is characterized geometrically by R_i = 12.3 nm and R_o = 14.5 nm. Evaluation of a number of different capsid types suggests that treating capsids as though they have a mean thickness of ≈1.5 nm suffices for the level of model being considered here. For the purposes of computing the internal stresses within the capsid we begin with a statement of equilibrium from continuum mechanics which requires that at every point in the capsid,

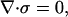where σ is the stress tensor comprising three normal stresses and three shear stresses. For a problem with spherical symmetry, like that considered here, the stresses reduce to a radial stress σ_R and a circumferential stress σ_T; see Fig. 4. Solution of the equilibrium equations results in stresses of the form

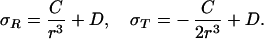Using the boundary conditions σ_R|_r=Ri = −p_i and σ_R|_r=Ro = −p_o the constants C and D can be determined with the result

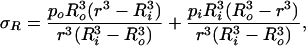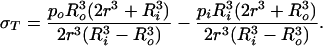The stress σ_T is our primary concern because it acts so as to tear the sphere apart. By looking at the expressions above we can see that this stress is maximum at r = R_i and the maximum value is given by

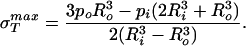We note that elasticity theory in and of itself is unable to comment on σ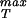 because this is effectively a material parameter that characterizes the contacts between the various protein monomers that make up the capsid. As a result, we first examine how the rupture strength depends on capsid dimensions in abstract terms and then turn to a concrete estimate of σ 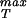itself from several complementary perspectives. If Eq. 25 is rewritten with p_i = p_o + Δp and R_o = R_i + ΔR and further, it is realized that for typical capsid dimensions ΔR/R_i ≪ 1, it can be shown by rearranging Eq. 25 that the maximum sustainable pressure difference is of the form

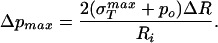For the case in which σ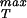 is much larger than p_o, this further simplifies to

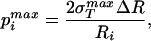where p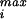 is really the quantity of interest, namely, the maximum sustainable internal pressure.

Fig 4.

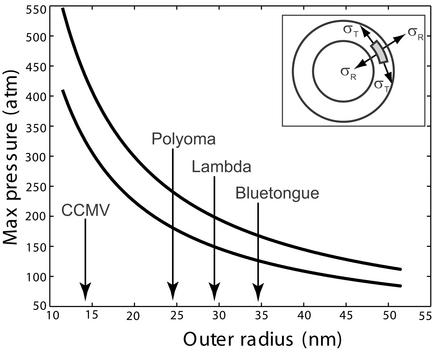
Rupture pressure as a function of capsid radius for x* = 0.3 nm (upper curve) and x* = 0.4 nm (lower curve). The width of the capsid walls was set to ΔR = 1.5 nm, while V₀ = 125 pN/nm. CCMV, cowpea chlorotic mottle virus. (Inset) The radial and circumferential stress on a capsid wall element.

To estimate the rupture stress we consider capsids for which the structure is known and for which the bonds between the monomers making up the capsid are understood at least approximately. We note that in the language of fracture mechanics, what we seek is a cohesive surface model that provides a measure of the energy of interaction between two surfaces as a function of their separation (20). There are a number of different ways to go about estimating the effective interaction between the monomers making up the capsid, one of which is by appealing to atomic-level calculations like those made by Reddy et al. (21). The Viper web site (11) has systematized such information for a number of capsids and one of the avenues we take to estimate σ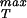 is to appeal directly to their calculations. To that end, we assume that the energy of interaction per unit area, as a function of separation x between adjacent monomers making up the capsid can be written in the form

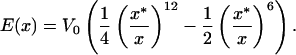The motivation for this functional form is the idea that the energy of interaction between adjacent monomeric units making up the capsid is the result of van der Waals contacts. Hence, our cohesive surface law has inherited the properties of the underlying atomic force fields. To proceed to an estimate of σ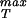 itself, we must determine the parameters V₀ and x* in Eq. 28. To that end, we note that Reddy et al. (21) have computed the association energies of various inequivalent contacts throughout a number of different icosahedral capsids. Their calculations result in a roughly constant value of ≈−45 cal/mol Ų for the association energy, which in the language of our cohesive potential results in V₀ ≈ 125 pN/nm. This may be seen by noting that the association energy is given by E(x*) = −V₀/4. [Note that this estimate for the protein–protein association energy is roughly a factor of 2 larger than the −25 cal/mol Ų (22) sometimes used as a rule of thumb. This value will result in an overall downward shift by roughly a factor of 2 in the curves shown in Fig. 4.]

Once we have chosen a particular x* that amounts to choosing the equilibrium separation between two monomers, then the material parameter σ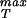 is obtained by evaluating ∂E(x)/∂x at a value of x corresponding to the point of inflection [∂²E(x)/∂x² = 0] in the cohesive surface function. For the cohesive surface function used above, this results in a maximum stress of the form

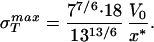With σ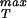 in hand, the maximum sustainable pressure is obtained from Eq. 27 and the results are shown in Fig. 4. These estimates suggest that the pressures within capsids as a result of packed DNA, while large, are still substantially smaller than our estimated rupture stresses.

We note in passing that we have used a second strategy similar to that described here in which we explicitly count the van der Waals contacts between adjacent monomers on the assumption that adjacent monomers are connected by parallel β-strands, and that such strands each contribute ≈10 van der Waals contacts. Such bond counting arguments result in σ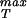 ≈ 107 MPa for x* = 0.4 nm whereas for x* = 0.3 nm we find σ 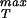≈ 280 MPa. The estimates for the maximum sustainable internal pressure in this case are roughly a factor of 2 lower than the ones obtained from the cohesive model that is likely to be the more reliable estimate because of its reliance on all-atom calculations. In any case, it appears that typical viral capsids are packed in a way that brings them in the vicinity of their strength limits. To more completely examine this question we have undertaken finite element elasticity calculations to examine the stresses in capsids exhibiting irregularities in both shape and thickness. In addition, further atomistic analysis of σ 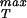is needed with special reference to its dependence on distance between protein units. It would also be of interest to examine mutant versions of the monomeric units making up the capsid to see the implications of such mutations for σ.

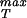Concluding Remarks

Recent single-molecule experiments have quantified various features of the packing of DNA in bacteriophage. The aim of the current work is to respond to this experimental data in the form of analytic models of the DNA packing process. In particular, we have computed the internal force within the capsid for several representative capsid shapes and found that the force vs. packing fraction curve is in excellent accord with experimental data. However, when considered in conjunction with the work of Kindt and coworkers (8, 9), these models reveal several intriguing features of the problem of DNA packing in bacteriophage. We find that in the repulsive conditions characteristic of experiments by Smith et al. (7), the mean spacing between parallel segments of DNA is larger than the ≈2.5-nm spacing seen in earlier work (5, 18) (compare Fig. 2). Furthermore, our arguments suggest that experiments using the same solvent as that used by Smith et al. but instead with λ phage would require a maximum packing force in excess of that found in φ29, suggesting either (i) that λ would not be able to package to completion or (ii) that λ has a more powerful motor than does φ29. In either case, there are clearly interesting experiments to be done to measure the DNA spacing in φ29 under the repulsive conditions considered here and to examine the packing forces in viruses other than φ29.