Detecting Maternal-Fetal Genotype Interactions Associated with Conotruncal Heart Defects: A Haplotype-based Analysis with Penalized Logistic Regression

Abstract

Non-syndromic congenital heart defects (CHDs) develop during embryogenesis as a result of a complex interplay between environmental exposures, genetics and epigenetic causes. Genetic factors associated with CHDs may be attributed to either independent effects of maternal or fetal genes, or the inter-generational interactions between maternal and fetal genes. Detecting gene-by-gene interactions underlying complex diseases is a major challenge in genetic research. Detecting maternal-fetal genotype (MFG) interactions and differentiating them from the maternal/fetal main effects has presented additional statistical challenges due to correlations between maternal and fetal genomes. Traditionally, genetic variants are tested separately for maternal/fetal main effects and MFG interactions on a single-locus basis. We conducted a haplotype-based analysis with a penalized logistic regression framework to dissect the genetic effect associated with the development of non-syndromic conotruncal heart defects (CTD). Our method allows simultaneous model selection and effect estimation, providing a unified framework to differentiate maternal/fetal main effect from the MFG interaction effect. In addition, the method is able to test multiple highly linked SNPs simultaneously with a configuration of haplotypes, which reduces the data dimensionality and the burden of multiple testing. By analyzing a dataset from the National Birth Defects Prevention Study (NBDPS), we identified seven genes (GSTA1, SOD2, MTRR, AHCYL2, GCLC, GSTM3 and RFC1) associated with the development of CTDs. Our findings suggest that MFG interactions between haplotypes in 3 of 7 genes, GCLC, GSTM3 and RFC1, are associated with non-syndromic conotruncal heart defects.

1. INTRODUCTION

Genetic interactions, or epistatic effects, are believed to exist pervasively in biological pathways [Moore 2003]. Maternal-fetal genotype (MFG) interaction is a particular type of interaction, which occurs when an MFG combination jointly alters the phenotype or risk of disease in offspring. A well-known example of an MFG interaction is Rh incompatibility [Kulich and Kout 1967]. The Rh locus on chromosome 1p35 is bi-allelic with a null allele and a coding allele. Individuals homozygous for the null allele are Rh-negative, while those with a coding allele are Rh-positive. Rh incompatibility occurs between an Rh-negative mother and her Rh-positive fetus, because the mother can produce immune antibodies to the Rh antigens on the fetal red blood cells at birth, leading to Rh isoimmunization. Rh isoimmunization may have severe adverse effects, including anemia, hyperbilirubinemia, fetal hydrops and adverse fetal neurodevelopment [van Gent, et al. 1997]. Over the past decade, evidence has accumulated demonstrating that MFG interactions may be a common mechanism for various complex human diseases and birth defects, such as neural tube defects [Relton, et al. 2004], schizophrenia [Palmer, et al. 2002] and autism [Zandi, et al. 2006]. Discovering and characterizing MFG interactions will contribute significantly to increasing our understanding of the etiology of birth defects and improving both maternal and fetal health.

Congenital heart defects (CHDs) are the most common type of birth defect with an estimated incidence of 6–8 per 1,000 live births [Hoffman and Kaplan 2002]. We and others, using candidate gene and pathway studies have identified maternal and fetal genetic susceptibilities that are associated with CHDs [Goldmuntz, et al. 2008; Hobbs, et al. 2011; Wessels and Willems 2010]. Though it is natural to wonder how pervasively MFG interactions exist, and how many possible interactive mechanisms there are [Sinsheimer, et al. 2010], relatively few studies have been conducted to detect the MFG interaction in regard to the development of CHDs [Lupo, et al. 2010].

Congenital heart defects are classified into various subgroups. Conotruncal heart defects (CTDs), a large subgroup of CHD, includes truncus arteriosus, transposition of the great arteries, double outlet right ventricle, tetralogy of fallot, pulmonary atresia, malalignment ventricle septal defect, and interrupted aortic arch. CTDs are among the most common and severe birth defects worldwide. Although survival of infants with CTDs has increased significantly over the last few decades, both mortality and morbidity remain high for these affected infants [van der Linde, et al. 2011]. Understanding the genetic mechanism underlying CTDs is of great importance to reduce morbidity and mortality related to these defects.

A potential difficulty encountered when evaluating the impact of genotypes from mother-offspring pairs is the correlation between maternal and fetal genotypes. Independent analyses of maternal or fetal effects are likely to confound each other, such that a single model that simultaneously includes both maternal and fetal effects is preferred [Shi, et al. 2008]. In pioneering work, a log-linear model was proposed to differentiate fetal genetic effects from maternally mediated genetic effects [Umbach and Weinberg 2000; Weinberg, et al. 1998; Wilcox, et al. 1998]. Since then, a number of methods have been proposed to investigate the possible MFG interaction effect by extending the log-linear model [Ainsworth, et al. 2011; Childs, et al. 2010; Sinsheimer, et al. 2003]. These log-linear-based methods typically divided family samples into different strata by their parental mating genotype combinations, and model the number of cases and controls in each stratum assuming a Poisson distribution. The maternal effects, fetal effects and MFG interaction effects can be specified by various parameters, which are further estimated by maximizing the likelihood function. These proposed methods have been useful tools for association studies with mother-offspring genotype data. Because the fetal effect is estimated conditionally on parental genotypes, it is robust to population stratification.

Recently, we and others proposed a penalized logistic regression approach to detect single SNP-SNP interactions and two-SNP haplotype-haplotype interactions [Li, et al. 2010; Li, et al. 2009]. Our method utilized Least Absolute Shrinkage and Selection Operator (LASSO), a machine learning technique that allows simultaneous effect estimation and variable selection. In this article, we extend our previously developed method to detect multi-SNP haplotype-haplotype interactions in the context of mother-offspring pair data. Our proposed method has several appealing properties. First, the LASSO estimator provides an automatic inference for the underlying genetic mechanisms. No individual test is required to differentiate maternal, fetal and MFG interaction effect. Second, the proposed method is nested with a haplotype phasing strategy, which simultaneously handles multiple SNPs that are in Linkage Disequilibrium (LD). Such a haplotype analysis strategy may potentially yield more information than single SNPs alone [Wang, et al. 2012], and reduce the burden of multiple testing. In this study, we applied the proposed method to dissect the maternal, fetal and MFG interaction effect associated with CTDs using genetic data from a candidate gene study. We identified a number of haplotype blocks with potential association to CTD, and adjusted for multiple testing by the number of blocks instead of number of SNPs. Finally, we explore the possible mechanisms in regard to the MFG combinations that jointly alter the disease risk.

2. METHODS

2.1 Study Population

The dataset was part of the National Birth Defects Prevention Study (NBDPS), a large-scale case control study covering an annual birth population of 482,000, or 10% of U.S. births. CTD cases were ascertained from birth defect registries in ten participating states that had identical inclusion criteria: Arkansas, California, Georgia, Iowa, Massachusetts, New Jersey, New York, North Carolina, Texas, and Utah. All offspring, including both cases and controls, were born between 1997 and 2010. A detailed description of NBDPS methods have previously been published [Gallagher, et al. 2011; Rasmussen, et al. 2002; Yoon, et al. 2001]. In this study, we included all available genotyped mother-offspring pairs, including 331 case pairs and 875 control pairs. Case pairs were defined as those where the child had a conontruncal heart structural malformation, whereas control pairs were defined as those where the child did not have any structural birth defect. Maternal characteristics were similar between cases and controls (Table I).

Table I.

Maternal Characteristics

		Case (N=331)	Control (N=875)
Age at delivery, mean (SD)		28.4 (6.0)	27.7 (5.9)
Mother’s race
	African American	23 (7%)	88 (10%)
	Caucasian	237 (72%)	620 (71%)
	Hispanic	51 (15%)	124 (14%)
	Others	19 (6%)	42 (5%)
	Missing information	1	1
Mother’s education, N (%)
	<12 years	32 (10%)	117 (13%)
	High school degree or equivalent	92 (28%)	209 (24%)
	1–3 years of college	89 (27%)	244 (28%)
At least 4 years of college or Bachelor degree		118 (36%)	305 (35%)
	Missing information	0	0
Household income, N (%)
	Less than 10 Thousand	46 (15%)	112 (14%)
	10 to 30 Thousand	78 (25%)	236 (29%)
	30 to 50 Thousand Dollars	63 (20%)	190 (23%)
	More than 50 Thousand	128 (41%)	285 (35%)
	Missing information	16	52
Folic acid supplementation, N (%)
	Unexposed	159 (48%)	372 (43%)
	Exposed	172 (52%)	503 (57%)
	Missing information	0	0
Alcohol consumption, N (%)
	Unexposed	247 (75%)	681 (78%)
	Exposed	84 (25%)	191 (22%)
	Missing information	0	3
Cigarette smoking, N (%)
	Unexposed	264 (80%)	720 (82%)
	Exposed	66 (20%)	154 (18%)
	Missing information	1	1
Maternal BMI, N (%)
	Underweight (BMI <18.5)	13 (4%)	35 (4%)
	Normal weight (18.5 <=BMI <25)	165 (51%)	462 (54%)
	Overweight (25 <=BMI <30)	81 (25%)	194 (23%)
	Obese (>=30)	63 (20%)	158 (19%)
	Missing information	9	26

No significant differences were found between cases and controls at 5% level

2.2 Genotyping and Quality Control

Our research team commissioned a custom panel of 1,536 SNPs covering 62 genes in the homocysteine, folate, and transsulfuration pathways potentially related to the development of CHD, using the Illumina GoldenGate custom genotyping platform, as described by Chowdhury et al. [Chowdhury, et al. 2012]. The whole genome amplified DNA was used for genotyping. Initial genotype calls were generated using GenCall, Illumina’s proprietary algorithm, with subsequent analysis performed using SNPMClust, a bivariate Gaussian model-based genotype clustering and calling algorithm developed in-house. To ensure high-quality genotypes, we applied stringent quality control measures and excluded SNPs with obviously poor clustering behavior (60 SNPs), no-call rates > 10% (328 SNPs), Mendelian error rates > 5% (11 SNPs), minor allele frequencies < 5% (204 SNPs), or significant deviation from Hardy-Weinberg Equilibrium in at least one racial group (p < 10e-4, 12 SNPs). After genotyping and subsequent quality control checks, genotyping data was available for 921 bi-allelic SNPs in 60 candidate genes for each mother-child pair.

2.3 Determination of Haplotype Blocks

The haplotype blocks were phased by using software Haploview version 4.2 [Barrett, et al. 2005]. Linkage Disequilibrium (LD) was first measured by the D′ statistic between two neighboring genetic variants. The Solid Spine of LD criterion, an internally developed method by Haploveiw, was further used to determine the haplotype blocks by using a threshold of D′ > 0.6. After applying Haploview, a total number of 112 haplotype blocks were identified for association analysis.

2.4 Statistical Method

We previously proposed a penalized logistic regression approach to detect two-SNP haplotype-haplotype interactions [Li, et al. 2010], and through simulations showed that the method has a low false positive rate and reasonable power for detecting haplotype-haplotype interactions. In this article, we briefly explain our method in the context of a flexible number of SNPs, more theoretical details can be found elsewhere [Cui, et al. 2007; Li, et al. 2010].

Assume we have a study population of n mother-offspring pairs, with n₁ case pairs and n₀ control pairs (n = n₁ + n₀). Denote y_i as the disease status for the i-th mother-offspring pair; y_i = 1 for case and y_i = 0 for control. Suppose we are interested in a particular haplotype block with K bi-allelic loci that are in LD. Two alleles at the k-th locus may form three possible genotypes, denoted as A_kA_k, A_kB_k and B_kB_k ; 1 ≤ k ≤ K.

Mapping Composite Diplotypes

Without loss of generality, denote H=[A₁A₂ ……A_K] as a “risk” haplotype that may alter the likelihood of disease. The K-locus genotype within the haplotype block can then be mapped into three possible composite diplotypes, namely HH, HH̅ and H̅H̅; where H̅ represents all haplotypes that are different from the “risk” haplotype H. The haplotype block may have a large number of multi-locus genotypes (i.e. up to 3^K). However, the number of composite diplotypes is always reduced to three after the haplotype configuration, which significantly lessens data dimensionality. It is worthwhile to note that a “risk” haplotype is defined here for the purpose of dimension reduction. In practice, a “risk” haplotype may have a protective effect that corresponds to a lower likelihood of disease. Such a modeling strategy was also adopted in previous studies [Lin, et al. 2007; Liu, et al. 2004; Liu, et al. 2011; Zhang, et al. 2012]. A potential challenge for the diplotype mapping is phase-ambiguity. The phase-ambiguous genotypes were treated as missing data, and phase determined probabilistically via an expectation-maximization (EM) algorithm described below.

In practice, every haplotype with an appreciable frequency (e.g. greater than 5%) may serve as a potential “risk” haplotype. Different choices of “risk” haplotypes would lead to various mapping strategies for composite diplotypes. The haplotype that gives the best model fit (minimum BIC statistic described below) will be selected as the optimal “risk” haplotype.

Epistasis Model

Denote the composite diplotypes for the i-th mother-offspring pair as G_i,m for the mother’s diplotype and G_i,f for the fetus’s diplotype. We use a logistic regression framework to model the genetic effects of the maternal block, the fetal block and their possible interactions:

$$\text{logit}(p(y_i=1))=\mathrm{\mu }+{\mathrm{a}}_{\mathrm{m}}{x}_{i,\mathrm{m}}+{\mathrm{a}}_{\mathrm{f}}{x}_{i,\mathrm{f}}+{\mathrm{d}}_{\mathrm{m}}{z}_{i,\mathrm{m}}+{\mathrm{d}}_{\mathrm{f}}{z}_{i,\mathrm{f}}+i_{\mathrm{a}\mathrm{a}}{x}_{i,\mathrm{m}}{x}_{i,\mathrm{f}}+i_{\mathrm{a}\mathrm{d}}{x}_{i,\mathrm{m}}{z}_{i,\mathrm{f}}+i_{\mathrm{d}\mathrm{a}}{z}_{i,\mathrm{m}}{x}_{i,\mathrm{f}}+i_{\mathrm{d}\mathrm{d}}{z}_{i,\mathrm{m}}{z}_{i,\mathrm{f}};$$ Eq. (1)

$$\text{where}{x}_{i,\mathrm{m}}=\{\begin{array}{ccc}\hfill 1& \hfill \mathit{\text{for}}\hfill & \hfill G_{i,\mathrm{m}}=HH\hfill \\ \hfill 0& \hfill \mathit{\text{for}}\hfill & \hfill G_{i,\mathrm{m}}=H\mathrm{H̅}\hfill \\ \hfill -1& \hfill \mathit{\text{for}}\hfill & \hfill G_{i,\mathrm{m}}=\mathrm{H̅}\mathrm{H̅}\hfill \end{array}\text{and}{z}_{i,\mathrm{m}}=\{\begin{array}{ccc}\hfill -1/2& \hfill \mathit{\text{for}}\hfill & \hfill G_{i,\mathrm{m}}=HH\hfill \\ \hfill 1/2& \hfill \mathit{\text{for}}\hfill & \hfill G_{i,\mathrm{m}}=H\mathrm{H̅}\hfill \\ \hfill -1/2& \hfill \mathit{\text{for}}\hfill & \hfill G_{i,\mathrm{m}}=\mathrm{H̅}\mathrm{H̅}\hfill \end{array};$$

and x_i,f and z_i,f are similarly defined. This coding strategy follows Cockerham’s orthogonal partition method [Cockerham 1954; Kao and Zeng 2002] where a_m(f) and d_m(f) can be interpreted as the additive and dominance effects for the risk haplotype at a maternal (fetal) block; i_aa, i_ad, i_da, and i_dd can be interpreted as the additive × additive, additive × dominance, dominance × additive, and dominance × dominance interaction effect between the maternal and fetal blocks, respectively.

The coefficients of genetic effect, β = (a_m,a_f,d_m,d_f, i_aa, i_ad, i_da, i_dd), are estimated by minimizing the −2 times log-likelihood with an adaptive LASSO penalty.

$$L\prime =-2L+\mathrm{\lambda }\sum {\mathrm{\omega }}_j|{\mathrm{\beta }}_j|;$$ Eq. (2)

Where L is the log-likelihood; λ is a tuning parameter between the likelihood and penalty term, and is chosen to minimize Bayesian Information Criterion (BIC); ω_j is a weight corresponding to the j-th genetic effect, 1 ≤ j ≤ 8, and is chosen as the j-th component of 1/β_MLE; where β_MLE is the maximum likelihood estimate of β. Previous studies have shown that the coefficients estimated using this adaptive LASSO are consistent and thus asymptotically converge to their true values [Zou 2006].

MFG combinations and Likelihood Function

For simplicity, we first assume that all multi-locus genotypes are phase-known, and each can be mapped to a unique composite diplotype. Consistent with Mendelian transmission, seven maternal-fetal genotypes (MFG) combinations may be formed and numerically denoted as 11, 12, 21, 22, 23, 32, 33 (Table II). Further, for each MFG combination, a likelihood function can be calculated according to the logistic regression model in Eq. (1). For example, if the i-th mother-offspring pair has MFG=11 (i.e. G_i,m = HH and G_i,f = HH), its likelihood of being a case pair is:

$${\mathrm{\pi }}_{i,11}=p(y_i=1|G_{i,\mathrm{m}}=HH,G_{i,\mathrm{f}}=HH)=p(y_i=1|x_{i,\mathrm{m}}=1,z_{i,\mathrm{m}}=-1/2,x_{i,\mathrm{f}}=1,z_{i,\mathrm{f}}=-1/2)=\frac{\mathit{\text{exp}}(\mathrm{\mu }+{\mathrm{a}}_{\mathrm{m}}+{\mathrm{a}}_{\mathrm{f}}-\frac{1}{2}{\mathrm{d}}_{\mathrm{m}}-\frac{1}{2}{\mathrm{d}}_{\mathrm{f}}+i_{\mathrm{a}\mathrm{a}}-\frac{1}{2}{i}_{\mathrm{a}\mathrm{d}}-\frac{1}{2}{i}_{\mathrm{d}\mathrm{a}}+\frac{1}{4}{i}_{\mathrm{d}\mathrm{d}})}{1+\mathit{\text{exp}}(\mathrm{\mu }+{\mathrm{a}}_{\mathrm{m}}+{\mathrm{a}}_{\mathrm{f}}-\frac{1}{2}{\mathrm{d}}_{\mathrm{m}}-\frac{1}{2}{\mathrm{d}}_{\mathrm{f}}+i_{\mathrm{a}\mathrm{a}}-\frac{1}{2}{i}_{\mathrm{a}\mathrm{d}}-\frac{1}{2}{i}_{\mathrm{d}\mathrm{a}}+\frac{1}{4}{i}_{\mathrm{d}\mathrm{d}})};$$ Eq. (3)

and its likelihood of being a control pair is:

$$1-{\mathrm{\pi }}_{i,11}=\frac{1}{1+\mathit{\text{exp}}(\mathrm{\mu }+{\mathrm{a}}_{\mathrm{m}}+{\mathrm{a}}_{\mathrm{f}}-\frac{1}{2}{\mathrm{d}}_{\mathrm{m}}-\frac{1}{2}{\mathrm{d}}_{\mathrm{f}}+i_{\mathrm{a}\mathrm{a}}-\frac{1}{2}{i}_{\mathrm{a}\mathrm{d}}-\frac{1}{2}{i}_{\mathrm{d}\mathrm{a}}+\frac{1}{4}{i}_{\mathrm{d}\mathrm{d}})}.$$

The likelihood for other MFG combinations can be calculated.

Table II.

Numerical Notations for Maternal Fetal Genotype Combinations

MFG		Fetal Diplotype
		HH	HH̅	H̅H̅
Maternal Diplotype	HH	11	12	--a
	HH̅	21	22	23
	H̅H̅	--a	32	33

^aCombination not possible under Mendelian transmission

If the multi-locus genotype G_i,m and G_i,f is phase-ambiguous, then it will map to two possible composite diplotypes, HH̅ or H̅H̅. To construct the likelihood function in Eq. (2), we define a set of indicator variables for MFG combinations as:

$$D_{i,11}=\{\begin{array}{cccc}\hfill 1\hfill & \hfill \mathit{\text{if}}\hfill & \hfill G_{i,\mathrm{m}}=HH\hfill & \hfill G_{i,\mathrm{f}}=HH\hfill \\ \hfill 0\hfill & \hfill \mathit{\text{if}}\hfill & \hfill \mathit{\text{otherwise}}\hfill & \hfill \hfill \end{array};$$

D_i,12, D_i,21, D_i,22, D_i,23, D_i,32, and D_i,33 can be defined similarly. Then the likelihood function in Eq. (2) takes the following form:

$$L=\sum _{i=1}^N\sum _{MF{G}_i}{D}_{i,MF{G}_i}\text{log}[{\mathrm{\pi }}_{i,MF{G}_i}^{y_i}{(1-{\mathrm{\pi }}_{i,MF{G}_i})}^{1-y_i}],\text{where}MF{G}_i\in \{11,12,21,22,23,32,33\}.$$

Because of phase-ambiguity, the indicators, D_i,11…D_i,33, are treated as missing data, and the likelihood function above is maximized iteratively with an EM algorithm. The computational details can be found in Li et al. [Li, et al. 2010].

After the coefficients are estimated, the likelihood of being a case pair can be computed for each MFG combination. It should be noted that the adaptive LASSO simultaneously estimates parameters and performs model selection through shrinkage. Coefficients that do not significantly differ from 0 are expected to be shrunk to 0. As a result, some of the MFG combinations may have the same likelihood of disease. Given a simple example when the maternal additive effect is the only no-zero coefficient (e.g. a_m ≠ 0,d_m = a_f = d_f = i_aa = i_ad = i_da = i_dd = 0), the MFG combinations in the same row of Table II would have the same likelihood of disease. According to Eq. (3), the 7 maternal/fetal genotype combinations can be partitioned into 3 risk groups:

• R1 = {H̅H̅ / HH̅; H̅H̅ / H̅H̅} with a likelihood of disease as $\frac{\mathit{\text{exp}}(\mathrm{\mu }-{\mathrm{a}}_{\mathrm{m}})}{1+\mathit{\text{exp}}(\mathrm{\mu }-{\mathrm{a}}_{\mathrm{m}})}$;

• R2 = {HH̅ / HH̅; HH̅ / HH̅; HH̅ / H̅H̅} with a likelihood of disease as $\frac{\mathit{\text{exp}}(\mathrm{\mu })}{1+\mathit{\text{exp}}(\mathrm{\mu })}$;

• R3 = {HH / HH; HH / HH̅} with a likelihood of disease as $\frac{\mathit{\text{exp}}(\mathrm{\mu }+{\mathrm{a}}_{\mathrm{m}})}{1+\mathit{\text{exp}}(\mathrm{\mu }+{\mathrm{a}}_{\mathrm{m}})}$.

When the coefficient a_m is positive, group R1 would have the lowest likelihood of disease and can be denoted as a reference group. Compared to group R1, group R2 and R3 would have increased risks of disease with odds ratios (OR) of exp(a_m) and exp(2a_m), respectively. Standard errors and thus confidence intervals for the OR are computed using bootstrap resampling [Tibshirani 1996]. Partitioning of risk groups with other non-zero coefficients can be obtained in a similar fashion and are not detailed here.

3. RESULTS

Using Haploview, we identified 112 haplotype blocks for analysis [Barrett, et al. 2005]. Within each block, all haplotypes with a frequency greater than 5% were examined as potential “risk” haplotypes, and the haplotype with a minimum BIC was selected as the optimal “risk” haplotype. Application of our method identified 7 haplotype blocks with non-zero coefficients, indicating a potentially significant genotype-phenotype association. The identified blocks were located in 7 genes: GSTA1, GCLC, SOD2, GSTM3, MTRR, AHCYL2 and RFC1. Information for the identified haplotypes is summarized in Table III. The frequencies of “risk” haplotypes were estimated based on the entire study population, including both cases and controls.

Table III.

Seven Haplotype Blocks Identified with Non-zero Genetic Effects

Genea	Chro.	Block Size	SNP in Block	Position	Allele	“Risk” Haplotype
GSTA1	6p12.1	18.1 KB	rs9474321	52756236	A/G	G
			rs6917325	52774232	A/G	A
			rs10948723	52774364	A/G	G
	Frequency of “Risk” Haplotype:		among mothers: 34.5%		among offspring: 34%
GCLC	6p12	22.6 KB	rs13437220	53476035	C/G	G
			rs13437395	53476268	A/G	A
			rs2277108	53477973	A/G	G
			rs661603	53478066	A/G	A
			rs524553	53478354	A/G	G
			rs12524494	53479419	A/G	A
			rs1555903	53480104	A/G	A
			rs9474576	53481064	A/G	A
			rs16883912	53481730	A/G	G
			rs546726	53485081	A/G	G
			rs634657	53485509	A/G	A
			rs648595	53486328	A/C	A
			rs617066	53491877	A/G	G
			rs572494	53492134	A/G	A
			rs13212365	53493043	A/G	G
			rs1555906	53498668	A/G	G
	Frequency of “Risk” Haplotype:		among mothers: 44.6%		among offspring: 43.2%
SOD2	6q25.3	29.2 KB	rs732498	160011550	A/G	A
			rs8031	160020630	A/T	A
			rs5746151	160021310	A/G	G
			rs2758331	160025060	A/C	C
			rs5746105	160032628	A/G	G
			rs6912979	160040789	A/G	G
	Frequency of “Risk” Haplotype:		among mothers: 24.0%		among offspring: 23.2%
GSTM3	1p13.3	10.5 KB	rs4970776	110072980	A/T	T
			rs1927328	110077267	A/G	A
			rs7483	110081224	A/G	G
			rs10735234	110083464	A/G	G
	Frequency of “Risk” Haplotype:		among mothers: 36.9%		among offspring: 36.5%
MTRR	5p15.31	4.1 KB	rs16879259	7919821	A/G	G
			rs1801394	7923973	A/G	A
	Frequency of “Risk” Haplotype:		among mothers: 5.82%		among offspring: 7.97%
AHCYL2	7q32.1	28.0 KB	rs6467244	128836743	A/G	G
			rs6958637	128844858	A/G	A
			rs822040	128853158	C/G	G
			rs4728164	128854289	A/G	A
			rs6971551	128859260	A/G	A
			rs691807	128863439	C/G	G
			rs587499	128864767	A/C	C
	Frequency of “Risk” Haplotype:		among mothers: 27.1%		among offspring: 26.5%
RFC1	4p14-p13	50.9 KB	rs2381375	38990224	A/G	A
			rs11096991	38997026	A/G	A
			rs6815859	39003739	A/G	G
			rs6531712	39006691	A/T	A
			rs11727502	39015795	A/C	C
			rs16995255	39041083	C/G	G
	Frequency of “Risk” Haplotype:		among mothers: 5.13%		among offspring: 5.18%

^aGSTA1: glutathione S-transferase alpha 1; GCLC glutamate-cysteine ligase, catalytic subunit; SOD2: superoxide dismutase 2; GSTM3: glutathione S-transferase mu 3; MTRR5-methyltetrahydrofolate-homocysteine methyltransferase reductase; AHCYL2: adenosylhomocysteinase-like 2. RFC1: replication factor C (activator 1) 1.

The LASSO estimator provides a direct inference of the underlying genetic mechanism. Based on the non-zero coefficients, the 7 identified blocks fell into three possible categories: maternal main effect (i.e. a_m,d_m ≠ 0), fetal main effect (a_f,d_f ≠ 0), or MFG interaction effect (i.e. i_aa, i_ad, i_da, i_dd ≠ 0). To further investigate the underlying genetic mechanisms, the likelihood of being a case pair was estimated for each MFG combination. The seven possible MFG combinations were partitioned into various risk groups according to their likelihoods of disease, as exemplified in method section. For simplicity, the risk group with the lowest likelihood of disease was used as reference group. The odds ratios (ORs), corresponding 95% confidence intervals and p-values were empirically estimated by using 100 bootstrap samples. The results are summarized in Table IV. All identified haplotype blocks had empirical p-values significant at the nominal level of 5%. We further applied the Storey’s q-value method to adjust for the multiple testing of 112 blocks [Storey 2002]. Although all 7 blocks had a false discovery rate (FDR) < = 0.25, only two blocks remained significant with a FDR less than 5%. These blocks were located within the glutathione S-transferase alpha 1 (GSTA1) and the glutamate-cysteine ligase, catalytic subunit (GCLC) genes. Three genetic mechanisms were observed for the identified haplotype blocks.

Table IV.

Genetic Risk Groups for the Identified Haplotype Blocks

Gene	MFG Combinationa Maternal/Fetal	OR [95% CI]	p-valueb	Overall p-valuec	FDR
Haplotype Blocks with Maternal Main Effect Only
GSTA1	R1 : HH / HH;HH / HH̅;H̅H̅ / HH̅ H̅H̅ / H̅H̅	Ref	--	3.89e-04	0.041
	R2 : HH̅ / HH;HH̅ / HH̅;HH̅ / H̅H̅	1.50[1.18,1.89]	3.89e-04
SOD2	R1 : H̅H̅ / HH̅;H̅H̅ / H̅H̅	Ref	--	0.0026	0.094
	R2 : HH̅ / HH;HH̅ / HH̅;HH̅ / H̅H̅	1.34[1.10,1.63]	0.0026
	R3 : HH / HH;HH / HH̅	1.78[1.18,2.70]	0.0026
Haplotype Blocks with Fetal Main Effect Only
MTRR	R1 : HH / HH;HH̅ / HH	Ref	--	0.0045	0.101
	R2 : HH / HH̅;HH̅ / HH̅;H̅H̅ / HH̅	1.7[1.15, 2.51]	0.0045
	R3 : HH / H̅H̅;HH̅ / H̅H̅;H̅H̅ / H̅H̅	2.9[1.30, 6.51]	0.0045
AHCYL2	R1 : HH / HH;HH̅ / HH	Ref	--	0.0070	0.130
	R2 : HH / HH̅;HH̅ / HH̅;H̅H̅ / HH̅	1.35[1.07, 1.71]	0.0070
	R3 : HH / H̅H̅;HH̅ / H̅H̅;H̅H̅ / H̅H̅	1.81[1.14, 2.92]	0.0070
Haplotype Blocks with MFG Interaction Effect
GCLC	R1 : H̅H̅ / H̅H̅	Ref	--	7.40e-04	0.041
	R2 : H̅H̅ / HH̅	1.42[1.04, 1.94]	1.23e-02
	R3 : HH / HH	1.69[1.15, 2.51]	4.39e-03
	R4 : HH̅ / HH;HH̅ / HH̅;HH̅ / H̅H̅	1.85[1.33, 2.59]	1.57e-04
	R5 : HH / HH̅	2.41[1.54, 3.78]	7.70e-05
GSTM3	R1 : HH / HH̅;H̅H̅ / H̅H̅	Ref	--	0.0033	0.094
	R2 : HH̅ / HH;HH̅ / HH̅;HH̅ / H̅H̅	1.28[1.08, 1.53]	0.0033
	R3 : HH / HH;H̅H̅ / HH̅	1.63[1.15, 2.32]	0.0033
RFC1	R1 : HH / HH;H̅H̅ / HH̅	Ref	--	0.016	0.252
	R2 : HH̅ / HH;HH̅ / HH̅;HH̅ / H̅H̅	1.70[1.04, 2.77]	0.016
	R3 : HH / HH̅;H̅H̅ / H̅H̅	2.88[1.10, 7.54]	0.016

^aPartition of MFG combinations into various risk groups according to their likelihoods of disease. R1 is the reference group with the lowest likelihood of disease.

^bBased on 100 bootstrap samples

^cBased on 100 bootstrap samples. Null hypothesis assumes all MFG combinations have the same likelihood of disease.

1) Two blocks exhibited maternal main effect only

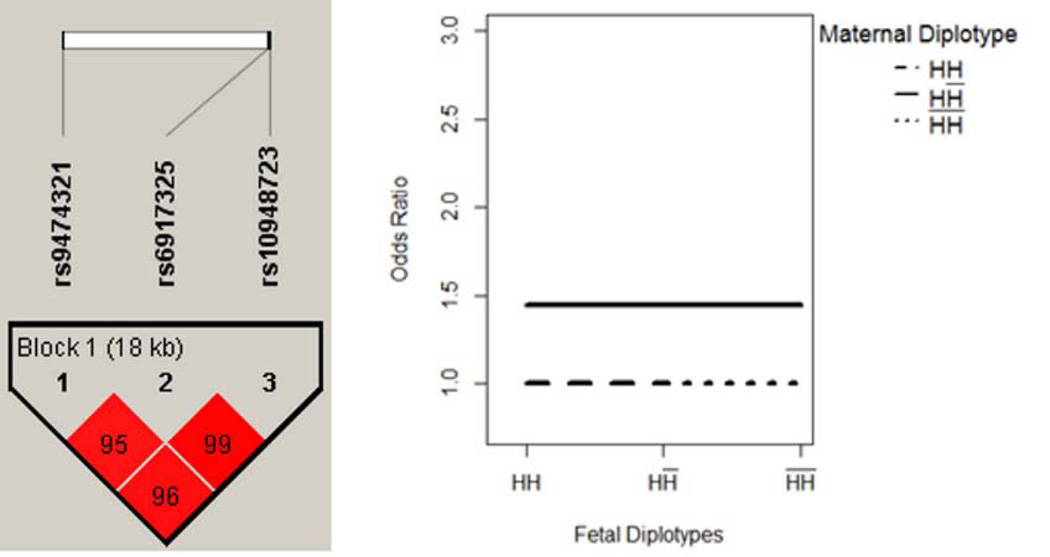
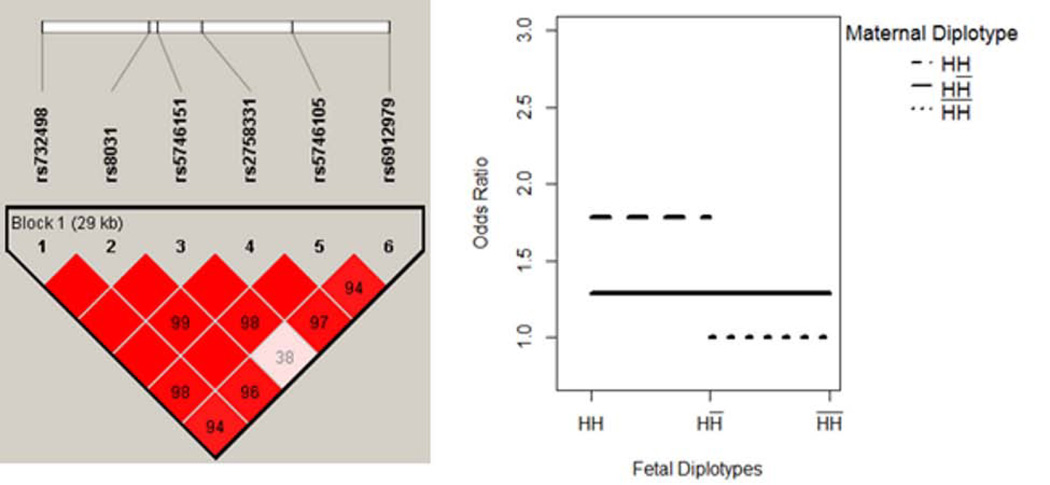
The results are summarized in Table IV. One block with 3 SNPs was located within the GSTA1 gene on chromosome 6. The haplotype structure showed three highly linked SNPs, rs9474321, rs6917325 and rs10948723, covering an 18 KB region (Figure 1A). Further, the MFG combinations were partitioned into two risk groups. Four MFG combinations had relatively lower likelihood of disease, and were used as reference group. We denoted the maternal/fetal genotype combinations in the reference group as R1 = {HH / HH; HH / HH̅; H̅H̅ / HH̅; H̅H̅ / H̅H̅}. Compared to the reference group, three other MFG combinations had an elevated likelihood of disease, denoted as R2 = {HH̅ / HH; HH̅ / HH̅; HH̅ / H̅H̅}. The corresponding OR between R1 and R2 was estimated to be 1.50 (95% CI: 1.18, 1.89). In such a scenario, the maternal haplotype H showed dominance effect that will increase the risk of disease, while the risk of disease was unchanged by fetal genotypes (Figure 1B). Similarly, our results show that a maternal haplotype of 6 SNPs within the gene SOD2 (Figure 2) may have an additive effect that increases the risk of disease.

Figure 1. GSTA1 - Maternal Main Effect Only.

Maternal haplotype H showed a dominance effect that will increase the risk of disease, while the risk of disease was unchanged by fetal genotypes.

Figure 2. SOD2 - Maternal Main Effect Only.

Maternal haplotype H showed an additive effect that will increase the risk of disease, while the risk of disease was unchanged by fetal genotypes.

2) Two blocks exhibited fetal main effect only

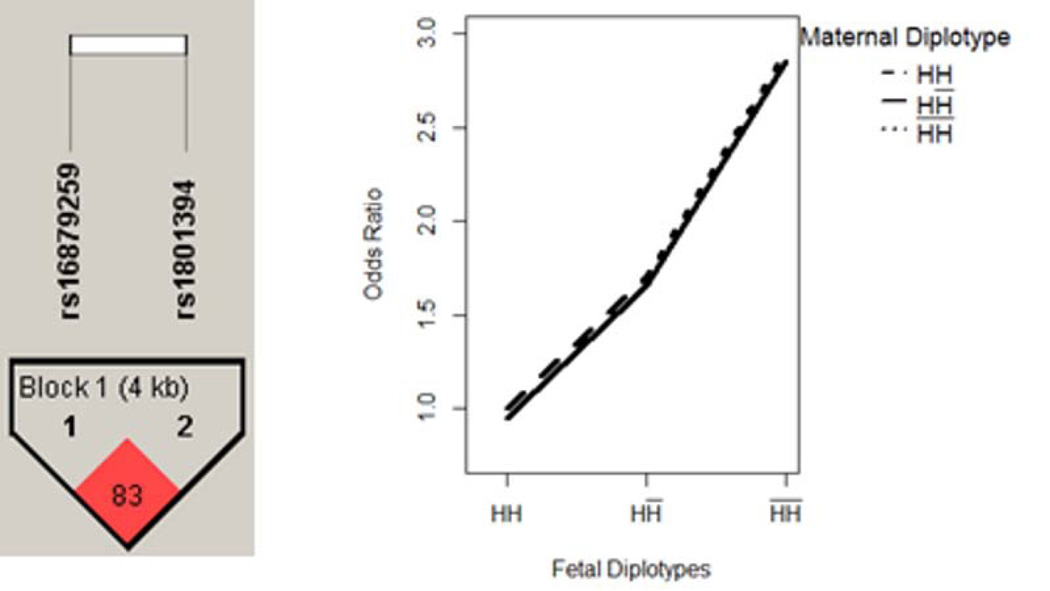
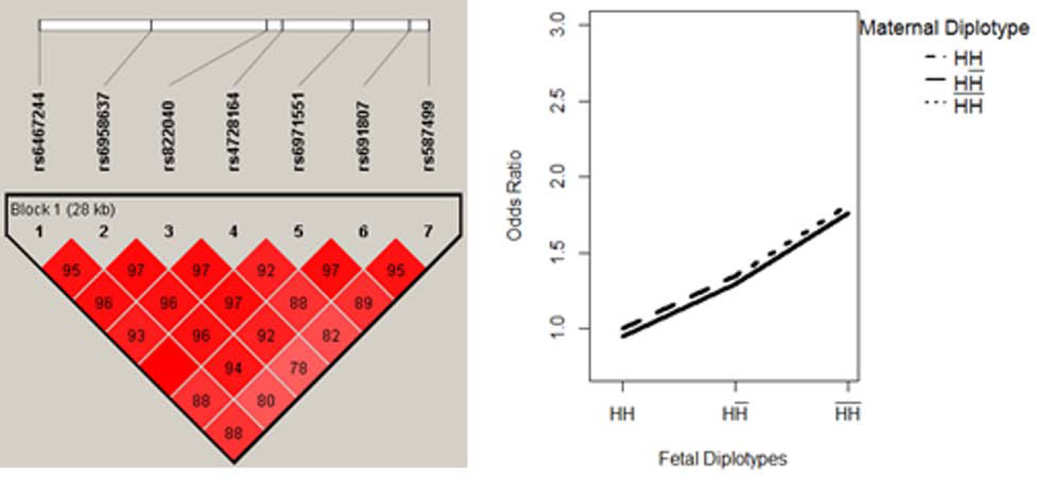
Two blocks were located within gene MTRR and AHCYL2, comprising 2 and 7 SNPs, respectively. The results are summarized in Table IV. For both blocks, the MFG combinations can be partitioned into three risk groups, according to the fetal genotypes. In each block, a fetal haplotype H showed an additive effect that was protective of the disease. The disease risk increased as the copy of haplotype decreased in the fetal genome, and was unchanged with maternal genotypes. We illustrated the pattern in Figure 3–4.

Figure 3. MTRR - Fetal Main Effect Only.

Fetal haplotype H showed an additive effect that was protective of the disease, while the risk of disease was unchanged by maternal genotypes.

Figure 4. AHCYL2 - Fetal Main Effect Only.

Fetal haplotype H showed an additive effect that was protective of the disease, while the risk of disease was unchanged by maternal genotypes.

3) Three blocks exhibited MFG interaction effect

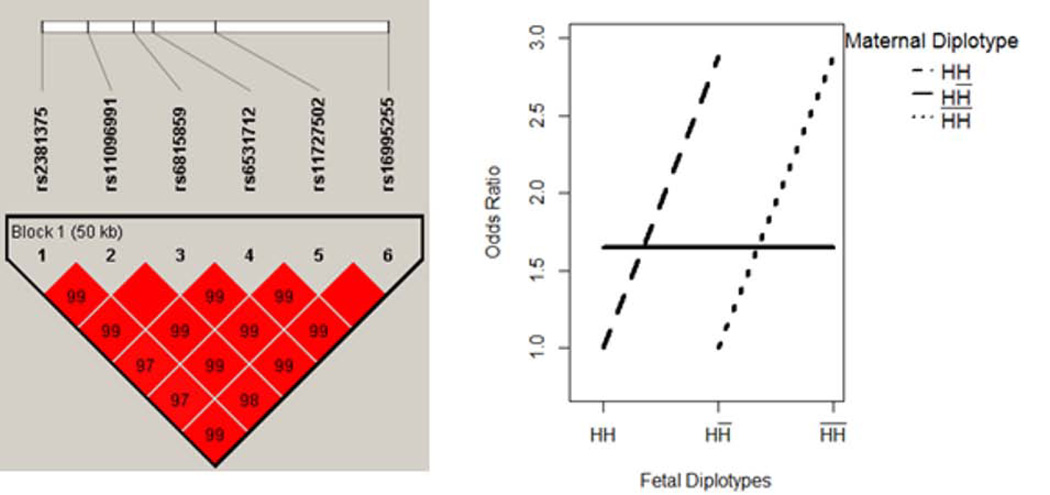
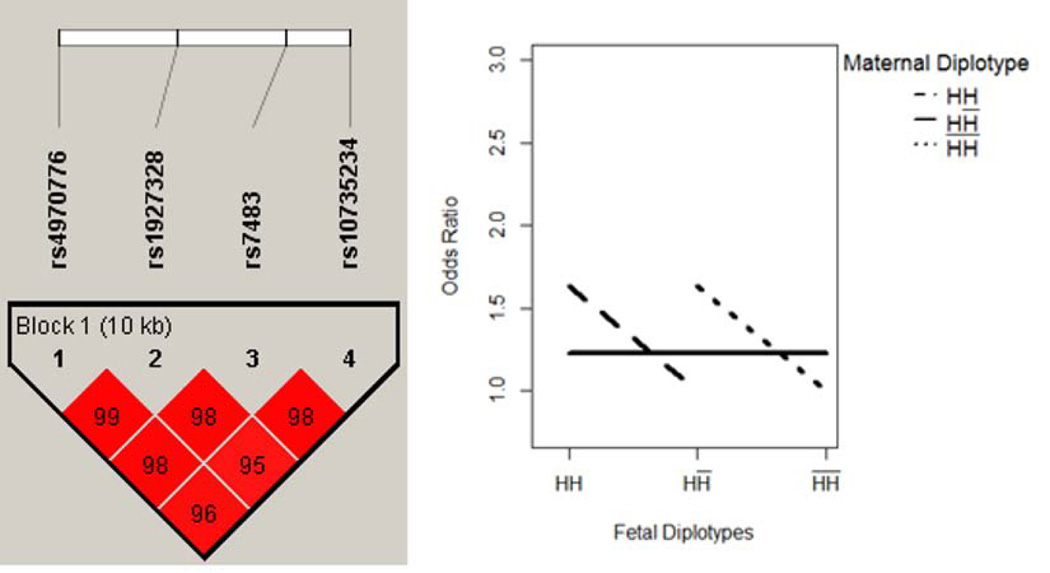
Three blocks were identified with MFG interaction effect (i.e. i_aa, i_ad, i_da, i_dd ≠ 0). These three blocks were located within genes GCLC, RFC1 and GSTM3, respectively on chromosome 6, 4, and 1. The results were summarized in Table IV. The block within gene GCLC had the most complicated interactive mechanisms. This block comprised 16 SNPs, covering a 22 KB region on chromosome 6. Based on the estimated coefficients, the MFG combinations were partitioned into 5 risk groups. As illustrated in Figure 5, when maternal genotype was HH̅, the risk of disease was unchanged with the fetal genotypes. However, when maternal genotype was HH (H̅H̅), the risk of disease showed increasing (decreasing) pattern with the fetal genotype. This pattern of “cross-over” was an indication of the potential MFG interaction effect. Similarly, the interactive pattern of the blocks in gene RFC1 and GSTM3 is illustrated in Figure 6–7.

Figure 5. GCLC – Both Maternal Main Effect and MFG Interaction Effect.

Maternal and fetal genotypes showed interactive pattern in terms of disease risk, which is indicated by a pattern of “cross-over”. Maternal haplotype H also showed an additive effect that will increase the risk of disease.

Figure 6. RFC1 - MFG Interaction Effect Only.

Maternal and fetal genotypes showed interactive pattern in terms of disease risk.

Figure 7. GSTM3 - MFG Interaction Effect Only.

Maternal and fetal genotypes showed interactive pattern in terms of disease risk.

4. DISCUSSION

Complex diseases are increasingly seen to be caused by the interplay of multiple genetic variants and environmental factors through complicated mechanisms. Detecting gene-gene interactions has been a major difficulty in genetic association studies [Cordell 2009], and can be especially challenging in maternal and perinatal research. Two types of gene-gene interactions are possible during pregnancy: intra-generational interaction within either maternal or fetal genome, and inter-generational interaction between maternal and fetal genomes. The inter-generational effect may lead to either conflicting or beneficial environment for fetal growth, which may influence the phenotypes of both mothers and babies [Sinsheimer, et al. 2010]. In addition, both maternal and fetal genes may have non-interactive main effects associated with the phenotypes. The effects of maternal genes may influence maternal metabolites, which are associated with the risk of having a CHD-affected pregnancy. For example, previous studies by our research group and others have described an association between gene MTHFR polymorphisms and maternal homocysteine levels that affect the risk of congenital anomalies [Botto and Yang 2000; Hobbs, et al. 2006]. Meanwhile, the correlation between maternal and fetal genomes imposes great difficulties on the statistical analyses to differentiate maternal, fetal and MFG interaction effects. In this study, we adopt a haplotype-based method, which utilizes a logistic regression framework with adaptive LASSO. This method serves to estimate maternal, fetal and MFG interaction effects, and allows modeling of multiple SNPs within a haplotype block simultaneously, thus reducing the burden of multiple testing. Using this method to examine the association between haplotypes in 60 candidate genes and the occurrence of CTD, we identified 7 genes potentially associated with this birth defect. Further analyses of these results suggest that the identified genes may influence the phenotype through various genetic mechanisms, corresponding to maternal main effect, fetal main effect and MFG interaction effects.

In our result, haplotypes within two genes, the glutathione S-transferase alpha 1 (GSTA1) and the glutamate-cysteine ligase, catalytic subunit (GCLC), were significantly associated with the occurrence of CTDs at a FDR level of 5%. The haplotype within the GSTA1 gene exhibited a significant maternal main effect only. This gene belongs to the Glutathione S-Transferase family, and its enzyme plays a key role in the detoxification of many toxic compounds [Coles and Kadlubar 2005]. A recent study in an Italian population also found that maternal variation in GSTA1 is associated with the risk of recurrent miscarriage [Polimanti, et al. 2012]. The haplotype within the GCLC gene exhibited both a significant maternal main effect and a significant MFG interaction effect. This gene encodes an enzyme for glutathione synthesis, thereby, preventing damage from oxidative stress. Variants with GCLC are known to make the enzyme less biologically active and lead to increased oxidative stress that may alter embryongenic processes. Population-based association studies have found an association between GCLC variants and cardiovascular events, such as myocardial infarction [Campolo, et al. 2007; Koide, et al. 2003].

In the current study, we also identified haplotypes in five additional genes, SOD2, GSTM3, MTRR, AHCYL2 and RFC1, potentially associated with CTDs, although the overall FDR for these 5 genes exceeded the 5% threshold. This is partly due to the limited sample size of our study (i.e. 331 case pairs and 875 control pairs), especially for the number of case pairs. We expect the power to increase in our on-going follow-up studies with larger sample sizes, which will improve the overall FDR. Considering the fact that most of them are functionally related to cardiovascular outcomes, we think that these genes may also play a role in the development of CTD, and are worth examining in further studies.

A few limitations should also be noted. First, the current study only included common SNPs that have minor allele frequencies (MAFs) of 5% or higher. Evidence from Phase III of the International HapMap Project and 1,000 Genome Project have supported that rare variants with lower MAFs may contribute considerately to the development of complex human diseases [Abecasis, et al. 2012; Altshuler, et al. 2010]. However, because of their low MAFs, the rare variants are less easy to be phased through LD blocks, and were not included in the current haplotype analysis. Second, the genetic etiology of non-syndromic CTDs may be highly complex, involving both inter-generational and intra-generational interactions among genes from either different genomes or different genomic regions. Our current analysis only considered the inter-generational interactions between maternal and fetal genes from the same genomic region (LD block). While MFG interactions may also exist between genes from different genomic regions, investigation of these interactions will significantly increase the number of statistical tests and is beyond the scope of the current study.