A General Class of Test Statistics for Van Valen’s Red Queen Hypothesis

Abstract

Van Valen’s Red Queen hypothesis states that within a homogeneous taxonomic group the age is statistically independent of the rate of extinction. The case of the Red Queen hypothesis being addressed here is when the homogeneous taxonomic group is a group of similar species. Since Van Valen’s work, various statistical approaches have been used to address the relationship between taxon age and the rate of extinction. We propose a general class of test statistics that can be used to test for the effect of age on the rate of extinction. These test statistics allow for a varying background rate of extinction and attempt to remove the effects of other covariates when assessing the effect of age on extinction. No model is assumed for the covariate effects. Instead we control for covariate effects by pairing or grouping together similar species. Simulations are used to compare the power of the statistics. We apply the test statistics to data on Foram extinctions and find that age has a positive effect on the rate of extinction. A derivation of the null distribution of one of the test statistics is provided in the supplementary material.

1. Introduction and Literature Review

Extinction plays an important role in evolutionary theory. Studying the extinction patterns and lifetime distributions among different taxonomic groups can help to determine the underlying causes of extinction. Extinction data contains extinction times, origination times, and may also contain other covariate information. This structure allows for the use of many traditional survival analysis techniques and an easy formulation of a statistical hypothesis. The Red Queen hypothesis is a theory of evolution which describes the relationship between taxon duration (age of a taxon or the total amount of geological time that a taxon has been in existence) and its rate of extinction (or hazard rate for extinction). Formally, it states that the hazard for extinction is independent of taxon duration. In our approach, the hazard for extinction is treated as a function of geological time and an individual is at risk on the interval of time for which they are in existence. This approach treats age as a time-varying covariate on the hazard for extinction. This is in contrast to the approach taken by Van Valen in which age is treated as a fixed covariate. The focus of this work is to test the effect of age of subject on their hazard for extinction. The age parameter can be used as a fixed covariate or a time-varying covariate. If age is treated as a time-varying covariate the effect of age on the hazard for extinction will also depend on geological time. If age is treated as a fixed covariate then the age effect on the hazard would only depend on the time since taxon origination. Van Valen brought this relationship to the forefront with his Red Queen hypothesis, which will be discussed later [22].

In 1973 Van Valen used survival (survivorship) curves to show that within a given taxon, group of organisms, the extinction rate appeared to be constant. He graphed multiple survival curves at the species level, genera level, and the family level using lifetime data on over 25,000 subtaxa and based on the results he obtained he formulated the Red Queen hypothesis, which states that extinction of a taxonomic group is independent of the age of that group [22]. This hypothesis is more easily described using a hazard function, or the instantaneous extinction rate. A taxonomic group that has a hazard function which does not depend on age would satisfy the Red Queen hypothesis. In Van Valen’s survivorship curves he graphed the living taxa and the extinct taxa separately. In his survivorship curves for the living taxa the individual points represent total number of subtaxa that have been in existence for at least that particular duration of time. The coordinates of the survivorship curves for the extinct taxa represented the total number of taxa that existed for at least that amount of time. For most of the survival curves that he graphed, he found that the slope was constant (on a log scale). Constant extinction rate can be interpreted as a constant hazard function in survival analysis, which corresponds to an exponential lifetime distribution. This is a special case of the Red Queen Hypothesis and it helps to give the foundation of the statistical testing applied to the Van Valen data since he began his work.

Since Van Valen’s work there have been a variety of statistical approaches used to test the Red Queen hypothesis. These approaches include both testing for a constant hazard for extinction [15, 17, 19] and regression model methods that include age as a covariate over geological time [4, 5, 9].

In 1975, Raup used one of the procedures developed by Epstein [6, 7] to test for exponentiality of the lifetime distribution. When Raup applied this test to one of Van Valen’s graphs for Ammonoid families, the null hypothesis of constant extinction rates, exponential lifetimes, was rejected.

In 1992 Pearson introduced the Corrected Survivorship Score (CSS) as an alternative unit to be used in graphing survival curves as opposed to the taxon duration. The concern was that the survivorship curves used by Van Valen compared taxa from different eras without taking into account the variation in extinction rates throughout the entire fossil record provided by the data. The Corrected Survivorship Score is given by, $\mathrm{CSS}=\frac{\mathrm{L}\cdot {\mathrm{R}}_e\left(\mathrm{extant}\right)}{R_e\left(\text{total}\right)}$, where L is the duration of the taxon, R_e(extant) is the average per-taxon disappearance rate in the group while the taxon is ‘alive’ and R_e(total) is the average per-taxon extinction rate for the whole time interval under consideration. Pearson showed that for the Paleogene planktonic foraminifera the Van Valen survivorship curve was a straight line (on a log scale) indicating constant extinction, while in contrast, a survivorship curve using the CSS was convex indicating a non-exponential lifetime distribution and a departure from the constant extinction. The Epstein Total Lifetimes [6, 7] test rejected the null hypothesis of constant extinction rate [17].

Parker and Arnold [15] modelled cenozoic planktonic foraminifera using the exponential and Weibull distribution. Using the estimates of the shape and scale parameters (β and α, respectively) of the Weibull model, they conducted a likelihood ratio test [13] of H₀ : β = 1 vs H_a : β ≠ 1. Since they rejected H₀, they also rejected the exponential model because the Weibull model yields the exponential model when the shape parameter is 1.

Doran et al. used a semi-parametric Cox proportional hazards model to test the Red Queen hypothesis in planktonic foraminifera [4, 5]. Doran et al. fit a Cox model which included species age as a time-varying covariate and found the coe cient of age to be positive and highly significant in this model.

Finnegan et al. [9] studied the extinction of phanerozoic marine animal genera and found that genus age had a negative effect on extinction risk throughout the majority of the time periods within the Phanerozoic eon. This was done by fitting logistic regression models on consecutive disjoint intervals of time with all possible combinations of the covariates and then assessing the fit of the models that included age versus those that didn’t by using Akaike weights [2].

Some of the limitations of the previous methods such as Weibull regression, exponential regression, and Epstein’s test include distributional assumptions on the data. If the data fail to follow these parametric assumptions, these approaches will be invalid. The natural alternative to the parametric assumptions of the previous regression models was the Cox model used by Doran et al. [4, 5], but if the proportional hazards assumption fails or if the covariate effects vary with time then this model will also be invalid. The logistic regression approach of Finnegan et al [9] also makes very strong assumptions on the covariate effects; moreover, their division of time into relatively short intervals (of about 11 million years) is not suitable for smaller data sets such as the foram data that we analyze, since it would leave us with too few extinctions in each interval to reach reliable conclusions.

In this paper we propose general statistical methods to test the Red Queen hypothesis. These methods address some of the limitations of the previously used methods. In comparison to the regression modelling approaches we don’t assume any model for the covariate effects. Our methods are applied to extinction data on Forams. The data that we use in this paper is the same data used by Doran et al. [5]. It contains origination times, extinction times, and morphological covariates. These morphological covariates represent measurements on the structure of the Forams. A more detailed description of the data will be provided in Section 4.

2. Methods

The motivation for this methodology is to provide a method in which covariate effects on the hazard are allowed to vary over time and the assumptions on the distributional and functional form of the hazard can be relaxed. The test statistic is computed by partitioning risk-groups into clusters of individuals that are similar on covariates known to be associated with the hazard for extinction. The clusters are formed so as to remove the possible effect of these covariates on the hazard for extinction.

Van Valen’s Red Queen hypothesis states that in a group of similar species the extinction rate is the same for all species, regardless of their age. Here, similar species refer to species in the same adaptive zone. An adaptive zone captures the interaction between an organism and its habitat and is quantified through changes in its phylogeny [21]. Since changes in morphology indicate changes in phylogeny [14], the adaptive zone in this study will be groups of species that share similar morphological covariates. As species evolve over time they are constantly adapting to their environment so that at different points in time a species may be in different adaptive zones [21]. The methodology used will have similar species grouped together at distinct time points, and then use these different groups to test for age effects on extinction in order to directly test the Red Queen hypothesis.

Proposed Method

The proposed method consists of two parts which can be varied independently of each other: grouping and scoring. In one part at risk species are placed in groups of similar species at each extinction (death) time. Species are considered at risk at a particular time if they originated and have not gone extinct prior to that time. In the other part a test statistic (denoted J) is incremented at each extinction time by a score which depends on the particular species which goes extinct and the group to which it has been assigned.

In this section we propose several grouping schemes that use important morphological covariates to form clusters of at risk species. The grouping methods are based on matched pairs and k-means clustering. Then we propose several test statistics to test for age effects on extinction for each of the different grouping schemes. A derivation of the distribution of the test statistic J under a special case of the null hypothesis (the Red Queen hypothesis) is provided in the supplementary material.

Before the methodology is introduced we provide a quick review of the logrank test statistic since statistic J resembles the logrank statistic.

Logrank Statistic

The logrank statistic is used when comparing the hazard rates of two populations. Specifically it tests the null hypothesis that the hazard rates are equal in both populations:

$$H_0:{\lambda }_1\left(t\right)={\lambda }_2\left(t\right)\forall t$$

Suppose two samples of individuals are randomly selected from populations 1 and 2 with sample sizes n1 and n2 respectively. Let (T_i;U_i) represent the failure and censoring times of individual i in the combined sample of the two samples where i = 1, …, n, for n = n1 + n2. Also let X_i be the observed time and Z_i be the indicator for which group (or population) individual i belongs to: X_i ≡ min(T_i,U_i) and Z_i = I_{[i∈group 2]}. Y_i(t) and N_i(t) are indicators of whether or not individual i is at-risk at time t and whether or not individual i has failed by time $t:Y_i\left(t\right)=I_{[{\mathrm{x}}_i\ge t]}$ and $N_i\left(t\right)=I_{[{\mathrm{x}}_i\le t]}$. A counting process representation for the logrank statistic U is:

$$U=\sum _{i=1}^n{\int }_0^{\infty }\left\{Z_i-\frac{{\Sigma }_{j=1}^n{Y}_j\left(s\right)Z_j}{{\Sigma }_{j=1}^n{Y}_j\left(s\right)}\right\}d{N}_i\left(s\right)$$ (1)

[10]

The logrank statistic is incremented each time an individual fails by a score comprised of their group indicator (0 or 1 for population 1 or 2) subtracted by average group indicator of the individuals at risk. The integral shown in equation (1) reduces to be the single term inside of the curly braces whenever an at risk individual fails and is zero otherwise.

2.1 Grouping Schemes

In this section we introduce three grouping schemes. The first two grouping schemes group at risk species into pairs based on the distance between any two species. The third grouping scheme is used to form groups of size 2 or more. The distance measure is computed using the covariate values of the species.

Grouping Scheme 1: Matched Pairs

For grouping scheme 1 the first step is to compute the normalized Euclidean distance between the covariate vectors for each pair of species. In the second step at risk are paired at any time t by initially pairing the closest two species. Continue pairing the closest remaining species as long as possible, that is, until only one or zero species remain. Matched pairs could also be constructed based on the Mahalanobis distance or any other suitable distance measure.

Grouping Scheme 2: Matched Pairs using Age Differences

This is the same as Grouping Scheme 1 except that in forming the pairings at time t the distance between species i and j is divided by their age difference:

$$d{2}_{i,j}=\frac{d{1}_{i,j}}{\mid A_i\left(t\right)-A_j\left(t\right)\mid }$$ (2)

where A_i(t) ≡ age of species i at time t and d1_i,j and d2_i,j denote the distance between species i and j under grouping schemes 1 and 2, respectively. The rationale behind dividing by the age differences is to possibly increase the power: the greater the difference in ages between two species, the smaller will be the distance measure and the more likely they are to be paired, so that Grouping Scheme 2 will tend to produce pairs which are well-matched on the covariates but differ substantially in age. Thus if there exists an age-related difference in extinction rates, this pairing increases our chances to detect it.

Grouping Scheme 3: K-means Clustering

Under grouping scheme 3, at each extinction time t the at risk species are grouped together using k-means clustering based on the Euclidean distance between their covariate vectors. For n species at risk with covariate vectors x₁, …, x_n, k-means clustering partitions the species into k groups (or clusters) C₁, C₂, …, C_k so as to minimize the within cluster sum of squares

$$\underset{C}{\arg \min }\sum _{i=1}^k\sum _{x_j\in C_i}{\mid \mid x_j-{\mu }_i\mid \mid }^2$$ (3)

where μ_i is the mean of cluster i, C_i, and C = {C₁, …, C_k}.[12]

2.2 Test Statistics

In addressing the question of age-dependency we formulate several different statistics for testing the null hypothesis of no age effect on the extinction rate. All of these statistics have the same general form: scores are assigned to all species at all times; and at the time a species is observed to go extinct, the value of the statistic is incremented by the score associated with that species and time. Let S_i(t) be the score assigned to species i at time t. Suppose there are r distinct extinction times t₁, t₂, …, t_r with t₁< t₂< ⋯ < t_r. Species are censored at the present time, τ. Let I_kbe the set of species which goes extinct at time t_k. (In our theory, we may assume there are no exact ties in the extinction times so that I₁, …, I_r will be singletons; but because of rounding and limited resolution, there may be ties in the data.) The general form of the test statistic that we use is

$$J=\sum _{j=1}^r\sum _{i\in I_j}{S}_i\left(t_j\right)$$ (4)

Statistics of this form can be given a counting process representation. Below is a brief description of the notation that is used:

• L_i and R_i are the origination time and extinction time of species i, respectively, where i = 1, …, n.

• N_i(t) = I_{Ri≤t} is the indicator that the species i goes extinct by time t.

• Y_i(t) = I_{Li<t≤Ri} is the indicator that species i is in existence and thus at risk for extinction at time t.

The counting process representation of J is given below:

$$J=\sum _{i=1}^n{\int }_{\gamma }^{\tau }{S}_i\left(t\right)Y_i\left(t\right)d{N}_i\left(t\right)$$ (5)

where γ is the first origination time.

For each of our statistics only the scoring function S_i(t) will be discussed since the basic structure is the same in all cases.

Our first two statistics are based on the use of matched pairs; at each extinction time the at-risk species are placed in pairs having similar covariate values as described earlier.

Statistic 1

Our first statistic is easily described: at each extinction time we score +1 if the species that went extinct was the older species in its matched pair, and −1 if it was the younger. If the total score J is large positive (negative), there is a tendency for the older (younger) species to go extinct first, which corresponds to an age effect. If the species are closely matched on all the covariates which a ect the extinction rate, then under the null hypothesis (H₀) of no age effect (the Red Queen hypothesis), the species in each pair are equally likely to go extinct at any given time, and the score arising from each extinction will take the values +1 or −1 with equal probability. Thus, under H₀, the random scores from each extinction have mean zero and variance one so that, conditional on the total number of species which go extinct (equal to $M\equiv {\sum }_{j=1}^r\mid I_j\mid$ where |I_j| is the cardinality of I_j), the total score J has mean zero and variance M. If M is sufficiently large, J will be approximately normal so that $J∕\sqrt{M}$ will have approximately a N(0, 1) distribution under H₀.

The test statistic described above is statistic J (4) with scoring function S_i(t) given by

$$S_i\left(t\right)=\{\begin{array}{cc}-1,\text{if species}i\text{is the younger species in its pair at time}t\hfill & \hfill \\ 1,\text{if species}i\text{is the older species in its pair at time}t\hfill & \hfill \\ 0,\text{if species}i\text{is not at risk at time}t\hfill & \hfill \end{array}\phantom{\}}$$ (6)

Summarizing the earlier discussion: under H₀, conditional on the total number of extinctions M our statistic J has E(J) = 0 and var(J) = M, and $J∕\sqrt{M}$ is approximately N(0, 1) when M is sufficiently large.

Statistic 2

This statistic is similar to Statistic 1, but instead of adding +1 or −1 to the score function at each extinction, we add the positive (negative) age difference if the older (younger) species in the pair goes extinct. This corresponds to using the scoring function

$$S_i\left(t\right)=A_i\left(t\right)-A_{i^{\prime }}\left(t\right)$$ (7)

where A_i(t) is the age of species i at time t and i′ is the species which is paired with species i at time t. The interpretation of this statistic is similar to Statistic 1 in that large positive (negative) values of the total score J indicate that there is a tendency for the older (younger) species in the pair to go extinct first.

Statistic 3

This statistic is different from the statistics previously mentioned because it is based on the species at risk being placed in groups of size 2 or more. When a species goes extinct their assigned score is the deviation of their age away from the mean age of their group (i.e. score = [age of species] − [mean age of group]). The score for species i at time t is defined by

$$S_i\left(t\right)=A_i\left(t\right)-B_i\left(t\right)$$ (8)

where B_i(t) is the mean age of the group G_i(t) that species i belongs to at time t. As before, if the species within the clusters are well matched on the covariates that effect the hazard for extinction, then under H₀ each of the species within a group are equally likely to go extinct and the score arising from an extinction will take on the value of any of the deviations from the mean age with equal probability.

Variance Estimation

For our statistic J we give a variance estimate V. These variance estimates have the same general form as J: they are incremented every time a species goes extinct, that is, we may write

$$V=\sum _{j=1}^r\sum _{i\in I_j}{V}_i\left(t_j\right)$$ (9)

where V_i(t) denotes the amount by which the variance estimate would be incremented if species i were to die at time t. The counting process representation for V is

$$V=\sum _{i=1}^n{\int }_{\gamma }^{\tau }{V}_i\left(t\right)Y_i\left(t\right)d{N}_i\left(t\right)$$ (10)

When species are arranged in pairs, the variance increment for our statistic is

$$V_i\left(t\right)={\left[S_i\right(t\left)\right]}^2.$$ (11)

This is because, if species i is paired with species i′ at time t, our scores are defined so that S_i(t) = −S_i′(t). If the paired species are truly similar, then under H₀ species i and species i′ are equally likely to die so given that one of them dies the score increment is ±S_i(t) with variance [S_i(t)]².

For groups based on k-means clustering (or other methods), we choose scores S_i(t) so that they sum to zero within each group. If species i in group G_i(t) dies at time t, the variance increment is taken to be

$$V_i\left(t\right)=\frac{1}{d_i\left(t\right)}\sum _{j\in G_i\left(t\right)}{\left[S_j\right(t\left)\right]}^2$$ (12)

where d_i(t) ≡ |G_i(t)|. The rationale is again that, if the grouped species are truly similar, then under H₀ they are all equally likely to be the species which goes extinct.

If more than one species in a group dies at time t, then using the finite population correction we have:

$$V_i\left(t\right)=\frac{d_i\left(t\right)-D_i\left(t\right)}{d_i\left(t\right)-1}\left[\frac{1}{d_i\left(t\right)}\sum _{j\in G_i\left(t\right)}{\left[S_j\right(t\left)\right]}^2\right]$$ (13)

where D_i(t) is the number of species that go extinct in group G_i(t) at the time t. Under H₀, given that D_i(t) species in group G_i(t) die at time t, the score increment is the sum of D_i(t) scores sampled without replacement from {S_j(t) : j ∈ G_i(t).

The Null Distribution of J

Under H₀, we expect the distribution of $J∕\sqrt{V}$ to be approximately normally distributed with mean zero and variance one (N(0, 1)) when the number of extinctions is sufficiently large.

Remark

In grouping schemes 1 and 2 risk sets that contain an odd number of species will have one species that does not get paired. If this species is the species that goes extinct, then their extinction is not counted and the statistic is not incremented. We will refer to this extinction as a wasted death. Clearly

$$\text{total extinctions}=\text{total wasted deaths}+\text{total increments}$$ (14)

The total number of increments is one of the factors a ecting the power of the test based on J.

3. Simulation Studies

In section a a simulation study was used to evaluate the performance of the test statistics under the null and alternative hypotheses. In section 4 we apply our test statistics to the foram data used in Doran et al. [5], and the simulations in this section are designed to justify or validate this analysis by showing that our procedures work well on simulated data sets which resemble the foram data. This will be evaluated based on sample Type I error rates and sample power estimates. The details of the simulations are motivated by the foram data.

Under each hypothesis (the null (H₀) and alternative (H_a)), 1000 samples of 286 species were simulated at each parameter value selected. There were 4 parameter values selected to evaluate the Type I error and 10 parameter values selected to evaluate the power. The covariates x_i (i = 1, …, n) and the origination times, L_i where i = 1, …, 286 used in the simulation come directly from the foram data. The origination times range from 1.77 to 70.64 million years ago. The covariate effects used in the simulations were chosen by fitting a Cox model to the foram data (and using the resulting parameter estimates). In essence, in our simulation studies we apply our procedures to simulated versions of the foram data in which the actual extinction times R_i are replaced by simulated values

$$R_i=L_i+{\Psi }_i$$ (15)

where the durations (lifetimes) Ψ_i were generated from the Cox proportional hazard model,

$$h(t\mid x(t\left)\right)=h_0\left(t\right)e^{x\left(t\right)\beta }.$$ (16)

where x(t) is a vector that contains fixed covariates from the foram data and a time-varying covariate for the age parameter which is a function of geological time t. Under H₀ (H_a), the coe cient of age is zero (nonzero).

In H₀ and H_a simulations we will apply all of our methods to the same set of simulated data. Therefore, the Type I error rates and the empirical power estimates for our statistics will be correlated. In order to conduct pairwise comparisons of the power of our test statistics under each of our simulation alternatives we will perform tests based on the difference in dependent binomial proportions.

Let x_ai be the indicator that statistic a rejected H₀ in the i^th sample of our power simulation and define ${\widehat{p}}_a=\frac{1}{m}{\sum }_{i=1}^m{x}_{ai}$. Then ${\widehat{p}}_a$ is an estimate of the power p_a of statistic a. Similarly define x_bi, ${\widehat{p}}_b$, and p_b for statistic b. A 100(1−α)% confidence interval for p_a − p_b is given by:

$${\widehat{p}}_a-{\widehat{p}}_b\pm \frac{z_{\alpha ∕2}\left({\widehat{p}}_a\right(1-{\widehat{p}}_a)+{\widehat{p}}_b(1-{\widehat{p}}_b)-2({\widehat{p}}_{ab}-{\widehat{p}}_a{\widehat{p}}_b\left)\right)}{\sqrt{n}}$$ (17)

where ${\widehat{p}}_{ab}=\frac{1}{n}{\sum }_{i=1}^n{x}_{ai}\cdot x_{bi}$ is the average cross product of the binomial trials. In our simulations, we reject H₀ : p_a = p_b whenever zero falls outside this interval.

The size of the risk set is also a factor that effects the power. At each sampled value of the parameter space the average risk set size is computed in each sample and then averaged across all 1000 samples.

The coefficients of the covariates for the simulation were selected by using the estimated coe cients of a Cox regression model fit to the foram data which included species age and the following variables: Keeledness, Width to height ratio of aperture, Angle between geometric centroids of various chambers, Circularity ratio of final chamber compared to a circle of equal area, Number of chambers in final whorl (viewed from dorsal side), Height in side view, and Clavateness. These variables were chosen because they were found to be significant in Doran et al. [5]. They will be explained in more detail in section 4. The estimates of the coe cients of these variables, excluding age, are given in Table 1. Also displayed in Table 1 are the estimates of the coe cients when the variables are standardized.

Table 1.

Estimated coefficients of the Cox model.

Variables	β estimate	standardized β	β values used
Keeledness	0.0145	0.004275397	0.0304011
Width to height ratio of aperture	−1.68489	−0.003405692	−3.159953
Clavateness	0.36015	0.00248234	−1.349819
Circularity ratio of final chamber compared to a circle of equal area	0.55887	0.001409179	−0.0006472
Height in side view	−0.000645	−10.71521889	0.0030524
number of chambers in final whorl	−0.00107	−0.001253322	−0.0043704
Angle between geometric centroids of penultimate and antepenultimate chamber	0.000373	0.287198337	0.000373
Angle between geometric centroids of antepenultimate and 4th chamber	−0.0000324	−0.023744172	0.0006349

3.1 Cox model simulations with baseline hazard rate that grows exponentially

In this set of null and alternative simulations the baseline hazard rate grows exponentially with respect to geological time. Table 1 displays the coe cients used in the model.

H₀ simulation

Under the null hypothesis of no age effect on the hazard rate, the hazard model for species i is:

$$h(t\mid {\mathrm{x}}_i)=e^{{\beta }_0+\gamma t}{e}^{{\mathrm{x}}_i\beta },L_i<t.$$ (18)

Note that when γ < 0 the resulting survival distribution is degenerate, assigning positive probability to the species surviving forever.

In the null simulation study for this model there were four values selected for γ: −0.02513, −0.01820, −0.01380, and −0.00813 listed in table 2. The value selected for β₀ was 2.8668. The mean number of extinctions across the 1000 samples was 72, 139, 187, and 238 respectively. The mean of the average risk set size across all 1000 samples were 119, 87, 63, and 36. Table 2 displays the results of this simulation.

Table 2.

Type I error estimates under the Cox proportional hazards model (18), where γ₀₁ = −0.02513, γ₀₂ = −0.01820, γ₀₃ = −0.01380, and γ₀₄ = −0.00813. * and ** denote significance level 0.05 and 0.01 respectively.

	γ0 parameter	γ 01	γ 02	γ 03	γ 04
Group Scheme 1	Stat 1	0.054	0.049	0.054	0.054
	Stat 2	0.039	0.05	0.048	0.049
Group Scheme 2	Stat 1	0.046	0.05	0.044	0.082**
	Stat 2	0.042	0.051	0.052	0.069**
Kmeans	Stat 1	0.041	0.044	0.046	0.059
	Stat 3	0.047	0.052	0.048	0.046

H_a simulation

For the simulation under the alternative hypothesis we allow for an age-effect by including the covariate age in the model. The proportional hazards model for species i is:

$$h(t\mid {\mathrm{x}}_i)=h_0\left(t\right)e^{{\mathrm{x}}_i\beta +{\beta }_{age}(t-L_i)}=e^{(\gamma t+{\beta }_0)}{e}^{{\mathrm{x}}_i\beta +{\beta }_{age}(t-L_i)},L_i\left(t\right)<t$$ (19)

As seen in the previous model this alternative model allows species to live forever when γ + β_age < 0. In this power simulation γ = −0.0172 and there were 10 values selected for β_age: −0.200, −0.056, −0.024, −0.008, 0.008, 0.024, 0.040, 0.056, 0.072, and 0.088.The mean number of extinctions for the 1000 samples at each γ_age value was: 74, 144, 174, 188, 201, 211, 219, 226, 230, and 235. The mean of the average risk set size across all samples for each value of β_age: 93, 72, 62, 57, 52, 48, 44, 41, 38, and 36, respectively.

In Table 3 the power estimates are displayed and it shows that among the statistics that we developed (Section 2.2), Statistic 3 and Statistic 2 under grouping scheme 2 appear to have the highest power when the age effect is positive. For negative age effects Statistic 2 with grouping scheme 2 appears to have the highest power. Statistic 1 and 2 also appear to have more power under grouping scheme 2 than grouping scheme 1. Also displayed in Table 3 are the power estimates for the Wald test for H₀ : β_age = 0 in the Cox model:

$$h(t\mid {\mathrm{x}}_i)=e^{\left({\beta }_0\right)}{e}^{{\mathrm{x}}_i\beta +{\beta }_{age}(t-L_i)}\text{for}t>L_i$$ (20)

The Wald statistic was more powerful than our methods for positive age effects but for negative age effects Statistic 1, 2 (grouping scheme 2) and Statistic 3 appeared to have more power than the Wald statistic. Along with comparing our methods to the Wald Statistic we also compared our grouping schemes to random pairing (Table 3), i.e., randomly assigning species into pairs as opposed to using grouping schemes 1 or 2 and then applying Statistics 1 and 2. Our results also indicate that grouping scheme 2 provides significantly more power to Statistics 1 and 2 than random pairing.

Table 3.

Power under the Cox proportional hazards model (19).

	Group Scheme 1		Group Scheme 2		Random		K-means	Cox Model
β parameter	Stat 1	Stat 2	Stat 1	Stat 2	Stat 1	Stat 2	Stat 3	Wald
βage = −0.05	0.995	1	1	1	0.999	1	1	1
βage = −0.034	0.765	0.982	0.99	1	0.877	0.994	0.995	0.95
βage = −0.018	0.273	0.509	0.614	0.789	0.389	0.632	0.65	0.488
βage = −0.002	0.07	0.096	0.14	0.164	0.116	0.16	0.118	0.062
βage = 0	0.055	0.052	0.066	0.056	0.059	0.069	0.043	0.072
βage = 0.014	0.057	0.09	0.063	0.098	0.042	0.049	0.106	0.501
βage = 0.03	0.232	0.383	0.369	0.52	0.147	0.25	0.534	0.942
βage = 0.046	0.488	0.786	0.699	0.915	0.393	0.628	0.913	0.999
βage = 0.062	0.731	0.927	0.905	0.989	0.613	0.867	0.988	1
βage = 0.078	0.847	0.985	0.976	1	0.781	0.957	1	1
βage = 0.094	0.927	0.998	0.992	1	0.885	0.989	1	1

After performing pairwise comparisons for the differences in power among our test statistics using the confidence interval test (equation (17)) we found that the power of Statistic 2 (Grouping Scheme 2) is not significantly different from Statistic 3 for positive age effects. Our results indicate that our statistics have significantly more power under Grouping Scheme 2 than Grouping Scheme 1. They also indicate that Statistic 2 and 4 have significantly more power than Statistic 1.

The simulation studies in other simulation models were also used, leading to similar results [24]. In addition to trying other simulation models we also tried to use alternative distance measures in the grouping schemes of the pairwise statistics. We compared using Mahalanobis distance to using Euclidean distance in grouping schemes 1 and 2. The results showed that Euclidean distance has significantly more power than Mahalanobis distance [24].

4. Application to Foraminifera Data

In this section we will apply our statistical methods that were developed in Section 2 to foraminifera fossil data. In Section 4.1 we give a brief description of the data and in Section 4.2 our statistical methods are applied to the data.

4.1 The Data

Forams are a phylum that belong to the kingdom protista. They are single-celled organisms whose fossilizable structure comprises of a test or shell. The test has one or more chambers. Initially in the life cycle of a foram there is a single chamber. Over the remainder of the life cycle chambers are added to the test most commonly in a spiral like form. Each time a new set of chambers completes a 360 degree coil around the test it is called a whorl. There is an opening in the shell called the aperture. One of the many functions of the aperture is feeding. A keel is formed when the chamber wall ‘collapses’ along the external perimeter forming an edge. The part of the wall that protrudes out is called the keel. Forams are mainly found in marine environments that receive sunlight and their fossil record is well preserved on the ocean floor. Variations in their shell pattern have been linked to climate change over geological time. Biostratigraphy uses microfossils to determine the geological age and composition of sedimentary rock. Biostratigraphy also provides good evolutionary sequence. Since forams are heavily used in biostratigraphy they have wide ranging applications to areas such as oil exploration [11].

The above discussion indicates why foraminifera fossil data is a perfect candidate for tests of the Red Queen Hypothesis. The foraminifera dataset was obtained from Doran et al. [5]. Included in the dataset was species origination and extinction time which were given in millions of years. The sample size was 288 species and there were 236 extinctions. The data set also contained morphological covariates. The morphological covariates that were found to be significant in the Cox model proposed by Doran et al. [5] were the covariates used in our data analysis. A description of these variables was provided by Doran [3]:

• Keeledness: ratio of area of the final chamber and keel to the final chamber.

• Ratio of the height of the aperture to the width of the aperture.

• Clavateness: ratio of the distance from the coiling axis to the chamber furthest away from the coiling axis compared to the distance from the coiling axis to the point on the border of the previous chamber that is furthest away from the coiling axis. This ratio is averaged over all chambers in the final whorl.

• Number of chambers in the final whorl

• Height in side view (micrometers)

• Ratio of the circumference of circle with equal area of final chamber compared to the circumference of the final chamber.

• The mean number of degrees of the angle formed by the geometric centroid of a chamber, the axis of rotation and the geometric centroid of the previous chamber for last four chambers.

• The angularity of the lateral periphery of the final chamber (in degrees).

Figure (1) [16] gives a depiction of what these covariates represent on a foraminiferan.

Figure 1.

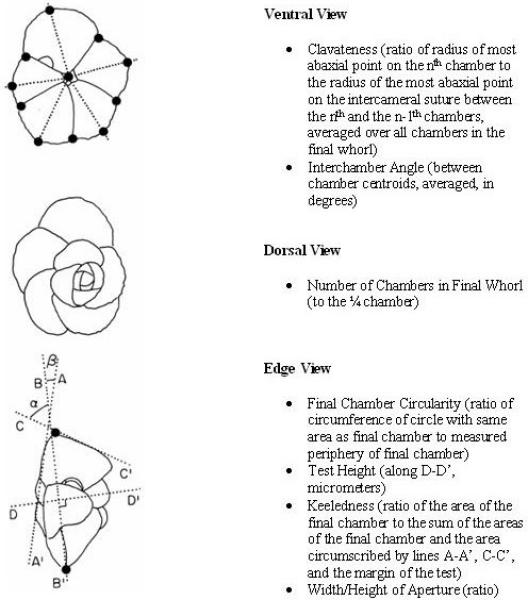
Foraminifera Morphological structure [16].

4.2 Results and Discussion

Table 4 displays the results from methods described in Sections 2.1 and 2.2 applied to this dataset. The distance measure in grouping scheme 1 was calculated using Euclidean distance of the covariate vectors of the paired species. The distance measure used in grouping scheme 2 was the distance measure used in grouping scheme 1 divided by the difference in ages between two species. The third grouping scheme grouped at-risk species into groups of size 2 or more using k-means clustering at each extinction time. The clusters were initialized to be of size 3.

Table 4.

Z-scores for the tests performed on the Foraminifera database

	Group Scheme 1		Group Scheme 2 (Euc)		Random		K-means
	Stat 1	Stat 2	Stat 1	Stat 2	Stat 1	Stat 2	Stat 3
Z-scores	5.19	4.29	5.88	4.47	3.92	3.37	4.56

The results in table 4 show that there is a highly significant positive age effect. This would mean that age is positively associated with the hazard for extinction. At any fixed time, older species are more likely to go extinct than younger species. This is evidence against the Red Queen hypothesis and it suggests that it does not hold in this case.

For some of our statistics, Statistic J has an easy interpretation because the interpretation is closely related to the magnitude of the age effect. Statistic 1 is the difference between the number of older and younger species that go extinct which amounts to be 71 and 85 in grouping schemes 1 and 2 respectively. It directly answers the question ‘Does the older (younger) species in the pair go extinct at a statistically significant larger number of times than the younger (older) species in the pair?’ This means that in grouping scheme 2 with euclidean distance, Statistic 1 shows that there are 85 more times that the older species in the pair dies than when the younger species in the pair dies. This is equivalent to saying there were 41% (Table 5) more older deaths than younger deaths. Let m be the total number of times a species goes extinct in all pairs. If we divide Statistic 1 by m then another way to interpret Statistic 1 is as the difference in the proportion of the number of times the younger species goes extinct in a pair and the proportion of the number of times that the older species goes extinct in the pair (as seen in Table 5). Statistic 2 is the sum of the age differences in all the pairs of species in which one species goes extinct. If we divide Statistic 2 by m, then another interpretation of this statistic is the mean age difference between the species that goes extinct and the species that it is paired with. The mean age difference in the pairs of species that go extinct in grouping scheme 2 is 2.9 myr (Table 5). Statistic 3 is the deviation of the age of the species that goes extinct from the mean age of the group to which the species belongs. Similarly, if we divide Statistic 3 by the number of species that go extinct in each of these groups then the interpretation of this statistic is the average deviation of the age of the species that goes extinct from the mean age of the group to which it belongs. Statistic 3 now tells us that the species that goes extinct in their group is on average a duration that is 0.11 myr higher than their mean group duration (Table 5).

Table 5.

Statistic J scaled by the number of deaths for the tests performed on the Foraminifera database

	Group Scheme 1		Group Scheme 2 (Euc)		Random		K-means
Test Statistics	Stat 1	Stat 2	Stat 1	Stat 2	Stat 1	Stat 2	Stat 3
J/m	0.38	2.21	0.41	2.90	0.28	1.93	0.11
Extinctions	187		209		190	194	221

In grouping scheme 1 and grouping scheme 2 if there are an odd number of species at-risk then one of the species do not get paired. If the unpaired species is the species that goes extinct then their extinction is not counted and the test statistic is not incremented. In the grouping scheme that uses k-means clustering, if the species that goes extinct is not grouped with any of the other species in the group then similarly the test statistic is not incremented by this extinction. In Table 5 the number of extinctions that were used to increment the test statistic in each of these grouping schemes is displayed.

Another area of interest is the quality of matching in the grouping schemes. To access this the sum of the squared distances between the covariate vectors of species mean vector of covariates in each group at each risk time was computed. The distances were computed using Euclidean distance. Grouping scheme 1, grouping scheme 2, random pairing, and K-means clustering each had a total sum of squares across all risk groups of 6,465.37, 9,202.46, 36,974,384, and 5,539.46 respectively. This shows that K-means clustering has minimum total sum of squared distances in comparison to the other grouping methods that we used. The K-means clustering method and the grouping scheme 1 used in Table 4 both use Euclidean distance as the distance measure in their grouping algorithms. Therefore we expect both of those methods to have a smaller sum of squared distances than grouping scheme 2 when using Euclidean distance as the distance measure. When using the distance measure defined in Grouping scheme 2 (Section 2.1) to compute the sum of squared distances within each group we found the sum of squares to be 9.37E+29, 261,784.07, 3.94E+33, and 11,376.94 for Grouping scheme 1, Grouping scheme 2, random pairing, and K-means clustering, respectively. Though the K-means clustering method did not use this distance measure to form the clusters it again shows to have the minimum sum of squares. This suggests that the K-means clustering method performs the other methods in providing a grouping methods in which species are well matched on the covariates. Also noted is that the sum of squares in Grouping scheme 2 is much smaller than that of Grouping scheme 1. This is also expected since the grouping scheme 1 used a different distance measure to form the pairs(groups), namely Euclidean distance.

5. Discussion

In Darwin’s theory of evolution by natural selection he proposed that organisms that are the most fit in their environment will have the greatest chance for survival and reproduction [18]. The Red Queen hypothesis states that within a homogeneous taxonomic group the probability of extinction is independent of the taxon age. Under the Red Queen hypothesis, when taxa compete with each other for survival and a (taxon) species becomes well adapted (or the most adapted) to the environment, that taxon will have to continuously increase their fitness because the environment is constantly changing. As a result of this changing environment, all of the species are equally likely to go extinct at any fixed time, regardless of their age. [22]

An interpretation of our results is that the positive age-effects could be a result of the small number of short range species (species < 4 myr) in the dataset. There were some time periods in the datasets where there were no short range species. This was also seen by Doran et al. [5]. This could could have resulted from limited resolution, i.e. the species could have been in existence but at same time absent from the fossil record. Shorter range species are less likely to appear in the fossil record than longer ranged species because when speciation occurs the size of the population may start out small then increase over time. Another reason for the small number of short range species could be that research on speciation occurrences has been highly concentrated on a small subset of intervals of geologic time.

The shortage of short range species in our data set is an issue unrelated to the Red Queen hypothesis. To handle this we will remove short range species from our analysis in way that will not bias our result and then try to test for an age effect. Doran et al. [5] performed a similar procedure using the Cox model. Let’s consider changing our definition of when a species becomes at-risk from $Y_i\left(t\right)=I_{\{L_i<t\le R_i}\}$ to $Y_i^k\left(t\right)=I_{\{t-L_i>k\}\cap \{t\le R_i}\}$. This new definition will now allow for us to specify an age (duration) k that a species will reach before it becomes at-risk. If a species goes extinct in shorter than k myr after it originates then their extinction will not be accounted for in our testing procedure. Our test statistic will not be incremented and that species will not be included in our grouping scheme. Looking at our most powerful statistics, Statistic 2 grouping scheme 2 (Euclidean distance) and Statistic 3 both with no weights, in Table 6 we see that once we consider species at risk only if they are greater than 4 myr, the age effect is no longer statistically significant. This would imply that there is not a statistically significant age-effect on extinction (or age-dependent extinction) for species with durations greater than 4 myr.

Table 6.

Z-scores for the tests performed on the Foraminifera database when imposing a threshold duration for the entering risk set. There were no weight functions used in this table.

At-Risk age (in myr)	Grouping Scheme 2 (Euc) Statistic 2	K-means Grouping Statistic 3
>1	3.67	3.01
>2	2.80	2.68
>3	2.09	2.24
>4	1.19	1.50

One of the issues that arise from the results at the end of Section 4 is the challenge of comparing groupings that are formed using different distance measures. Grouping Scheme 1 and 2 both use different distance measures when forming the groups but the method of forming the groups is actually the same. This poses a problem when trying to use a summary measure, such as the sum of squared distances, to assess the quality of the grouping. For example, the sum of squared deviations is a function of the distance measure therefore when using this summary statistic will tend to favour the method which uses that distance measure. Rosenbaum [20] refers to the method of pairing that was introduced in Section 2.1 as ‘Greedy Matching’ and suggests that it is not necessarily ‘optimal’. That remains true in our case as well since K-means clustering provides groups with a lower sum of squares than our grouping schemes.

In this paper we have attempted to develop a statistical method for testing the Red Queen hypothesis. We translated this evolutionary theory problem into a survival analysis problem where we tested the Red Queen hypothesis by testing for a covariate effect of age on the hazard for extinction within a homogeneous taxonomic group. This was done by providing a method of grouping species on other covariates that effect the hazard for extinction and a statistical testing procedure to test H₀ within the different groups. A proof of the null distribution for one of the test statistics is also provided. Simulation studies under variations of the Cox model were conducted to evaluate the power of the different test statistics. A hypothesis test was performed on Foram data using the most powerful test statistics. The results indicate a rejection of the Red Queen hypothesis.

An area of future work that could be considered is to look at the alternative interpretation of the Red Queen hypothesis. This interpretation of the Red Queen hypothesis looks at the speciation rate as opposed to the extinction rate. In this approach to the hypothesis is the speciation occurs at a constant rate. Some of the recent work in this area include Venditti, Meade, and Pagel [23] and Benton [1]. In Ezard, Aze, Pearson, and Purvis [8], the Red Queen hypothesis (where evolution is considered to be driven by (biotic) internal factors such as morphology) was contrasted with the Court Jester model (in which evolution was considered to be driven by abiotic factors such as mass extinction events and climate change).There two sets of models used to compare these different approaches to evolution: a model with discrete time and a model with continuous time. In the discrete time model clade growth ($\ln (\frac{N_{t+1}}{N_t}$, where N_t was the number of species at time t) was regressed on climate, species diversity and species ecology using a generalized additive model. In the continuous time models the growth rate was estimated using an exponential growth rate was estimated using a ODE developed by Lotka and De Roos. Included in the models were terms for the hazard function for extinction and the hazard model for speciation. Both hazard models used Weibull lifetimes. This study also showed age-dependent extinction in which increases in age were associated with an increase in extinction risk.