Transactional Database Transformation and Its Application in Prioritizing Human Disease Genes

Abstract

Binary (0,1) matrices, commonly known as transactional databases, can represent many application data, including gene-phenotype data where “1” represents a confirmed gene-phenotype relation and “0” represents an unknown relation. It is natural to ask what information is hidden behind these “0”s and “1”s. Unfortunately, recent matrix completion methods, though very effective in many cases, are less likely to infer something interesting from these (0,1)-matrices. To answer this challenge, we propose IndEvi, a very succinct and effective algorithm to perform independent-evidence-based transactional database transformation. Each entry of a (0,1)-matrix is evaluated by “independent evidence” (maximal supporting patterns) extracted from the whole matrix for this entry. The value of an entry, regardless of its value as 0 or 1, has completely no effect for its independent evidence. The experiment on a gene-phenotype database shows that our method is highly promising in ranking candidate genes and predicting unknown disease genes.

1 Introduction

A key task in biomedicine in postgenomic era is to understand the gene-phenotype relationships. In humans, such knowledge leads to the discovery of genes causing or relating to (disease) phenotypes. The gene-phenotype relationships can be exactly described by a binary matrix if we associate each phenotype with confirmed causative genes. However, since our knowledge on causative disease genes are still limited, this binary matrix is far from complete. Recovering a matrix with partly known entries is a general problem with growing interest. Recent advances in matrix completion techniques [10], [31], [15], [5], [27] provide very good solutions to many applications. Thus, motivated by discovering unknown gene-phenotype relationships, a natural question appears here: is it possible to use current matrix completion methods to recover such a binary matrix describing gene-phenotype relationships? Unfortunately, we find that the answer is no. The reason will be explained immediately in the following section.

Nevertheless, the efforts to discover unknown gene-phenotype relationships never stop. In addition to the traditional methods of genetic discovery, such as linkage analysis and positional cloning (See [8] for a review), recent advances in computational methods provide researchers many choices in testing gene-phenotype relationships through large number of genes, or even the entire genome. These methods often prioritize genes for a given phenotype, and the performance are often measured by fold enrichment, which measures how well the known causative genes are ranked among all candidate genes for a given phenotype. However, there are two main weaknesses in current methods. First, it is hard to make the fold-enrichment evaluation both unbiased and complete. Second, it is difficult to justify the resulting rank of each individual candidate gene (imagine a clinician asks why one gene is ranked among the top genes, or why one gene is ranked higher than another gene).

Other than modeling gene-phenotype relationships, these binary matrices exist in many biomedicine applications. They are also well known as transactional databases [25] in the data mining area. The term “transactional” implies that the database is composed of many transactions, e.g., a store record showing what items are included in each transaction. It is easy to see that a transactional database can be presented by a (0,1)-matrix. In this work, we propose a novel transactional-database-transformation problem that always leads to unbiased solutions. Our method not only produces results with a high fold enrichment that is both unbiased and complete, but also provides a unique feature to support our rank of every candidate gene for a given phenotype by clear evidence, whose details can be easily reconstructed as needed. The experiment on a typical gene-phenotype database shows that our method is highly promising in ranking candidate genes and predicting unknown disease genes.

1.1 Related Work

Matrix Completion

The problem of matrix completion is of general interest: given a sampling of m entries of a matrix M, how to recover the complete matrix? Several methods [10], [31], [15], [5], [27] have been proposed recently to recover a low-rank matrix with some samplings. It is even proven in [11] that the recovery is most likely to be successful when the number of samplings is larger than a threshold, which is a function of the matrix size and its rank. However, this sample model does not apply to transactional databases such as gene-phenotype data, because “1” is the only nonzero value. Each entry is either 0, which means unsampled, or 1, which means sampled and the result is positive. When there are enough sampled entries being 1 only, there is little reason to believe an unsampled entry to be a value other than 1 (or not close to 1 when floating-point operation applies). We tried Opt-Space [31] on gene-phenotype data and the results (every entry is getting close to 1 after some iterations) confirmed our analysis.

Readers may wonder, what if gene-phenotype data are not simply a transactional database? For example, if it contains negative entries that completely exclude some gene-phenotype associations. In this case, it is still not clear whether matrix completion methods will work. As suggested in [11], the possibility to recover a matrix depends on the number of samplings, the matrix size, and its rank. Low-rank matrices are considered to have high redundancy in their entries and thus it is possible to recover them with only a small percent of samplings. Here, we only know a very small percent of gene-phenotype associations and there is no clear evidence that actual gene-phenotype relationships can make up a matrix with a correspondingly low enough rank.

Prioritizing candidate genes by computational methods

Recent advances in computational biology made it possible to study the gene-phenotype relationships between many genes and phenotypes quickly [20], [46], [55], [57], [2], [3], [19], [21], [33], [58], [37], [29], [53], [13], [12]. A couple of the latest work (e.g., [21], [58], [37]) can be used to study such relationships over the whole genome. A number of recent work (e.g., [3], [19], [21], [33], [58], [37], [12]) share some common workflow. First, they use text mining to establish similarities among phenotypes. Then, they use various Protein-Protein Interaction databases to study the relationships among genes. Finally, various scoring methods were developed to prioritizing genes. After these somewhat complicated steps, one may wonder that how reliable the final results are. Most of the available work relies on fold enrichment as an objective measurement of the effectiveness of their methods.

The fold enrichment is a measurement of how good the tested known genes are ranked with respect to their associated phenotypes. The detailed computational method and the test selection make the fold-enrichment value somehow tricky, and it should be interpreted with the complete details of how it is obtained. Without those details, it could be hard to tell whether there is any systematic bias toward known gene-phenotype relations. To make fold enrichment unbiased, the information of a known gene phenotype is removed in [21], [58], and [37] before testing its rank. This definitely makes the result more sound, but it greatly increases the testing time. Thus, the fold enrichment in [21], [58], and [37] is based on a small number of tested cases only, making it hard to perform a complete unbiased evaluation of the method and the results.

In addition, since there is no reason to believe unknown gene-phenotype relations are not important, a highest fold enrichment does not necessarily imply that the corresponding results are the best for predicting unknown disease genes. Thus, other than the fold enrichment, evidence that supports each individual rank will be very helpful but not always available.

Mining bicliques for biomarkers

In most graphs that model real life, dense subgraphs are often indication of important patterns. Various algorithms for finding dense components, such as cliques and quasi cliques [1], [36], [50], [51] from graphs, have been developed (See [34] for a survey). Since bipartite graphs are essentially (0,1)-matrices or transactional databases, there are quite a few methods for mining them in the data mining community. Compared to traditional biclustering or coclustering [26], [41], methods powered by frequent item set mining techniques [25] take into account the exponential number of patterns, and thus are possible to produce results much closer to optimal for many problems. Bicliques discovered by these methods often have other names, such as tiles [22], [23], hyperrectangles [59], and blocks [28], but essentially they are considered to be representative patterns of the transactional database. Clique or biclique patterns are very likely to be associated with important patterns in real applications. For example, in [47] and [44], authors mine clique patterns for candidate biomarkers. In [32], authors find biclusters of drug-gene associations. In [28], we also show that some block patterns are candidate biomarkers for breast cancer. These patterns in the form of dense subgraph components hint us to find evidence to support a gene-phenotype relation from its covering patterns.

1.2 Our Contributions

Motivated by the related work as discussed above, in this work we aim at proposing a succinct computational method to unbiasedly evaluate every entry in a (0,1)-matrix. Our main contributions are

• We propose a novel concept to transform transactional databases into matrices of features. It can be regarded as an extension of the matrix completion concept to (0,1)-matrices.

• Each original entry of the (0,1)-matrix, regardless of its value as 0 or 1, has no effect on its independent evidence. This makes our final results unbiased. In addition, it is easy to obtain a complete and unbiased fold-enrichment evaluation for human gene-phenotype relationships, without the need to do any extra leave-one-out validation (i.e., test a known gene phenotype after removing such knowledge, see [58]).

• Unlike previous methods that simply give a score or rank to a candidate gene, we can support our evaluation for each individual gene phenotype (an entry in the (0,1)-matrix) with clear evidence, whose details can be reconstructed as needed.

• As our method uses evidence hidden in the given data, it is a general framework to evaluate any transactional databases, including gene-phenotype data. Our algorithms are succinct and easy to implement or incorporate into other methods.

• Our problem formulation leads to $\mid \mathcal{T}\mid \ast \mid \mathcal{I}\mid$ NP-hard problems, where $\mid \mathcal{T}\mid$ is the number of transactions in the transactional database (i.e., the number of rows in the (0,1)-matrix), and $\mid \mathcal{I}\mid$ is the number of items in the transactional database (i.e., the number of columns in the (0,1)-matrix). However, we propose a very succinct and efficient solution for our problem.

• The study on a very sparse gene-phenotype data shows the effectiveness of our method. Using only a very sparse gene-to-phenotype data itself, our method achieves a very high fold enrichment that is both unbiased and complete. Detailed case studies also show that our method is highly promising in ranking candidate genes and predicting unknown disease genes.

2 Problem Formulation

Recently, by formulating the disease and gene relationships as a bipartite graph, disease networks and the corresponding gene networks have been derived [24], [38], [6]. This also implies that by matching a group of related disease phenotypes with a group of corresponding genes, we can predict previously unknown gene and disease phenotype relationships, and generate new hypotheses for experimental and clinical study. Our problem formulation is motivated by this notion.

Let M be a transactional database in the form of (0,1)-matrix; let $\mathcal{T}$ be the complete set of transactions (rows), and $\mathcal{I}$ be the complete set of items (columns). For simplicity, we assume transactions are numbered continuously from 1, and the same for items. Let M(i, j) denote the value of entry (either 0 or 1) at row i and column j of M, where $1\le i\le \mid \mathcal{T}\mid$ and $1\le j\le \mid \mathcal{I}\mid$. A (0,1)-matrix is equivalent to a bipartite graph, if we model the set of rows as a set of vertices, and the set of columns as another set of vertices, with one entries corresponding to edges. In the following, the term (0,1)-matrix (or matrix for short) implies its corresponding bipartite graph.

Let P = T × I = {(x, y) : x ∈ T, y ∈ I} be a pattern of M where $T\subseteq \mathcal{T}$ and $I\subseteq \mathcal{I}$. P is essentially a Cartesian product between a subset of rows and a subset of columns, and equivalent to a submatrix of M. Note that a biclique (i.e., a submatrix of all 1s) is a pattern but the reverse is not necessarily true. An entry (i, j) is covered by P if and only if (i, j) ∈ P. We say a pattern P is a supporting pattern for entry (i, j) if and only if P covers (i, j) and, M(x, y) = 1 for any entry (x, y) ∈ P\{(i, j)}. Note that here the value M(i, j) itself is NOT considered when defining a supporting pattern for (i, j).

To avoid redundant supporting patterns, we only consider supporting patterns that are maximal. A supporting pattern P for an entry (i, j) is maximal if and only if there does not exist another supporting pattern P′ for (i, j) such that $P\subset P^{\prime }$.

Let S(i, j) be the set of all maximal supporting patterns for the entry (i, j). We consider S(i, j) to be the independent evidence to support the hypothesis that entry (i, j) is 1. Since S(i, j) may contain a good number of supporting patterns, we will extract the most important feature from it. Let $\mathcal{F}$ be the function for feature extraction. Then, $\mathcal{F}(i,j)$ is the feature extracted from S(i, j).

Thus, one very general problem is: How to efficiently transform M into $\mathcal{F}$, such that $\mathcal{F}$ can unbiasedly predict the unknown transaction-item relationships?

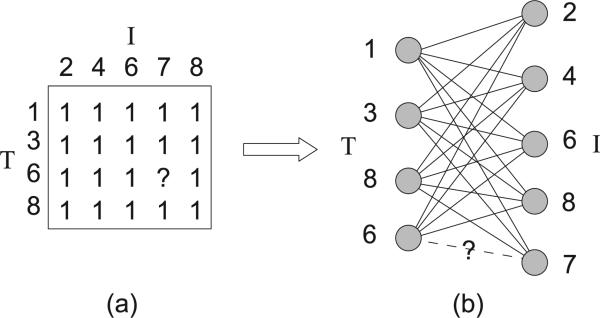
Fig. 1a is an example of a supporting pattern for an entry (6, 7). Fig. 1b is the graph representation of the supporting pattern.

Fig. 1.

(a) A supporting pattern for (6; 7). (b) The visualization of this supporting pattern by a bipartite graph.

As suggested in [24], [38], and [6], if a set A of genes causing a set B of diseases also cause disease k, and if there appears another gene causing the set B of diseases, it is more or less reasonable to conjecture this gene can also cause disease k. Such inference is also the basis for various associate rule mining applications [25]. The strength of the inference is proportional to the size of A and the size of B. Thus, in this work, we simply define the $\mathcal{F}(i,j)$ to be

$$\mathcal{F}(i,j)=\underset{T\times I\in S(i,j)}{\text{max}}(\mid T\mid -1)\ast (\mid I\mid -1),$$

and our specific problem in this paper is: How to efficiently transform M into $\mathcal{F}$ defined above, such that $\mathcal{F}$ can unbiasedly predict the unknown gene-phenotype relationships?

In the next section, we will primarily focus on answering the above specific question. We will see that $\mathcal{F}(i,j)$ is equal to the area of a maximum edge biclique of a specific submatrix corresponding to entry (i, j). A maximum edge biclique in a bipartite graph is often defined as a maximal biclique with the largest number of edges. There could be more than one maximum edge biclique in a bipartite graph. A maximal biclique is commonly known as a biclique which is not a subgraph of any other biclique. For readers’ convenience, we summarize major notations and definitions in Table 1.

TABLE 1.

Summary of Notations and Definitions

Notation/Name	Defined in	Definition
M	Section 2	transactional database in the form of (0,1)-matrix
$\mathcal{T}$	Section 2	complete set of transactions (rows) of M
$\mathcal{I}$	Section 2	complete set of items (columns) of M
M(i, j)	Section 2	value of entry (either 0 or 1) at row i and column j of M
pattern (Cartesian product)	Section 2	P = T × I = {(x, y) : x ∈ T, y ∈ I} where $T\subseteq \mathcal{T}$ and $I\subseteq \mathcal{I}$
supporting pattern P for entry (i, j)	Section 2	Pattern P covers (i, j) and, M(x, y) = 1 for any entry (x, y) ∈ P\{(i, j)}
maximal supporting pattern P for entry (i, j)	Section 2	There does not exist another supporting pattern P′ for (i, j) such that $P\subset P^{\prime }$
S(i, j) (independent evidence for hypothesis M(i, j) == 1)	Section 2	the set of all maximal supporting patterns for entry (i, j)
$\mathcal{F}(i,j)$ (feature extracted from S(i, j))	Section 2	maxT × I ∈ S(i,j)(|T| – 1) * (|I| – 1)
M[X; Y] (submatrix of M)	Section 3.1	a matrix formed by selecting rows in X and columns in Y from M, where $X\subseteq \mathcal{T}$ and $Y\subseteq \mathcal{I}$
supporting biclique for entry (i, j)	Section 3.1	biclique in M[X;Y] where $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\}$, $Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$.
maximal supporting biclique for entry (i, j)	Section 3.1	maximal biclique in M[X;Y] where $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\}$, $Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$.
maximum supporting biclique for entry (i, j)	Section 3.1	maximum edge biclique in M[X;Y] where $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\}$, $Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$.

3 IndEvi and IndEviRe Algorithms

In this section, we mainly focus on solving the specific problem proposed in Section 2. First, we show how to find independent evidence S(i, j) and calculate $\mathcal{F}(i,j)$ for one entry (i, j) in the (0,1)-Matrix. Then, we propose an efficient algorithm IndEvi to calculate $\mathcal{F}(i,j)$ for all entries in the (0,1)-Matrix. Since IndEvi calculates $\mathcal{F}(i,j)$ for all entries without building S(i, j) for all entries, we will discuss how to efficiently reconstruct S(i, j), the details of the independent evidence, either completely or partly, for a desired entry (i, j).

3.1 Find Independent Evidence S(i, j) and Calculate $\mathcal{F}(i,j)$ for One Entry

S(i, j) is defined in Section 2 as the set of all maximal supporting patterns for the entry (i, j). In the following, we will show that S(i, j) has one-to-one correspondence with the set of maximal bicliques in a submatrix of M. Let M[X; Y], where $X\subseteq \mathcal{T}$ and $Y\subseteq \mathcal{I}$, be a matrix formed by selecting rows in X and columns in Y from M. Then, we have the following lemma:

Lemma 1. Given an entry (i, j), let $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\},Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$. Then, S(i, j) has to one correspondence with (but not equal to) the set of maximal bicliques in M[X; Y].

Proof. To proof this lemma, we will show that 1) “⇒” A pattern T × I ∈ S(i, j) is corresponding to a maximal biclique (T{i}) × (I{j}) of M[X; Y]. 2) “⇐” A maximal biclique T × I of M[X; Y] is corresponding to a pattern $(T\cup \left\{i\right\})\times (I\cup \left\{j\right\})\in S(i,j)$.

Proof of 1. We only need to show (T\{i}) × (I\{j}) is a maximal biclique M[X; Y]. First, according to the definition of S(i, j) and M[X; Y], it is easy to see that $(T\backslash \left\{i\right\})\subseteq X$ and $(I\backslash \left\{j\right\})\subseteq Y$. Thus, (T\{i}) × (I\{j}) is a biclique of M[X; Y]. If it is not maximal, then there must exist another biclique T′ × I′ of M[X; Y], such that $(T\backslash \left\{i\right\})\times (I\backslash \left\{j\right\})\subset T^{\prime }\times I^{\prime }$. Then, we can construct a pattern $(T^{\prime }\cup \left\{i\right\})\times (I^{\prime }\cup \left\{j\right\})\supset (T\times I)$, which is a support pattern for (i, j). Thus, it is a contradiction to the fact that T × I is a maximal supporting pattern.

Proof of 2 is similar as proof of 1 and thus omitted.

Given Lemma 1, it is easy to see the following corollary holds.

Corollary 1. Given entry (i, j), $\mathcal{F}(i,j)$ is the area, i.e., the number of edges, of a maximum edge biclique of M[X; Y], where $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\},Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$.

From Lemma 1, one can see that the task of finding all maximal supporting patterns for entry (i, j) is equivalent to finding all maximal bicliques of M[X; Y] where $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\},Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$. To facilitate our discussion, in the following we call bicliques, maximal bicliques, and maximum edge bicliques of M[X; Y] as supporting bicliques, maximal supporting bicliques, and maximum supporting bicliques, respectively, for (i, j). For example, in Fig. 1, {1, 3, 6, 8} × {2, 4, 6, 7, 8} is a supporting pattern for (6, 7), while {1, 3, 8} × {2, 4, 6, 8} is a supporting biclique for (6, 7). In many places of the following, we will use maximal supporting bicliques instead of maximal supporting patterns since they have one-to-one correspondence as suggested by Lemma 1.

Unfortunately, the problem of listing all maximal cliques (or just a maximum clique) for a graph is well known to be NP-hard [30]. For finding a maximum edge biclique for a bipartite graph, it is also proved to be NP-hard [45]. It is easy to see that listing all maximal bicliques (which include every maximum edge biclique) for a bipartite graph is NP-hard too.

Nevertheless, algorithms for frequent closed item set mining [25] provide practical solutions. It is not difficult to understand that a maximal biclique in a bipartite graph corresponds to a closed item set in the corresponding transactional database (See [35] for additional details). In [35], authors use frequent closed item set mining results for mining maximal biclique subgraphs. The main advantage of frequent closed item set mining is that it takes frequency (often called “support”) as a user-specified parameter. The lower the frequency, the closer the results to the exact solution. If there are $\mid \mathcal{T}\mid$ rows (i.e., transactions), the final results are exact if the frequency is set to be $1∕\mid \mathcal{T}\mid$ or lower. Thus, users can set up a frequency as lower as possible, with respect to the input data and the computational resource. To give some idea on how long it takes to list all maximal bicliques for a typical graph, we cite a result in [35]: it takes LCM [56], a state-of-art frequent item set mining algorithm, 126.294 hours to list all closed item sets for a transactional database with $\mid \mathcal{T}\mid =8,000$ and $\mid \mathcal{I}\mid =8,000$ (which is the adjacency matrix of a graph with 8,000 vertices and 319,959 edges). We will not go into detail of closed item set mining in this paper. Interested readers may refer to [25]. It is sufficient to know there are data mining algorithms that can list all maximal bicliques or close, for the following discussion.

The above discussion is for finding independent evidence S(i, j) and calculate $\mathcal{F}(i,j)$ for one entry only. It is not a good idea to directly extend the above method to calculate $\mathcal{F}(i,j)$ for all $\mid \mathcal{T}\mid \mid \mathcal{I}\mid$ entries. This will make the running time $\mid \mathcal{T}\mid \mid \mathcal{I}\mid$ times as long as the average running time for finding independent evidence for one entry under the same settings, making it impractical to get a nontrivial result in most cases. Thus, in the next section, we propose an efficient algorithm IndEvi to calculate $\mathcal{F}(i,j)$ for all entries. IndEvi also makes it possible to efficiently reconstruct S(i, j) for any desired entry (i, j).

3.2 Calculate $\mathcal{F}(i,j)$ for All Entries and Reconstruct Independent Evidence S(i, j) for Desired Entries

As indicated by Lemma 1, S(i, j), the independent evidence for one entry (i, j), is corresponding to the set of maximal bicliques of M[X; Y] where $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\},Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$. Since M[X; Y] is a submatrix of M, a maximal biclique of M[X; Y], is at least a biclique (although it may not be maximal) of M. It is easy to see that any biclique in a bipartite graph is covered by at least one maximal biclique in that graph. Hence, we conclude that any maximal biclique of M[X; Y] is covered by at least one maximal biclique of M. This observation clues us to find independent evidence for all entries by scanning all maximal bicliques of M.

To make our method easy to understand, we start with entries that are 0. Then, we consider entries that are 1. It is better to emphasize again that although we consider entry values here for algorithm design, the problem formulation has never been changed, and the value of any entry has completely no effect on its independent evidence. That is, by changing the value of an entry only, no matter from 1 to 0, or from 0 to 1, its independent evidence remains the same.

3.2.1 Entries of Value 0

It is easy to observe that for a maximal biclique C of M, its corresponding part in submatrix M[X; Y], if any, is a biclique. Formally, the following lemma holds.

Lemma 2. Given an entry (i, j), let $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\},Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$. Let C = T_C × I_C be a maximal biclique of M which contains S = T_S × I_S, a maximal supporting biclique for (i, j). Then, $C\cap (X\times Y)=(T_C\cap X)\times (I_C\cap Y)=T_S\times I_S=S$.

Proof. It is not difficult to verify that $C\cap (X\times Y)=(T_C\times I_C)\cap (X\times Y)=(T_C\cap X)\times (I_C\cap Y)$. In the following, we will prove that $(T_C\cap X)=T_S$ and $(I_C\cap Y)=I_S$.

Assume $(T_C\cap X)\ne T_S$. Then, at least one of the following cases must hold: 1) $\exists t\in T_C\cap X$ such that $t\notin T_S$, 2) $\exists t\in T_S$ such that $t\notin T_C\cap X$.

Case 1. Since t ∈ T_C where T_C × I_C is a maximal biclique, it is easy to see {t} × I_C is a biclique. Given $I_S\subseteq I_C$ and t ∈ X, we conclude that $(\left\{t\right\}\cup T_S)\times I_S$ is a biclique in M[X; Y], a contradiction to the fact that S = T_S × I_S is a maximal biclique in M[X; Y]. Hence, case 1 cannot hold.

Case 2. Since T_S × I_S is a maximal clique in M[X; Y], we conclude $T_S\subseteq X$. Given t ∈ T_S and $T_S\subseteq X$, we conclude that $t\notin T_C\cap X$ implies $t\notin T_C$, contradiction to the fact that $T_S\subseteq T_C$. Hence, case 2 cannot hold.

Thus, we proved by contradiction that $(T_C\cap X)=T_S$. In the similar way, we can also prove that $(I_C\cap Y)=I_S$.

The purpose of introducing Lemma 2 will be clear in the following. It leads to two corollaries, which make an efficient algorithm possible.

Corollary 2. Given an entry (i, j) that M(i, j) = 0, let $X^{\prime }=\{x:x\in \mathcal{T},M(x,j)=1\},Y^{\prime }=\{y:y\in \mathcal{I},M(i,y)=1\}$. Let C = T_C × I_C be a maximal biclique of M which contains S= T_S × I_S, a maximal supporting biclique for (i, j). Then, $(T_C\cap X^{\prime })\times (I_C\cap Y^{\prime })=T_S\times I_S=S$.

Proof. Since M(i, j) = 0, we conclude that $i\notin X^{\prime }$ and $j\notin Y^{\prime }$.

Thus, X′ = X and Y′ = X, where $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\},Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$. According to Lemma 2, we conclude $(T_C\cap X^{\prime })\times (I_C\cap Y^{\prime })=T_S\times I_S$.

Note that in Corollary 2, X′ only depends on column j and Y′ only depends on row i. This observation suggests that given a maximal biclique T_C × I_C of M, we can first get $T_C\cap X^{\prime }$ for each column and $I_C\cap Y^{\prime }$ for each row. Then, a $\mathcal{F}(i,j)$ for every zero entry can be easily calculated.

3.2.2 Entries of Value 1

Interestingly, we find it is not necessary to treat 1 and 0 entries completely different. The following corollary suggests that entries of value 1 can also be handled similarly as entries of value 0.

Corollary 3. Given an entry (i, j) that M(i, j) = 1, let $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\},Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\},X^{\prime }=\{x:x\in \mathcal{T},M(x,j)=1\},Y^{\prime }=\{y:y\in \mathcal{I},M(i,y)=1\}$.

Let C = T_C × I_C be a maximal biclique of M which contains S = T_S × I_S, a maximal supporting biclique for (i, j). Then, $((T_C\backslash \left\{i\right\})\cap X^{\prime })\times ((I_C\backslash \left\{j\right\})\cap Y^{\prime })=C\cap (X\times Y)=T_S\times I_S=S$.

Proof. Since M(i, j) = 1, we have i ∈ X′ and j ∈ Y′. Thus, X = X′\{i} and Y = Y′\{j}. Further, we have $T_C\cap X=T_C\cap (X^{\prime }\backslash \left\{i\right\})=(T_C\backslash \left\{i\right\})\cap X^{\prime }$, and $I_C\cap Y=I_C\cap (Y^{\prime }\backslash \left\{j\right\})=(I_C\backslash \left\{j\right\})\cap Y^{\prime }$. According to Lemma 2, we conclude $((T_C\backslash \left\{i\right\})\cap X^{\prime })\times ((I_C\backslash \left\{j\right\})\cap Y^{\prime })=C\cap (X\times Y)=T_S\times I_S=S$.

3.2.3 Final Algorithms

Hinted by Corollaries 2 and 3 (both can find a maximal supporting biclique S from C by set operations on X′ and Y′, instead of X and Y), we propose Algorithm 1, IndEvi for Independent-Evidence-based transactional database transformation. The input $\mathcal{C}$ for IndEvi is a set of maximal bicliques.

Algorithm 1.

$\mathrm{INDEVI}(M,\mathcal{C})$

1:	for each $C=T_C\times I_C\in \mathcal{C}$ do
2:	$\{C_{\mathcal{T}},C_{\mathcal{I}}\}=\text{Preprocess}(M,C)$;
3:	for each entry (i, j) of M do
4:	$loca{l}_{\mathcal{T}}=C_{\mathcal{T}}\left(i\right)$;
5:	$loca{l}_{\mathcal{I}}=C_{\mathcal{I}}\left(j\right)$;
6:	if M(i, j) = 1 then
7:	if i ∈ TC then $loca{l}_{\mathcal{I}}=loca{l}_{\mathcal{I}}-1$; end if {Note the update is on $loca{l}_{\mathcal{I}}$, not $loca{l}_{\mathcal{T}}$, if i ∈ TC}
8:	if j ∈ IC then $loca{l}_{\mathcal{T}}=loca{l}_{\mathcal{T}}-1$; end if {Note the update is on $loca{l}_{\mathcal{T}}$, not $loca{l}_{\mathcal{I}}$, if j ∈ IC}
9:	end if
10:	${\mathcal{F}}_C(i,j)=loca{l}_{\mathcal{T}}\ast loca{l}_{\mathcal{I}}$
11:	if ${\mathcal{F}}_C(i,j)>0$ then
12:	$\mathcal{G}(i,j)=\mathcal{G}(i,j)+1$;{A counter of maximal bicliques of M that contain supporting bicliques for (i, j). It is an auxiliary information for tie breaking.}
13:	if $\mathcal{F}(i,j)<{\mathcal{F}}_C(i,j)$ then
14:	$\mathcal{F}(i,j)={\mathcal{F}}_C(i,j)$;
15:	$c(i,j)=\text{index}\text{of}C\text{in}\mathcal{C}$;{An index for reconstructing evidence of maximum supporting biclique.}
16:	end if
17:	end if
18:	end for
19:	end for
20:	return $\mathcal{F}$, $\mathcal{G}$, c;
Procedure Preprocess(M, C)
1:	for all $i\in \mathcal{T}$ do
2:	$C_{\mathcal{T}}\left(i\right)=\mid I_C\cap Y^{\prime }\mid$ where $Y^{\prime }=\{y:y\in \mathcal{I},M(i,y)=1\}$;
3:	end for
4:	for each $j\in \mathcal{I}$ do
5:	$C_{\mathcal{I}}\left(j\right)=\mid T_C\cap X^{\prime }\mid$ where $X^{\prime }=\{x:x\in \mathcal{T},M(x,j)=1\}$;
6:	end for
7:	return $C_{\mathcal{T}}$, $C_{\mathcal{I}}$

In Algorithm 1, we completely eliminate the huge burden of calculating $\mathcal{F}(i,j)$ for every entry as discussed in Section 3.1. Rather, it is done by two fast batch processes for every $C\in \mathcal{C}$.

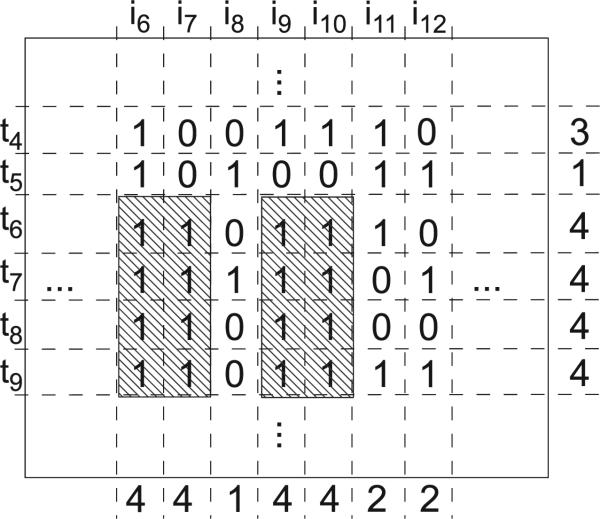
In the first step, we preprocess a maximal biclique C into $C_{\mathcal{T}}$, a list of numbers corresponding to rows (shown on Fig. 2 as the rightmost list of numbers), and $C_{\mathcal{I}}$, a list of numbers corresponding to columns (shown on Fig. 2 as the lowermost list of numbers). In this step, we only need to project the biclique C to every row and every column of M, rather than individual entries.

Fig. 2.

Numbers on the left-most column are transaction ids, and number on the upper most row are the item ids. The shaded part is a maximal biclique of M.

Then, in the second step (line 3-18), each entry can get a ${\mathcal{F}}_C(i,j)$ by using the previously computed $C_{\mathcal{T}}$ and $C_{\mathcal{I}}$ value, with additional consideration of itself (i.e., 0 or 1) and whether it is covered by the maximal biclique C.

Fig. 2 is an example to understand the algorithm. The shaded part is a maximal biclique T_C × I_C of M. Each number on the lower most row is $\mid T_C\cap X^{\prime }\mid$ where $X^{\prime }=\{x:x\in \mathcal{T},M(x,j)=1\}$. Each number on the right most column is $\mid I_C\cap Y^{\prime }\mid$ where $Y^{\prime }=\{y:y\in \mathcal{I},M(i,y)=1\}$. Then, let us some representative entries: M(t₄, i₁₂) = 0, ${\mathcal{F}}_C(t_4,i_{12})=3\ast 2=6;M(t_5,i_{11})=1,{\mathcal{F}}_C(t_5,i_{11})=1\ast 2=2;M(t_7,i_{11})=0,{\mathcal{F}}_C(t_7,i_{11})=4\ast 2=8;M(t_5,i_6)=1,{\mathcal{F}}_C(t_5,i_6)=(1-1)\ast 4=0;M(t_8,i_9)=1,{\mathcal{F}}_C(t_8,i_9)=(4-1)\ast (4-1)=9$. Here, ${\mathcal{F}}_C(i,j)$ is the area (i.e., the number of edges) of a maximum edge biclique of $M[X\cap T_C,Y\cap I_C]$ where $X=\{x:x\in \mathcal{T}\backslash \left\{i\right\},M(x,j)=1\},Y=\{y:y\in \mathcal{I}\backslash \left\{j\right\},M(i,y)=1\}$. Given these examples, it shall be easy to figure out how IndEvi works.

Combining Corollaries 2, 3, and related analyses, we have the following theorem of unbiasedness for IndEvi.

Theorem 1. $\mathcal{F}$ returned by Algorithm 1, IndEvi, is an unbiased predicting function for every gene-phenotype pair (or transaction-item pair in general). That is, by changing a value of an entry (i, j), either from 1 to 0, or from 0 to 1, $\mathcal{F}(i,j)$ remains the same.

IndEvi also returns two other functions, $\mathcal{G}$ and c. $\mathcal{G}(i,j)$ is the number of maximal bicliques of M that contain supporting bicliques for (i, j). g is used as a heuristic information for tie breaking when prioritizing genes which have the same $\mathcal{F}$ value. Since it is generally impractical to have enough memory or disk space to store complete S(i, j) for all entries, we use c(i, j) to save the index of the maximal biclique of M that contains a maximum supporting biclique for (i, j). Function c can be used to reconstruct a maximum supporting biclique for any desired entry (i, j). The reconstruction follows the principles as suggested in Corollaries 2 and 3. Algorithm 2 is the pseudocode.

Algorithm 2.

$\mathrm{INDEVIRE}(M,\mathcal{C},c,(i,j))$

1:	Let C = TC × IC be the biclique in $\mathcal{C}$ indexed by c(i, j);
2:	Let $X^{\prime }=\{x:x\in \mathcal{T},M(x,j)=1\}$, $Y^{\prime }=\{y:y\in \mathcal{I},M(i,y)=1\}$;
3:	if M(i, j) = 0 then
4:	return $(T_C\cap X^{\prime })\times (I_C\cap Y^{\prime })$;
5:	else
6:	return $((T_C\backslash \left\{i\right\})\cap X^{\prime })\times ((I_C\backslash \left\{j\right\})\cap Y^{\prime })$;
7:	end if

In Algorithm 2, we only reconstruct a maximum supporting biclique for (i, j). However, with reasonably large storage space, it is still practically possible to quickly reconstruct all the details of the independence evidence, i.e., all maximal supporting bicliques, for (i, j) (thus, the complete S(i, j)). To realize this, we only need to let c(i, j) record the set of indices for all supporting bicliques, instead of just a maximum supporting biclique. When reconstructing, we also need to compare and eliminate supporting bicliques that are not maximal. Under limited storage settings, we may also choose to reconstruct partly the maximal supporting bicliques (e.g., the top 100 maximal supporting bicliques with largest areas). The implementation is not difficult by revising Algorithms 1 and 2.

4 Experimental and Case Study

There have been many efforts for archiving the gene-phenotype relationships such as the OMIM database [40], [4]. In this paper, we select the gene-to-phenotype data set¹ (“G2P” for short in the following) for our experimental study. Although G2P is small, containing $1,807(=\mid \mathcal{T}\mid )$ genes and $5,560(=\mid \mathcal{I}\mid )$ phenotypes, and 34,503 confirmed gene-to-phenotype relations (i.e., only 0.3434 percent entries are 1), it is derived from sources including OMIM and is well curated with strict criterion [48], [49].

For maximal biclique generation (closed item sets), we use MAFIA² [9], one of the popular publicly available tools for generating frequent closed item sets. For data set G2P, we set the frequency to be 0.05 percent, a value low enough to obtain a complete set of maximal bicliques. Our algorithms are implemented in C++, and tested on Linux with a 2.6 kernel.

We cross validate our gene ranks by web tool www.geneanswers.com³ (“GACOM” for short in the following), which is based on a newly developed disease ontology [17], [18].

4.1 Fold Enrichment

The details for calculating fold enrichment vary among literature. We feel it is necessary to make the rule unequivocal. By referring to some recent work [21], [58], [37], we use the following rule:

• Let E′ be a subset of E, the set of confirmed gene-phenotype relations. Let |E′|/|E| = x%. If for any element (i, j) ∈ E′, gene i is ranked among top y percent of the candidate genes (i.e, all the genes involved in ranking) for phenotype j, the fold enrichment of E′ over E is x/y.

• A gene is ranked in y percent of the candidate genes if and only if there are 100 – y)% candidate genes ranked lower.⁴

In papers that aim at providing unbiased fold enrichments [21], [58], [37], the set E refers to the sampled known gene-phenotype relations, rather than the complete set of all known gene-phenotype relations as we do in this work. To the best of our knowledge, there is no reported fold enrichment that satisfies both completeness and unbias as ours. Nevertheless, to facilitate comparison with others, we list our statistics as follows.

Given the closed item sets outputted by MAFIA, our IndEvi implementation finishes transforming the G2P data set within an hour, with less than 1 GB memory requirement, on an AMD Opteron 2.4 GHZ machine. For a phenotype, genes are ranked by $\mathcal{F}$ (high to low), with $\mathcal{G}$ (high to low) for tie breaking (recall $\mathcal{F}$ in Sections 2 and 3.1, and $\mathcal{G}$ in Section 3.2). After transformation of G2P by IndEvi, we obtain the following results: among all 34,503(=|E|) known gene-phenotype relations, 4,598(=|E′|) of them with gene ranked among the top 0.1107%(= y%) of the $1,807(=\mid \mathcal{T}\mid )$ candidate genes for it, achieving 120.4(=x/y = 13.3264/0.1107) fold enrichment. The number 120.4 itself is among the highest fold enrichment values [33], [21], [58], [37] to the best of our knowledge.

Nevertheless, as we mentioned before, the fold enrichment should be handled with care. If we simply comment out line 6-9 of IndEvi, then we can achieve a 270.4 fold enrichment. However, in this case it is not difficult to see that the transformation is biased toward the entries of value 1.

4.2 Rank Cutoff

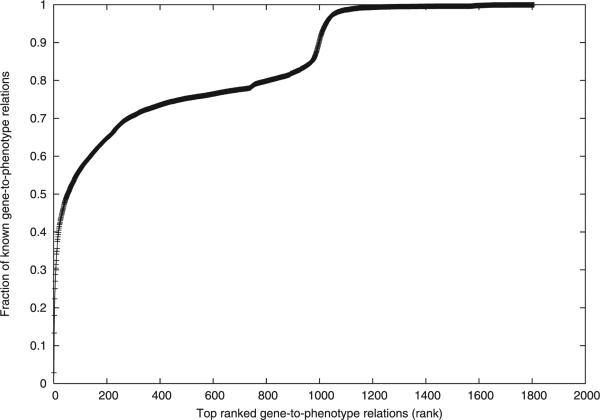
Although every gene has a rank with respect to a given phenotype, it remains a good question what percentage of top ranked gene-to-phenotype relations are most significant for prediction. To answer this question, we plot the fraction of known gene-to-phenotype relations over the top ranked gene-to-phenotype relations in Fig. 3, which shows the aggregated results over all 5,560 phenotypes.

Fig. 3.

The fraction of known gene-to-phenotype relations contained in the top-ranked gene-to-phenotype relations.

From Fig. 3, we can observe that at the beginning, the percentage of known gene-to-phenotype relations increases sharply when rank increases. However, the increase rate changes significantly twice: one is around rank 200-400, and the other is around rank 1,000. For the two rate changes, we found that more than 70 percent of known gene-to-phenotype relations are ranked within top 16 percent gene-to-phenotype relations, and more than 98 percent of known gene-to-phenotype relations are ranked within top 60 percent gene-to-phenotype relations.

This suggests that in most cases a known gene-to-phenotype relation will not get a very low rank. Thus, if we mark top ranked (e.g., top 15 percent) gene-to-phenotype relations as positive results, and bottom (e.g., bottom 15 percent) ranked as negative results, with others being neutral, then, known gene-to-phenotype relations will not be falsely tagged as negative in nearly all cases. Moreover, the rank around 200-400 provides a good cutoff for prediction. Biologists may primarily focus on the top 200 gene-to-phenotype relations on average for a given phenotype.

4.3 Case Study

In this section, we use three well-known syndromes, colon cancer, breast cancer, and osteoarthritis, to evaluate results generated by IndEvi on data set G2P.

4.3.1 Colon Cancer

For colon cancer, there are nine confirmed gene-phenotype relations in the data set G2P. The $\mathcal{F}$, $\mathcal{G}$, rank, and percentile of them are listed in Table 2. We can see most of them are ranked among the top 5 percent of the 1,807 genes.

TABLE 2.

Nine Confirmed Genes for Colon Cancer in G2P

Gene	$\mathrm{INDEVI}\text{-}\mathcal{F}$	$\mathrm{INDEVI}\text{-}\mathcal{G}$	rank	percentile
MLH1	22	1436	3	0.22%
MSH2	22	1436	3	0.22%
HRAS	19	4634	6	0.33%
RPS19	16	4509	11	0.60%
TP53	12	1443	43	2.37%
BMPR1A	11	1968	44	2.49%
SMAD4	11	1968	44	2.49%
CDKN2A	8	1425	794	43.94%
APC	8	1404	795	43.99%

Next, in Table 3 we list the top 10 ranked genes for colon cancer. We cross validate these 10 genes by GACOM, and three genes that are not known causative genes for colon cancer in G2P are confirmed by GACOM. For the remaining fours genes, we performed a literature search, and found documents supporting that they are directly related to colon cancer (PMS2 [54], MAP2K1 [43], [52], MAP2K2 [7], PTPN11 [42]). Interestingly, the somatic mutation of MAP2K2 in colon cancer is a very recent discovery [7].

TABLE 3.

Top Ten Ranked Genes for Colon Cancer

rank	Gene	$\mathrm{INDEVI}\text{-}\mathcal{F}$	$\mathrm{INDEVI}\text{-}\mathcal{G}$	percentile	in G2P	in GACOM
2	MSH6	24	107	0.11%	No	Yes
2	PMS2	24	107	0.11%	No	No
4	MLH1	22	1436	0.22%	Yes	Yes
4	MSH2	22	1436	0.22%	Yes	Yes
5	KRAS	20	4563	0.28%	No	Yes
6	HRAS	19	4634	0.33%	Yes	Yes
7	BRAF	19	4552	0.39%	No	Yes
8	MAP2K1	19	4519	0.50%	No	No
8	MAP2K2	19	4519	0.50%	No	No
10	PTPN11	18	4412	0.55%	No	No

4.3.2 Breast Cancer

Although there are many identified genes for breast cancer, the G2P data set contains only 19 confirmed genes (for details see Table 4; note BRCA1 is not even in $\mathcal{T}$, the gene set of G2P). Nearly half of them are ranked among the top 5 percent of the 1,807 genes. Again, we perform a cross validation of the top 10 genes (for details see Table 5) by GACOM. Two genes that are not known causative genes for colon cancer in G2P are confirmed by GACOM. For the other five unconfirmed genes, we found four of them relating to breast cancer in the literature. (BRAF [16], MAP2K1 [39], MAP2K2 [7], MED12 [No literature found], FBN1 [14]). This time, a confirmed gene KRAS in G2P does not appear in the GACOM for breast cancer, showing that GACOM may not be complete either.

TABLE 4.

Nineteen Confirmed Genes for Breast Cancer in G2P

Gene	$\mathrm{INDEVI}\text{-}\mathcal{F}$	$\mathrm{INDEVI}\text{-}\mathcal{G}$	rank	percentile
KRAS	69	13974	2	0.11%
FGFR2	54	13817	6	0.33%
TWIST1	32	10978	7	0.39%
PTEN	24	11241	11	0.61%
MLH1	22	6592	16	0.94%
MSH2	22	6592	16	0.94%
TP53	20	6711	69	3.87%
PIK3CA	20	6698	73	4.04%
SLC22A18	18	6671	744	41.17%
PARK2	18	6622	745	41.23%
STK11	18	5198	746	41.28%
CTNNB1	18	3442	747	41.34%
AKT1	18	3428	748	41.39%
RAD54L	18	3415	749	41.62%
PPM1D	18	3415	749	41.62%
RB1CC1	18	3415	749	41.62%
BRIP1	18	3415	749	41.62%
CDKN2A	18	3221	749	41.67%
TIMP2	18	3195	749	41.73%

TABLE 5.

Top Ten Ranked Genes for Breast Cancer

rank	Gene	$\mathrm{INDEVI}\text{-}\mathcal{F}$	$\mathrm{INDEVI}\text{-}\mathcal{G}$	percentile	in G2P	in GACOM
1	BRAF	70	14045	0.06%	No	No
2	KRAS	69	13974	0.11%	Yes	No
4	MAP2K1	67	13727	0.22%	No	No
4	MAP2K2	67	13727	0.22%	No	No
5	FGFR1	55	13393	0.28%	No	Yes
6	FGFR2	54	13817	0.33%	Yes	Yes
7	TWIST1	32	10978	0.39%	Yes	Yes
8	MED12	26	12837	0.44%	No	No
9	FBN1	24	13875	0.50%	No	No
10	FLNA	24	12350	0.55%	No	Yes

An interesting observation is that for gene MED12 we cannot find any literature to link it with breast cancers. However, we found that in a large set of public microarray data (GDS2250) from the NCBI Gene Expression Omnibus (http://www.ncbi.nlm.nih.gov/geo/) for human biopsy samples from 40 breast cancer patients and seven normal subjects, MED12 shows a 1.94 fold decrease in cancer patients (one-tailed Student t-test p-value = 0.00057). In addition, in the BioGRID database, the protein of MED12 is shown to directly interact with estrogen receptor (ER) alpha (ESR1) with experimental confirmation using two different methods. ESR1 is a well-known critical gene in ER+ breast cancers. These results suggest that MED12 could be a potential candidate breast cancer associated gene.

4.3.3 Osteoarthritis and Examples of Using IndEviEr

Table 6 shows the top 10 genes for disease osteoarthritis. Since GACOM currently does not contain an entry for osteoarthritis, the last column in Table 6 is marked with “N/A.” Again, it is easy to find in literature relationships between these genes and osteoarthritis. To understand why a gene is currently ranked for osteoarthritis, we run IndEviRe (Algorithm 2), and find its supporting maximum biclique T × I. For example, for a known disease gene TNXB in Table 6, IndEviRe returns:

TABLE 6.

Top Ten Ranked Genes for Osteoarthritis

rank	Gene	$\mathrm{INDEVI}\text{-}\mathcal{F}$	$\mathrm{INDEVI}\text{-}\mathcal{G}$	percentile	in G2P	in GACOM
1	COL1A1	44	882	0.06%	No	N/A
2	COL5A1	42	538	0.11%	Yes	N/A
4	COL5A2	42	536	0.17%	Yes	N/A
4	COL3A1	21	555	0.22%	Yes	N/A
5	COL1A2	16	862	0.28%	No	N/A
6	ADAMTS2	16	738	0.33%	No	N/A
7	PLOD1	16	736	0.39%	No	N/A
8	TNXB	15	799	0.44%	Yes	N/A
9	FBN1	12	933	0.50%	No	N/A
10	VWF	12	747	0.55%	No	N/A

T_TNXB = {COL3A1, COL5A1, COL5A2}; I_TNXB = {AUTOSOMAL DOMINANT INHERITANCE, ECCHYMOSES, JOINT DISLOCATION, MITRAL VALVE PROLAPSE, SOFT SKIN};

Since TNXB is a known disease gene for osteoarthritis, we also known that the supporting pattern for (TNXB, OSTEOARTHRITIS), i.e., {COL3A1, COL5A1, COL5A2, TNXB} × {AUTOSOMAL DOMINANT INHERITANCE, ECCHYMOSES, JOINT DISLOCATION, MITRAL VALVE PROLAPSE, SOFT SKIN, OSTEOARTHRITIS} is a biclique. Actually, we can also show it is a maximal biclique, as indicated by the following lemma (proof is simple and omitted):

Lemma 3. For an entry (i, j) with M(i, j) = 1, any pattern in S(i, j) (independent evidence defined in Section 2) is a maximal biclique of M.

For an unknown disease gene VWF in Table 6, IndEviRe returns:

T_VWF = {COL3A1, COL5A1, COL5A2, TNXB}; I_VWF = {AUTOSOMAL DOMINANT INHERITANCE, ECCHYMOSES, MITRAL VALVE PROLAPSE,};

Being related to all the phenotypes in I_VWF, the genes in T_VWF are related to osteoarthritis; gene VWF is related to all the phenotypes in I_VWF too. This provides a clue for biologists to confirm whether gene VWF is related to osteoarthritis too.

5 Discussion and Conclusion

In this paper, we present a novel transformation algorithm for transactional databases. This method will have impact on many biomedical data mining applications, since many biomedical relationships can be formulated using transactional databases and the lack of complete knowledge in these relationships is a ubiquitous problem. Using the independent-evidence-based transactional database transformation approach, new hypotheses with strong evidence can be generated and prioritized for further experimental or clinical studies. We demonstrated the effectiveness of this method using a relatively small human gene-phenotype database to prioritize potential clinically significant genes. Even though the genes in this database are less than 10 percent of the known human genome and many well-known disease genes are not included (e.g., BRCA1), our algorithm was able to predict missed relations for which many can be confirmed by other sources in our case study. It can be conceived that if more information such as linkage, disease ontology, and protein-protein interaction can be incorporated like used in other studies [3], [19], [21], [33], [58], [37], [29], [53], [13], [12], our method could yield an even larger repertoire of hypotheses.

In addition, we leave the flexibility to readers to revise our algorithms easily. First, there are various ways to define $\mathcal{F}(i,j)$ according to different applications. For example, $\mathcal{F}(i,j)$ can be defined as the maximum number of vertices of a supporting biclique, i.e., $\mathcal{F}(i,j)={\text{max}}_{T\times I\in S(i,j)}((\mid T\mid -1)+(\mid I\mid -1))$. Comparing to our current definition, this $\mathcal{F}(i,j)$ definition does not prioritize supporting patterns with balanced transactions and items. Nevertheless, it provides a different angle of view on the supporting patterns. More important, It is not difficult to see that our algorithms IndEvi and IndEviRe can be slightly adjusted to fit this new $\mathcal{F}(i,j)$ definition. Second, readers may choose to supply IndEvi with different $\mathcal{C}$, such as bicliques corresponding to maximal frequentC item sets [25], and quasi-bicliques [1], [36], to approximate maximal bicliques. Though it is clear that the results depend on the input, it is interesting to observe that Theorem 1 always holds.

We expect to see in the future both applications of our algorithms (and their variations) on many available data sets, and improvements of our algorithms for very large data sets or data sets other than binary matrices.

Biography

Yang Xiang received the PhD degree in computer science from Kent State University in 2009. He is a computing innovation fellow (CIFellow) of US National Science Foundation (NSF)/CRA/CCC in the Department of Biomedical Informatics, The Ohio State University. Before he received the CIFellow award in 2010, he held a postdoctoral researcher position in Comprehensive Cancer Center, The Ohio State University. His research focuses on algorithmic graph theory, graph databases, data/graph mining, and biomedical informatics. He is a member of the IEEE.

Philip R.O. Payne received the PhD degree with distinction in biomedical informatics from Columbia University in 2006. From 2006 to 2010, he served as an assistant professor in the Department of Biomedical Informatics at The Ohio State University. In 2010, he was appointed as an associate professor and chair in the Department of Biomedical Informatics at The Ohio State University, where he also serves as the executive director of Center for IT Innovations in Healthcare (CITIH). His research focuses on the design and evaluation of novel informatics platforms and methodologies that enable foundational hypothesis generation and testing in the translational bioinformatics and clinical research domains.

Kun Huang received two BS degrees in biology and computer science from Tsinghua University, Beijing, China, in 1996. In addition, he received the MS degree in physiology in 1998, the MS degree in electrical engineering in 2000, the MS degree in mathematics in 2002, and the PhD degree in electrical and computer engineering in 2004, all from the University of Illinois at Urbana-Champaign. Currently, he is an associate professor in the Department of Biomedical Informatics, The Ohio State University (OSU), Columbus, Ohio, and the codirector of the OSU Comprehensive Cancer Center Biomedical Informatics Shared Resources. His research interests include systems biology, bioinformatics, biomedical imaging analysis, computer vision, and machine learning. He is a member of the IEEE.