A Structural Approach to Address the Healthy-Worker Survivor Effect in Occupational Cohorts: an Application in the Trucking Industry Cohort

Abstract

Background

Occupational cohort studies are often challenged by the Healthy Worker Survivor Effect, which may bias standard methods of analysis. G-estimation of structural failure time models is an approach for reducing this type of bias. Accelerated failure time models have recently been applied in an occupational cohort but cumulative failure time models have not.

Methods

We used g-estimation of a cumulative failure time model to assess the effect of working as a long-haul driver on ischaemic heart disease mortality in a cohort of 30,448 males employed in the unionized US trucking industry in 1985. Exposure was defined by job title and based on work records. We also applied g-estimation of an accelerated failure time model as a sensitivity analysis and approximated hazard ratios from both models to compare them.

Results

The Risk Ratio (RR) obtained from the cumulative failure time model, comparing the observed risk under no intervention to the risk had nobody ever been exposed as a long-haul driver, was 1.09 (95% CI: 1.02 – 1.16). The RR comparing the risk had everyone been exposed as long-haul driver for 8 years to the risk had nobody ever been exposed was 1.20 (95% CI: 1.04 – 1.46). After hazard ratio approximations, accelerated failure time model results were similar.

Conclusions

The cumulative failure time model can effectively control time-varying confounding by Healthy Worker Survivor Effect, and provides an easily interpretable effect estimate. Risk ratios estimated from the cumulative failure time model indicate an elevated ischaemic heart disease mortality risk for long-haul drivers in the US trucking industry.

INTRODUCTION

Occupational cohort studies often present researchers with the challenge of dealing with the Healthy Worker Effect¹. This bias can be broken into two components. The first, known as the healthy hire effect, stems from the better overall health status and favorable survival of actively employed individuals compared to the general population. The other aspect, the healthy worker survivor effect (HWSE), results from less-healthy workers accumulating less occupational exposure because they take more time off work, retire earlier than healthier workers, or switch to a job with lower exposure levels. The HWSE usually leads to a downward bias and underestimation of the effects of possibly harmful occupational exposures.

While the healthy hire effect is simply dealt with by means of internal comparisons within a working population², the HWSE is less straightforward. A number of methods have been proposed to control for this bias, including restricting analysis to workers who have been unemployed for a period of time, lagging exposure, or adjusting for time since hire, time since termination and/or employment status^3–7. However, if less healthy workers take time off work or terminate employment, then health status and time off work may be confounders of future exposure and the outcome. In fact, if time off work or termination of employment is affected by prior occupational exposure, then applying these methods to studies with time-varying variables using standard regression models may introduce additional bias. It has been shown that even under the null hypothesis standard models conditional on time-varying confounders affected by previous exposure (e.g. variables that are proxies for health status) may result in biased estimates, while failure to adjust for them also results in bias^8–9.

G-methods were developed in order to adjust correctly for time-varying confounders affected by previous exposure. These include the g-computation algorithm⁹, marginal structural models and inverse probability weighting¹⁰, and g-estimation of structural nested failure time models^11–12. The causal framework for these g-methods was originally proposed by Robins in the context of occupational epidemiology⁹. Early attempts to apply the methods were incomplete, though they identified the challenge^13–14. Recently Cole et al. applied the parametric g-formula in an occupational cohort¹⁵, while Chevrier et al. reported a successful application of g-estimation of accelerated failure time models in a cohort of autoworkers to reduce HWSE¹⁶.

We propose g-estimation of a cumulative failure time model, as a novel alternative for the analysis of the health effects of exposures based on occupational survival data. Under assumptions of no unmeasured confounding, correct classification of all variables, and correct model specification, this method is also unbiased in the presence of time-varying confounding affected by previous exposures. Moreover the cumulative failure time model has advantages compared to either Cox proportional hazards analysis or the accelerated failure time model. For example, the estimating equations for the cumulative failure time model are more easily solved than for the accelerated failure time model¹⁷. The proposed cumulative failure time model also allows for the estimation of marginal (unconditional) cumulative risks and estimands on the absolute scale. Such estimands are easier to interpret and of more direct use in public health than the ratio of median survival times estimated by the accelerated failure time model or the hazard ratios (HR) obtained with Cox proportional hazards analysis.

Drivers have higher exposure to vehicle exhaust fumes than other jobs in the trucking industry. Previous findings from the Trucking Industry Particles Study (TrIPS) have suggested that all-cause and ischaeamic heart disease (IHD) mortality are associated with being a driver^18–20. Bias from HWSE in occupational studies of cardiovascular outcomes has been highlighted as a particular concern in several previous studies^{2, 16, 21}, raising a question about underestimation of IHD risk. This concern motivated us to apply g-estimation of a cumulative failure time model to quantify the effects of being a long-haul driver on marginal cumulative risks of all-cause and IHD mortality in the TrIPS cohort.

METHODS

Study Population

The study population used in the analysis has been described in detail elsewhere¹⁸. Briefly, detailed computerized work records for unionized employees employed in 1985 (54,319 men and 4,007 women) were obtained from four large national companies. These employees were followed up through the year 2000. Participants from one of the companies (n=5,717) contributed data for the time period of 1993–2000. Primary analysis was limited to men forty years or older at baseline, with at least one year of work in the trucking industry. Duration of employment was calculated as years of work in specific trucking industry jobs, through information on start date, retirement and layoff dates for each job title. Lack of detailed records represented only 1.5% of all person-years, and the primary analysis sample included only participants with complete covariate data (n=30,448).

Exposure Assessment

Job title in the industry was defined in eight different job categories, based on a review of job titles and duties, information on historical use of diesel and other vehicles by workers in the industry²² as well as an industrial hygiene exposure assessment^23–25. The exposure of interest in this study was working as a long-haul driver, a specific job classification from the work history files, which is consistent across the 4 participating companies. Long haul drivers deliver freight from terminal to terminal, as opposed to pick up and delivery drivers who pick up and/or deliver freight to consumers locally, other jobs involving driving forklifts or tractors in terminal docks and yards, or no driving-related duties^19–20. While participants could have contributed person time in multiple job titles, the majority of person-years were spent in the same job title. Job titles and related duties were the same for all participating companies and participants. Throughout follow-up, the time-varying dichotomous annual exposure variable took the value of 1 if a participant worked as a long-haul driver at any point during the year and 0 otherwise.

Mortality Follow-up

Vital status, date of death and cause-specific mortality from 1985 to 2000 was obtained through searching the National Death Index [National Center for Health Statistics (NCHS), Hyattsville, MD]. Matching criteria included social security number, month and year (±1) of birth, and first name, middle initial and last name. IHD mortality was defined as ICD-941.0-414.9 and ICD-10 I20-I25.9 codes.

Evidence of HWSE

To examine evidence of HWSE as a time varying confounder also affected by previous exposure we fit a series of models to estimate associations amongst exposure, surrogates of unmeasured health status, such as employment status and intermittent time off work, and outcome. Standard Cox models were fit to assess the association between health status surrogate and mortality, adjusted for baseline characteristics such as age, race and region. We also fit models to assess the exposure-related risk of leaving work, adjusting for the same baseline covariates.

G-estimation of Structural Nested Cumulative Failure Time Models

We applied a structural nested cumulative failure time model to estimate the causal effect of working as a long-haul driver in the trucking industry on all-cause and IHD mortality. The method is described in detail in the Appendix. Briefly, the process requires two models: (a) a structural model for the ratio of counterfactual risks that differ only in exposure a single year, as a function of observed exposure and a causal parameter ψ_cft and (b) a model predicting annual exposure to adjust for confounding.

The effect estimate in the structural model is a counterfactual risk ratio that compares the risks assessed in any year j under two scenarios. The numerator is the risk under a given exposure history up to some earlier year k (k<j) and unexposed thereafter. The denominator is the risk under the same exposure history up to the previous year k-1 and unexposed thereafter. Both risks are conditional on the same covariate history up to time k–1. This risk ratio is then modelled as a function of observed exposure at time k, the length of time from the final exposure to the time at which the risks are assessed (j–k), and an unknown coefficient to be estimated (ψ_cft). Under this model, the impact of a final year of exposure at time k on risk at time j decreases as the length of time between k and j increases. (See Appendix for model.)

The logistic model for the (binary) annual exposure allows us to adjust for time-varying confounding. We predict annual exposure as a function of previous exposure, previous time off work and other covariates. Under the (conditional exchangeability) assumption of no unmeasured confounders, counterfactual risks are statistically independent of observed exposure given the observed confounders.

The g-estimation procedure uses optimization methods to estimate the unknown coefficient in the structural model for which this independence is satisfied in the exposure model. After this coefficient ψ_cft is estimated, the counterfactual risks under no exposure are estimated for each year of follow up, using the observed risks and removing the effect of any observed exposure. Subsequently counterfactual risks for hypothetical exposure interventions can be estimated by adding effects of exposure to the counterfactual risks under no exposure. The exposure effect estimate can be transformed to obtain cumulative counterfactual risks over the duration of follow-up for specific interventions on exposure¹⁷.

In this study we assessed three specific interventions: (1) nobody in the study population ever worked as a long-haul driver, (2) everybody in the population worked as a long-haul driver for the first 8 years of follow-up (the median duration of employment during follow-up) and was unexposed thereafter, and (3) everybody in the population worked as a long-haul driver for the full duration of follow-up (up to 15 years).

We used a pooled logistic model for annual exposure to adjust for covariates. This model for exposure was restricted to active employment time, because the probability of exposure for non-active employment is zero by definition. Exposure history was entered in the model as two variables: an indicator for exposure in the previous year and a continuous variable for cumulative exposure up to two years ago. Time-varying confounding variables were time spent off work in the preceding year, as a percentage, and a continuous variable for cumulative time off work up to two years ago.

Additional covariates entered in the exposure model were pre-baseline cumulative exposure (years as a long-haul driver prior to baseline), age at baseline, race, geographical region, ambient air pollution levels near each participant’s residence and cumulative time spent in other jobs titles up to the preceding year^{20, 26}. Follow-up time was also entered in the model as a continuous variable along with year of hire to account for left truncation bias.

Inverse probability of censoring weighting was used to control for differential loss to follow-up and for competing risks in the case of IHD mortality²⁷. Censoring models included the covariates listed above for the exposure model as well as the dichotomous annual exposure variable. G-estimation of the cumulative failure time model was performed in SAS (SAS version 9.3; SAS Institute Inc., Cary, NC) invoking the SNCFTMshell SAS macro available at: http://www.hsph.harvard.edu/causal.

G-estimation of Structural Nested Accelerated Failure Time Models

As a sensitivity analysis we also fitted a structural nested accelerated failure time model, described in detail in the Appendix. This accelerated failure time model assesses counterfactual unexposed survival time as a function of observed survival time and exposure. It allows us to compare median counterfactual survival times under population interventions of always exposed (T_α) and never exposed (T₀).

Similar to the cumulative failure time model, the accelerated failure time method uses two models: a) a structural model for counterfactual survival time under no exposure (T₀) as a function of observed exposure and an unknown coefficient to be estimated (ψ_aft) and b) a model for annual exposure to adjust for confounding. We again rely on the (conditional exchangeability) assumption of no unmeasured confounders under which counterfactual survival times are independent of observed exposure, and use optimization methods estimate a ψ_aft value for which that independence is satisfied.

The same covariates were controlled for in the exposure models of the two structural methods. Natural cubic splines were used for follow-up time with 3 degrees of freedom, and for year of hire with 6 degrees of freedom (approximately one for each decade in the time span), as opposed to linear terms used in the model for the cumulative failure method. Control for loss to follow up and competing risks was achieved using IPCW as described above. G-estimation of the accelerated failure time model was performed using R software (version 2.15.1, see web supplement for R code).

RESULTS

Study Population and Mortality Outcomes

Characteristics of the study population are summarized in Table 1. Briefly, participants were predominantly white (85%), with mean age at baseline of 49 (±6) years, and the most common job was long haul driver (32%). The median duration of employment was 8 years.

Table 1.

Population characteristics in primary analysis sample of men aged 40 years or more at baseline with complete covariate data.

Characteristic	Overall (n=30,448)	Long-Haul Drivers (n=10,642)	Other job titles (n=19,846)
	Mean ± SD
Age at baseline	49.04 ± 6.01	49.89 ± 6.05	48.59 ± 5.94
Age when leaving active emp.	59.18 ± 4.73	60.04 ± 4.68	58.71 ± 4.68
Year of Hire	1972 ± 8.53	1973 ± 8.10	1972 ± 8.73
Average Pollutant Levels Near Home Residence
PM10 (µg/m3)	26.83 ± 5.87	26.49 ± 5.62	27.01 ± 6.00
NO2 (ppb)	14.18 ± 7.11	12.55 ± 5.89	15.03 ± 7.54
SO2 (ppb)	4.85 ± 2.91	4.80 ± 2.85	4.88 ± 2.94
Census Region of Residence		No. (%)
South	11,505 (37.7)	4,220 (39.7)	7,285 (36.7)
Midwest	9,736 (31.9)	3,745 (35.2)	5,991 (30.2)
Northeast	4,477 (14.7)	1,046 (9.8)	3,471 (17.5)
West	4,730 (15.5)	1,631 (15.3)	3,099 (15.6)
Race, White	25,872 (84.9)	9,385 (88.2)	16,487 (83.1)

All-cause and IHD mortality are summarized overall and by job title in Table 2. There were 4,201 deaths during study follow-up, 1,253 of them due to IHD. Most deaths (72%) and most IHD deaths (68%) occurred after termination of employment. The HR for mortality associated with leaving active employment was 1.09 (95% CI: 0.99 – 1.20). Leaving active employment was not associated with IHD mortality after covariate adjustment, however, intermittent time off was strongly associated with both all-cause and IHD mortality. The HR for leaving active employment associated with exposure was 1.07 (95% CI: 1.04 – 1.11).

Table 2.

Total and cause-specific mortality by job title and employment status^a

Exposure	Person Years		Total Deaths		IHD Deaths
	Total	Active emp.	Total	Active emp.	Total	Active emp.
Long Haul Driver	144,525	98,993	1706	506	563	204
Other jobs	275,047	182,710	2495	659	690	199
Totals	419,572	281,703	4,201	1,165	1,253	403

^aPerson years and deaths presented both for totals during follow up based on job title at baseline, and also based on years and deaths occurring during active employment

Job Title and Mortality Associations

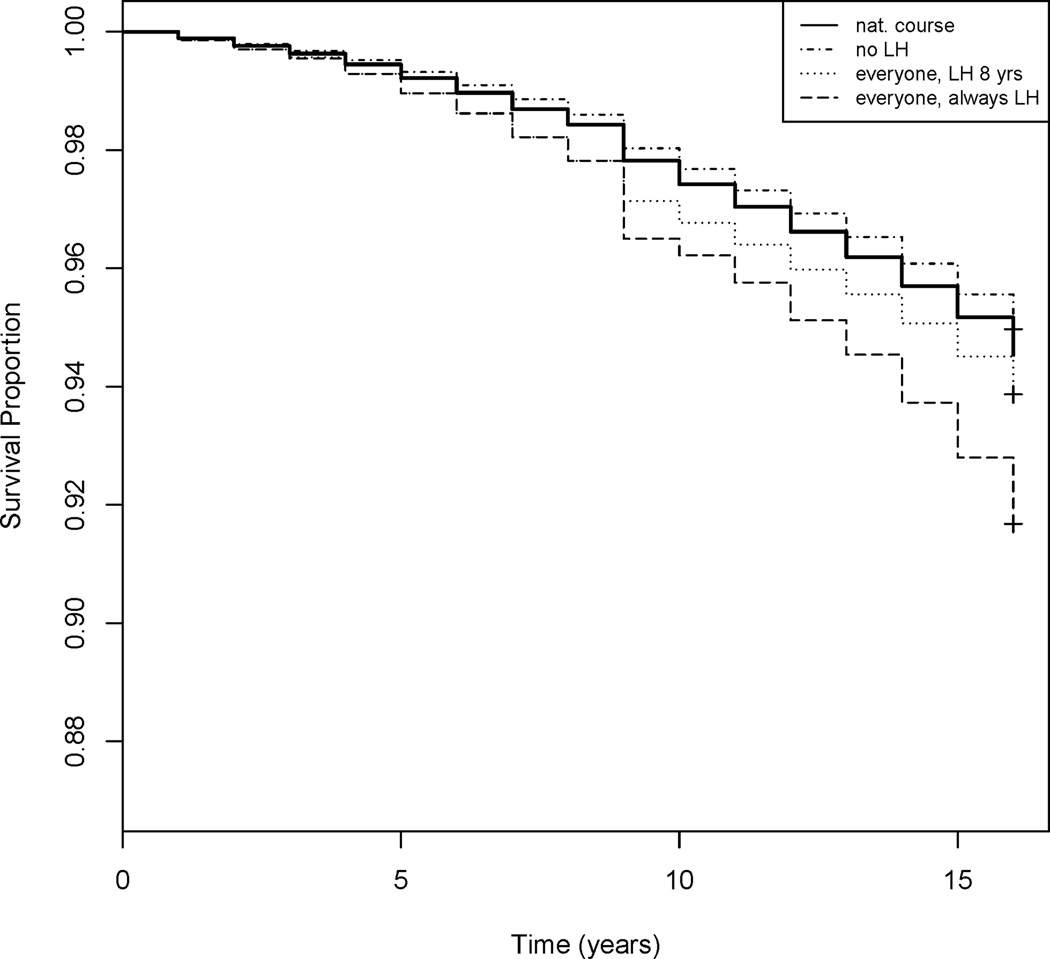
The Risk Ratios (RR) comparing the observed risk for the cohort under the natural course (i.e., under observed exposure and covariate history) to the risk under different interventions are illustrated in Table 3. Being a long-haul driver increased the risk of all-cause and IHD mortality with similar magnitudes on the multiplicative scale. Survival graphs for the observed survival times in the study population (natural course), as well as for the three interventions on the exposure, are presented in Figure 1.

Table 3.

15-year cumulative Risk (%) for all-cause and IHD mortality under natural course and “never exposed”, “exposed through 8 first years of follow-up” and “always exposed”, interventions, along with marginal Risk Ratios (RR, 95% CI), from the CFT model for the exposure Long-Haul Driver.

Intervention	All-cause Mortality		IHD mortality
	Risk (%)	RR vs. “never ex” (95% CI)	Risk (%)	RR vs. “never ex” (95% CI)
Natural Course	16.75	1.09 (1.05 –1.12)	5.46	1.09 (1.02 – 1.16)
Never Exposed	15.47	.	5.05	.
8-year exposure	18.97	1.23 (1.12 – 1.36)	6.08	1.20 (1.04 – 1.46)
Always Exposed	25.39	1.64 (1.34 – 2.06)	8.03	1.59 (1.12 – 2.47)

Figure 1.

Survival graphs for IHD mortality under natural course and the interventions everyone never exposed as long-haul driver (LH), everyone exposed as long-haul driver for first 8 years of follow up, and everyone always exposed as long-haul driver.

Inverse probability of censoring weights for competing risks did not affect parameter estimates of the cumulative failure time model for IHD mortality. Effect estimates and their 95% CIs with inverse probability of censoring weights only for loss to follow up were very similar to those controlling for both loss to follow up and competing risks. Results are presented based on models controlling for both loss to follow up and competing risks throughout this report for reasons of simplicity.

Hazard ratio approximations for the cumulative failure time and accelerated failure time models were very similar for IHD mortality (Table 4). In the case of total mortality, the HR approximation from the cumulative failure time model was slightly higher than that from the accelerated failure time model. (Note: these hazard ratios are only comparable under specific assumptions. See Appendix.)

Table 4.

Hazard ratio approximations (95% CIs) from cumulative failure time (CFT) and accelerated failure time (AFT) models for the exposure Long Haul drivers.

	HR approx.a
All-cause Mortality
CFT model	1.43 (1.24 – 1.66)
AFT model	1.34 (1.15 – 1.59)
IHD Mortality
CFT model	1.38 (1.08 – 1.82)
AFT model	1.39 (1.05 – 1.84)

^bHR approximation from CFT model Risk Ratio estimate, is the conditional HR at time t ∈(k, k+1] (assumed to approximate the marginal HR) for the effect of exposure up to year k, compared to exposure up to year k-1 and unexposed afterwards

HR approximation from the AFT model based on Weibull distribution assumption for survival time T, and approximates the HR comparing “always” exposed to “never exposed” at time t.

DISCUSSION

This application of the cumulative failure time model to the trucking industry study is the first in any occupational cohort. Given that not all of the assumptions required by different structural methods are shared, it can be useful to consider alternatives for any particular study based on the causal question at hand and the possible biology behind it¹⁷. Considering the application of the accelerated failure time model as a sensitivity analysis allows us to assess the robustness of the results to changes in the method of analysis. Differences in results may lead to better understanding of the strengths and limitations of both the data and the methods.

Results from the g-estimation of the cumulative failure time model in this study indicate that working as a long-haul driver in the trucking industry leads to an increased risk of both IHD and all-cause mortality. Long-haul drivers are exposed to high levels of vehicle exhaust^{23, 25}. Exposure to particulate matter from vehicle exhaust and other sources has been linked to cardiovascular and all-cause mortality in a growing body of literature^28–31. Increased cardiovascular disease risk has also been reported in professional drivers in other studies^32–35. Our finding of increased IHD mortality risk among long-haul drivers is consistent with previous analyses in which the IHD risk associated with ever being a driver was elevated^{18, 20}. It is also consistent with previous findings of increased risk for myocardial infarction in long-distance truck drivers in Sweden³⁵.

A major data limitation of this retrospective cohort mortality study was lack of personal information on potential risk factors for heart disease mortality, such as smoking, BMI, and other lifestyle related factors. The observed effect of being a long-haul driver on mortality may reflect differences in these characteristics across job titles, in addition to differences in vehicle exhaust exposures. Furthermore, all subjects in the TrIPS cohort were hired before start of follow-up. Despite steps taken to address left truncation, survivor bias may still exist. We expect the direction of this bias to be towards the null³⁶. Generalizability of our findings may also be limited as non-unionized sectors of the industry as well as trucking industries in other countries may have different practices that affect exposure.

The methods used in this paper have several strengths. G-estimation of the cumulative failure time model is a structural approach. Under specific assumptions, it correctly adjusts for time-varying covariates affected by prior exposure, an issue inherent in the HWSE as described above. This analysis is thus an improvement over standard methods, which are biased in the presence of a time varying confounder affected by prior exposure. Additionally, failure time models like either the accelerated and cumulative failure time models, unlike standard Cox models, are not affected by potential limitations of the hazard ratio, such as crossing of hazards due to depletion of susceptibles³⁷. They can also be used to obtain survival graphs, which (though less familiar) may be more informative than hazard ratios.

Results from accelerated and cumulative failure time models were similar in the sensitivity analysis. HR approximations were virtually identical for IHD mortality and were similar for all-cause mortality. It is important to note, however, that these approximations of hazard ratios answer different causal questions, and are comparable only under specific assumptions³⁸. Specifically, the cumulative failure time model approximates a hazard ratio for the effect of a one-year difference in exposure assessed over a one-year period, conditional on exposure and covariate history. The accelerated failure time model approximates a marginal hazard ratio comparing the interventions always and never exposed, much like the estimate of a Cox marginal structural model, and in the context of the accelerated failure time model it is also the effect of exposure in each year.

Cumulative failure time models have two advantages over accelerated failure time models. First, they have a smooth estimating function with respect to their parameters that can be solved using standard optimization procedures (e.g. the Newton-Raphson procedure). By contrast, the estimating function of an accelerated failure time model is not differentiable in the model parameters in the presence of administrative censoring, and requires a grid search or non-gradient-based optimizers^{17, 38–39}. Second, cumulative failure time models can be used to obtain marginal cumulative risks, as long as there is no effect modification by time-varying confounders, an assumption satisfied by the model used in this study. Cumulative risks and risk ratios are more easily interpretable than ratios of median survival times as estimated by an accelerated failure time model.

One limitation of the cumulative failure time model is that estimates are valid only under the “rare failure” assumption. This assumption may have been violated in the case of all-cause mortality in the latter stages of follow-up in this study. Accelerated failure time models do not require the “rare failure” assumption and are potentially a better option for less rare outcomes.

General limitations of our analyses include the fact that estimates are only valid under the assumption of conditional exchangeability, which is not a testable assumption in observational studies. This, however, is a limitation of all observational studies. Additionally, the function of the cumulative failure time model used in this study assumes no interactions, and validity of results depends on correct specification of the model. The estimating equation used in our analysis was a simple form, as described by Picciotto et al.¹⁷, and does not result in a doubly-robust, locally efficient estimator.

Censoring by differential loss to follow up and competing risks may be sources of selection bias inherent in survival data⁴⁰. Under the assumption that the censoring models for both mechanisms are correctly specified and account for all censoring factors, use of inverse probability of censoring weights will lead to unbiased estimates but may present an interpretation problem. The weight-corrected effect estimates represent the effect of the exposure “had nobody been lost to follow up or competing risks”. In cause-specific mortality analysis, no deaths due to competing risks is an unrealistic scenario, and causal effects “had nobody been lost to competing risks” may not be a useful causal estimate for a real world public health issue. In our analysis results with and without use of inverse probability of censoring weights for competing risks were very similar. Assuming that our censoring model was correctly specified, this suggests that any selection bias due to loss to competing risks in this cohort with respect to the exposure is of small magnitude.

To conclude, the cumulative failure time model is an alternative structural method for the analysis of observational data in the presence of time-varying confounders affected by prior exposure. It is applicable to occupational studies with longitudinal data in the presence of HWSE. Cumulative failure time models have advantages over previously proposed methods, but come with their own limitations. Overall it may be beneficial to consider more than one structural method when possible. Although in this instance the two g-methods considered had similar results, this may not always be the case. Given the number of assumptions required for each model, a sensitivity analysis using different models may provide insights as to the appropriateness of each in light of the specific causal questions and exposure scenarios considered, as well as sensitivity to data limitations such as residual confounding and measurement error.

What this paper adds

The Healthy Worker Survivor Effect, caused by time varying confounders affected by prior exposure, is a bias that can be avoided by applying g-methods.

One such method, g-estimation of a structural accelerated failure time model, has previously been used in an occupational cohort.

This paper proposes g-estimation of a structural cumulative failure time model for use in occupational survival analyses.

While it shares strengths with the accelerated failure time model as compared to standard Cox analysis, the cumulative failure time model, under a rare failure assumption, also provides further advantages, such as simpler estimating functions and easily interpretable effect estimates.