Abstract
Analysis of molecular interaction networks is pervasive in systems biology. This research relies almost entirely on graphs for modeling interactions. However, edges in graphs cannot represent multiway interactions among molecules, which occur very often within cells. Hypergraphs may be better representations for networks having such interactions, since hyperedges can naturally represent relationships among multiple molecules. Here, we propose using hypergraphs to capture the uncertainty inherent in reverse engineering gene-gene networks. Some subsets of nodes may induce highly varying subgraphs across an ensemble of networks inferred by a reverse engineering algorithm. We provide a novel formulation of hyperedges to capture this uncertainty in network topology. We propose a clustering-based approach to discover hyperedges. We show that our approach can recover hyperedges planted in synthetic data sets with high precision and recall, even for moderate amount of noise. We apply our techniques to a data set of pathways inferred from genetic interaction data in S. cerevisiae related to the unfolded protein response. Our approach discovers several hyperedges that capture the uncertain connectivity of genes in relevant protein complexes, suggesting that further experiments may be required to precisely discern their interaction patterns. We also show that these complexes are not discovered by an algorithm that computes frequent and dense subgraphs.
Index Terms: Biology and genetics, hypergraphs, graphs and networks
1 Introduction
Interaction networks are increasingly used to represent cellular processes and reason about them [28]. Methods have been developed to reconstruct gene regulatory networks from gene expression profiles [18], to predict molecular interactions [13], to classify cellular states [8], and to compute cellular response networks [30]. An overwhelming majority of these approaches use directed or undirected connections between pairs of molecules to model interaction networks. However, pairwise interactions cannot accurately represent coordinated activity of assemblages of more than two molecules, such as a protein complex that acts as a unit, modifier proteins that bind to and modulate the activity of transcription factors (TF), and metabolic reactions that may involve multiple substrates and products and be catalyzed by one or more enzymes [19].
Hypergraphs are attractive alternatives to graphs to represent such facets of cellular processes [6], [11], [12], [15], [32]. Informally, a hyperedge (an edge in a hypergraph) is simply a set of one or more nodes; therefore, every edge in a graph is a hyperedge composed of exactly two nodes. Hypergraphs are increasingly being recognized for their utility in accurately representing cellular processes. Many databases and interaction storage formats support hyperedges of different types, either explicitly or implicitly [7], [25]. Such formats have proven useful for converting existing interaction pathways and processes into hypergraph representations.
The power of hypergraphs for representing uncertainty in experimentally and computationally derived interactions is less well recognized. For example, pairwise interactions are inappropriate for representing protein complexes pulled down by tandem affinity purification; it is widely recognized that the spoke and matrix models are both incorrect representations of purified complexes [26]. While techniques have been developed to infer which pairs of proteins physically interact in each complex [26], representing each protein complex by a hyperedge is natural [23].
More generally, methods that reconstruct gene networks [3], [21] from systems biology data sets may be able to infer only that there is some set of interactions among a group of molecules but may not be able to precisely discern pairwise interactions within the group. Furthermore, since experimental data are noisy and limited, there may be multiple network topologies that fit the experimental data equally well. Existing algorithms for inferring and representing molecular interaction networks make simplifying assumptions to account for the underdetermined nature of the system [18] or compute a single network that is the consensus of multiple high-scoring networks [9]. The central thesis of our work is that hypergraphs are natural candidates for representing uncertainty in the topology of the inferred network.
1.1 Contributions
Our primary contribution is formulating the novel problem of reverse engineering hypergraphs from systems biology data sets. Many network inference techniques, for example, those discovering Bayesian networks, search the landscape of possible networks until they converge to local optima, thereby generating ensembles of networks with scores that are close to optimal [3], [21]. Although these networks have very similar scores, they may have different dependence and connectivity structures [9], [21]. We take as our starting point a set
 of graphs computed by such an algorithm. In our formulation, a set S of nodes constitutes a hyperedge if S induces very different subgraphs in each of the graphs in
of graphs computed by such an algorithm. In our formulation, a set S of nodes constitutes a hyperedge if S induces very different subgraphs in each of the graphs in
 . Intuitively, across the ensemble
. Intuitively, across the ensemble
 , there is no consensus on which specific edges should connect pairs of nodes in S. We deem such a set of nodes to be a hyperedge. We formalize this notion by incorporating parameters that are lower bounds on the number of distinct subgraphs on S that appear in
, there is no consensus on which specific edges should connect pairs of nodes in S. We deem such a set of nodes to be a hyperedge. We formalize this notion by incorporating parameters that are lower bounds on the number of distinct subgraphs on S that appear in
 and the number of times each such subgraph occurs in
and the number of times each such subgraph occurs in
 .
.
Our second contribution is an algorithm that discovers hyperedges by computing heavily weighted clusters in an appropriately defined summary graph. As far as we know, ours is the first paper to explicitly propose using hypergraphs to represent uncertainty in the structure of reverse-engineered gene networks, to propose a formal definition of hyperedges in this context, to develop an efficient algorithm to compute hyperedges supported by a set of varying graphs, and to show that hyperedges as well as the hypergraph itself are biologically interesting.
An implementation of our hyperedge miner is available as part of the Biorithm software suite at http://bioinformatics.cs.vt.edu/~murali/software/biorithm/.
1.2 Results
First, we demonstrate that our approach recovers hyperedges planted in synthetic data sets with high precision and recall, even when there is a moderate amount of noise in the data and when the planted hyperedges overlap. Second, we highlight an application where we use hyperedges to capture the variations in an ensemble of networks inferred from quantitative genetic interaction (GI) data in S. cerevisiae [3]. Upon analysing this data, we observe that our method discovers hyperedges that capture specific pathways and complexes in the ER for whom the GI data do not support well-defined interactions.
2 Related Research
Here, we highlight how our question is conceptually distinct from related areas of research.
2.1 Network Inference
Our knowledge of molecular interactions that take place within the cell is highly incomplete. To surmount this difficulty, methods have been developed to predict or “reverse engineer” interactions from data sets of information on gene and protein expression, under the assumption that an interaction may be inferred between two genes if they show similar patterns of activities in multiple experimental conditions. Based on this hypothesis, many methods have been developed to infer interactions between pairs of genes [18]. As far as we know, these methods have not been generalized to predict hyperedges.
2.2 Gene Modules and Network Clustering
A functional module may be defined as a set of molecules that interact to execute a discrete biological function. A vast number of approaches have been developed to find modules or communities from one or more molecular networks [16], [20], [28]. All existing methods start from one or more graphs and find dense clusters within these graphs. The clusters may exist within a single graph, be composed of edges arising from different graphs, or occur simultaneously in many graphs (the last version of the problem is often termed frequent subgraph mining in relational graphs). In contrast, in our work, we focus on a completely different type of property: a set of nodes that do not exhibit any consistent pattern of connectivity in any graph.
2.3 Molecular Hyperedges
Some approaches do exist to reverse-engineer specific types of hyperedges from systems biology data. For instance, the MINDY [31] algorithm predicts post-translational modulators of transcription factors. In other words, it predicts directed hyperedges with the TF and its modulator in the tail of the hyperedge and the target gene in the head of the hyperedge. Another example arises in the work by Battle et al. on identifying pathways from genetic interaction data [3]. They reconstruct an ensemble of high-scoring Bayesian networks that represent pathway structures from quantitative phenotypes of double knockout strains of budding yeast. They identify sets of nodes that are connected by some path in many graphs in the ensemble, while allowing the specific ordering to vary in different graphs. They call such sets of nodes collapsed nodes. In principle, collapsed nodes are similar to the hyperedges we compute. However, the paths induced by a collapsed node do not necessarily vary widely across the graphs in
 , i.e., only a few of the possible paths among the nodes may be represented in
, i.e., only a few of the possible paths among the nodes may be represented in
 . Our methodology differs significantly, as we explicitly seek sets of nodes whose induced subnetworks exhibit high variation across the collection of graphs. Moreover, our important contributions include a formal definition of hyperedges and an algorithm to systematically compute hyperedges. In Section 5.2, we demonstrate the value of our approach by applying our hyperedge discovery technique to their ensemble of networks.
. Our methodology differs significantly, as we explicitly seek sets of nodes whose induced subnetworks exhibit high variation across the collection of graphs. Moreover, our important contributions include a formal definition of hyperedges and an algorithm to systematically compute hyperedges. In Section 5.2, we demonstrate the value of our approach by applying our hyperedge discovery technique to their ensemble of networks.
3 Definitions
Let
 be a set of n graphs computed by multiple runs of a network inference algorithm. We assume that each graph in
be a set of n graphs computed by multiple runs of a network inference algorithm. We assume that each graph in
 is undirected, unweighted, and has the same set V of vertices. There are a number of ways to define how one set of nodes induces different subgraphs in
is undirected, unweighted, and has the same set V of vertices. There are a number of ways to define how one set of nodes induces different subgraphs in
 . We propose one such formulation in this work.
. We propose one such formulation in this work.
Given a set S ⊆ V of k nodes and a graph G ∈
 , let G(S) denote the subgraph of G induced by S. Let
, let G(S) denote the subgraph of G induced by S. Let
 (S) denote the multiset of these subgraphs as we vary the graphs in
(S) denote the multiset of these subgraphs as we vary the graphs in
 and let
and let
 (S) denote the set of
possible graphs on the nodes in S. Note that the number of distinct subgraphs in
(S) denote the set of
possible graphs on the nodes in S. Note that the number of distinct subgraphs in
 (S) is at most
. Consider a graph H ∈
(S) is at most
. Consider a graph H ∈
 (S). Let ψ(H) denote the number of occurrences of H in
(S). Let ψ(H) denote the number of occurrences of H in
 (S). Ideally, as we vary H ∈
(S). Ideally, as we vary H ∈
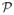 (S), we desire the counts ψ(H) to be as uniform as possible. We capture this notion using the following definition. Given parameters 0 < β, σ ≤ 1, we say that S is a (β, σ)-hyperedge if ψ(H) ≥ βn for at least
graphs in
(S), we desire the counts ψ(H) to be as uniform as possible. We capture this notion using the following definition. Given parameters 0 < β, σ ≤ 1, we say that S is a (β, σ)-hyperedge if ψ(H) ≥ βn for at least
graphs in
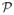 (S). The parameters β and σ ensure that the counts ψ(H) are balanced for at least some number of graphs in
(S). The parameters β and σ ensure that the counts ψ(H) are balanced for at least some number of graphs in
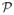 (S).
(S).
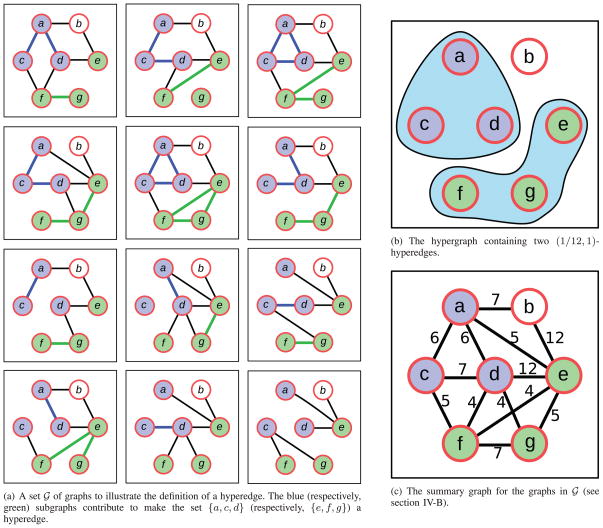
Fig. 1a illustrates these ideas using a set
 of 12 graphs on the set of nodes {a, b, c, d, e, f, g}. Consider the set of nodes {a, c, d}. Each of the eight possible graphs among these nodes occurs as a subgraph of at least one graph in
of 12 graphs on the set of nodes {a, b, c, d, e, f, g}. Consider the set of nodes {a, c, d}. Each of the eight possible graphs among these nodes occurs as a subgraph of at least one graph in
 in the figure, with some graphs occurring exactly once. By our definition, {a, c, d} is a (1/12, 1)-hyperedge. Fig. 1b displays all (1/12, 1)-hyperedges supported by the set of graphs in Fig. 1a. Observe that four out of the eight possible graphs among {a, c, d} appear twice in
in the figure, with some graphs occurring exactly once. By our definition, {a, c, d} is a (1/12, 1)-hyperedge. Fig. 1b displays all (1/12, 1)-hyperedges supported by the set of graphs in Fig. 1a. Observe that four out of the eight possible graphs among {a, c, d} appear twice in
 . Therefore, {a, c, d} is also a (2/12, 4/8)-hyperedge. As another example, consider the set of nodes {e, f, g}. All eight graphs among these nodes appear in
. Therefore, {a, c, d} is also a (2/12, 4/8)-hyperedge. As another example, consider the set of nodes {e, f, g}. All eight graphs among these nodes appear in
 , with two graphs appearing twice each and one graph appearing thrice. Thus, {e, f, g} is a (1/12, 1)- and a (2/12, 3/8)-hyperedge. While this set is also a (3/12, 1/8)-hyperedge, in practice, we do not consider the pair of parameters (3/12, 1/8) as suggesting a hyperedge, since this means that only one out of eight possible subgraphs is present in the graphs in
, with two graphs appearing twice each and one graph appearing thrice. Thus, {e, f, g} is a (1/12, 1)- and a (2/12, 3/8)-hyperedge. While this set is also a (3/12, 1/8)-hyperedge, in practice, we do not consider the pair of parameters (3/12, 1/8) as suggesting a hyperedge, since this means that only one out of eight possible subgraphs is present in the graphs in
 . In contrast to these examples, consider the set of nodes {a, b, e}. Only two of the eight possible subgraphs occur in
. In contrast to these examples, consider the set of nodes {a, b, e}. Only two of the eight possible subgraphs occur in
 , five and seven times, making {a, b, e} a (5/12, 2/8)-hyperedge. Here, the β parameter is quite large (5/12) but the σ parameter is quite small (2/8). Since {a, b, e} induces only two different subgraphs, we do not consider it as a hyperedge.
, five and seven times, making {a, b, e} a (5/12, 2/8)-hyperedge. Here, the β parameter is quite large (5/12) but the σ parameter is quite small (2/8). Since {a, b, e} induces only two different subgraphs, we do not consider it as a hyperedge.
Fig. 1.
An illustration of a set
 of graphs, two hyperedges defined by
of graphs, two hyperedges defined by
 , and the summary graph of
, and the summary graph of
 . In Fig. 1c, to aid clarity, we show the number of occurrences of each edge in a graph in
. In Fig. 1c, to aid clarity, we show the number of occurrences of each edge in a graph in
 , rather than the fraction of graphs in which the edge occurs.
, rather than the fraction of graphs in which the edge occurs.
Note that since the ensemble contains 12 graphs, every four-node set is a hyperedge only for values of σ less than ; thus, no four-node set is likely to constitute an interesting hyperedge. More generally, the largest (β, σ)-hyperedge has nodes.
We now state the problem we solve in this work:
“Given a set of graphs
, an integer k > 0, and parameters 0 < β, σ ≤ 1, enumerate all (β, σ)-hyperedges containing k nodes.”
We consider other formulations of the problem in the conclusions (see Section 6).
4 Algorithm
In this section, we describe an algorithm that formulates the problem of discovering hyperedges in terms of computing clusters in an appropriate summary graph (see Fig. 1c). To motivate the algorithm, consider a (β, σ)-hyperedge S that contains k nodes such that σ = 1, i.e., each of the
possible graphs on S occurs as a subgraph of some graph in
 . For such a hyperedge, the largest possible value of β is
. In this situation, each pair of nodes in S will appear as an edge in precisely half the graphs in
. For such a hyperedge, the largest possible value of β is
. In this situation, each pair of nodes in S will appear as an edge in precisely half the graphs in
 . Therefore, we can compute such a hyperedge by constructing the average of all graphs in
. Therefore, we can compute such a hyperedge by constructing the average of all graphs in
 and searching for cliques in which each edge has weight equal to 0.5.
and searching for cliques in which each edge has weight equal to 0.5.
We now generalize these observations to arbitrary (β, σ) hyperedges. We first prove lower and upper bounds on the “density” of a hyperedge. We use these bounds to transform the edge weights in the average of all graphs in
 . Finally, we use a clustering algorithm to enumerate all dense subgraphs in this transformed graph.
. Finally, we use a clustering algorithm to enumerate all dense subgraphs in this transformed graph.
4.1 Bounds on Hyperedge Densities
We start by defining some notation. Given a set
 of undirected, unweighted graphs, let μ(G) denote the average of
of undirected, unweighted graphs, let μ(G) denote the average of
 , i.e., μ(G) is an undirected, weighted graph such that the edge set of μ(G) is the union of the edge sets of all the graphs in
, i.e., μ(G) is an undirected, weighted graph such that the edge set of μ(G) is the union of the edge sets of all the graphs in
 and the weight of each edge in μ(G) is the fraction of graphs in
and the weight of each edge in μ(G) is the fraction of graphs in
 that contain the edge. Given a (β, σ)-hyperedge S, let μS(G) denote the subgraph of μ(G) induced by the nodes in S. If S contains k nodes, then μS(G) contains at most
edges. In general, any particular edge in μS(G) may have a weight in the interval (0, 1]. However, we can establish lower and upper bounds on the density of μS(G), where we define the density of a graph to be the total weight of the edges in the graph divided by the number of possible edges in the graph. The following two lemmas state the lower bound and the upper bound, respectively. For the sake of convenience, we assume that
is an integer.
that contain the edge. Given a (β, σ)-hyperedge S, let μS(G) denote the subgraph of μ(G) induced by the nodes in S. If S contains k nodes, then μS(G) contains at most
edges. In general, any particular edge in μS(G) may have a weight in the interval (0, 1]. However, we can establish lower and upper bounds on the density of μS(G), where we define the density of a graph to be the total weight of the edges in the graph divided by the number of possible edges in the graph. The following two lemmas state the lower bound and the upper bound, respectively. For the sake of convenience, we assume that
is an integer.
Lemma 1
If S is a (β, σ)-hyperedge with k nodes, then the density of μS(G) is at least
where l is the smallest integer such that
Proof
To prove this lower bound, we consider the sparsest graphs in
 (S) that enable S to be a hyperedge. To assist this analysis, we partition
(S) that enable S to be a hyperedge. To assist this analysis, we partition
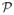 (S) into
sets
(S) into
sets
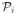 (S),
where
(S),
where
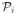 (S) is the set of graphs on the nodes in S that contain exactly i edges. By construction,
(S) is the set of graphs on the nodes in S that contain exactly i edges. By construction,
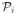 (S) contains
graphs. It is easy to see that the lower bound is achieved when the following conditions are satisfied:
(S) contains
graphs. It is easy to see that the lower bound is achieved when the following conditions are satisfied:
if a nonempty graph H ∈
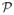 (S) occurs at least once in
(S) occurs at least once in
 (S), i.e., ψ(H) > 0, then H is one of the
sparsest graphs in
(S), i.e., ψ(H) > 0, then H is one of the
sparsest graphs in
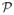 (S), i.e., the graphs with the smallest number of edges,
(S), i.e., the graphs with the smallest number of edges,for each such graph H, ψ(H) = βn, and
each of the remaining graphs (for which ψ(H) < βn) in
 (S) is the empty graph, i.e., the only graph in
(S) is the empty graph, i.e., the only graph in
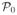 (S).
(S).
Using the definition of l in the statement of the lemma, we select the
sparsest graphs in
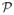 (S) as follows: 1) pick all the graphs in the sets
(S) as follows: 1) pick all the graphs in the sets
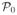 (S),
(S),
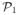 (S), …,
(S), …,
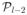 (S),
(S),
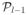 (S) and 2) pick as many graphs as necessary from
(S) and 2) pick as many graphs as necessary from
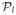 (S) so as to obtain
graphs. To obtain the lower bound on the density, we simply compute the total number of edges in these graphs and divide that number by
. Each graph in
(S) so as to obtain
graphs. To obtain the lower bound on the density, we simply compute the total number of edges in these graphs and divide that number by
. Each graph in
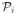 (S), 1 ≤ i < l contributes i edges, whereas each of the
graphs from
(S), 1 ≤ i < l contributes i edges, whereas each of the
graphs from
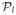 (S) contributes l edges.
(S) contributes l edges.
Lemma 2
If S is a (β, σ)-hyperedge, then the density of μS(G) is at most
where u is the largest integer such that
Proof
To obtain the upper bound on the density of μS(G), we pack the densest graphs in
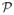 (S) into the set of
graphs that occur at least βn times in
(S) into the set of
graphs that occur at least βn times in
 (S). Using the definition of u from the statement of the lemma, these graphs belong to the sets
, …,
(S). Using the definition of u from the statement of the lemma, these graphs belong to the sets
, …,
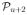 (S),
(S),
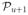 (S) and as many graphs as necessary from
(S) and as many graphs as necessary from
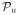 (S). To maximize the density, each of these graphs, other than the complete graph in
, must occur exactly βn times in
(S). To maximize the density, each of these graphs, other than the complete graph in
, must occur exactly βn times in
 (S). The number of such graphs is
. The remaining occurrences correspond to the complete graph in
, i.e., it must occur
times. Summing up the total number of edges in these graphs and dividing the sum by
gives rise to the upper bound. Specifically, we use
edges from the complete graph in
, i edges from each of the graphs in
(S). The number of such graphs is
. The remaining occurrences correspond to the complete graph in
, i.e., it must occur
times. Summing up the total number of edges in these graphs and dividing the sum by
gives rise to the upper bound. Specifically, we use
edges from the complete graph in
, i edges from each of the graphs in
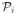 (S),
, and u edges from each of
(S),
, and u edges from each of
graphs in
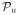 (S) for computing the total number of edges. Finally, we need the indicator function [
] to avoid double counting in the special case when
.
(S) for computing the total number of edges. Finally, we need the indicator function [
] to avoid double counting in the special case when
.
Given the parameters 0 < β, σ ≤ 1 and an integer k > 0, let λ(k, β, σ) and γ(k, β, σ) denote the lower and upper bounds defined by Lemmas 1 and 2, respectively, on the density of a (β, σ)-hyperedge with k nodes. For purposes of brevity, we denote the bounds by λ and γ when the parameters are clear from the context.
Lemma 3
If l is the smallest integer such that
and u is the largest integer such that
then .
We can prove this lemma by changing the variable i to in the definition of either l or u. By using the previous three lemmas and some simplifications, we can prove the following corollary.
Corollary 4
If S is a (β, σ)-hyperedge with k nodes, then λ (k, β, σ) + γ(k, β, σ) = 1.
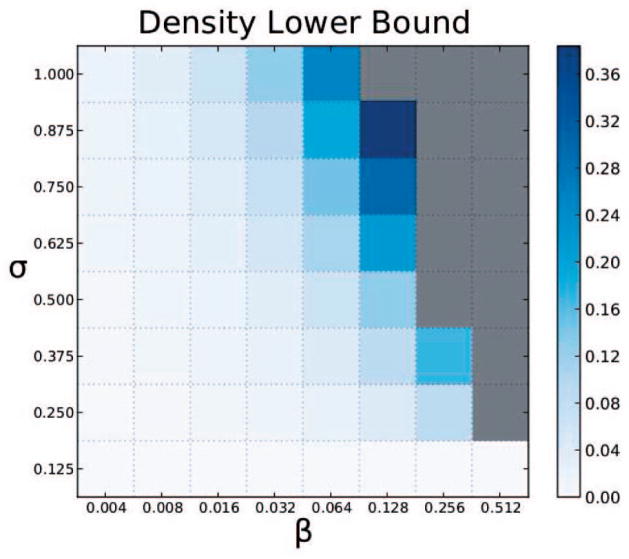
Fig. 2 illustrates how the theoretical lower bound on density λ(3, β, σ) varies with the parameters β and σ for hyperedges of size three. In general, after fixing β (respectively, σ), the lower bound monotonically increases with an increase in σ (respectively, β). For small values of β or σ, the lower bound is zero. Note that we only plot the lower bounds since for a given value of β, σ, and k, the sum of λ and γ is one, by Corollary 4.
Fig. 2.
Variation of lower bound on density of three-node hyperedges across different values of β and σ. Gray cells indicate the values of β and σ for which no hyperedge can exist.
4.2 Clustering Algorithm
Our algorithm consists of the following steps, illustrated in Fig. 3:
Fig. 3.

A flowchart that illustrates how our method computes (1/12, 1)-hyperedges in the ensemble of graphs displayed in Fig. 1a. Solid lines (respectively, dashed lines) in the summary graph indicate edges whose weights fall inside (respectively, outside) the interval spanned by the theoretical lower and upper bounds on the density of a (1/12, 1)-hyperedge. Line widths in both summary graphs are proportional to the corresponding edge weights.
Compute μ(
 ) =
) =
 G, the union of the graphs in
G, the union of the graphs in
 .
.Assign each edge (u, v) in μ(
 ) a weight w(u, v) equal to the fraction of graphs in
) a weight w(u, v) equal to the fraction of graphs in
 that contain (u, v) as an edge.
that contain (u, v) as an edge.-
For each edge (u, v) in μ(
 ), transform its weight using the function
), transform its weight using the function
where τ is a large positive number.
Compute all highly dense subgraphs of k nodes in μ(
 ).
).
The first two steps simply compute the average μ(
 ) of the graphs in
) of the graphs in
 . The third step transforms the edge weights in μ(
. The third step transforms the edge weights in μ(
 ) so that all edge weights in the interval [λ, γ] are close to one and all edge weights outside this interval are small. Note that the value of the maximum in the transformation function is negative iff w(u, v) lies in the interval [λ, γ]. Hence, by choosing τ = 100, we ensure that the transformed weights are close to one for edges whose weights lie in the interval [λ, γ] and are close to zero otherwise.
) so that all edge weights in the interval [λ, γ] are close to one and all edge weights outside this interval are small. Note that the value of the maximum in the transformation function is negative iff w(u, v) lies in the interval [λ, γ]. Hence, by choosing τ = 100, we ensure that the transformed weights are close to one for edges whose weights lie in the interval [λ, γ] and are close to zero otherwise.
Finally, in this transformed graph, we compute all subgraphs with sufficiently high density, and report the node sets of these subgraphs as hyperedges. For a hyperedge S, our intuition is that this transformation will convert μS(
 ) into a dense (heavily weighted) subgraph of μ(
) into a dense (heavily weighted) subgraph of μ(
 ). To enumerate all sufficiently dense subgraphs, we extended the ODES algorithm [17]. We describe this extension below.
). To enumerate all sufficiently dense subgraphs, we extended the ODES algorithm [17]. We describe this extension below.
Given an unweigthed graph, ODES enumerates all clusters in the graph with density above a given threshold, provided this threshold is at least 0.5. Starting from each individual edge in the input graph, ODES iteratively extends each potential cluster by adding any node whose addition to the cluster does not decrease its density below the input threshold. If a cluster cannot be so extended, ODES reports it as a maximal dense cluster. ODES hinges on the property that every subgraph with density at least 0.5 contains a node whose removal does not disconnect the graph or decrease the density. We extended this property for weighted graphs (see the supplemental material, which can be found on the Computer Society Digital Library at http://doi.ieeecomputersociety.org/10.1109/TCBB.2013.71).
Also, we forced our algorithm to compute dense subgraphs with exactly k nodes rather than enumerate all dense subgraphs.
4.2.1 Remarks
Our algorithm is a heuristic that is not guaranteed to compute all (β, σ)-hyperedges. Moreover, some sets of nodes computed by our algorithm may not satisfy the properties of a (β, σ)-hyperedge. This discrepancy can arise because the lower and upper bounds apply to the density of a hyperedge but we transform each edge weight individually. Yet our approach works well on both synthetic and real biological data, as we demonstrate below. The worst-case running time of our algorithm can be exponential in k. However, in practice, our algorithm runs very efficiently, as we report below.
5 Results
We divide our results into two parts: 1) synthetic data (see Section 5.1) and 2) the pathway structures inferred from double knockout budding yeast strains [3] (see Section 5.2). We used a Dell R515 server with two 2.8-GHz AMD Opteron 4,184 CPUs for all operations. In each execution of our algorithm, we computed all subgraphs in the summary graph with density at least 0.9.
5.1 Synthetic Data
5.1.1 Generation
We generated synthetic data sets by implanting hyperedges in a “background graph.” We used the BioGRID (version 3.1.74) [29]. S. cerevisiae protein-protein interaction network as the background graph. This graph contained 168,599 interactions among 6,063 genes. Three parameters governed the data generation: k, the number of nodes in the hyperedges we implanted; ω, the maximum fraction of node overlap between an implanted hyperedge and any other implanted hyperedge(s); and η, a fraction representing the amount of noise that we introduced. We used the values of 3 and 4 for k, 0 and 0.5 for ω, and the elements in the set {0, 0.1, 0.2, 0.3, 0.4, 0.5} for η, giving 24 combinations of parameters. For each setting of the parameters (k, ω, η), we generated 10 graph ensembles, with each ensemble containing 1,024 graphs. We used 1,024 graphs to support hyperedges of size four. We created ten ensembles so that we could compute the average and standard deviation of the results. To generate one ensemble for the parameters (k, ω, η), we performed the following sequence of steps:
We created 1,024 copies of the background graph. These graphs formed the ensemble
 .
.-
We implanted 100 hyperedges of size k among these copies. To create a single hyperedge with k nodes, we used two steps:
We selected k nodes uniformly at random from the set of nodes in the background graph, while ensuring that at most an ω fraction of these k nodes overlapped with hyperedge(s) that were already implanted.
To implant a hyperedge among these k nodes, we replaced the subgraph induced by them in each graph in
 with a random subgraph generated by the Erdös-Rényi (k, 0.5) model. By adding each possible edge with probability 0.5, we aimed to ensure that the distribution of edges among these k nodes was relatively uniform across
with a random subgraph generated by the Erdös-Rényi (k, 0.5) model. By adding each possible edge with probability 0.5, we aimed to ensure that the distribution of edges among these k nodes was relatively uniform across
 .
.
-
To add noise, we performed the following steps on each graph G in
 :
:We removed each edge in G with probability η.
We generated a graph G′ using the degree-preserving randomization of the background graph.
We added each edge of G′ to G with probability η.
Observe that when the noise parameter η = 0, step 3 does not change G. On the other hand, when η = 1, G equals G′. In this situation, we replace the graph containing all the implanted hyperedges by a randomized version of the background graph. Values of η between zero and one create a graph that interpolates between these two extremes.
5.1.2 Evaluation
We applied our algorithm on each of these data sets using five values of σ, {i/8, 3 ≤ i ≤ 7}, and (its largest feasible value). We did not consider σ equal to 1/8 or 2/8, reasoning that these values were two small for our purpose. Neither did we consider σ = 1, since our hyperedge implantation method was unlikely to generate all possible subgraphs corresponding to a hyperedge.
To compare the computed hyperedges with the planted hyperedges, we defined precision and recall in the following manner. Let R denote the set of planted hyperedges and C denote the set of computed hyperedges. We defined
Note that the numerators of both quantities measured the planted hyperedges that we also found by our algorithm. For precision, we compared the size of this set to the total number of computed hyperedges, whereas for recall, we compared this number to the total number of planted hyperedges. For each setting of the parameters, we computed the average and standard deviation of precision and recall values across all 10 runs.
5.1.3 Results
We ran our algorithm on each of the ten ensembles for each of the 24 parameter sets. Our algorithm ran in an average of 5.6 seconds across all the data sets. When the noise parameter η is 0.5, both precision and recall were zero. Therefore, we do not display results for this value of noise. For smaller values of η, we observed that both precision and recall were equal to one for many parameter sets. Moreover, precision was not less than 0.9 for any parameter set, but recall decreased with increasing values of noise. Hence, we focus only on the recall values in the rest of this section.
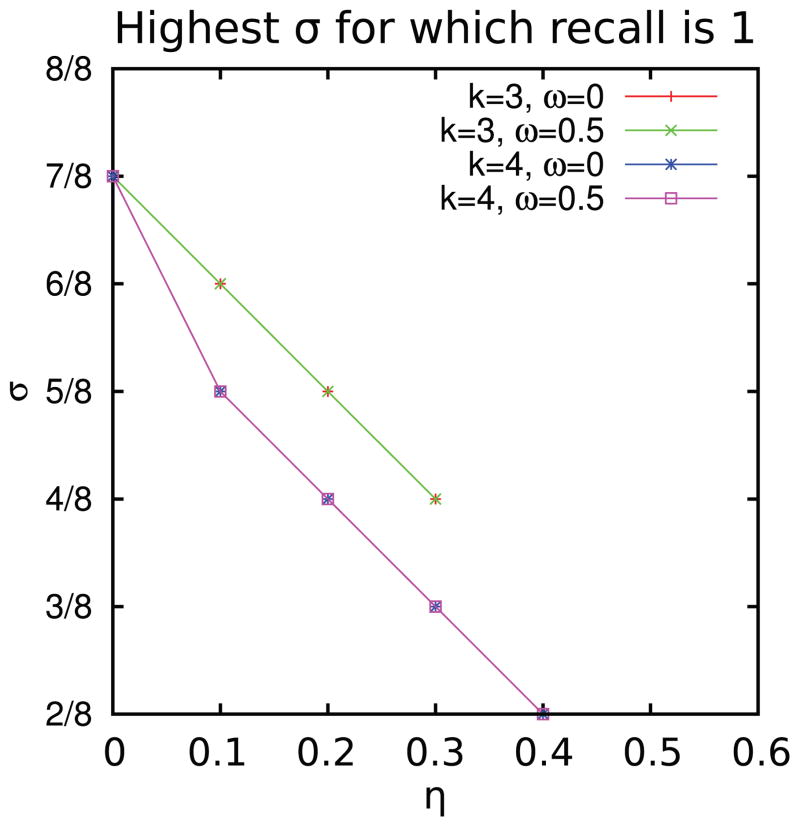
For each value of η between 0 and 0.4, Fig. 4 plots the highest value of σ such that recall is one. Note that the two curves (for the two values of hyperedge overlap parameter ω) for three node hyperedges are identical, as are the two curves for four node hyperedges. These plots show that as noise increased, the highest value of σ for which we could recover the implanted hypergraphs perfectly decreased. Moreover, noise had a more deleterious effect on the algorithm’s ability to recover four node hyperedges than on three node hyperedges.
Fig. 4.
Plot of the highest value of σ for which recall is 1, as the noise parameter η varies.
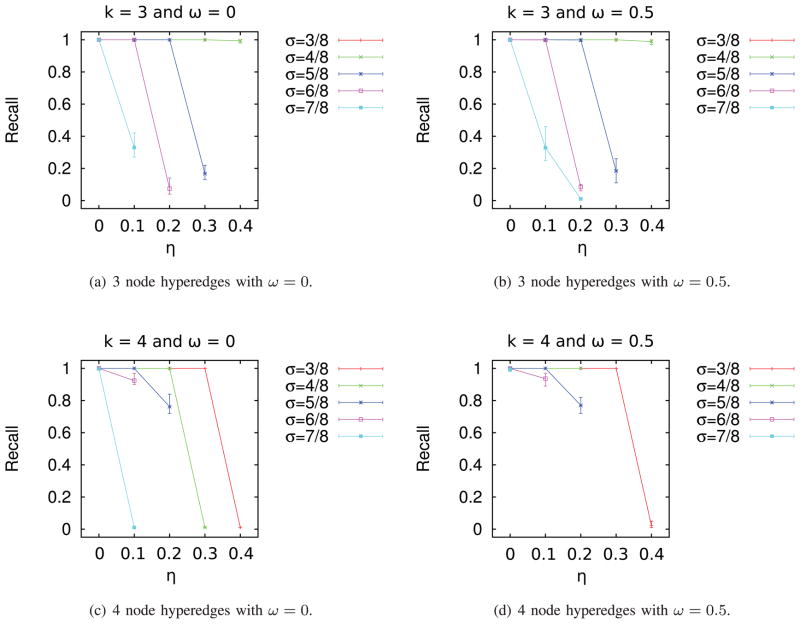
The graphs in Fig. 5 illustrate the precise relationship between noise and recall. Several salient trends emerge from these plots. For three node hyperedges (with overlaps of 0 and 0.5, Figs. 5a and 5b), the curves for σ = 4/8 and σ = 3/8 are almost identical. For three node hyperedges, noise had no appreciable effect on recall for the two lowest values of σ we experimented with (3/8 and 4/8). However, for four node hyperedges, recall dropped dramatically with increase in noise. As can be expected, this drop-off occurred at a larger value of noise (0.4) when σ is 3/8 compared to when σ is 4/8 (noise of 0.3). In fact, our algorithm was unable to recover any implanted four node hyperedges when the overlap was 0.5 and noise was larger than 0.2. In general, recall dropped with increase in noise or σ, with the magnitude of the decrease being largest for the largest values of these parameters. We concluded that for σ ≤ 5/8, our algorithm can recover the implanted hyperedges with high precision and recall for moderate amounts of noise (0.1–0.2) even when the hyperedges overlapped.
Fig. 5.
Recall as a function of noise parameter η for synthetic data.
5.2 Analysis of Battle et al. Data
Given quantitative phenotype measurements for a set of single and double knockout organisms, Battle et al. [3] computed activity pathway networks (APNs) that represented functional dependences between genes and their combined effects on the phenotype. Each APN terminated in a node called “Reporter” that represented the quantitative phenotype. They sampled the space of APNs using a Markov chain Monte Carlo method, thereby creating an ensemble of networks. Analogous to our definition of hyperedges, they were interested in sets of genes that occurred in a single linear chain (in any order). For each such set, they computed the probability that the genes in it occurred in a linear chain across the ensemble of APNs. When this probability was at least 0.6 and exceeded the probability of occurrence of any specific linear ordering of the genes in G by a factor of 1.8, they collected these genes into a collapsed node similar to our notion of hyperedge. They applied their method to quantitative GI data between pairs of genes [14] whose single mutants upregulated the unfolded protein response (UPR) in the endoplasmic reticulum.
We obtained the 500 APNs computed by them. We treated each APN as an undirected, unweighted graph so as to focus purely on the network topology rather than on the directionality of the probabilistic dependences. Here, we discuss the properties of the hyperedges we computed and what light they shed on the interactions between these genes. We divided our analysis into multiple parts:
parameter selection,
degree distribution in the hypergraph,
comparison of hyperedges to collapsed nodes, and
comparison to NetsTensor.
5.2.1 Parameter Selection
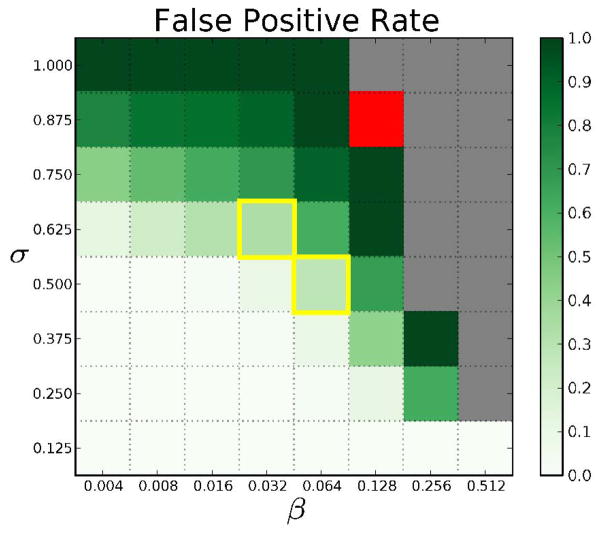
We executed our algorithm on the ensemble of 500 networks with k = 3, 4, and 5, eight values of σ, {i/8, 1 ≤ i ≤ 8}, and β = 2j/500, . For each dense subgraph computed by our algorithm, we evaluated whether it was truly a (β, σ)-hyperedge. If it was not, we deemed this hyperedge a false positive, and measured the false-positive rate (FPR) as the ratio of the number of false positives to the total number of computed dense subgraphs. As pointed out earlier, our approach may also have false negatives. However, we do not have a method for estimating their count.
Fig. 6 illustrates how the FPR varies with β and σ. When both parameters are small (lower left corner), the FPR is close to 0. When σ is high (top) or when both parameters are high (center), the FPR is close to one, suggesting that our algorithm computes many dense subgraphs that do not satisfy the constraints laid down by β and σ. We selected two pairs of the parameters that had FPR less than 0.5: (0.032, 0.625) and (0.064, 0.5), with FPR 0.34 and 0.29, respectively. In the first case, 5/8 possible subgraphs each appear at least 16 times in the set of 500 graphs. In the second case, 4/8 possible subgraphs each appear at least 32 times in the 500 graphs. The first case has the advantage of having a higher value of σ. The second case has a lower value of σ, but involves more networks overall from the input ensemble. We observed that the (0.032, 0.625)-hyperedges formed a superset of the (0.064, 0.5)-hyperedges. Hence, we focused our attention on the parameters β = 0.032 and σ = 0.625. Using these parameter values, we obtained 398 3-node hyperedges, out of which 262 were true hyperedges (see the online supplemental Table S1 for details). Our method took 1.54 seconds to compute these hyperedges. Note that we did not find any hyperedge having four or more nodes with these values of β and σ. In fact, this set of 500 networks did not support any four-node hyperedges unless the values of β and σ were very small, which are uninteresting for our purpose. Hence, we focused our attention on three-node hyperedges in the rest of the analysis.
Fig. 6.
Visualization of the false-positive rates in the hyperedges computed from the ensemble of APNs. Red cells correspond to parameter values for which our algorithm did not compute any cluster for k = 3. Gold boxes highlight pairs of β and σ we used for further biological analysis. Gray cells indicate pairs of β and σ that are invalid, i.e., no collection of graphs can support hyperedges with such high values of β and σ. In other words, βσ > 1/23.
5.2.2 Analysis of Degree Distribution in the Hypergraph
High degree nodes (a.k.a. hubs) in protein-protein interaction networks are known to carry out important biological functions [10]. We asked whether the same property held true in our hypergraph, i.e., whether genes participating in many hyperedges were highly enriched in any biological function. Accordingly, we computed the degree distribution of the hypergraph, i.e., we ranked genes in decreasing order of the number of hyperedges in which they participated. We computed Gene Ontology (GO) biological processes enriched in this ranked list of genes using FuncAssociate [5], which is a functional enrichment software package that can take ranked lists of genes as input. We asked FuncAssociate to compute enriched terms using the list of genes studied by Battle et al. as background. We set the number of simulations to 10,000 and significance cutoff to 0.01 in FuncAssociate. We reasoned that this analysis would help us identify biological processes whose genes participated in numerous hyperedges, i.e., processes whose genes were connected in multiple ways both to each other and to genes external to the process.
Table 1 displays the top four enriched GO terms (see the online supplemental Table S2 for all the enriched terms). Note that FuncAssociate may report closely related GO terms, in which case we focus on the most specific term. The most enriched GO term was the molecular function transferase activity, transferring hexosyl groups. This term annotates genes that encode enzymes responsible for catalyzing the transfer of hexosyl groups from one compound to another during the glycosylation reaction [24]. The genes annotated with this term either participate in protein N-linked glycosylation (ALG3, ALG5, ALG6, ALG8, ALG9, ALG12, DIE2, OST3, OST5) or in mannosylation (ANP1, MNN2, PMT1, PMT2) [14]. Both of these reactions are vital for protein folding because (i) during the N-linked glycosylation of a protein in ER, an oligosaccharide is attached to a protein as a marker of the state of its folding [1] and (ii) inhibition of O-mannosylation has been implicated in the activation of unfolded protein response [2]. On average, each of the genes in these two terms participated in 13 hyperedges (in at least 2 and as many as 28 hyperedges), indicating that the interactions between their corresponding enzymes and several ER proteins are quite unclear, at least from the APN-based analysis of the genetic interaction data.
TABLE 1.
GO Terms Enriched in the List of Genes Sorted in Descending Order of Their Degrees in the (0.032, 0.625)-Hypergraph
| Rank | GO Term ID | GO Term Name | Adjusted P-value | LOD |
|---|---|---|---|---|
| 1 | GO:0016758 | Transferase activity, transferring hexosyl groups | 0.0004 | 1.384 |
| 2 | GO:0016757 | Transferase activity, transferring glycosyl groups | 0.0004 | 1.384 |
| 3 | GO:0016020 | Membrane | 0.0034 | 1.219 |
| 4 | GO:0006486 | Protein glycosylation | 0.0008 | 1.167 |
LOD stands for log-odds ratio. We have sorted the rows by the values in the LOD column.
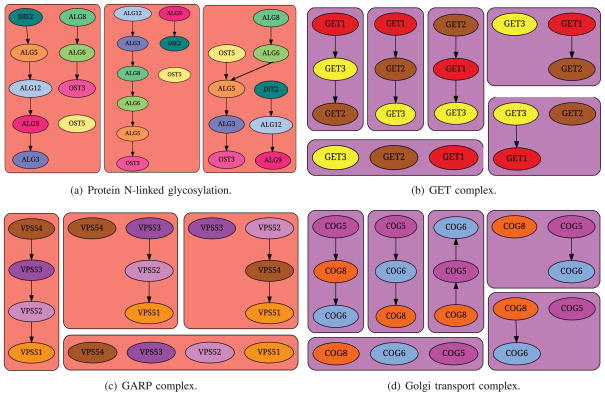
We also noticed that there were 34 hyperedges such that each of them contained three genes from Protein N-linked glycosylation (GO:0006487), suggesting that the pairwise connections among these genes are difficult to estimate. In contrast, Battle et al. reported that their method accurately predicted the ordering of the genes participating in N-linked glycosylation. Their observation appears to contradict our results. Upon examining the subgraphs induced by this set of genes in the ensemble of 500 networks, we observed that they involved only 32 unique edges (reinforcing their findings) but in numerous combinations (supporting our result), thus resolving the apparent contradiction. See Fig. 7a for some of the subgraphs induced by this set of genes in the APNs.
Fig. 7.
Illustration of different subgraphs induced in the ensemble by genes annotated to GO terms enriched in hyperedges or collapsed nodes.
Note that we did not perform a similar analysis for collapsed nodes computed by Battle et al. since they did not overlap each other.
5.2.3 Comparison between Hyperedges and Collapsed Nodes
From the supplementary data provided by Battle et al., we collected all six collapsed nodes containing three or more genes. The largest collapsed node contained six genes. Treating all these collapsed nodes as the ground truth, we computed the precision and recall of our hyperedges in the following manner. Let Ri denote the ith collapsed node and Cj denote the jth hyperedge, where i ranges over the collapsed nodes and j over the hyperedges. We defined
For this calculation, we only considered hyperedges that did not involve the Reporter node. There were 281 such hyperedges out of which 193 were true hyperedges. These hyperedges had a recall of 0.83 and a precision of 0.21. Such a high recall resulted from the fact that most of the collapsed nodes were small in size (four of them contained three or four nodes) and thereby were comparable to the hyperedges. Overall, these statistics indicated that our algorithm succeeded in discovering almost all the collapsed nodes computed by Battle et al. In addition, our method discovered many hyperedges not computed by Battle et al.
To better understand the similarities and differences between hyperedges and collapsed nodes, we computed the functional enrichment of each hyperedge and each collapsed node. For this analysis, we used the MGSA algorithm [4]. We did not select FuncAssociate since we did not need to analyze ranked lists. Moreover, MGSA selects a non-redundant set of GO terms enriched in a input set of genes. It computes a posterior probability for each GO term that reflects how well the genes annotated to that term overlap with the given set of gene while not overlapping with other GO terms. For our analysis, we used MGSA to compute the enrichment of GO cellular components. We reported all GO terms with posterior probability at least 0.4.
We found that 32 hyperedges were significantly enriched in seven protein complexes and two membrane-related GO terms (see Table 2 and the online supplemental Tables S3 and S4 for details). Of these, 27 hyperedges are true (0.032, 0.625)-hyperedges, suggesting that the true hyperedges are more likely to include biologically interesting sets of genes. This observation supports our FPR-based method of choosing parameters. Note that the majority of hyperedges were not significantly enriched in any GO term. We anticipated this result since each hyperedge involved only three genes, a number usually insufficient for significant enrichment.
TABLE 2.
GO Terms Enriched in (0.032, 0.625)-Hyperedges or in Collapsed Nodes Reported by Battle et al.
| GO term ID | GO term Name | Min posterior for a hyperedge | Max posterior for a hyperedge | #Enriched hyperedges | Posterior for a collapsed node |
|---|---|---|---|---|---|
| GO:0043529 | GET complex | 0.8082 | 0.9989 | 9 | 0.9988 |
| GO:0000938 | GARP complex | 0.4644 | 0.7498 | 8 | - |
| GO:0072546 | ER membrane protein complex | 0.9662 | 0.9709 | 5 | 0.9995 |
| GO:0000812 | Swr1 complex | 0.4198 | 0.9559 | 5 | 0.5819 |
| GO:0034272 | Phosphatidylinositol 3-kinase complex II | 0.4823 | 0.4842 | 2 | - |
| GO:0005942 | Phosphatidylinositol 3-kinase complex | 0.4830 | 0.4866 | 2 | - |
| GO:0030867 | Rough endoplasmic reticulum membrane | 0.4693 | 0.4728 | 2 | - |
| GO:0005791 | Rough endoplasmic reticulum | 0.4679 | 0.4801 | 2 | - |
| GO:0033254 | Vacuolar transporter chaperone complex | 0.4812 | 0.4812 | 1 | - |
| GO:0031310 | Intrinsic to vacuolar membrane | 0.4861 | 0.4861 | 1 | - |
| GO:0017119 | Golgi transport complex | - | - | - | 0.9991 |
For each GO term, we report the number of enriched hyperedges and the range of the posterior probabilities across the hyperedges. The last column reports the posterior probability for collapsed nodes. A dash (-) in the third, fourth, or sixth column indicates that the posterior probability is less than 0.4. We sorted the rows by the number of enriched hyperedges. Note that each GO term is enriched in at most one collapsed node.
A majority of the enriched complexes were involved in vesicular trafficking of proteins between ER and the Golgi body (GET complex, GARP complex, and vacuolar transporter chaperone complex) and/or sorting proteins (vacuolar transporter chaperone complex, phosphatidylinositol 3-kinase complex II). The GET complex is involved in Golgi to ER Traffic, especially in facilitating insertion of tail-anchored proteins into the ER membrane [27]. It contained three proteins: Get1, Get2, and Get3; Fig. 7b illustrates some of the different subgraphs induced by the corresponding genes in the ensemble. All three genes were members of a single hyperedge, suggesting that the APNs had considerable disagreement about how these proteins should be connected to each other. The Golgi-associated retrograde protein (GARP) complex (see Fig. 7c) is responsible for recycling of proteins from endosomes to the late Golgi. The original publication of the genetic interaction data used by Battle et al. [14] noted that a significant set of genes whose deletion caused up-regulation of the UPR were involved in the late Golgi. This complex contains four proteins: Vps51, Vps52, Vps53, and Vps54. Among them, the last three constituted a hyperedge, suggesting that the precise connections among these proteins are unclear (according to the genetic interaction data). The ER membrane protein complex (EMC) was highly enriched, as well. Loss of this complex causes misfolding of membrane proteins [14]. The SWR1 complex, which is involved in chromatin remodeling, was also highly enriched in three hyperedges.
Table 2 compares the GO terms enriched in hyperedges to the terms enriched in collapsed nodes. Four collapsed nodes were enriched, each in one distinct GO term. Three out of four GO terms enriched in collapsed nodes were also enriched in hyperedges. Interestingly, seven of the 11 GO terms enriched in hyperedges were not enriched in any collapsed node. On the other hand Golgi transport complex was enriched in a collapsed node, but not in any hyperedge. In Fig. 7d, we display some of the subgraphs induced by the three genes (Cog5, Cog6, and Cog8) annotated to this term in the ensemble of APNs. Although some subgraphs were partially or fully disconnected, a vast majority of the subgraphs were paths. Thus, our algorithm did not consider these genes as constituting a hyperedge. We concluded that hyperedges and collapsed nodes were somewhat complementary to each other in capturing interesting sets of genes, although hyperedges do seem to involve a larger space of ER-related functions than the collapsed nodes.
5.2.4 Comparison to NetsTensor
Finally, we sought to demonstrate that our notion of hyperedges is quite dissimilar to other types of analyses on graph ensembles, notably that of finding frequent dense subgraphs. We chose the NetsTensor [16] algorithm, whose goal is to find dense subgraphs that are frequent, i.e., appear in many graphs in the ensemble. To obtain clusters comparable to our hyperedges (for which k = 3, β = 16/500), we asked NetsTensor to compute clusters of size at least 3 and frequency at least 16. However, we could not find any clusters, even with the low density cutoff of 1/3. This result shows the usefulness of hyperedges in identifying interesting sets of genes that cannot be computed by more well-established methods for computing dense modules in graph ensembles.
6 Conclusions
In this paper, we have proposed hypergraphs as a novel representation for capturing the uncertainty inherent in inferring gene interaction networks from systems biology data sets. Our main theoretical contributions are twofold: a formal definition of (β, σ)-hyperedges supported by an ensemble of networks and an algorithm for computing (β, σ)-hyperedges of a fixed size k. Our algorithm relied on a transformation of the input ensemble that enabled us to apply an existing clustering algorithm to discover hyperedges. We demonstrated that our algorithm could recover hyperedges planted in synthetic data sets with high precision and recall. The recall of our algorithm degraded gracefully with increase in the noise in the data.
Applying these techniques to a data set of 500 APNs inferred from quantitative genetic interaction data, we discovered 398 hyperedges. Each hyperedge included genes for which the APNs could not infer precise pairwise interactions. We were able to use the false-positive rate to select appropriate values of the parameters β and σ. We could settle on the value of k by examining the largest value for which our method was able to compute hyperedges. Examination of functional enrichment trends in the list of genes ranked in order of the number of hyperedges they participated in revealed several biological processes related to protein folding. Enrichment of individual hyperedges allowed us to discover interesting protein complexes, among which the genetic interaction data did not support precise pairwise interactions. These results suggest that more in-depth experiments may be needed to resolve the ambiguity in the connections among the members of these complexes.
We envision that this paper will serve as the basis for a rich body of research. Several extensions and generalizations of our ideas are immediate. For instance, we would ideally like to compute maximal hyperedges (those that are not contained in any other hyperedges). We would also like to systematically enumerate all hyperedges. It may be possible to employ the ideas from itemset mining here. Formulations of the problems other than enumeration are also interesting, for example, finding the (β, σ)-hyperedge with the largest number of nodes, computing a set of nonredundant (β, σ)-hyperedges, or discovering statistically significant hyperedges. Moreover, we will also consider other definitions of hyperedges, for example, a variation of the current formulation where each hyperedge will still induce highly varying subgraphs across the ensemble but we will consider subgraphs sharing a large fraction of edges to be identical. We plan to address these problems in the future. We are also considering extensions to weighted and directed graphs.
Ultimately, we are interested in directly inferring hyperedges from diverse data sets without going through the intermediate step of inferring an ensemble of graphs. By discovering such hypergraphs, we hope to pinpoint which set of genes and proteins might be ideal for further experimentation. Incorporating the data from these experiments might help to refine hyperedges and resolve the pairwise interactions among the nodes, resulting in a fruitful interplay and feedback between computational and experimental scientists.
Our method is directly applicable to any set of networks with varying topologies. Such a set of networks may naturally occur in a cell due to the dependence of molecular interactions on time, space, and/or cellular contexts [12], [22]. Hypergraphs derived from such networks may reveal new biological insights about condition-specific cellular processes.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health under grant R01-GM095955-01 and the US National Science Foundation (NSF) under grants CBET-0933225 and DBI-1062380. Chris Poirel was supported by an NSF Graduate Research Fellowship. The authors would like to thank Alexis Battle for sharing the data set of 500 APNs.
Biographies

Ahsanur Rahman received the BS degree in computer science and engineering from Bangladesh University of Engineering and Technology in 2008. He is currently working toward the PhD degree in the Computer Science Department at Virginia Tech. He is currently working as a research assistant under Dr. T.M. Murali. His research interests include computational systems biology, graph theory, hypergraphs, and data mining. He received the Best Paper Award at the 2012 ACM Conference on Bioinformatics, Computational Biology and Biomedicine.

Christopher L. Poirel received the BS degree in mathematics from the University of South Carolina Honors College, Columbia, and the PhD degree in computer science at Virginia Tech, Blacksburg. His research lies at the confluence of graph theory and molecular biology, where he seeks network-based formulations and solutions to challenging problems that arise in systems biology. His awards include the Graduate Research Fellowship (US National Science Foundation), Science Graduate Fellowship Finalist (US Department of Energy), Virginia Tech’s Computer Science Department Doctoral Fellowship, the Best Paper Award at the 2012 ACM Conference on Bioinformatics, Computational Biology and Biomedicine, and the Jeong S. Yang Award for Excellence in Mathematics.

David J. Badger received the BS degree in computer science from Virginia Tech, Blacksburg, in 2006. He is currently a software engineer at Virginia Tech, working in a research group led by Dr. T.M. Murali. His interests include database systems, graph visualization, graph theory, and gene-function prediction.

Craig Estep received the BS degree in computer science and mathematics from Virginia Tech in 2012. He is currently working toward the master’s degree in computer science at Virginia Tech and is working as a research assistant under Dr. T.M. Murali. His interests include algorithm analysis, computational systems biology, graph theory, and discrete mathematics.

T.M. Murali received the undergraduate degree in computer science from the Indian Institute of Technology, Madras, India, and the ScM and PhD degrees from Brown University. He is an associate professor in the Department of Computer Science at Virginia Tech. He codirects the ICTAS Center for Systems Biology of Engineered Tissues and is the associate director for the Computational Tissue Engineering Interdisciplinary Graduate Education Program. His research group develops phenomenological and predictive models dealing with the function, behavior, and properties of large-scale molecular interaction networks in the cell.
Footnotes
For information on obtaining reprints of this article, tcbb@computer.org, and reference IEEECS Log Number TCBBSI-2013-01-0024.
Contributor Information
Ahsanur Rahman, Email: ahsanur@vt.edu, Department of Computer Science, Virginia Tech, Blacksburg, VA.
Christopher L. Poirel, Email: poirel@vt.edu, Department of Computer Science, Virginia Tech, Blacksburg, VA
David J. Badger, Email: dbadger@vt.edu, Department of Computer Science, Virginia Tech, Blacksburg, VA
Craig Estep, Email: craigy@vt.edu, Department of Computer Science, Virginia Tech, Blacksburg, VA.
T.M. Murali, Email: murali@cs.vt.edu, Department of Computer Science and the ICTAS Center for Systems Biology of Engineered Tissues, Virginia Tech, Blacksburg, VA
References
- 1.Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. 4. Garland Science; 2002. The Endoplasmic Reticulum. [Google Scholar]
- 2.Arroyo J, Hutzler J, Bermejo C, Ragni E, García-Cantalejo J, Botías P, Piberger H, Schott A, Sanz AB, Strahl S. Functional and Genomic Analyses of Blocked Protein O-Mannosylation in Baker’s Yeast. Molecular Microbiology. 2011;79(6):1529–1546. doi: 10.1111/j.1365-2958.2011.07537.x. [DOI] [PubMed] [Google Scholar]
- 3.Battle A, Jonikas MC, Walter P, Weissman JS, Koller D. Automated Identification of Pathways from Quantitative Genetic Interaction Data. Molecular Systems Biology. 2010;6(1):379. doi: 10.1038/msb.2010.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bauer S, Gagneur J, Robinson PN. GOing Bayesian: Model-Based Gene Set Analysis of Genome-Scale Data. Nucleic Acids Research. 2010;38(11):3523–3532. doi: 10.1093/nar/gkq045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Berriz GF, Beaver JE, Cenik C, Tasan M, Roth FP. Next Generation Software for Functional Trend Analysis. Bioinformatics. 2009;25(22):3043–3044. doi: 10.1093/bioinformatics/btp498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Christensen T, Oliveira A, Nielsen J. Reconstruction and Logical Modeling of Glucose Repression Signaling Pathways in Saccharomyces cerevisiae, BMC Systems Biology. 2009;3(1):article 7. doi: 10.1186/1752-0509-3-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Demir E, et al. The BioPAX Community Standard for Pathway Data Sharing. Nature Biotechnology. 2010;28(9):935–942. doi: 10.1038/nbt.1666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dutkowski J, Ideker T. Protein Networks as Logic Functions in Development and Cancer. PLoS Computational Biology. 2011;7(9):article e1002180. doi: 10.1371/journal.pcbi.1002180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Friedman N, Koller D. Being Bayesian about Network Structure: A Bayesian Approach to Structure Discovery in Bayesian Networks. Machine Learning. 2003;50(1):95–125. [Google Scholar]
- 10.He X, Zhang J. Why Do Hubs Tend to Be Essential in Protein Networks? PLoS Genetics. 2006;2(6):article e88. doi: 10.1371/journal.pgen.0020088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Heath LS, Sioson AA. Semantics of Multimodal Network Models. IEEE/ACM Trans Computational Biology and Bioinformatics. 2009 Apr;6(2):271–280. doi: 10.1109/TCBB.2007.70242. [DOI] [PubMed] [Google Scholar]
- 12.Hu Z, Mellor J, Wu J, Kanehisa M, Stuart JM, DeLisi C. Towards Zoomable Multidimensional Maps of the Cell. Nature Biotechnology. 2007 May;25(5):547–554. doi: 10.1038/nbt1304. [DOI] [PubMed] [Google Scholar]
- 13.Huttenhower C, Haley EM, Hibbs MA, Dumeaux V, Barrett DR, Coller HA, Troyanskaya OG. Exploring the Human Genome with Functional Maps. Genome Research. 2009;19(6):1093–1106. doi: 10.1101/gr.082214.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jonikas MC, Collins SR, Denic V, Oh E, Quan EM, Schmid V, Weibezahn J, Schwappach B, Walter P, Weissman JS, Schuldiner M. Comprehensive Characterization of Genes Required for Protein Folding in the Endoplasmic Reticulum. Science. 2009;323(5922):1693–1697. doi: 10.1126/science.1167983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Klamt S, Haus UU, Theis F. Hypergraphs and Cellular Networks. PLoS Computational Biology. 2009;5(5):article e1000385. doi: 10.1371/journal.pcbi.1000385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li W, Liu C, Zhang T, Li H, Waterman M, Zhou X. Integrative Analysis of Many Weighted Co-Expression Networks Using Tensor Computation. PLoS Computational Biology. 2011;7(6):article e1001106. doi: 10.1371/journal.pcbi.1001106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Long J, Hartman C. ODES: An Overlapping Dense SubGraph Algorithm. Bioinformatics. 2010;26(21):2788–2789. doi: 10.1093/bioinformatics/btq514. [DOI] [PubMed] [Google Scholar]
- 18.Markowetz F, Spang R. Inferring Cellular Networks—A Review. BMC Bioinformatics. 2007;8(Suppl 6):article S5. doi: 10.1186/1471-2105-8-S6-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mithani A, Preston GM, Hein J. Rahnuma: Hypergraph-Based Tool for Metabolic Pathway Prediction and Network Comparison. Bioinformatics. 2009;25(14):1831–1832. doi: 10.1093/bioinformatics/btp269. [DOI] [PubMed] [Google Scholar]
- 20.Newman M. Modularity and Community Structure in Networks. Proc Nat’l Academy of Sciences USA. 2006;103(23):8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pe’er D. Bayesian Network Analysis of Signaling Networks: A Primer. Science Signaling. 2005;2005(281):pl4. doi: 10.1126/stke.2812005pl4. [DOI] [PubMed] [Google Scholar]
- 22.Rachlin J, Cohen DD, Cantor C, Kasif S. Biological Context Networks: A Mosaic View of the Interactome. Molecular Systems Biology. 2006 Nov;2(1) doi: 10.1038/msb4100103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ramadan E, Tarafdar A, Pothen A. A Hypergraph Model for the Yeast Protein Complex Network. Proc. 18th Int’l Parallel and Distributed Processing Symp; 2004. pp. 189–196. [Google Scholar]
- 24.Rini J, Esko J, Varki A. Essentials of Glycobiology. 2. Cold Spring Harbor Laboratory Press; 2009. Glycosyltransferases and Glycan-Processing Enzymes. [PubMed] [Google Scholar]
- 25.Schaefer CF, Anthony K, Krupa S, Buchoff J, Day M, Hannay T, Buetow KH. PID: The Pathway Interaction Database. Nucleic Acids Research. 2009;37:D674–D679. doi: 10.1093/nar/gkn653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schelhorn SE, Mestre J, Albrecht M, Zotenko E. Inferring Physical Protein Contacts from Large-Scale Purification Data of Protein Complexes. Molecular and Cellular Proteomics. 2011;10(6):article M110.004929. doi: 10.1074/mcp.M110.004929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schuldiner M, Metz J, Schmid V, Denic V, Rakwalska M, Schmitt H, Schwappach B, Weissman J. The GET Complex Mediates Insertion of Tail-Anchored Proteins into the ER Membrane. Cell. 2008;134(4):634–645. doi: 10.1016/j.cell.2008.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sharan R, Ideker T. Modeling Cellular Machinery through Biological Network Comparison. Nature Biotechnology. 2006;24(4):427–433. doi: 10.1038/nbt1196. [DOI] [PubMed] [Google Scholar]
- 29.Stark C, Breitkreutz BJJ, Chatr-Aryamontri A, Boucher L, Oughtred R, Livstone MS, Nixon J, Auken KV, Wang X, Shi X, Reguly T, Rust JM, Winter A, Dolinski K, Tyers M. The BioGRID Interaction Database: 2011 Update. Nucleic Acids Research. 2011;39:D698–D704. doi: 10.1093/nar/gkq1116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ulitsky I, Krishnamurthy A, Karp RM, Shamir R. DEGAS: De Novo Discovery of Dysregulated Pathways in Human Diseases. PLoS ONE. 2010;5(10):article e13367. doi: 10.1371/journal.pone.0013367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang K, Saito M, Bisikirska BC, Alvarez MJ, Lim WK, Rajbhandari P, Shen Q, Nemenman I, Basso K, Margolin AA, Klein U, Dalla-Favera R, Califano A. Genome-Wide Identification of Post-Translational Modulators of Transcription Factor Activity in Human B Cells. Nature Biotechnology. 2009;27(9):829–837. doi: 10.1038/nbt.1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhou W, Nakhleh L. Properties of Metabolic Graphs: Biological Organization or Representation Artifacts? BMC Bioinformatics. 2011;12(1):article 132. doi: 10.1186/1471-2105-12-132. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.