Rate-Dependent Behavior of the Amorphous Phase of Spider Dragline Silk

Abstract

The time-dependent stress-strain behavior of spider dragline silk was already observed decades ago, and has been attributed to the disordered sequences in silk proteins, which compose the soft amorphous matrix. However, the actual molecular origin and magnitude of internal friction within the amorphous matrix has remained inaccessible, because experimentally decomposing the mechanical response of the amorphous matrix from the embedded crystalline units is challenging. Here, we used atomistic molecular dynamics simulations to obtain friction forces for the relative sliding of peptide chains of Araneus diadematus spider silk within bundles of these chains as a representative unit of the amorphous matrix in silk fibers. We computed the friction coefficient and coefficient of viscosity of the amorphous phase to be in the order of 10⁻⁶ Ns/m and 10⁴ Ns/m², respectively, by extrapolating our simulation data to the viscous limit. Finally, we used a finite element method for the amorphous phase, solely based on parameters derived from molecular dynamics simulations including the newly determined coefficient of viscosity. With this model the time scales of stress relaxation, creep, and hysteresis were assessed, and found to be in line with the macroscopic time-dependent response of silk fibers. Our results suggest the amorphous phase to be the primary source of viscosity in silk and open up the avenue for finite element method studies of silk fiber mechanics including viscous effects.

Introduction

Spider silks provided by the major ampullate (MA) glands are used by the spider to form the web frame and the spider’s dragline. MA silk has been the most studied silk, as it has excellent mechanical properties and an unusual combination of high stiffness, toughness, strength, and extensibility, which are rarely observed in synthetic high-performance fibers (1,2). Silk fiber mechanics are ultimately defined by the nanoscale structure of the fiber. The repetitive segment of spider dragline silk is dominated by iterations of alanine- and glycine-rich regions. The alanine motifs are composed of a polyalanine (A)_n or polyalanylglycine segment (GA)_n, where n ranges from 4 to 15 amino acids (3–7). (A)_n- and (GA)_n-motifs form β-sheets that stack together and thereby form rigid crystals (8–10), which are 2–5 nm in length on a side (11). These constitute 10–25% of the fiber volume in spider silk (12,13). This glycine-rich sequence motifs form the amorphous phase, which is predominantly disordered (1,9,14), but also comprise GGX- and GPGXX-motifs, which have been suggested to form $3_1$ -helices and β-turns, respectively (15–21).

As first suggested by Termonia (22) and generally accepted today, the stiff β-sheet crystals furnish silk fibers with a high stiffness and yield strength, whereas the amorphous glycine-rich matrix provides extensibility. However, how the mechanical properties of these individual constituents and their interplay give rise to the typical highly nonlinear stress-strain behavior of silk fibers (12,23,24) is still largely unknown. We have recently developed a finite element model of spider silk fiber in a bottom-up approach based on molecular dynamics (MD) simulations, and were able to predict crystallinity-dependent fiber stiffness, strength, and toughness in agreement with experiments (25). However, this model relied on a linearly elastic stress-strain behavior of silk, and thus cannot help to understand or predict the intriguing nonlinearity of silk mechanics and its time-dependent behavior. Another recently developed nonlinear model made use of atomistic simulations for parameterization, but was otherwise based on an empirical formula to reproduce the particular stress-strain behavior observed in loading experiments (26), and also did not take its time-dependency into account.

Thus, correctly assessing plastic and viscous deformations of the crystalline and amorphous phases, respectively, are required to integrate their nanoscale mechanical response into a more realistic, purely bottom-up, and therefore, predictive macroscopic fiber model. The mechanical response of the crystalline phase of MA spider silk has been comparably well studied (25,27–29). The crystal component of silk largely behaves like an elastoplastic material, which undergoes nonreversible rupture in response to applied forces (30). The second component, the amorphous phase, in contrast, is much less well characterized. The large extensibility and viscous behavior as evidenced by the time-dependency of silk mechanics in tensile loading experiments (31–34) is likely to originate from the amorphous phase due to sliding of peptide chains, that is, internal molecular friction. Indeed, the amorphous phase can at low forces reversibly extend, as suggested by the increased orientation of chains along the fiber axis observed in stretching experiments (12,35,36). Similarly, the large hysteresis (∼65%) observed in such loading experiments is thought to arise from the internal friction in the amorphous phase (12,34,37).

The historic concept for friction encountered when two materials in contact move, or tend to move, relative to each other, has become known as the Amontons-Coulomb model (38,39). This model is stating that friction force is proportional to normal load but independent of apparent contact area and sliding velocity. In the presence of adhesive contacts and for low sliding velocities, the crossover to viscous friction, where friction force becomes proportional to sliding velocity, is described by Schallamach’s phenomenological model (40,41), which treats the stochastic breakage and rebinding of individual adhesive bonds. Recent studies started to bridge the considerable conceptual gap between models for friction between adhesive macroscopic bodies and the way friction is invoked in protein folding studies. Namely, valuable insight was gained into single-molecule friction by using MD simulations of adsorbed peptides on surfaces (42,43). Furthermore, recent work on viscous friction of hydrogen-bonded matter addressed the issue of peptide friction on polar surfaces, and used stochastic theory to extrapolate simulation data into the experimentally important viscous friction regime (44).

This work focuses on the rate-dependent behavior of the amorphous phase of MA silk fibers. We assessed friction forces between the peptide chains of the amorphous phase by using MD simulations. This allowed us to deduce a friction coefficient and coefficient of viscosity at the viscous limit. We employed the coefficient of viscosity in proof-of-principle finite element models of the amorphous phase of silk. Our quantitative analysis of the viscoelasticity of the amorphous phase presents an important step toward developing a bottom-up viscoelastoplastic model for MA silk fibers.

Materials and Methods

MD simulations

We modeled the amorphous phase of spider silk from the MA gland of Araneus diadematus (12). The all-atom model comprises the 24-residue sequence (GPGGYGPGSQGPSGPGGYGPGGPG, where G, P, Y, S, Q are glycine, proline, tyrosine, serine, and glutamine, respectively) known to form the amorphous phase in Araneus diadematus spider silk fibers. We constructed bundles of 4, 8, and 24 fully stretched peptide chains using the software visual molecular dynamics (45). For subsequent MD simulation, we used the GROMACS 4.5.3 package (46), and the OPLS-AA force field (47) for the protein. Simulation boxes of ∼18.0 × 4.5 × 4.5, ∼18.0 × 6.5 × 6.5, and ∼19.0 × 8.7 × 8.5 ${\text{nm}}^3$ for the bundles of 4, 8, and 24 peptide chains were used, respectively. The bundles of the amorphous chains were subsequently solvated in TIP4P water (48). The solvent included Na and Cl ions with a concentration of 0.1 mol/liter, resulting in a system size ∼0.1 million atoms for the 8 peptide chains bundle, and ∼0.06 and ∼0.2 million atoms for the bundles of 4 and 24 peptide chains, respectively. Periodic boundary conditions were employed to remove artificial boundary effects. We chose a cutoff of 1.0 nm for nonbonded interactions, and the particle mesh Ewald method (49) to account for long-range electrostatic interactions. To increase the simulation time step, we used LINCS (50) to constrain all bond vibrations. A time step of 0.002 ps was used. Simulations were performed in the NpT (isothermal-isobaric) ensemble with a temperature of 300 K and a pressure of 1 bar. We used Nosé-Hoover (51,52) temperature coupling with a coupling time constant 0.1 ps, and Parrinello-Rahman (53,54) pressure coupling with a coupling time constant of 1 ps.

Each of the three simulation systems were relaxed by energy minimization. We then performed 500 ps position-restrained simulations to equilibrate the solvent, subjecting each protein atom to a harmonic potential with a force constant of 1660 pN. Finally, all models were fully equilibrated for 200 ns allowing the silk peptides to adopt relaxed conformations and to partially entangle within the bundle. The resulting equilibrated simulation systems served as starting points for force-probe molecular dynamics (FPMD) simulations (55).

In the FPMD simulations, half of the peptide chains were pulled in one direction and the other half pulled in the opposite direction, as schematically shown in Fig. 1, A and B. Force was applied by attaching one-dimensional harmonic springs with a force constant of 830 pN acting at the center of mass of the alanines at the C- and N-termini. The pulling direction for each peptide was chosen such that the peptide chains were maximally surrounded by peptide chains pulled in the opposite direction, as shown in Fig. 1 B. The springs were moved with constant velocities ranging between 0.01 and 100 nm/ns. There was no external force exerted on the peptides perpendicular to the pulling direction. The FPMD simulations were stopped after the amorphous peptide chains separated from each other.

Figure 1.

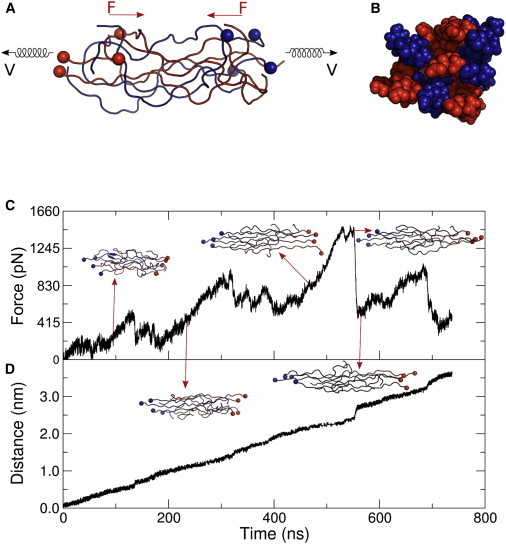
Setup and results of a representative FPMD simulation of an 8-chain bundle at 0.01 nm/ns. Schematic representation of the 8-chain bundle model in front view (A) and side view (B). For each peptide chain, a harmonic spring that moves with constant velocity V was connected to one terminal residue (solid spheres) and the other terminal residue is free. The friction force F is acting in the opposite direction to the applied velocity. In the pulling simulations, 4-peptides (in red color) are pulled in one direction and the remaining 4-peptides (in blue color) are pulled in the opposite direction. (C) Friction force of 4-peptide chains in one direction as a function of time, and (D) displacement of the terminal residue as a function of time. Snapshots show the sliding of peptide chains from each other taken at times that are marked by arrows.

To obtain a shear stress, which then can be converted into a coefficient of viscosity, we calculated the contact area between the peptide chains, which is the resistance area against sliding. Microscopic contact areas between a polymer surface and a crystalline surface as well as between polymer surfaces have been previously calculated on a molecular scale to determine shear stresses (56,57). Here, we used the solvent accessible surface area as the peptide-peptide contact area. We subtracted the solvent accessible surface area of the whole bundle from the sum of the areas of only the peptide chains pulled in one and in the other direction, when considered in isolation, which then, after division by two, gives the interface or contact area of the peptides between each other. We used a solvent probe of radius 0.14 nm, which is commonly used for water, and is also roughly an average radius of heavy atoms in proteins, i.e., relevant for peptides in contact with other peptides.

Finite element model

For the finite element (FE) modeling of the amorphous phase, the commercial solver LS-DYNA (version: ls971s R5.1.1) (Livermore Software Technology ) was used together with the Pre/Post tool LS-Pre-Post (Livermore Software Technology). A rectangular cube of the amorphous phase was modeled by using 8-node hexahedron (brick8) elements. The model of the rectangular cube was fixed at one end and pulled at another end. See Fig. 4 A, which shows the schematic representation of the model with boundary conditions. A viscoelastic material model, ^∗MAT_VISCOELASTIC (^∗MAT_006) (Livermore Software Technology), was used for these elements, which is based on the Power Law viscoelastic model. Hereby, the time-dependent shear modulus, $G\left(t\right)$,

$$G\left(t\right)=G_{\infty }+\left(G_0-G_{\infty }\right)\mathrm{ex}{\mathrm{p}}^{\left(-\alpha t\right)},$$ (1)

is a function of the long term shear modulus, $G_{\infty }$, the short term shear modulus, $G_0$, and the decay constant, α. The short term shear modulus, $G_0$ = 1.66 GPa, is dominant near t = 0, although near t = $\infty$, the long term shear modulus, $G_{\infty }$, is dominant (see the Supporting Material for the calculation of $G_0$). The decay constant, α, determines the rate at which the long term modulus starts dominating the material response. Here, the decay constant was defined as α = $G_0$ /η, where η is the coefficient of viscosity, and was set to η = 1.0 $\times {10}^4$ Ns/m². This coefficient was obtained from FPMD simulations as described previously.

Figure 4.

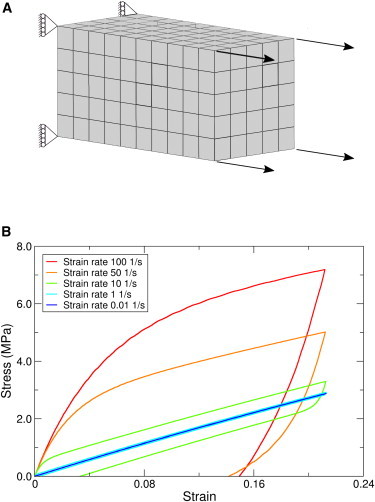
FE modeling of the amorphous phase. (A) Schematic picture of the FE model with boundary conditions. (B) Stress-strain curves for the amorphous phase of spider silk for the different constant strain rate loading and unloading. The area inside the hysteresis loop is the energy dissipated due to internal friction.

Results and Discussion

To assess the frictional forces within the amorphous phase of spider silk at atomistic scale, we used atomistic FPMD simulations. The simulation setup is depicted in Fig. 1, A and B, showing a front and side view of the 8-chain bundle model, respectively. In our simulations, we used 24-residue peptide chains of the amorphous phase of Araneus diadematus spider silk (for details on the model set up and boundary conditions see Materials and Methods). A harmonic spring was connected to one terminus of the peptide chain, and moved at constant velocity, although the other terminus of the peptide was kept free to move. By pulling half of the amorphous peptide chains in one direction, and the other half in the opposite direction, we could measure the force and displacements upon sliding the amorphous peptide chains relative to each other within the bundle. Fig. 1 C shows a typical force profile and related structures of the 8-chain bundle model. The resulting average displacement of the center of mass of the pulled peptide chains in one direction is shown in Fig. 1 D.

After an initial phase of local adhesive bond breaking between peptide-peptide and bond rotation, which occurred mostly near the point of load application (until 100 ns), we observed a number of stick-slip events involving collective adhesive bond breaking of the initially relaxed and entangled peptide bundle (horizontal bars in Fig. 1, C and D). Slipping of chains within the bundle is reflected by a sudden increase in the displacement of terminal residues (Fig. 1 D) along with a significant decrease in force (Fig. 1 C). At the peak force, a maximum number of adhesive bond breaking between peptide-peptide occurred in the amorphous phase, resulting in a sudden drop of interactions between chains, and the peptide chains continue to slide from each other with low resistance. Finally, four chains were detached from the 8-chain bundle (around 700 ns), and the remaining low frictional force was solely caused by dragging the bundles through water.

The obtained peak frictional force of ∼1450 pN comprises both peptide-peptide and peptide-solvent friction, as previously shown for a similar system (44). We next separated the frictional forces within the silk peptide bundle from frictional forces with water. To this end, we compared the peak forces obtained for the 8-chain bundle from FPMD simulations as described previously to the peak force required to pull a 4-peptide chain bundle with the same pulling velocity through water, as observed in additional FPMD simulations with all chains pulled in the same direction. Fig. 2 shows the frictional force per residue for dissociating the bundle (red), for dragging through water (green), and their difference, i.e., the peptide-peptide friction (black). Data was obtained at different pulling velocities, and averages and standard errors over four independent FPMD simulations are given. Note that the friction force corresponds to an effective mean force, i.e., we assume that force is on average equally shared by all residues.

Figure 2.

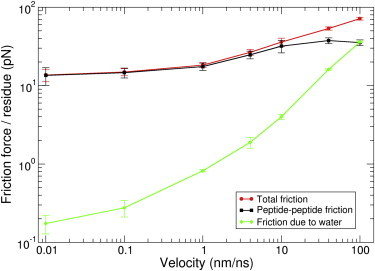
Friction force per residue $\left(F/N\right)$ as a function of pulling velocity (V) for the 8-chain bundle. Both peptide-peptide and peptide-water friction contribute to the total friction.

For low velocities (<4 nm/ns), total friction forces and peptide friction forces are of similar magnitude, i.e., water gives rise to an only minimal resistance on the peptide chain sliding. For velocities beyond 4 nm/ns, peptide-water friction substantially contributes to the total frictional force. We note that we did not observe water molecules within the peptide bundle, so that friction with water is effectively restricted to the outer peptide surface in our simulation system, i.e., peptide-peptide friction is dry. Fig. 2 shows that the water friction force grows nearly linearly with applied velocity. A straight line would follow the linear viscous law, $F_{\text{w}}/N={\gamma }_0\times V$ (44), where, $F_{\text{w}}$ is the water friction force, N the number of residues, and V the applied constant velocity. From the simulations, the per residue friction coefficient, ${\gamma }_0$, with water is $\sim 0.8\times {10}^{-12}$ Ns/m, which is very close to the experimental value of bulk water of $1\times {10}^{-12}$ Ns/m (60,61).

To assess the dependency of the computed forces on the size of the bundle, we repeated the FPMD simulations with two different amorphous peptide chain systems, namely a 4-chain bundle (with 2 chains pulled in each direction), and a 24-chain bundle (with 12 chains in each direction). We obtained similar results (within the error) for the total friction force per residue versus pulling velocity for the two systems, namely an 8- and 24-chain bundle (see Fig. S1), suggesting the frictional forces to be independent from the simulation system size beyond the 8-chain bundle. In the following, results for the 8-chain bundle are presented.

Viscous friction coefficient

In the presence of adhesive contacts and for low sliding velocities, the crossover to viscous friction is described by the general Schallamach’s phenomenological model (62,63). For large velocities, the linear viscous law describes the friction coefficient, and allows a rough estimate of the friction coefficient in the viscous regime. However, it does not describe the crossover from large and intermediate velocities to the regime of linear friction at small velocities. In the experiments, such as force spectroscopy experiments or when biological molecular motors are active, the applied external force causes molecular motions in the μm/s range. Thus, we are experimentally always in the viscous linear response regime, where friction forces are proportional to velocities. To extract the viscous friction coefficient from the sliding of silk peptide chains in our simulations, we have to extrapolate our data to the viscous regime.

To this end, we used a stochastic model that describes the full velocity dependence of the friction force per residue (44). The steady-state friction coefficient is obtained from the Fokker-Planck equation in the presence of an external force and a corrugated periodic potential. The model considers a single particle moving in a one-dimensional corrugated potential of the form of $U\left(x\right)=m{U}_{\text{bond}}\left(\text{cos}\left[2\pi x/a\right]-1\right)/2$, with a lattice constant, a, the cooperativity of bonds, m, and a bond strength, $U_{\text{bond}}$. In the Fokker-Planck equation, bond refers to a peptide-peptide adhesive bond. As proposed earlier (44), the modified equation of the friction coefficient per residue can be written as

$${\gamma }_{\text{resi}}={\gamma }_0+\frac{{\gamma }_0}{m}\text{Ψ}\left(\frac{ma{F}_{\text{amorph}}}{k_{\text{B}}TN},\frac{m{U}_{\text{bond}}}{k_{\text{B}}T}\right).$$ (2)

The first term on the right describes the friction in the high-velocity limit, which in all our fits we approximated by the friction coefficient in bulk water per residue, ${\gamma }_0=0.8\times {10}^{-12}$ Ns/m. The second term describes the friction due to the corrugated potential. It is proportional to the scaling function $\text{Ψ}$ that describes the friction coefficient, subject to the driving force, $F_{\text{amorph}}/N$ and diffusing in the sinusoidal potential, $U\left(x\right)$, which follows from the closed-form solution of the Fokker-Planck equation. Note that we here again assume the friction force $F_{\text{amorph}}$ to be equally distributed on all residues.

The stochastic model is used to fit the simulation data set by varying the bond cooperativity, the strength of bonds, or the lattice constant. Fig. 3 A shows different fits of the stochastic model to our simulations data. When fixing the strength of individual residue bonds to the value $m{U}_{\text{bond}}/k_{\text{B}}T$ = 17.6, and treating the periodicity a as fitting parameter, which controls the lateral position of the scaling function (red lines in Fig. 3 A), we obtained a value $ma$ of $3.1\pm 0.7$, which covers the range of the simulation data. Fixing the parameter $ma$ to 3.15 and varying the strength of individual residue bonds (red solid and black lines in Fig. 3 A) yields a strength of $m{U}_{\text{bond}}/k_{\text{B}}T$ = $17.6\pm 0.7$.

Figure 3.

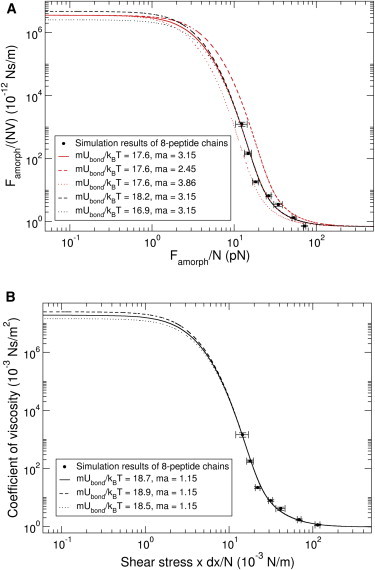
Comparison of the simulation data set with the solution of the Fokker-Planck equation. (A) Peptide friction coefficient per residue as a function of peptide friction force per residue. Red and black lines present from fits of the stochastic model to the simulation data with varying $ma$ and $m{U}_{\text{bond}}/k_{\text{B}}T$, respectively. The solid red line shows the best fit to the data. (B) Simulated coefficient of viscosity per residue as a function of shear stress $\times dx/N$. Black lines present from fits of the stochastic model to the simulation data with varying $m{U}_{\text{bond}}/k_{\text{B}}T$. The most suitable fitting scheme is the solid black line.

Using these fit parameters, for high velocities, individual residues experience the dominant resistance from water, therefore, the friction coefficient obtained from simulations is $\sim 0.8\times {10}^{-12}$ Ns/m, which is very close to the experimental value of bulk water of $1\times {10}^{-12}$ Ns/m (60,61). The extrapolation to low velocities gives a friction coefficient per residue for the amorphous phase of spider silk of $3.5\pm 1.0\times {10}^{-6}$ Ns/m.

On this basis, we next extracted the primary quantity of interest, the coefficient of viscosity η for the amorphous phase of spider silk, from our MD simulations. η is defined by Newton’s law of shear viscosity, with $\tau =\eta \times dv/dx$, where τ is the shear stress, and $dv/dx$ is the shear velocity or velocity gradient. The calculation of the velocity gradient is detailed in the SI. The shear stress τ, causing a shear deformation of the material by relative sliding, is defined as the sliding frictional force per unit contact area. We here calculated the peptide-peptide contact area from the solvent accessible area of the peptides. Fig. 3 B shows the coefficient of viscosity per residue, $\eta =\tau \times dx/\left(VN\right)$ from the solution of the Fokker-Planck equation, as a function of $\tau \times dx/N$. Fits with varying potential heights are given, with $m{U}_{\text{bond}}/k_{\text{B}}T$ of 18.71 and $ma$ of 1.15 representing the data best (solid line), especially in the regime of the steep increase of the coefficient of viscosity. From the simulation results at high velocity, the coefficient of viscosity or dynamic viscosity per residue with water is ∼0.8 $\times {10}^{-3}$ Ns/m², which is very close to the experimental value of the dynamic viscosity of water $1\times {10}^{-3}$ Ns/m² (64,65).

From the extrapolation to low velocities, we obtained a coefficient of viscosity of the amorphous phase of spider dragline silk of $1\pm 0.5\times {10}^4$ Ns/m², which is in the range of polymer melts (${10}^3$ to ${10}^5\text{Ns}/{\text{m}}^2$) (66,67).

FEM to the amorphous phase

We next determined the rate-dependent behavior of the amorphous phase by finite element modeling, using the coefficient of viscosity determined from MD simulations as described previously. Viscoelasticity is the property of materials that exhibit both viscous (dashpot-like) and elastic (spring-like) characteristics when undergoing deformation.

In our previous work, the amorphous phase was studied as an elastic material with a Young’s modulus of 2.7 GPa and a Poisson’s ratio to 0.33, and the elastic parameters were determined by MD studies (25). In this work, we assessed the time-dependent stress-strain behavior of a representative rectangular box (Fig. 4 A) of the amorphous phase in terms of three typical mechanical properties, namely stress relaxation (Fig. S3, A and B), creep (Fig. S3, C and D), and hysteresis. Hysteresis, the dissipation of mechanical energy under cyclic loading of a material, is a common feature of viscoelastic spider silks. Hysteresis is defined as the area under the stress-strain curve of one loading-unloading cycle. We considered strain rates between 100 and 0.01 ${\text{s}}^{-1}$, which is the range commonly applied to spider silk fibers in experiments (12,68–70). In loading-unloading tests, the amorphous phase sample was loaded to a strain of 0.2 and unloaded to zero strain. Fig. 4 B shows the stress-strain curves for the loading of the viscoelastic amorphous material with different constant strain rates. As expected, stress-strain curves are dependent on the rate of straining, that is, the faster the stretching, the larger the stress required. We observed for most of the strain rates a significant hysteresis. Load cycle experiments by Gosline (12) gave a hysteresis for MA silks of ∼65% for a constant strain rate in the range of 20–50 ${\text{s}}^{-1}$. In close agreement, our studies suggest a hysteresis of ∼70% in this range of constant strain rates.

We note that our model only includes the amorphous phase, which supposedly is the major player in the viscoelastic response of silk, but it is also likely to be altered in its mechanical response by the incorporation with crystals.

Conclusion

Here, we have quantified the viscous friction inherent to the amorphous phase of Araneus diadematus silk using MD simulations. The friction coefficient of the amorphous phase is in the order of 10⁻⁶ Ns/m, which is similar to the one derived for other protein bundles (71), and a coefficient of viscosity in the order of 10⁴ Ns/m², which is similar to polymer melts. According to a finite element analysis of only the amorphous phase, this magnitude of the coefficient of viscosity can account for the strain-rate-dependent hysteresis commonly observed in loading-unloading tests of silk fibers. This suggests the amorphous matrix, i.e., the disordered sequences in spidroins, to be the major determinant of the viscosity of spider silk. Crystals, instead, can be primarily considered as elastoplastic materials.

Our analysis thus paves the way for a finite element model of silk fibers as a viscoelastoplastic material, which combines elastoplastic crystals and a viscoelastic amorphous matrix, to assess the determinants of its outstanding toughness.

Dragline silks are generally composed of two major protein components, which are spidroin type I and II proteins. Dragline of Araneus diadematus, which is the silk investigated here, consists of ADF-3 and ADF-4 (Araneus diadematus fibroin), and it remains unclear whether additional proteins play a significant role in silk assembly and the final silk structure (5,72). It is assumed that, based on amino acid composition, within the dragline fiber the molecular ratio between ADF-4 and ADF-3 is ∼3–2 (5,72). In the amorphous matrix, GPGXX and GGX motifs in ADF-3 are likely to form β-turn spirals and 3₁-helices, respectively, whereas ADF-4 features only the GPGXX motif with a propensity to form β-turn spirals (73). Our study has been restricted to ADF-4, for which we did not impose any particular secondary structure content, resulting in a largely disordered bundle to represent the amorphous phase. Although the order of magnitude of the forces for rupture, and thus of the newly determined coefficient of viscosity, are likely to remain unaffected by details of the sequence and secondary structure, it remains to be investigated what the effect of mixing two different spidroins and of including particular secondary structure motifs might be on the internal molecular friction.