Microstructures in the Organ of Corti Help Outer Hair Cells Form Traveling Waves along the Cochlear Coil

Abstract

According to the generally accepted theory of mammalian cochlear mechanics, the fluid in the cochlear scalae interacts with the elastic cochlear partition to generate transversely oscillating displacement waves that propagate along the cochlear coil. Using a computational model of cochlear segments, a different type of propagating wave is reported, an elastic propagating wave that is independent of the fluid-structure interaction. The characteristics of the propagating wave observed in the model, such as the wavelength, speed, and phase lag, are similar to those observed in the living cochlea. Three conditions are required for the existence of the elastic propagating wave in the cochlear partition without fluid-interaction: 1), the stiffness gradient of the cochlear partition; 2), the elastic longitudinal coupling; and 3), the Y-shaped structure in the organ of Corti formed by the outer hair cell, the Deiters cell, and the Deiters cell phalangeal process. The elastic propagating waves in the cochlear partition disappeared without the push-pull action provided by the outer hair cell and Deiters cell phalangeal process. The results suggest that the mechanical feedback of outer hair cells, facilitated by the organ of Corti microstructure, can control the tuning and amplification by modulating the cochlear traveling wave.

Introduction

The current theory of mammalian cochlear mechanics has been built upon the observations of cochlear traveling wave first reported by Békésy (1). According to this theory, differential hydrodynamic pressures between the cochlear scalae deflect the elastic cochlear partition to create displacement waves propagating along the length of the partition from the base toward the apex. Fluid mechanical models of the cochlea have been developed to account for the major characteristics of Békésy’s traveling waves such as the direction of travel, the several cycles of phase accumulation that develop as the wave travels toward the apex, and the asymmetric wave envelope (2).

Most theoretical studies of the cochlea share two simplifications in representing the mechanics of the elastic cochlear partition. First, the mechanics of the organ of Corti complex (OCC), consisting of the organ of Corti, the tectorial membrane (TM), and basilar membrane (BM), is reduced to a system with one to three degrees of freedom. Second, there is no elastic coupling between the OCC resonators arrayed along the cochlear length. As more data on the fine structures in the OCC and their mechanics accumulate, however, there are increasing demands for more detailed OCC models to explain new findings and to test hypotheses more rigorously. For example, observations of the relative motions between OCC microstructures (3–5) suggest that the modes of vibration are too complicated for a simplistic mechanical system to explain. These observations led to more detailed OCC models to consider TM resonance (6), inner hair cell bundle motion (7), or longitudinal coupling (8). This study uses a highly detailed electromechanical model of the OCC that has been developed previously using the finite element method (9,10). The model incorporates three-dimensional (3D) characteristics of the OCC, such as the Y-shaped structure formed by the outer hair cell, Deiters cell, and Deiters cell phalangeal process (DCpp). Mechanical properties were validated by comparing simulated point stiffnesses and longitudinal space constants with experimental measurements (9). The amplification by outer hair cell motility was incorporated and validated by reproducing stimulus level-dependent phase relations between OCC structures (10) using realistic outer hair cell electrical properties (11).

I report an unconventional type of propagating waves along the cochlear partition using the electromechanical OCC model. They are named the elastic propagating waves because they are distinguished from the traveling waves of existing theories in that they are independent of fluid-structure interactions in the cochlear scalae. Such elastic propagating waves have wavelengths, velocities, and phases similar to experimentally observed traveling waves. The objectives of this study were to characterize the elastic propagating waves, to account for the conditions of their existence, and to compare them with measured cochlear traveling waves.

Methods

The following summary emphasizes updates to the model reported in previous publications (9,10,12). The stiffness gradient predominantly determined by the geometry was found to be central for the conclusions of this work. The geometrical properties at two locations were based on available anatomical data (13,14) of the gerbil cochlea. Mechanical properties of longitudinal elements were adjusted to match known mechanical responses of the gerbil cochlea (9,15,16). After determining geometrical and material parameters at 2 and 10 mm from the basal end, all geometrical and material parameters were interpolated/extrapolated from the properties at the two locations. Because the change in the width and the collagen fiber layer thickness of the basilar membrane along the cochlear length is steeper in the basal turn (13,14,17), this slope of mechanical parameters could be underestimated in the basal model and overestimated in the apical model. OCC mechanical parameters are listed in Table S1 and Fig. S1 in the Supporting Material. Transduction channel and membrane electrical properties of the outer hair cell are in Table S2.

Finite element model of the OCC

The gerbil cochlea sections near 2 and 10 mm from the basal end were chosen for the creation of full 3D finite element models of the OCC. Structurally significant structures such as the BM, TM, pillar cells, Deiters cells (with DCpps), reticular laminar, and outer hair cells were represented by either beam or link elements (Fig. 1). The stereociliar (hair) bundles were represented by a hinged link between the reticular lamina and the TM with a rotational spring at the bundle rootlet. Structurally insignificant cells such as Claudius cells, Hensen’s cells, and inner hair cells were omitted, but their masses were lumped with the BM (Fig. S1). There are three to four rows of outer hair cells along the cochlear coil. In the model, they were merged to one row of outer hair cells for simplicity. The radial sections repeating every 10 μm were connected along the longitudinal direction by five different elastic structures (Fig. 1 B). Three of them are aligned with the Z axis—longitudinal elements of BM, reticular lamina, and TM, whereas the Y-shaped structure formed by outer hair cell, Deiters cell, and DCpp is 3D (inclined in the Y-Z and X-Y plane, Fig. 1, B and C). To capture the wave envelope properly, longitudinal sections with spans of 1600 and 1200 μm at the apex and base, respectively, were simulated (a shorter section is drawn in Fig. 1 to show better details). Different from the previous work with this model, the arcuate zone is thinner than the pectinate zone by a factor of five, and the edge of the arcuate zone is simply supported, whereas the edge of the pectinate zone is clamped to better represent the radial deforming pattern of the BM (18).

Figure 1.

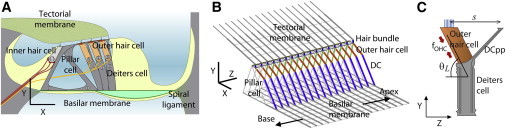
Cochlear partition model. (A) The organ of Corti microstructures. The pillar cells, outer hair cells, and Deiters cell are structurally significant in the organ of Corti. The organ of Corti is sitting on the basilar membrane and connected to the tectorial membrane through the outer hair cell hair bundle. (B) The 3D finite element model of the OCC includes all the structurally significant components. The outer hair cell, Deiters cell, and DCpp (indicated by orange, blue, and green colors, respectively) form the Y-shaped structure that repeats along the Z axis. The scale bars in (A) and (B) are 30 μm. (C) The Y-shaped structure shown in the Y-Z plane. In the present model θ_L = 80°–70° and s = 20 μm. To see this figure in color, go online.

The mass of the OCC can be divided into four components—the mass of TM, BM, organ of Corti, and the mass added by extra-OCC fluid. For the TM, the mass matrix is consistent with stiffness matrix. For the BM, the thickness used to compute the stiffness was that of collagen fiber layers, although the thickness used to compute mass included the thickness of nonstructural layers such as the ground substance and tympanic layer. Structurally insignificant parts of the organ of Corti (such as Hensen’s and Claudius cells) were considered to follow the motion of the BM rather than the TM. Therefore, the BM mass-thickness was increased by 50% to include the mass of the structurally insignificant parts in the organ of Corti. Assuming that the extra-OCC fluid mass primarily interacts with the BM, fluid thickness was added to the mass thickness of the BM. The fluid thickness was 75 μm and zero at the apex and the base, respectively. Without this added fluid mass the best responding frequency of the apical model increases from 0.7 to 1.0 kHz. Viscous forces were assumed to consist of two components: the damping within the cleft between the TM and the reticular lamina, and the viscous resistance acting on other parts of the OCC. When there was no outer hair cell motility (active force), the passive mechanical system was slightly underdamped so that it oscillated two to four cycles after an impulse.

Electromechanics of the outer hair cell

Mechanotransduction in the outer hair cell bundle is modulated by the relative displacement between the TM and the reticular lamina, which equals the hair bundle shear displacement (x_HB). The transducer channel kinetics was based on the previous work (12,19). The only parameter slightly adjusted from the previous work (Nam and Fettiplace, 2012 (10)) is the single-channel gating force defined by the product of the gating swing and the gating spring stiffness (Table S2, the gating swing was reduced from 0.8 to 0.6 nm at the base). It was 2.4 and 3.6 pN at the apex and the base, respectively. With this gating force, a hair bundle can generate up to 14 and 70 pN at the apex and the base, respectively ($f_{MET}=N\gamma b{k}_{GS}$, where N is the number of tip links, γ is the geometric gain of hair bundle, b is the gating swing, and k_GS is the stiffness of tip link complex including the gating spring (12)). In the model, the endolymphatic potential remains the same despite the OCC vibration. Therefore, there was no electrical interaction between the hair cells. The electrical representation of the outer hair cell has two parts: the apical part representing the hair-bundle’s mechanotransduction and the basal part representing the lateral membrane. Voltage-dependent membrane conductance and strain/voltage-dependent membrane capacitance were incorporated to represent the outer hair cell membrane’s electromechanical feedback. The outer hair cell membrane motility could generate more than one order of magnitude greater force than the hair bundle force. Two relative displacements within the OCC were involved with the electromechanical feedback from the outer hair cells: the displacement between the TM and the reticular lamina, and the displacement between the reticular laminar and the BM. Outer hair cell electrical properties were the same as previously reported (10) (Table S2).

Y-shaped structure of the organ of Corti

The outer hair cell together with the Deiters cell forms a Y-shaped structure (Fig. 1, B and C). The standard longitudinal (along the Z axis) tilt of the outer hair cells was 5 μm toward the base. This corresponds to tilt angles (θ_L) of 80° and 70° for the apex and the base model, respectively (Fig. 1 C). The distance between the tips of the outer hair cell and the DCpp (s) was 20 μm. It has been reported that the DCpp has stiffness in transverse flexion between 0.02 and 0.44 mN/m (20). The stiffness in transverse flexion of DCpp in the present model was 0.01 and 0.45 mN/m in the apex and base model, respectively. The axial stiffness of the DCpp was 135 and 645 mN/m in the apex and base model, respectively.

Computation

The program was written in MATLAB (ver. 8.10, The MathWorks, Natick, MA). No MATLAB toolbox was used. The code was run on an IBM PC (Intel i7-3770 processor, 3.40 GHz, 16 GB RAM). Typical time step size for the integration of differential equations was 40 and 1 μs for the apex and the base model, respectively. Approximately 4 min were required to simulate 1 ms response of the base model. The computer code is available upon request.

Results

Instead of modeling the entire length of the cochlear coil, a fraction of the coil was modeled and simulated because 1), a single tone stimulus principally vibrates a finite span of the cochlea; and 2), the numerical size of the model (150 mechanical degrees of freedom per 10 μm section) makes it inefficient to model the entire cochlea. Two pieces of the gerbil cochlea were analyzed that represent the low and high frequency regions of the cochlea: Z = 9.2–10.8 mm and Z = 1.4–2.6 mm, where the origin of the Z axis is at the basal end of the 12 mm long gerbil BM. Within each section, longitudinal variations in OCC properties were present, per the interpolation noted previously. Hereafter, the two models are referred to as the apex and base model, respectively. The boundary effects proved to be confined to within 100 μm from the edges (Z = Z_min and Z_max), which is reasonable because the longitudinal space constants are <50 μm (9,15). All the analyses were done in the time domain to consider the nonlinearity of mechanotransduction.

Elastic propagating wave without fluid-structure interaction

3D vibration patterns at low stimulus level are shown in Fig. 2. When a force that was sinusoidal in time and uniform in space was applied along the length of the BM, both apex and base models developed vertically vibrating waves in the TM and the BM. There were qualitative differences in the deforming patterns at the apex and the base though. The maximum BM deformation occurred in the pectinate zone in the apex model, but it occurred at the junction between arcuate and pectinate zones in the base model. The TM vibrated in its second mode at the base as opposed to the primary vibration mode of the apical TM. These differences are ascribed to the relative stiffnesses between the BM, the organ of Corti, and the TM that depend on location. At the base, the BM dominates the overall stiffness of the OCC, but at the apex the BM stiffness is comparable to the stiffness of the TM or the organ of Corti. A radial deformation pattern of the BM similar to that shown in Fig. 2 B has been observed in the basal turn of gerbil cochlea (21) and analyzed (18).

Figure 2.

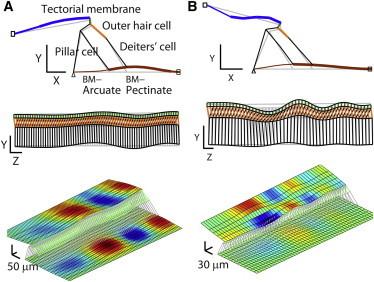
Deformed shape of the organ of Corti complex. 3D finite element models of the gerbil cochlea were subjected to pure tone stimulation uniformly distributed along the Z axis, where the origin of the Z axis is at the basal end of the cochlear coil. The stimulating frequency was 0.7 and 21.5 kHz for the apex and base model, respectively. The deformation at one moment in time is shown. Maximum displacement of the basilar membrane is ∼100 nm and 1 nm for the force equivalent to 5 and 2 mPa of pressure at the apex and base, respectively (the deformed shapes were exaggerated). (A) Apex model deformation. (B) Base model deformation. Top: deformation in the X-Y plane. Middle: deformation in the Y-Z plane. The top (green) and the bottom (black) lines represent the tectorial and the basilar membrane, respectively. In the two-dimensional plots, the structures in each plot are not in the same plane (e.g., the OHC is tilted three-dimensionally). Bottom: 3D deformation patterns. Colors encode vertical (Y-) displacement of the tectorial and the basilar membrane. To demonstrate the vibrating pattern better, only a part of the simulated span was shown (e.g., shown Z-span = 0.7 mm in the base, simulated Z-span = 1.6 mm in the apex). To see this figure in color, go online.

Spatially, the amplitude of the propagating wave developed its peak within its first cycle from the base and decayed during the next two to three cycles toward the apex (Fig. 3). This number of wave cycles in space corresponds to the overall phase lag with respect to the stimulating force. The sequence of longitudinal vibration patterns clearly demonstrates that displacement waves were produced, propagating toward the apex. At a low stimulation level (1 nN distributed along the BM, equivalent to 2–5 mPa in pressure), the span of wave envelope (defined by 90% decay from the wave peak) was 1.6 and 0.7 mm at the apex and base, respectively (Fig. 3, A and B, shaded area plots in top row).

Figure 3.

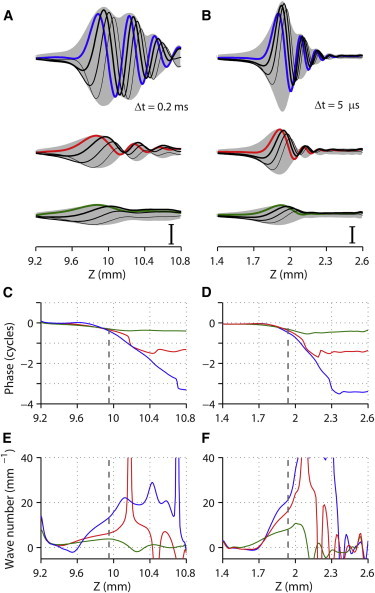
Elastic propagating wave on the basilar membrane under uniformly distributed stimulation. Finite element models of the cochlear partition were subjected to pure tone stimulations. The stimulating frequency was 0.7 and 21.5 kHz for the apical (span of 1.6 mm centered at 10 mm from the basal end) and basal (span of 1.2 mm centered at 2 mm from the basal end) model, respectively. The force was uniformly distributed along the midline of the basilar membrane. (A) A sequence of basilar membrane vibration patterns of the apical model. As time advances, the wave propagates from thicker to thinner curves. The interval between curves is 0.2 ms. The shaded area indicates the envelope swept by the basilar membrane displacement waves. From top to bottom, the force amplitude was increased so that the amplitude of outer hair cell transduction current increases from 10%, 40%, and 90% of its maximum value. The basilar membrane displacement was normalized by the applied force. Scale bar: 70 nm/Pa. (B) Vibration patterns of the basal section. The time interval between the curves is 5 μs. Scale bar: 0.4 nm/Pa. The phase of the basilar membrane displacement with respect to the applied force at the apex (C) and the base (D). The wave number along the longitudinal location at the apex (E) and the base (F). The line colors correspond to the force amplitude in (A) and (B). Broken lines indicate the peak response location.

The stimulation level affected the wave pattern. For the lower two rows in Fig. 3, A and B, the force amplitude was increased to 20 and to 100 times the low stimulation level, respectively. As the amplitude of applied force increased, the number of wave cycles decreased. The compliance of the OCC decreased to nearly passive (no feedback force from the outer hair cells) level as the stimulation level increased. The compliance of the active OCC (2 × 10⁻⁴ m/Pa at the apex and 5 × 10⁻⁷ m/Pa at the base) was 9–18 times higher than the passive OCC. As the stimulation level increased, the phase lag at the peak locations decreased (apex: from 0.4 to 0.3 cycles; base: 0.5 to 0.3 cycles). The maximum phase lag between the applied force and displacement of the BM was ∼3.5 cycles when the stimulus level was low (Fig. 3, C and D). The maximum phase lag decreased to 1.5 and 0.5 cycles, respectively, as the stimulus levels were increased. For low stimulation levels, the wave number at the peak locations was 13 and 22 radian/mm in the apex and the base, respectively (Fig. 3, E and F), corresponding to respective wavelengths of 480 and 280 μm. The wavelength increased to 1600 μm (apex) and 770 μm (base) as the stimulation level increased. The speed of the wave (phase velocity v_W = 2πf/k, where f is the frequency in kHz and k is the wave number in radian/mm) gets slower as it propagates. At the low stimulus level, the wave speed at the peak responding location was 0.34 m/s for the apex model (0.7 kHz stimulation) and 6.0 m/s for the base model (21.5 kHz stimulation). When stimulated at different frequencies, the cochlear partition vibrations peaked at different locations specific to each frequency, but the wave patterns were consistent at different frequencies (Fig. 4).

Figure 4.

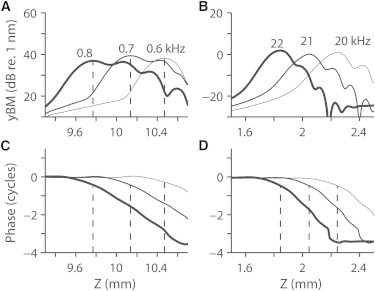
Response to different stimulating frequencies. Sinusoidal force was uniformly distributed along the midline of the basilar membrane. Three different frequencies were simulated for the apex and the base model, respectively. Basilar membrane vibration amplitudes along the length at the apex (A) and at the base (B). The phase lag along the length with respect to the stimulation at the apex (C) and the base (D).

Stiffness gradient, longitudinal coupling, and the Y-shaped structure determine the elastic propagating waves

A stiffness gradient along the cochlear coil (Z axis) was required for the existence of the elastic propagating wave. To test the effect of the stiffness gradient, four cases in addition to the standard case were simulated—steep, shallow, reverse, and no gradient (Fig. 5). Stiffness measured from point force application was 2.1 N/m at Z = 2 mm and 0.029 N/m at Z = 10 mm. Thus, the stiffness gradient was 4.6 dB/mm, consistent with experimentally measured values (16). The gradient was adjusted by doubling or halving the gradient of geometric dimensions and Young’s modulus of OCC structures (steep and shallow gradient). When there was no gradient, the entire section oscillated in phase without forming a wave pattern. The wave envelope (shaded area) became broader as the stiffness gradient decreased (Fig. 5 A). Accumulated phase lag increased from 2.5 to 5.5 cycles as the stiffness gradient decreased (Fig. 5 B). The wave number at the peak responding location modestly increased from 19 to 24 radian/mm as the stiffness gradient became steeper (Fig. 5 C). The direction of the wave propagation was determined by the stiffness gradient. When the stiffness gradient was reversed such that the apical end was stiffer than the basal end, the wave propagated toward the base (Fig. 5 A, bottom plot). In this simulation with the reverse-stiffness gradient, the direction of outer hair cell tilt remained the same (tilt toward the base), which indicates that the stiffness gradient, not the microstructure, determines the direction of wave propagation.

Figure 5.

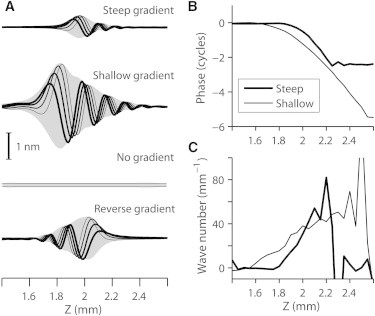
Effect of stiffness gradient. Cochlear partitions with three different stiffness gradient values were simulated. With the parameter values at z = 2 mm fixed, the slope of material, geometric, and electrical properties (property change per unit z-length) were doubled (steep gradient), reduced to half (shallow gradient) of the default gradient, removed (no gradient), or reversed (getting stiffer toward the apex). All simulation parameters are the same other than the mechanical properties relevant to stiffness gradient, but in the no-gradient case the gating swing of transduction channel was reduced from 0.6 to 0.45 nm to maintain stability. Pure tone (21.5 kHz) oscillatory force equivalent to 2 mPa was uniformly distributed to the basilar membrane. (A) Basilar membrane vibration patterns with 5 μs interval (from thick to thin curve along time). (B) Phase lag along the length. (C) Wave number along the length.

Cochlear mechanical models, including this work, can be considered to be a series of mechanical resonators arranged tonotopically along the length of the cochlear coil. Most existing models derived from conventional traveling-wave theory have neglected elastic longitudinal coupling between the resonators. A few exceptional works (8,22) considered the implication of the longitudinal coupling to find that the coupling blunts the sharpness of tuning. In this work, longitudinal coupling was required for the series of cochlear resonators to produce propagating waves. When there was no elastic longitudinal coupling, the propagating wave disappeared (Fig. 6, the longitudinal decoupling was achieved by removing all the structural elements in the Z-direction and the DCpps). When the present model without longitudinal coupling was subjected to sinusoidal stimulation distributed uniformly along the length, the vibration peaked at the characteristic place for that frequency similar to that shown in Fig. 3. However, the OCC oscillated like a series of simple resonators—half a cycle phase lag at most.

Figure 6.

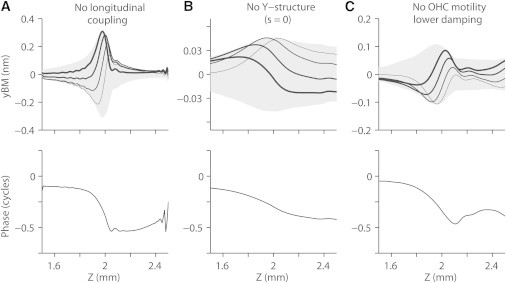
Conditions for the elastic propagating waves in the OCC model to appear under uniformly distributed stimulation. Besides the stiffness gradient, three conditions were required for the existence of the propagating wave under uniform stimulation. Sinusoidal force (21.5 kHz) was uniformly distributed along the midline of the basilar membrane. The basilar membrane displacement (top) and the phase with respect to the stimulation (bottom) were plotted. (A) When there was no elastic longitudinal coupling (all longitudinal beams and the DCpp were removed), the propagating waves were not present. The Z-degrees of freedom were constrained (dZ = 0) to stabilize the structure. (B) When the distance between the tips of the outer hair cell and the DCpp was set to zero (s = 0), the propagating waves were not present. (C) Without outer hair cell motility, despite reduced viscous damping, there were no propagating waves.

The Y-shaped structure formed by the outer hair cell, Deiters cell, and DCpp affected the cochlear amplification and the elastic propagating wave. The span s played a more prominent role in outer hair cell motility and wave propagation than the tilt angle θ_L. When the span remained the same (s = 20 μm) and the tilt was changed from θ_L = 70° to 100°, the amplification and the wave propagation persisted. However, when s = 0, two obvious differences were observed. First, the amplification of the OCC vibrations by the outer hair cells was greatly decreased. Even with greater outer hair cell feedback sensitivity (the gating swing of the mechanotransduction channel increased from 0.6 to 1.8 nm for the basal model), the amplification was minimal (<5 dB). Second, the elastic propagating waves disappeared completely despite the existence of a longitudinal stiffness gradient, longitudinal coupling, and θ_L <90°.

Elastic propagating waves can be observed in a series of resonators like von Békésy’s reed model (Figs. 12–43 in (1)). Perhaps, the observed propagating waves could also be the results of highly tuned resonators oscillating with slight phase differences along the length. Although the simulation protocol (uniformly distributed stimulation along the length) prevents the development of such a propagating wave, the possibility of propagating waves in simple series resonators was further explored. To demonstrate the role of outer hair cells, the feedback of the outer hair cells was turned off, and the viscous damping of the model was reduced so that the quality factor of vibrations became comparable to the model with the outer hair cell feedback (Fig. 6 C). In other words, only outer hair cell feedback was selectively removed from the model. Without the outer hair cell feedback, no propagating wave was observed, at least within the simulated span.

Discussion

Elastic propagating wave versus experimentally observed traveling wave

Without the fluid-structure interaction, which is generally accepted to be the generating mechanism of cochlear traveling wave, the present computational model exhibited propagating waves. The elastic propagating waves resemble the observed cochlear traveling wave, having several key quantities in good agreement. First, the accumulated phase lag is more than three cycles. Second, the wavelength (280–770 μm at the base) is comparable to measured values (23). Finally, the propagating speeds at the peak responding locations (0.34 m/s at the apex and 6.0 m/s at the base under low stimulation) agree with physiological measurements (23–26).

On the other hand, there are two characteristics that distinguish the simulated elastic propagating wave from the traveling waves of the existing fluid-structure interaction theory. First, the level-dependence of peak response location: in the present simulations, the peak response location remained the same across different stimulation levels (Fig. 3, A and B). Despite different theoretical interpretations (27,28), it has been consistently observed that the peak responding location shifts toward the base as the stimulation level increases (29,30). It is expected that if fluid-interaction were to be incorporated, the level-dependence would appear because of the level-dependent wavelength in the present model (i.e., the wavelength became longer as the stimulus level increased, Fig. 3). The wavelength is proportional to the added fluid mass (31) that reduces the resonant frequency and shifts the peak location. Second, the asymmetry of the wave envelope: the wave envelope in the apical turn of the cochlea observed by von Békésy (1) is asymmetrical such that the apical slope is steeper than the basal slope. Although rather symmetrical wave envelopes have been measured by Ren in the basal turn of the gerbil cochlea (32,33), cochlear fluid mechanical models reproduced this asymmetry more prominently (e.g., (34,35)). For comparison, the observed wave envelopes are rather symmetrical. It is unclear if this symmetry is due to the exclusion of the fluid-interaction and/or to the inclusion of elastic longitudinal coupling.

The role of the Y-shaped structure formed by the outer hair cell, Deiters cell, and DCpp

An interesting finding of this study is the effect of the Y-shaped structure in the organ of Corti formed by the outer hair cell, Deiters cell and DCpp. It has been suggested that outer hair cell tilt renders cochlear amplification more efficient (called the feed-forward effect in (34,36,37)), although others found that the feed-forward effect is negligible (27). According to the results, the amplification and the elastic propagating wave are consequences of the longitudinal gaps (s) between the apical tips of outer hair cell and the DCpp rather than outer hair cell tilt itself. Without the Y-shaped structure (i.e., s = 0), the outer hair cells did not amplify despite outer hair cell tilt (θ_L < 90°). That could be because the rigidity of DCpp, placed in parallel with the outer hair cell, overwhelmed the outer hair cell’s motility: in this model, the axial stiffness of the DCpp is 2–5 times greater than outer hair cell axial stiffness. Even when the stiffness of the DCpp was reduced by a factor of 30, propagating waves did not appear without the Y-shaped structure and there was little amplification. This implies that a push-pull action performed by the two cellular structures is needed for the development of elastic propagating waves.

When outer hair cells are depolarized so that they shrink, the Y-shaped structure causes a characteristic longitudinal warping of the basilar membrane (Fig. 7 A). This longitudinal warping disappears when there is no DCpp (Fig. 7 B). Despite the existence of the DCpp, the radial (X-Y plane) deformation patterns at the middle of the model are similar in both cases. The basilar membrane was subjected to upward and downward force by the DC and the outer pillar cell, respectively, so that the basilar membrane deformed nonmonotonically (top plots in Fig. 7). However, the deformation patterns along the length (Y-Z plane) are very different depending on the existence of DCpp, whereas the basilar membrane warped like the radial section in the standard case with the DCpp, it was deflected monotonically in the case without DCpp (see arrows of the second row plots in Fig. 7). As was shown in the previous study (9), despite significant basilar membrane displacement, there was minimal volume displacement of the basilar membrane in the standard case. This longitudinal warping of the basilar membrane caused by the outer hair cells and the DCpp explains why the elastic propagating waves in this model become more prominent when the stimulation level is low (when the relative contribution of the outer hair cell’s active force is higher, Fig. 3).

Figure 7.

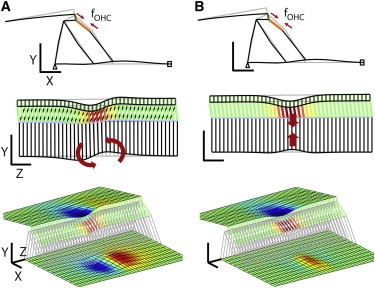
Deformation patterns due to outer hair cell force depending on the DCpp. Outer hair cells in the middle of the modeled section were depolarized. The generated axial forces (f_OHC) deflect the OCC in different patterns according to the existence of the DCpp. (A) Organ of Corti with the DCpp. (B) Organ of Corti without the DCpp. From top to bottom, the deformed shape in the X-Y plane, Y-Z plane, and in 3D view. The thick arrows in the middle plots indicate the primary deforming mode of each case. The colors of the tectorial and basilar membrane indicate transverse (Y) displacement (blue: downward, red: upward). The colors of the outer hair cells indicate the length change (red: maximal shrinkage, green: no strain). Scale bars are 50 μm. To see this figure in color, go online.

Unfortunately, there are few systematic anatomical data regarding the Y-shaped structure in the organ of Corti. The only available data to my knowledge indicate that the outer hair cells are tilted slightly toward the apex (θ_L = 93°–95° (38)). More information regarding the geometry and mechanical properties of the Deiters cell would help to further clarify its contribution to the development of elastic propagating waves.

Implication of the elastic propagating wave

Two reservations should be noted. First, despite several similarities, the elastic propagating waves in this model are different from the cochlear traveling waves, especially in their generation mechanisms. Because of this difference in generating mechanism, it is possible that the elastic propagating waves can disturb or modify the fluid-induced cochlear traveling waves. Second, the scope of this study is the waves in the cochlear partition (not general elastic propagating waves). Any elastically connected system can carry transient propagating waves, and depending on its physical properties, the propagating waves can look similar to the cochlear traveling waves. For example, with a physical model, von Békésy (1) demonstrated that a series of resonators can carry traveling waves when they are connected by elastic elements. The simulated elastic propagating waves also require the elastic longitudinal coupling. Besides that basic characteristic shared by elastic waves in general, the OCC elastic propagating waves of this work are characteristic in that: their generation is greatly enhanced by 1), the active feedback from the outer hair cells and 2), the unique kinematics provided by the Deiters cells. Therefore, the present OCC model is more than a series of resonators in that it was carefully adjusted to match available mechanical measurements (15,16,39) using reasonable mechanical and anatomical properties (including the longitudinally oriented Y-complexes) and it incorporated the active feedback of the outer hair cell to address the level-dependent phase relations between the OCC fine structures (10).

This study demonstrates that 1), There exist elastic propagating waves in the cochlear partition that are distinguished from the classical traveling waves in their generation mechanism; 2), The model’s elastic propagating waves have very similar wave properties to the experimentally observed traveling waves; 3), The model’s elastic propagating waves are enhanced by the push-pull action provided by the outer hair cell and DCpp. Because of their similarity, the elastic propagating waves can modify the traveling waves. Therefore, the present results suggest that the micromechanical push-pull action of outer hair cells, facilitated by the Y-shaped structure, can control the tuning and amplification by modulating the cochlear traveling wave. Despite the differences in the interpretation of the feed-forward effect, the observation of the push-pull effect by the Y-shaped structure is in line with the feed-forward and feed-backward mechanism of Yoon et al.’s full-scaled cochlear model (28).