Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 11;4:5248. doi: 10.1038/srep05248

Tunable chiral spin texture in magnetic domain-walls

J H Franken 1, M Herps 1, H J M Swagten 1,a, B Koopmans 1
PMCID: PMC4052744  PMID: 24919162

Abstract

Magnetic domain-walls (DWs) with a preferred chirality exhibit very efficient current-driven motion. Since structural inversion asymmetry (SIA) is required for their stability, the observation of chiral domain walls in highly symmetric Pt/Co/Pt is intriguing. Here, we tune the layer asymmetry in this system and observe, by current-assisted DW depinning experiments, a small chiral field which sensitively changes. Moreover, we convincingly link the observed efficiency of DW motion to the DW texture, using DW resistance as a direct probe for the internal orientation of the DW under the influence of in-plane fields. The very delicate effect of capping layer thickness on the chiral field allows for its accurate control, which is important in designing novel materials for optimal spin-orbit-torque-driven DW motion.

Current-induced motion of magnetic DWs in materials with perpendicular magnetic anisotropy (PMA) could be used to transport data in next-generation storage devices5. Recently, it has been suggested that in addition to conventional bulk STT contributions6, various current-induced torques relating to the high spin-orbit coupling in these materials could play a dominant role7,8,9. Most notably, the sources of these so-called spin orbit torques include the Rashba field, which enters as a current-dependent transverse Hy field10,11,12, and the spin Hall effect13, which leads to a vertical spin current with transverse polarization σy. In a previous work14, we demonstrated that the Spin Hall effect has the correct characteristics to describe the effect of current on domain walls in Pt/Co/Pt. It was observed that the efficiency of current-induced DW motion is practically zero, since the Bloch wall that is expected to be stable does not have the correct symmetry to be moved by a SHE-induced torque (Figure 1(a)), i.e. the cross product of the injected spin direction and magnetization direction within the DW vanishes14,15. Efficient motion arose when the internal structure was forced to the Néel type by applying a field along the current direction. However, this still contradicts the uniform motion of all DWs, at zero in-plane field, that was observed in other materials where the magnetic layer was sandwiched between two different materials10,16,17. Subsequently, it was recognized by several authors1,2,3,18,19 that in the case of structural inversion asymmetry (SIA), the Dzyaloshinskii-Moriya interaction (DMI)20 gives rise to chiral spin structures, in this case chiral Néel walls21,22,23, which are moved uniformly by a spin-Hall-effect-induced effective field (HSHE in Figure 1(b)).

Figure 1. Tuning the chirality of magnetic DWs.

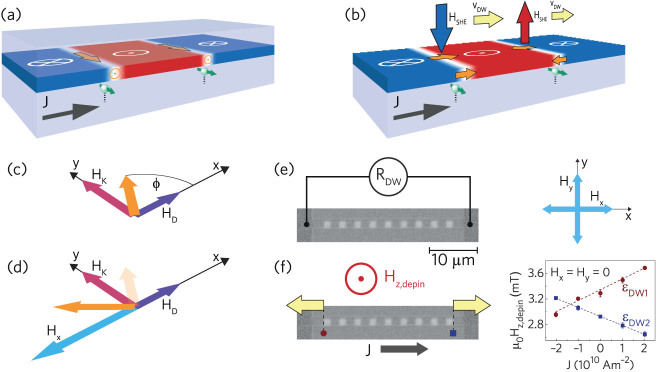
Figure 1

Open in a new tab

(a) In a symmetric layer system, Bloch walls are favored (orange arrows), on which the spin Hall current (green spins) cannot exert a torque. (b) If SIA is introduced, chiral Néel walls with alternating orientation become stable, which are moved uniformly (yellow arrows) by the effective spin Hall field HSHE ∝ cos ϕ. (c) The in-plane DW angle ϕ (orange) is determined by the competition of the DMI field HD (violet) and the DW anisotropy field HK (pink). (d) The internal angle can be further tuned using an external magnetic field Hx (light blue) or Hy (not shown). (e) DW resistance measurements can be used to verify the DW angle ϕ under influence of Hx and Hy. This can be linked to DW motion measurements on the same samples (f), where the depinning field Hz,depin as a function of current density J is measured for the two outermost DWs. The slope of this relation defines the depinning efficiency Inline graphic of each DW, which scales with cos ϕ. The Kerr micrographs show the well-controlled alternating pattern of up (white) and down (grey) domains, realized by Ga irradiation of the white areas.

In this work, we demonstrate by current-assisted depinning measurements that a measurable DMI is also present in Pt/Co/Pt4, which is surprising at first since the top and bottom interfaces are in principle the same. The DMI effect is found to be highly tunable by varying the top layer thickness, and becomes very large when the top Pt layer is substituted by AlOx. In fact, the tuning is so delicate that the DW can have any in-plane angle ϕ in between the Bloch (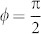Inline graphic) and Néel (ϕ = 0) states at remanence, due to the competition between the effective longitudinal DMI field HD and transverse DW anisotropy field HK, as visualized in Figure 1(c). Our data can be explained by a very simple model1 of the internal DW angle ϕ under influence of HD, HK, and externally applied in-plane fields Hx and Hy (Figure 1(d)). The efficiency of DW depinning is simply proportional to cos ϕ, as expected from a field-like torque by the SHE1. To prove that the DW angle ϕ is responsible for the efficiency, we measure the DW resistance as a function of in-plane fields (Figure 1(e)) and observe that the DW structure is indeed changing from Bloch to Néel, which is often just assumed based on elementary micromagnetics without any convincing experimental proof. These measurements allow us to directly correlate a high DW efficiency to the presence of Néel walls, which we show to be stabilized by the DMI in a tunable way.

To allow for DW resistance as well as DW depinning measurements, 1.5 µm wide strips with varying layer configurations were fabricated. Irradiation with Ga ions is employed to locally reduce the PMA in 1.5 µm long areas in these strips, allowing us to introduce a well-defined number of DWs into the strip24,25. The Kerr microscopy image in Figure 1(e) visualizes the controlled domain structure that is essential for the DW resistance measurements presented later. When the perpendicular field strength is increased from this state, DWs are randomly depinning from the edges of the irradiated regions, as indicated in Figure 1(f). We analyze the effect of current on the depinning of two particular DWs, indicated by the red circle and blue square in Figure 1(f). The graph shows how the depinning field of these domain walls change with increasing current density in a Pt(4)/Co(0.4)/Pt(2) sample (all thicknesses in nm). The slopes define the depinning efficiency 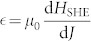Inline graphic of each DW. The opposing slopes of the 2 DWs actually imply a small but uniform action of the current on the DWs: since the field pushes both DWs outwards (in opposite directions), the current reduces the depinning field of DW2 (negative efficiency) and increases the depinning field of DW1 (positive efficiency). It is worth noting that the sign of current-induced domain wall motion opposes the electron flow direction and is therefore unlikely to be caused by conventional STT. Instead, we propose that the DWs have a small degree of built-in chirality, which leads to their uniform motion driven by the SHE. This is a refinement to our observations on similar samples in14, where we assumed that domain-walls are of the non-chiral Bloch type at zero in-plane field. To prove the presence of a favored chirality in Pt/Co/Pt, we will use in-plane fields to either oppose or assist the built-in chiral field HD.

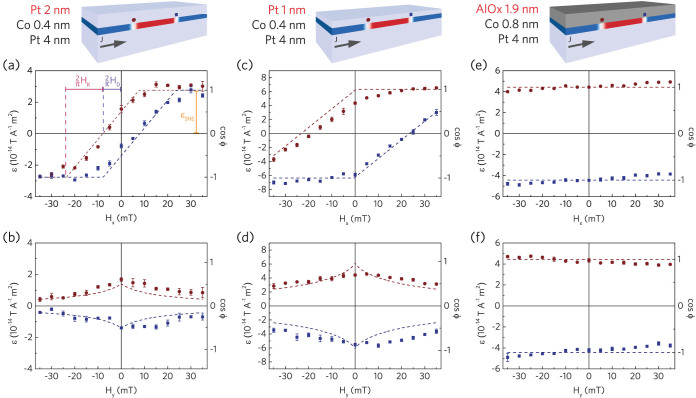
Figure 2 shows the measured current-induced depinning efficiency 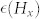Inline graphic (top panes) and 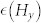Inline graphic (bottom panes) on three samples with different compositions. We first discuss Figure 2(a–b), representing the sample with the lowest degree of inversion asymmetry, Pt(4)/Co(0.4)/Pt(2). The Hx and Hy data have been fitted simultaneously using the efficiency expected from the 1D-model with only the SHE as driving force1,

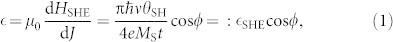graphic file with name srep05248-m1.jpg

with θSH the spin Hall angle, Ms the saturation magnetization, t the magnetic layer thickness, ν a loss factor due to compensating spin Hall currents from the bottom and top Pt layers14, and ϕ the internal DW angle prescribed by energy minimization of

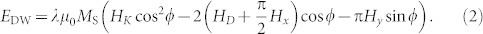graphic file with name srep05248-m2.jpg

Here, λ is the DW width (assumed constant), HK the shape anisotropy field of the DW, and HD = πD/(2µ0Msλ) the effective chiral magnetic field (with D an energy constant characterizing the strength of the DMI). The free parameters of the fit are HK, HD, and 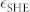Inline graphic as indicated in Figure 2(a). This graph clearly shows that there is a contribution from DMI: the red and blue curves have been shifted to the left and right, respectively, due to the effective chiral magnetic field HD ≈ 12.5 ± 0.4 mT, which has opposite sign for domain walls of opposite polarity (up-down vs down-up). We should note that HD could be lower than in an unpatterned film, since the Ga irradiation locally reduces the anisotropy and increases λ. 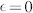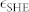Apart from the observed horizontal shift, there is a linear increase from Inline graphic to Inline graphic over a field range πHK/2, which is attributed to the transition from Bloch to Néel. Replacing Hx by Hy in Figure 2(b), the efficiency simply decreases with |Hy|, because Hy gradually pulls the wall to a Bloch state. Interestingly, the DW at zero in-plane field is neither a Bloch nor a Néel wall. From the efficiency at zero in-plane field, it can be deduced that the DW angle at remanence is ϕ ≈ 60°, rather than the 90° that is expected in a system without SIA. The stability of such an in-between wall type, observed before on epitaxial Co/Ni multilayers23, might be interesting for specific device applications of sputtered PMA films.

Figure 2. Depinning efficiency Inline graphic under in-plane fields in systems with varying SIA.

Figure 2

Open in a new tab

(a) in almost symmetric Pt(4)/Co(0.4)/Pt(2), 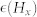Inline graphic shows a small opening between the two domain walls (red discs and blue squares) of opposite polarity, indicative of a DMI field HD. The slope of the transition from 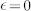Inline graphic to its saturation level 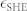Inline graphic is characterized by the DW anisotropy HK. To determine these parameters, a global fit (dashed lines) is performed together with the Hy-data in (b). (c,d) Increasing the stack asymmetry by reducing the top Pt layer to 1 nm gives a higher DMI opening. (e,f) Replacing the top Pt layer by AlOx, the DMI opening becomes too large to measure in our setup. The DMI is so strong that the DW angle ϕ is hardly influenced by Hx and Hy. The fit corresponds to the average level.

To explore the tunability of the small DMI in Pt/Co/Pt, samples with a thinner 1 nm Pt capping layer were fabricated, in order to increase the apparent SIA. Indeed, in Figure 2(c) it is observed that HD has increased significantly to the value 37 ± 1 mT. The change of efficiency εSHE matches with the change in layer thickness as discussed in the Supplementary Information. The SIA can be increased much more by replacing the top Pt layer by a different material, AlOx, as shown in Figure 2(e–f). In fact, HD has become so large that we cannot quantify it within our setup. Regardless of the in-plane field, the domain-walls are chiral Néel walls which are pushed uniformly in the direction of current flow, hence opposite to conventional STT. A small linear effect of the in-plane field on the efficiencies appears to be present, which is either an experimental artifact or caused by mechanisms beyond our simplified 1D model. We verified this effect does not have the correct characteristics to be described by the Rashba effect, by quasi-statically reproducing the depinning process in the dynamic 1D DW model1 including a current-dependent Hy Rashba field. Crucially, these results suggest that our Pt/Co/AlOx is not fundamentally different from Pt/Co/Pt, but only has a higher built-in chiral field due to the increased asymmetry.

Although the results presented so far here and by other authors1,2,3,18,19 match well with a SHE-induced torque dictated by the DW angle ϕ, it is not at all trivial that the DW indeed has the structure that these experiments suggest. In fact, the transition from a Bloch-like to a Néel state by an in-plane field was to our knowledge not measured before. We believe that using DW resistance as a probe for the DW structure is much more direct than using the DW mobility, since the resistance does not rely on any of the spin torques. Therefore, we have performed measurements of the DW resistance as a function of in-plane field. To be able to accurately measure tiny resistance changes induced by the DWs, we use lock-in measurements on an on-sample Wheatstone bridge25,26 consisting of four nominally identical wires, one of which has a Ga-irradiation pattern. To exclude magnetoresistive effects in the domains from polluting the measured resistance of the DWs, we measure the bias of the bridge for the monodomain state at each in-plane field, and subtract it from the bias in the presence of the multidomain state shown in Figure 1(e) (see also Methods section). When the resistance of a Bloch wall is measured (Figure 3(a)), the dominant contribution comes from the intrinsic resistance RLZ ~ 1/λ dictated by the Levy-Zhang model27 for which we recently found experimental evidence25,26. However, when the magnetization within the DW obtains a component parallel to the current flow (Figure 3(b)), an additional contribution RAMR from anisotropic magnetoresistance arises28, simply proportional to λ cos2 ϕ.

Figure 3. Bloch-Néel transition revealed by DW resistance measurements.

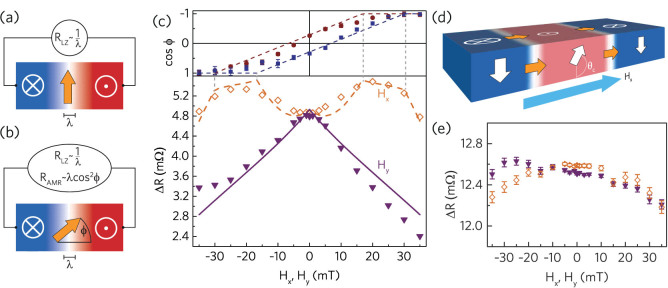
Figure 3

Open in a new tab

(a) a Bloch wall yields only an intrinsic contribution RLZ to the DW resistance. (b) As ϕ approaches 0 (Néel wall), an additional contribution from the AMR effect arises. (c) (top) Depinning efficiency as a function of Hx and (bottom) Resistance change induced by 20 DWs of alternating polarity, as a function of Hx (open diamonds) and Hy (filled triangles), measured on the same Pt(4)/Co(0.5)/Pt(2) sample. The dashed orange and solid purple line are a fit including the two resistance contributions, in which HK and HD have been taken from the fit of the depinning data. The DW resistance peaks around Hx = 20 mT due to the transition from Bloch to Néel. A decreasing background signal is present in both the Hy and the Hx data due to canting of the magnetization in the irradiated domain (d), leading to a lower intrinsic contribution RLZ. (e) DW resistance in Pt/Co/AlOx does not show the Bloch-Néel transition since Néel walls are highly stable.

Looking at the measured DW resistance in Pt(4)/Co(0.5)/Pt(2) as a function of Hx (open orange diamonds in Figure 3(c)), we indeed see an increase when the in-plane field increases, owing to the transformation to a Néel wall. However, beyond Hx = 30 mT, the measured DW resistance starts to decrease again. This decrease is seen over the entire Hy-field range (purple triangles), which can be regarded as a kind of background measurement. We attribute this to a change of RLZ related to the domain structure. Since the anisotropy in one of the domains is reduced strongly by the Ga irradiation treatment29, this region tends to be pulled in plane, modifying the domain-wall profile as sketched in (Figure 3(d)). This has a strong effect on RLZ, and also a small effect on RAMR (see Supplementary Information for details of the model). From the DW-depinning data (top pane of Figure 3(c)), we can deduce ϕ(Hx, Hy), and use this as input in our resistance model. The best-fit to this model is presented as the dashed orange and solid purple lines in Figure 3(c)), where the free parameters are the anisotropy in the irradiated domain, the AMR resistivity, and the strength of the intrinsic DWR. The model reproduces the measurements, apart from two kinks at each field polarity (when the angles of either the ‘red’ or the ‘blue’ domain walls saturate, compare to top panel). It is not surprising that these sharp features from the 1D model become smooth in reality, especially since we measure the sum of 20 DWs, each with slightly different local properties.

Looking at the DW resistance measurements in Pt/Co/AlOx in Figure 3(e)), only minor changes as a function of in-plane field are observed, and there is no clear difference between the Hx and Hy data. Similar to the DW-depinning results, this suggests that the Néel character of the DWs is stabilized by a strong built-in chiral field and is not significantly influenced by the range of applied in-plane fields. The background due to magnetization canting is largely absent here, because the anisotropy in the irradiated domain is much higher. Although any change as a function of in-plane field is relatively small compared to the Pt(4)/Co(0.5)/Pt(2) sample, a small asymmetry appears in the Hy data, which may have the same unknown origin as the slight asymmetry in the DW depinning data in Figure 2(f).

We should note that, in our analysis so far, we assumed that the DW is oriented perpendicular to the nanowire, whereas it was recently demonstrated that the DW boundary might tilt in the xy-plane in systems with a significant DMI18,30. Such tilting will occur when the DW moves at high speed (which is not applicable in depinning measurements), or when Hy fields are applied30. We estimate that the highest applied Hy of ~ 40 mT, could induce a tilting of at most 10° in Pt/Co/AlOx, which has the highest DMI. We do not observe significant tilting in the Kerr images (within the ~ 300 nm resolution), nor do we observe a dramatic difference between the DW resistance as a function of Hy and Hx in this material, hence the influence of this possible tilt angle is limited. Furthermore, in Pt/Co/Pt samples the DMI is an order of magnitude smaller, hence a tilting of at most 1 or 2 degrees might be induced, which is hardly significant and therefore not taken into account in the analysis.

We now briefly discuss the origin of the unexpected chiral effective fields in Pt/Co/Pt. It was recently calculated31 that a significant DMI can arise in a Pt/Co bilayer, leading to a effective chiral field of several 100 mT. Since the chiral field in Pt/Co/Pt is the result of two canceling interfaces, we should stress that an imbalance between the DMI at the top and bottom interface of only a few percent is enough to achieve the measured magnitude. Ryu et al.3 also studied the effect of stack asymmetry on the effective chiral field in Co/Ni multilayers, and concluded that the DMI originates at Pt/Co interfaces and scales with the thickness of the neighboring Co layer, which they attributed to proximity-induced moments in Pt. They concluded that DW motion in the direction of current flow implies that the DMI at the bottom interface dominates over the top interface. In the current manuscript, we appear to have tuned the DMI through the thickness of the Pt layers themselves. Due to growth-related phenomena, it is known that the top and bottom interface can have different characteristics, for example evidenced by a different contribution to the effective PMA32. Apparently, the DMI at the top interface decreases when reducing the top layer thickness, such that the net DMI increases. It is worth noting that although the DMI at the top layer appears to decrease, the PMA constant increases for thinner Pt top layers (see Supplementary Information Table 1). In an inverted Pt(2)/Co/(0.5)/Pt(4) sample (Supplementary Information, Figure S1), it was found that the DMI almost vanishes, but does not change sign, thus the interfaces appear to become more symmetric for thick capping layers. This indeed suggests that interface characteristics are key, rather than the thickness of the layers themselves. Reasons for the top interface to vary with thickness can be changes to the mode of growth, different interdiffusion32 or even slight oxidation at the top Co/Pt interface in case of thin capping layers.

To summarize, the effective chiral magnetic field in Pt/Co systems turns out to be tunable by varying the top layer thickness and material. The effect scales with the degree of structural inversion asymmetry and leads to a gradual change of the stable wall type from Bloch to Néel. Furthermore, by using the DW resistance as an independent measurement of the internal DW structure, a change of the internal structure from Bloch-like to Néel under longitudinal fields was evidenced, and correlated to the high efficiency of DW motion of Néel walls. These findings firmly establish SHE and DMI as a tandem for efficient and uniform domain wall motion.

Methods

A. Sample fabrication

All samples consisted of 1.5 µm wide strips fabricated on Si/SiO2 substrates by Electron-Beam lithography, DC sputtering, and lift-off. The Pt(4)/Co(0.8)/Al(1.5) samples were oxidized in a 15 W, 0.1 mbar O2 plasma for 10 minutes to obtain Pt/Co/AlOx. These samples were annealed for 20 minutes at 573 K. The Pt/Co/Pt samples did not undergo an annealing treatment. The samples were designed to form an on-sample Wheatstone bridge configuration to be able to measure resistance changes accurately (for details see25). The samples were locally irradiated with a 30 keV Ga FIB to make it possible to create a stable domain pattern with a well-defined number of domain walls. At the same time, the edges of the irradiation boundaries acted as pinning sites, to enable the well-controlled depinning measurements. The Ga doses were chosen to ensure that all DWs are stable during DWR measurements and amounted to 1.13 × 1013 ions/cm2 on Pt/Co/AlOx, 0.50 × 1013 ions/cm2 on Pt(4)/Co(0.5)/Pt(2) and Pt(4)/Co(0.4)/Pt(2), and 0.81 × 1013 ions/cm2 on Pt(4)/Co(0.4)/Pt(1). Table S1 (Supplementary Information) provides the material parameters (PMA constant and Ms) obtained by VSM-SQUID magnetometry on unpatterned films.

B. DW depinning measurements

Very low DC current densities in the range ±2 × 1010 A/m2 were used to exclude significant effects from Joule heating and Oersted fields. The current and in-plane field are kept constant, while the z-field is being ramped up until both DWs have depinned which is automatically detected by an image analysis routine. This is repeated at least 10 times for each current point to obtain sufficient signal to noise. Table S1 presents the fit parameters of the 1D model (HK, HD and 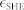Inline graphic) for each used material composition, and compares the latter to the expected efficiency 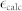Inline graphic based on the layer thicknesses.

C. DW resistance measurements

Our measurement routine is very similar to what we described in25. We use a combination of an on-sample Wheatstone bridge and a lock-in technique to measure the resistance change due to the presence of domain walls. The in-plane field is applied constantly, and first the wire is saturated (zero DWs) by a negative Hz, and the lock-in voltage at Hz ≈ −1 mT is recorded. Then, the domain walls are created by a positive Hz, the field is reduced to Hz ≈ 1 mT and the lock-in voltage is recorded again. The difference is presented in Figure 3 as ΔR, and represents the resistance change due to all the DWs (20 or 18 for Pt/Co/Pt and Pt/Co/AlOx, respectively). Since the background voltage is recorded at the same in-plane field as the voltage in the presence of DWs, magnetoresistive effects within the bulk of the domains, such as AMR due to canting or the magnon contribution33, are automatically filtered out, leaving only resistance changes in the DW region.We always check the number and positions of the DWs present by real-time comparison to a Kerr-microscopy image. Furthermore, we always ensure that the magnetization underneath the 20 nm thick Pt contacts and the three reference strips in the bridge does not switch, as this can give rise to additional magnetoresistive signals. The small Hz during measurements serves to ensure the DW pattern remains stable during measurements. An AC probe current of 1 mA (0.75 mA) at 500 Hz was sent through two parallel series of Pt(4)/Co(0.5)/Pt(2) (Pt(4)/Co(0.8)/AlOx) wires and it was verified that a lower amplitude does not significantly alter the results. Because the bridge is not perfectly balanced, a bias of typically 10 mV occurs, even when all strips are magnetized in the same direction. When we introduce domain walls into one of the strips, the signal typically changes by 10 µV. Note that a sample with slightly thicker tCo = 0.5 nm had to be used, because the samples with tCo = 0.4 turned out to be very easily switched by the spin Hall effect from the probe current. Therefore, much lower probe currents have to be used, and the thinner magnetic Co layer further deteriorates the signal/noise. Details on the modeling of in-plane field effects on the measured DW resistance are presented in the Supplementary Information, and the individual contributions to the modeled resistance are plotted in Figure S2.

Author Contributions

J.H.F. designed the experiments and prepared the manuscript. M.H. and J.H.F. performed the experiments and the data analysis. H.J.M.S. and B.K. assisted in the analysis and commented on the final manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep05248-s1.pdf (120.2KB, pdf)

Acknowledgments

This work is part of the research programme of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO).

References

  1. Thiaville A., Rohart S., Jué E., Cros V. & Fert A. Dynamics of Dzyaloshinskii domain walls in ultrathin magnetic films. Europhys. Lett. 100, 57002 (2012). [Google Scholar]
  2. Emori S., Bauer U., Ahn S.-M., Martinez E. & Beach G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–6 (2013). [DOI] [PubMed] [Google Scholar]
  3. Ryu K.-S., Thomas L., Yang S.-H. & Parkin S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 8, 527–33 (2013). [DOI] [PubMed] [Google Scholar]
  4. Je S.-G. et al. Asymmetric magnetic domain-wall motion by the Dzyaloshinskii-Moriya interaction. Phys. Rev. B 88, 214401 (2013). [Google Scholar]
  5. Parkin S. S. P., Hayashi M. & Thomas L. Magnetic domain-wall racetrack memory. Science 320, 190–4 (2008). [DOI] [PubMed] [Google Scholar]
  6. Thiaville A., Nakatani Y., Miltat J. & Suzuki Y. Micromagnetic understanding of current-driven domain wall motion in patterned nanowires. Europhys. Lett. 69, 990 (2005). [Google Scholar]
  7. Miron I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–194 (2011). [DOI] [PubMed] [Google Scholar]
  8. Liu L. et al. Spin-Torque Switching with the Giant Spin Hall Effect of Tantalum. Science 336, 555–558 (2012). [DOI] [PubMed] [Google Scholar]
  9. Garello K. et al. Symmetry and magnitude of spin-orbit torques in ferromagnetic heterostructures. Nat. Nanotechnol. 8, 587–93 (2013). [DOI] [PubMed] [Google Scholar]
  10. Miron I. M. et al. Fast current-induced domain-wall motion controlled by the Rashba effect. Nat. Mater. 10, 419–23 (2011). [DOI] [PubMed] [Google Scholar]
  11. Wang X. & Manchon A. Diffusive Spin Dynamics in Ferromagnetic Thin Films with a Rashba Interaction. Phys. Rev. Lett. 108, 117201 (2012). [DOI] [PubMed] [Google Scholar]
  12. Kim K.-W., Seo S.-M., Ryu J., Lee K.-J. & Lee H.-W. Magnetization dynamics induced by in-plane currents in ultrathin magnetic nanostructures with Rashba spin-orbit coupling. Phys. Rev. B 85, 180404(R) (2012). [Google Scholar]
  13. Hirsch J. Spin Hall Effect. Phys. Rev. Lett. 83, 1834–1837 (1999). [Google Scholar]
  14. Haazen P. P. J. et al. Domain wall depinning governed by the spin Hall effect. Nat. Mater. 12, 299 (2013). [DOI] [PubMed] [Google Scholar]
  15. Khvalkovskiy A. V. et al. Matching domain-wall configuration and spin-orbit torques for efficient domain-wall motion. Phys. Rev. B 87, 020402 (2013). [Google Scholar]
  16. Moore T. A. et al. High domain wall velocities induced by current in ultrathin Pt/Co/AlOx wires with perpendicular magnetic anisotropy. Appl. Phys. Lett. 93, 262504 (2008). [Google Scholar]
  17. Koyama T. et al. Current-Induced Magnetic Domain Wall Motion in a Co/Ni Nanowire with Structural Inversion Asymmetry. Appl. Phys. Express 6, 033001 (2013). [Google Scholar]
  18. Emori S., Martinez E. & Bauer U. Spin Hall torque magnetometry of Dzyaloshinskii domain walls. arXiv 1308.1432 (2013). [Google Scholar]
  19. Torrejon J. et al. Interface control of the magnetic chirality in TaN—CoFeB—MgO heterosctructures. arXiv 1308.1751 (2013). [Google Scholar]
  20. Moriya T. New mechanism of anisotropic superexchange interaction. Phys. Rev. Lett. 4, 228 (1960). [Google Scholar]
  21. Heide M., Bihlmayer G. & Blügel S. Dzyaloshinskii-Moriya interaction accounting for the orientation of magnetic domains in ultrathin films: Fe/W(110). Phys. Rev. B 78, 140403 (2008). [Google Scholar]
  22. Chen G. et al. Novel Chiral Magnetic Domain Wall Structure in Fe/Ni/Cu(001) Films. Phys. Rev. Lett. 110, 177204 (2013). [DOI] [PubMed] [Google Scholar]
  23. Chen G. et al. Tailoring the chirality of magnetic domain walls by interface engineering. Nat. Commun. 4, 2671 (2013). [DOI] [PubMed] [Google Scholar]
  24. Franken J. H. et al. Precise control of domain wall injection and pinning using helium and gallium focused ion beams. J. Appl. Phys. 109, 07D504 (2011). [Google Scholar]
  25. Franken J. H., Hoeijmakers M., Swagten H. J. M. & Koopmans B. Tunable Resistivity of Individual Magnetic Domain Walls. Phys. Rev. Lett. 108, 037205 (2012). [DOI] [PubMed] [Google Scholar]
  26. Aziz A. et al. Angular Dependence of Domain Wall Resistivity in Artificial Magnetic Domain Structures. Phys. Rev. Lett. 97, 206602 (2006). [DOI] [PubMed] [Google Scholar]
  27. Levy P. M. & Zhang S. Resistivity due to Domain Wall Scattering. Phys. Rev. Lett. 79, 5110–5113 (1997). [Google Scholar]
  28. Koyama T. et al. Observation of the intrinsic pinning of a magnetic domain wall in a ferromagnetic nanowire. Nat. Mater. 10, 194–197 (2011). [DOI] [PubMed] [Google Scholar]
  29. Franken J. H., Hoeijmakers M., Lavrijsen R. & Swagten H. J. M. Domain-wall pinning by local control of anisotropy in Pt/Co/Pt strips. J. Phys. Cond. Matter 24, 024216 (2012). [DOI] [PubMed] [Google Scholar]
  30. Boulle O. et al. Domain Wall Tilting in the Presence of the Dzyaloshinskii-Moriya Interaction in Out-of-Plane Magnetized Magnetic Nanotracks. Phys. Rev. Lett. 111, 217203 (2013). [DOI] [PubMed] [Google Scholar]
  31. Freimuth F., Blügel S. & Mokrousov Y. Berry phase theory of Dzyaloshinskii-Moriya interaction and spin-orbit torques. arXiv 1308.5983 (2013). [DOI] [PubMed] [Google Scholar]
  32. Bandiera S., Sousa R. R., Rodmacq B. B. & Dieny B. Asymmetric Interfacial Perpendicular Magnetic Anisotropy in Pt/Co/Pt Trilayers. IEEE Magn. Lett. 2, 3000504 (2011). [Google Scholar]
  33. Nguyen V. D. et al. Detection of Domain-Wall Position and Magnetization Reversal in Nanostructures Using the Magnon Contribution to the Resistivity. Phys. Rev. Lett. 107, 136605 (2011). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep05248-s1.pdf (120.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES