Automated Factor Slice Sampling

Abstract

Markov chain Monte Carlo (MCMC) algorithms offer a very general approach for sampling from arbitrary distributions. However, designing and tuning MCMC algorithms for each new distribution, can be challenging and time consuming. It is particularly difficult to create an efficient sampler when there is strong dependence among the variables in a multivariate distribution. We describe a two-pronged approach for constructing efficient, automated MCMC algorithms: (1) we propose the “factor slice sampler”, a generalization of the univariate slice sampler where we treat the selection of a coordinate basis (factors) as an additional tuning parameter, and (2) we develop an approach for automatically selecting tuning parameters in order to construct an efficient factor slice sampler. In addition to automating the factor slice sampler, our tuning approach also applies to the standard univariate slice samplers. We demonstrate the efficiency and general applicability of our automated MCMC algorithm with a number of illustrative examples.

1 Introduction

Markov chain Monte Carlo (MCMC) algorithms provide the knowledgeable researcher with a very general approach for generating samples from and approximating integrals (expectations) with respect to a wide range of complicated distributions. However, while the theory underlying the MCMC algorithm guarantees that the accuracy of these integrals will eventually get arbitrarily close to the truth, in practice the precision of these approximations depends upon how well the algorithm is tailored to the particular distribution of interest.

While the standard sampling techniques such as the random-walk Metropolis-Hastings algorithm appear adequate for many simple statistical models, the necessary sampling time to estimate covariance structures, non-linear link functions, and/or more complicated hierarchical models vastly diminishes their utility as a generic MCMC sampler. For many complicated models and distributions, the resulting Markov chain does not result in accurate estimates of the interesting features of the target distribution. In addition, standard samplers like the random-walk algorithm are serial in nature and are not typically designed in a manner to take advantage of modern parallelized computing hardware. In recent work, Tibbits et al. (2011) demonstrate that it is possible to construct versions of the slice sampler (Neal, 2003) that take advantage of parallel computing.

In this manuscript, we provide a significant improvement to the approach in Tibbits et al. (2011) by constructing proposals within a rotated reference frame. By sampling within a transformed space, the rotated or “factor” slice sampler can generate nearly independent draws from a highly correlated, high dimensional target distribution, eliminating the construction of an expensive approximate multivariate slice as required by Tibbits et al. (2011). The factor slice sampler offers a potentially robust, general sampler which can be applied to a wide range of distributions. In addition we will also address another, seldom discussed, challenge of constructing an efficient MCMC sampling: the selection of optimal tuning parameters. Although identifying reasonable tuning parameters is often thought of as more art than science, we demonstrate that a heuristic optimization technique can robustly identify efficient interval widths (the only tuning parameter for a univariate slice sampler) with minimal, if any need for supervision. In addition, we incorporate the techniques for parallelizing the univariate slice sampler from our previous work utilizing modern computational hardware (multi-threaded CPUs, graphics cards, etc.). This allows us to provide an automatic, efficient, and parallelizeable Markov chain Monte Carlo sampling algorithm with an example implementation in R (R Development Core Team, 2009).

The outline for the manuscript is as follows. In Section 2, we introduce the rotated or “factor” slice sampler and demonstrate its utility within the context of a toy example. In Section 3, we describe a procedure for automatically tuning univariate slice samplers. In Section 4, we describe, in detail, a fully automated factor slice sampler (AFSS). Working in concert with parallelization techniques, we demonstrate via examples that the AFSS algorithm obtains a dramatic improvement in computational efficiency over the standard slice sampler. Furthermore, we demonstrate the automated factor slice sampler's performance for high dimensional distributions. We conclude in Section 5 by summarizing the AFSS algorithm's performance and outlining areas of future research.

2 Factor Slice Sampling

The slice sampling algorithm (e.g. Damien et al., 1999; Mira and Tierney, 2002; Neal, 1997, 2003) exploits the equivalence between drawing directly from a K-dimensional probability distribution and drawing uniformly from the K + 1-dimensional region which lies below the corresponding probability distribution. Constructing a K + 1-dimensional random walk, the slice sampler uses uniform deviates to draw from an arbitrary density function. Although the algorithm for slice sampling, Algorithm 1, does not depend on the dimensionality of the target distribution, f (β), in this manuscript we will restrict our attention to single-dimension (univariate) implementations of the slice sampler. When applying the univariate slice sampler to a multivariate target distribution, we sample component-at-a-time, augmenting each dimension with its own auxiliary variable. For clarity, the subscript k will index the dimension of the parameter, β_k. The superscript (i) will index the iteration of the Markov chain.

Algorithm 1: Slice Sampling Update Algorithm for Parameter β with density ∝ f(β)

1. Sample h(i) ∼ Uniform {0, f(β(i−1)}

2. Sample β(i) ∼ Uniform on A={β: f(β) ≥ h(i)}

The slice sampler augments the target distribution, adding the h parameter, to more easily sample from a complicated target distribution, f(β). The i^th step of the algorithm may be described as follows. First, a “height” under the density function, h⁽ⁱ⁾, is drawn uniformly from the interval (0, f(β⁽ⁱ⁻¹⁾)). This height, h⁽ⁱ⁾, then defines a horizontal slice across the target density, A = {β: f(β) ≥ h⁽ⁱ⁾}. Second, a sample, β⁽ⁱ⁾, is drawn uniformly from A. Typically a closed-form solution for the boundary of A is unavailable; hence, an intermediate step is usually inserted to construct an approximation, Ã⁽ⁱ⁾, to A from which β⁽ⁱ⁾ is drawn subject to the constraint: β⁽ⁱ⁾ ∈ A. Note that in the univariate case the set A is either an interval or the union of several intervals (for example, in the presence of multiple modes). In a multivariate setting, A may have a much more complicated geometry. We will assume for the remainder of Section 2, that an efficient means for constructing an approximating interval à exists (for the univariate slice sampler) and proceed as if A is known precisely.

It has been known for some time that a simple rotation of the sampling reference frame or block updating can dramatically improve the efficiency of an MCMC algorithm. This fact is often utilitized in practice through either correlated multivariate updates (e.g. Roberts and Rosenthal, 2009; Roberts and Sahu, 1997), or through a reparameterization of the target distribution to minimize the dependence amongst parameters (e.g. Gelfand et al., 1996; Gilks and Roberts, 1996; Yan et al., 2007). While these approaches offer improved mixing, they can often be challenging to implement. The first approach requires either an adaptive scheme capable of navigating complicated dependence structures or prior knowledge of the correlation structure to avoid highly autocorrelated samples. The second approach is often unusable as it may not be possible to construct orthogonal reparameterizations.

The primary contributions of our work are as follows: (1) we propose a factor slice sampler, which can be automatically constructed using a rotated orthogonal basis without prior knowledge of the correlation structure, and (2) we provide an approach for automatically tuning the proposed sampler. In Algorithm 2, shown below, updates are proposed using linear combinations, Γ_k's, of the vector components, β_k, in such a way that Γ forms an orthogonal basis which spans the parameter space and leaves the target distribution unaltered.

Algorithm 2: Univariate Factor Slice Sampling Update Algorithm for β ∈ ℝK with density proportional to f(β). Note: ηk ∈ ℝ1 is a parameter in the orthogonalized space. The basis vectors, Γk ∈ ℝK are chosen as eigenvectors of the covariance matrix of β.

1. Sample h(i) ∼ Uniform on {0, f(β(i−1))}

2. Set β(*) = β(i−1)

3. For each basis vector Γk ∈ Γ:

(a) Sample ${\eta }_k^{(i)}\sim \text{Uniform on}A=\{{\eta }_k:f({\eta }_k{\mathrm{\Gamma }}_k+{\mathit{\beta }}^{(\ast )})\ge h^{(i)}\}$

(b) Update ${\mathit{\beta }}^{(\ast )}={\mathit{\beta }}^{(\ast )}+{\eta }_k^{(i)}{\mathrm{\Gamma }}_k$

4. Set β(i) = β(*)

It is particularly difficult to create an efficient sampler when there is strong dependence among the variables in a multivariate distribution. The benefit of the factor slice sampler is that univariate updates of η_(k) are performed in an orthogonalized space where correlation between the steps of the Markov chain is minimized. Further, a priori knowledge of the correlation structure of f(β) is unnecessary. In such cases, one may construct a quadratic approximation, $f\ast \left(\mathit{\beta }\right)\propto {\left|\mathrm{\Lambda }\right|}^{-\frac{1}{2}}exp\left(-\frac{1}{2}{\left(\mathit{\beta }-{\mathit{\mu }}_f\right)}^T{\mathrm{\Lambda }}^{-1}\left(\mathit{\beta }-{\mathit{\mu }}_f\right)\right)$, of the target distribution, f(β), where μ_f and Λ represent the mean and covariance of the target distribution respectively. One can compute the eigenvectors of Λ which form an orthogonal basis, Γ̂. The columns of Γ̂ are then used to construct linearly independent updates of the original parameters following Algorithm 2. The examples which follow demonstrate that an iterative approximation of Γ using a sample covariance matrix is sufficient for efficient exploration of f(β). Further, one can use the summation in step five of Algorithm 3 during an initial tuning phase to gauge the accuracy of the approximation, Γ̂, to Γ.

Algorithm 3: Iterative Procedure for Parameter Covariance Estimation

1. Set Γ̂(0) =I, Λ(0) = I, and t = 1, where I is an identity matrix.

2. Draw N samples using Γ̂(t−1), an orthogonal basis for the factor slice sampler.

3. Compute Λ(t) and its corresponding eigenvectors Γ(t).

4. Find A, where A is a rotation matrix such that Λ(t−1)A = Λ(t). Set t = t + 1.

5. Repeat steps 2 through 4 until Σ (A− I) is below a preset threshold.

There are clear limits to the factor slice sampler. The factor-based technique will only reduce the impact of linear dependence among the parameters β and will not help in the case of non-linear dependence (as seen in the Appendix). Further, if the covariance matrix, Λ, is highly ill-conditioned, the factor slice sampler may perform less than optimally; however if Λ is ill-conditioned it is possible to utilize the left-singular vectors from a singular value decomposition of Λ and allow Λ to be singular. In this case the factor slice sampler would gracefully decay to sequentially lower dimensional subspaces even if a given distribution was overparameterized or partially non-identifiable. This would be useful, for example, when one desires to sample from a distribution with imposed linear constraints: given a vector whose elements are constrained to sum to one, the distribution can be sampled efficiently by using the basis of the space, P┴, orthogonal to the linear (sum-to-one) constraint. However, for purposes of this manuscript, we limit our scope to models whose parameters have a full-rank covariance matrix. If the parameters β of a distribution f(β) exhibit strong linear dependence, then the factor slice sampler will provide a significant performance improvement, as can be demonstrated using a stylized example of Bayesian linear regression.

Example 1 (Linear Regression with an Intercept)

Consider a simple linear regression model using k predictors. We assume that the errors ∊_j are i.i.d. standard normal:

$$\begin{array}{ccc}{Y}_j={\mathbf{X}}_j\mathit{\beta }+{∊}_j& {∊}_j\sim N(0,1)& j=1,\dots ,N\end{array}$$

We use a Bayesian approach to model specification and complete the model by assigning flat priors to the regression coefficients: 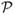(β) ∝ 1.

This is a toy example as we can sample directly from the posterior distribution; however, it provides a nice test bed for studying our algorithm. By rearranging terms, we see that the posterior covariance of the coefficients, β, is given by (X^TX)⁻¹. Hence, we can obtain the optimal sampling basis explicitly by calculating the eigenvectors Γ_k of (X^TX)⁻¹. To compare the performance of Algorithms 1 and 2 we generate 20, 000 pairs {Y_j, X_j} according to the above model with 10, 50, 100, and 500 correlated predictors as follows:

Algorithm 4: Data Generation Procedure for Regression Example (# 1)

1. Set ${\sum }_{m,n}\equiv \{\begin{array}{cc}1.0& \text{if}m=n\\ 0.6& \text{if}m\ne n\end{array}$ 3. Draw Xj ∼ N(0, Σ*)

2. Draw $\sum \ast \sim \text{Wishart}(\frac{1}{2p}\sum ,2p)$ 4. Draw Yj ∼ N(Xjβ, 1)

The Wishart draw in step 2 of Algorithm 4 was simply used to perturb the off-diagonal elements of the correlation matrix while ensuring that it remains positive definite. We drew the correlated predictors, X_j, according to step 3, and similarly the response observations according to step 4 (from the model in Example 1) using a vector of known coefficients β. The efficiency of competing MCMC algorithms can be compared using effective sample size (ESS) and effective samples per second (ES/sec) as described by Kass et al. (1998) and Chib and Carlin (1999). ESS is defined as the ratio of the number of steps in a Markov chain over its autocorrelation time, τ, given by $\tau =1+2\sum _{i=1}^N\rho \left(m\right)$ where ρ(m) is the autocorrelation at lag m. This summation is often truncated when the autocorrelation drops below 0.1, though more sophisticated approaches are possible (cf. Geyer, 1992). Hence, ESS estimates the number of i.i.d. draws to which a given Markov chain is equivalent. ESS weighted by computation time is also reported as a metric of computational efficiency.

For comparison, we ran three univariate (component-at-a-time) update algorithms to sample from the posterior distribution of β as described in Example 1 using data generated via Algorithm 4. We varied the length of the tuning phase as well as the tuning parameters values between the three samplers to ensure that each sampler functioned at peak performance. The ES/sec times reflect the total run time (including time spent in the tuning phase) so that a fair comparison can be made. The univariate slice sampler was run for a shorter tuning phase of 10, 000 samples during which the interval widths were tuned to ensure optimal performance (see Algorithm 5 in Section 3.2). The univariate factor slice sampler ran for a much longer tuning phase of 120, 000 samples during which the interval widths were also tuned to ensure optimal performance using Algorithm 5 of Section 3.2. Algorithm 3 was used to tune the factor slice sampler for iteration number 10, 000 through 110, 000. The univariate random-walk Metropolis-Hastings sampler was tuned via the method outlined in Roberts and Rosenthal (2009) to an acceptance rate of 0.44 during a tuning phase of 100, 000 samples.

In comparing the performance of the samplers, we see that the factor slice sampler clearly dominates the performance of the other two algorithms in both mixing efficiency, generating nearly independent draws, as well as computational efficiency, with the highest ES/sec. The univariate factor slice sampler requires roughly 50% more time to run than the univariate slice sampler (including the tuning period), but this time is easily recouped in ES/sec as the generated samples are nearly independent (ESS is nearly 500, 000). The model from Example 1 may unfairly favor the factor slice sampler because the complicated dependency between the β coefficients can be easily removed by orthogonalizing the covariates. In an uncorrelated setting, the factor slice sampler will have identical performance with the standard univariate slice sampler, but one would, algorithmically, require a longer tuning phase; hence, the ES/sec of the factor slice sampler will be slightly lower than the ES/sec of the standard slice sampler, but only with a perfectly linearly-independent distribution. However, with more challenging models which employ non-linear link functions or complicated hierarchies, removing the collinearity among the parameters may be difficult if not impossible and there the true utility of the AFSS algorithm becomes evident, as we shall see in Section 4.

3 Automated Interval Width Selection

In practice the most challenging aspect of using a slice sampler is constructing an efficient approximation to the slice A = {β : f(β) ≥ h} because for most models one lacks a closed form representation for A. We overcome this by following the method from Neal (2003) for constructing and sampling from an approximate slice and propose a method for automatically identifying efficient tuning parameters (initial interval widths) for this method. In Tibbits et al. (2011), we discussed how in a multivariate slice sampler, approximating A is a challenging or impossible problem; however, in a single dimension, it is quite straightforward to find an upper and lower bound which are guaranteed to contain A (given that f(β) is a proper probability distribution). The computational cost of constructing an approximate slice depends directly on the number of likelihood evaluations which are required. We start by quantifying the functional dependence of the computational cost on the choice of the initial interval width. We then show how a Robbins-Monroe recursion from the optimization literature may be used to automatically tune the slice sampler, thereby minimizing the computational burden.

3.1 Computational Cost Estimation

To quantify the computational cost of our general slice sampling approach, we must account for both the time spent constructing the approximate slice, Ã, as well as the time needed to sample from A using Ã. There are clearly tradeoffs between these two. A highly accurate approximate slice will require many likelihood evaluations to construct, but only a few proposals as à is very similar to A. Conversely, a poor approximate slice will require few (if any) likelihood evaluations to construct, but many more proposals as à is a very inefficient approximation to A.

3.1.1 Approximate Slice Construction

We first explain how to construct an approximation to the slice. Two methods for iteratively constructing an approximate slice in one dimension were outlined in Neal (2003): “step-out” and “doubling”. To clearly illustrate our approach we will examine the step-out method in detail and derive the functional dependence of the computational cost (the expected number of likelihood evaluations) on the choice of tuning parameter (initial interval width). The approximation methods of Neal both construct à by randomly positioning an initial interval width and then expanding it until both bounds fall outside the target slice. Initially, we assume that the target distribution is unimodal as this provides a well-defined stopping criterion for the interval approximation, that is, once the approximate interval bounds fall outside the target slice, then A ⊆ Ã. We then extend our approach to consider multimodal distributions where A is a collection of disjoint intervals and hence, while a portion of A must be contained in Ã, à may not contain all of A.

In the step-out algorithm proposed by Neal (2003), an initial interval of width ω is randomly positioned such that it overlaps the current location, and then the lower and upper bounds are examined and extended in steps equal to ω until they fall outside the target slice. We let s represent the true (unknown) width of the target slice A, and define κ to be the ratio $\frac{s}{\omega }$. Let X denote the number of expansions required so that the approximate interval completely contains A. Intuitively, κ is the expected value of X. If ω is $\frac{s}{2}$, half the size it must be to fully contain s, then the interval will be expanded twice. Similarly, if ω is 3 × s, then the interval will only expand (exactly once) a third of the time. We now formally construct this result.

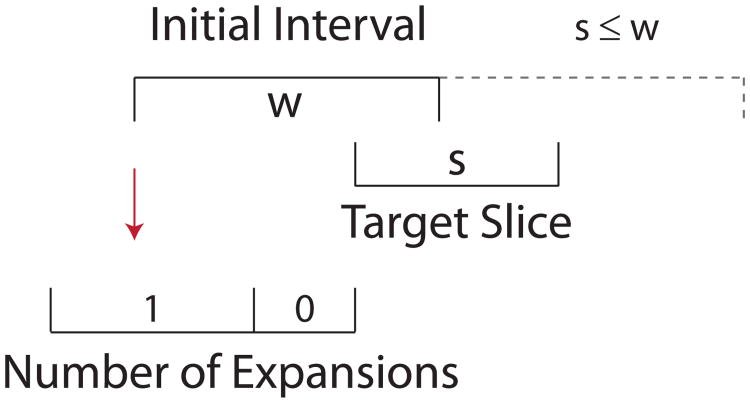
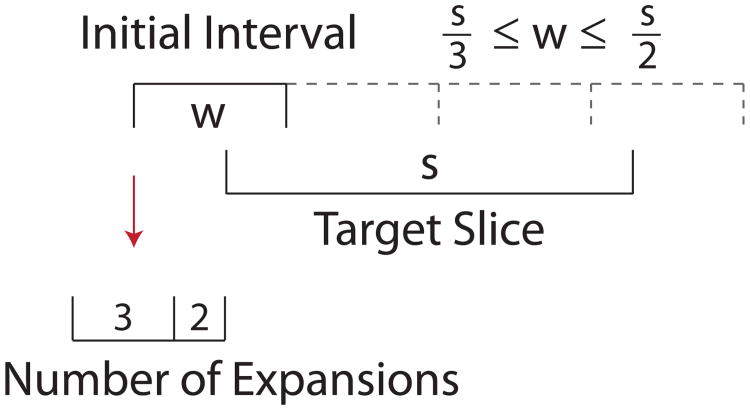
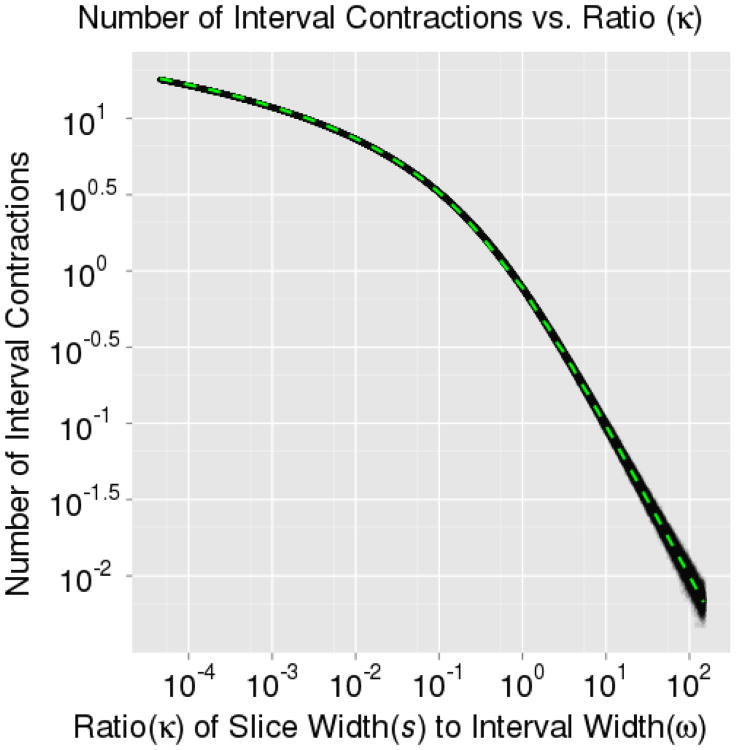
If we first consider the case where the target slice is smaller than the initial interval width (κ < 1), as in the example shown in Figure 1, we see that either (1) the initial interval will completely cover the target slice and not expand, or (2) one of the bounds (either the upper, or the lower, but not both) will need to be extended exactly once. Further, if we consider the placement of the lower bound with respect to the target slice, we see that the probability of expanding is equal to the probability of the lower bound falling within a region of size s divided by its total flexibility ω. When κ > 1, as in the example in Figure 2, X can only take the integer values of either ⌈κ⌉ or ⌊κ⌋. In Figure 2, where $\kappa \equiv \frac{8}{3}$, the initial interval will either be expanded ⌊κ⌋ = two times or ⌈κ⌉ = three times. As a result, the expected number of expansions for all values of κ can be summarized in Equation 1.

Figure 1.

Expansion of a randomly positioned initial interval of width $\omega \equiv \frac{3s}{2}$. Hence $\kappa \equiv \frac{2}{3}$, and we make either ⌈κ⌉ = 1, or ⌊κ⌋ = 0 expansions.

Figure 2.

Expansion of a randomly positioned initial interval of width $\omega \equiv \frac{3s}{8}$. Hence $\kappa \equiv \frac{8}{3}$, we make either ⌈κ⌉ = 3, or ⌊κ⌋ = 2 expansions.

$$\begin{array}{c}\mathcal{P}(X=\lceil \kappa \rceil )=\frac{s-\lfloor \kappa \rfloor \omega }{\omega }=\kappa -\lfloor \kappa \rfloor \mathcal{P}(X=\lfloor \kappa \rfloor )=\frac{\omega -(s-\lfloor \kappa \rfloor \omega )}{\omega }=\lceil \kappa \rceil -\kappa \\ E\left[X\right]=\lceil \kappa \rceil \mathcal{P}(X=\lceil \kappa \rceil )+\lfloor \kappa \rfloor \mathcal{P}(X=\lfloor \kappa \rfloor )\Rightarrow E\left[X\right]=\kappa \end{array}$$ (1)

The expected number of interval expansions derived in Equation 1 is interesting as it does not depend on the actual size of the target slice, but only on the ratio κ of the target slice to the initial interval width. In practice, as s is unknown, we can only vary ω, not κ. However, if ω remains fixed after a small tuning phase and is not varied by height h or for different values of s, then ω and s are independent. Hence, for a given initial interval width, ω⁽⁰⁾, we can compute $E[X|\omega ={\omega }^{\left(0\right)}]=E[\kappa |\omega ={\omega }^{\left(0\right)}]=\frac{1}{{\omega }^{\left(0\right)}}\times E[s|\omega ={\omega }^{\left(0\right)}]=\frac{1}{{\omega }^{\left(0\right)}}\times E[s]$ where the expectation of s is integrated with reference to target probability distribution and the distribution of the auxiliary variable, h.

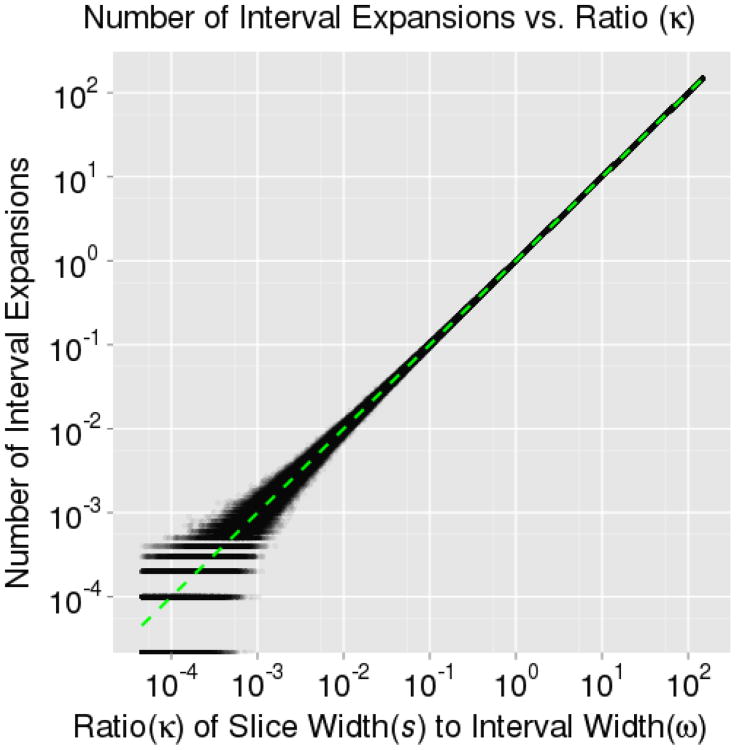
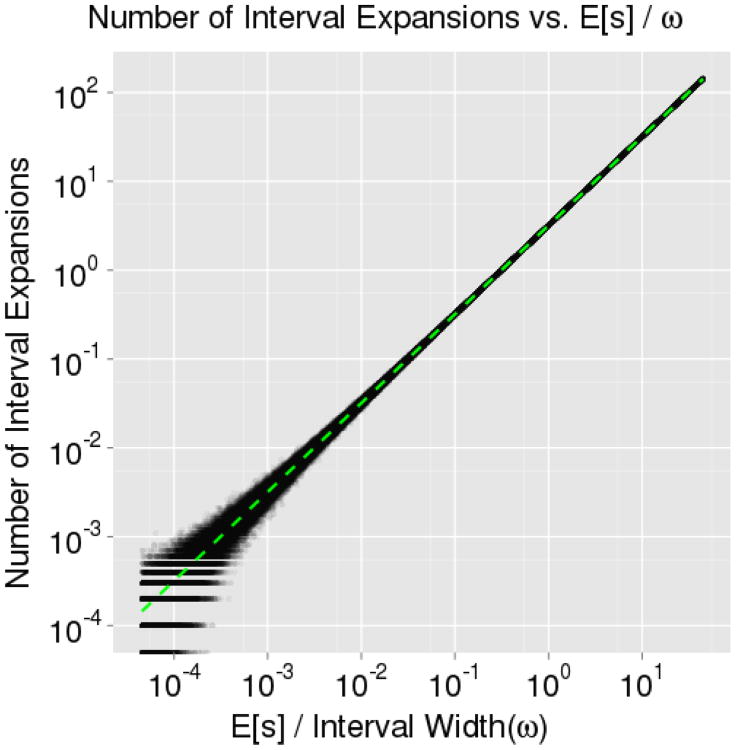
To examine Equation 1, we used a univariate, step-out slice sampler to sample from a standard normal distribution in ℝ¹. In the first of two simulations, we analytically computed the target slice width at each iteration – as it is easily determined for the standard normal distribution – varying ω in each iteration to keep κ fixed and then recorded the average number of expansions over 10, 000 iterations at different levels of κ. In Figure 3, we see that the result, E[X] = κ, is an exact fit to the simulation. In the second simulation, we varied ω, and likewise, we see in Figure 4 that $E[X]=\kappa =\frac{1}{\omega }E[s]$ also provides an exact fit to the results. Note that the value E [s] for the standard normal distribution is an integral which can be evaluated using Maple:

Figure 3. Number of Expansions vs κ.

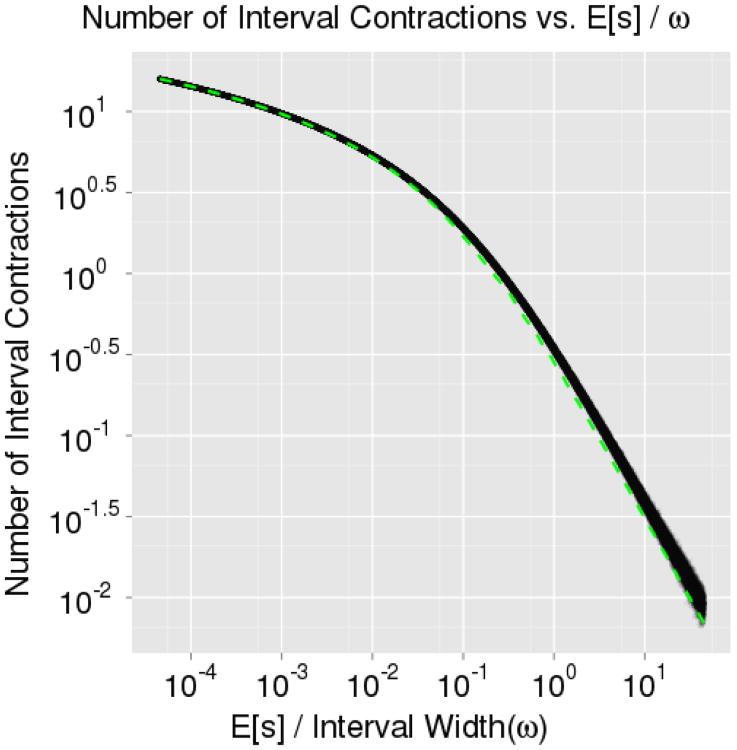
Figure 4. Number of Expansions vs s/ω.

$$E[s]=\sqrt{\frac{2}{\pi }}{\int }_0^{\infty }{\int }_{-\mathrm{\infty }}^{\infty }\left(\sqrt{x^2+2y}\right)e^{-y}{e}^{-\frac{x^2}{2}}\mathit{\text{dxdy}}=4\sqrt{\frac{2}{\pi }}\approx 3.19154$$

Note that $E[X]=\frac{1}{\omega }E[s]$ regardless of the skew, kurtosis, or other higher order moments of the target distribution, as long as the underlying distribution is unimodal. Two additional terms must be added to Equation 1 for each additional mode in the distribution. Further, these two terms are multipled by the probability of the approximate slice overlapping both modes without expansion. This probability is important because the step-out approximation method may now violate our assumption that: “expansion of the initial interval width will only cease after s is wholly contained in the approximate interval”. If this probability (of overlapping both modes initially) is near zero, then the step-out approximation method will tend to stick in one mode (Neal, 2003). The doubling method of Neal (2003) was devised to mitigate the possibility of being trapped in one mode; however, the doubling method also requires a costly construction to ensure that moving from the proposed location back to the initial location is possible. This additional step to ensure reversibility makes the identification of an optimal initial interval width for the doubling slice sampler highly distribution dependent and beyond the scope of this manuscript.

3.1.2 Sampling from the Approximate Slice

To aid in situations where à grossly over-estimated the size of A, an interval shrinkage procedure was also devised in Neal (2003). The interval is contracted toward the current parameter value after each rejected proposal. By construction, à is guaranteed to contain a portion of the target slice with probability one. Hence, there is a well-defined stopping criterion for the proposal phase because eventually a proposal must fall within the target slice, A. This leads us to estimate the number of interval contractions, C, required before a generated proposal falls within the target slice – as this will be one less than the number of proposals (and likelihood evaluations) needed. Let ϖ denote the width of the approximate slice (after expansion). If we again consider only unimodal distributions for the moment, the approximate slice is guaranteed to contain the entirety of the slice A. The expanded interval width ϖ is then equal to the width of the target slice s plus some additional region ∊ falls outside the target slice. As in deriving E[X], we find it useful to work with a ratio, and here we define $\mathrm{\xi }\equiv \frac{∊}{s}$.

We first note that no contractions are necessary if the first proposal falls within A; therefore, we can easily construct $\mathcal{P}(C=0)=\frac{s}{\varpi }=\frac{1}{1+\mathrm{\xi }}$. If the first proposal does not fall within the target slice, then the second proposal will be sampled (uniformly) from a smaller interval. Since the first proposal was rejected, the only portion of the interval to shrink is the excess, ∊, as the proposal must have fallen within this region to be rejected. We denote the width of this contracted proposal interval by s + λ∊, where λ is the fraction of the excess which remains after contraction. However, this formulation is slightly misleading because in general a portion of the excess, ∊, falls below the lower bound (∊_l) and a portion of the excess falls above the upper bound (∊_u). While λ is random, every proposal is independent given the interval width, so the expected value can easily be computed, $E[\mathrm{\lambda }]=\frac{5}{8}$. To calculate the probability of a successful second proposal (C = 1), we must first condition on the selection of the left or right tail:

$$\mathcal{P}(C=1)=\left(\mathcal{P}\right({\beta }^{\left(1\right)}\in A|{\beta }^{\left(0\right)}\in {∊}_l)\mathcal{P}({\beta }^{\left(0\right)}\in {∊}_l)+\mathcal{P}({\beta }^{\left(1\right)}\in A|{\beta }^{\left(0\right)}\in {∊}_u\left)\mathcal{P}\right({\beta }^{\left(0\right)}\in {∊}_u\left)\right)$$

where β^(j) denotes the j^th proposal. We compute the expected number of interval contractions as a weighted summation across a binary tree of proposals. We define a recursive set of equations and numerically estimate the expected number of interval contractions. Note that all probabilities below are computed given {β⁽⁰⁾,…,β^(j−1)} ∉ A, $N_u^{\left(j\right)}$, and $N_l^{\left(j\right)}$. These are abbreviated to "−" for brevity where $N_l^{\left(j\right)}$ denotes the number of proposals in {β⁽⁰⁾,…, β^(j−1)} which led to the contractions of the excess in the lower bound, ∊_l and similarly $N_u^{\left(j\right)}$, for the upper bound.

$$\mathcal{P}({\beta }^{\left(j\right)}\in {∊}_l|-)=\frac{\frac{\mathrm{\xi }}{2}\mathrm{\lambda }(N_l^{\left(j\right)})}{1+\frac{\mathrm{\xi }}{2}({\mathrm{\lambda }}^{(N_l^{\left(j\right)})}+{\mathrm{\lambda }}^{(N_u^{\left(j\right)})})},\mathcal{P}({\beta }^{\left(j\right)}\in {∊}_u|-)=\frac{\frac{\mathrm{\xi }}{2}{\mathrm{\lambda }}^{(N_u^{\left(j\right)})}}{1+\frac{\mathrm{\xi }}{2}({\mathrm{\lambda }}^{\mathrm{(}{N}_l^{\left(j\right)})}+{\mathrm{\lambda }}^{(N_u^{\left(j\right)})})},\mathcal{P}({\mathrm{\beta }}^{\left(j\right)}\in A|-)=\frac{1}{1+\frac{\mathrm{\xi }}{2}({\mathrm{\lambda }}^{(N_l^{\left(j\right)})}+{\mathrm{\lambda }}^{(N_u^{\left(j\right)})})},\text{and}E[C]=\sum _{m=1}^{\infty }m\sum _{n=1}^{m+1}(\mathcal{P}({\beta }^{\left(n\right)}\in A|-)\times \prod _{t=1}^m\mathcal{P}({\beta }^{\left(t\right)}\notin A|-)).$$ (2)

As with earlier notations in this manuscript, superscripts here reflect an iteration index. For example, the term ${\mathrm{\lambda }}^{\left(N_l^{\left(j\right)}\right)}$ represents the fraction of excess interval remaining below the lower bound after $N_l^{\left(j\right)}$ proposals were made in the region less than the lower bound of the target slice (out of j rejected proposals). Note that Equation 2 does not reduce to a binomial random variable as the probabilities of proposing in s, ∊_l or ∊_u are not constant. Further, the term 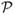(β^(j) ∉ s|−) must account, recursively, for the order in which the lower, ∊_l and upper, ∊_u, excesses were contracted. However, the computation of E[C] was greatly simplified by summing across the m + 1 leaves of binary tree instead of eliciting all 2^m possible paths. We truncated the infinite summation in Equation 2 to the first 100 terms, and overlayed it (dashed line) on the experimental results in Figures 5 and 6.

Figure 5. Number of Contractions vs κ.

Figure 6. Number of Contractions vs ω.

We numerically verified Equation 2 by sampling from a standard normal distribution in ℝ¹. In the first simulation, we analytically computed the target slice width, s, at each iteration and allowed ω (and hence ϖ) to vary allowing us to record the average number of contractions over all 10, 000 iterations at fixed levels of κ. For large values of $\kappa \equiv \frac{s}{\omega }$ in our simulations, many expansions led to an interval which closely approximates the target slice and very few contractions occurred. For small values of κ, the initial interval width was too large, few expansions were made, many proposals were rejected, and, hence, many contractions occurred. Note that as κ decreases, more contractions will occur; hence, this will require larger and larger trees to yield an accurate approximation. This will become computationally burdensome, but by only using the first 100 terms, we see a near perfect fit to the simulation results in Figure 5. In the second simulation, we recorded the average number of contractions over 10,000 iterations at fixed levels of ω. In Figure 6, we use an approximate value, ω/E [s], in place of κ when constructing ξ for Equation 2 and find a reasonable fit to the second simulation results. While the results presented apply chiefly to unimodal distributions, one could consider extending these results to multimodal situations. However, it would be highly distribution dependent as it is possible to contract and remove entire modes from the approximate interval (altering both ∊ and s).

3.2 Tuning by Heuristic Optimization

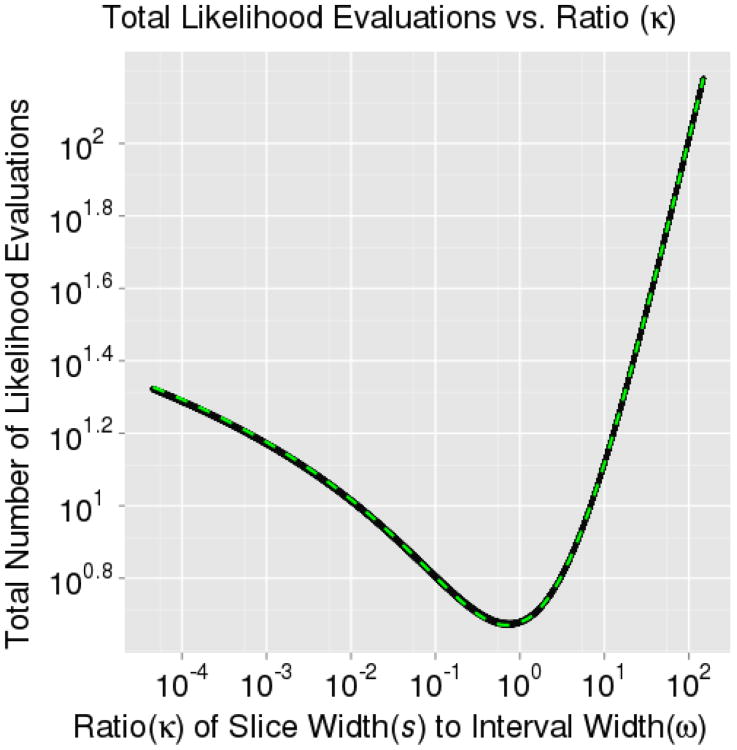
The efficiency of the univariate slice sampler depends on the number of likelihood evaluations required. Therefore, we want to find values of ω that minimize E[X|ω] + E[C|ω]. The second contribution of this manuscript is to propose an automated algorithm for identifying efficient ω's. As evidenced in Sections 3.1.1 and 3.1.2, E[X] and E[C] as functions of κ are quite well behaved. Almost any optimization technique could find the minimum in Figure 7; however, these estimates of E[X] and E[C] were generated by integrating over the space of all true target widths, s, globally across the distribution. If the Markov chain is randomly initialized in the tails of the distribution, a local grid search, for example, might limit the slice sampler's ability to efficiently explore the rest of the distribution. Hence, we propose an adaptive optimization technique to sequentially adjust the slice sampler's initial interval width as it explores a larger fraction of the distribution.

Figure 7. Total Number of Likelihood Evals vs κ.

Instead of continually adapting with “diminishing magnitude” as in Roberts and Rosenthal (2009), our approach stops tuning after a pre-specified threshold is met or a pre-specified number of tuning iterations is exceeded. Then, ω is fixed and the proposals are constructed using a constant (non-adaptive) transition kernel. To tune the univariate slice sampler, we propose a simple heuristic approach which utilizes the ratio of the number expansions to the total number of expansions and contractions. We construct a simple Robbins-Monro recursion (cf. Benveniste et al., 1990; Borkar, 2008). The standard form of this recursion is: ω^(t+1) ← ω^(t) + γ^(t)(h(ω^(t)) − α), where h(ω) is some approximation to an unobservable function of interest g(ω) (with E[h(ω)|ω] = g(ω)), and it is used to find the roots of the equation g(ω) − α = 0, (cf. Shaby and Wells, 2010). Hence, we derive Algorithm 5 by taking $\alpha =\frac{1}{2}$, γ^(t) = 2ω^(t), and $g(\omega )=\frac{E\left[X\right|\omega ]}{E\left[X\right|\omega ]+E[C\left|\omega \right]}$:

Algorithm 5: Heuristic Algorithm for Initial Interval Width Selection

1. Draw N(0) samples using an initial guess, ω(0). Set t = 0.

2. Tally the number of expansions, X(t) & contractions, C(t)

3. Set ${\omega }^{\left(t+1\right)}={\omega }^{\left(t\right)}\times 2\left(\frac{X^{\left(t\right)}}{X^{\left(t\right)}+C^{\left(t\right)}}\right)$ and N(t+1) = 2 × N(t). Set t = t + 1.

4. Repeat steps 2 and 3 until $\left(\frac{X^{\left(t\right)}}{X^{\left(t\right)}+C^{\left(t\right)}}\right)-\frac{1}{2}\in [-\phi ,\phi ]$

In practice, if X^(t) is zero for a given iteration, we set it equal to one to prevent an undefined update. Note also that using the interval contraction procedure, it is much better to consider an ω that is too large versus an ω that is too small (see Figure 7). To prevent multiple draws from using an ω which is too small, we generally choose N⁽⁰⁾ (the initial number of samples drawn before adjusting ω) to be a small number, often a single sample. Note that Neal (2003) also proposed terminating the interval expansion after performing an arbitrary number of expansions which will also help with an initially undersized ω while maintaining the integrity of the heuristic procedure. In addition, we must also select an appropriate tolerance for the stopping criterion. In practice, we recommend φ ≈ 0.1 as the minimum in Figure 7 is nearly two orders of magnitude wide.

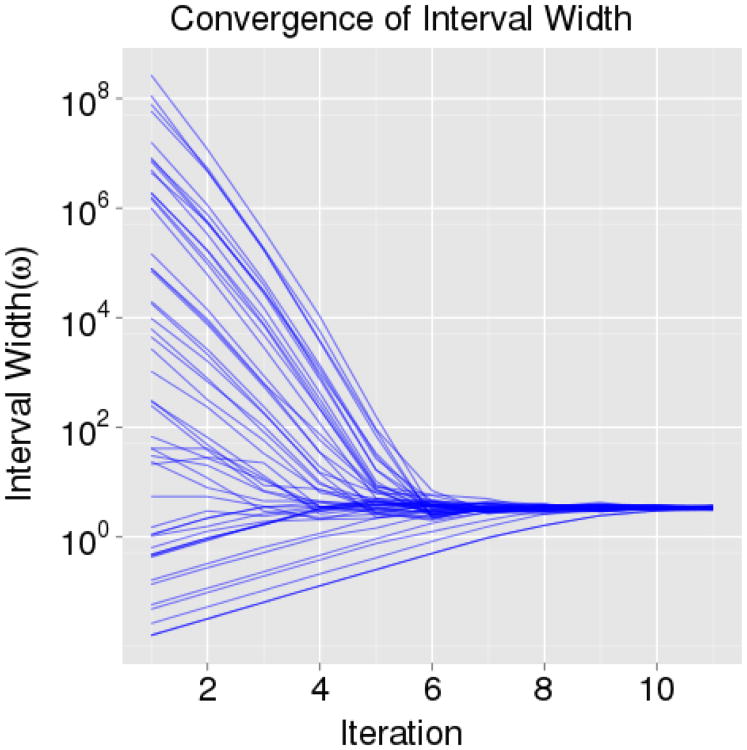
To test the performance of Algorithm 5, we again sampled from a standard normal distribution in ℝ¹. We initialized 50 samplers to a uniform distribution for ω⁽⁰⁾ of roughly thirteen orders of magnitude on the interval [e⁻⁵, e²⁰]. We see in Figure 8, that the convergence is quite rapid. The sampler interval widths (ω) have all converged to within a single order of magnitude of the posterior mean in under eight iterations. Because the number of slice sampler draws are increased in powers of two after each iteration of Algorithm 5, eight iterations require only 512 samples. In the examples presented in Sections 4.1 and 4.2, the samplers also often require fewer than eight tuning iterations (with N⁽⁰⁾ = 1, and φ = 0.1) to find a nearly optimal initial interval width. However, we typically desire at least 10 tuning iterations to allow more time for the samplers to reach the general vicinity of posterior support. Further, when applying Algorithm 5 to the univariate factor slice sampler which also uses Algorithm 3, we reset i = 0 and N⁽ⁱ⁾ = 1 in Algorithm 5 every time the factors are updated to obtain an optimal selection of ω with regard to the newly rotated frame of reference. Algorithm 5 appears to very efficiently tune the standard and factor slice samplers (initial interval widths). With a reasonable initial guess of the spread of the target distribution, the convergence will be faster; however, it appears that starting even from a naive guess of 1.0 for the initial interval width and tuning using Algorithm 5 will work in general and provide reasonable performance.

Figure 8. Convergence of Interval Width (ω).

4 Applications to Data Examples

In Section 2, we demonstrated the utility of rotating the sampling reference frame within the context of a stylized example. To demonstrate the robustness of these approaches we consider two more challenging and realistic examples from spatial statistics where an orthogonalizing transformation of the target parameterization does not exist. While one could generate perfectly uncorrelated draws from the distribution in our toy example, there are no such simplifications for these two examples. The improved performance of the univariate factor slice sampler over the the standard univariate slice sampler translates directly to an improved ability to utilize these ubiquitous Gaussian process models.

An efficient univariate slice sampler will, on average, only require five likelihood evaluations (where at most only two or three are performed simultaneously). Hence, the algorithm doesn't provide as much of an opportunity for parallel decomposition as, for example, a multivariate slice sampler; however, the improved efficiency due to the rotation of the factors more than compensates for this drawback and further, additional parallel processing capacity can then be dedicated to each likelihood computation. We find that an optimal level of parallelism is obtained for these models by using either three cores of an Intel Core i7 processor through OpenMP, or utilizing two GTX 480 graphics cards from nVidia through CUDA. For details on the parallel implementation, we refer the interested reader to Tibbits et al. (2011).

4.1 Linear Gaussian Process Model

In the next example, we use a linear Gaussian process to model the mean surface temperature over the month of January, 1995 on a 24 × 24 grid covering Central America. This dataset was obtained from the NASA Langley Research Center Atmospheric Science Data Center.

Example 2 (ASDC Surface Temperature Dataset)

We model the mean surface temperature as a spatially-referenced response, Y(s_j), measured at 576 locations s_j with a set of covariates, X(s_j), including an intercept, the latitude, and the longitude of each s_j. The responses, Y(s_j), are correlated based on their magnitude of separation and it decays exponentially:

$$Y({\mathbf{s}}_j)=X({\mathbf{s}}_j)\mathit{\beta }+∊({\mathbf{s}}_j),∊({\mathbf{s}}_j)\sim N(0,\sum )\text{with}{\sum }_{mn}=\{\begin{array}{cc}\sigma +\psi & m=n\\ \sigma exp\left(\frac{{\Vert s_m-s_n\Vert }^2}{\varphi }\right)& m\ne n\end{array}$$

We place a uniform prior on β as in Example 1. We place inverse gamma (shape = 2, scale = 1) priors on σ and ψ so that the prior means for σ and ψ are 1.0 and the prior variance is infinite. Finally, we place a uniform [0.005, 1.2] prior on the effective range parameter φ (the distance matrix has been rescaled to the unit square).

The univariate factor slice sampler achieves an ESS roughly roughly 23 times that of standard univariate slice sampler, and it is actually able to draw 100, 000 samples slightly faster than the non-factor approach. In terms of computational efficiency, the factor slice sampler is 26 times better at generating effectively independent samples per second (ES/sec). Using OpenMP, we see that both univariate slice samplers gain a 30% performance improvement. With reference to the non-parallel standard slice sampler, the factor slice sampler using OpenMP achieves an overall 36 to 38 fold improvement. Given the ease with which OpenMP can be incorporated to an existing codebase, the parallelized factor slice sampler represents an automated and efficient statistical sampling technique, which requires a minimum amount of development time.

Utilizing the more intricate parallelism of CUDA, we wrote graphics kernels to estimate the Gaussian process log likelihood and thereby attain nearly a fifty fold improvement in sampling efficiency. This magnitude of speedup changes the way in which the modeler approaches this class of problems. Instead of waiting a week or more to compare two or three models for variable selection or requiring huge, costly high performance computing centers, the factor approach allows the statistician to examine hundreds of possible models within the same time frame using a single desktop computer. Hardware for parallel implementations also continues to get less expensive. (Note that at the time of submission, an nVidia GTX 480 graphics card retailed for less than $225.)

4.2 Logistic Gaussian Process Model

To better characterize the performance of the automated factor slice sampling algorithm within the context of a high dimensional distribution, we used the Gaussian process model of Section 4.1 as a tool to fit the spatial dependence amongst the odds of observing a Pennsylvania native songbird, the Hermit Thrush, using a spatial generalized linear model (cf. Haran, 2011). This dataset, collected in a joint effort by the Carnegie Museum of Natural History, the Powdermill Nature Reserve, and the Pennsylvania Game Commission, will be published in the Second Pennsylvania Breeding Bird Atlas (Powdermill Avian Research Center, 2012). The Hermit Thrush is a species found across North America; however, surprisingly little is known of its demographic characteristics (cf. Hughes et al., 2011). For the purpose of illustration, we have selected a random subset of 500 observations.

Example 3 (Logistic Gaussian Process Model)

We consider a logistic Gaussian process model with an exponential covariance function. We model the presence or absence of the Hermit thrush, as a spatially-referenced response Z(s_j) measured at locations s_j with covariates X(s_j) (j ∈ {1… N}) where we have included four predictors of scientific interest as well as an intercept. We model a second spatial process w(s_j) and assume that the responses Z(s_j)'s are conditionally independent given w = (w(s₁),…, w(s_N)) and that the Z(s_j)'s are conditionally Bernoulli, where for j ∈ {1… N} we have:

$$\begin{array}{c}E[Z({\mathbf{s}}_j)|\mathbf{w}]=\mu ({\mathbf{s}}_j)\text{and}log(\frac{\mu \left({\mathbf{s}}_j\right)}{1-\mu \left({\mathbf{s}}_j\right)})\equiv X({\mathbf{s}}_j)\mathit{\beta }+\mathrm{w}({\mathbf{s}}_j)\\ \text{where}\mathbf{w}\sim N(0,\sum (\mathbf{s},\varphi ))\text{with}{\sum }_{mn}=\{\begin{array}{cc}1.0& m=n\\ exp\left(\frac{{\Vert s_m-s_n\Vert }^2}{\varphi }\right)& m\ne n\end{array}\end{array}$$

The spatial dependence is imposed by modeling w as a stationary Gaussian process with an exponential covariance function. However, to preserve the identifiability, we must force Σ(s, φ) to be a correlation matrix. As in Example 2, we place a flat prior on β and a uniform [0.005, 1.2] prior on the effective range parameter φ (the distance matrix was again rescaled).

This example is not only more computationally expensive than Example 2, but also much more challenging as the target distribution has 506 dimensions: a vector β of five regression coefficients (including an intercept), a scalar φ which determines the degree of spatial dependence, and 500 spatial random effect parameters, w. Unlike in Example 2, the distributions of β, φ, and w cannot be sampled from directly; hence, we will use slice samplers for β, φ and w. For the purpose of illustration, we have included the results (and sampling efficiencies) for four distinctly different blocking and sampling approaches. Note that one could construct a univariate factor slice sampler to update the regression coefficients (β) jointly and a separate univariate factor slice sampler to update the location mean parameters (w). We could then utilize a standard univariate slice sampler to sample the remaining parameter, φ. For convenience, we label this scheme by IV and denote it by (φ,{β},{w}) where the braces, {}, denote the use of a joint/factor update. There are ten possible blocking schemes with the four included in Table 3 starred below:

Table 3.

Comparison of effective sample size (ESS), effective samples per second(ES/sec), and relative speedup of ES/sec for φ, β, and w from Example 3. All algorithms were run for 120, 480 iterations, but the first 20, 480 were discarded to allow for sampler tuning. For brevity we provide only the average efficiency β̄ for the fixed effects β, and the average efficiency ω̄ for the spatial random effects w.

		φ			β̄			ω̄
Sampling Approach	Parallel API	ESS	ES/sec	ES/sec Speedup	ESS	ES/sec	ES/sec Speedup	ESS	ES/sec	ES/sec Speedup
φ, β, w	—	1561	0.04		3614	0.08		2370	0.05
	OpenMP	1548	0.05	(1.46)	3360	0.11	(1.37)	2364	0.08	(1.47)
φ, β, {w}	—	1564	0.03	(0.88)	5171	0.10	(1.26)	5587	0.11	(2.07)
	OpenMP	1679	0.05	(1.68)	4246	0.13	(1.62)	6165	0.19	(3.42)
φ, {β}, w	—	1504	0.03	(0.96)	1316	0.03	(0.36)	2343	0.05	(0.96)
	OpenMP	1484	0.05	(1.36)	2207	0.07	(0.88)	2403	0.08	(1.45)
φ, {β, w}	—	1673	0.03	(0.94)	35141	0.70	(8.56)	39424	0.79	(14.64)
	OpenMP	1777	0.06	(1.56)	34706	1.08	(13.11)	38568	1.19	(22.21)

Note that {θ₁, θ₂} denotes a joint update of parameters θ₁ and θ₂ using a factor slice sampler. The first sampling approach: “φ, β, w” employs standard univariate slice samplers for all parameters and was used as the baseline for determining the algorithmic speedups shown above.

$$\begin{array}{ccccc}\mathbf{I}\ast \varphi ,\mathit{\beta },\mathbf{w}& \mathbf{III}\ast \varphi ,\left\{\mathit{\beta }\right\},\mathbf{w}& \mathbf{V}\{\varphi ,\mathit{\beta }\},\mathbf{w}& \mathbf{VII}\{\varphi ,\mathbf{w}\},\mathit{\beta }& \mathbf{IX}\ast \varphi ,\{\mathit{\beta },\mathbf{w}\}\\ \mathbf{II}\ast \varphi ,\mathit{\beta },\left\{\mathbf{w}\right\}& \mathbf{IV}\varphi ,\left\{\mathit{\beta }\right\},\left\{\mathbf{w}\right\}& \mathbf{VI}\{\varphi ,\mathit{\beta }\},\left\{\mathbf{w}\right\}& \mathbf{VIII}\{\varphi ,\mathbf{w}\},\left\{\mathit{\beta }\right\}& \mathbf{X}\{\varphi ,\mathit{\beta },\mathbf{w}\}\end{array}$$

We note that when blocking the regression coefficients, β, and/or the spatial random effects, w, with the covariance parameter φ, care must be taken as this adds a significant computational cost. Each time the parameter φ is altered, the likelihood evaluation requires a costly Cholesky decomposition and back substitution (which is more efficient than inverting the matrix directly for the density computation). To improve the computational efficiency, often a discrete uniform distribution is substituted for the prior on φ where the Cholesky decomposition at each location can be precomputed and stored (cf. Section 7.5.4 of Diggle and Ribeiro, 2007); however, no such concessions were made here. Note that one could also consider varimax or other such rotations to minimize the number of non-zero loadings in Γ and thereby minimize the number of factors which require Cholesky decompositions to update. In testing the blocking strategies IV through VIII and X, we found that the ESS of φ marginally improved while the ES/sec of all parameters were significantly lower than the reference strategy, I, due to the significantly increased computational burden. As such, we also do not include the results from the samplers using CUDA. Computationally expensive matrix operations are only required for updates to φ and the improved vector performance of CUDA is outweighed by the cost of transferring updated β and w vectors after each iteration. For further discussion on blocking strategies, please refer to Roberts and Sahu (1997), Liu et al. (1994), and the references therein.

In Table 3, we contrast the performance of the four sampling approaches. The first sampling approach (I): “φ, β, w” uses standard univariate slice samplers for all parameters. It is used as the baseline for determining the algorithmic speedups shown above. Blocking strategy II uses a factor slice sampler to update the 500 random effects {w}. Blocking strategy III uses a factor slice sampler update the 5 fixed effects {β}. Finally, blocking strategy IX uses a single factor slice sampler to update the 5 fixed and the 500 random effects jointly ({β, w}). We see that blocking the random effects improves sampling efficiencies, but it also leads to longer sampling times. Also, the blocking of the random effects in approach II, (φ, β, {w}), only triples the sampling efficiency whereas blocking the random effects with the fixed effects in approach IX, (φ, {β, w}), leads to a factor of twenty-two improvement in sampling efficiencies for the random effects. The blocking strategy in approach IX also leads to a thirteen-fold improvement in the fixed effects sampling efficiency.

4.3 Summary of Results

In the simple toy example, we find that even in high dimensional distributions with strong dependence, the ease with which the factor slice sampler can adapt to distributional dependence allowed it generate nearly independent samples unlike the strong autocorrelation present in the traditional random walk and standard slice sampler approaches. The factor slice sampler attained a near twenty-seven-fold improvement in ES/sec, a measure of sampling and computational efficiency. In Example 4.1, we fit a linear Gaussian process model to a 576 location surface temperature dataset obtained from the NASA Langley Research Center Atmospheric Science Data Center. Blocking the three covariance parameters and utilizing the automatically tuned factor slice sampler, we obtained a forty-six and forty-seven fold improvement in ES/sec for the two covariance parameters. In Example 4.2, we fit a logistic Gaussian process model to 500 observations of the prescence/abscence of Hermit Thrush, obtained from the Second Pennsylvania Breeding Bird Atlas (Powdermill Avian Research Center, 2012). The factor slice sampler obtained thirteen and twenty fold improvements in ES/sec for the 5 covariate coefficients, β, and the 500 random effects, w, respectively.

5 Discussion

We develop an automated approach to selecting an efficient coordinate basis using a simple sample covariance estimate (obtained during an initial tuning phase) and constructed a rotated or “factor” slice sampler to address the challenge of sampling from high dimensional distributions which exhibit moderate to strong dependence. Further, we describe a new approach to automatically tune slice samplers. Our approach for tuning is general and appears to be effective for both the factor slice sampler and the regular slice sampler. We then examined the performance of the standard and factor univariate slice samplers within the context of several examples, including two challenging examples from spatial data analysis.

We believe we have demonstrated that the factor slice sampler is efficient, providing thirteen to forty-seven fold improvements in computational efficiency (as measured in ES/sec) over carefully tuned alternative MCMC algorithms. Furthermore, we show how the algorithm can be fully automated, which makes it very useful for routine application by modelers who are not experts in MCMC. The automated and parallelized factor slice sampler provides an efficient technique which has broad application to statistical sampling problems. It requires little or no user intervention to identify an efficient basis for sampling and also optimal tuning parameters. Hence, we hope that these algorithms will facilitate a broader audience to access the power of MCMC methods for complicated problems, while efficiently utilizing increasingly parallelized hardware.

We chose not to include the multivariate slice sampler results because it was computationally infeasible for more than 8 dimensions given our current hardware. The results of Section 4.1 do translate directly to those of Section 4.3 in Tibbits et al. (2011), except that in this manuscript we utilized graphics cards capable of handling all 576 locations (whereas we had previously limited our analysis to only 500 data points). Further, the multivariate slice sampler also required a grid search to identify optimal tuning parameters whereas the factor slice sampler is easily tuned as explained in Section 3.2.

In the future, we wish to consider alternative factor selection methods, as well as orthogonal and oblique rotation techniques. We also wish to revisit the multivariate slice sampler extensions explored in Tibbits et al. (2011) as they apply to the factor slice sampler.

Table 1.

Toy example for performance comparison of MCMC sampling algorithms for β, a vector of regression coefficients from Example 1 with P = 10, 50, 100, and 500 dimensions. All ESS estimates were obtained from 500, 000 “post-tuning” draws. Note: The computation time used in ES/sec includes time spent in the tuning phase. (RWMH ≡ Random-Walk Metropolis Hastings)

Algorithm	P = 10		P = 50		P = 100		P = 500
	ESS	ES/sec	ESS	ES/sec	ESS	ES/sec	ESS	ES/sec
Univariate RWMH	20195	2684	15822	180	15865	32	17004	0.30
Univariate Slice Sampler	75169	3462	39576	150	36235	25	19763	0.13
Univariate Factor Slice Sampler	498808	14376	495132	1130	490794	241	457337	2.64

Table 2.

Comparison of effective sample size (ESS), effective samples per second(ES/sec), and relative speedup of ES/sec for σ, ψ, and φ from Example 2. All algorithms were run for 110, 240 iterations, but the first 10, 240 were discarded to allow for sampler tuning (using Algorithms 3 and 5). The sampling algorithms were parallelized using OpenMP with three processor cores and using CUDA with two nVidia GTX 480s as described in Tibbits et al. (2011).

		ψ			σ			φ
Algorithms	Parallel API	ESS	ES/sec	ES/sec Speedup	ESS	ES/sec	ES/sec Speedup	ESS	ES/sec	ES/sec Speedup
Univariate Slice Sampler	—	64616	2.06		2267	0.07		2234	0.07
	OpenMP	64920	2.70	(1.27)	2210	0.09	(1.31)	2178	0.09	(1.27)
	CUDA	65497	2.70	(1.31)	2293	0.09	(1.31)	2262	0.09	(1.31)
Univariate Factor Slice Sampler	—	58723	2.10	(1.02)	52291	1.87	(25.82)	51937	1.85	(26.02)
	OpenMP	57129	2.89	(1.40)	51267	2.60	(35.93)	52996	2.68	(37.69)
	CUDA	66086	4.25	(2.06)	51770	3.33	(46.07)	51641	3.32	(46.63)

Note: Table 2 uses the standard univariate slice sampler's single processor run time as the baseline for determining algorithmic speedups shown above.