The optimal rate of chromosome loss for the inactivation of tumor suppressor genes in cancer

Abstract

Many cancers are characterized by chromosomal instability (CIN). This phenotype involves the deletion and duplication of chromosomes or chromosome parts and results in a high degree of aneuploidy. The role of CIN for cancer progression is a very important, yet unresolved question. It has been argued that CIN contributes to cancer initiation because chromosome loss can unmask a mutated tumor suppressor (TSP) gene. At the same time, CIN is costly for the cell because it destroys the genome and therefore compromises clonal expansion. Here, we use mathematical models to determine whether CIN can accelerate the generation and expansion of TSP^-/- cells in the context of this tradeoff. Comparing cells with different degrees of CIN, we find that the emergence and growth of TSP^-/- cells is optimized if the rate of chromosome loss is of the order of 10^-3 to 10^-2. This result is very robust, is independent of parameter values, and coincides with experimental measures using colon cancer cell lines. However, if we consider all of the steps in the pathway, including the generation of the CIN phenotype from stable cells, then it turns out that the emergence and growth of TSP^-/- cells is never accelerated by CIN. Therefore, CIN does not arise because it accelerates the accumulation of adaptive mutations. Instead, it arises for other reasons, such as environmental factors, and is subsequently finetuned by selection to minimize the time to further cancer progression by means of the inactivation of TSP genes.

Numerous observations suggest that cancer cells are often characterized by gross chromosomal abnormalities (1, 2). Those abnormalities include losses of whole chromosomes, chromosomal arms, or large chunks of chromosomes, as well as chromosomal rearrangements, duplications, and mitotic recombinations. A high degree of aneuploidy is very common among cancer cells (3). It has been suggested that the abnormal karyotypes are the result of an increased rate at which chromosomal changes are accumulated in cells. The corresponding phenotype is termed chromosomal instability (CIN) phenotype. It has been reported that as much as 87% of all colon cancers are characterized by CIN (1, 4). CIN has also been observed in a variety of other cancers. The molecular basis of CIN in human cancers is still uncertain (5, 6). Whereas several candidate CIN genes have been identified in yeast (7, 8), corresponding mutations in unstable cancer cell lines have rarely been found (4, 9–12). Alternatively, it has been suggested that CIN may be brought about by epigenetic mechanisms (13–15), or that it might even be nongenetic (16). The role of CIN in cancer initiation and progression is equally mysterious. A prominent theory is that CIN allows for faster somatic adaptive evolution of cells (17). This notion applies particularly to the inactivation of tumor suppressor genes, which requires the loss of both alleles. Whereas it can take a very long time until a cell has inactivated both alleles by successive point mutations, the acquisition of one point mutation followed by a fast loss of heterozygocity may occur within a shorter period.

Whereas CIN can speed up the inactivation of tumor suppressor (TSP) genes, it can also have a negative effect on cancer progression. Cells with inactivated TSP genes undergo clonal expansion, and clonal expansion can be compromised by CIN. The reason is that chromosomal material containing important genes can be lost at a high rate. This loss can lead to cell death and reduce the fitness of the cells. Given this tradeoff, we would like to address the following questions with mathematical models: Can an elevated loss of chromosomes enhance the generation and growth of TSP^-/- cells, or is it a burden for the cancer? Can we define an optimal rate of CIN for the accumulation of inactivated TSP genes? How do theoretical results compare to experiments that measure the rate of chromosome loss in colon cancer cell lines? We would like to point out that these considerations apply specifically to the loss of chromosomes (18). Other chromosomal alterations, such as mitotic recombination, can also occur (19–21). Mitotic recombination does not, however, contribute (to the same degree) to the destructive genomic alterations and the aberrant karyotypes. Hence, the tradeoff examined here does not apply to this situation.

We provide a mathematical description of a system in which cancer initiation occurs by the inactivation of a TSP, followed by a phase of clonal expansion. A specific and well studied example is colon cancer. Loss of both alleles of the adenomatous polyposis coli (APC) gene results in dysplastic cells that clonally expand. Starting with wild-type cells, we will calculate the average time it takes for a TSP^-/- cell clone to reach a certain size. We assume that two processes can contribute to cancer initiation: (i) point mutations that have been estimated to occur at a rate of 10^-7 per gene per cell division, and (ii) loss of chromosomes. The probability that a given chromosome suffers a loss event is captured in the variable p and may range in principle from 0 to 1. If p = 0, there is no loss of chromosomes and only point mutations occur. If p = 1 each chromosome is certain to suffer a loss at every cell division. In the following, we consider two scenarios. (i) First, we compare the rate at which TSP^-/- cells are generated and grow, assuming different degrees of chromosome loss (different values of p). Is there an optimal rate, p, of chromosome loss for the generation and emergence of TSP^-/- cells? (ii) We expand the model to include an extra step: the generation of the CIN phenotype from stable cells. How does this extra step influence the relationship between CIN and the generation and growth of TSP^-/- cells?

Mathematical Model of TSP Inactivation and Clonal Expansion

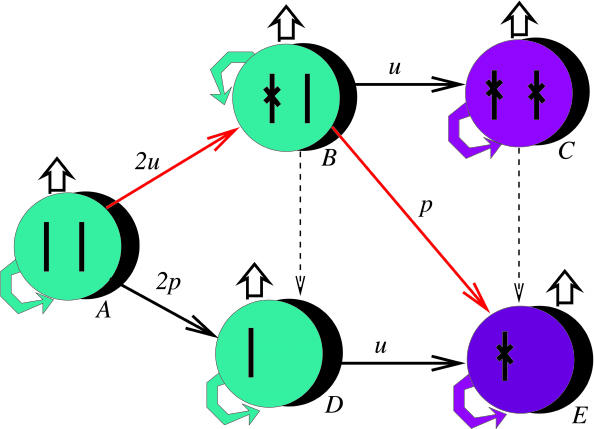
We start with a robust mathematical model that includes the loss of a TSP gene and the subsequent clonal expansion of the TSP^-/- cell clone (Fig. 1). It describes the dynamics of a population of cells as a birth–death process with mutations and quantifies the probability (over time) for cells to have a certain genotype. All of the relevant types are shown in Fig. 1: type A (cells with two wild-type alleles of the TSP); type B (cells with one mutated allele and one wild-type allele); type C (cells with two mutated alleles of the TSP); type D (cells that have lost one chromosome with TSP and retained the other); and type E (cells that have lost one chromosome with the TSP and have mutated the remaining allele). Loss of both chromosome copies is assumed to be lethal. Clonal expansion occurs only in cell populations that do not have a wild-type copy of the TSP. There are several pathways of TSP inactivation (Fig. 1). For example, starting with a cell with two wild-type copies of the TSP gene, first one of the alleles and then the other might get an inactivating mutation that corresponds to the path A → B → C. Alternatively, the first allele may acquire a mutation, and then the other allele may be inactivated by a chromosome loss event (the path A → B → E). Or, in the beginning, one of the alleles might get lost and then the other may acquire a mutation (the path A → D → E). A mutation event can happen with the rate u whereas a chromosome loss event occurs with the rate p. The phenotype corresponding to an inactivated TSP gene is marked in purple (Fig. 1); such cells have a faster net turn-over rate compared with the wild type.

Fig. 1.

Schematic diagram illustrating the principles of the mathematical model. The model considers the chromosome pair that bears the TSP gene. We start with a cell that has two wild-type copies of the TSP gene. Relevant genetic alterations comprise two processes: point mutations occur with a rate u = 10^-7 and can inactivate a copy of the TSP gene; chromosome loss can occur with a rate p, which can unmask an already mutated TSP gene. Therefore, a TSP gene can be inactivated in two basic ways: by two successive point mutations (A → B → C), or by a combination of a point mutation and a chromosome loss. The latter can occur through various pathways. The most likely pathway is indicated in red (A → B → E). That is, first a point mutation inactivates one copy of the TSP gene, and the other copy is eliminated by chromosome loss. Dashed arrows indicated possible but irrelevant steps because they do not have the potential to speed up the inactivation of the TSP gene. Cells with an inactivated TSP gene are marked in purple. They are assumed to undergo clonal expansion.

So far, we have captured only the effect of CIN on a chromosome that carries the TSP gene. What is the effect of CIN on the other chromosomes and the overall fitness of the cell? Because the answer is not known, we consider two extreme scenarios. (i) In the most benign case for the cell, loss of one copy of any chromosome will not result in a decrease in fitness. Cell death requires the loss of both copies of a chromosome. An alternative interpretation is that loss of a single chromosome copy would reduce fitness, but that this is buffered by duplication events. (ii) In the most destructive scenario, loss of any one copy of a chromosome results in immediate death of the cell. The reality is somewhere between these extreme scenarios.

We would like to point out that, whereas the model does not take chromosome duplications explicitly into account (because it would result in intractable complexity), it is included implicitly. That is, we take account of the fact that duplications can work against the effect of chromosome loss by assuming that the fitness reduction caused by a chromosome loss event is less severe (scenario i above). Either a duplication might be coupled with a loss event, or they can occur independently.

Results and Discussion

Because uncertainties remain about the nature of the cell population that gives rise to cancer, we have investigated different assumptions. According to one scenario, we assume that cancer is initiated in adult stem cells. There is a single stem cell per compartment, such as the crypt of the colon. Division of the stem cell is assumed to be asymmetric, and these dynamics are described by a stochastic model. When a TSP gene becomes inactivated in the stem cell, clonal expansion occurs, which is described with deterministic equations. Alternatively, we can assume that a healthy compartment contains a population of (stem or differentiated) cells that is kept at a constant size. Depending on the number of cells, this scenario is described either with a stochastic or a deterministic model (see Supporting Methods, which is published as supporting information on the PNAS web site). Again, inactivation of a TSP gene results in clonal expansion. It turns out that the results presented here remain the same in the context of the different assumptions. The results cited in the text are based on the model, which assumes the existence of one stem cell per compartment.

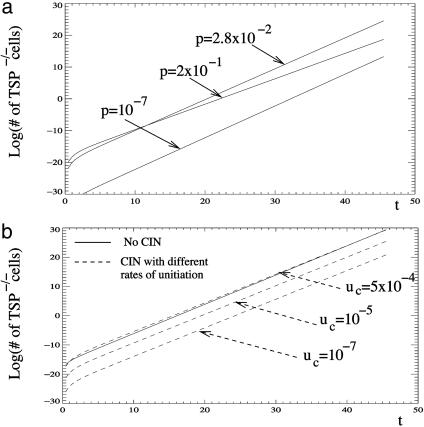
How does the rate of chromosome loss influence the generation and growth of TSP^-/- cells? We can calculate how long it takes, on average, for the TSP^-/- clone to reach a certain size. The answer will depend on the parameters of the system, and in particular, on the rate of chromosome loss, p. Let us first suppose that the rate of chromosome loss is zero, p = 0. In this case, a TSP gene can be inactivated only by two consecutive, independent (small scale) genetic events that have to happen in each of the alleles of the gene (path A → B → C). The basic rate at which such mutation events occur in stable cells has been estimated to be approximately u = 10^-7 per cell division per gene. Having two such slow events would therefore take a comparatively long time. Next, let us consider the opposite extreme, where the rate of chromosome loss is very high (p ≈ 1). Now, even though a TSP mutation is unmasked at a very fast rate, the price that the cell lineage has to pay is a very high death rate due to loss of chromosomal material. This cost can considerably slow down the expansion of the TSP-negative phenotype. Therefore, there must be an intermediate, optimal (for cancer!) value of the rate of chromosome loss, for which cells have a high chance of inactivating the TSP gene, without having to pay too high a price in nonviable or nonreproductive mutants (Fig. 2a). With this optimum value of p = p*, the cancer will progress fastest. The result, p*, of this optimization problem turned out to be amazingly robust. It depends very weakly (logarithmically) on the combination of variables, κ = aβM/u (see Supporting Methods), where log 2/(aβ) is the doubling time (measured in number of cell cycles), and M is the target number of cells. It turns out that, as we vary these parameters over many orders of magnitude, so that κ stays within 10⁵ to 10²⁰, the result for the optimal value of p does not vary significantly. Interestingly, it also does not significantly depend on the overall fitness cost for the cell brought about by chromosome loss. Consider the two extreme scenarios described above. (i) For the most benign scenario (no fitness reduction when one chromosome copy is lost), we obtain p* between 3 × 10^-2 and 6 × 10^-2 per chromosome per generation. (ii) For the most destructive scenario (immediate death upon loss of a single chromosome copy), it is between 5 × 10^-4 and 10^-3 per chromosome per generation. The optimal value of p is lower in scenario ii, which is not surprising because this case assumes a higher penalty for chromosome loss events. The true value is expected to lie somewhere between these two extremes. The remarkable fact is that the values of p* for the two scenarios are so close to each other, and that they depend so little on the assumptions of the model.

Fig. 2.

The effect of chromosome loss (CIN) on the generation and growth of TSP^-/- cells. (a) This graph plots the number of TSP^-/- cells against time, assuming that all cells have the CIN phenotype and are characterized by different rates of chromosome loss, p. An intermediate chromosome loss rate (of the order of magnitude of ≈10^-2 to 10^-3) results in the fastest growth of the TSP^-/- cell population. The simulations are based on the mathematics presented in Supporting Methods. Parameters were chosen as follows: a = 1, u = 10^-7, k = 1. (b) This graph plots the expansion of TSP^-/- cells assuming that, before chromosome loss can occur, the cell has to generate the CIN phenotype at a rate u_c. Dashed lines represent simulations that assume that CIN is generated. The solid line assumes that CIN is not generated and cancer initiation occurs by two successive point mutations. The figure shows that the generation and growth of TSP^-/- cells in the context of CIN is significantly slower than in the context of two successive point mutations unless the CIN phenotype is acquired at rates that are orders of magnitude higher than the physiological mutation rate (10^-7). Simulations are based on the mathematics presented in Supporting Methods. Parameters were chosen as follows: a = 1, u = 10^-7, k = 23. Genetically unstable cells are characterized by the optimal rate of chromosome loss whereas, in the stable cell population, chromosome loss is assumed not to occur.

What is even more encouraging is that we were able to compare our results with the value for the rate of chromosomal loss obtained by in vitro experiments using several CIN colon cancer cell lines (22). The value that emerges from these experiments is p = 10^-2 per chromosome per cell division, which is almost exactly in the middle of the range that we obtained theoretically. This is a thought-provoking result. We can hypothesize that the rate at which cancerous cells lose chromosomal material is under selection pressure, and, as a result, the optimal rate, p*, is the one that survives and progresses fastest. Alternatively, if the rate of chromosome loss differs significantly from the optimum value, the tumor is never detected because it cannot progress fast enough.

The optimal rate of chromosome loss for the accumulation of inactivated TSP genes calculated here is also optimal during later stages of cancer progression. For instance, adding another tumor suppressor gene to the pathway that we considered will not change the value of p* significantly. The reason is that every new tumor suppressor gene takes much less time to inactivate than a previous one; this result is a consequence of a growing population size of the lesion. However, we did not include the accumulation of mutated oncogenes into our model. In phases of cancer progression where the activation of oncogenes is the driving force, our results do not apply. Indeed, to turn on an oncogene, a small-scale mutation is often needed, rather than a chromosome loss event or another crude chromosomal change. Moreover, a chromosome loss event may lead to the inactivation of a functioning oncogene, which will revert the process of oncogenesis.

The above analysis has established that, once a cell has acquired a CIN phenotype, there is an optimal rate of chromosome loss that maximizes the ability of cancer cells to inactivate TSP genes and to expand. We have, however, ignored the generation of a CIN cell from wild-type cells. Here, we include this step and ask how this influences the effect of CIN on the generation and growth of TSP^-/- cells. In contrast to the previous model, we distinguish between two types on noncancerous cells: stable cells and those that have acquired CIN. The CIN phenotype is acquired at a rate u_c. In principle, CIN can be acquired at two stages in phenotypically healthy cells: either before the first copy of the TSP gene has been inactivated, or after the first copy of the TSP gene has been inactivated. We can show mathematically (see Supporting Methods) that this event must happen after the inactivation of the first TSP gene. (In this case, the advantages of CIN can be used to the fullest without having to pay the price of deleterious mutations for too long!) A rather straightforward calculation shows the following. If CIN is generated by a genetic event that happens at a rate comparable to the basic mutation rate, u, or even a couple of orders of magnitude larger, then a CIN cell, even with the optimal value of p*, cannot accelerate the generation and growth of a TSP^-/- cell line, simply because it requires this extra event, the “activation” of the CIN phenotype (see Fig. 2b and Fig. 3). In this scenario, CIN can accelerate the emergence and growth of TSP^-/- cells only if healthy cells acquire the CIN phenotype at a rate that is several orders of magnitude higher than the physiological mutation rate (Fig. 2b).

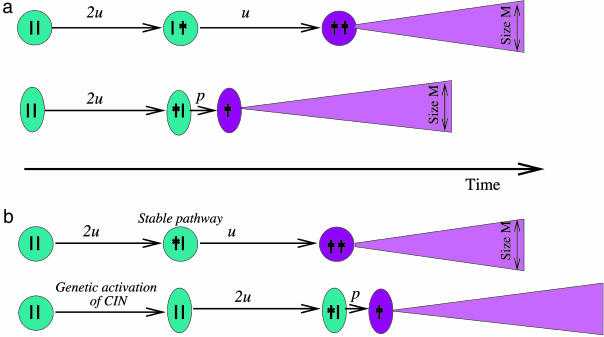
Fig. 3.

Schematic summary of the results about the effect of chromosome loss on the generation and growth of TSP^-/- cells. (a) We compare the growth rate of TSP^-/- cells in two scenarios: The TSP^-/- phenotype is generated by two successive point mutations in cells that do not have CIN; or the TSP^-/- phenotype is generated in CIN cells by the combination of a point mutation and a chromosome loss event. In this case, we observe an optimal rate of chromosome loss, for which the generation and growth of TSP^-/- cells occur fastest and which is better for the cancer than being stable. (b) On the other hand, if we assume that CIN first has to be generated before chromosome loss can occur, the generation and growth of TSP^-/- cells is always slower with the CIN pathway compared with the stable pathway (unless stable cells acquire CIN at a very high rate that is orders of magnitude larger than the basic mutation rate).

What are the implications of this result (summarized in Fig. 3)? Our analysis leads to the important insight that CIN does not arise simply because it allows the faster accumulation of carcinogenic mutations. Instead, CIN must arise because of alternative reasons, such as environmental factors. For example, if cells are exposed to high degrees of DNA damage (as a result of carcinogens and metabolic radicals), CIN can be selected for because it avoids frequent cell cycle arrest upon damage (23). The effect of DNA damage on the selection of genetically unstable cells has been explored mathematically (24). Alternatively, CIN might be the consequence of another mutation that confers an advantage to the cell (17). It has been proposed that a mutation in the adenomatous polyposis coli (APC) gene itself leads to the development of CIN and the generation of aneuploidy in colon cancer (25, 26). Another possibility is that CIN arises as a result of a virus infection. It has been suggested that JC virus infection can result in an unstable phenotype in colon cells (27). Once the CIN phenotype has been generated for whatever reason, our work suggests that there exists an optimal rate of chromosome loss at which the cancer can accumulate inactivated TSP genes fastest. Interestingly, the optimal rate of chromosome loss derived from our models is very robust and independent from parameter values and coincides with the rate of loss observed in colon cancer cell lines.

Our work has implications for the long-standing debate about whether so-called mutator phenotypes are necessary for the initiation and progression of cancers (28, 29). We emphasize that different types of instabilities observed in cancer cannot be lumped together into a class of mutator phenotypes. Different instabilities confer different types of costs and benefits to cells, and this balance determines whether they can accelerate the initiation of cancers or not. For example, our arguments do not apply to smaller scale instabilities, such as microsatellite instability. The effect of such smaller scale instabilities needs to be studied separately.