Offline Analysis of Context Contribution to ERP-based Typing BCI Performance

Abstract

Objective

To increase the symbol rate of the electroencephalography (EEG) based brain computer interface (BCI) typing systems by utilizing the context information.

Approach

Event related potentials (ERP) corresponding to a stimulus in EEG can be used to detect the intended target of a person for BCI. This paradigm is widely utilized to build letter-by-letter BCI typing systems. Nevertheless currently available BCI-typing systems still requires improvement due to low typing speeds. This is mainly due to the reliance on multiple repetitions before making a decision to achieve a higher typing accuracy. Another possible approach to increase the speed of typing while not significantly reducing the accuracy of typing is to use additional context information. In this paper, we study the effect of using a language model as additional evidence for intent detection. Bayesian fusion of an n-gram symbol model with the EEG features is proposed, and specifically regularized discriminant analysis ERP discriminant is used to obtain EEG-based features. The target detection accuracies are rigorously evaluated for varying language model orders, as well as the number of ERP-inducing repetitions.

Main Results

The results demonstrate that the language models contribute significantly to letter classification accuracy. For instance, we find that a single-trial ERP detection supported by a 4-gram language model may achieve the same performance as using 3-trial ERP classification for the non-initial letters of words.

Significance

Overall, fusion of evidence from EEG and language models yields a significant opportunity to increase the symbol rate of a BCI typing system.

1. Introduction

Worldwide, there are millions of people with severe motor and speech disabilities which prohibit them from participating in daily functional activities, such as personal care (Smith and Delargy, 2005). While many individuals may understand language fully and retain cognitive skills, they have no way to produce speech. Communication with other people, especially with their family members and care providers, becomes a significant challenge. Various assistive technologies have been developed to increase the quality of life and functions for these individuals (Fager et al., 2012). These technologies depend on the extraction and interpretation of various physiological signals at any anatomical site, such as eye movements blinks, or movements of hand, foot or head. However there is a group of individuals with locked-in syndrome (LIS) who may not have sufficient neuromuscular control to reliably and consistently use switches or intentionally direct their eye gaze, putting them into a state referred to as total locked-in syndrome. Bypassing all neuromuscular activity by relying on use of the brain activity as a switch activator has been developed as an interface for assistive technologies that allow communication and environmental control (Wolpaw and Wolpaw, 2012; Sellers et al., 2010).

Brain computer interface(BCI) is a technology that uses neural signals as the physiological input for various assistive technology applications (Brunner et al., 2011; Pfurtscheller et al., 2000; Farwell and Donchin, 1988; Renard et al., 2010; Pfurtscheller et al., 2010). BCI systems are based on invasive or noninvasive recording techniques. The noninvasive use of scalp electroencephalography (EEG) has drawn increasing attention due to portability, feasibility, and relative low cost. EEG has been used in BCIs for various communication and control purposes, such as typing systems or controlling robot arms. One of the biggest challenges encountered by most of these systems is to achieve sufficient accuracy or speed with the existence of a low signal-to-noise ratio and the variability of background activity (Schalk, 2008; Cincotti et al., 2006). To ameliorate this problem in letter-by-letter BCI typing systems, researchers have turned to various hierarchical symbol trees (Wolpaw et al., 2002; Serby et al., 2005; Treder and Blankertz, 2010). Additionally, there exist attempts to make stimuli more interesting to increase the attention level of the subjects (Kaufmann et al., 2011). Even though using various approaches on the presentation of the options may improve the performance, most BCI researchers agree that BCI is a maturing field and there is still a need for improvement on the typing speed (Brunner et al., 2011; Mak et al., 2011; Wolpaw and Wolpaw, 2012; Millán et al., 2010). Low accuracy rates for symbol selection considerably reduce the practical usability of such systems. One way to overcome this condition is to increase the number of the repetitions of the stimuli to achieve a sufficient level of typing accuracy, by sacrificing the typing speed (Aloise et al., 2012; Kaufmann et al., 2011). Another approach is to incorporate the context information directly to the decision making process to obtain speedups and to improve the efficiency of such systems. In the case of letter-by-letter typing BCIs, placing a computational language model, which can predict the next letter from the previous letters, within the decision making process can greatly affect performance by improving the accuracy and speed. If the symbol decisions are made using only the EEG evidence, that is, without using the context information in the language, decisions might not be sufficiently accurate with low number of repetitions. Under such conditions further word prediction without improving decision accuracy might not be feasible (Ryan et al., 2010). Thus, we propose to incorporate context information directly to the decision making process and to make symbol classification based on the tight fusion of language model and EEG evidence.

As the application of this proposed language model (LM) and EEG feature fusion methodology, we investigate the performance of context based decision making in RSVP Keyboard^TM, a BCI typing system that uses rapid serial visual presentation (RSVP) (Mathan et al., 2008). RSVP is a paradigm that presents each stimulus, in this case letters and symbols, one at a time at a visually central location on the screen, instead of using the matrix layout of the popular P300-Speller (Krusienski et al., 2008; Farwell and Donchin, 1988) or the hexagonal two-level hierarchy of Berlin BCI (Treder and Blankertz, 2010). In RSVP based BCI, the sequence of stimuli are presented at relatively high speeds, each subsequent stimulus replacing the previous one, while the subject tries to perform mental target matching between intended and presented stimuli. Accordingly, RSVP does not require an individual to perform extensive visual scanning or precise direction of gaze control. The RSVP Keyboard^TM is particularly suited for the most severely restricted users including those with LIS.

LIS might be the result of traumatic brain injury, brain-stem stroke, spinal cord injury or a neurodegenerative condition such as amyotropic lateral sclerosis (ALS). It is characterized by near total paralysis, despite the individual being cognitively intact. Motor control deterioration might extend to eye movements even though vision is intact. Even achieving a reliable twitch of a muscle or eye blink might become challenging. Therefore, using complex interactions requiring precise control of muscles or eyes might not be feasible for users with the most severe conditions. Consequently, simpler interactions via BCI holds great promise for effective text communication by such individuals. Yet, these simple interfaces have not been taking full advantage of language models (LM) to ease or speed-up typing.

In this paper, we demonstrate a methodology to expand the EEG-LM fusion concept introduced earlier (Orhan et al., 2011). We use a graphical model between EEG features and previously written text. An estimation of conditional probability density functions of the EEG features, assuming they are continuous-valued, and a predictive n-gram language model are employed. This approach can be used with most letter-by-letter typing systems including the audio BCI systems and most EEG feature extraction methods, including linear or nonlinear projections, and classification algorithms with a probabilistic output. To test the proposed method, an offline analysis using EEG data collected with RSVP Keyboard ^TMcan be obtained using this fusion framework. Based on experimental work, we designed an operational real time typing system, RSVP Keyboard^TM (Hild et al., 2011; Orhan et al., 2012).

2. Rapid Serial Visual Presentation based BCI

RSVP is an experimental psycho-physics technique in which visual stimuli are displayed on a screen over time at a fixed focal area and in rapid succession (Mathan et al., 2006; Huang et al., 2009). In contrast, the Matrix-P300-Speller (Krusienski et al., 2008; Farwell and Donchin, 1988) used by Wadsworth and Graz groups relies on spatially distributed presentation of the symbols, highlighting them using various subset organizations (e.g. a column, a row, checkerboard or an individual symbol) and orders to elicit responses to detect the intent of the user. Berlin BCI’s recent variation of their Hexo-Spell utilizes a 2-layer tree structure (Treder and Blankertz, 2010) where the subject chooses among six units (symbols or sets of these) while the subject focuses on a central focal area that uses RSVP-like paradigm to generate responses induced by the intent. Recently, the researchers started to investigate and compare these alternative presentation methodologies (Treder et al., 2011). In both of these BCIs an awareness of the full screen is required. On the other hand, the approach in RSVP Keyboard^TM is to distribute the stimuli temporally and present one symbol at a time using RSVP. Correspondingly, a binary answer is sought for each presented symbol. The latter method has the advantage of not requiring the user to fixate at different regions of the screen. This can be particularly useful for users with with weak or no gaze control, and for those whose cognitive skills do not allow processing of a matrix presentation (Brunner et al., 2010). Two example screens from the matrix presentation and RSVP are given in Fig. 1.

Figure 1.

Sample visual presentation screens; matrix presentation (on the left) and rapid serial visual presentation (on the right)

The presentation paradigm of RSVP Keyboard^TM includes stimulus sequences consisting of the 26 letters in the English alphabet, plus symbols for space and backspace. The set of symbols can easily be extended to a set containing various symbols for word completion or additional commands and punctuation. During the presentation of the sequence, the symbols are ordered randomly for the purpose of strengthening the response for the intended symbol. During the selection of a single symbol in the typing process, which we call an epoch, all symbols might be shown multiple times or sequences to improve accuracy. We call the single presentation of a symbol as a trial, which represents a single stimulus. The user is expected to react positively only for the target symbol. The problem reduces into decision making between positive and negative intended target for each symbol.

The human brain generates a natural response, an event related potential (ERP), to the infrequent target stimulus shown in RSVP sequences. The most prominent component of the target ERPs is the P300 wave. It is a positive deflection in the scalp voltage mainly in the centro-parietal areas with a latency of roughly 300 ms. However, the regions, latency, and amplitude of this signal may significantly vary between subjects. This target matching response allows us to build BCI systems by detecting them.

The detection of single trial ERPs solely from EEG is not accurate enough using current approaches. Therefore, it would be extremely beneficial to use additional context information during the sensing of ERPs. For a given probabilistic EEG feature extraction methodology for detecting ERPs, we propose the incorporation of a probabilistic language model, which is explained next.

3. Language Modeling

Language modeling is very important for many text processing applications, such as speech recognition, machine translation, as well as for the kind of typing application being investigated here (Roark et al., 2010). In BCI field, there exist recent attempts to use word prediction to speed up the typing process (Ryan et al., 2010). Typically, these approaches do not directly influence the decision making for an individual epoch, but instead give options for word completion. On the other hand, if the language models are incorporated into the decision making process, it might be possible to increase the speed and accuracy of the selection. To utilize this idea, the prefix string (what has already been typed) is used to predict the next symbol(s) to be typed, as the language model. Consequently, the next letters to be typed become highly predictable in certain contexts, particularly word-internally. In applications where text generation/typing speed is very slow, the impact of language modeling can become much more significant. BCI-spellers, including the RSVP Keyboard paradigm presented here, can be extremely low-speed letter-by-letter writing systems, and thus can greatly benefit from the incorporation of probabilistic letter predictions from an accurate language model during the writing process.

The language model used in this paper is based on the n-gram sequence modeling paradigm, widely used in all of the application areas mentioned above. An L-gram model, it estimates the conditional probability of every letter in the alphabet given L − 1 previous letters using a Markov model of order L − 1. In this context, let 𝗌_t : Ω → 𝒮 be the random variable corresponding to the correct symbol for epoch t, i.e. during t^th symbol selection, where 𝒮 is the set of possible symbols. Since there might be an operation of deletion, the total number epochs might be larger than the number of characters written. Hence, we can define the number of characters written as a function of epoch index; in other words let i_t be the number of characters already typed until epoch t. With this notation, we have i_t < t. Additionally, the corresponding random sequence of the last L − 1 characters written prior to epoch t are represented as 𝗐_j : Ω → 𝒜 where j ∈ {i_t − L + 2, ⋯;, i_t − 1, i_t} and 𝒜 ⊂ 𝒮 is the set containing the symbols which are characters, e.g. letters, punctuation and space. For representation simplicity, let 𝗐_t = [𝗐_it, 𝗐_it−1, ⋯, 𝗐_it−L+2] correspond to the random string of last L−1 characters during the selection of the target of t^th epoch and w = [w₁, w₂, ⋯, w_L−1] corresponds to a character string of length L − 1. In n-gram models, the symbol prediction is made using the latest string of length L as

$$P({\mathbf{𝗌}}_t=s|{\mathbf{𝗐}}_t=\mathbf{w})=\frac{P({\mathbf{𝗌}}_t=s,{\mathbf{𝗐}}_t=\mathbf{w})}{P({\mathbf{𝗐}}_t=\mathbf{w})},$$ (1)

from Bayes’ Theorem. In this equation, the joint probability mass functions are estimated using a large text corpus.

If the language model order is 1, the prediction probability is equal to the context-free letter occurrence probabilities in the English language, which is not dependent on the previous letters, i.e. P(𝗌_t = s|𝗐_t = w) = P(𝗌_t = s). Zero-gram model is defined as, having no active language model or equivalently P(𝗌_t = s) is assumed to be a uniform distribution over the alphabet, i.e. P(𝗌_t = s) = 1/|𝒮|. If the number of characters that are already typed is less than the language model order, a truncated model using all the characters that had been typed is used. As an example, if the second letter is being written, a 6-gram model is truncated to a 2-gram model. However this only happens in the very beginning of typing process, and it doesn’t restart at the beginning of words.

For the current study, all n-gram language models were estimated from a one million sentence (210M character) sample of the NY Times portion of the English Gigaword corpus. Corpus normalization and smoothing methods were as described in (Roark et al., 2010). Most importantly for this work, the corpus was case normalized, and we used Witten-Bell smoothing for regularization (Witten and Bell, 1991). For the offline analysis conducted in this paper, we sampled contexts from a separate 1M sentence subset of the same corpus. More specifically, for each letter, 1000 contexts were randomly sampled (without replacement).

4. Fusion of EEG Features and the Language Model

The evidence obtained from EEG and the language model can be used collaboratively to make a more informative decision about the class that each symbol belongs to. An epoch, i.e. multiple repetitions of each sequence, is going to be shown for each symbol to be selected. Each symbol is assumed to belong to the class of either positive or negative attentional focus or intent. Let 𝖼 : Ω → {0, 1} be the random variable representing the class of intent, where 0 and 1 corresponds to negative and positive intents, respectively and 𝗑 : Ω → ℝ^d be a random vector of EEG features corresponding to a trial. For example, an ERP discriminant function that projects the EEG data corresponding to a trial into a single dimension may be used as a feature extraction method. In this case, since d = 1, which represents there is only one EEG feature per trial. The fusion methodology explained here does not depend on the feature extraction method, and practically can be used with any feature vector in ℝ^d. The only requirement is an estimate of the conditional probability density function of EEG features given the class label, i.e. f(𝗑 = x|𝖼 = c) ∀c ∈ {0, 1}.

Specifically, let 𝗑_t,s,r be the random EEG feature vector corresponding to a trial for epoch t ∈ ℕ, symbol s ∈ 𝒮 and repetition r ∈ {1, 2, ⋯, R}, R is the total number of repetitions or sequences of the symbols per epoch. Furthermore, let 𝖼_t,s be the random variable representing the class of epoch t and symbol s. Consequently, for a symbol s, the posterior probability of the class being c using the L−1 previous symbols and EEG features for all of the repetitions of symbol s in epoch t can be written as,

$$Q=P({𝖼}_{t,s}=c|{\mathbf{𝗑}}_{t,s,1}={\mathbf{x}}_1,{\mathbf{𝗑}}_{t,s,2}={\mathbf{x}}_2,\cdots ,{\mathbf{𝗑}}_{t,s,R}={\mathbf{x}}_R,{𝗐}_{i_t}=w_1,{𝗐}_{i_t-1}=w_2,\cdots ,{𝗐}_{i_t-L+2}=w_{L-1}),$$ (2)

where x_R ∈ ℝ^d for r ∈ {1, 2, ⋯, R}. Using Bayes’ Theorem on (2), we obtain

$$Q=\frac{f({\mathbf{𝗑}}_{t,s,1}={\mathbf{x}}_1,\cdots ,{\mathbf{𝗑}}_{t,s,R}={\mathbf{x}}_R,{\mathbf{𝗐}}_t=\mathbf{w}|{𝖼}_{t,s}=c)P({𝖼}_{t,s}=c)}{f({\mathbf{𝗑}}_{t,s,1}={\mathbf{x}}_1,\cdots ,{\mathbf{𝗑}}_R={\mathbf{x}}_R,{\mathbf{𝗐}}_t=\mathbf{w})}.$$ (3)

We can assume that the EEG features corresponding to the symbol in question and the text that has been written already are conditionally independent given the class label of the symbol. This assumption is reasonable, because after the subject decides on a target symbol by considering the previously typed text, he/she is expected to show positive intent for the target and negative intent for the others, and after the class of a symbol is decided the EEG response is expected not to get affected by the text already written. This assumption can formally be written as 𝗑_t,s,1, ⋯, 𝗑_t,s,R ⫫ 𝗐_t|𝖼_t,s. Accordingly, (3) transforms to,

$$Q=\frac{f({\mathbf{𝗑}}_{t,s,1}={\mathbf{x}}_1,\cdots ,{\mathbf{𝗑}}_{t,s,R}={\mathbf{x}}_R|{𝖼}_{t,s}=c)P({\mathbf{𝗐}}_t=\mathbf{w}|{𝖼}_{t,s}=c)P({𝖼}_{t,s}=c)}{f({\mathbf{𝗑}}_{t,s,1}={\mathbf{x}}_1,\cdots ,{\mathbf{𝗑}}_R={\mathbf{x}}_R,{\mathbf{𝗐}}_t=\mathbf{w})}.$$ (4)

It can be further assumed that the EEG responses for each repetition of the symbol are conditionally independent given the class of the symbol. This assumption expects intents to be independent and identically distributed for a symbol in an epoch. As an example, if the subject shows a stronger intent for the second repetition, then the assumption fails. Since estimating such a joint conditional probability density function would be difficult as the number of repetitions gets higher, this assumptions constitutes a useful simplifying approximation. More formally, this can be written as 𝗑_t,s,1 ⫫ 𝗑_t,s,2 ⫫ ⋯ ⫫ 𝗑_t,s,R|𝖼_t,s, reducing (4) to,

$$Q=\frac{({\prod }_{r=1}^{R}f({\mathbf{𝗑}}_{t,s,r}={\mathbf{x}}_r|{𝖼}_{t,s}=c))P({\mathbf{𝗐}}_t=\mathbf{w}|{𝖼}_{t,s}=c)P({𝖼}_{t,s}=c)}{f({\mathbf{𝗑}}_{t,s,1}={\mathbf{x}}_1,\cdots ,{\mathbf{𝗑}}_{t,s,R}={\mathbf{x}}_R,{\mathbf{𝗐}}_t=\mathbf{w})}.$$

Using Bayes’ Theorem once again on P(𝗐_t = w_t|𝖼_t,s = c), we obtain,

$$Q=\frac{({\prod }_{r=1}^{R}f({\mathbf{𝗑}}_{t,s,r}={\mathbf{x}}_r|{𝖼}_{t,s}=c))P({𝖼}_{t,s}=c|{\mathbf{𝗐}}_t=\mathbf{w})P({\mathbf{𝗐}}_t=\mathbf{w})}{f({\mathbf{𝗑}}_{t,s,1}={\mathbf{x}}_1,\cdots ,{\mathbf{𝗑}}_{t,s,R}={\mathbf{x}}_R,{\mathbf{𝗐}}_t=\mathbf{w})}.$$ (5)

We can apply the likelihood ratio test for 𝖼_t,s to make a decision between two classes. The likelihood ratio of 𝖼_t,s, can be written from (2) as,

$$\mathrm{\Lambda }({𝖼}_{t,s}|{\mathbf{𝖷}}_{t,s}=\mathbf{X},{\mathbf{𝗐}}_t=\mathbf{w})=\frac{P({𝖼}_{t,s}=1|{\mathbf{𝖷}}_{t,s}=\mathbf{X},{\mathbf{𝗐}}_t=\mathbf{w})}{P({𝖼}_{t,s}=0|{\mathbf{𝖷}}_{t,s}=\mathbf{X},{\mathbf{𝗐}}_t=\mathbf{w})},$$

where 𝖷_t,s = {𝗑_t,s,1, 𝗑_t,s,2, ⋯, 𝗑_t,s,R} and X = {x₁, x₂, ⋯, x_R}. Using the form we obtained after simplifications and approximations from (2) to (5), likelihood ratio can be rewritten as

$$\mathrm{\Lambda }({𝖼}_{t,s}|{\mathbf{𝖷}}_{t,s}=\mathbf{X},{\mathbf{𝗐}}_t=\mathbf{w})=\frac{({\prod }_{r=1}^{R}f({\mathbf{𝗑}}_{t,s,r}={\mathbf{x}}_r|{𝖼}_{t,s}=1))P({𝖼}_{t,s}=1|{\mathbf{𝗐}}_t=\mathbf{w})}{({\prod }_{r=1}^{R}f({\mathbf{𝗑}}_{t,s,r}={\mathbf{x}}_r|{𝖼}_{t,s}=0))P({𝖼}_{t,s}=0|{\mathbf{𝗐}}_t=\mathbf{w})}.$$

In terms of the probabilities obtained from the language model, some of the probabilities can be rewritten as P(𝖼_t,s = 1|𝗐_t = w) = P(𝗌_t = s|𝗐_t = w) and P(𝖼_t,s = 0|𝗐_t = w)) = 1 − P(𝗌_t = s|𝗐_t = w). Finally, ratio of class posterior probabilities can be estimated as,

$$\mathrm{\Lambda }({𝖼}_{t,s}|{\mathbf{𝖷}}_{t,s}=\mathbf{X},{\mathbf{𝗐}}_t=\mathbf{w})=\frac{({\prod }_{r=1}^{R}f({\mathbf{𝗑}}_{t,s,r}={\mathbf{x}}_r|{𝖼}_{t,s}=1))P({\mathbf{𝗌}}_t=s|{\mathbf{𝗐}}_t=\mathbf{w})}{({\prod }_{r=1}^{R}f({\mathbf{𝗑}}_{t,s,r}={\mathbf{x}}_r|{𝖼}_{t,s}=0))(1-P({\mathbf{𝗌}}_t=s|{\mathbf{𝗐}}_t=\mathbf{w}))}.$$ (6)

In this equation, f(𝗑_t,s,r = x_r|𝖼_t,s = c) is to be estimated using the feature extraction algorithm and P(𝗌_t = s|𝗐_t = w) is to be estimated using the language model. Therefore the decision on the class label of symbol 𝗌_t for epoch t, ĉ_t,s may be done comparing the likelihood ratio with a risk dependent threshold, τ, i.e.

$$\mathrm{\Lambda }({𝖼}_{t,s}|{\mathbf{𝖷}}_{t,s}=\mathbf{X},{\mathbf{𝗐}}_t=\mathbf{w}){\gtrless }_{{ĉ}_{t,s}=0}^{{ĉ}_{t,s}=1}\tau ,$$ (7)

or in other words,

$${ĉ}_{t,s}=\{\begin{array}{cc}1,\hfill & \text{if}\mathrm{\Lambda }({𝖼}_{t,s}|{\mathbf{𝖷}}_{t,s}=\mathbf{X},{\mathbf{𝗐}}_t=\mathbf{w})>\tau \hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$

5. EEG Feature Extraction Case Study with RSVP Keyboard

There exist numerous ways to extract features from EEG. They might consist of bandpass filtering, artifact reduction, channel selection, linear or nonlinear projections, extraction of power features from various frequency bands, spatial pattern analysis, extraction of independent components, wavelet filtering etc. The method to extract features highly depends on the application.

In RSVP Keyboard^™, the goal for each stimuli is to decide if it corresponds to an intended symbol or not. Consequently, intent detection for a stimulus is equivalent to deciding if its ERP is induced from the target or non-target category. If we assume that ERPs last only for a limited duration of time, the problem reduces into a binary classification problem. This can easily be achieved by windowing the the signals after the stimuli using a sufficiently long window. For the analysis in this paper, we apply a 500 ms window.

To extract well separated features, we use the following methodology. Firstly, the time windowed EEG signals are filtered by a 1.5–42 Hz bandpass filter (FIR, linear phase, length 153) to remove low frequency signal drifts and noise at higher frequencies for each channel. Secondly, temporal feature vectors containing the filtered&windowed signals from each channel are further projected to a slightly lower dimensional space by linear dimension reduction. For this paper, this is applied using principal component analysis (PCA) by removing zero variance directions. Afterwards, the feature vectors corresponding to each feature channel are concatenated to create a single aggregated vector. This process amounts to a channel-specific energy preserving orthogonal projection of raw temporal features. Finally, using regularized discriminant analysis (RDA) (Friedman, 1989), a nonlinear projection to ℝ on the aggregate feature vector is applied. Without a doubt, one can employ one of the numerous other feature extraction methodologies, which might perform better or worse. The main purpose of this paper is not to find the best feature extraction methodology, but to demonstrate the effectiveness of the usage of context information.

5.1. Regularized Discriminant Analysis (RDA)

RDA is a modified quadratic discriminant analysis (QDA) model. If the feature vector corresponding to each class is assumed to have multivariate normal distribution, the optimal Bayes classifier resides in the QDA family. This is due to the fact that the logarithm of the ratio of two multivariate normal density functions is a quadratic function. Under the Gaussianity assumption, QDA depends on class means, class covariance matrices, class priors and a risk based threshold. All of these are to be estimated from the training data, in this case, from a calibration session, except for the risk-dependent threshold. The calibration session is a supervised data collection done to learn the signal statistics. When there exist a small number of samples for high dimensional problems, singularities in the estimation of these covariance matrices become problematic. This is generally the case for ERP-classification, since the duration of the calibration session is limited. Henceforth the maximum likelihood estimate of the covariance matrices will not be invertible, which is needed for the corresponding QDA solution.

RDA is proposed as a remedy to this obstacle. It modifies the covariance estimates to eliminate the singularities by applying shrinkage and regularization on them. The shrinkage procedure makes the class covariance matrices closer to the overall data covariance, and therefore to each other. Thus, it makes the discriminant closer to being a linear function of the feature vectors instead of a quadratic one. Let y_υ ∈ ℝ^p be the set of feature vectors used to learn the discrimination function of RDA from, where p is the number of features to administer RDA on and υ ∈ {1, 2, ⋯, N} is the index of the samples. Correspondingly, the maximum likelihood estimates of the means and covariances are given by

$${\mathit{\mu }}_k=\frac{1}{N}\sum _{c(\upsilon )=k}{\mathbf{y}}_{\upsilon }$$

and

$${\mathbf{\Sigma ̂}}_k=\frac{{\mathbf{S}}_k}{N_k}=\frac{1}{N_k}\sum _{c(\upsilon )=k}({\mathbf{y}}_{\upsilon }-{\mathit{\mu }}_k){({\mathbf{y}}_{\upsilon }-{\mathit{\mu }}_k)}^T,$$

where c(υ) ∈ {0, 1} is the class label of sample υ, k ∈ {0, 1} represents the class label and N_k is the number of samples belonging to class k, i.e. |{υ : c(υ) = k}|. The shrinkage procedure is administered as, ∀k ∈ {0, 1}

$${\mathbf{\Sigma ̂}}_k(\lambda )=\frac{{\mathbf{S}}_k(\lambda )}{N_k(\lambda )}$$ (8)

where

$${\mathbf{S}}_k(\lambda )=(1-\lambda ){\mathbf{S}}_k+\lambda \mathbf{S}$$

and

$$N_k(\lambda )=(1-\lambda )N_k+\lambda N,$$

with

$$N=\sum _{k\in \{0,1\}}{N}_k,\mathbf{S}=\sum _{k\in \{0,1\}}{\mathbf{S}}_k.$$

The shrinkage parameter, λ, determines how much the individual covariance matrices are to be shrinked towards the pooled estimate and takes a value between 0 and 1, i.e. λ ∈ [0, 1]. Further regularization is applied as,

$${\mathbf{\Sigma ̂}}_k(\lambda ,\gamma )=(1-\gamma ){\mathbf{\Sigma ̂}}_k(\lambda )+\frac{\gamma }{p}\mathrm{t}\mathrm{r}[{\mathbf{\Sigma ̂}}_k(\lambda )]\mathbf{I},$$

where Σ̂_k(λ) is given by (8), tr[·] is the trace operator and I is the p × p identity matrix. For a given λ, the regularization parameter, γ ∈ [0, 1] controls the shrinkage towards the circular covariance.

RDA provides a broad family of regularization options. The four special cases of λ and γ represent various well-known classifiers:

• λ = 0, γ = 0 : quadratic discriminant analysis

• λ = 1, γ = 0 : linear discriminant analysis

• λ = 0, γ = 1 : weighted nearest-means classifier

• λ = 1, γ = 1 : nearest-means classifier

For γ = 0, varying λ corresponds to the models between QDA and LDA.

The illustrate how much these operations are effective on decreasing the singularities, we can investigate the ranks of the covariance matrices before and after. Before shrinkage rank[Σ̂_k] ≤ N_k, after shrinkage,

$$\text{rank}[{\mathbf{\Sigma ̂}}_k(\lambda )]\le \{\begin{array}{cc}{N}_k,\hfill & \text{if}\lambda =0\hfill \\ N,\hfill & \text{otherwise}\hfill \end{array}.$$

With the further application of regularization ranks of the covariance estimates become,

$$\text{rank}[{\mathbf{\Sigma ̂}}_k(\lambda ,\gamma )]\{\begin{array}{cc}\le N_k,\hfill & \text{if}\lambda =0,\gamma =0\hfill \\ \le N,\hfill & \text{if}\lambda >0,\gamma =0\hfill \\ =p,\hfill & \text{otherwise}\hfill \end{array}.$$

Since N_k ≪ p and N < p most of the cases, shrinkage and regularization steps are both expected to be helpful to reduce the singularities.

After carrying out classifier shrinkage and regularization on the estimated covariance matrices, the Bayes classifier (Duda et al., 2001) is defined by the comparison of log-posterior-ratio with a risk-dependent threshold. The corresponding discriminant score function is given by,

$${\delta }_{\mathrm{R}\mathrm{D}\mathrm{A}}(\mathbf{y})=\text{log}\frac{f_{𝒩}(\mathbf{y};{\mathit{\mu ̂}}_1,{\mathbf{\Sigma ̂}}_1(\lambda ,\gamma )){\mathrm{\pi ̂}}_1}{f_{𝒩}(\mathbf{y};{\mathit{\mu ̂}}_0,{\mathbf{\Sigma ̂}}_0(\lambda ,\gamma )){\mathrm{\pi ̂}}_0}$$

where μ_k, π̂_k are estimates of class means and priors respectively; f_𝒩(y;μ, Σ) is the pdf of a multivariate normal distribution and y is the feature vector to apply RDA on. In this paper, we will consider the discriminant score function as a nonlinear projection from 𝗒 to 𝗑, i.e. 𝗑 = δ_RDA(𝗒). Subsequently, x = δ_RDA(y) will be the one dimensional EEG feature for the fusion with language models as explained in Section 4.

As a final step, the conditional probability density function of 𝗑 given the class label, i.e. f(𝗑 = x|𝖼 = k) needs to be estimated. It is nonparametrically done using kernel density estimation on the training data using a Gaussian kernel as

$$\mathrm{f̂}(𝗑=x|𝖼=k)=\frac{1}{N_k}\sum _{c(\upsilon )=k}{K}_{h_k}(x-x(\upsilon )),$$ (9)

where x(υ) is the discriminant score corresponding to a sample υ in the training data, that is to be calculated during cross validation, and K_hk(․) is the kernel function with bandwidth h_k. For Gaussian kernel, the bandwidth h_k is estimated using Silverman’s rule of thumb (Silverman, 1998) for each class k. This assumes the underlying density has the same average curvature as its variance-matching normal distribution. Using the conditional pdf estimates from (9) and language model probabilities from (1) in (6), we can finalize the fusion process.

6. Experimental Analysis

6.1. Offline Study

Two healthy subjects, one man and one woman, were recruited for this study. Each subject participated in the experiments for two sessions. In each session 200 letters are selected (with replacement, out of 26) according to their frequencies in the English language and randomly ordered to be used as target letters in each epoch. In each epoch, the designated target letter and a fixation sign are each shown for 1s, followed by 3 sequences of randomly ordered 26 letters in the English alphabet with 150 ms inter-stimuli interval. Correspondingly each sequence takes 4.9 seconds including the 1 second fixation duration. Subjects are asked to look for the target letter shown at the beginning of the epoch.

The signals are recorded using a g.USBamp biosignal amplifier using active g.Butterfly electrodes from G.tec (Graz, Austria) at 256Hz sampling rate. The EEG electrodes are applied with g.GAMMAcap (electrode cap) and the positioned according to the International 10/20 System were O1, O2, F3, F4, FZ, FC1, FC2, CZ, P1, P2, C1 C2, CP3, CP4. Signals were filtered by a nonlinear-phase 0.5–60 Hz bandpass filter and a 60 Hz notch filter (G.tec’s built-in design). Afterwards signals filtered further by the previously mentioned 1.5–42 Hz linear-phase bandpass filter (our design). The filtered signals were downsampled to 128Hz. For each channel, stimulus-onset-locked time windows of [0,500)ms following each image onset was taken as the stimulus response.

Let us denote by e_j the jth epoch in a given session and let 𝔼 be the ordered set containing all epochs in the session. 𝔼 is partitioned into 10 equal-sized nonintersecting blocks, 𝔼_k; for every e_j there is exactly one k_j such that e_j ∈ 𝔼_kj. For every e_j acting as a test sample, the ERP classifier is trained on the set 𝔼/𝔼_kj. During training, the classifier parameters λ and γ are determined using this 10-fold cross-validation approach and grid search within the set 𝔼/𝔼_kj. The kernel density estimates of the conditional probabilities of classification scores for EEG classifiers are obtained using scores obtained from 𝔼/𝔼_kj. The trained classifiers are applied to their respective test epochs to get the 10-fold cross-validation test results presented in the tables.

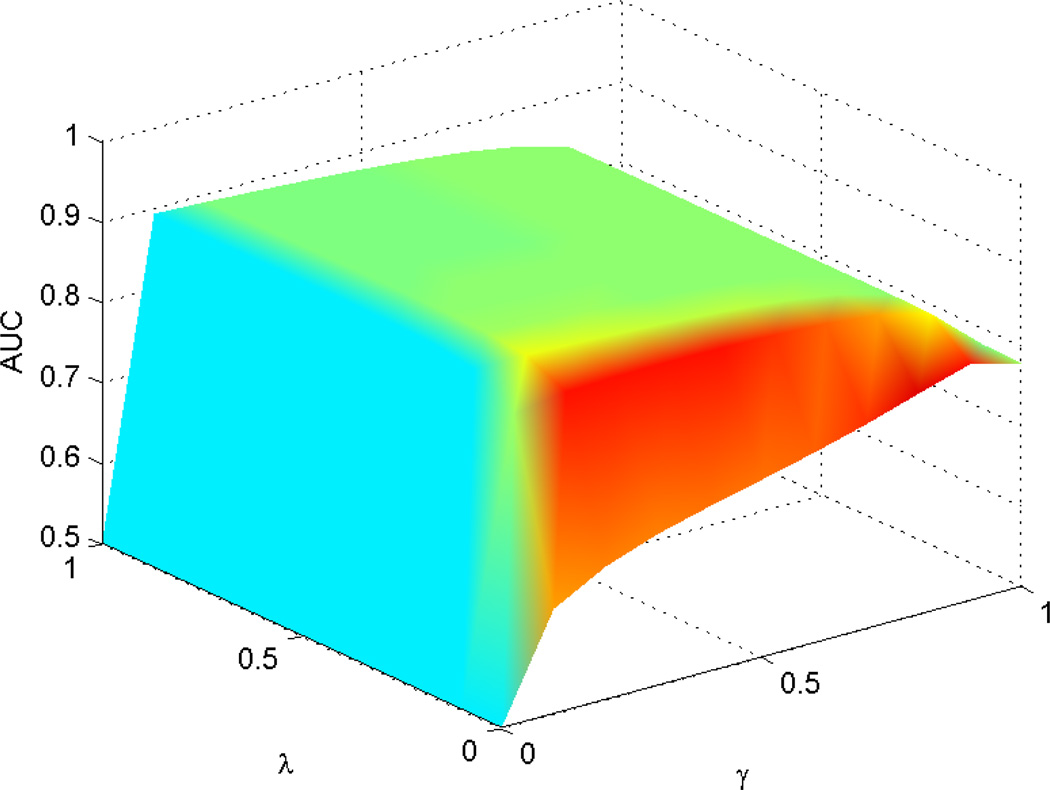
An example of the change in AUC during the grid search is given in Fig. 2 for single sequence with no language model (0-gram). This figure demonstrates that the regularization and shrinkage are both necessary and significantly effective. However if the regularization is applied too much it might degrade the performance.

Figure 2.

An example of the change in AUC while searching shrinkage (λ) and regularization (γ). Highest AUC is obtained for λ = 0.6 and γ = 0.1.

The language model was trained as described in Section 3. For each letter in the alphabet, 1000 random samples were drawn from the same corpus (separate from the language model training data) for testing purposes. For each letter sample we simulate the fusion of EEG responses and the language model in the following way: (i) each sample is assumed to be the target letter of a typing process using BCI; (ii) the predecessor letters of the target letter for each epoch are taken from the corpus to calculate the letter probabilities of the n-gram language models for each letter in the alphabet (Since subjects only focus on a single target letter without knowing the predecessor letters of the typing process in this experiment, it is assumed that the EEG responses created during an epoch are independent from the predecessors.); (iii) under the assumption of independence of EEG responses with the previous letters selected, for each epoch, the EEG responses for every letter is converted to EEG classifier scores; (iv) matching model probabilities for each letter are obtained from the language model; (v) and the fusion of ERP classifier scores and language model predictions was achieved as described above, resulting in a joint discriminant score that needs to be compared with a threshold depending on risk ratios for missing a target letter and a false selection.

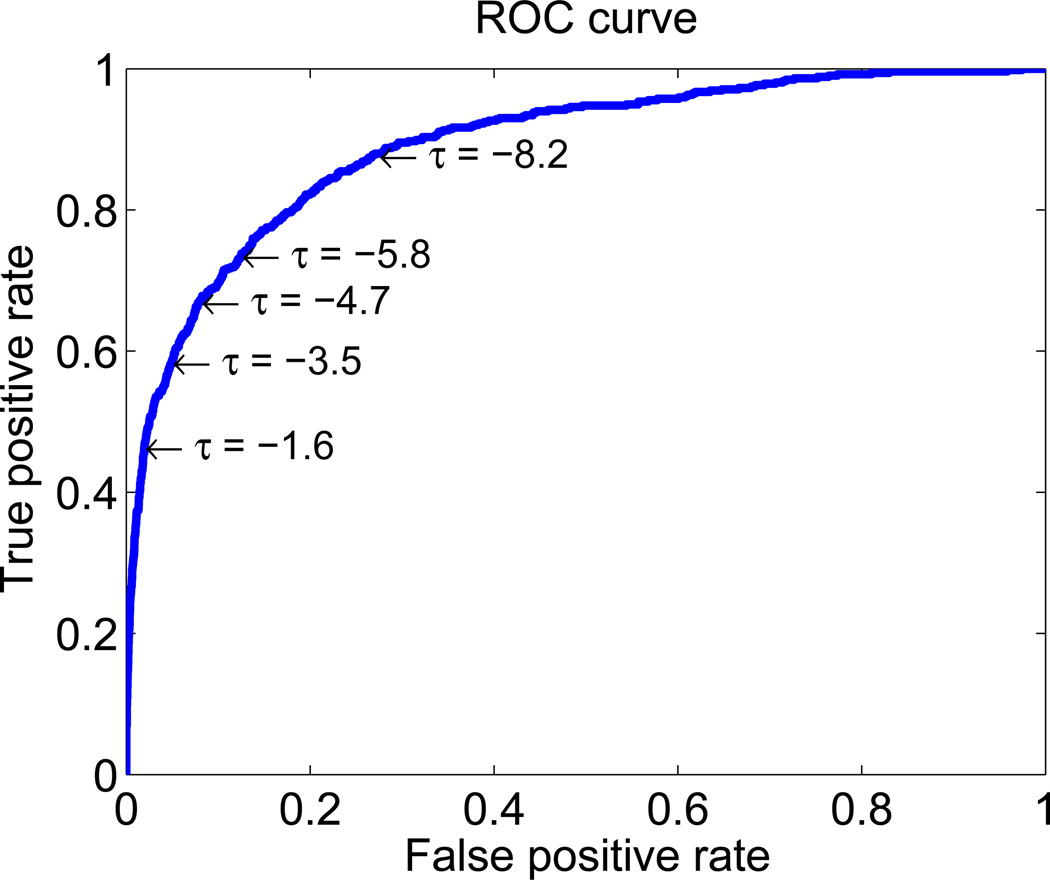
Fusion results were obtained for n-gram model orders L = 0, 1, 4, and 8. The EEG scores were assumed to have been evaluated for R = 1, 2, and 3 sequences (to evaluate the contribution of multi-trial information) to decide if a letter under evaluation was a desired target letter or not. In the results, only EEG data from the first R sequences of each epoch were used to classify each selected sequence count. Receiver operating characteristics (ROC) curves were obtained using the decision rule given in (6) by changing the risk based threshold, τ. An example ROC curve is given in Fig. 3. Area under the ROC curves were calculated for different orders of the language model, for different number of sequences used and for different positions of the sample target letter in the corresponding word from the corpus. In Table 1, the area under the ROC curves (AUC) are compared. Each entry contains the pair of minimum and maximum AUC over the sessions, i.e. each pair represent the performance of the worst and best session. In Table 2, Table 3, and Table 4 the correct detection rates are given for false positive rates of 1%, 5%, and 10%, respectively. These correspond to different values of the τ, since selecting a point on the ROC curve correspond to a false alarm rate, true positive rate and τ triplet.

Figure 3.

An example of an ROC curve corresponding to single sequence and 0-gram language model.

Table 1.

The minimum and the maximum values of the area under the ROC curves obtained using fusion classifier under different scenarios. The comparison is made using different number of sequences for classification, different letter positions in the word and different language model orders.

		1 sequence	2 sequences	3 sequences
0-gram		(0.812, 0.884)	(0.907, 0.956)	(0.957, 0.985)
1-gram		(0.892, 0.922)	(0.944, 0.973)	(0.972, 0.986)
4-gram	If 1st letter	(0.892, 0.941)	(0.954, 0.983)	(0.977, 0.991)
	If not 1st letter	(0.975, 0.983)	(0.985, 0.992)	(0.991, 0.997)
8-gram	If 1st letter	(0.905, 0.945)	(0.960, 0.984)	(0.979, 0.992)
	If not 1st letter	(0.991, 0.993)	(0.995, 0.997)	(0.995, 0.998)

Table 2.

The minimum and the maximum values of the detection rates for 1% false detection rate using fusion classifier under different scenarios.

		1 sequence	2 sequences	3 sequences
0-gram		(0.101, 0.348)	(0.500, 0.532)	(0.625, 0.698)
1-gram		(0.255, 0.371)	(0.468, 0.583)	(0.591, 0.698)
4-gram	If 1st letter	(0.263, 0.416)	(0.434, 0.774)	(0.621, 0.810)
	If not 1st letter	(0.597, 0.684)	(0.748, 0.849)	(0.848, 0.927)
8-gram	If 1st letter	(0.294, 0.448)	(0.465, 0.782)	(0.647, 0.835)
	If not 1st letter	(0.810, 0.854)	(0.886, 0.932)	(0.936, 0.972)

Table 3.

The minimum and the maximum values of the detection rates for 5% false detection rate using fusion classifier under different scenarios.

		1 sequence	2 sequences	3 sequences
0-gram		(0.453, 0.548)	(0.700, 0.810)	(0.828, 0.889)
1-gram		(0.556, 0.660)	(0.767, 0.841)	(0.900, 0.953)
4-gram	If 1st letter	(0.606, 0.688)	(0.740, 0.884)	(0.886, 0.971)
	If not 1st letter	(0.842, 0.899)	(0.912, 0.966)	(0.960, 0.989)
8-gram	If 1st letter	(0.614, 0.716)	(0.766, 0.905)	(0.899, 0.971)
	If not 1st letter	(0.951, 0.971)	(0.972, 0.990)	(0.986, 0.996)

Table 4.

The minimum and the maximum values of the detection rates for 10% false detection rate using fusion classifier under different scenarios.

		1 sequence	2 sequences	3 sequences
0-gram		(0.550, 0.661)	(0.800, 0.906)	(0.900, 0.969)
1-gram		(0.633, 0.797)	(0.817, 0.905)	(0.917, 0.984)
4-gram	If 1st letter	(0.692, 0.836)	(0.857, 0.961)	(0.948, 0.990)
	If not 1st letter	(0.933, 0.961)	(0.966, 0.991)	(0.983, 0.996)
8-gram	If 1st letter	(0.729, 0.840)	(0.873, 0.964)	(0.950, 0.990)
	If not 1st letter	(0.983, 0.990)	(0.992, 0.997)	(0.995, 0.998)

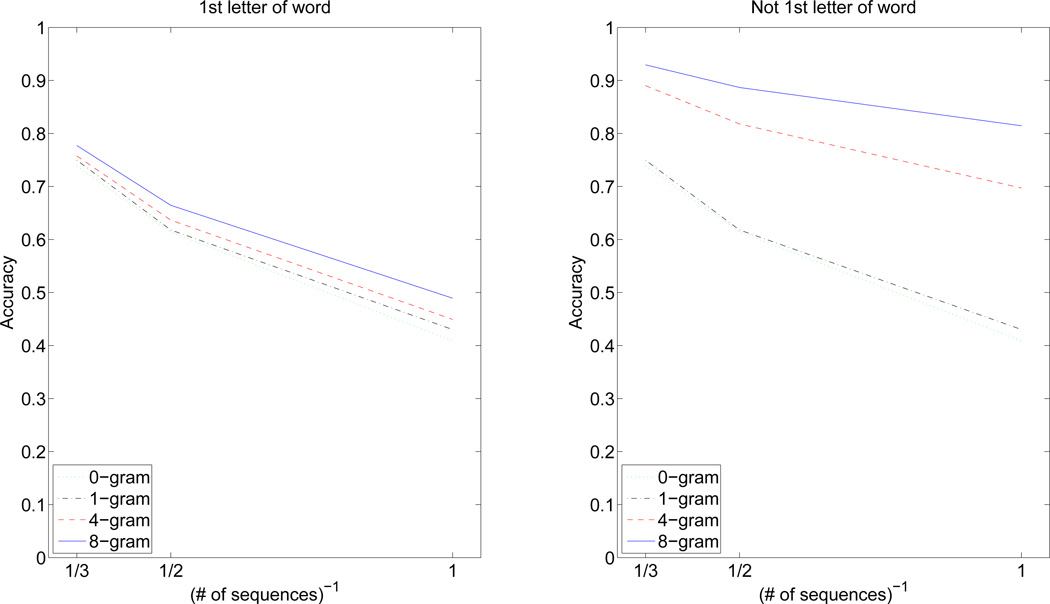
The letter decisions after an epoch may be made by selecting the symbol with maximum likelihood ratio. This corresponds to selecting the symbol with maximum Λ(𝖼_t,s|𝖷_t,s = X,𝗐_t = w) from (6). If applied with our offline analysis structure, the correct letter selection probabilities averaged over subjects are given by Fig. 4. The plots show correct letter selection probabilities vs inverse of number of repetitions. Since the number of repetitions is a direct measure of epoch duration, we used its inverse as a speed indicator. These curves indicate that usual speed/accuracy trade-offs apply to the proposed typing system and better language models result in better performance.

Figure 4.

The average correct letter selection probability vs inverse of the number of repetitions for various language model orders and letter locations in the word.

Obtaining expected typing duration from probability of correct decision

The typing duration can be directly related to the correct decision accuracy. If the correct decision making probability, p, is constant and greater than 0.5, the expected symbol selection duration becomes

$$\frac{T_s{N}_s}{2p-1},$$

where T_s is the duration of the of a sequence, and N_s is the number of sequences. If p < 0.5, with a nonzero probability the system will not be able to type the intended symbol, since it won’t be able to correct its mistakes. Therefore p < 0.5 is considered to be failure as subject might get stuck at a symbol. A similar relationship between expected time and probability of detection is also independently obtained independently in (Dal Seno et al., 2010). An alternative derivation for the formula is given in the Appendix.

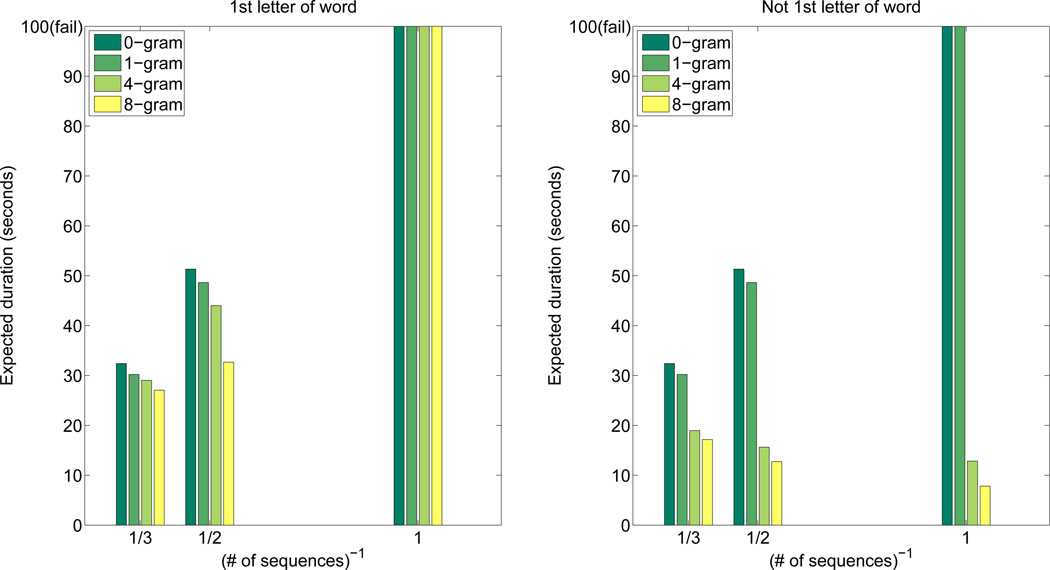
Typing duration per symbol, estimated using this relation, for various number of sequences, language model orders are given in Fig. 5 after averaging over sessions and subjects.

Figure 5.

The average expected value of typing duration vs inverse of the number of repetitions for various language model orders and letter locations in the word. In the graphs 100 seconds mark is used jointly with the failure case. If the subject has a probability of getting stuck it is considered as a failure.

6.2. Online System

The proposed fusion approach is implemented in RSVP Keyboard^™. Consequently, the real time system is trialed in typing by healthy subjects as well as people with LIS. Both groups were able to successfully operate the system for typing. To be able to demonstrate the applicability of this approach, we present results from (Orhan et al., 2012). In the online system, we employ a confidence based dynamic stopping criteria in addition to the online setting proposed here, with a maximum of 6. The language model used in the online system was limited to be a 6-gram model, due to the memory limitations in 32-bit Windows OS.

In the online setting, the symbol with the highest posterior probability is decided as the intended symbol. Consequently, no risk based threshold, τ, is selected. This means we employ a maximum a posteriori decision rule, which inherently assigns equal risk to every discrete decision candidate. These candidates are the elements of the alphabet. The ROC for the EEG discriminant is shown as an indicator for the quality of the EEG evidence, however, that ROC is not directly used in the decision process. Therefore the risk assignments associated with the τ that traces the ROC is not directly relevant to the final typing performance. Hence, a value is not selected.

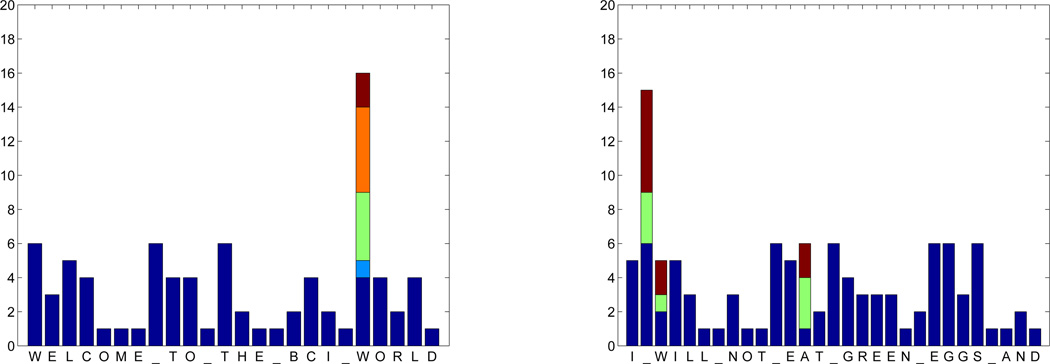
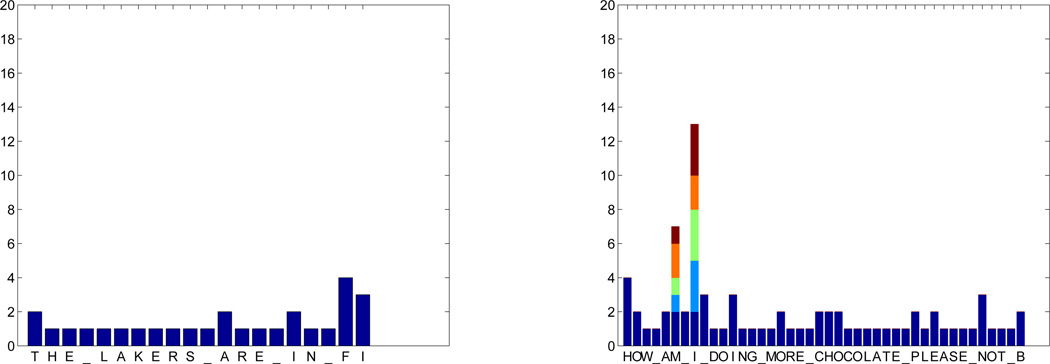
The experiments are done on two healthy subjects and one subject with LIS. The typing performances corresponding to the healthy subjects are given in Fig. 6 and Fig. 7. The locked-in subject successfully wrote HELLO_THERE_PEOP and THIS_IS_FAMILY__. Unfortunately the sequence information for each decision was not recorded for the locked-in subject. As extracted from the triggers, overall symbol typing duration was 74.7 and 45 seconds/symbol, respectively.

Figure 6.

HS1 number of sequences used to type each symbol. If there are multiple epochs needed to correctly type a symbol, unintended decisions and backspaces to correct it are represented with different colors. Typing duration was 17.8 and 23.2 seconds/symbol, respectively.

Figure 7.

HS2 number of sequences used to type each symbol. If there are multiple epochs needed to correctly type a symbol, unintended decisions and backspaces to correct it are represented with different colors. Typing duration was 17.1 and 23.8 seconds/symbol, respectively.

7. Discussion

The analysis done in this paper supports the hypothesis that using context information to support ERP classification can improve the performance of BCI typing systems. As the number of stimulus repetitions and as the order for language models increase, the accuracy of letter classification increases. A 0-gram language model (EEG only) performs the worst and context priors from the the language model makes significant contribution in single-trial decision making. The language model contributes more to letters that are internal in words than those appear at the beginning. The language model is not as influential for the first letters whereas the number of repetitions is. When the context is from the beginning of a word, the language model has a high entropy, i.e. uncertainty on the symbols. Therefore it doesn’t substantially improve the decision making process. However when the context is more internal to the word, the language model becomes more peaked for some symbols. Consequently, this phenomenon makes the language model more influential. Thus, the results suggest that the BCI system increase the number of trials for the beginning of each word and decrease it for the subsequent letters. Reduction in the number of stimulus repetitions is a direct multiplier factor for reduction in time to type a given length text, hence significant speed-up in typing may be possible.

The context information fusion approach proposed in this paper can be integrated with almost any ERP-based BCI typing system in the field, e.g. P300-speller, by satisfying two main requirements. Firstly, there needs to exist a language model that makes a probabilistic prediction on the following selection based on the context. Secondly, a probabilistic conditional likelihood estimator for the trials is required. This can easily be achieved while using a probabilistic classifier. Alternatively, a parametric or non-parametric estimator, e.g. KDE, may be used to estimate conditional likelihoods. Meeting these conditions allows a BCI typing system to use the proposed approach to make a more informed decision, consequently an increase in typing speed and accuracy is highly possible to be accomplished.

Appendix A. Accuracy and Speed Analysis

Catalan numbers: Catalan numbers arise in various counting problems (Stanley, 2011). One of the problems that results with Catalan numbers is the nested parenthesis problem. The number of the ways k left parenthesis and k right parenthesis can be ordered so that it becomes a properly nested ordering, correspond to k^th Catalan number. Explicitly it is, $C_k=\frac{1}{k+1}\left(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\right)$. If we replace left parenthesis with 0 and right parenthesis with 1, the problem can equivalently be restated as the number of ways to order k 0s and k 1s so that no initial segment contains more 1s than 0s.

Lemma 1: Let 𝖡_n ∈ {0, 1} be i.i.d. Bernoulli random variables with success probability of p, i.e. P(𝖡_n = 1) = p. Let b₁b₂ ⋯ b_l be a successful serie if following two conditions are satisfied,

1. ∀r ∈ {1, 2, ⋯, l − 1} b₁b₂ ⋯ b_r, contains at least as many 0s as 1s,

2. b₁b₂ ⋯ b_l contains more 1s than 0s.

The probability of achieving a successful serie is

$$P(\text{success})=\{\begin{array}{cc}1,\hfill & \text{if}p\ge 0.5\hfill \\ \frac{1-2p}{1-p},\hfill & \text{if}p<0.5\hfill \end{array}.$$

Proof. Using binomial series expansion

$${(1+y)}^{\upsilon }=\sum _{k=0}^{\infty }\left(\begin{array}{c}\upsilon \hfill \\ k\hfill \end{array}\right)y^k,$$ (A.1)

where $\left(\begin{array}{c}\hfill \upsilon \hfill \\ \hfill k\hfill \end{array}\right)$ is the Binomial coefficient at y = −4z and $\upsilon =-\frac{1}{2}$,

$${(1-4z)}^{1/2}=\sum _{k=0}^{\infty }\left(\begin{array}{c}\hfill 1/2\hfill \\ \hfill k\hfill \end{array}\right){(-4z)}^k=\sum _{k=0}^{\infty }\frac{{\prod }_{r=0}^{k-1}(\frac{1}{2}-r)}{k!}{(-4)}^k{z}^k=1+\sum _{k=1}^{\infty }-\frac{{\prod }_{r=1}^{k-1}(2r-1)}{k!}{2}^k{z}^k=1+\sum _{k=1}^{\infty }-\frac{(2k-2)!}{2^{k-1}(k-1)!k!}{2}^k{z}^k=1-2\sum _{k=1}^{\infty }\frac{1}{k}\left(\begin{array}{c}\hfill 2(k-1)\hfill \\ \hfill k-1\hfill \end{array}\right)z^k=1-2z\sum _{k=0}^{\infty }\frac{1}{k+1}\left(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\right)z^k.$$

This converges if |4z| ≤ 1. Rearranging the equation,

$$\sum _{k=0}^{\infty }\frac{1}{k+1}\left(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\right)z^k=\frac{1-{(1-4z)}^{1/2}}{2z}.$$ (A.2)

Let s_m be the number of 1s in b₁b₂ ⋯ b_m. ∀m ∈ ℕ, s_m+1 ≤ s_m + 1, with the equality condition is satisfied only if b_m+1 = 1. If b₁b₂ ⋯ b_l is a successful serie, s_l ≥ ⌈(l + 1)/2⌉ from condition (ii), and s_l−1 ≤ ⌊(l−1)/2⌋ from condition (i), where ⌊․⌋ and ⌈․⌉ represent the floor and ceil operators, respectively. Combining these three inequalities, we obtain

$$\lceil (l+1)/2\rceil \le s_l\le s_{l-1}+1\le \lfloor (l-1)/2\rfloor +1=\lfloor (l+1)/2\rfloor \le \lceil (l+1)/2\rceil .$$

Consequently, ≤ s_l = s_l−1 + 1, and ⌊(l + 1)/2⌋ = ⌈(l + 1)/2⌉. Hence b_l = 1 and l is odd, i.e. l = 2k + 1. Therefore P(Success using 2k trials) = 0. Furthermore s_l = ⌈(2k + 1 + 1)/2⌉ = k + 1. As a conclusion, a successful serie of length l = 2k + 1 contains k zeros and k + 1 ones. Since each element of the serie is obtained via independent Bernoulli trials, achieving a given successful serie of length 2k + 1 has the probability of p^k+1(1−p)^k. The probability of achieving success with 2k+1 trials is

$$P(\text{Success using}2k+1\text{trials})=p^{k+1}{(1-p)}^k{C}_k,$$ (A.3)

where C_k is the number of different successful series with length 2k+1. In all successful series, b_2k+1 = 1, therefore C_k is the number of different ways k 0s and k 1s where ∀r ∈ {1, 2, ⋯, 2k}, b₁b₂ ⋯ b_r has no more 1s than 0s. Hence C_k is k^th Catalan number, $C_k=\frac{1}{k+1}\left(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\right)$. Correspondingly the probability of success becomes,

$$P(\text{Success})=\sum _{l=1}^{\infty }P(\text{Success using }l\text{ trials})=\sum _{k=0}^{\infty }P(\text{Success using }2k+1\text{ trials})=\sum _{k=0}^{\infty }{p}^{k+1}{(1-p)}^k\frac{1}{k+1}\left(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\right)$$

Using (A.2) for z = p(1 − p),

$$P(\text{Success})=p\frac{1-{(1-4p(1-p))}^{1/2}}{2p(1-p)}=\frac{1-{(1-4p+4p^2))}^{1/2}}{2(1-p)}=\frac{1-|2p-1|}{2(1-p)}=\{\begin{array}{cc}1,\hfill & \text{if}p\ge 0.5\hfill \\ \frac{p}{1-p},\hfill & \text{otherwise}\hfill \end{array}.$$

Corollary. If p < 0.5, with $\frac{1-2p}{1-p}$ probability there will never be a success.

Lemma 2: If p ≥ 0.5, the expected length of the series with success is 1/(2p−1), i.e.

$$𝔼[𝖫]=\frac{1}{2p-1},$$

where L is a rv representing the length of the successful series.

Proof. Similar to Lemma 1, using Binomial series for (A.1) for y = −4z and υ = −1/2,

$${(1-4z)}^{-1/2}=\sum _{k=0}^{\infty }\left(\begin{array}{c}\hfill -1/2\hfill \\ \hfill k\hfill \end{array}\right){(-4z)}^k=\sum _{k=0}^{\infty }\frac{{\prod }_{r=0}^{k-1}(-\frac{1}{2}-r)}{k!}{(-4)}^k{z}^k=\sum _{k=0}^{\infty }\frac{{\prod }_{r=0}^{k-1}(2r+1)}{k!}{2}^k{z}^k=\sum _{k=0}^{\infty }\left(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\right)z^k$$

For z = p(1 − p),

$$\sum _{k=0}^{\infty }\left(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\right)p^k{(1-p)}^k={(1-4p(1-p))}^{-1/2}=\frac{1}{2p-1}$$ (A.4)

Since from Lemma 1, all of the probability mass is contained by successful series for p > 0.5, using (A.3) we obtain,

$$𝔼[𝖫]=\sum _{l=0}^{\infty }lP(\text{Success with}l\text{trials})=\sum _{k=0}^{\infty }(2k+1)P(\text{Success with}2k+1\text{trials})=\sum _{k=0}^{\infty }(2k+1)p^{k+1}{(1-p)}^k{C}_k=\sum _{k=0}^{\infty }(2k+1)p^{k+1}{(1-p)}^k\frac{1}{k+1}\left(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\right)=\sum _{k=0}^{\infty }{p}^{k+1}{(1-p)}^k\frac{1}{2}\left(\begin{array}{c}\hfill 2(k+1)\hfill \\ \hfill k+1\hfill \end{array}\right)=\frac{1}{2(1-p)}(-1+\sum _{k=0}^{\infty }{p}^k{(1-p)}^k(\begin{array}{c}\hfill 2k\hfill \\ \hfill k\hfill \end{array}\left)\right)$$

Using A.4,

$$𝔼[𝖫]=\frac{1}{2(1-p)}(-1+\frac{1}{2p-1})=\frac{1}{2(1-p)}·\frac{2(1-p)}{2p-1}=\frac{1}{2p-1}$$

Appendix A.1. BCI perspective

Assume that the correctness of a decision at the end of each epoch be i.i.d. Bernoulli random variables with success probability of p and the duration of the epoch, the duration a decision is made, to be T.

To be able to type a symbol accurately, we have the following tree.

Whenever the number of correct selections is more than the number of incorrect selections, the target symbol is typed correctly. The correct typing of a symbol is equivalent to having a successful serie as defined in Lemma 1. As an example, the successful conditions using 7 epochs are,

• 0101011

• 0100111

• 0011011

• 0010111

• 0001111.

Let the duration of an epoch is T. If we assume that the success of the decisions are independent and identically distributed, than the problem becomes equivalent to Lemma 2. Correspondingly we can calculate the expected symbol typing duration. If p > 0.5, expected duration of typing a symbol becomes $\frac{T}{2p-1}$ by Lemma 2. If p < 0.5, the system wouldn’t be able to operate, since the there is a nonnegative probability of failure.