The effect of echo time and post-processing procedure on blood oxygenation level-dependent (BOLD) functional connectivity analysis

Abstract

While spontaneous BOLD fMRI signal is a common tool to map functional connectivity, unexplained inter- and intra-subject variability frequently complicates interpretation. Similar to evoked BOLD fMRI responses, spontaneous BOLD signal is expected to vary with echo time (TE) and corresponding intra/extravascular sensitivity. This may contribute to discrepant conclusions even following identical post-processing pipelines. Here we applied commonly-utilized independent component analysis (ICA) as well as seed-based correlation analysis and investigated default mode network (DMN) and visual network (VN) detection from BOLD data acquired at three TEs (3T; TR=2500 ms; TE = 15 ms, 35 ms, and 55 ms) and from quantitative R2* maps. Explained variance in ICA analysis was significantly higher (P<0.05) when R2*-derived maps were considered relative to single-TE data with no post-processing. While explained variance in the BOLD data increased with motion correction, R2* derived DMN and VN were minimally affected by motion correction. Explained variance increased in all data when physiological noise confounds were removed using CompCor. Notably, the R2*-derived connectivity patterns were least affected by motion and physiological noise confounds in a seed-based correlation analysis. Intermediate (35 ms) and long (55 ms) TE data provided similar spatial and temporal characteristics only after reducing motion and physiological noise contamination. Results provide an exemplar for how 3T spontaneous BOLD network detection varies with TE and post-processing procedure over the range of commonly acquired TE values.

1. INTRODUCTION

Functional magnetic resonance imaging (fMRI) using evoked or spontaneous blood oxygenation level-dependent (BOLD) contrast is frequently used to infer information regarding neuronal activity (Fox and Raichle, 2007; Kwong et al., 1992; Ogawa et al., 1990). However, both evoked and spontaneous BOLD contrast arises from changes in cerebral blood flow, cerebral blood volume and the cerebral metabolic rate of oxygen consumption. Furthermore, BOLD signal contains contributions from intravascular blood water, extravascular tissue, and cerebrospinal fluid (CSF) water at typical field strengths of 1.5–3.0T, and it is well known that the relative effects from each of these contributions will vary with echo time (TE) choice (Donahue et al., 2011; Yacoub et al., 2005). For evoked BOLD fMRI experiments, whereby a specific task is administered and corresponding oxygenation-induced susceptibility changes in capillaries and veins are detected, substantial work has already been conducted demonstrating the dependence of the BOLD hemodynamic response function on TE. It is now generally accepted that TE ~ tissue T2* is desired for most applications (Triantafyllou et al., 2005).

Alternatively, while spontaneous BOLD fMRI has grown substantially in popularity over the past decade, important gaps in our knowledge remain regarding how spontaneous BOLD activity is related to intravascular sensitivity and corresponding imaging parameter choice, which frequently varies between studies. Much work is aimed at improving post-processing strategies and network identification of spontaneous BOLD data (Damoiseaux et al., 2006; Joel et al., 2011a; Smith et al., 1999; Smith et al., 2012). There is however, comparatively less work that has shown conclusively which imaging parameters are ideal for spontaneous BOLD acquisition and how post-processing analysis varies for different experimental input (i.e., BOLD data acquired at different TE). For instance, TE choice for BOLD functional connectivity studies at 3.0T frequently varies from 30–45 ms, and it is unclear whether networks detected at these different TEs will provide comparable information at a single-subject or group level. Furthermore, recent work has demonstrated that baseline BOLD data acquired at different TE can be used to help distinguish neuronally-derived signal fluctuations from nuisance fluctuations derived from motion, physiology, and related sources (Kundu et al., 2012).

Baseline BOLD networks of interest are generally reported to oscillate at low frequencies (< 0.1 Hz) and are commonly measured at a sampling rate of 2–3 sec. It is also feasible to acquire whole-brain multi-TE BOLD data at this temporal resolution to generate connectivity maps with varying extravascular sensitivity and also to derive quantitative measurements of R2*. At such typical TR values, not only will the physiological noise be aliased into the baseline signal fluctuations, but slow variations including scanner drift may also contribute significantly to the baseline signal fluctuations, thereby potentially increasing inter-subject variability (Fransson, 2005; Mantini et al., 2007). Analyses of spontaneous BOLD data often involve high-pass frequency filtering to remove the effects of such variations, which in turn de-sensitizes such acquisitions to the very low frequency regime that may contain additional information regarding functional networks. However, compared to single-TE data, R2*-derived maps are likely to be less sensitive to baseline drift and motion artifacts, and can provide an alternative approach to study functional networks. Unfortunately, extremely limited information is available on how outputs from typical functional connectivity analysis pipelines vary with choice of TE, and furthermore to what extent R2* maps themselves can be utilized for connectivity mapping.

Here we assess how BOLD functional connectivity varies with choice of TE. We investigate the application of multi-TE BOLD and the derived R2* fluctuations to detect default mode network (DMN) and visual network (VN) using commonly employed independent component analysis (ICA) algorithms as well as seed region approaches (Beckmann et al., 2005; Beckmann and Smith, 2005; Joel et al., 2011b). The hypothesis to be investigated is that similar to evoked BOLD responses, spontaneous BOLD connectivity characteristics vary with experimental input choice (i.e., TE or R2*). Specifically, voxels acquired at short TE will correlate spatially less well with group level results owing to the large and variable intravascular contributions from draining veins, whereas long TE functional connectivity mapping will provide better spatial specificity.

Results are intended to provide an exemplar for how spontaneous BOLD network detection varies with TE and choice of post-processing procedure.

2. MATERIAL AND METHODS

All volunteers provided informed, written consent in accordance with the Health Insurance Portability and Accountability Act (HIPAA) and Vanderbilt Institutional Review Board (IRB; Study 101567). This study was divided into two parts. First, we acquired multi-TE BOLD data in healthy volunteers and assessed how network detection varied with TE and the quantified R2* inputs for minimally processed data. Second, for the same data, we varied the processing steps to understand how experimental input as well as analysis pipeline influenced network detection.

2.1 Experiment

Adult male volunteers (n=18; age=21±3 yrs) with no history of neurological disorders were enrolled. All data were acquired at 3.0T (Philips Medical Systems, Best, The Netherlands) using quadrature body coil radiofrequency (RF) transmission and SENSE 8-channel reception.

Experimental scan parameters

Multi-echo BOLD fMRI: Single-shot, gradient echo, echo planar imaging (EPI), spatial resolution = 3.5 × 3.5 × 3.5 mm³, slices = 29, field-of-view = 224 × 224 × 101.5 mm³, TR = 2500 ms, SENSE-factor = 2. Note that parallel imaging (or a similar acceleration strategy) is required to allow all TEs to be acquired in a single TR with moderate temporal resolution (i.e., TR = 2–3s). Data were acquired at three TEs: 15 ms, 35 ms, and 55 ms. R2* maps were calculated according to:

$$R{2}^{\ast }=-\frac{\ln (S_i∕S_0)}{{\mathrm{TE}}_i}i=15,35\text{and}55\mathrm{ms}$$ [1],

where S_i is the signal intensity at TE_i, and S₀ is the equilibrium signal intensity (common for all measurements). The R2* maps were calculated on a voxel-wise basis and preserved for functional connectivity analysis. Considerations regarding Rician noise and the use of a linear, rather than exponential fit are addressed in the Discussion.

T1-weighted anatomical images were acquired for co-registration using the following parameters: 3D turbo field echo, spatial resolution 1 × 1 × 1 mm³, slices = 150, flip angle = 8°, TR/TE = 8.8/4.6 ms.

The purpose of the functional connectivity analysis was to apply commonly used approaches (both ICA and seed region correlation testing) to understand how experimental input choice led to different observed connectivity patterns. The analysis details of these common approaches are summarized below.

2.2 Independent component analysis (ICA)

Data were grouped according to BOLD acquisition at TE = 15 ms, TE = 35 ms, TE = 55 ms, and quantified R2*, and referred to as BOLD_TE=15, BOLD_TE=35, BOLD_TE=55, and R2*, respectively, from here on. To allow signal to reach steady state; the first five volumes were removed from each subject's time course. All fMRI and anatomical data were registered to a standard 3.5 mm (isotropic) MNI atlas. Next, data were pre-processed in three ways (Table 1):

• 1)Basic processing (BASIC): Spatial smoothing with FWHM=3 mm (Jenkinson et al., 2002; Jenkinson and Smith, 2001)
• 2)Motion correction (MOCO): BASIC and motion correction (Jenkinson et al., 2002; Jenkinson and Smith, 2001)
• 3)MOCO+COMPCOR: MOCO and physiological noise correction using the CompCor technique with anatomical masks (Behzadi et al., 2007).

Table 1.

Data processing strategies.

	Spatial Smoothing (FWHM=3 mm)	Motion Correction (MOCO)	Physiological Noise Reduction (CompCor)
1. BASIC	Yes	No	No
2. MOCO	Yes	Yes	No
3. MOCO + COMPCOR	Yes	Yes	Yes

BASIC: Minimally Processed, MOCO: Motion corrected, MOCO+COMPCOR: Reduced physiological noise (in addition to motion-corrected)

Motion correction was performed using the FMRIB Software Library (FSL) MCFLIRT routine (Jenkinson et al., 2002; Jenkinson and Smith, 2001). Motion regressors were obtained from BOLD_TE=15 and the transformation matrices for each volume were then applied to all data of the same subject. Therefore, identical motion correction was applied to all fMRI data for each subject. We found this method to reduce artifacts derived from differences in motion correction performance at each TE, yet this approach assumes that minimal motion occurs over the duration of the multi-TE readout.

CompCor (Behzadi et al., 2007) was implemented using the NeuroImaging Analysis Kit (NIAK, www.nitrc.org/projects/niak/). To achieve this, the T1-weighted structural data from each subject were segmented into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) using the FSL FAST routine (Zhang et al., 2001). Masks were then co-registered to the MNI atlas using the transformation matrices obtained during the registration of the T1-weighted anatomical images to MNI space. These masks were thresholded at a probability value of 0.99 and eroded by 2 voxels in FSL. Next, the separate, eroded, WM and CSF masks were combined into one binary mask containing voxels with either WM or CSF. The CompCor routine was applied in NIAK, which included extraction of the relevant time courses from the WM and CSF voxels in the mask, construction of the covariance matrix, and principal component analysis (PCA). The most significant components from the PCA were extracted as outlined in the literature (Behzadi et al., 2007). These components were then used as confounds and regressed from all the baseline time courses using FSL.

For individual subject analysis, ICA components were estimated with MELODIC (Beckmann and Smith, 2005). The number of ICA components was fixed at 20, based on literature recommendation (Smith et al., 2009) to reduce network decomposition, which was not the target of this investigation. The DMN and VN components were selected by comparing all 20 MELODIC outputs with template ICA-derived maps of the same networks (Damoiseaux et al., 2006; Smith et al., 2009). Briefly, the DMN and VN maps from the ICA atlas (Damoiseaux et al., 2006; Smith et al., 2009) were first downsampled to 3.5 mm to match the experimental data. Next, spatial correlation was assessed between these downsampled template maps and all 20 components obtained from the individual subject and group ICA output. The component with the maximum correlation (Pearson's correlation) to the standard atlas template was selected as the desired network.

Explained variance, which describes how much of the total signal variation is contributed by the particular component, was computed for all data inputs and processing strategies. To test for significant differences in the explained variances, a two-tailed Student's t-test with criteria for significance P≤0.05 was applied.

Next, group level analysis was performed using MELODIC (Beckmann and Smith, 2005) by temporally concatenating the individual, co-registered subject data. The DMN and VN was identified from the BOLD_TE=15, BOLD_TE=35, BOLD_TE=55, and R2* data using the template procedure as outlined above; explained variances for group analysis were recorded. Paired difference testing was avoided owing to different amplitudes of the spontaneous BOLD fluctuations and SNR inherent in the different TE and R2* data.

To evaluate SNR in all analyses, pair-wise difference images were acquired by subtracting the even acquisitions from the odd acquisitions. Signal from all odd acquisitions was multiplied by a correction factor (1.414) and divided by the standard deviation in the difference images to calculate SNR values for each data set in a homogeneous white matter tissue region.

2.3 Seed voxel correlation analysis

DMN and VN maps were also evaluated by measuring synchrony using a common seed region approach and Pearson's correlation (r) tests. For this purpose, a 7 mm region-of-interest (ROI) around a standard seed voxel (Harrison et al., 2008) was chosen in the posterior cingulate (MNI coordinates: [−3 −54 30]) to characterize DMN and in the visual cortex (MNI coordinates: [10 −73 30]) to characterize VN. The mean time course in the seed ROI was evaluated and r was calculated at each voxel in the acquired brain volume. The correlation values, r, were then converted to Fisher's Z scores using

$$z=\frac{1}{2}\ln \left(\frac{1+r}{1-r}\right)$$ [2].

Individual and averaged DMN and VN maps were evaluated at TE=15 ms, 35 ms, 55 ms, and for R2* each for BASIC, MOCO, and MOCO+COMPCOR post-processing pipelines.

3. RESULTS

3.1 SNR calculation

Mean SNR values from BOLD_TE=15, BOLD_TE=35, BOLD_TE=55, and R2* were 216±60, 158±35, 116±20, and 94±12 respectively in the white matter. As expected, SNR was significantly (P<0.001) different across the four data input types and approximately consistent with literature values after correcting for differences in spatial resolution (Triantafyllou et al., 2005).

3.2 ICA analysis: component detection

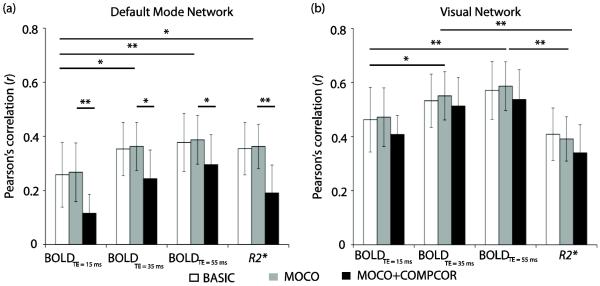
Figure 1 details the maximum correlation (r) that was measured between the DMN and VN template and the ICA component. The corresponding component was therefore, chosen as the desired network in the individual analysis. The DMN correlation range was r = 0.12 – 0.38 and VN correlation range was 0.35 – 0.58, with actual values depending on input data and post-processing method. For reference, the mean spatial correlation (r) of all other individual subject ICA components with the template ICA maps were 0.03±0.02, 0.04±0.03, 0.05±0.02, and 0.02±0.02 for BOLD_TE=15, BOLD_TE=35, BOLD_TE=55, and R2* data respectively. Note that the spatial correlations of the DMN and VN components decreased significantly in MOCO+COMPCOR data. DMN and VN were identified in the group analysis using the same approach. Group r values are shown in Table 2. These values summarize how the DMN and VN were selected from the 20-component ICA decomposition without rater bias.

Figure 1.

Spatial correlation (r) values for the independent component analysis (ICA)-derived component that correlated highest with the default mode network (DMN; a) and visual network (VN; b) templates obtained from the literature. Note that these networks were obtained from ICA analysis of single-TE BOLD data, and therefore it is not surprising that the R2* maps had a slightly lower correlation with the template maps than the BOLD data (*P<0.05, **P<0.01). By performing network selection in this manner, subjective selection of networks is reduced. Error bars represent standard deviation.

Table 2.

Component selection summary for group analysis. The table enumerates the Pearsons' correlation (r) values of the detected DMN and VN components when compared to the template maps.

	TE = 15 ms	TE = 35 ms	TE = 55 ms	R2*
Default mode network (DMN)
BASIC	0.62	0.66	0.66	0.71
MOCO	0.60	0.68	0.74	0.67
MOCO+COMPCOR	0.50	0.69	0.69	0.64
Visual network (VN)
BASIC	0.80	0.79	0.80	0.68
MOCO	0.79	0.79	0.76	0.67
MOCO+COMPCOR	0.86	0.86	0.85	0.68

Spatial (highest) correlation of ICA component with the template DMN and VN map

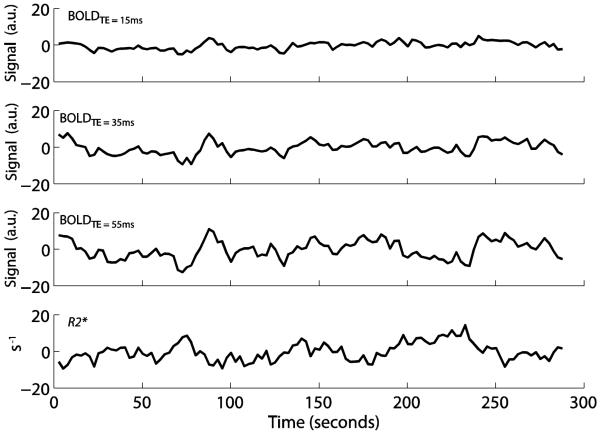
Figure 2 shows representative de-meaned time courses of all voxels in DMN for the different experimental inputs for a representative subject. The amplitude of fluctuations, measured as the standard deviation of the de-meaned time courses, increases significantly (P<0.01) with increasing TE (n=18; BOLD_TE=15 = 2.32±0.83 a.u., BOLD_TE=35 = 4.07±1.22 a.u., BOLD_TE=55 = 5.35±1.51 a.u.). Note that the R2* fluctuations (5.06±0.1.11s⁻¹) are opposite in direction relative BOLD signal, as expected. The correlations between the DMN time courses for BOLD_TE=15, BOLD_TE=35, BOLD_TE=55 with the R2* time course for this representative volunteer shown were −0.01, −0.35, and −0.55, respectively, demonstrating that the R2* data correlated most closely with the long TE data, and much more weakly with the short TE data. This finding was preserved when all subjects were considered. Correlation (n=18; mean ± std. deviation) of R2* with: BOLD_TE=15 = −0.10±0.23, BOLD_TE=35 = −0.23±0.21, BOLD_TE=55 = −0.36±0.21. Correlation values within BOLD acquisitions for all subjects: BOLD_TE=15 vs. BOLD_TE=35 = 0.85±0.07, BOLD_TE=15 vs. BOLD_TE=55 = 0.77±0.13, BOLD_TE=35 vs. BOLD_TE=55 = 0.93±0.08. The VN component showed a similar trend. Here, the average correlation of the R2* time course with BOLD_TE=15, BOLD_TE=35, and BOLD_TE=55 was −0.25±0.27, −0.42±0.23, and −0.50±0.21, respectively. Correlation values of the VN time courses within the BOLD acquisitions for all subjects were: BOLD_TE=15 vs. BOLD_TE=35 = 0.87±0.12, BOLD_TE=15 vs. BOLD_TE=55 = 0.79±0.15, BOLD_TE=35 vs. BOLD_TE=55 = 0.94±0.08. In both the DMN and VN, the correlation values between BOLD data at different TEs were significantly higher (P<0.001) than the correlation values between any single TE-BOLD time course and the R2* time course.

Figure 2.

De-meaned BOLD_TE=15, BOLD_TE=35, BOLD_TE=55 and R2* time courses in default mode network (DMN) for a representative subject. The amplitude of the baseline BOLD fluctuations increases with echo time (TE). The R2* time courses yield fluctuations that are opposite in magnitude from single-TE BOLD time courses, as expected.

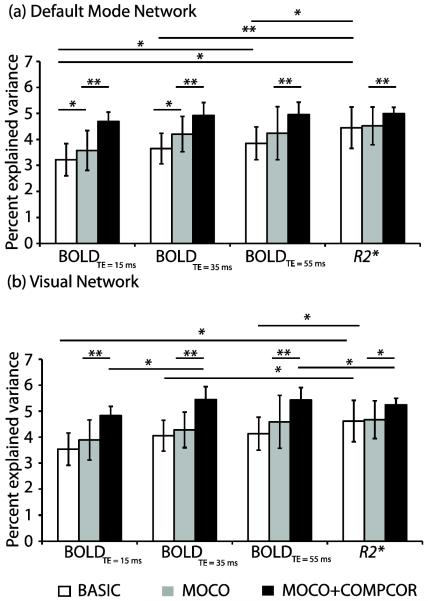
3.3 ICA analysis: percent explained variance

The percentages of variance, explained by the DMN components, were compared between the four data (i.e., BOLD_TE=15, BOLD_TE=35, BOLD_TE=55, and R2*) and for the three processing strategies (i.e., BASIC, MOCO, and MOCO+COMPCOR). Figure 3a shows that the percent explained variance for the DMN component was significantly higher for R2* (4.45±0.79) in the BASIC data than BOLD_TE=15 (3.22±0.62; P<0.01), BOLD_TE=35 (3.64±0.59; P<0.01), and BOLD_TE=55 (3.85±0.63; P<0.05). While percent explained variance in the single-TE BOLD MOCO data at 15 and 35 ms showed significant increases (P<0.05), it did not change significantly in MOCO data at TE = 55 or with R2*. Significant increases (P<0.01) were noted in the percent explained variance in all MOCO+COMPCOR data. No significant difference was detected in the percent explained variance between the four MOCO+COMPCOR data.

Figure 3.

Percent explained variance in the individual independent component analysis (ICA) for different experimental inputs and processing possibilities for (a) default mode network (DMN) and (b) visual network (VN). For minimally processed data, R2* maps provide the most explained variance, however in (MOCO+COMPCOR) data, there is less discrepancy in explained variance between data inputs, especially at intermediate and long TE. Error bars represent standard deviation. * P<0.05, **P<0.01

Group analysis revealed a greater percent explained variance for the DMN component using R2* data with BASIC (6.30) as well as MOCO (6.24) compared to BOLD_TE=15 (BASIC: 5.02, MOCO: 4.66), BOLD_TE=35 (BASIC: 5.50, MOCO: 5.58), and BOLD_TE=55 (BASIC: 5.42, MOCO: 5.70). Percent explained variance in the MOCO+COMPOR data was comparable across BOLD data at TE = 35 ms and 55 ms and R2*.

The percent explained variance of R2* in the VN component for individual subjects for BASIC was also significantly higher (P<0.01) compared to BOLD_TE=15, BOLD_TE=35, BOLD_TE=55ms (Figure 3b). While MOCO data showed a trend toward increased percent explained variance for the BOLD data, MOCO+COMPCOR data showed significant (P<0.01) increases in percent explained variance compared to BASIC and MOCO. The percent explained variance of the VN detected using R2* data was unaltered in MOCO but increased significantly (P<0.05) after physiological confound removal. VN group analysis reveals that MOCO and MOCO+COMPCOR components at TE = 55 ms contributed more (percent explained variance = 5.85 and 6.00, respectively) to the baseline signal compared to other single TE-data as well as R2* (Table 3).

Table 3.

Percent explained variances for default mode network (DMN) and visual network (VN) for group analysis using independent component analysis (ICA).

	TE = 15 ms	TE = 35 ms	TE = 55 ms	R2*
Percent explained variance in DMN
BASIC	5.02	5.50	5.42	6.30
MOCO	4.66	5.58	5.70	6.24
MOCO+COMPCOR	4.82	5.17	5.33	5.21
Percent explained variance in VN
BASIC	5.47	5.77	5.78	5.84
MOCO	5.58	5.93	5.85	5.49
MOCO+COMPCOR	5.66	5.82	6.00	5.45

In summary, these findings demonstrate that minimally processed R2* data provide more explained variance than minimally processed BOLD data acquired at a single TE. Furthermore, motion correction had no effect on percent explained variance in R2* data. Physiological noise removal in MOCO+COMPCOR data significantly increased the percent explained variance. This suggests that signal variations due to motion are minimized in the R2* fitting process, however physiological confounds remain.

3.4 ICA analysis: spatial features

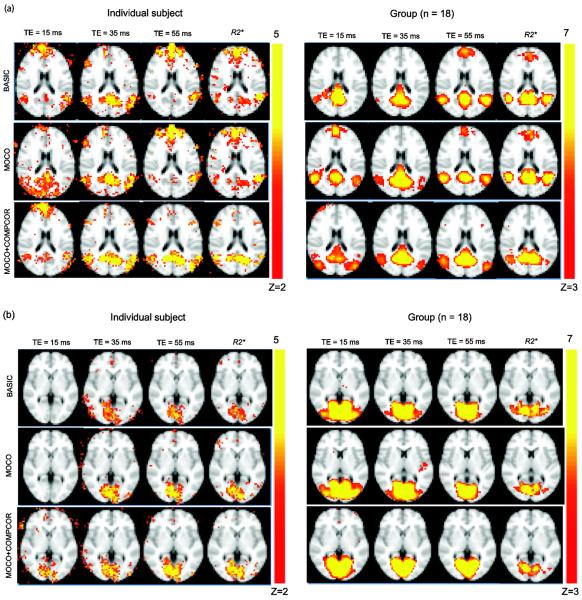
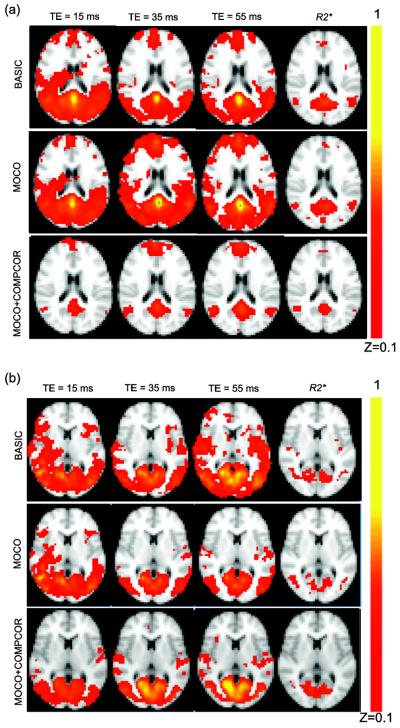
Figure 4a shows the DMN maps for a single subject and the group using BOLD_TE=15, BOLD_TE=35, BOLD_TE=55, and R2* with BASIC, MOCO, MOCO+COMPCOR data. Anterior DMN regions varied with processing strategy as well as TE (and R2*) as seen in the individual and group maps. These data provide evidence that experimental input as well as post-processing strategy influence spatial specificity of the detected network. Application of CompCor reduced the anterior DMN component in BOLD data TE = 55ms and R2* along the draining sagittal sinus in individual as well as group analysis. Similar to recent studies (Kim and Lee, 2011); the anterior DMN regions exhibited high variability compared to the posterior DMN regions and were not detected in the group analysis. No significant differences were observed between different acquisitions and processing strategies in the VN (Figure 4b). Similar to the observation regarding percent explained variance, motion correction had minimal effect on the R2* derived DMN and VN maps in individual data as well as group analysis.

Figure 4.

(a) Single-subject maps of the default mode network (DMN) using BOLD data acquired at TE = 15 ms, 35 ms, 55 ms and R2* with BASIC, MOCO and MOCO+COMPCOR processing strategies for a representative slice. Motion correction influences the R2* maps the least, as these confounds are partly reduced in the fitting procedure. However, the removal of physiological confounds influences the DMN maps in all data (b) VN map obtained with BOLD at TE = 15 ms, 35 ms, and 55 ms and R2* data with BASIC, MOCO, and MOCO+COMPCOR processing scenarios. The VN maps show less obvious differences across TEs for different processing strategies. *P<0.05, **P<0.01

3.5 Seed-voxel correlation analysis

Figure 5a shows the correlation maps in MNI space obtained using BOLD_TE=15, BOLD_TE=35, BOLD_TE=55, and R2* inputs using standard seed regions in the posterior cingulate. The correlation maps using BASIC and MOCO data show non-specific connectivity to other cortical gray matter regions, which reduces in the MOCO+COMPCOR data. The BOLD-derived VN showed similar non-specific connectivity to the cortical gray matter in the BASIC and MOCO data but not in the MOCO+COMPCOR data (Figure 5b). The R2* DMN and VN maps however show reduced effects of motion and physiological variations that increase non-specific correlation in the cortex, especially in gray matter and large vessels, regardless of processing strategy.

Figure 5.

(a) Average Fisher Z coefficient maps obtained from the Pearson's correlation, r in the default mode network (DMN) time course. Note that the R2* DMN maps were least altered for different processing strategy. BASIC BOLD data showed highest correlation to non-DMN gray matter regions, consistent with the most respiratory and cardiac noise contributions here. These non-specific spatial regions are reduced following nuisance reduction in MOCO+COMPCOR. (b) Fisher Z maps for VN demonstrate similar trends.

4. DISCUSSION

This work utilizes multi-echo BOLD fMRI to evaluate how baseline BOLD signals at different echo times (TEs) and the quantified R2* signals contribute to variability in functional connectivity patterns in two common functional networks: default mode network (DMN) and visual network (VN). The major findings are (i) quantitative R2* maps yield similar explained variance and spatial specificity to single TE BOLD maps in individual subjects at typically-used 3.0T echo times (TE = 30–55 ms), however DMN maps derived from BOLD data acquired at TE = 15 ms are more variable. (ii) R2* derived DMN and VN networks demonstrate greater explained variance relative to single-TE BOLD when only very basic processing is performed (i.e., no motion correction or physiological noise reduction). While motion correction (MOCO) did not affect R2* connectivity features substantially, percent explained variance of single-TE BOLD data increased when MOCO data was used. Physiological noise correction significantly altered DMN and VN maps for all four data, further increasing the explained variance. (iii) Seed-based detection of DMN and VN networks from R2* data were least affected by signal processing (MOCO or MOCO+COMPCOR) compared to BOLD data acquired at a single TE.

A log linear fit was used to evaluate R2* due to its lower computational costs, which are important to consider when evaluating such large data sets. It is well known that a linear fit to the log of the data may give biased results because of the Rician nature of noise in MRI data, particularly when SNR is low. However, the multi-echo data acquired in this study have relatively high SNR (SNR>>10) and therefore the noise is approximately Gaussian (Gudbjartsson and Patz, 1995). We simulated how different fitting procedures would influence the corresponding results, and for our SNR range found only a trace difference in accuracy or precision of linear vs. non-linear fitting for Gaussian or Rician noise. However, when computational time is not an issue, or rather when SNR is much lower, multi-exponential fitting procedures may be pursued. Acquisition of additional echoes may reduce temporal resolution beyond 3s, however with the ongoing development of multiplexing and compressed sensing, achieving multi-TE acquisitions with a temporal resolution of TR=2s or below should be feasible in the near future (Feinberg and Yacoub, 2012; Smith et al., 2012).

Global signal contributions, likely arising from systematic drifts show minimal effect on R2* data as evinced by the small effect that motion correction had on it. Since R2* values are derived by fitting the multi-echo data following a single excitation, where signal drifts are primarily synchronous, it is likely that these contributions are inherently reduced in the fitting procedure. Aliased physiological signals however will not be completely resolved in the R2* time course. Indeed CompCor significantly increased the percent explained variance in all acquisition strategies, including R2*. The R2* fitting for CSF may be suboptimal due to the long T2* of CSF and the relative small echo time range utilized here. We therefore additionally performed CompCor with only the WM mask as the anatomical ROIs. For the ICA analysis, percent explained variance increased slightly, although non-significantly for individual and group analysis. Seed-based correlation maps were also largely unchanged.

The number of ICA components was restricted to 20, which is generally accepted as a reasonable number to identify the most common functional networks without decomposing these networks extensively (Smith et al., 2009). However, we also investigated how our results would change if the dimensionality was automatically estimated from MELODIC. In this case, the R2* approach produced 25±6 components as opposed to BOLD data which produced 48±4, 43±5, 39±5 components at TE = 15 ms, 35 ms, and 55 ms respectively for individual subject analysis and 32, 32, 31, and 16 components from BOLD data at TE = 15 ms, 35 ms, and 55 ms, and R2* for group analysis. The reduced number of components in R2* may be due to the reduced signal variations from motion and physiological confounds since the network maps were not statistically different with inclusion of these correction processes. Thus R2* is likely to have reduced splitting of RSNs. Consequently, the percent explained variance with such an automatic component detection algorithm was significantly (P<0.01) higher for R2* (3.75±0.83) than BOLD at TE = 15 ms (1.82±0.38), TE = 35 ms (2.18±0.52), and TE = 55 ms (2.42±0.59).

Multiple studies have investigated the noise characteristics in BOLD fMRI at different TEs and field strengths. For instance, Triantyfallou et al. (Triantafyllou et al., 2005), have shown that while BOLD fMRI contrast is preferred at TE ~ tissue T2*, BOLD-like physiological noise also peaks at a similar TE range at 3.0T and non-BOLD physiological noise increases with TE. Much of this BOLD-like physiological noise is the source of spontaneous BOLD connectivity analysis. The modified BOLD model proposed by Kruger et al. (Kruger and Glover, 2001) suggests maximum task-related activation at TE = tissue T2* due to reduced contributions of non-BOLD like noise (comprising of cardiac, respiratory fluctuations, and scanner related noises) and reduced sensitivity to draining venous blood water which has short T2* relative to tissue water at intermediate (e.g., 3.0T) to high (e.g., 7.0T) field strengths. Increased percent explained variance in the MOCO+COMPCOR DMN and VN component at TE = 55 ms compared to BASIC and MOCO is consistent with reduction of such non-BOLD physiological noise. This may also improve specificity of resting state networks at long TEs. Functional connectivity analysis is commonly not performed at such long TE, likely owing to SNR concerns and additional susceptibility-induced artifacts during single-shot EPI readouts. However, with improved field homogeneity schemes, readouts, and multi-array coils, long TE connectivity analyses may be warranted.

Finally, it is important to note that although the DMN and VN templates enable network identification without rater bias, (i) the template is based on ICA analysis of single-TE BOLD measurements and (ii) R2* networks show spatial differences as noted in this study (Figure 4) compared to single-TE BOLD. While the template provided an excellent method for identifying the network components objectively, the lower correlations with R2* data (relative to single-TE BOLD data) are inherently biased. These templates were created at a TR = 0.8 s, which although short is not enough to eliminate aliased physiological noise. No physiological confound removal was performed when the templates were generated and could likely be the reason for a reduced spatial correlation of the DMN/VN components with the template when physiological confounds were regressed.

Multi-echo fMRI acquisitions have been applied to characterize how different intravascular weightings influence spontaneous and evoked BOLD signals (Gati et al., 1997; Poser and Norris, 2009; Posse et al., 1999; Speck and Hennig, 1998; Barth et al., 1999). Barth et al. (Barth et al., 1999) have characterized the effect of vessels on BOLD activation and Poser et al. (Poser and Norris, 2009) derived a mixed multi-echo metric with a higher contrast to noise ratio for detection of activated brain regions at high field strengths. Additional work (Kundu et al., 2012) has applied multi-echo BOLD approaches for denoising purposes, which is consistent with different regions exhibiting different function-related relaxivity (ΔR2*) effects that depend on local vasculature (Speck and Hennig, 1998; Van Den Heuvel and Hulshoff Pol, 2010) and corresponding physiological nuisance parameters. Here we have investigated the effect of multi-echo acquisitions in conjunction with various degrees of processing on detection of resting state networks.

5. CONCLUSION

This work demonstrates how common functional connectivity analysis procedures yield different results based on experimental inputs. We have shown that baseline R2* fluctuations show several advantages relative to single-TE BOLD data for identification of the default mode network and the visual network with minimal post–processing. Motion-corrected has minimal effect on R2* data. With physiological confound removal R2* provides similar connectivity patterns to those derived from single-TE BOLD data. The over-reaching conclusion from this work is that both spatial specificity and explained variance of BOLD functional connectivity analysis varies with post-processing pipeline (i.e., motion correction and physiological noise reduction) and experimental input (i.e., echo time) and this should be considered when interpreting results between experiments.

Highlights

1. Sensitivity and synchrony of BOLD connectivity metrics vary with echo time (TE)

2. R2* maps are less susceptible to motion artifacts compared to single-TE BOLD maps.

3. Seed-based R2* networks were least affected by motion and physiological noise correction.