Comparison of Structure Determination Methods for Intrinsically Disordered Amyloid-β Peptides

Abstract

Intrinsically disordered proteins (IDPs) represent a new frontier in structural biology since the primary characteristic of IDPs is that structures need to be characterized as diverse ensembles of conformational substates. We compare two general but very different ways of combining NMR spectroscopy with theoretical methods to derive structural ensembles for the disease IDPs amyloid-β 1–40 and amyloid-β 1–42, which are associated with Alzheimer’s Disease. We analyze the performance of de novo molecular dynamics and knowledge-based approaches for generating structural ensembles by assessing their ability to reproduce a range of NMR experimental observables. In addition to the comparison of computational methods, we also evaluate the relative value of different types of NMR data for refining or validating the IDP structural ensembles for these important disease peptides.

Introduction

Experimental approaches such as X-ray and electron crystallography and microscopy have traditionally excelled at determining the structure of single folded proteins^1,2 and large protein complexes.³ However, intrinsically disordered proteins (IDPs) are not amenable to these static structural determination methods.⁴ IDPs represent a new frontier in structural biology in that the IDP structure must be characterized as a diverse ensemble of interconverting conformational substates, as opposed to a single dominant 3D structure.⁵ This necessitates an adjustment in the core methodology of protein structure determination for this class of protein.

The experimental identification of proteins with global intrinsic disorder can be performed using various spectroscopic techniques including circular dichroism (CD), NMR, infrared spectroscopy (IR), UV spectroscopy, and fluorescence spectroscopy.^6,7 CD and IR report on the amount of secondary structure, while lack of chemical shift dispersion in NMR spectra is a good indication of high flexibility. Hydrodynamic techniques such as SAXS, gel filtration, and dynamic light scattering can also aid in IDP identification as they report on the radius of the protein, which is often larger for an IDP or denatured protein than a folded protein of the same mass. Lack of a cooperative folding transition, solubility at high temperatures, and proteolytic sensitivity are also attributes of IDPs that are useful in forming a complete picture of a certain protein’s level of disorder. A subset of these techniques is generally employed to determine that a protein is an IDP.

Recently increased importance has been placed on characterizing the conformational substates within IDP ensembles since they each may have distinct functional roles⁷⁻¹³ or could lead to hypotheses about disease origin.¹⁴ In order to achieve both better ensemble classification and a detailed description of conformational substates, we must critically assess how we build these complex structural ensembles from experimental data and theoretical models. NMR is the experimental tool of choice for characterizing the solution structure and dynamics of biological molecules since it reports on the native distribution of conformations in an aqueous environment, and more importantly is a dynamical experiment that probes the nanosecond to millisecond time scales of conformational motion.^4,15,16 Observables from these experiments include chemical shifts, which are characteristic of functional groups and their surrounding environment, and spin–spin couplings (J-couplings), which independently report on backbone dihedral angles. In addition, through-space dipole–dipole interactions give rise to the nuclear Overhauser effect (NOE) that reports on tertiary structure contacts, and more recently, residual dipolar couplings (RDCs) have been used to describe the relative orientation of spatially separated regions of a protein.¹⁷⁻²⁰ Paramagnetic relaxation enhancements (PREs), which can produce longer distance restraints than NOEs have also been used in the context of IDPs;²¹⁻²⁴ however, this measurement requires chemical modification of the protein with a nitroxide spin label or an amino-terminal copper binding motif, which sometimes requires sequence modification to attach the probe, and which may perturb the monomeric IDP conformations.^25,26

IDPs typically convert between conformations faster than the ca. nanoseconds–milliseconds time scale of the NMR experiment, leading to an averaging of the NMR observables across structural subpopulations. This uniform average hinders the structural characterization of all the conformational substates, and can even obscure the overall ensemble classification, as we will see for the amyloid peptides in this study. Building the connection between the averaged NMR observables and the complete IDP structural ensemble therefore depends critically on computational models.²⁷ The goal of the computational model is to provide a properly weighted set of the diverse subpopulations of the IDP most consistent with the NMR observables and perhaps other experimental measures such as circular dichrosim,²⁸ small-angle X-ray scattering,^29,30 or PREs.^23,31 Thus, multiple types of NMR or other experimental observables are necessary for validation of the computational model.^16,30

Currently there are two primary but very different computational approaches to building an IDP structural ensemble, which can be loosely contrasted as first principle or de novo molecular dynamics (MD) methods versus knowledge-based approaches. The de novo approach implements MD simulations based on the theoretical foundations of statistical mechanical sampling and model-derived potential energy force fields. De novo MD generates a structural ensemble that is representative of given thermodynamic conditions according to the force field employed, i.e., a Boltzmann weighted ensemble of conformational subpopulations and their time scales, independent of experimental input. The MD trajectories also allow calculation of the time correlation functions that underlie the NMR experiment. The complementary use of MD and NMR data to determine structure and dynamics of folded and unfolded proteins has been a highly active area over the last two decades,^32,33 particularly for relaxation measurements that require a dynamical interpretation of the NMR data at the picosecond and nanosecond time scales.³⁴ For the de novo MD method, multiple NMR or other experimental data are necessary to validate the MD ensemble through direct back-calculation of observables, many of which depend on the time scales of motion, in order to directly compare to the experiment. Once validated, MD simulations provide a prediction of the complete IDP structural ensemble, allowing overall classification as well as the study of individual conformational substates, which can be analyzed with some confidence.

In contrast, we define knowledge-based approaches as those that use experimental NMR information directly to derive the structural ensemble. Such methods are the foundation of NMR structure determination of folded proteins using experimentally derived conformational constraints based on chemical shifts, J-couplings, and NOE data embodied in software packages such as CANDID,³⁵ CYANA,³⁶ and X-Plor-NIH.^37,38 While MD is often used to generate atomistic predictions independent of NMR experimental input, as in our de novo method, a number of researchers have advanced the combination of applying knowledge from NMR to restrain the MD ensemble.^{22,24,39−41} For example, MD simulations have been combined with RDC restraint data for folded proteins⁴⁰ that then allows for the analysis of other features of the ensemble, such as conformational fluctuations. NMR restrained MD has also been applied to IDPs such as α-synuclein, a disease protein indicted in Parkinson’s disease. This study incorporated distance restraints derived from PRE experiments in order to guide the MD so that the protein’s radius of gyration distribution is in good agreement with the experimental value.³⁹

Other knowledge-based approaches for IDPs forego MD simulations altogether and instead use an extensive set of statistical coil conformations;^16,42 this starting pool, which can be generated using a variety of heuristics, can be thought of as a basis set of structures. Subsequently, the starting pool of structures is then culled for the subset of conformations that are in best agreement with experimental data to create the IDP ensemble. In the energy-minima mapping and weighting (EMW) method, Stultz and co-workers used end-to-end distance restraints to develop a pool of conformations with varying radii of gyration; they then selected, via Monte Carlo, a weighted ensemble of 15 structures to optimize the agreement with experimental ¹³C and ¹⁵N chemical shifts and J-couplings.^43,44 Blackledge and co-workers have developed the program Flexible-Meccano to create a pool of structures based on random coil backbone dihedral angles, on which they employ a genetic search algorithm in their ASTEROIDS software program to select structures that together best match experimental chemical shifts, PREs, or RDCs.^16,45,46

The ENSEMBLE method, developed by Forman-Kay and co-workers, typically defines the starting pool of IDP conformational states as an ensemble of extended or random coil states generated using TraDES, with an option for biasing the secondary structure of the ensemble at certain places in the sequence that are known to be partially structured.^23,29,42,47 Structures are selected from this pool using a Monte Carlo selection algorithm with an energy-weighting scheme for each type of experimental input. The ENSEMBLE program includes modules for several different experimental data types including chemical shifts, RDCs, PREs, J-couplings, and contact distances derived from NOEs, and is a user-friendly and publically available software package.⁴² Although there are some specific differences, ENSEMBLE is largely representative of the knowledge-based approaches and is qualitatively equivalent to the combination of Flexible-Meccano and ASTEROIDS software.^16,45,46 It is important to note that such techniques largely ignore the inherent dynamical information of certain types of the NMR data that can be important for discriminating between different IDP structural ensembles.

The primary objective of this work is to compare the de novo and knowledge-based approaches for deriving IDP structural ensembles in context of the intrinsically disordered Alzheimer’s disease peptides amyloid-β 1–40 (Aβ40) and amyloid-β 1–42 (Aβ42). We implement the ENSEMBLE knowledge-based method by building an ensemble from a pool of statistical coil structures, and compare this knowledge-based ensemble to MD generated ensembles, which are qualitatively different in that they are comprised of mostly cooperative secondary structure and tertiary contacts. This comparison also exposes the relative utility of different types of NMR data for refining or validating the IDP computational ensemble. We find that chemical shifts and J-coupling constants are not particularly useful for distinguishing between qualitatively different IDP ensembles of the amyloid-β peptides. Finally we show that the combination of de novo MD methods that provide Boltzmann weighted samples with the ability to measure time correlation functions, and knowledge-based methods for conformation selection, provides the best agreement with the NMR data.

Methods

Back-Calculation of NMR Observables

In order to evaluate the alternative ensembles produced by knowledge-based and de novo approaches, we need a method of calculating the chemical shifts, J-coupling constants, RDCs, and ¹H–¹H NOEs as averages over the entire computationally generated structural ensemble for comparison with experimental values.⁴⁸ General purpose chemical shift calculators such as SHIFTX⁴⁹ and SHIFTS⁵⁰ describe the isotropic shielding of the applied magnetic field for the given atom, a quantity that depends sensitively on the local electronic structure environment.⁴⁹⁻⁵¹ Even for folded proteins with a dominant native conformer, each atom type can exist in many different local environments, and for disordered peptides and proteins the ensemble average reflects an even more diverse set of chemical environments. This makes an accurate calculation of chemical shifts quite a challenge for IDPs. Whether one uses SHIFTX (used in ENSEMBLE) or SHIFTS to calculate chemical shifts, the results generated by the two programs are consistent when applied to amyloid-β and averaged over the structural ensembles.^14,48,52 We report results using SHIFTX in this work.

To calculate the scalar coupling constants, ³J_HNH^α, we used the Karplus equation⁵³

1

where ϕ indicates the protein backbone dihedral angle, with coefficients A = 6.51, B = −1.76, and C = 1.60 corresponding to the parameter set by Vuister and Bax.⁵⁴ However, Sgourakis and co-workers^55,56 and our own previous work on Aβ42^14,48 found that the MD results exhibited a systematic shift of calculated J-couplings with the experimental scalar couplings of Wang and co-workers. We delved into this issue more deeply and derived an analytical correction, described in recent work,¹⁴ that must be applied to the original experimental J-coupling data from Wang and co-workers.⁵⁷ In particular, it has been corrected for a missing relaxation that makes scalar couplings determined from the H_NH_α 3D experiment consistently lower than those from COSY splittings by a small amount⁵⁴ (from ∼1–5%). The J-coupling values are also averaged over all structures in the ensemble as in,^14,48,52 and then the calculations can be compared to the corrected experimental ³J_HNH^α values for both amyloid peptides.

The standard method in the field for calculation of RDCs is the PALES⁵⁸ program, which we have used previously for the Aβ40 and Aβ42 MD ensembles.^14,48,52 The program computes the RDC by using steric properties of the molecule to generate a global alignment orientation. Then, the angle between the backbone amide bond vectors and the external magnetic field is used to calculate the RDC for each conformation, and the RDCs are averaged over all conformations of a given ensemble. The ENSEMBLE program by contrast, evaluates RDCs using a local alignment program developed in the Forman-Kay lab, where 15 residue segments along the protein are aligned separately over the ensemble of structures.¹⁸ The local RDCs (L-RDCs) are also averaged over all conformations of a given ensemble. This local alignment has lower computational cost and has been shown to give similar results to PALES, hence L-RDCs, rather than RDCs generated from a global alignment algorithm, are optimized in the standard implementation of the ENSEMBLE approach. Similarly, the ASTEROIDS program by default employs a local alignment tensor to optimize ensemble agreement with experimental RDC data.⁵⁹ We also note that the PALES alignment and RDC calculation were developed for folded proteins, and their application to IDPs assumes individual IDP conformations behave similarly to folded proteins during the RDC experiment, which may not be the case for IDPs such as amyloid-β.

We also evaluate the ¹H–¹H NOESY (or ROESY) spectra as we have described in previous studies^14,48,52 by calculating the intensity of the NOE cross-peaks

2

where X and Λ are the eigenvectors and eigenvalues of the full relaxation matrix, composed of diagonal elements

3a

and off-diagonal elements

3b

that are comprised of appropriate combinations of the spectral density functions

4

evaluated at the relevant Larmor frequencies, ω, and where K is given by

5

γ_H is the gyromagnetic ratio of ¹H, μ₀ is the permeability of free space, and ℏ is Planck’s constant. r_eff is the distance between the hydrogen atoms raised to −6 power, averaged over all structures in the ensemble and then raised to the −1/6 power to convert back to units of distance. These calculations account for all hydrogen atoms explicitly (including all methyl or methylene groups) and hence r_eff and correlation functions for every pair of hydrogen atoms are evaluated.^14,48,52 The spectral density function for each atom pair is calculated as the Fourier transform of the correlation function for the pair vector and water proton coordinates are ignored, as is the standard assumption in the NMR experiment.

Finally we calculate ¹H–¹⁵N NOEs as we did in refs (14 and 48) by evaluating the steady state NOE enhancement factor of the ¹⁵N spin by the ¹H NOE according to

6

where γ_H and γ_N are the gyromagnetic ratios of ¹H and ¹⁵N, respectively. The ¹H–¹⁵N cross-relaxation rate constant is given by

7

and the ¹⁵N self-relaxation by

8

In this case, J_HN(ω) is the spectral density function for the ¹H–¹⁵N covalently bonded pair.

Note that the homonuclear and heteronuclear NOE calculations require correlation time information about the vector between each pair of atoms given by τ in eq 4. This dynamic information is naturally supplied by the de novo MD method, which allows direct measurement of the autocorrelation of the interatomic vector over the time of the simulation. However, dynamics are not considered in the generation of ensembles that are used in the knowledge-based approach. This is an inherent limitation of ensembles generated from a static perspective only, which we discuss further below.

Results

To determine an IDP’s level of disorder, we first generate several alternative ensembles, compare these ensembles to the available NMR data, and select the best validated ensemble. We consider the creation of three qualitatively different conformational ensembles that are typically used in the knowledge-based approaches^16,42,45,46 for the Aβ40 and Aβ42 peptides.

The common null hypothesis is that the disordered peptides can be well represented by a random coil (RC) ensemble. The second type of statistical coil (Pred-SS) ensemble is also random, but incorporates bioinformatics-based knowledge about what secondary structure category is more likely for a given residue in the amino acid sequence. In this case, the random ensemble is biased to contain a statistical probability of predicted secondary structure on a per residue basis, but no cooperative secondary structure such as α-helices, β-hairpins, or β-sheets are generated from the random secondary structure assignments. Computational methods such as TraDes and Flexible-Meccano are used to generate these type of random or statistical coil ensembles.^16,42 Finally, a fully knowledge-based approach is considered, which culls the RC or, in this case, Pred-SS ensembles to derive a subset of conformations that best agrees with the NMR data (Pred-SS-ENS). The ENSEMBLE software package provides a working example of the knowledge-based approach that performs this biased selection and which has been successfully applied to a range of IDPs. Each of the above three ensembles can then be compared against the ensembles generated by de novo MD for both of the IDPs Aβ40 and Aβ42. Details of the de novo MD approach applied to amyloid-β can be found in other publications.^14,48,52 We also consider an additional fifth ensemble (MD-ENS) that combines the knowledge-based and de novo MD approaches, by using ENSEMBLE to select structures from the de novo MD starting pool, and which is described in our recent study.¹⁴

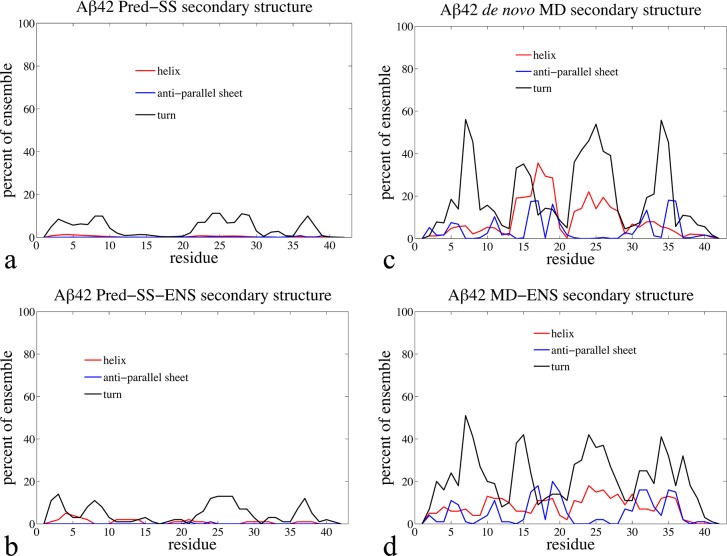
Table 1 shows the average radius of gyration (Rg) values for each type of ensemble. We see that the order from most extended to most compact proceeds as Pred-SS > RC > Pred-SS-ENS > MD ∼ MD-ENS, and thus the alternative ensembles span a range of IDP classifications by the ⟨Rg⟩ measure.¹⁴ Figure 1 provides the propensities for the Pred-SS, Pred-SS-ENS, de novo MD, and MD-ENS ensembles to form turns, antiparallel β-strands, or helical structure by residue for Aβ42. We do not show the secondary structure profiles for the RC ensemble since it is similar to the Pred-SS ensemble (see the Supporting Information).

Table 1. Comparison between Random Coil (RC), Predicted Secondary Structure (Pred-SS), de novo MD (MD), and ENSEMBLE Optimized Pred-SS-ENS and MD-ENS Ensembles^a.

Aβ40 peptide	average property
ensemble type	Rg (Å)	χδ2 (Hα)	χδ2 (HN)	χδ2 (Cα)	χδ2 (Cβ)	3JHNHα
RC	16.9 ± 3.2	0.20	0.13	0.29	0.34	0.80 (1.20)
Pred-SS	19.3 ± 3.6	0.45	0.10	0.67	0.49	1.09 (2.23)
Pred-SS-ENS	15.6 ± 3.3	0.41	0.11	0.52	0.45	0.88 (1.46)
MD	14.7 ± 4.8	0.58	0.36	0.69	0.70	0.99 (1.82)
MD-ENS	15.0 ± 4.1	0.30	0.34	0.46	0.36	0.62 (0.72)

Aβ42 peptide	average property
ensemble type	Rg (Å)	χδ2 (Hα)	χδ2 (HN)	χδ2 (Cα)	χδ2 (Cβ)	3JHNHα
RC	17.3 ± 3.3	0.22	0.15	0.41	0.25	0.49 (0.46)
Pred-SS	19.9 ± 3.8	0.49	0.10	1.06	0.38	0.85 (1.34)
Pres-SS-ENS	16.2 ± 3.6	0.40	0.12	0.71	0.29	0.67 (0.85)
MD	13.1 ± 4.3	0.54	0.48	0.98	0.52	0.99 (1.83)
MD-ENS	13.1 ± 2.8	0.33	0.37	0.51	0.34	0.60 (0.67)

^aFor the radius of gyration (Rg) values, we report both the ensemble average and RMSD. For chemical shifts, we report χ² that measures agreement between the computational ensembles and the experimentally measured chemical shifts: χ² < 1 indicates no disagreement with experiment within SHIFTX calculator error. We also report the ³J_HNH^α RMSD (χ²). Some data reproduced from ref (14).

Figure 1.

Percentage of Aβ42 simulated ensemble in different types of secondary structure by residue for (a) the Pred-SS, (b) Pred-SS-ENS, (c) de novo MD, and (d) MD-ENS ensembles. The red line represents helix, the blue line for antiparallel sheet, and the black line for β-turns. We note that the blue line represents only antiparallel sheet structure (the most common) and not all sheets.

This plot emphasizes that the MD-based ensembles are qualitatively different from the RC or Pred-SS ensembles, in that the Aβ40 and Aβ42 peptides samples some type of structured conformations in ∼99% of the MD ensemble, including complex βstrand formation.^14,48 From this, we conclude that the radius of gyration trends stem from the much larger propensity for the MD ensembles to form cooperative secondary structure and collapsed tertiary contacts, as opposed to the random or knowledge-based ensembles that do not generate contiguous blocks of secondary structure, and hence are more extended on average. Although the secondary structure content of the MD-ENS ensemble resembles that of the MD ensemble, Figure 1 shows that there is some variation in the percentages with which certain residues adopt different types of secondary structure.¹⁴

For analysis of Aβ40 and Aβ42 IDPs considered here, we have utilized a wide range of previously published NMR data including chemical shifts from the Zagorski group⁶⁰ as well as J-coupling constants, RDCs, and heteronuclear ¹H–¹⁵N NOEs for backbone amides from Wang and co-workers.^57,61,62 Our group has collected ¹H chemical shifts and NOESY ¹H–¹H homonuclear spectra for the full length Aβ40 and Aβ42 peptides as reported elsewhere.^14,48 The data for the longer peptides were processed as described in ref (48) in a similar approach to that used for the Aβ21–30 fragment.⁵²

First we consider the chemical shift data, for which we note that the calculated chemical shifts have an uncertainty that is independent of the quality or type of structural ensemble, and results from approximations of the SHIFTX⁴⁹ or SHIFTS⁵⁰ calculators themselves. Other research groups have reported the uncertainty, σ² (ppm), for these calculators, with the value depending on the atom type and its bonding chemistry.^49,50 Therefore the best way validate the various IDP ensembles with chemical shift data is to calculate the difference between the experimental chemical shift and the shift calculated from each of the structural ensembles, normalizing it by the calculator uncertainty, to generate χ_δ² values

9

Reported uncertainties (root mean squared difference, RMSD, from experiment) for the SHIFTX calculator⁴⁹ are σ = 0.23 ppm for H_α, σ = 0.49 ppm for H_N, σ = 0.98 ppm for C_α, and σ = 1.10 ppm for Cβ. Any dominant error due to the underlying structural ensemble would then correspond to values of χ_δ² > 1.

Table 1 displays the χ_δ² agreement between experimentally measured proton⁴⁸ and carbon⁶⁰ chemical shifts with those generated from each candidate ensemble for both Aβ40 and Aβ42.^14,48,52 Experimental chemical shift data reported for the monomeric Aβ40 and Aβ42 peptides do not differ greatly from random coil values, and therefore the RC ensemble falls within χ_δ² uncertainty.^14,48 Since the Pred-SS ensemble shows almost no DSSP defined secondary structure (Figure 1a), it remains largely equivalent to the RC ensemble as deduced by chemical shifts. The de novo MD structural ensemble is also in good agreement with the chemical shift data;^14,48 however, ∼99% of the MD generated Aβ conformations contain one or more elements of cooperative secondary structure somewhere along the peptide sequence (Figure 1b). The reason that the MD ensemble is also in good agreement with the experimental chemical shifts is that averaging over a large ensemble of cooperatively formed secondary structure and tertiary contacts yields average chemical shifts that are consistent with random coil values.^14,48 For example, averaging the chemical shifts of all folded proteins in the PDB results in averages very similar to random coil values.^48,63 We have found that the ENSEMBLE optimization of the Pred-SS and MD starting pools improves the χ_δ² values, but all are within the calculator uncertainty. Not surprisingly, if the knowledge-based ENSEMBLE approach were biased by chemical shift data alone, they would show little deviation from their starting “soup”, and the structural interpretation would be highly dependent on the starting ensemble. For this reason we conclude that NMR chemical shifts alone do not provide any qualitative discrimination between the alternative ensembles, at least not for the Aβ40 and Aβ42 disease IDPs.^14,48 It may still be useful to apply chemical shift constraints in combination with other experimental observables to optimize an IDP ensemble, as we have done when generating the MD-ENS ensemble. In this context the chemical shift constraints might provide a ‘sanity check’ against ensembles that fit other observables, such as NOEs, but lead to unphysical chemical shift values.

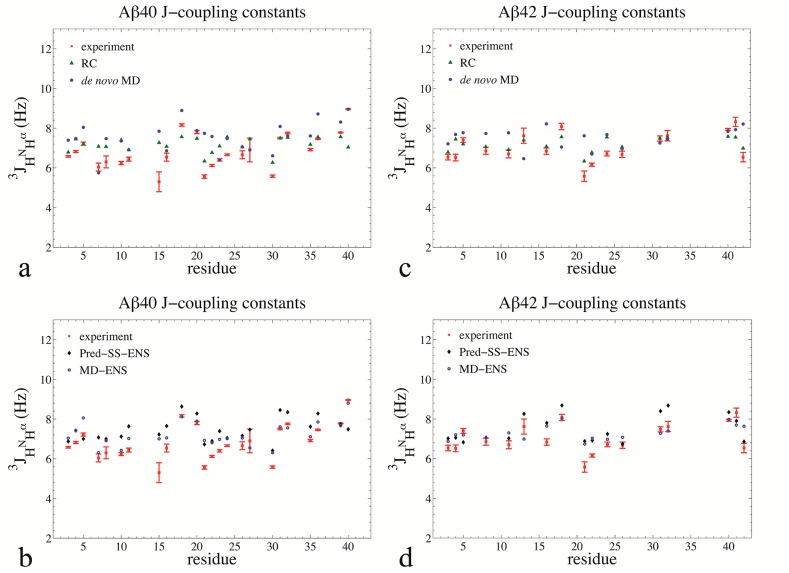
Similarly, J-couplings alone also do not discriminate between random coil IDPs and those that are more structured with cooperative secondary structure and tertiary structure contacts. Figure 2 illustrates this by plotting the agreement between experimentally measured ³J(H_N,H_α),^55,57 and those calculated from the RC, Pred-SS, Pred-SS-ENS, de novo MD, and MD-ENS ensembles for Aβ40 and Aβ4. Table 1 shows that all ensembles yield an RMSD across all residues of 0.60–1.09 Hz, and also reports

10

with σ_J = 0.73 Hz. J-couplings report on the backbone ϕ dihedral angle, and therefore could in principle distinguish between an unstructured peptide and a peptide with a defined secondary structure; however, in the case of the disease IDP Aβ, the presence of diverse secondary structure in the MD ensemble is not apparent from the calculated J-couplings. We believe that this stems from the fact that good agreement with scalar coupling data for IDPs can largely be predicted by sampling over the allowed regions of residue-specific Ramachandran plots without needing to assume any structure adopted by the full length sequence. Thus J-couplings also do not provide an experimental measure for discriminating among qualitatively different structural ensembles for the amyloid peptides.

Figure 2.

J-coupling constants for backbone amides for Aβ40 and Aβ42. (a) Aβ40 experimental J-coupling constants (red squares) compared to RC (green triangles) and de novo MD (solid blue circles). (b) Aβ40 experimental J-coupling constants (red squares) compared to Pred-SS-ENS (black diamonds) and MD-ENS (blue circles). (c) Aβ42 experimental, RC, and de novo MD J-coupling constants. (d) Aβ42 experimental, Pred-SS-ENS, and MD-ENS J-coupling constants. The experimental data are from Yan et al.⁵⁷ has been corrected to account for T_1sel relaxation and bring J-couplings determined from a H_NH_α 3D experiment to be consistent with those from COSY splittings.⁶⁰

Table 2 provides the assessment of the five alternative ensembles for Aβ40 and Aβ42 using RDC values evaluated residue by residue using the PALES program⁵⁸ and L-RDCs based on local alignments.¹⁸ While the RC and Pred-SS ensembles yield lower RMSD values, 1.3–1.5 Hz, they are marginally better than the de novo MD RMSD of 2.2 Hz.^14,48 This is in part due to the fact that experimental RDC uncertainties for IDPs are larger (∼0.9 Hz for Aβ40 and ∼0.5 Hz for Aβ42) than the uncertainty observed for folded proteins of ∼0.1 Hz.⁶⁴ In addition, there are large uncertainties in the accuracy of RDC calculators using programs such as PALES.⁵⁸ In fact, the reported RMSD of the PALES calculator for folded proteins is ∼2.0 Hz, on the same order as the RMSD for the de novo MD ensemble. While the ENSEMBLE method does significantly lower the RMSD for L-RDCs for the Pred-SS-ENS and MD-ENS ensembles, the corresponding RMSD based on the global alignment using PALES is marginally better than the Pred-SS and de novo MD starting pools.^14,48 Hence for this particular application on disordered amyloid peptides, we have found that RDCs are not a particularly good experimental metric for differentiating among the different ensembles, and substantial disagreement between RDCs based on local and global alignments are observed.

Table 2. Comparison between Random Coil (RC), Predicted Secondary Structure (Pred-SS), de novo MD (MD), and ENSEMBLE Optimized Pred-SS-ENS, and MD-ENS Ensembles^a.

Aβ40 peptide	average property
ensemble type	RDC-PALES (Hz)	RDC-Local (Hz)	H2O NOEs	D2O NOEs
RC	1.49	1.56	11.75 (0.47)	4.61 (0.54)
Pred-SS	1.54	1.36	4.68 (0.50)	3.75 (0.54)
Pres-SS-ENS	1.85	0.48	1.85 (0.68)	3.54 (0.52)
MD	2.22	1.88	1.15 (0.74)	3.22 (0.55)
MD-ENS	1.69	0.18	1.22 (0.70)	3.66 (0.51)

Aβ42 peptide	average property
ensemble type	RDC-PALES (Hz)	RDC-Local (Hz)	H2O NOEs	D2O NOEs
RC	1.35	1.42	7.25 (0.38)	3.77 (0.44)
Pred-SS	1.37	1.27	3.28 (0.52)	1.26 (0.67)
Pres-SS-ENS	1.17	0.42	1.81 (0.59)	0.75 (0.76)
MD	2.25	2.14	1.25 (0.67)	0.58 (0.80)
MD-ENS	2.13	0.33	1.51 (0.62)	0.73 (0.76)

^aWe report RMSDs for the RDC calculator PALES and L-RDCs evaluated with ENSEMBLE using local alignments. The NOEs are back-calculated from the structural ensembles as described in Section 4. We evaluate the RMSD normalized by the largest NOE intensity, RMSDN and (correlation coefficient, r) with the H₂O and D₂O experiments. Some data reproduced from ref (14).

Finally, we consider the performance of the different ensemble methods for reproducing ¹H–¹H homonuclear NOE cross-peaks. We have presented the NOE data collection for the Aβ42 peptide in which ∼700 cross-peaks are observed in the NOE spectra, but only ∼200 can be uniquely assigned from experimental information alone.^14,48 The remaining cross-peaks do not have a clear independent assignment (and in fact require a computational model to interpret them^14,48). Therefore we have only compared the different methods against the NOE cross-peaks that can be assigned by experiment alone. We note that quantitatively reproducing NOE intensities is a very high bar since peak volumes are extremely sensitive to r^–6 distance averaging, that also involve an appropriate time scale that is heterogeneous across proton pairs. Geometric imperfections in the conformational ensemble where contact differences differ by a factor of 2^1/6 (difference between 1 Å and 1.12 Å) will double the corresponding intensity value, thereby driving up the RMSD error for all ensembles.^14,48,52 Large absolute NOE intensities especially tend to dominate the RMSD error, and therefore we have mitigated this effect by normalizing the RMSD (RMSDN) by the experimental intensity for each NOE as in ref (14).

Table 2 shows that the predicted set of ¹H–¹H NOEs from de novo MD is better than any other ensemble, with RMSDNs that are lower than the RC and Pred-SS ensembles values by 2–3 fold and with much higher correlation coefficients.¹⁴ The Pred-SS-ENS ensemble performs better for Aβ40 and Aβ42 than the randomly generated ensembles because the NOE restraints are used in the knowledge-based ensemble selection. However, the Pred-SS-ENS ensemble still does not reproduce the data as well as the de novo MD ensemble. The NOE validation clearly indicates that the de novo MD ensemble with its cooperative secondary structure is a better representation of Aβ40 and Aβ42 than are the RC, Pred-SS, or Pred-SS-ENS ensembles, which have no cooperative secondary structure. Since time information is not available for the static ensembles, we can only evaluate the NOEs for the statistical ensembles under the assumption of one uniform correlation time applied to all pairs of protons, for which we use a 1 ns correlation time, which is on the same order as those observed in the MD simulations. Of course the de novo MD method can account for the time scales explicitly and more importantly for the fact that different pairs of hydrogen atoms do decay on different time scales. Thus the statistically generated and knowledge-based ensembles agree relatively poorly with the NOE observables since the heterogeneity in correlation times are unknown, and hence even the MD-ENS ensemble is in somewhat worse agreement with the experimental NOEs than the de novo MD ensemble (Table 2). The NOE validation emphasizes that an IDP’s diverse set of conformations gives rise to a heterogeneous set of correlation times that must be described in order to validate against experimental NOEs.

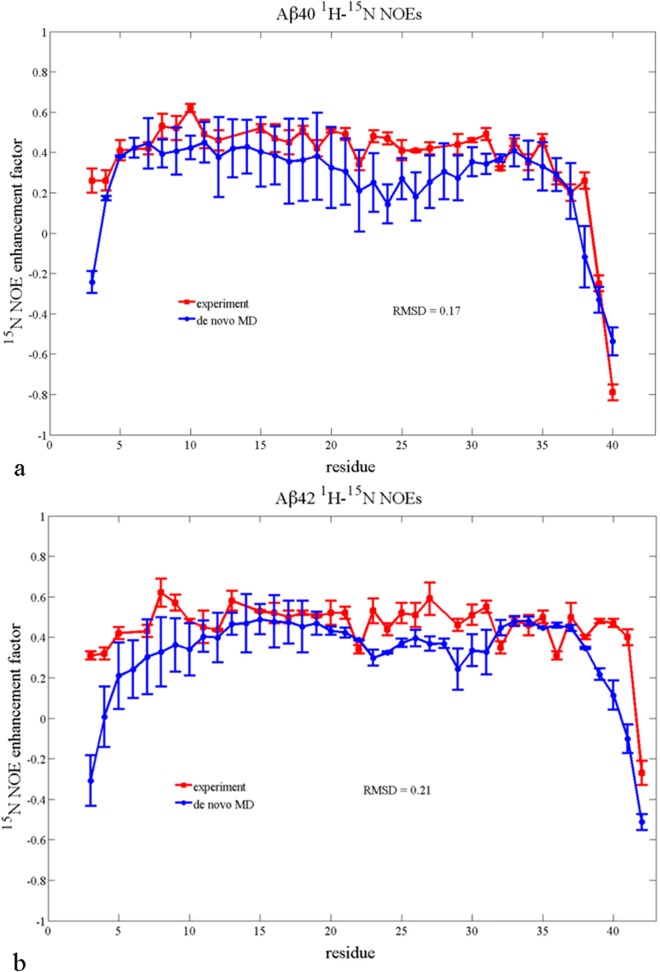
We further emphasize that the calculation of heteronuclear NOEs, being a purely dynamical measurement, is only possible with the de novo MD method. Figure 3 shows a comparison of the experimental ¹H–¹⁵N NOE intensities, measured by Yan and Wang,⁶² and those derived from our MD simulation for Aβ42 and Aβ40, showing overall excellent agreement.^14,48 Unlike the ¹H–¹H NOEs, these assignments are unambiguous from experiment. We find that, as in the experiment, there is an increase in ¹H–¹⁵N NOE intensities calculated from simulation for residues 35–40 for Aβ42 compared to Aβ40, indicating that the longer peptide experiences slower dynamics at the C-terminus.^14,48 This difference in experimental ¹H–¹⁵N NOEs for Aβ42 and Aβ40 has previously been interpreted as evidence that Aβ42 has greater structural rigidity in the C-terminus compared to Aβ40^62,65 and we provide more analysis on this point in recently published work.⁷

Figure 3.

Agreement with experiment of simulated (a) Aβ40 and (b) Aβ42 ¹H–¹⁵N NOE. The red squares are experimental data from Yan and Wang.⁶⁶ The blue circles are the data calculated from the de novo MD ensemble.

Discussion

We have shown that the MD and MD-ENS structural ensembles for the IDPs Aβ40 and Aβ42 previously characterized^14,48 yield substantially better agreement with a range of NMR data than the random coil or statistical ensembles that are typically used with knowledge based approaches. The MD ensembles are qualitatively different from random coil or statistical ensembles in that the subpopulations are richly structured, contain a diverse set of secondary structures including α-helix, β-turns, and β-strands, and span the full range of compact to fully extended conformations. Furthermore, while MD generated ensembles are Boltzmann weighted, the knowledge-based approaches give equal statistical weight to all conformations and thus are likely inconsistent with statistical mechanical weightings that are inherent to the NMR experiment.

We have also shown that some types of NMR data may not be helpful for discriminating among qualitatively different structural ensemble of IDPs. In particular, averages over a diverse set of cooperative secondary structure conformations yield experimental values of chemical shifts that are superficially consistent with values expected from a random coil ensemble. Furthermore, if the chemical shifts are not highly dispersed along the sequence of a particular IDP, such as is found for the amyloid-β peptides, then the chemical shifts have limited value as experimental refinement input or as a validation measure. J-couplings also do not provide discrimination between randomly generated conformations and a diverse population of cooperative secondary structure. In fact, we found that scalar couplings calculated as averages over the allowed regions of each residue-specific Ramachandran plot gave as good agreement with the experimental J-couplings for Aβ40 and Aβ42 as did averages over the structural populations.

Unlike others who have used RDC data to help interpret IDP or unfolded protein structural ensembles, we found RDCs to be only marginally useful for Aβ40 and Aβ42. This may be due to limitations of RDC calculators such as PALES,⁵⁸ which were originally developed and successfully applied to folded proteins, but which are reported to have large uncertainties in their predicted RDC values. Furthermore, calculated RDCs based on global alignment algorithms such as PALES⁵⁸ diverge significantly from RDCs evaluated from localized alignments¹⁸ for Aβ40 and Aβ42, indicating that in cases like this the ENSEMBLE package should be employed using the PALES calculator to fit RDCs, which is possible though not standard.⁶⁶ More research may be necessary to apply programs like PALES to disordered proteins, which likely do not align in an anisotropic medium in the same way as folded proteins, in part due to the time scale of interconversion of the conformational substates. For example, conventional methods for calculating RDCs cannot be applied to the motion of multidomain biomolecules,⁶⁷ and the local conformational sampling and long-range structure need to be simultaneously accounted for because they both affect the experimental RDC data.¹⁶ However, progress is being made in using RDCs to provide meaningful structural information for other IDPs.^{16,17,40,45,67,68} We speculate that success is greatest when all subpopulations of the IDP ensemble are homogeneously classifiable (as extended disordered conformations for example), so that the IDP global alignment properties are uniform and resulting averages provide meaningful and consistent structural information.

We have demonstrated that homonuclear ¹H–¹H NOE intensities and heteronuclear ¹⁵N–¹H NOEs are by themselves discriminating with regard to the tertiary contacts and backbone dynamics, respectively, that define the important validation of the MD-based ensembles over the statistical coil ensembles.^14,48 Furthermore, a correct picture of the IDP ensemble based on the experimental NOE data would not be possible without a computational model providing both details of individual structures and the time scales for their interconversion. In turn, although the homonuclear NOEs are averaged over all subpopulations, they are still vital for deducing whether a given ensemble contains subpopulations of structure with the right tertiary contacts to give rise to the observed cross-peaks in the spectra. Because these cross-peak intensities rely directly on the decay time scales of correlated proton distances, the NOEs for IDPs are reporting on a heterogeneous population of time scales. One of the primary limitations of the statically generated ensembles is that they are not associated with any information about motional time scales that can be used to calculate NOE observables. Relaxation times can be used with the ENSEMBLE method, although they are incorporated as structural rather than dynamic constraints.^29,30,42 This dynamic information is a genuine strength of the de novo MD methods, especially for ¹⁵N–¹H NOEs, which cannot be calculated from the static ensembles.

We believe that the primary limitation of knowledge-based methods applied to the difficult amyloidβ case is 3-fold. We note that while there will be quantitative differences between ENSEMBLE and other knowledge-based approaches such as ASTEROIDS, qualitatively the problems will be similar. First, there is no requirement for generating a complete and representative starting “basis set” of conformations to select the final ensemble from; i.e., these methods cannot use the NMR data effectively to select for compact structures with elements of cooperative secondary structure if the initial pool of structures is largely composed of extended random coil structures. Both ENSEMBLE and ASTEROIDS have relied on statistical coil ensembles as the starting pool of structures, and while some “on-the-fly” addition of new structures is possible with these methods, they do not yet support formation of complicated β-sheet motifs.^16,42 Metrics of ensemble heterogeneity, such as those developed by the Onuchic and Stultz research groups, will continue to be useful as we explore the range of IDPs that cannot be easily classified based on their level of disorder.⁶⁹⁻⁷¹ Second, for certain classes of IDPs such as amyloidβ optimization of structures to reproduce chemical shifts and scalar couplings does not discriminate among qualitatively different structural ensembles. Third, the optimization phase of the knowledge-based approaches relies on approximations to NMR observables, which may diverge from a global property, as for L-RDCs, or from the dynamical origins of NOE intensities.

At the same time, the de novo MD method is not quantitatively perfect, and therefore the MD ensemble provides an excellent start state for subsequent refinement by knowledge-based approaches. An unambiguous future direction for the structural biology of IDPs is the combined use of knowledge-based approaches and MD that supplies Boltzmann weighted conformational substates as well as heterogeneous time scales of motion.

All together, the productive interplay between NMR experiments, de novo MD simulations, and knowledge-based approaches, along with supporting models, algorithms, and computer hardware, gives us an ability to accurately identify structures present in IDP ensembles and use that knowledge to gain previously inaccessible functional insights.^{14,22,24,39,43,44,48,52,55,72−83} To further improve techniques for studying disordered proteins, we as a community could establish a high throughput computational infrastructure to predict IDP structural ensembles using a combination of MD and NMR. This would be similar to the establishment of X-ray crystallography beamlines for the rapid solution of folded protein structures that was launched during the structural genomics era. The ultimate goal in both cases is to use structural information to drive the formation of hypotheses about protein function. Based on the success of using structural information for functional characterization of folded proteins and complexes, we hope and expect that structural knowledge of IDP ensembles can provide similar insight into IDP function and enable development of molecular hypotheses for disease IDPs.

Supporting Information Available

A detailed description of how the five candidate .amyloid-β structural ensembles were generated, details on the use of the ENSEMBLE software, a table showing how the Pred-SS ensemble was biased to contain extended dihedral angles preferentially, and a figure showing the secondary structure present in the RC ensemble. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States