The Influence of Ca²⁺ Buffers on Free [Ca²⁺] Fluctuations and the Effective Volume of Ca²⁺ Microdomains

Abstract

Intracellular calcium (Ca²⁺) plays a significant role in many cell signaling pathways, some of which are localized to spatially restricted microdomains. Ca²⁺ binding proteins (Ca²⁺ buffers) play an important role in regulating Ca²⁺ concentration ([Ca²⁺]). Buffers typically slow [Ca²⁺] temporal dynamics and increase the effective volume of Ca²⁺ domains. Because fluctuations in [Ca²⁺] decrease in proportion to the square-root of a domain’s physical volume, one might conjecture that buffers decrease [Ca²⁺] fluctuations and, consequently, mitigate the significance of small domain volume concerning Ca²⁺ signaling. We test this hypothesis through mathematical and computational analysis of idealized buffer-containing domains and their stochastic dynamics during free Ca²⁺ influx with passive exchange of both Ca²⁺ and buffer with bulk concentrations. We derive Langevin equations for the fluctuating dynamics of Ca²⁺ and buffer and use these stochastic differential equations to determine the magnitude of [Ca²⁺] fluctuations for different buffer parameters (e.g., dissociation constant and concentration). In marked contrast to expectations based on a naive application of the principle of effective volume as employed in deterministic models of Ca²⁺ signaling, we find that mobile and rapid buffers typically increase the magnitude of domain [Ca²⁺] fluctuations during periods of Ca²⁺ influx, whereas stationary (immobile) Ca²⁺ buffers do not. Also contrary to expectations, we find that in the absence of Ca²⁺ influx, buffers influence the temporal characteristics, but not the magnitude, of [Ca²⁺] fluctuations. We derive an analytical formula describing the influence of rapid Ca²⁺ buffers on [Ca²⁺] fluctuations and, importantly, identify the stochastic analog of (deterministic) effective domain volume. Our results demonstrate that Ca²⁺ buffers alter the dynamics of [Ca²⁺] fluctuations in a nonintuitive manner. The finding that Ca²⁺ buffers do not suppress intrinsic domain [Ca²⁺] fluctuations raises the intriguing question of whether or not [Ca²⁺] fluctuations are a physiologically significant aspect of local Ca²⁺ signaling.

Introduction

The regulation of intracellular calcium (Ca²⁺) concentration ([Ca²⁺]) is a fundamental aspect of many cell signaling pathways (1). In many types of cells, spatially localized Ca²⁺ signals known as Ca²⁺ micro- or nanodomains regulate specific cellular processes in different subcellular regions. Significant examples include pre- and postsynaptic signaling in neuronal dendrites (2–4), contraction regulation in cardiac dyadic subspaces (3,5–7), localized control of mitochondria (8–10), and nuclear gene transcription (4,8), and localized mechanical and olfactory sensing in primary cilia (11–13).

Ca²⁺ buffers play an important role in modulating spatially localizing Ca²⁺ signals. The term “Ca²⁺ buffers” is generic and includes endogenous binding proteins, exogenous Ca²⁺ chelators (e.g., EGTA and BAPTA), indicator dyes (e.g., Fluo-4 and Rhod-2), and other nonspecific Ca²⁺ binding molecules (e.g., membrane phospholipids). In addition to regulating the levels of free Ca²⁺ in the cytoplasm, Ca²⁺ buffers influence the spatiotemporal dynamics of Ca²⁺ signaling. Because Ca²⁺ buffer binding rates, affinities, and diffusivities can range over several orders of magnitude (14), it is important to understand the influence of these parameters on Ca²⁺-dependent signaling. Using deterministic formulations for Ca²⁺ and buffer dynamics, investigators have derived analytical results pertaining to the influence of rapid mobile and immobile buffers on Ca²⁺ signaling, demonstrating that buffers can greatly alter the [Ca²⁺] profile in the proximity of Ca²⁺ channels (15–19). Immobile buffers have been shown to reduce the effective diffusivity of Ca²⁺, whereas mobile buffers can facilitate diffusion near an open Ca²⁺ channel and produce steep [Ca²⁺] gradients (20). Experimental and simulation studies have shown that the decay of residual Ca²⁺ after Ca²⁺ channel closure can be longer for rapid buffers than slow buffers (21,22). The influence of buffers on Ca²⁺ signaling can be counterintuitive, because it depends subtly on binding rate kinetics and competition between Ca²⁺-binding sites. For example, analytical results have shown that increased buffer diffusivity may increase or decrease the speed of a propagating Ca²⁺ wave, depending on the excitability of Ca²⁺ dynamics and buffer properties (23).

Assuming a rapidly equilibrating bimolecular association reaction between Ca²⁺ and buffer (B),

$${\text{Ca}}^{2+}+\text{B}\underset{k_{-}}{\overset{k_{+}}{\rightleftharpoons }}\text{CaB,}$$ (1)

the time evolution of [Ca²⁺], denoted by c below, can be described by the ordinary differential equation (ODE) (24)

$$\text{Ω}\dot{c}=\beta J,$$ (2)

where the dot indicates a time derivative, Ω is the compartmental volume, J = J_in – J_out is the net flux of Ca²⁺ molecules into the compartment, and the buffering factor β is the differential fraction of free-to-total Ca²⁺ that takes values between 0 and 1,

$$\begin{array}{c}\beta =\frac{1}{1+w}\text{,}\text{and}\\ w=\frac{b_T\kappa }{{\left(c+\kappa \right)}^2}.\end{array}$$ (3)

In this expression, total buffer concentration b_T = b + cb is the sum of free and Ca²⁺-bound buffer concentration, b and cb, respectively; κ = k₋/k₊ is the dissociation constant for Ca²⁺; and the ratio w = b_Tκ/(c + κ)² is the buffering capacity, i.e., the differential fraction of bound-to-free Ca²⁺. Concentration balance equations such as Eq. 2 are often written in the form

$${\text{Ω}}_{\text{eff}}\dot{c}=J,$$ (4)

where the effective volume Ω_eff is defined as Ω_eff = Ω/β ≥ Ω.

It is well known that the number of molecules in biochemical reaction networks randomly fluctuate, and the resulting concentration fluctuations for each chemical species are larger amplitude when the system size is small (25,26). For a sufficiently large system, i.e., large volume and number of molecules, concentration fluctuations become negligible and deterministic modeling is appropriate (26). However, in physiological settings of local Ca²⁺ signaling, i.e., Ca²⁺ microdomains, the system size is often small and concentration fluctuations may be significant. Intracellular [Ca²⁺] is very low in resting cells, typically 100 nM, and the volume of Ca²⁺ microdomains or subspaces are ∼10⁻¹⁷–10⁻¹⁵ liters, values that correspond to 0.6–60 Ca²⁺ ions at rest. A large amount of prior work has focused on the influence of stochastic gating of Ca²⁺-regulated Ca²⁺ channels on [Ca²⁺] (19,27–32), but only a few have considered the role of concentration fluctuations associated with the small number of Ca²⁺ ions typically present in domains (30,33,34). The relative size of [Ca²⁺] fluctuations can be characterized by their coefficient of variation (c_v), defined as the standard deviation of [Ca²⁺] divided by the mean [Ca²⁺]. In a spatially restricted domain and in the absence of Ca²⁺ buffers, the relative size of [Ca²⁺] fluctuations is given by (35)

$$c_v^0=\frac{1}{\sqrt{c_{ss}\text{Ω}}},$$ (5)

where c_ss is the steady-state [Ca²⁺] and Ω is the physical volume of the domain (the superscripted 0 indicates no buffers). Because c_ssΩ is the number of Ca²⁺ ions in the domain, this expression is consistent with the influence of system size on molecular fluctuations well known in statistical physics (26). For the small volume domains mentioned above, this $c_v^0$ is in the range of 1.3–0.13. Our prior work suggests that fluctuations in [Ca²⁺] of this magnitude could significantly influence the gating of Ca²⁺-regulated Ca²⁺ channels in Ca²⁺ microdomains, such as dyadic subspaces or dendritic spines (35).

Although prior work makes it clear that [Ca²⁺] fluctuations are a nonnegligible aspect of Ca²⁺ signaling, the influence of Ca²⁺ buffers on the dynamics of [Ca²⁺] fluctuations has not previously been studied. Based on the notion of effective volume, one might conjecture that buffers decrease [Ca²⁺] fluctuations and, consequently, mitigate the significance of small domain volume vis-a-vis downstream Ca²⁺ signaling (e.g., Ca²⁺-triggered events). Do Ca²⁺ buffers influence [Ca²⁺] fluctuations? If so, how do these fluctuations depend on Ca²⁺ buffer properties such as dissociation constant and total concentration (Ca²⁺ free plus bound)? To answer these questions, we develop and analyze a minimal stochastic model that includes Ca²⁺ and buffer in a domain of small volume.

Our analysis focuses on Ca²⁺ microdomains that arise from Ca²⁺ influx into a spatially restricted subcellular compartment that may contain Ca²⁺ buffers, e.g., a dendritic spine or cardiac dyadic subspace (Fig. 1, A and B). The theory is most directly applicable to Ca²⁺ signaling complexes with membrane configurations or other obstructions to diffusion (e.g., molecular crowding) resulting in spatially confined Ca²⁺ signaling, for example, the primary cilium (Fig. 1 C), mitochondria-endoplasmic reticulum (ER) junctions, and presynaptic boutons (2–13). Free Ca²⁺ and buffer (Ca²⁺-bound and -free) may exchange between domain and bulk via diffusion represented as a first-order reaction (Fig. 1 D). We specify the volume but not the detailed geometry of the spatially confined region that delimits the domain. Spatial gradients between domain and bulk are minimally represented in the model, but the microdomain itself is treated as a well-stirred compartment. The compartmental model formulation is most applicable and relevant to microdomains for which the time constant for domain escape is longer than the characteristic time for diffusion across the domain (36).

Figure 1.

The analysis of the effect of Ca²⁺ buffers on domain [Ca²⁺] fluctuations is applicable to microdomains that arise from Ca²⁺ influx into a spatially restricted subcellular compartment. (A) In a dendritic spine (Ω denotes volume of spine head), Ca²⁺ influx occurs via ionotropic receptors (e.g., NMDA) or plasma membrane (PM) Ca²⁺ channels downstream of metabotropic receptors (e.g., mGluRs) (2). (B) In the cardiac dyad, Ca²⁺ influx via PM L-type Ca²⁺ channels trigger Ca²⁺ influx from Ca²⁺-activated sarcoplasmic reticulum (SR) Ca²⁺ channels (ryanodine receptors) (7). Close associations of endoplasmic reticulum (ER) and PM are observed in many cell types. During ER depletion in Jurkat T cells, luminal Ca²⁺ sensor STIM1 aggregates on the ER membrane and binds the Ca²⁺ channel Orai1 providing store-operated Ca²⁺ entry. (C) In olfactory primary cilium, odorant detection induces a rise in second messenger cAMP, activating cyclic nucleotide-gated channels allowing entry of Ca²⁺ and Na⁺ ions (11). (D) Model components and fluxes employed in the microdomain model. The stochastic ODE model includes Ca²⁺ influx, association of Ca²⁺ and buffer, and passive exchange of Ca²⁺ and buffer between the domain of volume Ω and the bulk cytosol.

For clarity and readability, we first present the stochastic model representing [Ca²⁺] fluctuations in a microdomain with no Ca²⁺ buffer. This preliminary calculation illustrates our approach and provides a reference point in our interpretation of results that include influx and efflux of both Ca²⁺ and buffer. We perform parameter studies to determine how Ca²⁺ buffers influence the size of [Ca²⁺] fluctuations, derive the fluctuating rapid buffer approximation to the dynamics of domain [Ca²⁺] fluctuations, and illustrate how the influence of buffers on the effective system size and the time course of [Ca²⁺] fluctuations depend on buffer parameters. We conclude with a discussion of our findings.

Model Formulation

Domain [Ca²⁺] fluctuations in the absence of buffer

Deterministic ODE formulation

The deterministic ODE that minimally describes the time evolution of [Ca²⁺] in the domain depicted in Fig. 1 without buffer, constant influx j_in, and passive exchange with the bulk is

$$\dot{c}=j_{\text{in}}-k_c\left(c-c_{\infty }\right)\equiv f\left(c\right),$$ (6)

where k_c is the exchange rate (due to diffusion) that has physical dimensions of inverse time. Setting the left-hand side of Eq. 6 to zero, steady-state [Ca²⁺] is found to be

$$c_{\text{ss}}=j_{\text{in}}/k_c+c_{\infty }.$$ (7)

This deterministic formulation assumes that concentration fluctuations are negligible (i.e., large system size, Ω → ∞). The following section presents the corresponding stochastic ODEs that are valid for small domain volume.

Stochastic ODE (Langevin) formulation

In a domain with physical volume small enough that fluctuations are not negligible, but large enough that molecular concentrations can be modeled continuously, [Ca²⁺] dynamics may be described by a Langevin equation. This would be a stochastic differential equation (SDE) similar to the deterministic ODE (Eq. 6), but augmented by a fluctuating term, ξ_c(t), with properties determined by the elementary molecular events that drive concentration fluctuations (26,37,38),

$$\dot{c}=f\left(c\right)+{\xi }_c\left(t\right).$$ (8)

In this stochastic ODE, ξ_c(t) is Gaussian noise (specifically, a random function of time with zero mean),

$$\langle {\xi }_c\left(t\right)\rangle =0$$ (9)

and two-time covariance

$$\langle {\xi }_c\left(t\right){\xi }_c\left(t^{\prime }\right)\rangle ={\gamma }_c\delta \left(t-t^{\prime }\right),$$ (10)

where δ is the Dirac delta function and γ_c is given by

$${\gamma }_c=\frac{j_{\text{in}}+k_c\left(c+c_{\infty }\right)}{\text{Ω}}.$$ (11)

Note that the signs in the numerator are correct; γ_c is proportional to the sum of rates of the elementary processes leading to changes in [Ca²⁺], which includes increases through influx (j_in) as well as decreases and increases due to exchange with the bulk (k_cc and k_cc_∞). The reader who is unfamiliar with chemical Langevin equations may review the general form of the two-time covariance (see Appendix A in the Supporting Material).

Employing a linear noise approximation (26) for fluctuations around the stable steady-state c_ss transforms Eq. 8 into

$$\dot{\delta c}=-k_c\delta c+{\xi }_c^{ss}\left(t\right),$$ (12)

where δ_c is the deviation of the fluctuating [Ca²⁺] from the steady-state value, c_ss, that is,

$$\delta c\left(t\right)=c\left(t\right)-c_{ss},$$ (13)

and we have used f′(c_ss) = −k_c and 〈ξ_c^ss(t)〉 = 0. The two-time covariance of the random term takes the form

$$\langle {\xi }_c^{ss}\left(t\right){\xi }_c^{ss}\left(t^{\prime }\right)\rangle ={\gamma }_c^{ss}\delta \left(t-t^{\prime }\right),$$

where the constant ${\gamma }_c^{ss}$ is found by evaluating Eq. 11 at steady state, that is,

$${\gamma }_c^{ss}=\frac{2k_c{c}_{ss}}{\text{Ω}},$$ (14)

where we have used the balance of Ca²⁺ influx and efflux at steady state, j_in = k_c(c_ss – c_∞), to express the numerator as 2k_cc_ss rather than j_in + k_c(c_ss + c_∞) (compare to Eq. 14).

Analysis of concentration fluctuations

To understand the dynamics of [Ca²⁺] fluctuations implied by Eq. 12, consider an ensemble of domains with initial state c(0) = c_ss, that is, δ_c(0) = 0. The time evolution of the ensemble variance of the deviations δc, defined by σ_c(t) = 〈${\delta }_c^2$(t)〉, follows from Eq. 12,

$${\dot{\sigma }}_c=-2k_c{\sigma }_c+{\gamma }_c^{ss},$$ (15)

where k_c = |f′(c_ss)| is the relaxation rate. By assumption, the ensemble variance is initially zero, that is, δ_c(0) = 0 implies σ_c(0) = 0, but as time proceeds, σ_c(t) is given by the solution of Eq. 15,

$${\sigma }_c\left(t\right)={\sigma }_c^0\left(1-e^{-2k_{c}t}\right),$$ (16)

where steady-state ensemble variance ${\sigma }_c^0$ is found by setting ${\dot{\sigma }}_c=0$ in Eq. 15,

$${\sigma }_c^0=\frac{{\gamma }_c^{ss}}{2k_c}=\frac{c_{ss}}{\text{Ω}}.$$ (17)

The first equality in Eq. 17 relating ${\sigma }_c^0$ and ${\gamma }_c^{ss}$ is called the “fluctuation-dissipation theorem” (25,26,39).

Thus, the relative size of the steady-state [Ca²⁺] fluctuations in the Langevin formulation, given by the coefficient of variation of the fluctuating [Ca²⁺], is

$$c_v^0=\frac{\sqrt{{\sigma }_c^0}}{c_{ss}}=\frac{1}{\sqrt{c_{ss}\text{Ω}}}.$$ (18)

Using the Langevin equation for a fluctuating Ca²⁺ microdomain, we have derived the well-known result (35) that the relative magnitude of concentration fluctuations is inversely proportional to the square-root of the system size, i.e., the expected number of Ca²⁺ ions in the domain at steady-state (c_ssΩ). This result is a reference point for our analysis of domain [Ca²⁺] fluctuations in the presence of buffer.

Domain [Ca²⁺] fluctuations in the presence of buffer

Deterministic ODE formulation

In this section we characterize [Ca²⁺] fluctuations in a domain model that includes Ca²⁺ buffers, Ca²⁺ influx, and exchange of both Ca²⁺ and buffer with the bulk (see Fig. 1). Assuming mass-action kinetics and bimolecular association of Ca²⁺ and buffer (Eq. 1), we write the following deterministic system of ODEs,

$$\dot{c}=R+j_{\text{in}}-k_c\left(c-c_{\infty }\right),$$ (19a)

$$\dot{b}=R-k_b\left(b-b_{\infty }\right),$$ (19b)

$$\dot{\mathit{cb}}=-R-k_b\left(cb-c{b}_{\infty }\right),$$ (19c)

where k_c and k_b are the Ca²⁺ and buffer exchange rates, and the reaction terms are given by R = −k + c × b + k − cb, with c, b, and cb denoting free Ca²⁺, free buffer, and bound buffer, respectively. We assume that the free and Ca²⁺-bound buffer have the same exchange rate k_b and, furthermore, that the bulk concentrations b_∞ and cb_∞ are in equilibrium with the bulk free [Ca²⁺],

$$\begin{array}{c}{b}_{\infty }=\frac{\kappa b_T^{\infty }}{c_{\infty }+\kappa },\text{a}\text{n}\text{d}\\ c{b}_{\infty }=\frac{c_{\infty }{b}_T^{\infty }}{c_{\infty }+\kappa }.\end{array}$$

Setting the time derivatives of Eq. 19 to 0, we find that the steady-state domain [Ca²⁺], denoted by c_ss, solves the implicit expression

$$j_{\text{in}}-k_c\left(c_{ss}-c_{\infty }\right)-k_b\left(c{b}_{ss}-c{b}_{\infty }\right)=0,$$ (20a)

where the steady-state Ca²⁺-free and -bound buffer concentrations are given by

$$\begin{array}{c}{b}_{ss}=\frac{\kappa b_T^{\infty }+k_b{b}_{\infty }/k_{+}}{c_{ss}+\kappa +k_b/k_{+}},\text{a}\text{n}\text{d}\\ c{b}_{ss}=\frac{c_{ss}{b}_T^{\infty }+k_{b}c{b}_{\infty }/k_{+}}{c_{ss}+\kappa +k_b/k_{+}}.\end{array}$$ (20b)

In the presence of Ca²⁺ influx, j_in > 0, and because ∂cb_ss/∂c_ss > 0, c_ss > c_∞, cb_ss > c_∞, and b_ss > b_∞. Also note that cb_ss + b_ss = $b_T^{\infty }$ at this nonequilibrium steady state, because buffer in the bulk is at equilibrium, cb_∞ + b_∞ = $b_T^{\infty }$, and the exchange of Ca²⁺-bound buffer between domain and bulk, balances the exchange of Ca²⁺-free buffer, k_b(cb_ss − cb_∞) = k_b(b_∞ − b_ss) > 0.

Stochastic ODE (Langevin) formulation

As in the previous section, the Langevin-type stochastic Ca²⁺ domain model is found by adding the appropriate random terms to the deterministic ODEs (Eq. 19),

$$\dot{c}=R+j_{\text{in}}-k_c\left(c-c_{\infty }\right)+{\xi }_c\left(t\right),$$ (21a)

$$\dot{b}=R-k_b\left(b-b_{\infty }\right)+{\xi }_b\left(t\right),$$ (21b)

$$\dot{cb}=-R-k_b\left(cb-c{b}_{\infty }\right)+{\xi }_{cb}\left(t\right),$$ (21c)

where 〈ξ_i(t)〉 = 0 for i ∈ {c,b,cb}. Because the ξ_i(t) are correlated, the two-time covariances are most easily expressed in matrix form,

$$\langle \mathit{\xi }\left(t\right){\mathit{\xi }}^T\left(t^{\text{'}}\right)\rangle =\text{Γ}\left(c,b,cb\right)\delta \left(t-t^{\text{'}}\right),$$ (22)

where ξ is the column vector (ξ_c, ξ_b, ξ_cb)^T and Γ is the state-dependent covariance matrix (see Appendix A in the Supporting Material),

$$\text{Γ}\left(c,b,cb\right)=\left(\begin{array}{ccc}{\gamma }_r+{\gamma }_c& {\gamma }_r& -{\gamma }_r\\ {\gamma }_r& {\gamma }_r+{\gamma }_b& -{\gamma }_r\\ -{\gamma }_r& -{\gamma }_r& {\gamma }_r+{\gamma }_{cb}\end{array}\right),$$ (23a)

where

$$\begin{array}{c}{\gamma }_r\left(c,b,cb\right)=\frac{k_{+}c\times b+k_{-}cb}{\text{Ω}},\\ {\gamma }_c\left(c\right)=\frac{j_{\text{in}}+k_c\left(c+c_{\infty }\right)}{\text{Ω}},\\ {\gamma }_b\left(b\right)=\frac{k_b\left(b+b_{\infty }\right)}{\text{Ω}},\\ {\gamma }_{cb}\left(cb\right)=\frac{k_b\left(cb+c{b}_{\infty }\right)}{\text{Ω}}.\end{array}$$ (23b)

Denoting the fluctuations around steady state by δc = c – c_ss, δb = b – b_ss, and δcb = cb – cb_ss, the linear SDE system for the concentration fluctuations in the presence of buffer is

$$\dot{\mathit{\delta }}=H_{ss}\mathit{\delta }+{\mathit{\xi }}_{ss}\left(t\right),$$ (24)

where δ = (δc, δc, δcb)^T is a column vector, H_ss is the Jacobian of the full system of SDEs evaluated at steady state,

$$H_{ss}=\left(\begin{array}{ccc}-k_{+}{b}_{ss}-k_c& -k_{+}{c}_{ss}& k_{-}\\ -k_{+}{b}_{ss}& -k_{+}{c}_{ss}-k_b& k_{-}\\ k_{+}{b}_{ss}& k_{+}{c}_{ss}& -k_{-}-k_b\end{array}\right),$$

〈ξ_ss(t)〉 = 0, and 〈ξ_ss(t) ξ^T_ss(t′) 〉 = Γ_ssδ(t – t′) with steady-state covariance matrix (compare to Eq. 23),

$${\text{Γ}}_{ss}=\left(\begin{array}{ccc}{\gamma }_r^{ss}+{\gamma }_c^{ss}& {\gamma }_r^{ss}& -{\gamma }_r^{ss}\\ {\gamma }_r^{ss}& {\gamma }_r^{ss}+{\gamma }_b^{ss}& -{\gamma }_r^{ss}\\ -{\gamma }_r^{ss}& -{\gamma }_r^{ss}& {\gamma }_r^{ss}+{\gamma }_{cb}^{ss}\end{array}\right),$$ (25a)

where

$$\begin{array}{c}{\gamma }_r^{ss}=\frac{k_{+}{c}_{ss}\times b_{ss}+k_{-}c{b}_{ss}}{\text{Ω}},\\ {\gamma }_c^{ss}=\frac{j_{\text{in}}+k_c\left(c_{ss}+c_{\infty }\right)}{\text{Ω}},\\ {\gamma }_b^{ss}=\frac{k_b\left(b_{ss}+b_{\infty }\right)}{\text{Ω}},\\ {\gamma }_{cb}^{ss}=\frac{k_b\left(c{b}_{ss}+c{b}_{\infty }\right)}{\text{Ω}}.\end{array}$$ (25b)

If one prefers, the Langevin system for the fluctuations (Eq. 24) can be written as

$$\dot{\delta c}=-\left(k_{+}{b}_{ss}+k_c\right)\delta c-k_{+}{c}_{ss}\delta b+k_{-}\delta cb+{\xi }_c^{ss}\left(t\right),$$ (26a)

$$\dot{\delta b}=-k_{+}{b}_{ss}\delta c-\left(k_{+}{c}_{ss}+k_b\right)\delta b+k_{-}\delta cb+{\xi }_b^{ss}\left(t\right),$$ (26b)

$$\dot{\delta cb}=k_{+}{b}_{ss}\delta c+k_{+}{c}_{ss}\delta b-\left(k_{-}+k_b\right)\delta cb+{\xi }_{cb}^{ss}\left(t\right).$$ (26c)

Analysis of concentration fluctuations

Our analysis of concentration fluctuations in the presence of buffer begins by defining a symmetric 3×3 covariance matrix for the fluctuating concentrations, Σ(t) = (σ_ij) for i, j ∈{c,b,cb}, that is,

$$\text{Σ}\left(t\right)=\langle \mathit{\delta }\left(t\right){\mathit{\delta }}^T\left(t\right)\rangle =\left(\begin{array}{ccc}\langle \delta c^2\rangle & \langle \delta c\delta b\rangle & \langle \delta c\delta cb\rangle \\ \text{⋆}& \langle \delta b^2\rangle & \langle \delta b\delta cb\rangle \\ \text{⋆}& \text{⋆}& \langle \delta c{b}^2\rangle \end{array}\right),$$

where each star indicates a redundant entry. The time-dependent dynamics of Σ(t) follows from Eq. 24 (26),

$$\dot{\Sigma }=H_{ss}\text{Σ}+\text{Σ}{H}_{ss}^T+{\text{Γ}}_{ss},$$ (27)

which is the matrix version of Eq. 15. Solving Eq. 27 with the initial condition $\text{Σ}\left(0\right)=0$ corresponds to an ensemble of domains with initial state c(0) = c_ss, b(0) = b_ss, and cb(0) = cb_ss, that is, δc = δb = δcb = 0. This equation represents a linear system of 6 ODEs simultaneously solved by the six covariances 〈δc²〉, 〈δcδb〉,…, 〈δcb²〉.

The covariances Σ(t) that solve Eq. 27 are the focus of this article’s mathematical and computational analysis of domain [Ca²⁺] fluctuations in the presence of buffer. The solution of Eq. 27 with Σ(0) = 0 is (26),

$$\text{Σ}\left(t\right)=\underset{0}{\overset{t}{\int }}\text{exp}\left(H_{ss}\hat{t}\right){\text{Γ}}_{ss}\text{exp}\left(H_{ss}^T\hat{t}\right)d\hat{t}.$$ (28)

The steady-state ensemble variance is the limiting value of this expression as t → ∞,

$${\text{Σ}}_{ss}=\underset{0}{\overset{\infty }{\int }}\text{exp}\left(H_{ss}t\right){\text{Γ}}_{ss}\text{exp}\left(H_{ss}^{T}t\right)dt,$$ (29)

but the steady-state ensemble variance Σ_ss is often more conveniently found by solving the linear algebraic system for the steady state of Eq. 27, the continuous Lyapunov equation, and the more general form of the fluctuation-dissipation theorem,

$$H_{ss}{\text{Σ}}_{ss}+{\text{Σ}}_{ss}{H}_{ss}^T=-{\text{Γ}}_{ss}.$$ (30)

Equation 30 can be solved numerically using the command LYAP available in the software MATLAB (The MathWorks, Natick, MA). For symbolic and analytical calculations, we rewrite Eq. 30 as

$$\left(H_{ss}\oplus H_{ss}\right)\text{vec}\left({\text{Σ}}_{ss}\right)=-\text{vec}\left({\text{Γ}}_{ss}\right)$$ (31)

and then expand in terms of the parameters of the problem and the unknown entries of Σ_ss. In Eq. 31, I is the 3×3 identity matrix, H_ss ⊕ H_ss is a Kronecker sum given by

$$H_{ss}\oplus H_{ss}=I\otimes H_{ss}+H_{ss}\otimes I,$$

where ⊗ is the Kronecker product, the vec operation creates a column vector from a matrix by stacking its column vectors, and we have used

$$\text{vec}\left(AB\right)=\left(I\otimes A\right)\text{vec}\left(B\right)=\left(B^T\otimes I\right)\text{vec}\left(A\right).$$

Although H_ss ⊗ H_ss is 9×9 and vec(Σ_ss) and vec(Γ_ss) are 9×1, Σ_ss and Γ_ss are symmetric and thus Eq. 31 can be contracted to a 6×6 linear system by eliminating rows 4, 7, and 8 of vec(Σ_ss) and vec(Γ_ss) and the corresponding rows and columns of the H_ss ⊕ H_ss.

The remainder of this article communicates numerical and analytical results obtained using this Langevin formulation for domain [Ca²⁺] fluctuations in the presence of buffer.

Results

The influence of Ca²⁺ buffers on domain [Ca²⁺] fluctuations

Fig. 2 shows parameter studies that characterize the dependence of the relative magnitude of domain [Ca²⁺] fluctuations on Ca²⁺ buffer parameters. Results were obtained by numerically solving the continuous Lyapunov equation (Eq. 30) for a range of total buffer concentrations ($b_T^{\infty }$) and rate constants (k₊ and k₋), fast and slow exchange rates for Ca²⁺-free and -bound buffer with the bulk (k_b), and Ca²⁺ influx rates leading to steady-state free [Ca²⁺] of c_ss = 1, 10, and 100 μM. The relative magnitude of domain [Ca²⁺] fluctuations are characterized by the coefficient of variation

$$c_v=\frac{\sqrt{{\sigma }_c^{ss}}}{c_{ss}},$$ (32)

where the steady-state domain concentration c_ss is determined by the Ca²⁺ influx rate via Eq. 20 and ${\sigma }_c^{\mathit{ss}}$ = 〈δc²〉_ss is the germane element of Σ_ss found by numerical solution of Eq. 30. Numerically calculated c_v values that were generated from Monte Carlo simulations of an ensemble of domains using Gillespie’s stochastic simulation algorithm (40) agree with the linear noise approximation, validating our approach (see Fig. S1 in the Supporting Material).

Figure 2.

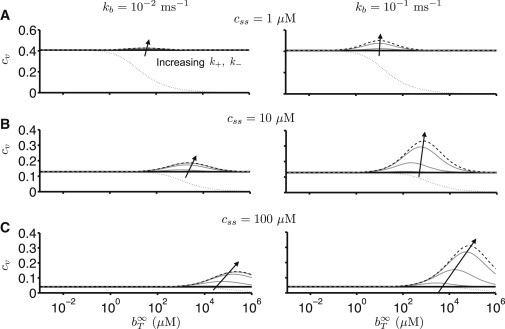
Dependence of the relative magnitude of domain [Ca²⁺] fluctuations probed by plotting the coefficient of variation (c_v) of the deviation of the fluctuating [Ca²⁺] on buffer parameters. (Shaded lines) c_v for different values of buffer binding reaction rate k₊. (Solid lines) $c_v^0$ in the absence of buffer (Eq. 5). (Dotted line) c_v predicted from a naive application of the concept of effective volume employed in deterministic models of Ca²⁺ signaling (Eq. 33). (Dashed lines) $c_v^{\prime }$, the (correctly derived) influence of buffer on c_v in the rapid buffer limit (Eq. 39). Parameters: c_ss = 1 (A), 10 (B), and 100 (C) μM, c_∞ = 0.1 μM, κ = 0.2 μM, k_c = 0.2 ms⁻¹, k₊ = 10⁻³, and 1 μM⁻¹ ms⁻¹. The domain volume Ω = 10⁻¹⁷L corresponds to 0.01 μm³ ≈ (0.22 μm)³.

Fig. 2 reveals that the relative magnitude of domain [Ca²⁺] fluctuations (c_v) is a biphasic (bell-shaped) function of the total buffer concentration $b_T^{\infty }$ (gray lines). For small or large total buffer concentrations ($b_T^{\infty }$), the relative fluctuation magnitude (c_v) asymptotically approaches the value obtained in the absence of buffer ($c_v^0=1/\sqrt{c_{ss}\text{Ω}}$, solid black line). This asymptotic value represents the minimum fluctuation size; c_v is enhanced for intermediate total buffer concentrations. Rapid Ca²⁺ buffers increase the relative fluctuation magnitude, that is, for fixed κ = k₋/k₊, the c_v increases with increasing k₊. High mobility Ca²⁺ buffer (represented in this compartmental formulation by increasing the exchange rate k_b) also enhances domain [Ca²⁺] fluctuations (compare left and right columns). High Ca²⁺ influx rates (j_in) amplify domain [Ca²⁺] fluctuations for intermediate, but not extreme, concentrations of buffer. Taken together, these results indicate that domain [Ca²⁺] fluctuations are significantly enhanced by Ca²⁺ buffer and nontrivially dependent on Ca²⁺ buffer properties.

The response of domain [Ca²⁺] to buffer parameters documented in Fig. 2 are counterintuitive in the sense that our numerical calculations are precisely the opposite of what one would predict using a naive application of the concept of effective volume. As mentioned in the Introduction, the effective volume derived from the rapid buffer limit of the deterministic equations for buffered Ca²⁺ dynamics (Eq. 19) is Ω_eff = Ω/β, where the buffering factor β is given by Eq. 3. If one replaces the physical volume Ω in Eq. 18 with this effective volume, one might conjecture that

$$c_v\stackrel{?}{=}\frac{1}{\sqrt{c_{ss}{\text{Ω}}_{\text{eff}}}}=\sqrt{\frac{{\beta }_{ss}}{c_{ss}\text{Ω}}},$$ (33)

where β_ss = β(c_ss). However, the numerical calculations presented in Fig. 2 show that this is incorrect (dotted line). In fact, this naive application of the concept of buffer-mediated increase in effective volume is quite misleading. Comparison of solid and dotted lines in Fig. 2 show that Eq. 33 incorrectly suggests that the size of [Ca²⁺] fluctuations is suppressed by buffer (by increasing the system size, c_ssΩ_eff > c_ssΩ). The conjecture of Eq. 33 also incorrectly suggests that domain [Ca²⁺] fluctuations can be eliminated (c_v → 0) as total buffer concentration $b_T^{\infty }$ increases and drives the differential fraction of free to total calcium to zero (β_ss → 0). On the contrary, the numerical results of this section (and analytical results presented below) are definitive: during periods of Ca²⁺ influx, Ca²⁺ buffers enhance domain [Ca²⁺] fluctuations.

The size of [Ca²⁺] fluctuations in the rapid buffer limit

Although closed-form analytical solution for the entries of the steady-state covariances Σ_ss (and in particular ${\sigma }_c^{\mathit{ss}}$) can be obtained beginning with Eq. 31, the algebra is tedious, the result is unwieldy, and little insight is gained from these expressions (not shown). On the other hand, numerical evaluation of symbolic solutions of Eq. 31 confirm the results of the previous section obtained by numerically solving the Lyapunov equation (Eq. 30).

To obtain more insight into the enhancement of domain [Ca²⁺] fluctuations mediated by Ca²⁺ buffers, we sought to derive a stochastic version of the rapid buffer approximation (RBA) that correctly accounts for the influence of fast Ca²⁺ buffering on domain [Ca²⁺] fluctuations. Two distinct approaches were identified and successfully employed, both yielding the same analytical result. In the first approach, the above-mentioned cumbersome analytical expression for ${\sigma }_c^{\mathit{ss}}$ was symbolically evaluated in the limit that k₊, k₋ → ∞ for fixed κ = k₋/k₊. The second approach involves no symbolic computations, but rather implements a general method for deriving a 0th-order approximation to the size of fluctuations in chemical reaction networks with widely separated timescales (26).

Briefly, beginning with the stochastic ODEs for buffered Ca²⁺ dynamics (Eq. 26), we identify the fluctuations in total calcium (δc_T = δc + δcb) and total buffer (δb_T = δb + δcb) as the slow variables. Differentiating these expressions and adding equations, we obtain the fast/slow system

$$\dot{\delta c}=-\left[k_{+}\left(c_{ss}+b_{ss}\right)+k_{-}+k_c\right]\delta c+\left(k_{+}{c}_{ss}+k_{-}\right)\delta c_T-k_{+}{c}_{ss}\delta b_T+{\xi }_c^{ss}\left(t\right),$$ (34a)

$$\delta {\dot{c}}_T=-\left(k_c-k_b\right)\delta c-k_b\delta c_T+{\xi }_{c_T}^{ss}\left(t\right),$$ (34b)

$$\delta {\dot{b}}_T=-k_b\delta b_T+{\xi }_{b_T}^{ss}\left(t\right),$$ (34c)

where δc is the fast variable, δc_T and δb_T are slow variables, and we define

$${\xi }_{c_T}^{ss}\left(t\right)={\xi }_c^{ss}\left(t\right)+{\xi }_{cb}^{ss}\left(t\right)\text{and}{\xi }_{b_T}^{ss}\left(t\right)={\xi }_b^{ss}\left(t\right)+{\xi }_{cb}^{ss}\left(t\right).$$

In the rapid buffer limit (k₊, k₋ → ∞ with κ = k₋/k₊ fixed), a quasistatic approximation for the average value of the [Ca²⁺] fluctuation that is valid on the slow (outer) timescale is

$${\langle \delta c\rangle }_{\text{∗}}\approx {\beta }_{ss}\left[\delta c_T-{\nu }_{ss}\delta b_T\right],$$ (35)

where we have written ν_ss = c_ss/(c_ss + κ), and 〈⋅〉_∗ indicates a time average (as opposed to an ensemble average) and we have used the fact that b_ss → b_Tκ/(c_ss + κ) in the RBA limit (compare to Eq. 20b). Replacing δc in the slow equations by this average value gives

$$\delta {\dot{c}}_T=-{\beta }_{ss}\left(k_c+w_{ss}{k}_b\right)\delta c_T+{\beta }_{ss}\left(k_c-k_b\right){\nu }_{ss}\delta b_T+{\xi }_{c_T}^{ss}\left(t\right),$$ (36a)

$$\delta {\dot{b}}_T=-k_b\delta b_T+{\xi }_{b_T}^{ss}\left(t\right),$$ (36b)

thereby expressing the slow SDEs in terms of δc_T and δb_T. Next, the 2×2 covariance matrix ${\text{Γ}}_{ss}^{\text{slow}}$ for ${\xi }_{c_T}^{ss}$ and ${\xi }_{b_T}^{ss}$ is calculated, and the 2×2 matrix ${\text{Σ}}_{ss}^{\text{slow}}$, whose entries correspond to 〈δ$c_T^2$〉, 〈δc_Tδb_T 〉, and 〈δ$b_T^2$〉, is found by solving a 2×2 Lyapunov equation (Eq. 30). Finally, the values of 〈δc²〉, 〈δcδc_T 〉, and 〈δcδb_T〉 consistent with Eq. 34 are found by solving a 3×3 Lyapunov equation for 〈δc²〉, 〈δcδc_T〉, and 〈δcδb_T〉. From the perspective of analytical work, this two-step process is far easier than solving the Lyapunov equation for the covariance matrix Σ_ss for δc, δb, and δcb, because the fast and slow versions of the Γ_ss and H_ss matrices are simpler than those that appear in the full calculation (see Appendix B in the Supporting Material for details).

Using both of the above-mentioned approaches (symbolic and analytical), we find that the variance of the free [Ca²⁺] fluctuations in the presence of rapid Ca²⁺ buffer (denoted by ${\sigma }_c^{\prime }$) is given by

$$\begin{array}{c}{\sigma }_c^{\text{′}}=\frac{c_{ss}}{\text{Ω}}\times \left(1+\chi \right),\\ \chi ={\beta }_{ss}\times \frac{w_{ss}{k}_b}{k_c+w_{ss}{k}_b}\times \frac{c_{ss}-c_{\infty }}{\kappa +c_{\infty }},\end{array}$$ (37)

where β_ss and w_ss are evaluated at the steady-state domain [Ca²⁺],

$$\begin{array}{c}{\beta }_{ss}=\frac{1}{1+w_{ss}},\\ w_{ss}=\frac{b_T^{\infty }\kappa }{{\left(c_{ss}+\kappa \right)}^2},\end{array}$$ (38)

and we note that c_ss ≥ c_∞ and thus χ ≥ 0. The variance ${\sigma }_c^{\prime }$ implies that in the rapid buffer limit the coefficient of variation for domain [Ca²⁺] fluctuations is given by

$$c_v^{\text{′}}=\frac{\sqrt{{\sigma }_c^{\text{′}}}}{c_{ss}}=\sqrt{\frac{1+\chi }{c_{ss}\text{Ω}}}=c_v^0\sqrt{1+\chi },$$ (39)

where $c_v^0=1/\sqrt{c_{ss}\text{Ω}}$ is the result in absence of buffer. Noting that χ ≥ 0, we find

$$\frac{c_v^{\text{′}}}{c_v^0}=\sqrt{1+\chi }\ge 1$$ (40)

and conclude that Ca²⁺ buffers may enhance but cannot suppress domain [Ca²⁺] fluctuations.

One way to represent the effect of rapid buffers on domain [Ca²⁺] fluctuations involves rewriting Eq. 37 as

$$\begin{array}{c}{\sigma }_c^{\text{′}}=\frac{c_{ss}}{{\text{Ω}}_{\text{eff}}^{\text{′}}},\\ {\text{Ω}}_{\text{eff}}^{\text{′}}=\frac{\text{Ω}}{1+\chi },\end{array}$$ (41)

where Ω′_eff denotes an effective volume that appropriately accounts for the influence of rapid Ca²⁺ buffers on [Ca²⁺] fluctuations. The fluctuating RBA is readily generalizable to multiple buffers (see Eq. S1 in the Supporting Material). We show that domain [Ca²⁺] fluctuations in the presence of two rapid buffers with different dissociation constants and exchange rates is given by the multiple buffer fluctuating RBA and not a naive weighted average utilizing total buffer concentration (see Fig. S2 in the Supporting Material).

Interpretation of the fluctuating rapid buffer limit

Some salient observations can be made regarding domain [Ca²⁺] fluctuations in the rapid buffer limit (Eqs. 37 and 41):

• 1.The effective volume in the fluctuating RBA is smaller than the physical volume (χ ≥ 0 and thus Ω^′_eff ≤ Ω). This is in marked contrast to the effective volume for the deterministic RBA that is greater than the physical volume (Ω^′_eff = Ω/β_ss > Ω). This is to say, we have analytically confirmed our previous numerical result demonstrating that rapid buffers typically increase the magnitude of domain [Ca²⁺] fluctuations (Fig. 2).
• 2.The χ in ${\sigma }_c^{\prime }$ is proportional to the concentration difference c_ss − c_∞ (Eq. 37). That is, the buffer-mediated enhancement of domain [Ca²⁺] fluctuations is an increasing function of the disequilibrium between the steady-state domain [Ca²⁺] (c_ss) and the bulk (c_∞).
• 3.The numerically observed biphasic dependence of the relative magnitude of domain [Ca²⁺] fluctuations (c_v in Fig. 2) corresponds to the factor β_ssw_ssk_b/(k_c + w_ssk_b) in χ that is a biphasic function of $b_T^{\infty }$ through β_ss and w_ss.
• 4.In several limiting parameter regimes, the steady-state variance of domain [Ca²⁺] fluctuations is not affected by Ca²⁺ buffer (χ = 0 and thus ${\sigma }_c^{\prime }$ = ${\sigma }_c^0$ = c_ss/Ω). These include the absence of Ca²⁺ influx (j_in = 0, c_ss = c_∞), immobile buffer that is unable to exchange with the bulk (k_b = 0), and extreme values for the total buffer concentration (both $b_T^{\infty }$ → 0 and $b_T^{\infty }$ → ∞). However, even in these limiting parameter regimes, buffers do not decrease [Ca²⁺] fluctuations to a size less than that observed in the absence of buffer.
• 5.
  The total buffer concentration that maximizes domain [Ca²⁺] fluctuations for a given fixed c_ss,

  $$b_{T\text{∗}}^{\infty }=\sqrt{\frac{k_c}{k_b}}\times \frac{{\left(c_{ss}+\kappa \right)}^2}{\kappa },$$ (42)

  is found as the $b_T^{\infty }$ that zeros ∂(1 + χ)/∂$b_T^{\infty }$ = ∂χ/∂$b_T^{\infty }$. This corresponds to

  $$w_{ss}^{\text{∗}}=\sqrt{k_c/k_b},$$

  $${\beta }_{ss}^{\text{∗}}=\sqrt{k_b/k_c}/\left(1+\sqrt{k_b/k_c}\right),$$

  and

  $$\begin{array}{c}{\text{Ω}}_{\text{eff}}^{\text{′}\text{∗}}=\frac{\text{Ω}}{1+{\chi }^{\text{∗}}},\\ c_v^{\text{′}\text{∗}}=\sqrt{\frac{1+{\chi }^{\text{∗}}}{c_{ss}\text{Ω}}},\\ {\chi }^{\text{∗}}=\frac{k_b/k_c}{{\left(1+\sqrt{k_b/k_c}\right)}^2}\times \frac{c_{ss}-c_{\infty }}{\kappa +c_{\infty }}.\end{array}$$ (43)
• 6.Equation 43 indicates that the maximum fluctuation magnitude is determined in part by the relative exchange rate k_b/k_c. Because χ^∗ is a monotone increasing function of k_b/k_c, domain [Ca²⁺] fluctuations can, formally, be made as large as possible by choosing k_b ≫ k_c and optimal $b_{T\text{∗}}^{\infty }$ (Eq. 42). However, the molecular weight of Ca²⁺-bound buffer is greater than Ca²⁺ and, consequently, one expects Ca²⁺-bound buffer to diffuse and exchange with the bulk more slowly than free Ca²⁺. This physical consideration implies that k_b ≤ k_c and, after imposing this constraint, the physiologically realistic parameter choice that maximizes domain [Ca²⁺] fluctuations (k_b ≈ k_c) leads to χ^∗ ≈ 1/4(c_ss –c_∞)/(c_∞ + κ) and thus

$${\frac{c_v^{\text{′}}}{c_v^0}|}_{\ast }=\sqrt{1+\frac{c_{ss}-c_{\infty }}{4\left(c_{\infty }+\kappa \right)}}.$$

• 7.The buffer dissociation constant κ influences buffer-mediated increase in [Ca²⁺] fluctuations in a complex manner. For example, the variance of free [Ca²⁺] fluctuations (${\sigma }_c^{\prime }$, Eqs. 37 and 38) depends on the relative (as opposed to absolute) concentrations of domain (c_ss/κ) and bulk (c_∞/κ) Ca²⁺ and total buffer ($b_T^{\infty }$/κ) via the dimensionless quantities β_ss and w_ss. This is because the buffering capacity can expressed as w_ss = ($b_T^{\infty }$/κ)/(1 + c_ss/κ)² and, similarly, the second factor of χ can be written as (c_ss/κ − c_∞/κ)/(1 + c_∞/κ). For a given steady-state [Ca²⁺], c_ss, the total buffer concentration with maximal effect ($b_{T\text{∗}}^{\infty }$, Eq. 42) is a u-shaped function of the buffer dissociation constant κ (see Supporting Results and Fig. S3 in the Supporting Material).

Applicability of the fluctuating rapid buffer approximation

In the spatial and deterministic formulation of the buffered diffusion of intracellular Ca²⁺, the rapid buffer approximation is valid when the equilibration time for buffers is much smaller than the time constant for Ca²⁺ diffusion. In this minimal model of domain [Ca²⁺] fluctuations, Ca²⁺ and buffer diffusion are represented as first-order reactions (rate constants k_c and k_b) that couple the domain with the bulk. The validity of the fluctuating RBA depends on buffer kinetics being faster than exchange. Consequently, the physical domain volume influences the validity of this approximate result.

The time constant for diffusion-mediated passive exchange between compartments can be characterized by the mean escape time for a Brownian particle with diffusion constant D leaving a domain of volume Ω via a small opening of radius a (36),

$$\tau =\frac{\text{Ω}}{4aD}.$$ (44)

As illustrated in Fig. 3 A, a cubical domain (Ω = L³) with an opening whose radius scales with linear dimension (ρ = a/L < 1) would yield rate constant k = 1/τ and thus k_i = 4ρD_i/L², where i ∈{c, b} and D_c and D_b are the diffusion coefficients for Ca²⁺ and buffer, respectively. Using parameters for the fast, mobile buffer BAPTA, Fig. 3 B plots the coefficient of variation of domain [Ca²⁺] fluctuations (c_v) and the buffer-mediated relative decrease in system size (${\sigma }_c^0$/${\sigma }_c^{\mathit{ss}}$, where ${\sigma }_c^0$ = c_ss/Ω) as functions of physical domain volume Ω for different values of the dimensionless escape radius ρ (shaded lines). As expected, both c_v and ${\sigma }_c^0$/${\sigma }_c^{\mathit{ss}}$ decrease with system size Ω. Narrowing the dimensionless escape radius (decreasing ρ) leads to an increase in c_v and a decrease in ${\sigma }_c^0$/${\sigma }_c^{\mathit{ss}}$ for any physical domain volume Ω. Comparison of the solid and dotted lines in Fig. 3 B shows that the fluctuating RBA agrees with the full calculation when the physical domain volume Ω is sufficiently large and/or the escape opening is sufficiently narrow (small ρ). Both situations lead to exchange rates (k_c and k_b) that are small compared to rate of buffer equilibration (an increasing function of both k₊ and k₋).

Figure 3.

The geometric parameters of a Ca²⁺ domain determine the time constant for escape of Ca²⁺ and buffer and the range of applicability of the fluctuating rapid buffer approximation (RBA). (A) Diagram of restricted subspace with volume Ω, linear dimension L, and radius of domain escape a. (B) (Shaded lines) Coefficient of variation of domain [Ca²⁺] fluctuations (c_v, top) and buffer-mediated relative decrease in system size (${\sigma }_c^0$/${\sigma }_c^{\mathit{ss}}$, bottom) as functions of physical domain volume Ω using four decades of dimensionless escape radii ρ = a/L = 10⁻⁴,…,10⁻¹. (Dashed black lines) Fluctuating RBA (Eq. 39) well approximates the full calculation when ρ is small. c_ss = 1 μM. (C) Illustration of three frequent spine shapes adapted from Harris et al. (41). (D, top) Relative increase in c_v in the presence of BAPTA, compared with the absence of buffer $c_v^0$, for different spine shapes. (D, bottom) Percent difference between c_v as calculated using the fluctuating RBA, $c_v^{\prime }$ and the full calculation, c_v. c_ss = 10 μM. Parameters: c_∞ = 0.1 μM, D_c = 0.2 μm²/ms. BAPTA (72): D_b = 0.1 μm²/ms, k₊ = 0.6 μM⁻¹ ms⁻¹ , κ = 0.2 μM, and $b_T^{\infty }$ = 100 μM. Spine geometries (41): thin (a = 0.05 μm, Ω = 4 × 10⁻¹⁷L), mushroom (a = 0.1 μm, Ω = 2.9 × 10⁻¹⁶L), and stubby (a = 0.16 μm, Ω = 3 × 10⁻¹⁷L).

[Ca²⁺] fluctuations in a physiological setting

Neuronal dendritic spines are a good setting to illustrate the influence of Ca²⁺ buffer on domain [Ca²⁺] fluctuations and explore the validity of the fluctuating RBA, in part because such spines are highly variable in shape and size. Although it is difficult to define an average spine geometry, most spines have a clearly defined neck (corresponding to the escape opening of radius a in the previous paragraph) and head (corresponding to the microdomain of volume Ω). Fig. 3 C illustrates three frequently observed spine shapes—thin, mushroom, and stubby—whose geometric parameters (a and Ω) have been experimentally quantified (41).

Fig. 3 D shows that over a wide range of concentrations, the fast buffer BAPTA increases the coefficient of variation, compared with the absence of buffer (c_v/$c_v^0$), by as much as a factor of 2 (top). The largest increase occurs in the case of the mushroom-shaped dendritic spine, for which the ratio of the spine-neck opening cross-sectional area, and the spine-head volume, is smallest (a/Ω).

For small and large BAPTA concentrations, there is a negligible difference between the fluctuating RBA and the corresponding full calculation, even measured in relative terms (Fig. 3 D, bottom). When the BAPTA concentration induces comparatively large [Ca²⁺] fluctuations, the fluctuating RBA overestimates the c_v (depending on spine shape by as much as 50–150% in the worst case). When the steady-state domain [Ca²⁺] (c_ss) is decreased, the disequilibrium between domain Ca²⁺ and buffer is attenuated, and the relative deviation between the RBA and full calculation is smaller (not shown). The fluctuating RBA works best for the mushroom-shaped dendritic spine, because a/Ω is smallest.

Influence of buffers on the relaxation time for domain [Ca²⁺] fluctuations

We have demonstrated that in the presence of Ca²⁺ influx (j_in > 0), Ca²⁺ buffer may significantly increase the steady-state covariance of [Ca²⁺] fluctuations, especially when buffers are mobile and rapid (Eq. 37). On the other hand, the fluctuating RBA shows that in the absence of Ca²⁺ influx (j_in = 0, c_ss = c_∞), fluctuation amplitude is not influenced by total buffer concentration ($c_v=c_v^0=1/\sqrt{c_{ss}\text{Ω}}$ as when $b_T^{\infty }$ = 0), a result that holds generally (e.g., when buffers are slow) in numerical simulations (not shown). This occurs because Γ_ss and H_ss scale in such a way that the steady-state covariance matrix Σ_ss is not a function of $b_T^{\infty }$ when j_in = 0 (Eq. 30). On the other hand, the time-dependent stochastic dynamics of the fluctuating concentrations (δc, δb, δcb) and the relaxation of the covariance matrix Σ to steady state are a function of buffer properties in both the absence or presence of Ca²⁺ influx (Eq. 27). For example, the relaxation rates governing the dynamics of Eq. 27 are given by the pairwise sums of the eigenvalues of H_ss (by properties of Kronecker sums and Eq. 31 (42)), and these are a function of $b_T^{\infty }$ in both the presence and absence of Ca²⁺ influx.

Fig. 4 A shows Monte Carlo simulations of domain [Ca²⁺], c(t), fluctuating around the steady-state c_ss that were generated by numerical integration of Eq. 21 using the Euler-Maruyama method. In the absence of buffer, the fluctuations δ_c(t) = c(t) – c_ss are typically small and long-lasting (Fig. 4 Aa). Similar dynamics are observed in the presence of slow buffers (Fig. 4 Ab). Conversely, in the presence of rapid buffer, free [Ca²⁺] fluctuations and subsequent relaxation to steady state occurs on a fast timescale (Fig. 4 Ac).

Figure 4.

Influence of buffer on the time evolution of [Ca²⁺] fluctuations. (A) Monte Carlo simulation of domain [Ca²⁺], c(t), for different buffer parameters. (B) Autocorrelation function (ϕ_c,c (τ), Eq. 45) and (C) power spectrum (s_c,c(ω), Eq. 46) in the presence of slow (open circles) and fast (dashed line) buffer and in the absence of buffer (solid line). Autocorrelation function curves are normalized by the steady-state variance such that ϕ_c,c (0) = 1. Parameters: c_ss = 0.1 μM, c_∞ = 0.1 μM, k_c = 0.2 ms⁻¹, and Ω = 10⁻¹⁷L. Buffer parameters: $b_T^{\infty }$ μM, κ = 0.2 μM, k_b = 10⁻¹ ms⁻¹, k₊ = 10⁻³ (slow), and 1 (fast) μM⁻¹ ms⁻¹.

One characterization of the influence of buffer on the time evolution of [Ca²⁺] fluctuations is given by the 3×3 steady-state correlation function Φ = (ϕ_i,j) with i,j ∈ {c,b,cb},

$$\text{Φ}\left(\tau \right)\equiv \langle \mathit{\delta }\left(\tau \right){\mathit{\delta }}^T\left(0\right)\rangle ,$$

where Φ(0) = Σ_ss. In the presence of buffer the correlation function for the domain [Ca²⁺] fluctuation δc is given by ϕ_c,c(τ), where −∞ < τ < ∞ and

$$\text{Φ}\left(\tau \right)=\text{exp}\left(-\left|\tau \right|H_{ss}\right){\text{Σ}}_{ss},$$ (45)

whereas in the absence of buffer ${\varphi }_{c,c}^0\left(\tau \right)={\sigma }_c^0\text{exp}\left(-k_c\left|\tau \right|\right)$ (26). Fig. 4 B plots ϕ_c,c(τ) using parameters that correspond to the three previously shown stochastic trajectories (Fig. 4 Aa–c). In the absence of buffer, ϕ_c,c(τ) decays by 50% when τ ≈ 5 ms, consistent with the time constant for Ca²⁺ exchange (k_c = 0.2 ms⁻¹, solid line). In the presence of slow buffer, ϕ_c,c(τ) is nearly identical (open circles), but in the presence of fast buffer the 50% decay occurs at a much shorter time (τ ≈ 0.1 ms, dashed line).

The time evolution of the domain [Ca²⁺] fluctuation δc(t) can also be characterized by its (colored) power spectrum, that is, the 3×3 matrix S(ω) = (s_i,j),

$$S\left(\omega \right)={\left(i\omega I+H_{ss}\right)}^{-1}{\text{Γ}}_{ss}{\left(-i\omega I+H_{ss}^T\right)}^{-1}$$ (46)

that reduces to

$$s_{c,c}^0\left(\omega \right)=2k_c{c}_{ss}/\left[\text{Ω}\left({\omega }^2+k_c^2\right)\right]$$

in the absence of buffer (26). Fig. 4 C shows the power spectrum s_c,c(ω) in the absence of buffer and in the presence of slow buffer (solid line, open circles). In both cases, the spectrum is low-pass, but for fast buffer, s_c,c(ω) drops off at higher frequency (smaller τ, dashed line), consistent with the higher frequency fluctuations observed in Fig. 4 A. In addition to clarifying the frequency content of domain [Ca²⁺] fluctuations, this power spectrum analysis illustrates how buffers influence fluctuations even in the absence of Ca²⁺ influx. Further analysis of the influence of buffers on the timescale of domain [Ca²⁺] fluctuations is provided in Fig. S4 and Fig. S5.

Discussion

Relation to prior work

The influence of Ca²⁺ buffers on Ca²⁺ diffusion, oscillations, propagating Ca²⁺ waves, and spatially localized Ca²⁺ elevations has received considerable attention in recent years (for reviews focused on local signaling, see Berridge (2,43), Smith et al. (45), and Augustine et al. (46)). Previous studies have presented theoretical analysis of buffered Ca²⁺ diffusion and localized Ca²⁺ elevations (16–18,20,47–49), as well as stochastic aspects of Ca²⁺-induced Ca²⁺ release, Ca²⁺ oscillations, and propagating Ca²⁺ waves (34,50–53). A subset of these studies utilized a Langevin formulation for the dynamics of intracellular Ca²⁺ channels (54–56).

Models of Ca²⁺-regulated ${\text{Ca}}^{2+}$ channels and stochastic Ca²⁺ release usually incorporate buffering into the domain description and, more rarely, consider the fluctuations in free [Ca²⁺] that result from the small volume of subcellular compartments (e.g., the cardiac dyadic subspace) (30,33–35). To our knowledge, this is the first study that formulates Langevin equations for the buffered dynamics of intracellular Ca²⁺ and, subsequently, characterizes the influence of Ca²⁺ buffers on [Ca²⁺] fluctuations that arise from the association and dissociation of Ca²⁺ and buffer. The analytical results pertaining to the fluctuating rapid buffer approximation (RBA) and the influence of buffers’ properties on fluctuation amplitude is, to our knowledge, entirely novel.

Previous studies have, of course, utilized Langevin equations to simulate concentration fluctuations in other biochemical systems (30,33,57–60) and the stochastic gating of plasma membrane and intercellular ion channels (54,55,61–64), and used the fluctuation-dissipation theorem to characterize concentration fluctuations in biochemical reaction networks, e.g., in models of gene networks and Michaelis-Menten enzyme reactions (65–68). However, to our knowledge, this is the first mathematical analysis of domain [Ca²⁺] fluctuations in the presence of Ca²⁺ buffers.

Summary of findings

The fluctuating RBA derived above shows how the Ca²⁺ and buffer exchange rates (k_c and k_b), total buffer concentration ($b_T^{\infty }$), and dissociation constant (κ) influence [Ca²⁺] fluctuations. Typically, fast buffer binding and high exchange rates increase the size of [Ca²⁺] fluctuations (${\sigma }_c^{\mathit{ss}}$ = 〈δc²〉). The fluctuating RBA derived here shows that the relative increase in fluctuation size due to buffers, i.e., the ratio of coefficients of variation (Eq. 40), is an increasing function of the steady-state domain [Ca²⁺] (c_ss) and thus an increasing function of Ca²⁺ influx rate (j_in). For fixed steady-state domain [Ca²⁺], c_ss > c_∞, Fig. 2 and Eq. 40 show that the relative fluctuation size $c_v^{\prime }$/$c_v^0$ is a biphasic function of the total buffer concentration $b_T^{\infty }$. At low $b_T^{\infty }$, the fluctuation amplitude approaches that observed in the absence of buffer ($c_v^{\prime }$ ≈ $c_v^0$, w_ss → 0 in Eq. 37). At high $b_T^{\infty }$, the ratio $c_v^{\prime }$/$c_v^0$ ≈ 1 because increased buffering capacity attenuates the buffer-mediated increase in free [Ca²⁺] fluctuations (β_ss → 0 in Eq. 37). The total buffer concentration that maximizes $c_v^{\prime }$/$c_v^0$ is given by Eq. 42. For a fixed Ca²⁺ influx rate j_in, c_ss is a decreasing sigmoidal function of $b_T^{\infty }$ that approaches c_∞ (Eq. 20). In this case, ${\sigma }_c^{\mathit{ss}}$ is a decreasing sigmoidal function that approaches c_∞/Ω. However, the buffer-mediated change in fluctuation size as measured by

$$c_v^{\text{′}}/c_v^0=\sqrt{1+\chi }\ge 1,$$

remains a biphasic function of $b_T^{\infty }$. For fixed c_ss and for fixed j_in, Ca²⁺ buffers increase the amplitude of domain [Ca²⁺] fluctuation.

We explore the validity of the RBA for realistic buffer parameters and microdomain geometries and find the fluctuating RBA is a good approximation when buffer kinetics are rapid compared to the Ca²⁺ and buffer exchange rates. Exchange rates on domain volume depends on the presumed relationship between escape target size and linear dimension of the domain. However, the fluctuating RBA agrees with the full calculation whenever the physical domain volume is sufficiently large and/or the escape passage is sufficiently narrow, because both situations lead to exchange rate constants (k_c and k_b) that are small compared to the buffer equilibration rate (an increasing function of both k₊ and k₋). As one would expect based on these considerations, the fluctuating RBA is a better approximation to the full equations for domain [Ca²⁺] fluctuations for mushroom-shaped (as opposed to thin or stubby) dendritic spine geometries (Fig. 3 D).

Our analysis shows that a buffer-mediated increase in intrinsic [Ca²⁺] fluctuations requires a nonequilibrium steady state, that is, a gradient between domain and bulk Ca²⁺ (c_ss > c_∞), which implies disequilibrium between Ca²⁺ and buffer within the domain. However, our primary result that buffers do not suppress intrinsic [Ca²⁺] fluctuations—due to the buffer’s contribution to these fluctuations—is true in the absence, as well as the presence, of elevated domain [Ca²⁺]. Although buffers do not influence the steady-state variance of domain [Ca²⁺] fluctuations in the absence of Ca²⁺ influx, power spectrum analysis shows that buffers do alter the temporal dynamics of domain [Ca²⁺] fluctuations. For fixed κ = k₋/k₊, a faster association rate constant (k₊) leads to higher frequency free [Ca²⁺] fluctuations and shorter autocorrelation times.

Buffers suppress extrinsic (not intrinsic) domain [Ca²⁺] fluctuations

As discussed in the Introduction, the effective volume that arises in the deterministic equations for the buffered diffusion of intracellular Ca²⁺ is

$${\text{Ω}}_{\text{eff}}=\text{Ω}/\beta \left(c\right),$$

where Ω_eff ≥ Ω because 0 < β(c) ≤ 1 (24). Because the relative size of concentration fluctuations decreases as system size increases, one might expect that domain [Ca²⁺] fluctuations would decrease as total buffer concentration increases. In marked contrast to this conjecture, the analysis of domain [Ca²⁺] fluctuations presented here demonstrates that buffers increase the size of [Ca²⁺] fluctuations (during periods of Ca²⁺ influx) or have no influence (when there is no influx). That is, buffers typically lead to domain [Ca²⁺] fluctuations with variance ${\sigma }_c^{\mathit{ss}}$ that is consistent with a domain that lacks buffers but has smaller physical volume.

Some clarity with regard to this counterintuitive result can be obtained by revisiting the fast/slow system of stochastic ODEs for buffered Ca²⁺ dynamics (Eq. 34) under the restriction that Ca²⁺-free or Ca²⁺-bound buffer do not exchange with bulk (k_b = 0),

$$\dot{\delta c}=-\left[k_{+}\left(c_{ss}+b_{ss}\right)+k_{-}+k_c\right]\delta c+\left(k_{+}{c}_{ss}+k_{-}\right)\delta c_T+{\xi }_c^{ss}\left(t\right),$$ (47a)

$$\delta {\dot{c}}_T=-k_c\delta c+{\xi }_{c_T}^{ss}\left(t\right).$$ (47b)

Here the fluctuation is free [Ca²⁺]. The value (δc) is the fast variable and δc_T is the only slow variable because the domain total buffer concentration is a conserved quantity given by initial conditions (b_T = b(0) + cb(0)) and does not fluctuate (δb_T = 0). Setting k_b = 0 in Eq. 37, we see that under this restriction χ = 0, and the fluctuating RBA result is identical to the case without buffers,

$$c_v^{\text{′}}=c_v^0=1/\sqrt{c_{ss}\text{Ω}},$$

because immobile buffers (k_b = 0) do not change the steady-state variance of domain [Ca²⁺] fluctuations. Note that when k_b = 0, the differential fraction of free to total calcium (β_ss) appears in the quasistatic approximation,

$${\langle \delta c\rangle }_{\text{∗}}\approx {\beta }_{ss}\delta c_T$$

and the slow equation,

$$\delta {\dot{c}}_T=-{\beta }_{ss}{k}_c\delta c_T+{\xi }_{c_T}^{ss}\left(t\right),$$ (48)

precisely as one would expect. Using the fluctuation-dissipation equation (Eq. 30), we calculate the steady-state covariance of the total calcium concentration,

$$\langle \delta c_T^2\rangle =\frac{{\gamma }_c^{ss}}{2{\beta }_{ss}{k}_c}=\frac{2k_c{c}_{ss}}{2{\beta }_{ss}{k}_c\text{Ω}}=\frac{c_{ss}}{{\beta }_{ss}\text{Ω}},$$ (49)

as well as the covariances that involve the fast variable δc. In the RBA limit with k_b = 0, the latter are given by

$$\langle \delta c\delta c_T\rangle ={\beta }_{ss}\langle \delta c_T^2\rangle =\frac{c_{ss}}{\text{Ω}}$$ (50a)

and

$$\langle \delta c^2\rangle =\frac{{\gamma }_r^{ss}}{2\left[k_{+}\left(c_{ss}+b_{ss}\right)+k_{-}\right]}+{\beta }_{ss}^2\langle \delta c_T^2\rangle$$ (50b)

$$=\left(1-{\beta }_{ss}\right)\frac{c_{ss}}{\text{Ω}}+{\beta }_{ss}\frac{c_{ss}}{\text{Ω}}=\frac{c_{ss}}{\text{Ω}},$$ (50c)

where for the second equality we have used β_ssw_ss = 1 – β_ss and the definition of ${\gamma }_r^{\mathit{ss}}$ (Eq. 23).

Equation 49 shows that the covariance of the total [Ca²⁺] fluctuation (〈δ$c_T^2$〉) responds to the elementary processes of Ca²⁺ influx and exchange with the bulk

$${\gamma }_c^{ss}=\left[j_{\text{in}}+k_c\left(c_{ss}+c_{\infty }\right)\right]/\text{Ω}=2k_c{c}_{ss}/\text{Ω}\text{.}$$

The covariance of the free [Ca²⁺] is also dependent on influx and exchange (${\gamma }_c^{\mathit{ss}}$) through the term ${\beta }_{ss}^2$〈δ$c_T^2$〉. The value 〈δc²〉 is influenced by the elementary processes of Ca²⁺ and buffer association and dissociation

$${\gamma }_r^{ss}=\left[k_{+}{c}_{ss}{b}_{ss}+k_{-}c{b}_{ss}\right]/\text{Ω,}$$

whereas 〈δ$c_T^2$〉 is not. Increasing buffer concentration ($b_T^{\infty }$) decreases β_ss and increases 〈δ$c_T^2$〉. The value $b_T^{\infty }$ also scales ${\gamma }_r^{\mathit{ss}}$ in such a way that 〈δc²〉 is unchanged. Stationary buffers do not influence the steady-state covariance of domain [Ca²⁺] fluctuations (k_b = 0), because the intrinsic nature of the fluctuating force ${\xi }_c^{ss}$ (t) causes ${\gamma }_r^{\mathit{ss}}$ and β_ss to be related in a manner that makes 〈δc²〉 = c_ss/Ω invariant to the buffer parameter $b_T^{\infty }$ and κ.

However, if the influx rate were modulated so that there was an extrinsic component to the fluctuations,

$$j_{\text{in}}\left(t\right)=j_{\text{in}}^0+j_{\text{in}}^1\left(t\right)$$

where

$$j_{\text{in}}^0=k_c\left(c_{ss}-c_{\infty }\right)\text{and}\langle j_{\text{in}}^1\left(t\right)j_{\text{in}}^1\left(t\text{'}\right)\rangle ={\gamma }_{\text{in}}^{ss}\delta \left(t-t^{\text{'}}\right),$$

where ${\gamma }_{\text{i}\text{n}}^{ss}$ = $j_{\text{ext}}^{ss}$/Ω, then the fluctuating terms in both Eqs. 47a and 47b would have greater variance and Eqs. 49 and 50b become

$$\langle \delta c_T^2\rangle =\frac{{\gamma }_c^{ss}+{\gamma }_{\text{in}}^{ss}}{2{\beta }_{ss}{k}_c}=\frac{c_{ss}}{{\beta }_{ss}\text{Ω}}\left(1+\frac{j_{\text{ext}}^{ss}}{2k_c{c}_{ss}}\right)$$

and

$$\begin{array}{c}\langle \delta c^2\rangle =\frac{{\gamma }_r^{ss}+{\gamma }_{\text{in}}^{ss}}{2\left[k_{+}\left(c_{ss}+b_{ss}\right)+k_{-}\right]}+{\beta }_{ss}^2\langle \delta c_T^2\rangle \\ =\left(1-{\beta }_{ss}\right)\frac{c_{ss}}{\text{Ω}}+{\beta }_{ss}\frac{c_{ss}}{\text{Ω}}\left(1+\frac{j_{\text{ext}}^{ss}}{2k_c{c}_{ss}}\right)=\frac{c_{ss}}{\text{Ω}}\left(1+{\beta }_{ss}\frac{j_{\text{ext}}^{ss}}{2k_c{c}_{ss}}\right),\end{array}$$

where we have used the fact that ${\gamma }_{\text{i}\text{n}}^{ss}$/k₊ → 0 in the RBA limit. From the last equality we conclude that the variance of the external drive ${\gamma }_{\text{i}\text{n}}^{ss}$ increases the steady-state variance of domain [Ca²⁺] fluctuations. The location of the coefficient β_ss in the term $\left(1+{\beta }_{ss}{j}_{\text{ext}}^{ss}/2k_c{c}_{ss}\right)$ shows that stationary buffers are able to suppress such extrinsic variability of Ca²⁺ influx/efflux rate, despite the fact that the buffers do not suppress intrinsic fluctuations (compare to Eq. 50b).

Analysis of the fluctuating RBA and intrinsic fluctuations

Analysis of the fluctuating RBA also provides insight into intrinsic (buffer-driven) fluctuations when both Ca²⁺ and buffer exchange with bulk (k_b ≠ 0). The quasistatic approximation for the average value of the [Ca²⁺] fluctuation in the fluctuating RBA (Eq. 35) shows that the free (δc) and total (δc_T) calcium fluctuations are related by the factor β_ss as expected. Also, Eq. 36a shows that total buffer concentration $b_T^{\infty }$ slows the relaxation of total calcium fluctuations (δc_T) through the factor β_ss. However, the relaxation of total buffer (δb_T) fluctuations are not slowed in this manner (Eq. 36b) and, importantly, the entries of the covariance matrix for the random terms ${\xi }_c^{ss}$, ${\xi }_{c_T}^{ss}$, and ${\xi }_{b_T}^{ss}$, are all proportional to the total buffer concentration $b_T^{\infty }$ (Eq. S18 and Eq. S20 in the Supporting Material).

To understand the interplay between the effect of $b_T^{\infty }$ on the random terms (fluctuation) and the relaxation rate (dissipation) in the case of mobile buffers (k_b > 0), we analyze the Langevin domain model when the exchange rates for Ca²⁺ and buffer are identical (k_c = k_b = k). Under this restriction, the covariances of the slow variables are given by

$$\begin{array}{c}\langle \delta c_T^2\rangle =\frac{c_{ss}+c{b}_{ss}}{\text{Ω}},\\ \langle \delta c_T\delta b_T\rangle =\frac{c{b}_{ss}+c{b}_{\infty }}{2\text{Ω}},\\ \langle \delta b_T^2\rangle =\frac{b_T^{\infty }}{\text{Ω}},\end{array}$$ (51)

where the c_ss + cb_ss value in the numerator of 〈δ$c_T^2$〉 is the steady-state total calcium concentration in the domain. The variance of the fast variable 〈δc²〉 can be written in terms of the covariances of the slow variables,

$$\langle \delta c^2\rangle ={\beta }_{ss}\left[w_{ss}\frac{c_{ss}}{\text{Ω}}+{\beta }_{ss}\left(\langle \delta c_T^2\rangle -2{\nu }_{ss}\langle \delta c_T\delta b_T\rangle +{\nu }_{ss}^2\langle \delta b_T^2\rangle \right)\right],$$ (52)

and it can be shown that 〈δcδb_T〉 is negative whereas 〈δcδc_T〉 and 〈δc²〉 are positive. Upon substitution of Eq. 51, we have

$$\langle \delta c^2\rangle =\frac{{\beta }_{ss}}{\text{Ω}}\left\{w_{ss}{c}_{ss}+{\beta }_{ss}\left[c_{ss}+c{b}_{ss}-{\nu }_{ss}\left(c{b}_{ss}+c{b}_{\infty }\right)+{\nu }_{ss}^2{b}_T^{\infty }\right]\right\},$$ (53a)

$$=\frac{1}{\text{Ω}}\left\{\left(1-{\beta }_{ss}\right)c_{ss}+{\beta }_{ss}^2\left[c_{ss}+c{b}_{ss}-{\nu }_{ss}\left(c{b}_{ss}+c{b}_{\infty }\right)+{\nu }_{ss}^2{b}_T^{\infty }\right]\right\}.$$ (53b)

In this case, the fluctuating RBA simplifies to

$$\begin{array}{c}{\sigma }_c^{\text{′}}=\frac{c_{ss}}{\text{Ω}}\times \left(1+\chi \right),\\ \chi =\frac{w_{ss}}{{\left(1+w_{ss}\right)}^2}\times \frac{c_{ss}-c_{\infty }}{\kappa +c_{\infty }}.\end{array}$$ (54)

This analysis of the fluctuating RBA under the restriction k_c = k_b shows that an increase in total buffer $b_T^{\infty }$ increases the absolute value of the slow covariances (Eq. 51). These covariances (the terms within square brackets in Eq. 53) combine to create a net positive impact on 〈δc²〉 that is attenuated to some extent by a decrease in the β_ss that scales these terms. The β_ss/Ω value outside the curly brackets in Eq. 53a might be interpreted as an effective volume that attenuates all of these contributions to 〈δc²〉, but this is misleading because β_ssw_ssc_ss = (1 − β_ss)c_ss is an increasing function of $b_T^{\infty }$ (compare to Eq. 53b). Furthermore, Eq. 54 shows that the variance of the free [Ca²⁺] fluctuations in the presence of buffer $b_T^{\infty }$ > 0 is never less than what would occur in the absence of buffer ($b_T^{\infty }$ = 0).

All of the expressions in this section have counterparts when the fluctuating RBA is derived in full generality (k_c ≠ k_b, see Appendix B in the Supporting Material). The derivation of the fluctuating RBA when k_c = k_b is shown in Appendix C in the Supporting Material.

Physiological implications

Ca²⁺ is an important signaling molecule in many cell types. Intracellular Ca²⁺ regulates cellular responses through Ca²⁺-regulated ion channels, Ca²⁺-dependent kinases, and phosphotases, and key processes in excitable cells, including muscle contraction and neurotransmitter release (1). Many of these signaling pathways occur in small spatially restricted volumes (microdomains) and, consequently, fluctuations in [Ca²⁺] may be physiologically significant. Our results are broadly applicable to subcellular Ca²⁺ domains, including dendritic spines, the dyadic cleft, and many other situations where localized Ca²⁺ elevations occur in spatially restricted subcellular compartments, such as the primary cilium, mitochondria-ER junctions, and endoplasmic reticulum/plasma membrane (ER/PM) junctional regions (Fig. 1). As a concrete example of an application of the theory, we found—using physiological values for dendritic spine shape—that the exogenous Ca²⁺ buffer BAPTA does not suppress intrinsic domain [Ca²⁺] fluctuations, and may increase the coefficient of variation (c_v) of domain [Ca²⁺] fluctuations by a factor of 2 or more (Fig. 3 D).

Spatially localized subcellular dynamics can greatly alter whole-cell or even tissue-level physiological processes. For example, in the cardiac dyadic subspace, the regenerative (i.e., positive feedback) nature of Ca²⁺-induced Ca²⁺-release creates a subcellular environment where the spontaneous opening of only a few Ca²⁺ channels can lead to opening of nearly all of the channels in a dyad (essentially an all-or-none response) (69). Ca²⁺ release that spontaneously initiates within one dyad may activate neighboring dyads resulting in propagating Ca²⁺ waves. In pathophysiological conditions this may lead to ectopic heart beats that are potentially arrhythmogenic. This is one of many examples where the spatially localized stochastic dynamics of a few Ca²⁺ channels may influence the global Ca²⁺ response and, for this reason, the regulation of Ca²⁺ channels by buffer-modulated [Ca²⁺] fluctuations may be physiologically significant.

In Weinberg and Smith (35), we developed and analyzed a minimal model of a Ca²⁺ microdomain that included a stochastically gating Ca²⁺-regulated Ca²⁺ channel and accounted for the small number of Ca²⁺ ions present in the domain at any given time. This prior work demonstrated that [Ca²⁺] fluctuations due to small domain volumes could alter the open probability of Ca²⁺ channels, typically reducing the open probability compared with larger volumes. The fluctuating RBA derived here shows that Ca²⁺ buffers typically enhance domain [Ca²⁺] fluctuations and, when combined with previous work, this suggests that buffers may influence the stochastic dynamics of Ca²⁺-regulated Ca²⁺ channels (the frequency and duration of channel openings) and potentially influence the stochastic properties of local Ca²⁺ release events (sparks and puffs).

Our analysis of the fluctuating RBA raises the intriguing question of whether or not domain [Ca²⁺] fluctuations are physiologically significant aspects of local (and perhaps global) Ca²⁺ signaling. This topic requires further study, in part because our mathematical analysis indicates that Ca²⁺ chelators and indictor dyes enhance intrinsic domain [Ca²⁺] fluctuations. The physiological relevance of domain [Ca²⁺] fluctuations on the dynamics of signaling complexes will presumably depend on the timescale of Ca²⁺ influx, the geometry of the microdomain, and the kinetics of downstream Ca²⁺-dependent signaling.

Limitations of this analysis

We have shown that [Ca²⁺] fluctuations in spatially restricted subcellular compartments cannot be suppressed by increasing the total concentration of Ca²⁺ buffer ($b_T^{\infty }$). Of course, this conclusion that Ca²⁺ buffers typically enhance domain [Ca²⁺] fluctuations pertains only to buffers whose dynamics are well represented by the bimolecular association reaction that was our starting point (Eq. 1). It is possible that Ca²⁺ buffers with more complicated and realistic Ca²⁺-binding kinetics (e.g., cooperative binding) may suppress free [Ca²⁺] fluctuations. This question could be addressed rigorously using chemical reaction network theory.

Although we consider Ca²⁺ and buffer transport via exchange between domain and bulk, this work does not use continuum modeling (partial differential equations) to explicitly represent spatial aspects of the buffered diffusion of intracellular Ca²⁺. Spatial correlations in fluctuations are of interest, but beyond the scope of this study, in part because the mathematical description of diffusion-mediated concentration fluctuations is less accessible than the analysis of stochastic differential equations presented here.

This article has focused on intrinsic Ca²⁺ and buffer concentration fluctuations around nonequilibrium steady states in the presence of Ca²⁺ influx (j_in > 0) and equilibrium steady states in the absence of Ca²⁺ influx (j_in = 0). Our analytical work is relevant and easily applied whenever a separation of timescales exists between the concentration fluctuations per se (that arise from finite size effects) and temporal variations in Ca²⁺ influx rate. For example, during the cardiac cycle, triggered release of junctional sarcoplasmic reticulum (SR) Ca²⁺ elevates dyadic subspace [Ca²⁺] for durations of ∼300 ms, and the low [Ca²⁺] of the diastolic interval persists for ∼500 ms. Because domain [Ca²⁺] fluctuations occur on a faster timescale (1–10 ms), it is straightforward to apply our theory to the cardiac dyad under the assumption that domain concentrations (expected values) are in quasistatic equilibrium with the time-varying influx rate, i.e., c_ss(t) = c_ss(j_in(t)) through Eq. 20 and similarly for b_ss(t) and cb_ss(t). Even when no such timescale separation exists, domain [Ca²⁺] fluctuations in the context of time-varying Ca²⁺ influx can be calculated by numerical integration of Eq. 27, with H_ss(t) and Γ_ss(t) evaluated at the time-varying expected values of the domain Ca²⁺ and buffer concentrations (26). Such quasistatic and nonstationary calculations agree with numerical simulations of domain [Ca²⁺] fluctuations during triggered release (see Fig. S6). Perhaps most importantly, such calculations confirm that buffers increase intrinsic domain [Ca²⁺] fluctuations during systole, and buffers do not suppress [Ca²⁺] fluctuations during diastole, just as one would expect from the nonequilibrium steady-state analysis that has been our focus.

In other physiological settings, domain [Ca²⁺] is elevated for longer or shorter durations. In pancreatic β-cells, for example, insulin secretion is regulated by minute-long duration [Ca²⁺] elevations in nuclear (8) and subplasma membrane (70) Ca²⁺ microdomains. In pituitary cells, minute-long spontaneous [Ca²⁺] oscillations have been observed in mitochondrial microdomains (71). In such cases, it is straightforward to apply our nonequilibrium steady-state analysis (e.g., the fluctuating RBA). This article’s conclusions are also directly applicable to the case of pulsatile Ca²⁺ influx with characteristic time shorter than the domain equilibration time (for buffers and escape). When the timescale for pulsatile influx is comparable to the domain time constant, quantitative studies will require simulation of the full system of stochastic ODEs. In numerical simulation of a stochastically gated influx with mean open time of 1 ms and mean closed time of 9 ms, we find that buffers do not decrease intrinsic domain [Ca²⁺] fluctuations (see Fig. S7), consistent with our analysis of constant and slowly changing Ca²⁺ influx.

It would be interesting to understand the impact of intrinsic fluctuations (due to the finite number of Ca²⁺ ions in a domain) on Ca²⁺-mediated effectors, including Ca²⁺-activated or inactivated channels, initiation of Ca²⁺ sparks, and so on. In complementary projects we have made some progress in that direction (35). It is important to understand that even when [Ca²⁺] fluctuations are much faster than the timescale of a downstream Ca²⁺-mediated process (e.g., opening of a Ca²⁺-activated channel), these fluctuations may (34) or may not (35) average-out over the slower timescale. Further studies could address such issues by including downstream signaling events in model formulations, but this article’s primary conclusion—that Ca²⁺ buffers do not suppress intrinsic [Ca²⁺] fluctuations—is an important first step in our developing understanding of the physiological significance of domain [Ca²⁺] fluctuations.